Multitask-Based Trajectory Planning for Redundant Space Robotics Using Improved Genetic Algorithm

Abstract

This work addresses the multitask-based trajectory-planning problem (MTTP) for space robotics, which is an emerging application of successively executing tasks in assembly of the International Space Station. The MTTP is transformed into a parameter-optimization problem, where piecewise continuous-sine functions are employed to depict the joint trajectories. An improved genetic algorithm (IGA) is developed to optimize the unknown parameters. In the IGA, each chromosome consists of three parts, namely the waypoint sequence, the sequence of the joint configurations, and a special value for the depiction of the joint trajectories. Numerical simulations, including comparisons with two other approaches, are developed to test IGA validity.

1. Introduction

Space robotics are now increasingly employed in outer space for various tasks, such as the assembly and maintenance of the International Space Station (ISS) [1], and Lunar Base construction [2]. Examples of space robotics include the Japanese Experiment Module Remote Manipulator System (JEMRMS) of the Japan Aerospace Exploration Agency (JAXA) [3] and the Canadarm 2 of MacDonald Dettwiler and Associates Ltd. (MDA) [4], while examples of performing tasks include the Experimental Test Satellite VII (EST-VII) [5] and the Robot Technology Experiment [6]. The free-flying space robot (FFSR1) and the free-floating space robot (FFSR2) are two main types of space robotics. The base attitude of FFSR1 is controlled, contributing to establishing a good connection between the ground and the base spacecraft. This is because the attitude of the base spacecraft should be well-managed when sending signals to, or receiving signals from, the ground. The base spacecraft of FFSR2 is in free-floating mode, contributing to saving energy, which is part of the superiority of FFSR2 since energy is precious in outer-space environments.

The trajectory planning for space robotics, aiming at generating the time histories of joints (or end effector) and contributing to the desired motion of robots, attracts extensive attention from both scientists and practitioners. The study of trajectory planning is essential for robots before physical manipulation and has been well developed. A primary trajectory-planning approach is based on the inverse kinematics of space robotics. Concepts such as the generalized Jacobian matrix [7], the enhanced disturbance map [8], the path independent workspace [9] and the reaction null-space [10] have been successively proposed for trajectory planning. The disadvantage of this approach is that it leads to kinematic singularity in some cases. Aiming at avoiding this kinematic singularity, an approach based on the direct kinematics of space robotics has been well-received. To begin with, mathematical functions such as the polynomial, trigonometric [11], or the Bézier function [12] are employed to depict the joint trajectories. Then, according to predefined conditions, mathematical functions are depicted with a set of unknown coefficients. In the aforementioned mathematical functions, the polynomial function denotes the combination of constants and variables with limited addition and multiplication calculations, the trigonometric function is an elementary function with variables of angles, and the Bézier function contributes to the derivation of a smooth curve based on four random points. Next, the trajectory-planning problem is converted into a parameter-optimization problem, with the objective function of minimum maneuver time or maximum manipulability of the robotic system, or minimum attitude disturbance acting on the free-floating base spacecraft during the robotic maneuver. Finally, the unknown coefficients are optimized by the optimization algorithms, including the basic heuristic algorithms such as the particle-swarm optimization algorithm (PSO) [13] and genetic algorithm (GA) [14,15], and the improved optimization algorithms such as hybrid PSO [16] and the constrained differential evolution algorithm (DE) [17]. In the aforementioned algorithms, the PSO is a random search algorithm based on group collaboration, more specifically, simulating the foraging behavior of a flock of birds. The DE, based on population, is a self-adaptive optimization algorithm with global search capability. To the authors’ knowledge, the approaches mentioned above aim at solving the point-to-point trajectory-planning problem, meaning that the space robot executes one task in each travel. If the robot executes two or more tasks in each travel, it could save much energy. Maneuvering time would also be reduced, which is a significant advantage in an emergency. Therefore, it is meaningful to study the multitask-based trajectory-planning problem (MTTP) for space robotics.

As a matter of fact, the MTTP for industrial robotics has been widely studied for its high productivity and low cost [18,19], and two categories of approaches were developed. For simplicity, the location of each task is usually considered to be a waypoint, which is also followed. One category of approaches aims at directly solving the MTTP. In [20], the MTTP is studied using the branch-and-bound method, where multiple inverse kinematic solutions of the robotic system are not considered. The branch-and-bound method aims at searching for solutions to solve optimization problems with constraints, where the feasible solution space is finite.

In [21], the MTTP is transformed into a mixed-integer nonlinear programming problem, where a solver is developed to improve calculation speed. The approach developed in [21] works well with a relatively small number of waypoints. In [22], an improved genetic algorithm (IGA) was developed where each chromosome consists of two parts. The first part represents the waypoint sequence, while the second part represents the sequence of the joint configurations at the waypoints, which corresponds to the first part. In [23], each chromosome consists of three parts, the waypoint sequence, the sequence of joint configurations, and the robot placement. The technique of dividing each chromosome into several parts was also employed in [24,25,26]. A common point of IGAs in [22,23,24,25,26] is that the parameter denoting the joint angular velocity is predefined as a constant. The other category of approaches aims at dividing MTTP into several subproblems which are then solved successively. In [27,28], MTTP is divided into two subproblems, the problem of the waypoint sequence, and the problem of joint trajectories. In [27], Tabu search was employed to optimize the waypoint sequence, after which joint trajectories were derived according to the inverse kinematics of industrial robotics. The Tabu search algorithm, a meta-heuristic algorithm, searches for the global optimal solution by constructing a Tabu table with the functions of cycling and memory. In [28], an improved lazy algorithm, according to the direct kinematics of industrial robotics, was developed to optimize the joint trajectories. Among MTTP documents for industrial robotics, manipulators are nonredundant, meaning that a point in the task space corresponds with finite points in the joint space. However, the redundant robot [29] provides the manipulator with high dexterity, contributing to the solution of problems such as obstacle avoidance, singularity avoidance, and joint limits. Unlike ground environments [30,31], there is microgravity in outer-space environments. Moreover, for FFSR2, strong coupling between manipulator and free-floating base is usually generated during a maneuver. Therefore, the aforementioned approaches, which were developed to solve MTTP for nonredundant industrial robotics, cannot be directly employed to solve MTTP for redundant space robotics.

In some cases, an urgent task should be performed in ISS, while the functional completeness of ISS should be guaranteed in advance. Component maintenance, assembly, and refueling of ISS should be finished successively, contributing to the functional completeness of ISS before performing the urgent task. Finishing a series of tasks successively also contributes to saving energy in outer space. Therefore, The MTTP for redundant space robotics is studied. In the MTTP, the location of each task is simplified as a task point, called waypoint. The position and attitude of each waypoint are predefined in the Cartesian space. First, the end effector is required to visit the waypoints with minimum time, thus the sequential order of visiting the waypoints should be optimized. Second, the joint configuration corresponding to each waypoint should be optimized, thus the feasible joint movements between adjacent waypoints can be guaranteed. Third, the joint movements should meet the predefined constraints. Piecewise continuous-sine functions with cubic polynomial arguments are employed to depict the joint trajectories along the waypoints, where each piece of sine function depicts one joint trajectory between adjacent waypoints. With predefined conditions, each piece of sine function is depicted with one unknown parameter which should be optimized. The MTTP is converted into a parameter-optimization problem. An IGA is developed to optimize the unknown parameters. In the IGA, each chromosome consists of three parts. The first part denotes the waypoint sequence, the second part denotes the sequence of joint configurations corresponding with the first part, and the third part denotes a special value corresponding with the depiction of the joint trajectories. Since the system is redundant, each waypoint corresponds with infinite joint configurations. Moreover, considering the sequence of joint configurations directly leads to combination explosion. An approach based on the concept of the dual-arm angle [32] was employed to formulate joint configurations. At each waypoint, eight joint configurations were derived with an assignment of the arm angle.

The rest is organized as follows. Preliminaries and adopted notation for space robotics are presented in Section 2. In the same section, the MTTP, the objective functions, the approach to depicting the joint configurations at each waypoint, and the approach of formulating the joint trajectories are explained. The IGA encoding and updating mechanisms, together with the IGA optimization process, are introduced in Section 3. In Section 4, numerical simulations are carried out to validate IGA, including comparisons with two other approaches. Section 5 concludes the work and gives an outlook for further research.

2. Preliminaries and Notation

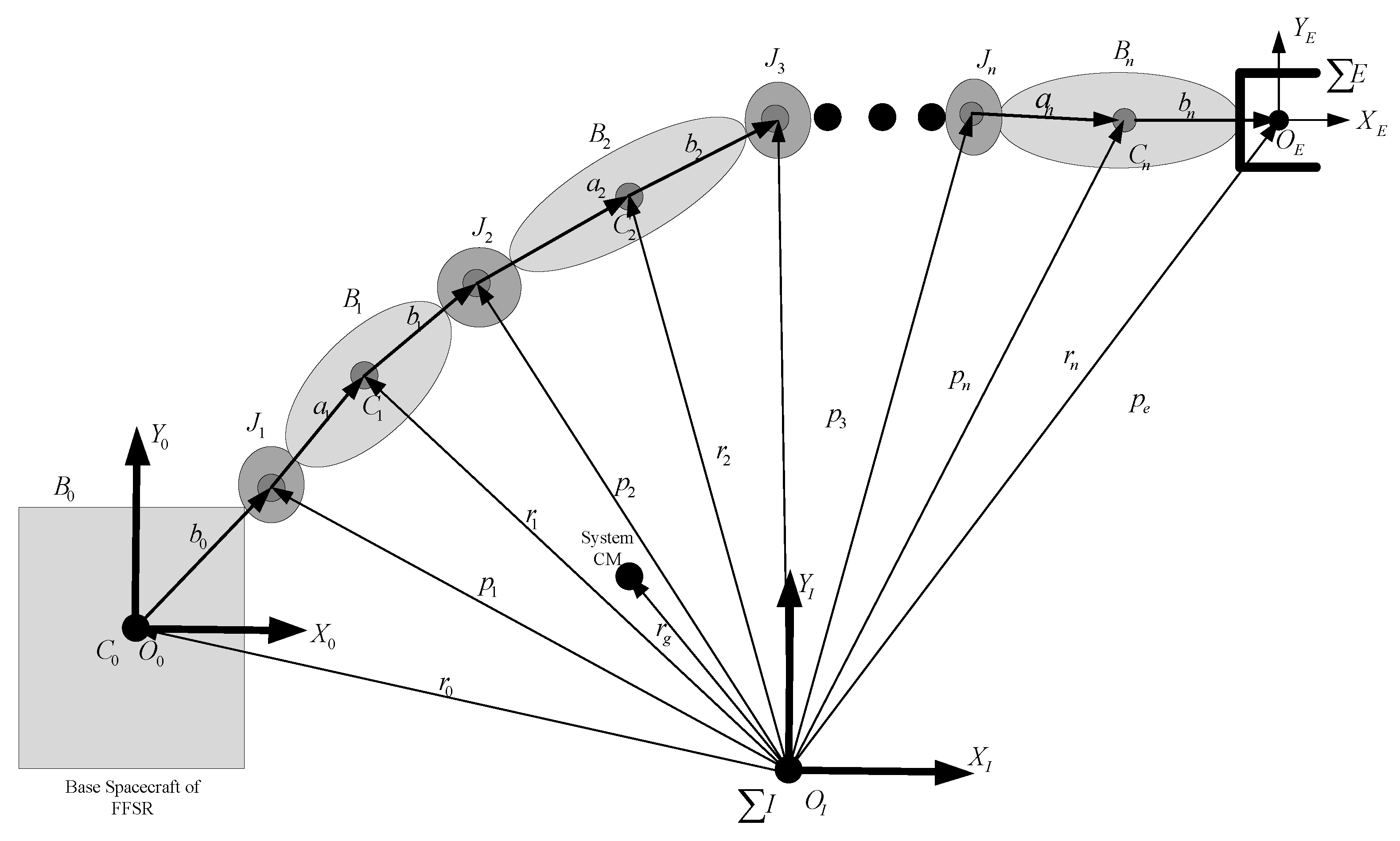
2.1. Kinematic Models of Space Robotic Systems

The 2D representation of a space robotic system is outlined in Figure 1, where the system consists of $n+1$ bodies $B_i(i=0,\dots ,n)$. $B_0$ denotes the base spacecraft, usually called base, and $B_i(i=1,\dots ,n)$ denotes the ith rigid link. The $n+1$ bodies are connected by n revolute joints $J_i(i=1,\dots ,n)$ and each joint provides the system with a single DOF (degree of freedom). Additional symbols in Figure 1 are explained as follows:

• $C_i\in {\mathit{R}}^1$ (i= 0,...,n): mass center of body i;
• ${\mathit{a}}_i\in {\mathit{R}}^3$ (i= 1,...,n): vector from joint i to mass center of body i with unit of [m; m; m], where m denotes the abbreviation of meter;
• ${\mathit{b}}_i\in {\mathit{R}}^3$ (i= 0,...,n): vector from mass center of body i to joint $i+1$ with unit of [m; m; m];
• ${\mathit{r}}_i\in {\mathit{R}}^3$ (i= 0,...,n): position of mass center of body i with unit of [m; m; m];
• ${\mathit{p}}_i\in {\mathit{R}}^3$ (i= 1,...,n): position of joint i with unit of [m; m; m];
• ${\mathit{r}}_g\in {\mathit{R}}^3$: position of system centroid with unit of [m; m; m];
• ${\mathit{p}}_e\in {\mathit{R}}^3$: position of end effector with unit of [m; m; m];
• ${\Sigma }_i$ (i= 0,...,n): coordinate frame fixed on $B_i$ with origin $O_i$ and axes $X_i$ and $Y_i$;
• ${\Sigma }_I$: inertial coordinate frame with origin $O_I$ and axes $X_I$ and $Y_I$; and
• ${\Sigma }_E$: coordinate frame fixed on end effector with origin $O_E$ and axes $X_E$ and $Y_E$.

The coordinate frame ${\Sigma }_I$ coincides with the coordinate frame ${\Sigma }_0$ at initial time, and the coordinate frame ${\Sigma }_i$ ($i=1,\dots ,n$) is established using the D-H approach [33,34]. The D-H approach aims at establishing a coordinate frame fixed on each link and computing the coordinate transformation between adjacent coordinate frames by four D-H parameters. The coordinate frame ${\Sigma }_i$ ($i=1,\dots ,n$) is defined as follows: $Z_i$-axis is chosen along rotational direction of $(i+1)$th joint, origin $O_i$ is located at intersection of $Z_i$-axis with common perpendicular line of $Z_{i-1}$- and $Z_i$-axis, $X_i$-axis is chosen along common perpendicular line of $Z_{i-1}$- and $Z_i$-axis with positive direction from ith joint to $(i+1)$th joint, and $Y_i$-axis is chosen to follow the right-handed rule. After the establishment of ${\Sigma }_i$ ($i=1,\dots ,n$), four D-H parameters $a_i$, ${\alpha }_i$, $d_i$, and ${\theta }_i$ are specified as follows: $a_i$ denotes the distance between $Z_i$- and $Z_{i+1}$-axis along $X_i$-axis; ${\alpha }_i$ denotes the angle from $Z_i$- to $Z_{i+1}$-axis around $X_i$-axis; $d_i$ denotes the distance between $X_{i-1}$- and $X_i$-axis along $Z_i$-axis; and ${\theta }_i$ denotes the angle from $X_{i-1}$- to $X_i$-axis around $Z_i$-axis.

Two categories of space robotic systems are usually employed for manipulation tasks, the FFSR1 and the FFSR2, which are collectively called FFSR in Figure 1. The base attitude of FFSR1 is controlled, while the base of FFSR2 is in free-floating mode. If both the position and attitude of the base are fixed, the differential kinematic equation is formulated as:

$$\left[\begin{array}{c}{\mathit{v}}_e\\ {\mathit{\omega }}_e\end{array}\right]={\mathit{J}}_m\dot{\mathit{q}}$$

(1)

$J_m$ in (1) is identical to the Jacobian matrix of industrial robotics. FFSR1 satisfies the linear momentum-conservation law, contributing to the following differential kinematic equation:

$$\left[\begin{array}{c}{\mathit{v}}_e\\ {\mathit{\omega }}_e\end{array}\right]=\left[\begin{array}{c}-{\displaystyle \frac{1}{M}}{\mathit{J}}_{bv}{\mathit{J}}_{tw}+{\mathit{J}}_{mv}\\ {\mathit{J}}_{mw}\end{array}\right]\dot{\mathit{q}}$$

(2)

However, FFSR2 satisfies the linear and angular momentum-conservation laws shown in Equation (3), where momentum value is usually set to 0 for simplicity.

$${\mathit{H}}_b{\dot{\mathit{x}}}_b+{\mathit{H}}_{bm}\dot{\mathit{q}}=\mathit{0}$$

(3)

Since matrix ${\mathit{H}}_b$ in Equation (3) is symmetric and positively definite,the velocity of the free-floating base can be expressed as:

$${\dot{\mathit{x}}}_b=\left[\begin{array}{c}{\mathit{v}}_b\\ {\mathit{\omega }}_b\end{array}\right]=-{\mathit{H}}_b^{-1}{\mathit{H}}_{bm}\dot{\mathit{q}}={\mathit{J}}_{bm}\dot{\mathit{q}}$$

(4)

Therefore, the differential kinematic equation of FFSR2 can be expressed as:

$$\left[\begin{array}{c}{\mathit{v}}_e\\ {\mathit{\omega }}_e\end{array}\right]={\mathit{J}}_b\left[\begin{array}{c}{\mathit{v}}_b\\ {\mathit{\omega }}_b\end{array}\right]+{\mathit{J}}_m\dot{\mathit{q}}=[{\mathit{J}}_m+{\mathit{J}}_b{\mathit{J}}_{bm}]\dot{\mathit{q}}={\mathit{J}}_g\dot{\mathit{q}}$$

(5)

The symbols in Equations (1)–(5) are explained as follows:

• $\mathit{q}\in {\mathit{R}}^n$: joint configuration with unit of each element of $\mathit{q}$ deg;
• $\dot{\mathit{q}}\in {\mathit{R}}^n$: angular velocity of joint configuration with unit of each element of $\dot{\mathit{q}}$ deg/s;
• ${\mathit{x}}_b\in {\mathit{R}}^6$: pose of base with unit of [m; m; m; deg; deg; deg];
• ${\dot{\mathit{x}}}_b\in {\mathit{R}}^6$: velocity of base with unit of [m/s; m/s; m/s; deg/s; deg/s; deg/s];
• ${\mathit{v}}_e\in {\mathit{R}}^3$: linear velocity of end effector with unit of [m/s; m/s; m/s];
• ${\mathit{\omega }}_e\in {\mathit{R}}^3$: angular velocity of end effector with unit of [deg/s; deg/s; deg/s];
• ${\mathit{J}}_b\in {\mathit{R}}^{6\times 6}$: Jacobian matrix of base;
• ${\mathit{J}}_m\in {\mathit{R}}^{6\times n}$: Jacobian matrix of manipulator;
• ${\mathit{J}}_{bm}\in {\mathit{R}}^{6\times n}$: coupling Jacobian matrix;
• ${\mathit{H}}_b\in {\mathit{R}}^{6\times 6}$: inertia matrix of base; and
• ${\mathit{H}}_{bm}\in {\mathit{R}}^{6\times n}$: coupling inertia matrix.

2.2. MTTP for Space Robotics

Space robots are required to execute a series of tasks, where the location of each task is simplified as a waypoint in the Cartesian space. The MTTP denotes that the end effector is constrained to visit a set of waypoints with minimum time. The position and attitude of the waypoints are predefined, while the optimal waypoint sequence is not given. Moreover, the space robot should meet the following constraints. First, the joint angular velocities need to be zero at each waypoint. Second, the joint angles and joint angular velocities are constrained to be within certain ranges. Third, for FFSR2, the attitude disturbance acting on the free-floating base should be minimized during the FFSR2 maneuver.

2.2.1. Objective Functions

A. Minimum Maneuver Time

In the MTTP for industrial robotics, minimum maneuver time [22,23] has been considered to improve the work efficiency of robots, which is also a factor for space robotics. Another key factor is to reduce the accident risk in outer space. In some cases, an urgent task should be performed in ISS, while the functional completeness of ISS should be guaranteed in advance. Component maintenance, assembly, and refueling of ISS should be finished in the shortest time, contributing to the functional completeness of ISS before performing the urgent task. Thus, urgent tasks are performed in time and the accident risk is reduced. One of the developed objectives is that the space robot is required to execute a series of tasks such as refueling with minimum maneuver time. Therefore, the end effector is required to visit a set of predefined waypoints with minimum time, which is expressed as:

$$\min F_1:=\sum _{j=1}^{N-1}{T}_j$$

(6)

In Equation (6), N denotes the number of waypoints and $T_j$ denotes the time period during which the end effector moves along the jth subpath, i.e., from the jth waypoint to the $(j+1)$th waypoint. $T_j$ is expressed as:

$$T_j=\underset{i}{max}\left(t_{jf}^i-t_{js}^i\right)$$

(7)

In Equation (7), $i(i=1,\dots ,n)$ denotes the ith joint. $t_{js}^i$ and $t_{jf}^i$ denote the initial and the final moving time instants of the ith joint, respectively, corresponding with the jth subpath. The n joints move for different time periods due to unequal angular distances and unequal angular velocities. The maximum of $\left(t_{jf}^i-t_{js}^i\right)(i=1,\dots ,n)$ is defined as the time period employed by the space robot for the jth subpath.

B. Minimum Base Attitude Disturbance

During the FFSR2 maneuver, minimum attitude disturbance acting on the free-floating base is required, which is expressed as:

$$\min F_2:=\sqrt{{\alpha }_0^2+{\beta }_0^2+{\gamma }_0^2}$$

(8)

In Equation (8), ${\alpha }_0$, ${\beta }_0$ and ${\gamma }_0$ are employed to depict the base attitude of FFSR2, denoting the Euler angles around the X-, Y-, and Z-axis of ${\Sigma }_0$, respectively. The order of rotation around the axes is $Z-Y-X$.

Remark 1.

The MTTP aims at searching for the optimal sequence of waypoints and the optimal joint movements. If not consider the optimal joint movements, the MTTP is the Traveling Salesman Problem (TSP) [18,20]. The TSP denotes that a salesman is required to visit a set of predefined cities with minimum time (or path length), while the time employed to stay at each city is not considered. This is because the time spent at each city has no influence on the optimal sequence of the cities, which also works in the MTTP. Therefore, the time period during which the end effector executes specific tasks at each waypoint is omitted.

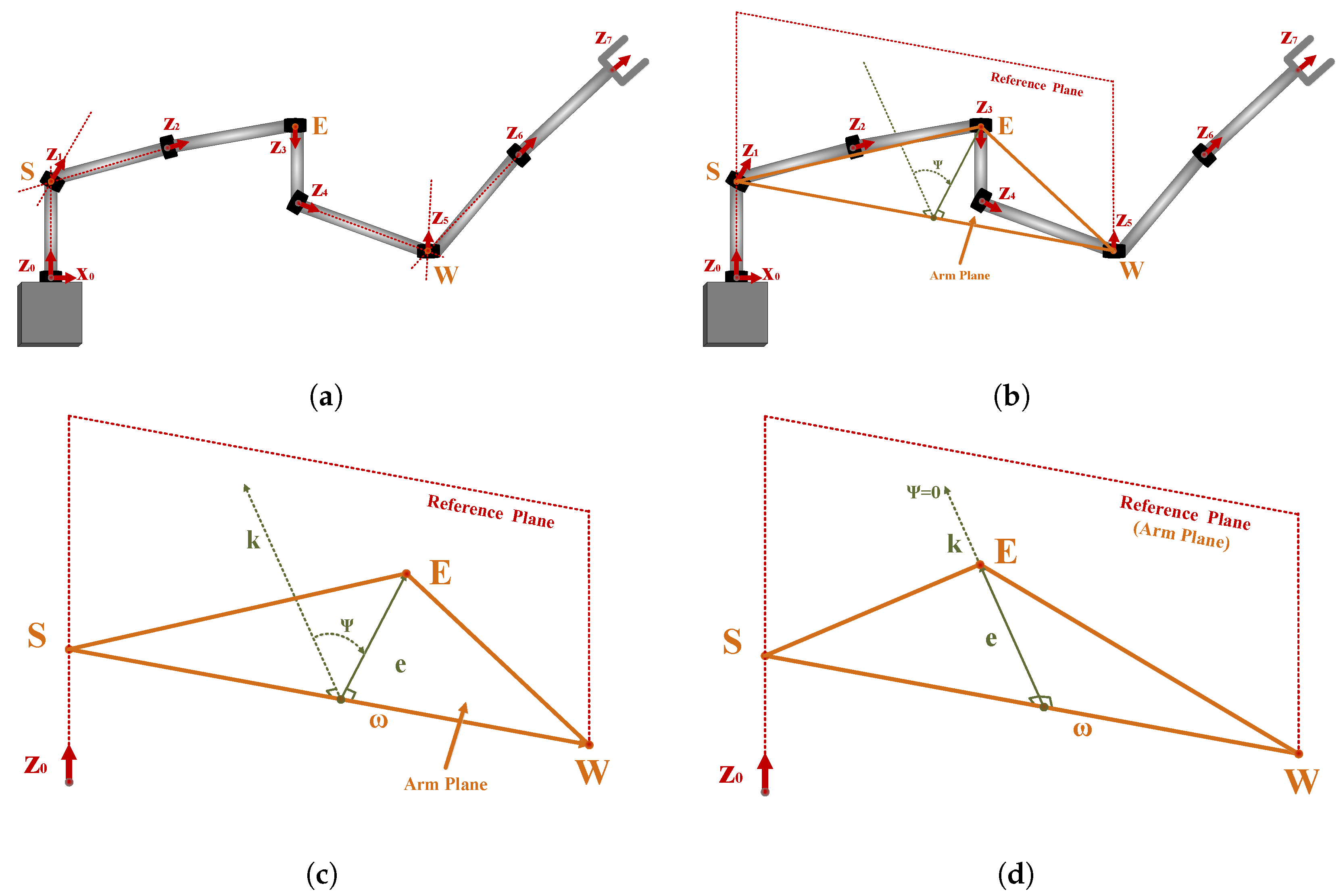
2.2.2. Depiction of Joint Configurations Corresponding to Each Waypoint

The inverse kinematics of redundant space robotics are complex, since one point in the task space corresponds to infinite points in the joint space. An approach based on the geometric construction of the robot, especially the robot called Spherical Revolute Spherical (SRS) [32,35,36,37], is well developed. Each component of the joint configuration is formulated as a function of the arm angle. By assigning a value to the arm angle, a finite number of joint configurations are obtained. Figure 2 presents the process for constructing the arm angle. The following legend is useful to understand the different subfigures. Figure 2a outlines the 7-DOF rotational robot SRS based on the D-H approach, together with the three main points S, E, and W. The shoulder point S denotes the intersection point of $Z_i$-axis ($i=0,1,2$), the elbow point E denotes the origin $O_3$ of ${\Sigma }_3$, and the wrist point W denotes the intersection point of $Z_i$-axis ($i=4,5,6$). Figure 2b outlines the reference plane constructed by $Z_0$-axis and $\omega$, the arm plane $SEW$, and the arm angle $\psi$ from the reference plane to the arm plane. Figure 2c coincides with Figure 2b, where $\omega$ denotes the vector from S to W. k and e denotes the vectors perpendicular to $\omega$ in the reference plane and the arm plane, respectively. Figure 2d outlines a case $\psi =0$, meaning that the reference plane coincides with the arm plane. The following procedure is carried out for the derivation of the joint configuration $\mathbf{q}={\left[q_1,\dots ,q_7\right]}^T$.

Step 1

Construction of the arm plane, the reference plane and the arm angle. First, the arm plane is constructed according to the points S, E, and W shown in Figure 2. Second, the reference plane is constructed based on $\omega$ and $Z_0$- or $X_0$-axis, since at least one of $Z_0$- and $X_0$-axes is not coincident with $\omega$. The arm angle $\psi$ is then depicted, shown in Figure 2.

Step 2

Derivation of the joint angle $q_4$. Project the arm plane $SEW$ to the plane perpendicular to the rotation axis of the elbow joint, namely $Z_3$-axis. According to the geometric construction of SRS and the Pythagorean theorem, two values of $q_4$ are derived.

Step 3

Derivation of the shoulder-joint angles $q_1$, $q_2$, and $q_3$. First, the rotation transformation, rotating around $\omega$ with the rotation angle $\psi$, is derived. Second, the orientation of ${\Sigma }_3$ relative to ${\Sigma }_0$ using the concept of the shoulder reference attitude matrix [32]. Finally, two groups of shoulder-joint angles are derived.

Step 4

Derivation of the wrist-joint angles $q_5$, $q_6$, and $q_7$. Two groups of wrist-joint angles are derived according to the predefined attitude of the end effector, the rotation transformation and the should reference attitude matrix derived in Step 3, and the rotation matrix from ${\Sigma }_3$ to ${\Sigma }_4$.

Remark 2.

A detailed explanation about the approach of computing $\mathbf{q}$ is expressed in [32]. According to the aforementioned procedure, eight groups of $\mathbf{q}$ are derived with an assignment of the arm angle ψ. ψ is set to zero considering the following aspects. First, the calculation accuracy of $\mathbf{q}$ corresponding to each waypoint declines as the absolute value of ψ increases. The result of $\mathbf{q}$ is derived with the highest accuracy in the case $\psi =0$. Second, the assignment of $\psi =0$ contributes to less computational cost [32]. Besides, the angular velocity of each joint is constrained to be zero at each waypoint, and is not affected by values of ψ.

Remark 3.

Inspired by the work of [32], the joint configuration $\mathbf{q}={\left[q_1,\dots ,q_7\right]}^T$ denotes that the number of joints is seven, which is also the manipulator DOF meaning that the DOF of each joint is one. This category of robots has simple geometrical structure and contributes to convenient operation when performing tasks and less computational cost when verifying a developed approach. Study and application of this category of robots can also be found in [11,12,13,17,32].

2.2.3. Formulation of Joint Trajectories among Waypoints

During the maneuver of the space robot when the end effector successively visits the waypoints, the joint trajectories are depicted with the piecewise-sine functions expressed in Equation (9). It can be seen that the sine function has the superiority of considering the physical limits on joint angles, and making the joint movements more practical.

$$q_j^i\left(t\right)=A·sin\left[a_{3j}^i{(t-T_{j-1})}^3+a_{2j}^i{(t-T_{j-1})}^2+a_{1j}^i(t-T_{j-1})+a_{0j}^i\right]$$

(9)

In Equation (9), $i=1,\dots ,n$, $j=1,\dots ,N-1$, and $T_0=0$. $q_j^i(·)$ denotes an angular trajectory of the ith joint, corresponding with a jth subpath along which the end effector moves from the jth waypoint to the ($j+1$)th waypoint. A denotes the physical limit on each joint angle, which is defined as $180\mathrm{deg}$. $a_{mj}^i(m=0,1,2,3)$ denotes the coefficients of the argument, where all $a_{3j}^i$ share the same absolute value. Based on Equation (9), joint angular velocities are given by:

$$\begin{array}{cc}\hfill {\dot{q}}_j^i\left(t\right)=& A·cos\left[a_{3j}^i{(t-T_{j-1})}^3+a_{2j}^i{(t-T_{j-1})}^2+a_{1j}^i(t-T_{j-1})+a_{0j}^i\right]·\hfill \\ & \left[3a_{3j}^i{(t-T_{j-1})}^2+2a_{2j}^i(t-T_{j-1})+a_{1j}^i\right]\hfill \end{array}$$

(10)

Corresponding with the jth subpath of the end effector, the angle of the ith joint is denoted as $q_{j0}^i$ at initial time $t_{js}^i$ ($t_{js}^i=T_{j-1}$), and denoted as $q_{jf}^i$ at final time $t_{jf}^i$, shown in Equations (11) and (12). To ensure the continuity of the joint movements during the whole travel, the space robot has the same joint configuration at the final time of jth subpath and at the initial time of $(j+1)$th subpath, shown in Equation (13).

$$\begin{array}{c}\hfill q_j^i\left(t_{js}^i\right)=q_{j0}^i\end{array}$$

(11)

$$\begin{array}{c}\hfill q_j^i\left(t_{jf}^i\right)=q_{jf}^i\end{array}$$

(12)

$$\begin{array}{c}\hfill q_{jf}^i=q_{(j+1)0}^i\end{array}$$

(13)

In Equation (13), $q_{N0}^i=q_{(N-1)f}^i$. Moreover, joint angular velocities are limited to be zero at each waypoint, given by:

$$\begin{array}{c}\hfill {\dot{q}}_{j0}^i={\dot{q}}_{jf}^i=0\end{array}$$

(14)

Substituting Equations (11)–(14) into Equations (9)–(10), the values of $a_{0j}^i$, $a_{1j}^i$, $a_{2j}^i$ and $t_{jf}^i$ are derived as follows:

$$\begin{array}{c}\hfill a_{0j}^i=arcsin\left(\frac{q_{j0}^i}{A}\right)\end{array}$$

(15)

$$\begin{array}{c}\hfill a_{1j}^i=0\end{array}$$

(16)

$$\begin{array}{c}\hfill a_{2j}^i=-\frac{3}{2}{a}_{3j}^i\left(t_{jf}^i-T_{j-1}\right)\end{array}$$

(17)

$$t_{jf}^i={\left\{\frac{2\left[a_{0j}^i-arcsin\left(\frac{q_{jf}^i}{A}\right)\right]}{a_{3j}^i}\right\}}^{\frac{1}{3}}+T_{j-1}$$

(18)

If the optimal value of $a_{3j}^i(i=1,\dots ,n;j=1,\dots ,N-1)$ is derived, the joint trajectories corresponding with the jth subpath of the end effector and time period $T_j$ are obtained. It should be noted that the case, $a_{3j}^i=0$, is meaningless and not considered.

3. Improved Genetic Algorithm

3.1. Basic GA

The basic GA [38,39], inspired by natural selection, is a heuristic optimization algorithm with global search abilities. A certain number of individuals, usually called initial solutions, are randomly generated and contribute to the globality of the search space. During evolution, each individual, corresponding to a chromosome, is evolved toward the best position in the whole search space. Furthermore, chromosomes are updated according to fundamental genetic operators, including reproduction, crossover, and mutation. The reproduction generator contributes to the replication of chromosomes with better fitness values from parents to offspring. Crossover and mutation generators contribute to generating new chromosomes. On the basis of a crossover generator, the paired chromosomes exchange part of their genes with each other. On the basis of the mutation generator, one or several genes of a chromosome are updated. The flowchart of basic GA is shown in Figure 3.

3.2. Improved GA

The basic GA is usually employed to optimize the polynomial coefficient or the path length in some problems, where chromosomes are assigned a category of meaning. Referring the composition mechanism of chromosomes studied in [22], an IGA was developed. Chromosomes were assigned three categories of meanings. Each IGA chromosome consists of three parts, as shown in Figure 4, where $\left\{W_1,W_2,\dots ,W_N\right\}$ denotes the waypoint sequence, $\left\{C_1,C_2,\dots ,C_N\right\}$ denotes the sequence of joint configurations, and $OPC$ denotes a special value corresponding with the cubic coefficients of the arguments in the piecewise-sine functions. Joint configuration $C_k\left(k=1,\dots ,N\right)$ corresponds with waypoint $W_k$.

Since the time period employed by the space robot for each subpath is positive, value ${\left\{\frac{2\left[a_{0j}^i-arcsin\left(\frac{q_{jf}^i}{A}\right)\right]}{a_{3j}^i}\right\}}^{\frac{1}{3}}$ in (18) is positive. Therefore, $a_{3j}^i$ is expressed as:

$$a_{3j}^i=sign\left(a_{0j}^i-arcsin\left(\frac{q_{jf}^i}{A}\right)\right)·abs\left(a_{3spe}\right)$$

(19)

In [24], $a_{3spe}$ denotes the special value after decoding $OPC$, where $abs\left(·\right)$ denotes the absolute value of $\left(·\right)$.

The encoding mechanism is an essential component of the IGA, which is studied first. Then, the IGA updating mechanism, including initialization, reproduction, crossover, and mutation, is studied. Finally, the IGA work mechanism is developed.

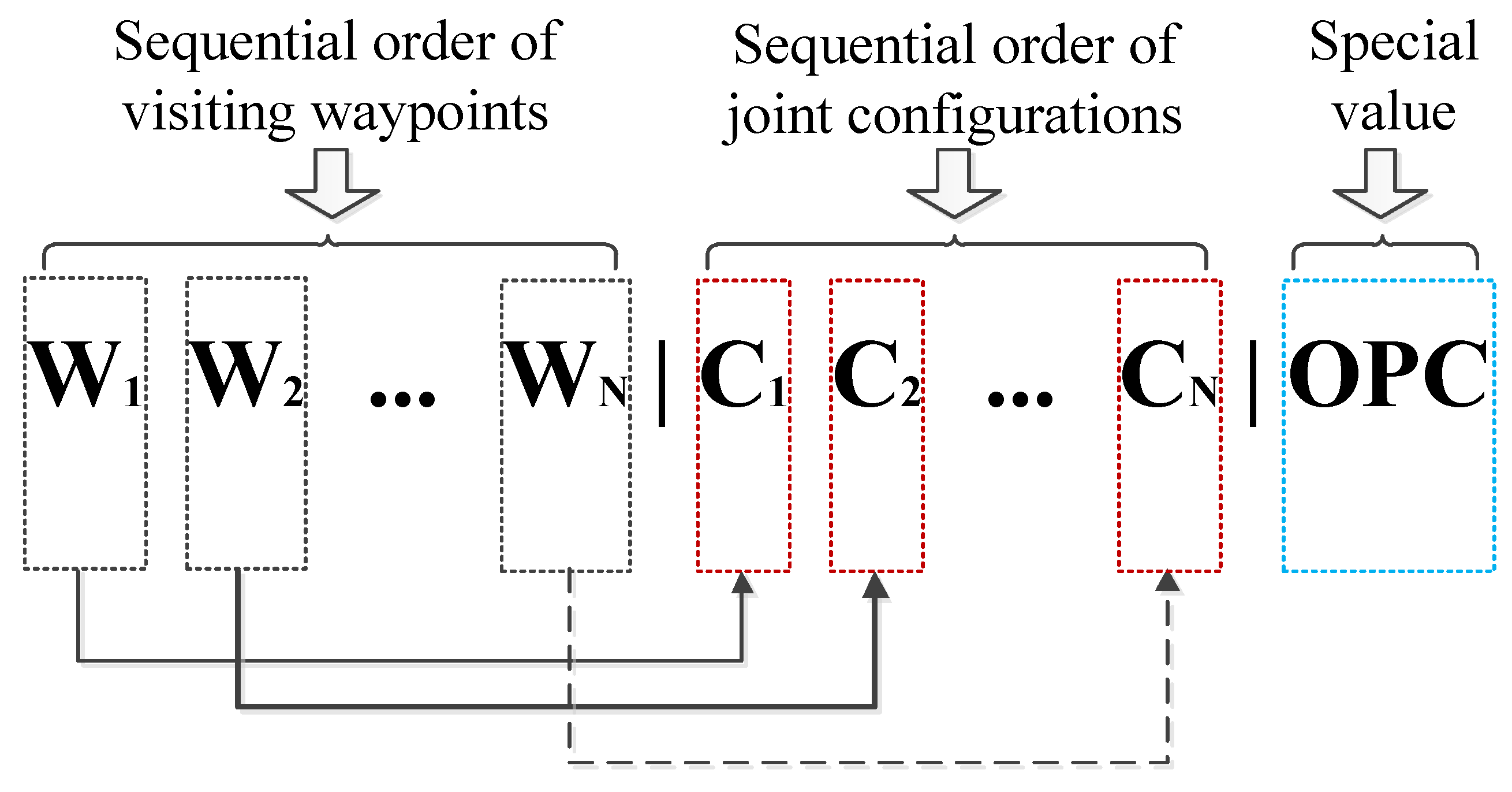
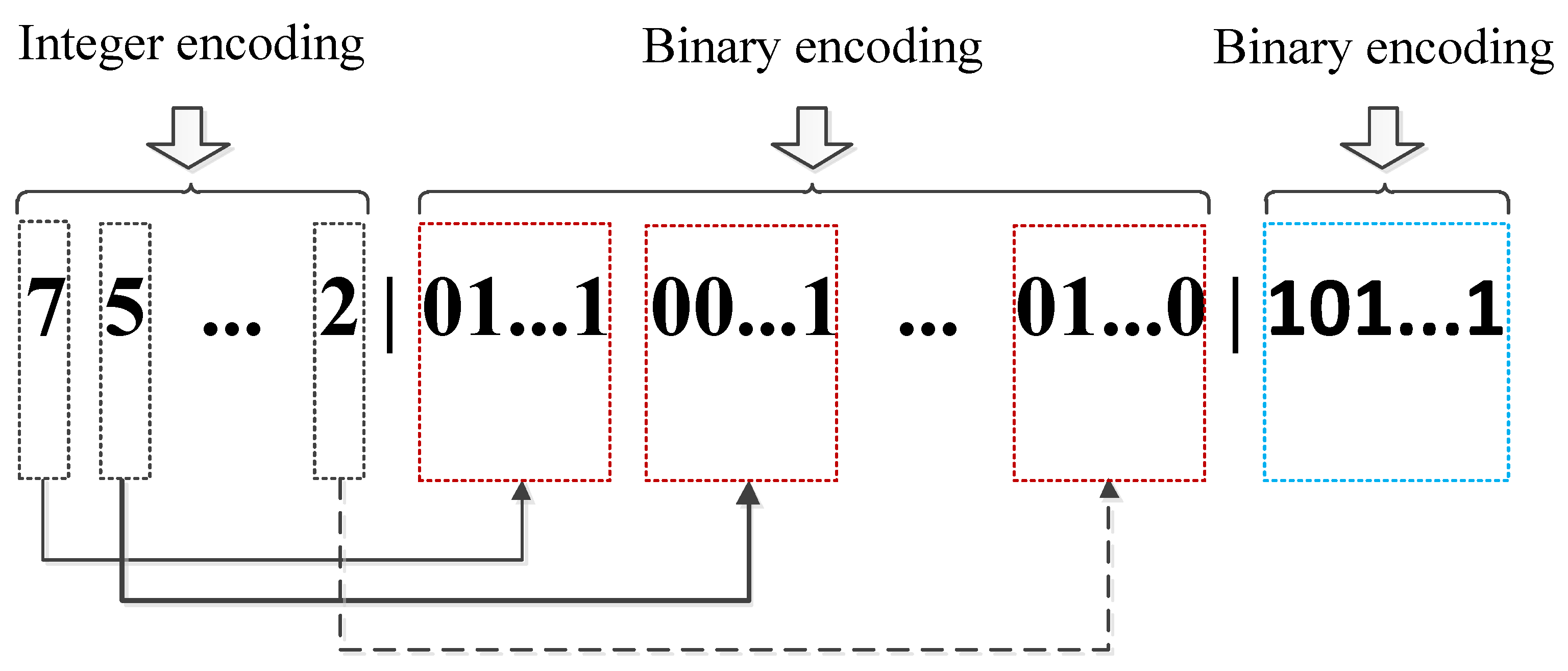
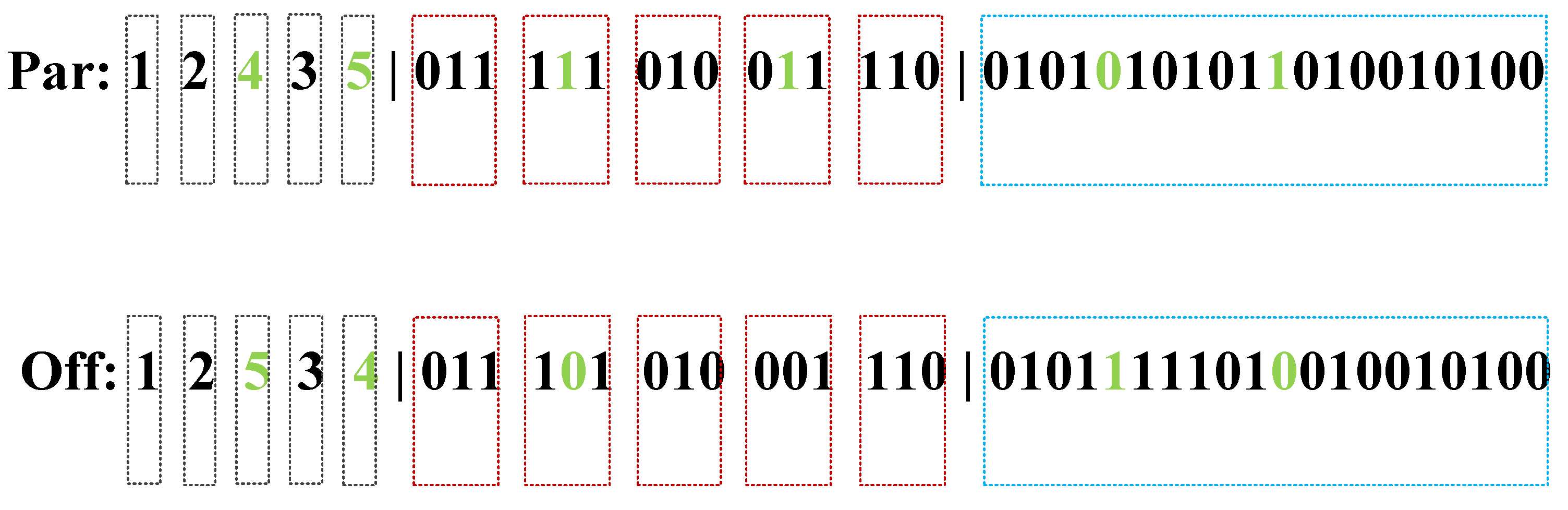
3.2.1. Encoding Mechanism

The encoding mechanism is essential, and the theoretical principle of IGA is implemented based on it. Traditional encoding mechanisms include the binary, the floating, the integer, and the symbol. The binary mechanism provides convenient encoding and decoding operations when solving discrete or continuous optimization problems. The floating mechanism provides results with high precision when solving continuous optimization problems with multidimensional functions. The integer mechanism is usually employed for solving combinatorial optimization problems such as the Traveling Salesman Problem [40]. The symbol mechanism contributes to the combination of GA and other algorithms. In IGA, the integer encoding mechanism is employed for the waypoint sequence, while the binary encoding mechanism is employed for the sequence of joint configurations and the special value corresponding with the cubic coefficients of the arguments, which is sketched in Figure 5.

A. First Part of Each Chromosome

In MTTP, the end effector is constrained to visit a set of predefined waypoints, and each waypoint is limited to being visited once. According to binary encoding, the random selection of the crossover and mutation mechanisms may lead to alphabet repetition, thus conflicting with the requirement of only visiting each waypoint once. Integer encoding is the best choice, where N positive integers correspond with N waypoints.

B. Second Part of Each Chromosome

The second part of each chromosome denotes the sequence of joint configurations corresponding to the first part of the chromosome, where binary encoding is implemented. Since eight special joint configurations corresponding to one waypoint are considered, each joint configuration is coded by one byte of three bits. Figure 6 represents the eight categories of bytes, where $CO{N}_{im}(i=1,\dots ,n;m=1,\dots ,8)$, also shown in Equation (20), and it denotes the mth joint configuration corresponding to the ith waypoint.

$$\mathcal{CON}=\left[\begin{array}{cccc}CO{N}_{11}& CO{N}_{11}& \dots & CO{N}_{18}\\ CO{N}_{21}& CO{N}_{21}& \dots & CO{N}_{28}\\ \dots \\ CO{N}_{n1}& CO{N}_{n1}& \dots & CO{N}_{n8}\end{array}\right].$$

(20)

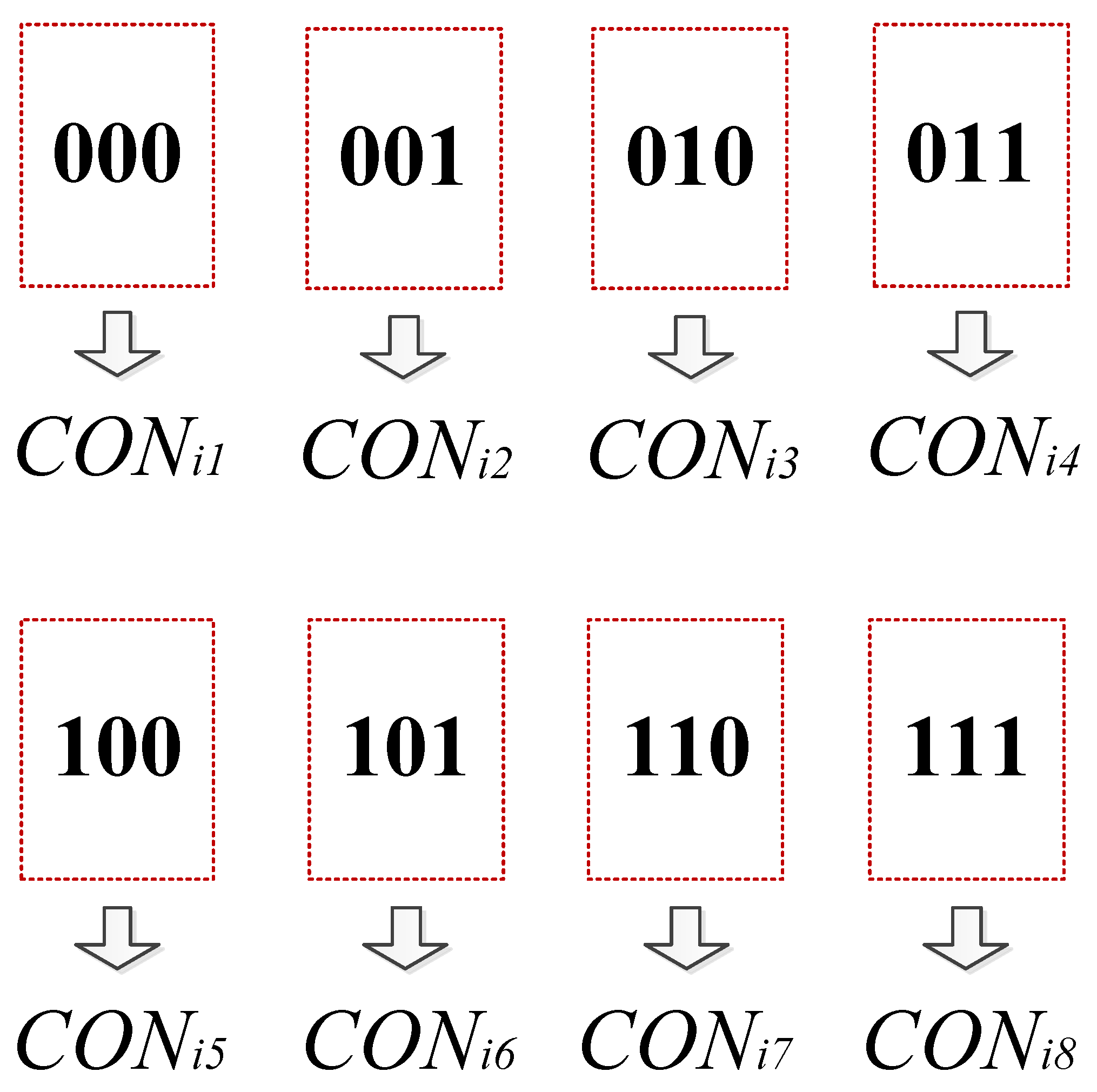
C. Third Part of Each Chromosome

The third part of each chromosome denotes a special value corresponding to the cubic coefficients of the arguments in the piecewise-sine functions. According to the relation between $a_{3j}^i$ and $a_{3spe}$, $a_{3spe}$ is limited to be within $\left[-\pi ,0\right)\cup \left(0,\pi \right]$. Moreover, optimization $a_{3spe}$ is constrained to be with an accuracy of $1e-5$, where $524,288=2^{19}<2\pi ·{10}^5<2^{20}=1,048,576$. Hence, the genes of this part of the chromosome consist of 20 bits.

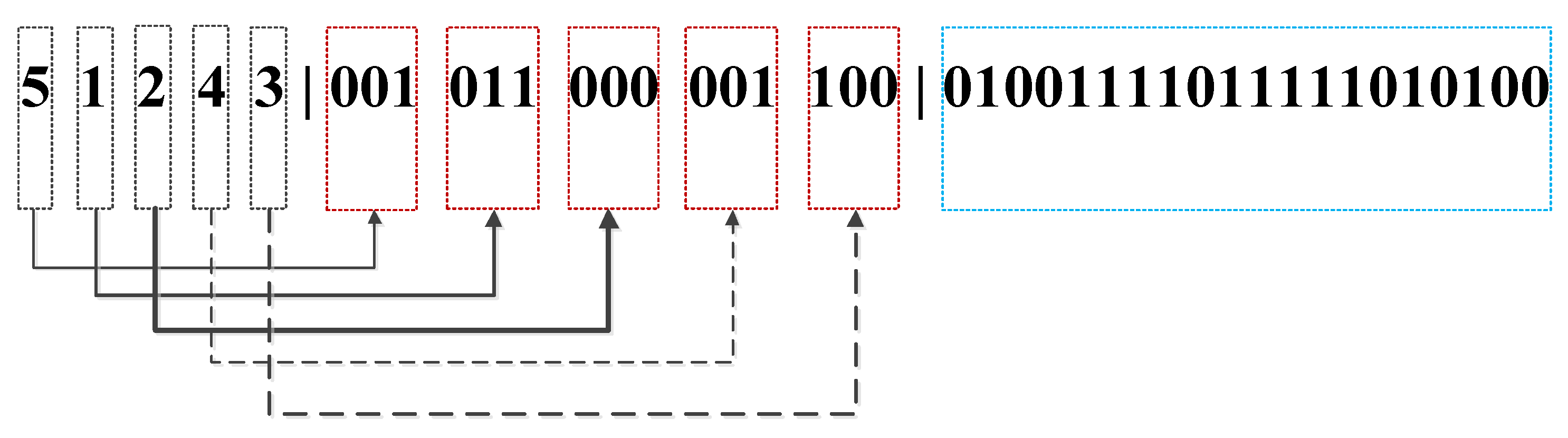
D. Example of Chromosome Depiction

In this example, a space robot is constrained to visit five waypoints, and a feasible chromosome is shown in Figure 7, where the waypoint sequence is $\left\{5,1,2,3,4\right\}$ according to the first part of the chromosome. By the second part of the chromosome, the encoding of the joint configuration corresponding with the 5th waypoint is 001, namely $CO{N}_{52}$ in Equation (20) according to Figure 6. Similarly, encoding the joint configurations corresponding to the 1st, 2nd, 4th, and 3rd waypoints are $CO{N}_{14}$, $CO{N}_{21}$, $CO{N}_{42}$, and $CO{N}_{35}$, respectively. The decimal number of the third part of the chromosome is $325,588$, and the corresponding value within the range of $\left[-\pi ,0\right)\cup \left(0,\pi \right]$ is given by: $-\pi +325,588\ast {\displaystyle \frac{\pi -(-\pi )}{2^{20}-1}}=-1.1906$.

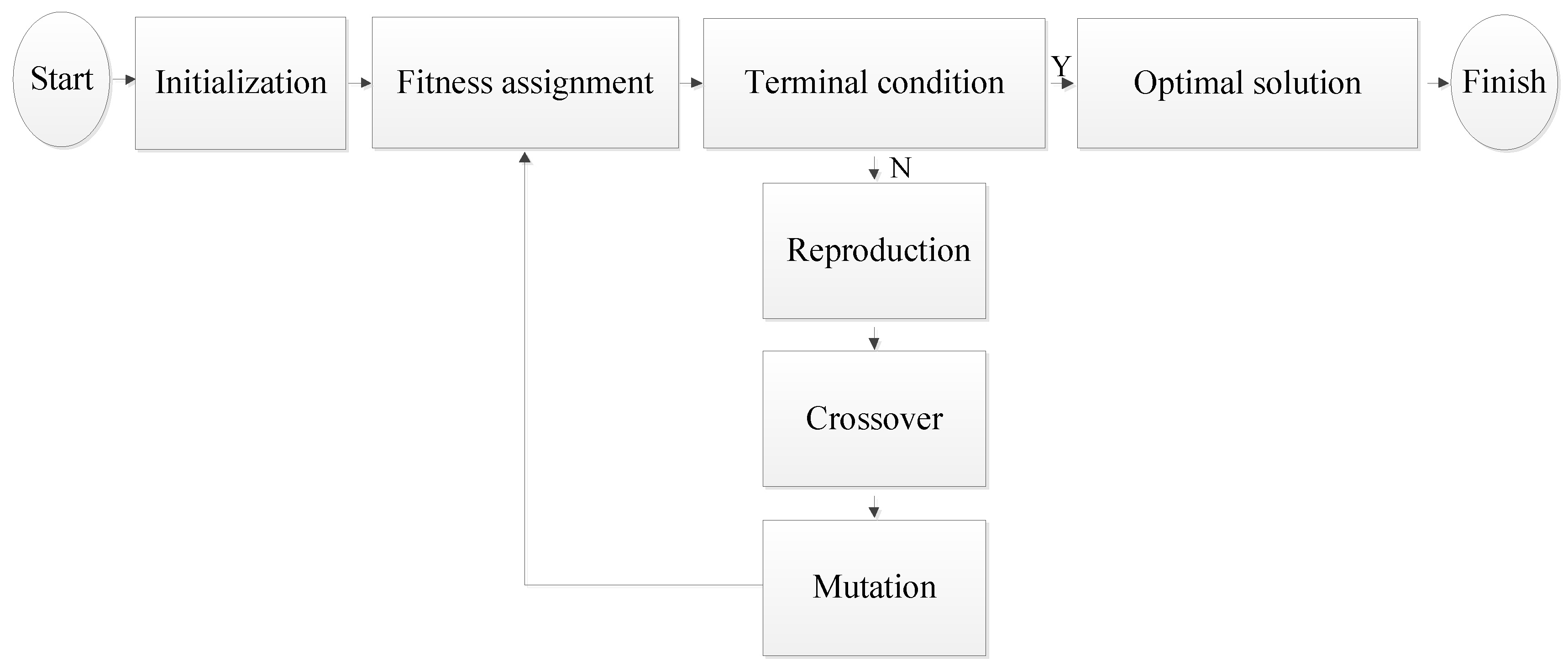
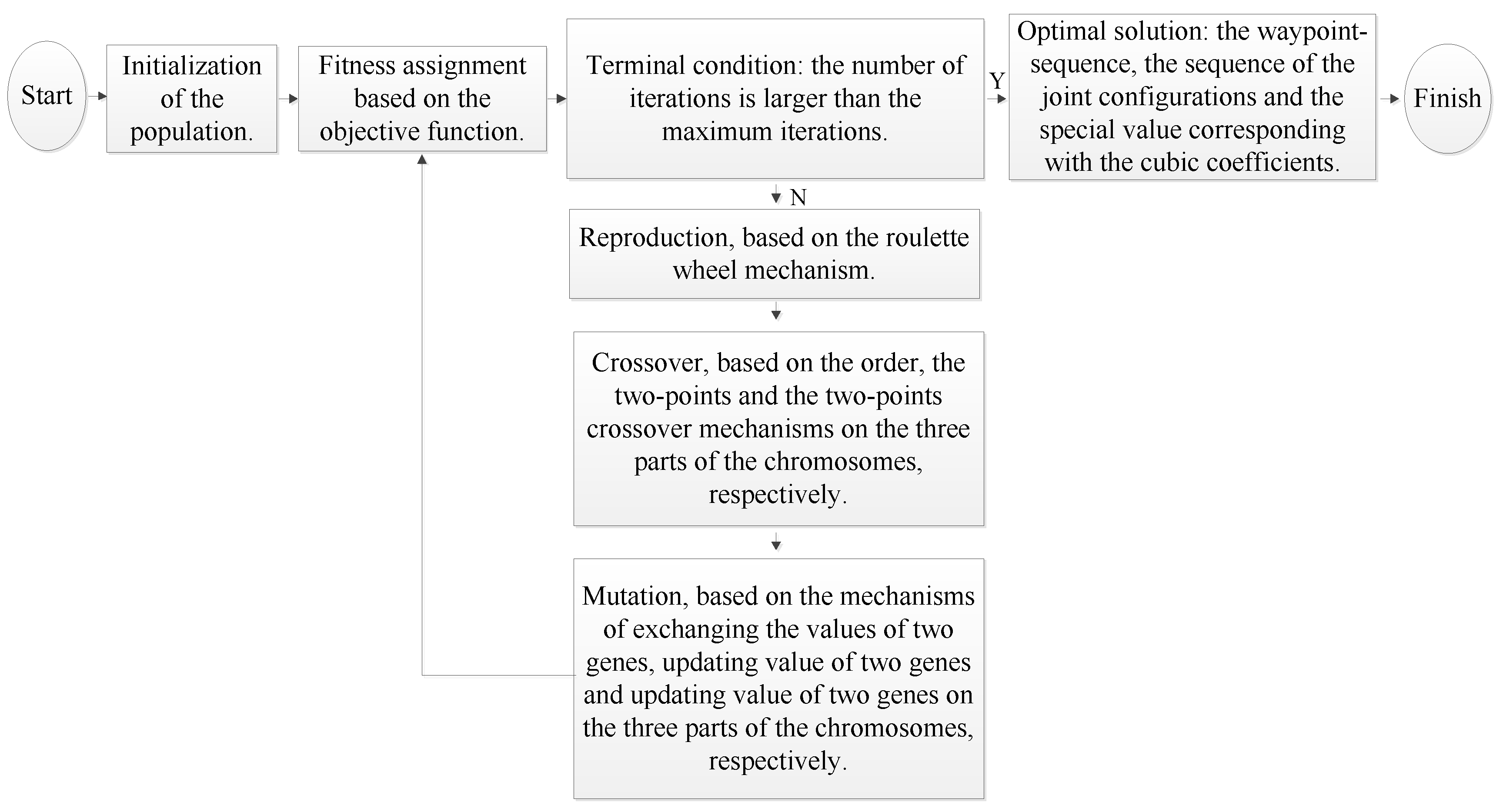
3.2.2. Updating Mechanism

A. Initialization

The initial population with 200 chromosomes is randomly generated. It should be noted that the first gene of each chromosome is 1, so that the first gene corresponds with the starting waypoint.

B. Reproduction

The reproduction operator aims at copying chromosomes from parents to offspring, where the roulette-wheel mechanism is employed in IGA. Each chromosome is assigned a proportion value, namely the fitness value of the chromosome to the sum of fitness values of the population. The chromosome with a large proportion of value is reproduced with high probability.

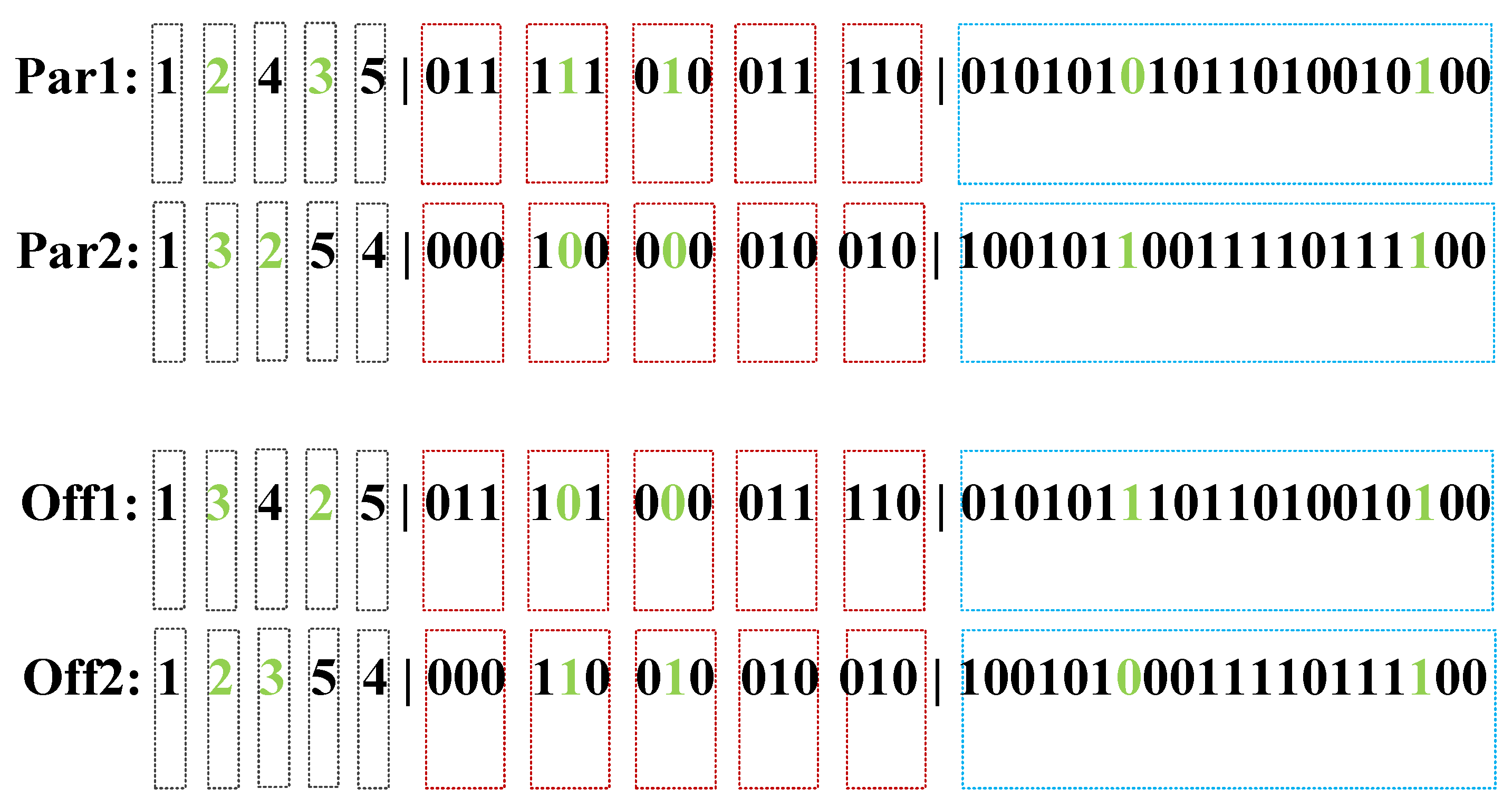
C. Crossover

The crossover operator is employed after the reproduction operator, where parent chromosomes are selected with a crossover probability defined as 0.6. The order, the two points, and the two-point crossover mechanisms are applied to the first, second, and third parts of every two selected and paired parent chromosomes, respectively. Figure 8 represents the crossover operation of two parent chromosomes and the offspring, where Par1 and Par2 denote two parent chromosomes, while Off1 and Off2 denote chromosomes after crossover operation.

D. Mutation

Mutation probability is defined as 0.15. For the first part of each chromosome, two genes are randomly selected to exchange values. Simultaneously, two random genes of the second part of the chromosome are selected, and the value of each selected gene is changed from ${}^{\prime }{1}^{\prime }$ to ${}^{\prime }{0}^{\prime }$ and vice versa. The mutation mechanism of the second part also works for the third part of the chromosome. Figure 9 shows the mutation operation of a chromosome, where Par denotes a selected parent chromosome, while Off denotes the chromosome after the mutation operation.

3.2.3. IGA Work Mechanism

Based on the above analysis, the IGA work mechanism is outlined in this part. Two-hundred individuals are randomly generated, where three parts of each chromosome are encoded according to Section 3.2.1. After this, the iterative loop starts. First, the fitness value of each chromosome, i.e., the value of the objective function, is computed after decoding. The chromosome with a minimum fitness value is denoted as the elite in each generation, which is saved directly for the next iteration. Second, the terminal condition is verified, where the maximum number of iterations is defined as 500. If the terminal condition is not followed, genetic operators, including reproduction, crossover, and mutation are successively executed as per Section 3.2.2. After this, the updated chromosomes, together with the saved elite, are denoted as the initial chromosomes for the next iteration. Once the terminal condition is satisfied, the loop stops, and the optimal solution is exported. Figure 10 shows the IGA flowchart.

4. Numerical Simulations

The space robotic system employed for simulation consists of a base spacecraft and a 7-DOF manipulator, and its parameters are shown in

Table 1. Physical parameters of the space robotic system.

Body	Mass	Length	Principle Moment of Inertial (kg $·{\mathbf{m}}^2$)
	(kg)	(m)	${\mathit{I}}_{\mathit{xx}}$	${\mathit{I}}_{\mathit{yy}}$	${\mathit{I}}_{\mathit{zz}}$
0	500	$0.2$	100	100	200
1	20	$0.1$	4	4	5
2	10	$0.3$	2	2	3
3	50	$0.4$	10	10	20
4	20	$0.5$	4	4	5
5	50	$0.3$	10	10	20
6	10	$0.2$	2	2	3
7	20	$0.1$	4	4	5

. Two categories of numerical simulations were developed by considering the state of the base spacecraft. For FFSR1, the base attitude is controlled, and only minimum maneuver time is required. For FFSR2, attitude disturbance acting on the free-floating base should also be minimized. Therefore, the objective function of MTTP for FFSR1 is $F:F=F_1$, while the objective function of MTTP for FFSR2 is $F:F=F_1+\alpha F_2$. $F_1$ and $F_2$ are shown in Equations (6) and (8), respectively. $\alpha$ denotes the weight and is defined as 2.

To validate the IGA, comparisons with two other algorithms were first developed. Afterward, two simulation cases on the detailed movements of space robotics using the IGA were developed.

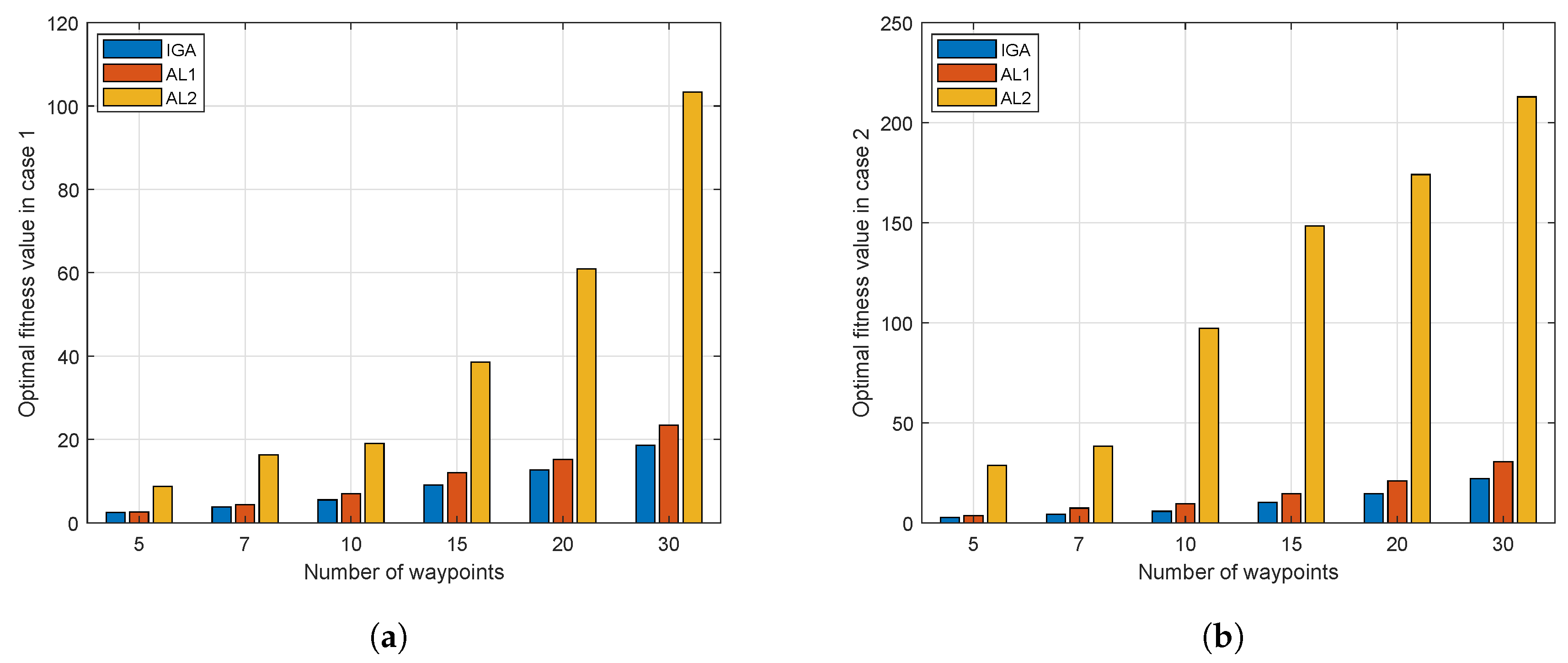
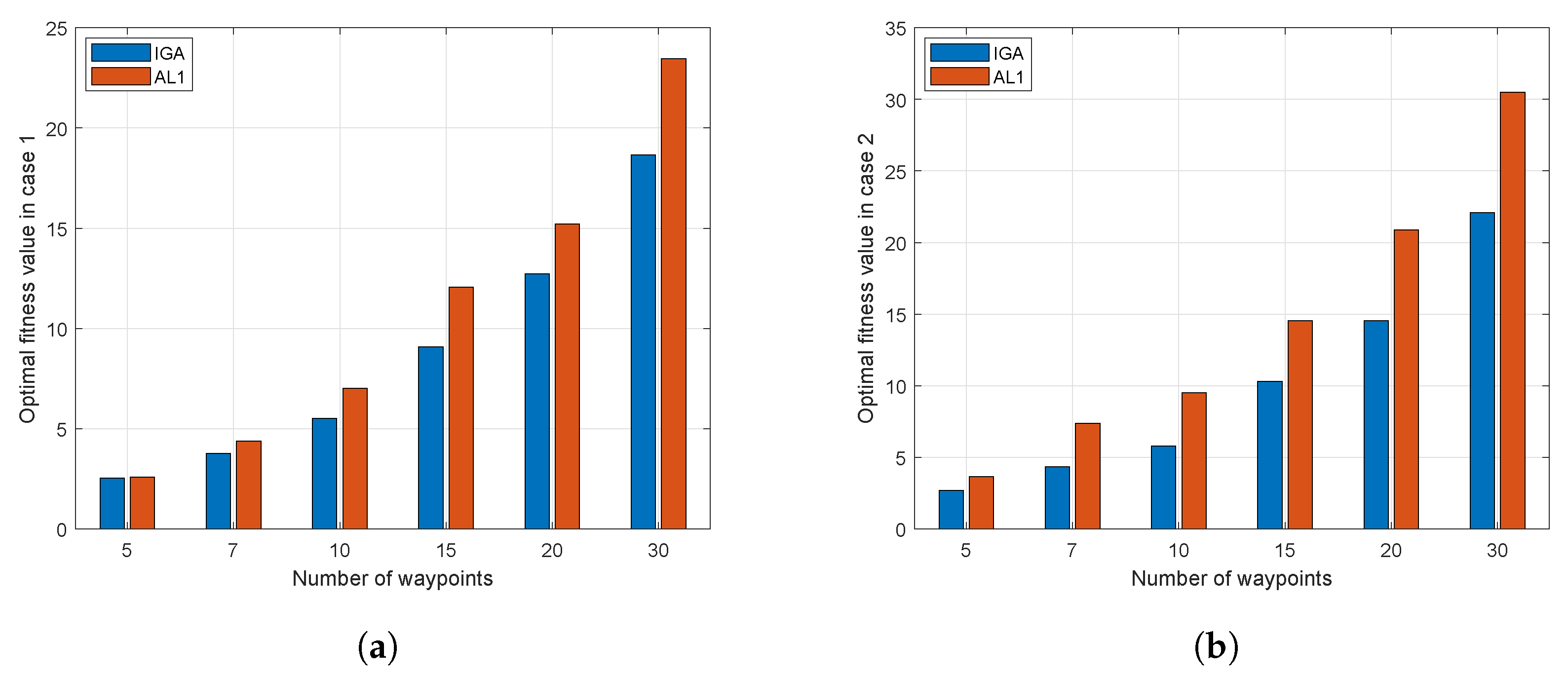
4.1. Comparisons

Comparisons between IGA and two other algorithms, AL1 and AL2, were developed. In the IGA, the second part of each chromosome is encoded with the binary mechanism. In AL1, the integer mechanism is employed to encode the second part. This comparison refers to [22]. In both the IGA and AL1, the variation trend of each joint between adjacent waypoints is depicted with a sine function, whose argument is a cubic polynomial. The angular velocity of each joint, shown in Equation (10), varies during the maneuver of the space robot. Therefore, the third part of each chromosome is variable. However, joint angular velocities are defined as a constant in [20,21,22,23,24,25,26,41], leading to joint trajectories being depicted with the linear functions, and the third part of each chromosome being depicted with a constant. In AL2, joint angular velocity is defined as $0.8\mathrm{rad}/\mathrm{s}\left(45.8\mathrm{deg}/\mathrm{s}\right)$ [41].

Based on the IGA, AL1, and AL2, the MTTP for space robotics is solved successively. Two cases of space robotics are considered, where the MTTPs for FFSR1 and for FFSR2 are solved in Case 1 and in Case 2, respectively. To further validate the developed approach, different numbers of waypoints, 5, 7, 10, 15, 20, and 30, are considered in each case. With the same number of waypoints, each algorithm is carried out for 25 times.

Table 2. Average execution time and fitness values of IGA.

No.	C1AET	C1WF	C1BF	C1AF	C2AET	C2WF	C2BF	C2AF
5	$29.6717$	$2.9690$	$2.4773$	$2.5280$	$87.2751$	$3.2721$	$2.6073$	$2.6871$
7	$41.7781$	$3.7754$	$3.7439$	$3.7680$	$102.3258$	$4.6112$	$4.1563$	$4.3424$
10	$62.6735$	$5.6198$	$5.3880$	$5.5059$	$130.2154$	$6.0007$	$5.5044$	$5.7854$
15	$88.4186$	$9.4253$	$8.6173$	$9.0766$	$165.2741$	$11.0144$	$9.5132$	$10.3125$
20	$118.4722$	$13.2953$	$12.0814$	$12.7159$	$201.4602$	$15.8477$	$14.0814$	$14.5411$
30	$168.7083$	$19.8873$	$16.9274$	$18.6520$	$268.4956$	$23.3607$	$21.0884$	$22.0983$

,

Table 3. Average execution time and fitness values of AL1.

No.	C1AET	C1WF	C1BF	C1AF	C2AET	C2WF	C2BF	C2AF
5	$30.2927$	$2.5802$	$2.5376$	$2.5734$	$87.7121$	$4.3226$	$2.9237$	$3.6392$
7	$43.4101$	$4.4033$	$3.9741$	$4.3858$	$105.3805$	$8.0266$	$6.9567$	$7.3691$
10	$63.5849$	$8.1634$	$6.4493$	$7.0059$	$132.4114$	$10.0733$	$9.1615$	$9.5277$
15	$89.5364$	$13.5983$	$10.9831$	$12.0514$	$170.8203$	$15.1020$	$13.8772$	$14.5412$
20	$123.4722$	$14.2953$	$16.0814$	$15.2159$	$206.5551$	$21.7545$	$19.0202$	$20.7822$
30	$175.4097$	$26.6370$	$21.8827$	$23.4604$	$275.3105$	$32.9934$	$28.1109$	$30.4985$

and

Table 4. Average execution time and fitness values of AL2.

No.	C1AET	C1WF	C1BF	C1AF	C2AET	C2WF	C2BF	C2AF
5	$17.5387$	$8.7288$	$8.7288$	$8.7288$	$40.7669$	$28.8014$	$28.8014$	$28.8014$
7	$19.4081$	$16.2850$	$16.2850$	$16.2850$	$45.7278$	$38.2449$	$38.2449$	$38.2449$
10	$24.9153$	$22.2850$	$16.4822$	$19.0011$	$53.4793$	$105.4628$	$90.2001$	$97.1588$
15	$35.6762$	$45.6080$	$34.0422$	$38.5686$	$70.6147$	$160.8218$	$138.5077$	$148.4189$
20	$46.5072$	$67.4052$	$58.3376$	$60.9117$	$86.0894$	$179.2049$	$167.3822$	$174.0670$
30	$68.3224$	$120.4871$	$98.7836$	$103.3427$	$130.1552$	$229.6452$	$200.9169$	$212.8989$

shows the average execution time (AET), the worst fitness (WF), the best fitness (BF) and the average fitness (AF) of 25 executions. The AET using AL2 is less than that using IGA or AL2. However, the optimization results using AL2 is much worse than results using IGA or AL1. Figure 11 represents the AF values. It should be noted that the optimal fitness value denotes the minimum value of $F_1$ in Figure 11a and denotes the minimum value of $F_1+\alpha F_2$ in Figure 11b. First, the fitness values of AL2 are much larger than those of IGA and AL1, meaning that the joint movements with constant joint angular velocity do not work well. Second, the fitness values of AL1 grow larger than those of IGA as waypoints increase. It can also be seen that the difference between fitness values of IGA and AL1 in each case is not large. To further analyze the results using IGA and AL1, fitness values of IGA and AL1 plotted in Figure 11 are once again shown in Figure 12. In Case 1, the difference generated by IGA and AL1 is smaller than 1 when the number of waypoints is less than 10. The difference gradually becomes large as waypoints increase, and the difference is about 5 when the number of waypoints is 30. In Case 2, the difference is 0.9 when the number of waypoints is 5, and the difference is 3 when the number is 7. However, difference grows faster as waypoints increase, compared with the case of MTTP for FFSR1. It can be seen in Figure 12b that the difference is 8 when the number of waypoints is 30.

According to the above analysis, the proposed approach is validated. It can be seen that depicting each joint angular trajectory with piecewise- and continuous-sine functions makes the joint angular velocity variable and contributes to a better solution. Generally, it is almost impossible for any optimization algorithm to find the best solution. However, compared with the integer mechanism of the second part in each chromosome, the binary encoding mechanism contributes to a preferable second-best solution.

4.2. Simulation Cases

Two cases of numerical simulation results, based on the IGA, were developed for detailed motion analysis of FFSR1 and FFSR2. In both cases, the end effector is constrained to visit 10 waypoints in the 3D Cartesian space. The position and attitude of the 10 waypoints are expressed in

Table 5. Position and attitude of ten waypoints.

No.	Position (m)	Attitude (deg)
1	$[1.61,0.15,0.15]$	$[148,-27,75]$
2	$[1.00,-0.50,-0.45]$	$[150,-30,80]$
3	$[1.50,0.00,0.00]$	$[100,0,100]$
4	$[1.00,-1.00,0.50]$	$[80,10,100]$
5	$[0.00,1.00,1.00]$	$[60,30,120]$
6	$[-0.50,0.50,1.00]$	$[80,80,80]$
7	$[0.60,-0.50,1.00]$	$[0,80,80]$
8	$[1.00,0.50,1.00]$	$[0,-10,10]$
9	$[1.00,-0.50,1.20]$	$[0,0,0]$
10	$[0.90,-0.50,1.40]$	$[20,0,-20]$

.

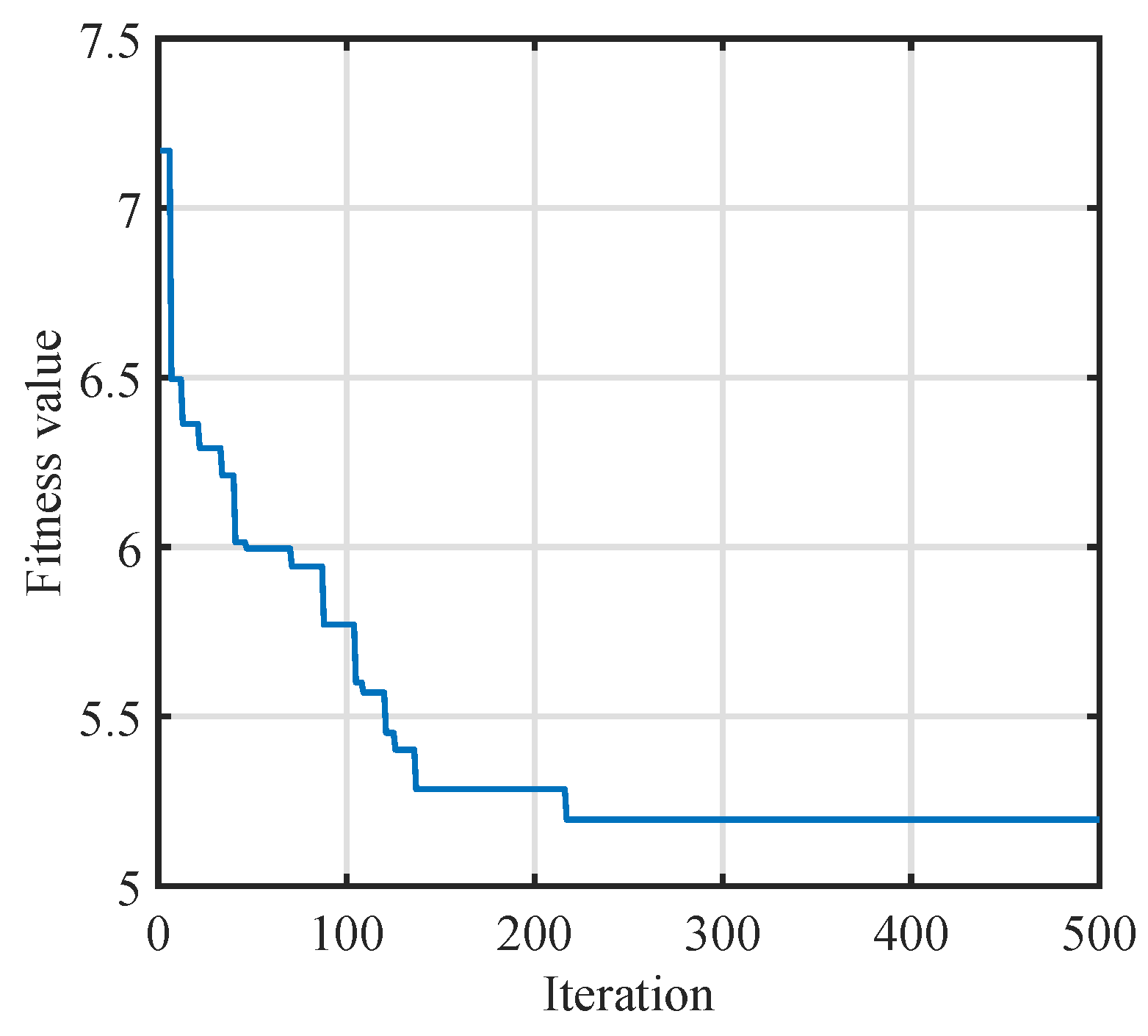
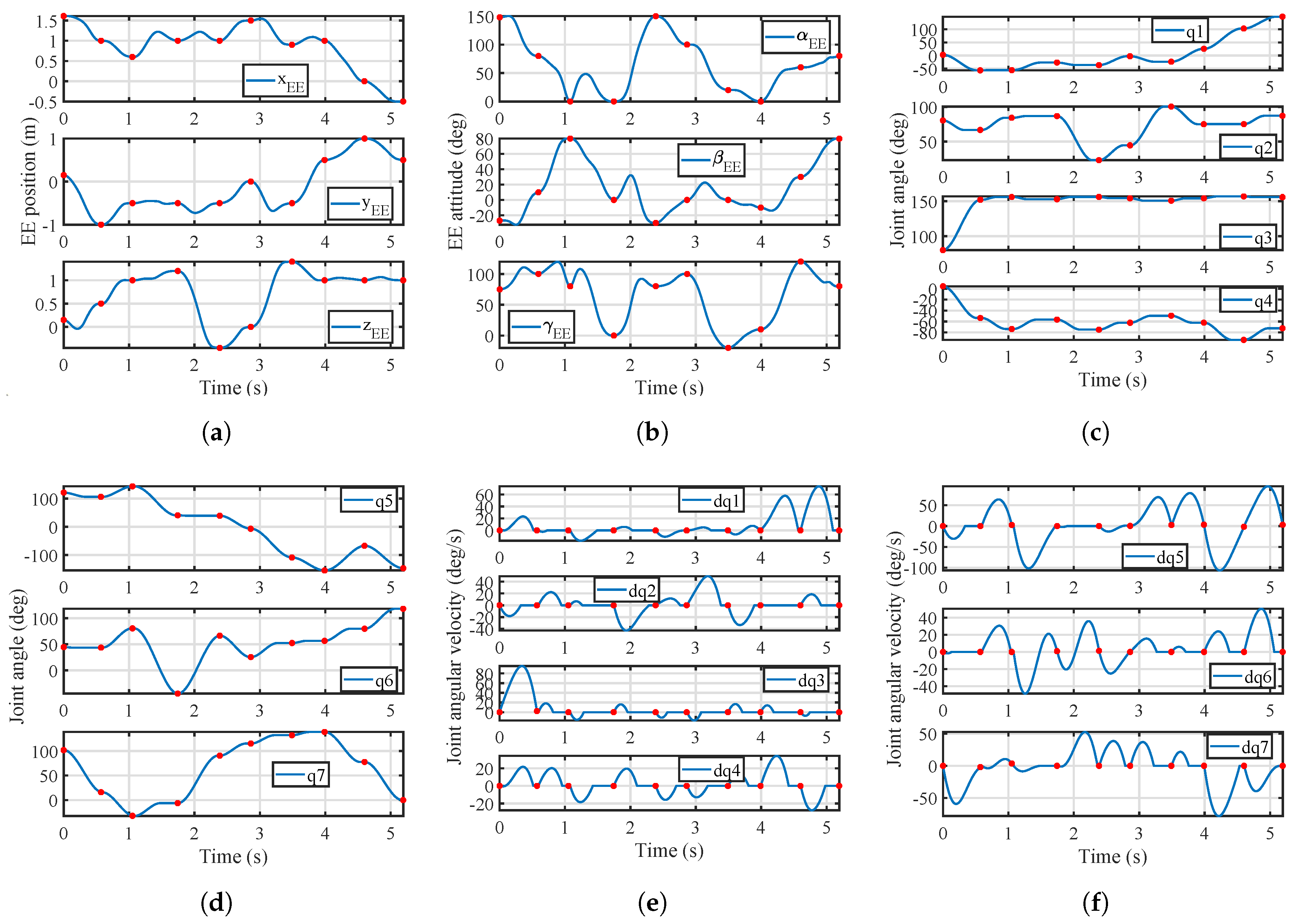
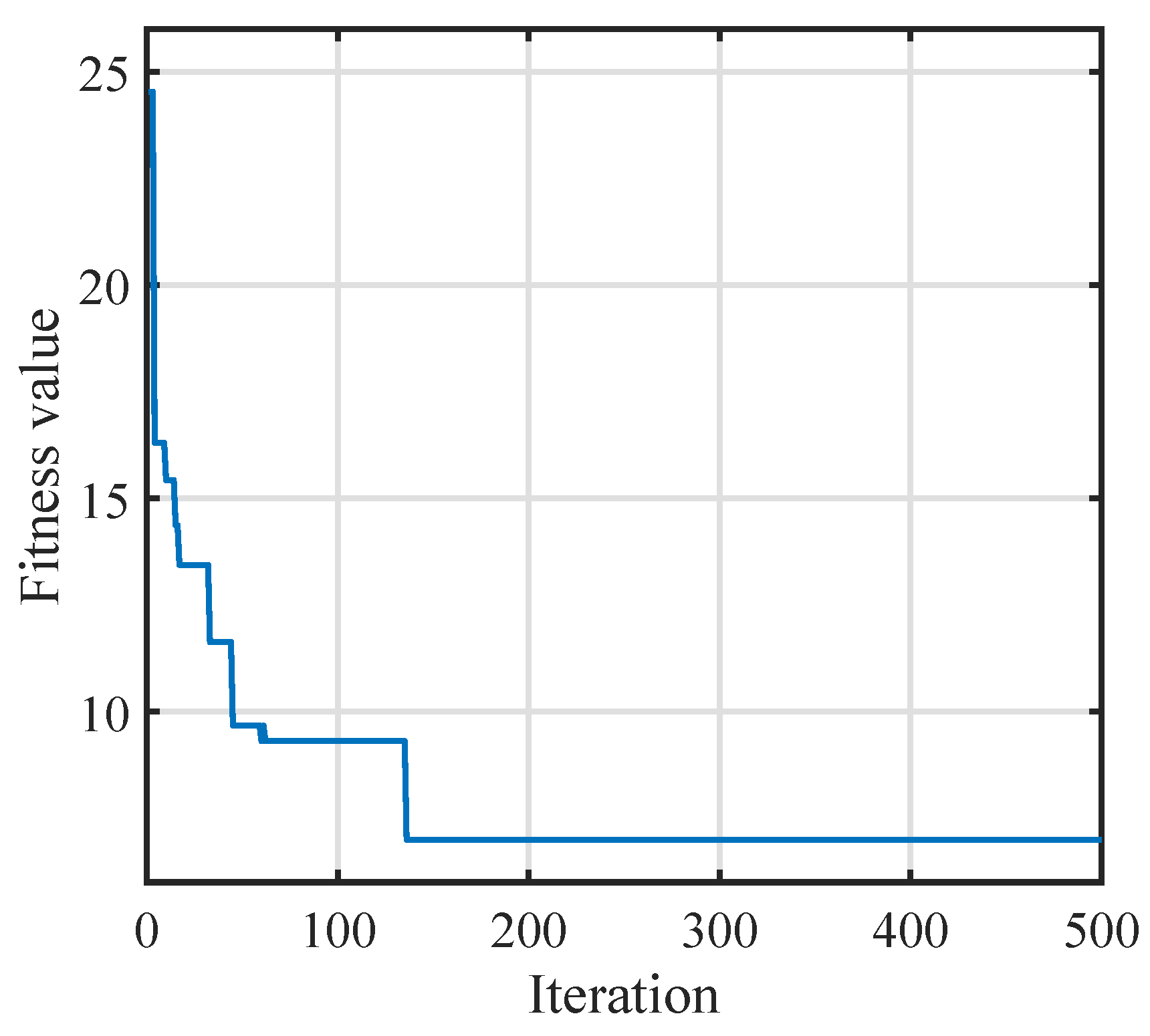
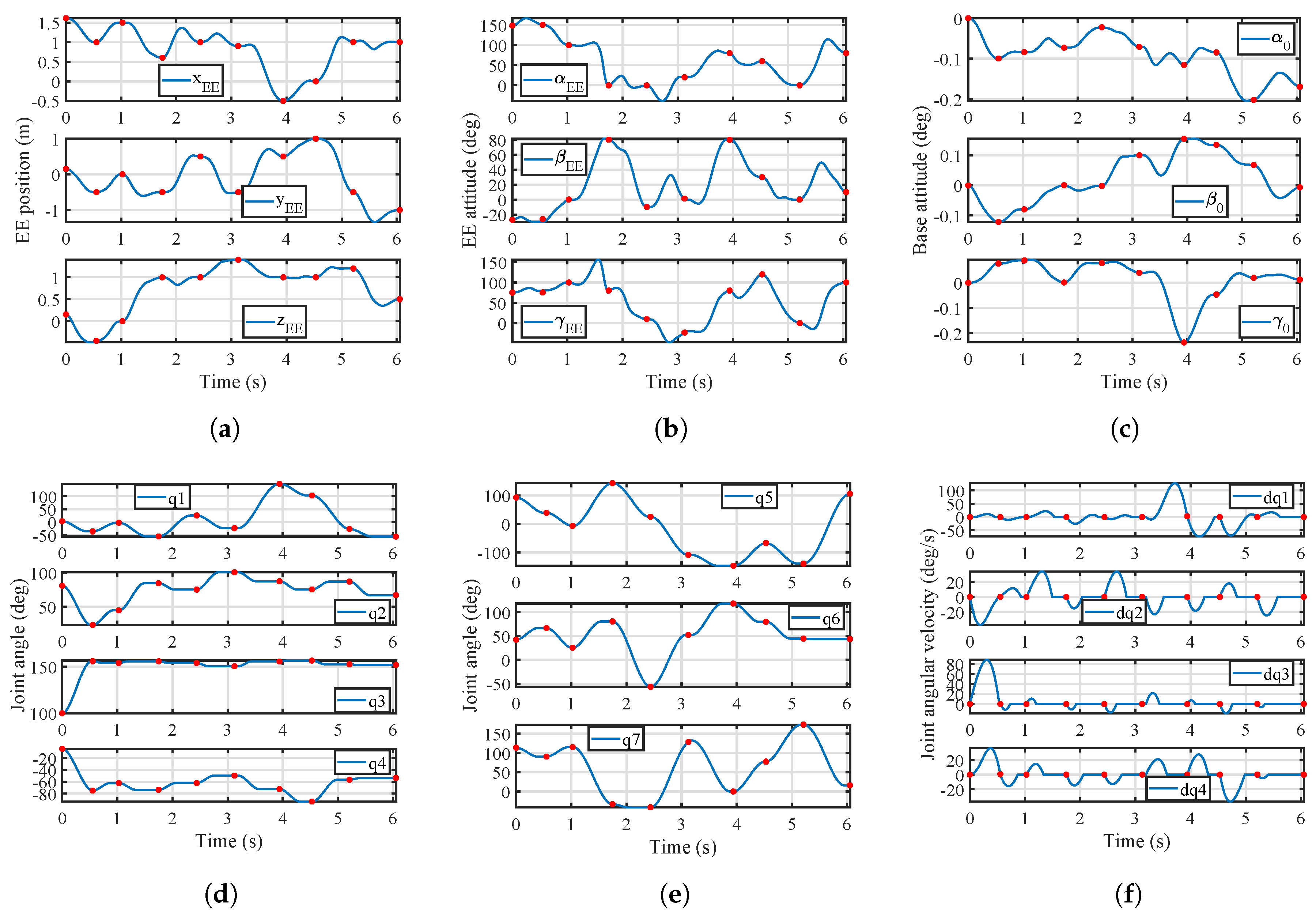
4.2.1. Case 1

In this case, the MTTP for FFSR1 is studied. Figure 13 represents the variation trends of fitness values using IGA, showing that the minimum maneuver time of FFSR1 is 5.196 s. Figure 14 represents the movements of FFSR1, where the red points in each subfigure denote the corresponding values at the waypoints. The following explanation is useful to understand the subfigures: Figure 14a,b represents the time histories of the position and attitude of the end effector, respectively; Figure 14c,d represents the time histories of the seven joint angles; Figure 14e,f represents the time histories of the seven joint angular velocities. Figure 14a,b shows that the optimal waypoint sequence is $1\to 4\to 7\to 9\to 2\to 3\to 10\to 8\to 5\to 6$, and all waypoints are accurately visited. Figure 14c,d shows that the joints move smoothly, while Figure 14e,f shows that the joint angular velocities at each waypoint are zero. Moreover, Figure 14c–f shows that the joint angles and the joint angular velocities are within the predefined region. In Figure 14, each joint angle $q_i(i=1,\dots ,7)$ denotes one component of the joint configuration $\mathbf{q}={\left[q_1,\dots ,q_7\right]}^T$, and each joint angular velocity $d{q}_i$ denotes the 1st derivative of $q_i$.

4.2.2. Case 2

In this case, the MTTP for FFSR2 is studied. Figure 15 represents the variation trends of the fitness values using IGA, where the minimum maneuver time of FFSR2 is $6.056$ s, and the module value of the base attitude in Equation (8) is $0.22$ deg. FFSR2 movements are represented in Figure 16, where the red parts in each subfigure denote the values at the corresponding waypoints. The legend of Figure 16 is explained as follows: Figure 16a,b represents the time histories of the position and the attitude of the end effector, respectively; Figure 16c represents the time histories of the base attitude; Figure 16d,e represents the time histories of the seven joint angles; Figure 16f,g represents the time histories of the seven joint angular velocities. Figure 16a,b shows that the optimal waypoint sequence is $1\to 2\to 3\to 7\to 8\to 10\to 6\to 5\to 9\to 4$, and all waypoints are accurately visited. It can be seen that the optimal waypoint sequence in this case is different from that obtained in Case 1, since one more objective function was considered in this case. Moreover, the randomness of IGA is a main factor. In Figure 16c, the variation amplitude of each Euler angle is less than 0.3 deg during the whole movement of FFSR2. Figure 16d,e shows that the joints move smoothly, while Figure 16f,g shows that the joint angular velocities at each waypoint are zero. Furthermore, Figure 16d–g shows that the joint angles and joint angular velocities are within the predefined region.

5. Conclusions

This work studied the MTTP for space robotics, including the free-flying space robot (FFSR1) and the free-floating space robot (FFSR2). The trajectory-planning problem was converted into an optimization problem by depicting the joint movements with piecewise- and continuous-sine functions. An IGA was proposed to solve the optimization problem. The main contributions are expressed as follows:

(i)

Cubic coefficients of arguments of piecewise-sine functions share the same absolute value, making the third part of each chromosome only consider one value after decoding. Therefore, computational cost is reduced.

(ii)

In contrast to the setting on joint angular velocities in most recent studies about the MTTP for industrial robotics, each joint angular velocity varies based on Equation (10), contributing to the high-precision results.

For future research, the MTTP for space robotics will be further studied in the case that one or more obstacles appear, especially the case when obstacles move. Furthermore, the corresponding trajectory-tracking control problem will be studied, which is of great significance for practical applications.