A Sparse Neural Network Based Control Structure Optimization Game under DoS Attacks for DES Frequency Regulation of Power Grid
Abstract
1. Introduction
- Sparse neural network based reinforcement learning is proposed to improve the frequency regulation of DES in control systems without using a power system analytical model, which involves adaptiveness, performance, and structure.
- The Stackelberg game model is used to derive the optimal control scheme and structure, so that the proposed frequency regulation system is robust to the worst case of DoS attacks. In addition, the reliability of proposed frequency regulation system is enhanced.
2. Problem Formulation
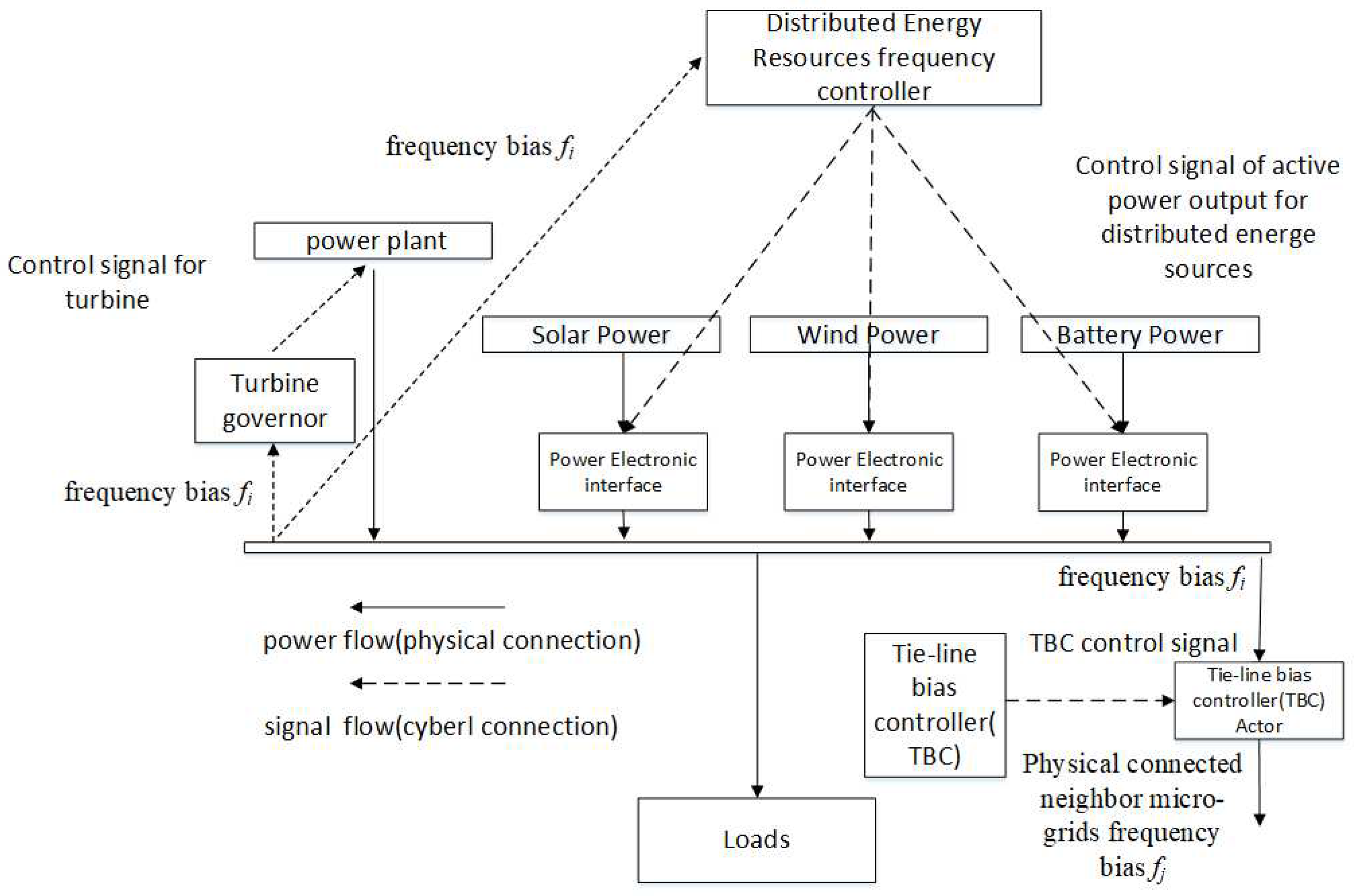
2.1. Power Grid Frequency Dynamic Model
2.2. DoS Attack Model
2.3. Control, Structure Design and Optimization Problem
3. Control and Structure Design
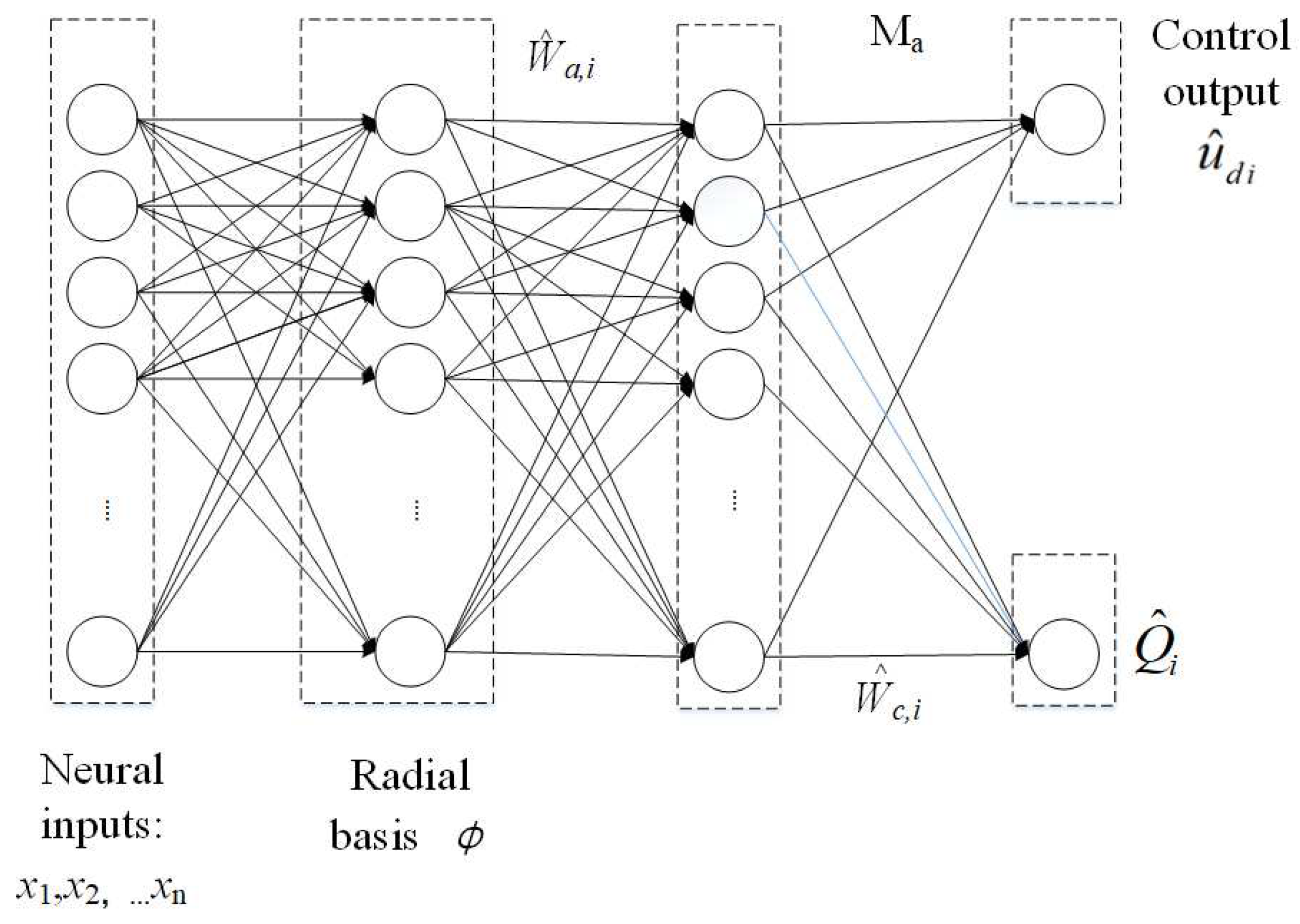
3.1. Control Design by Reinforcement Learning
3.2. Structure Design by Sparse Neural Networks
4. Structure Optimization under DoS Attacks
4.1. Stackelberg Game Formulation
4.2. Structure Optimization under Dos Attacks
| Algorithm 1 Algorithm of Structure Optimization under DoS Attacks |
|
5. Experiments and Analysis
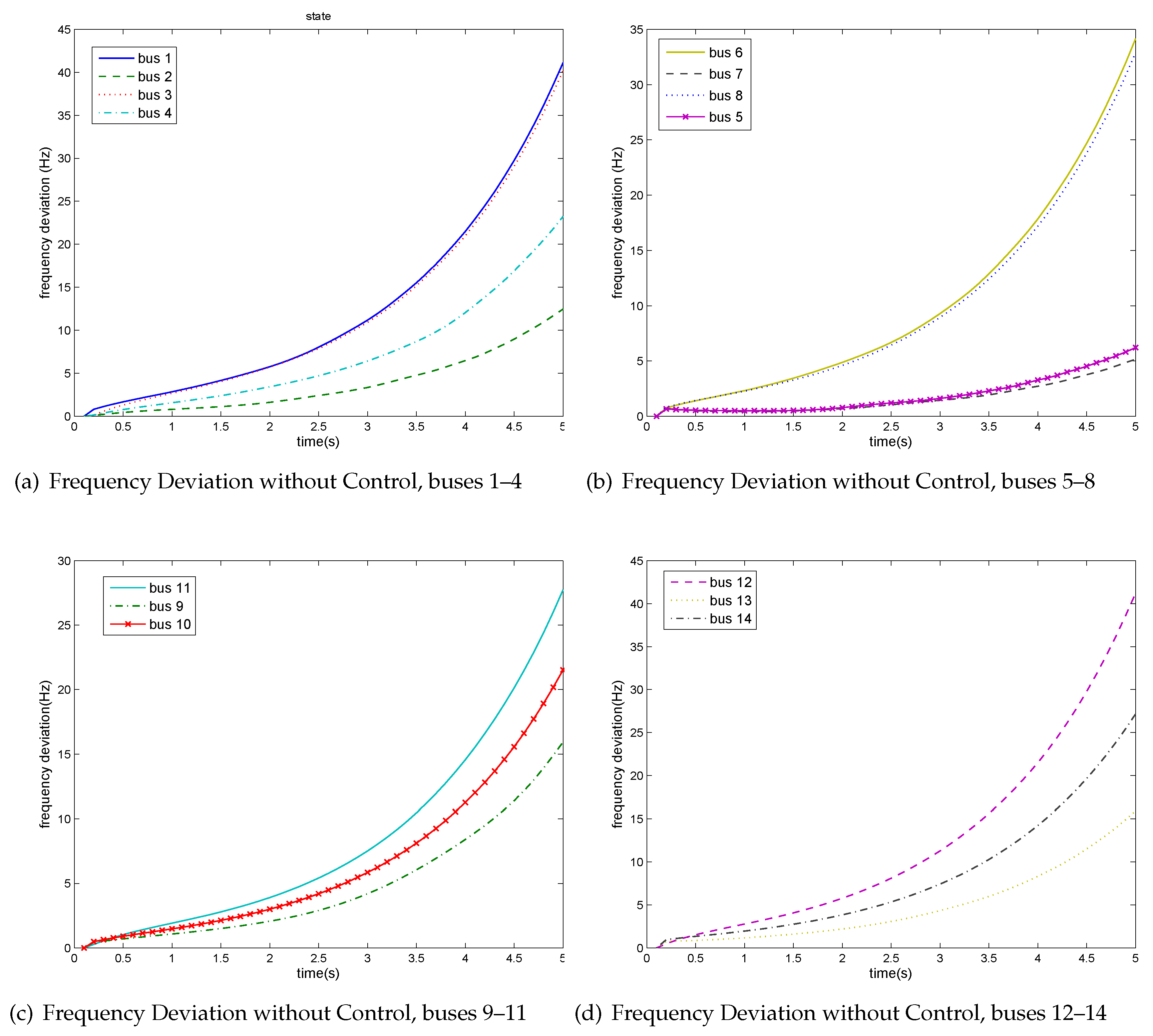
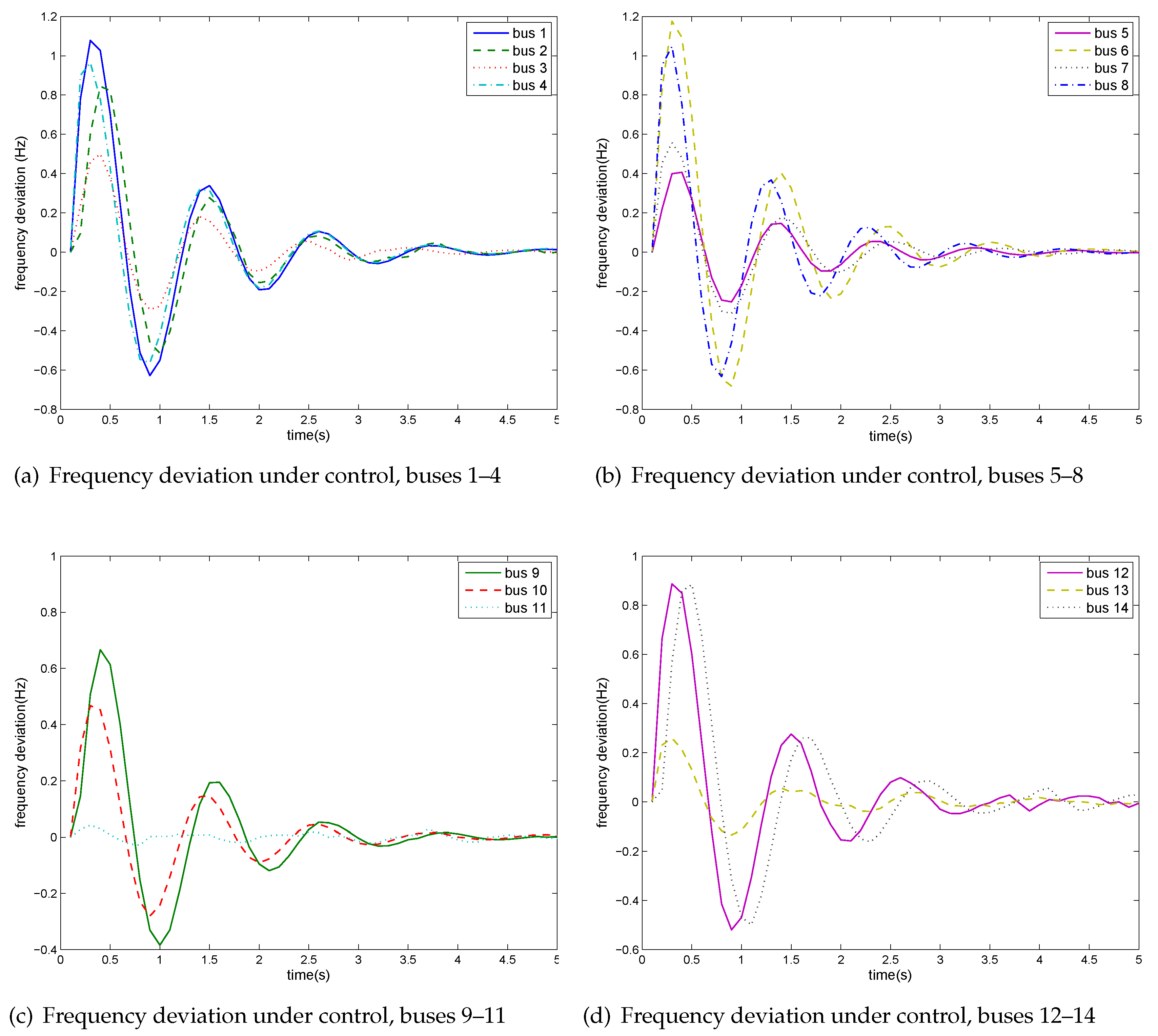
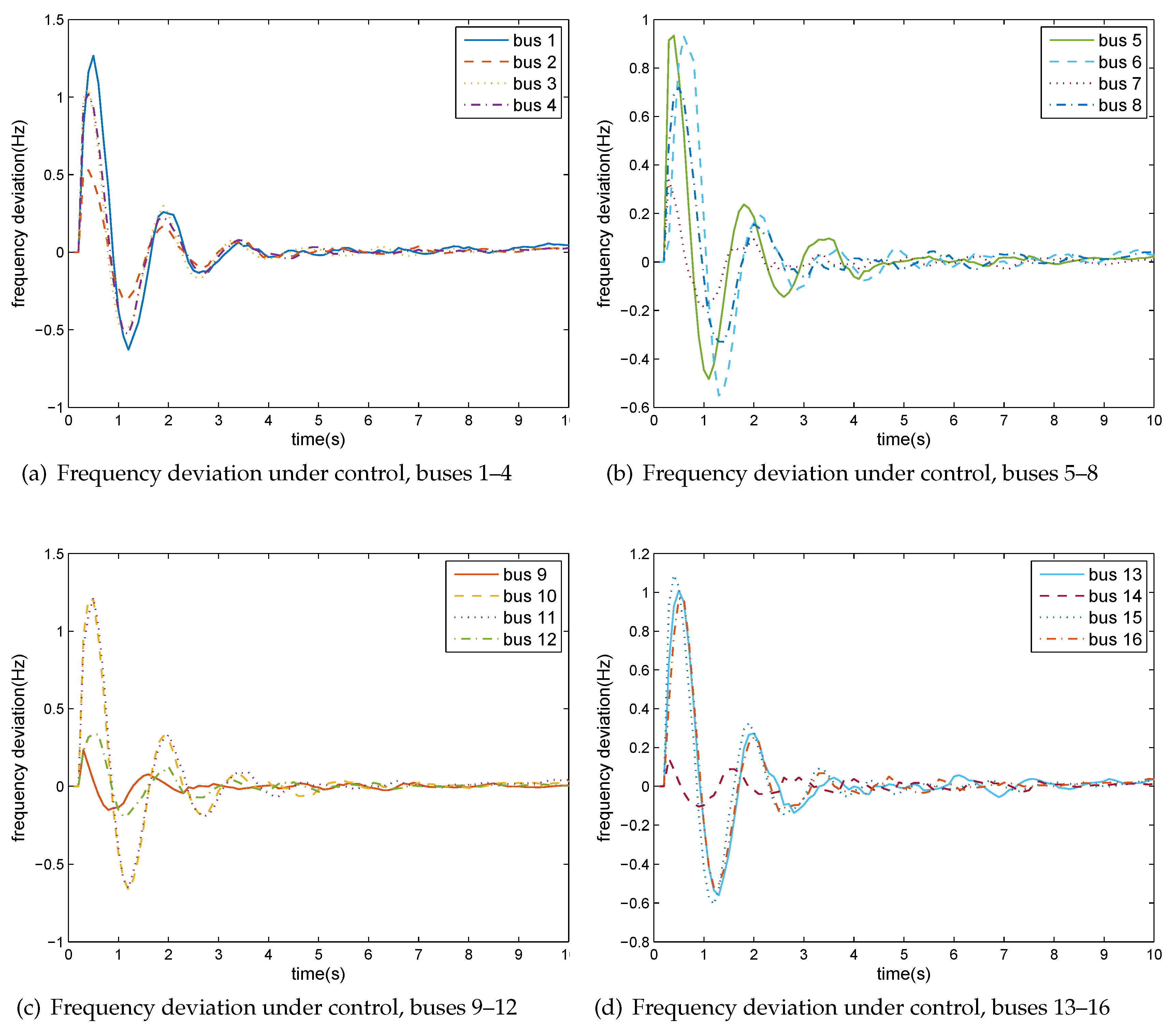
5.1. Case I: IEEE 14 Bus Test System
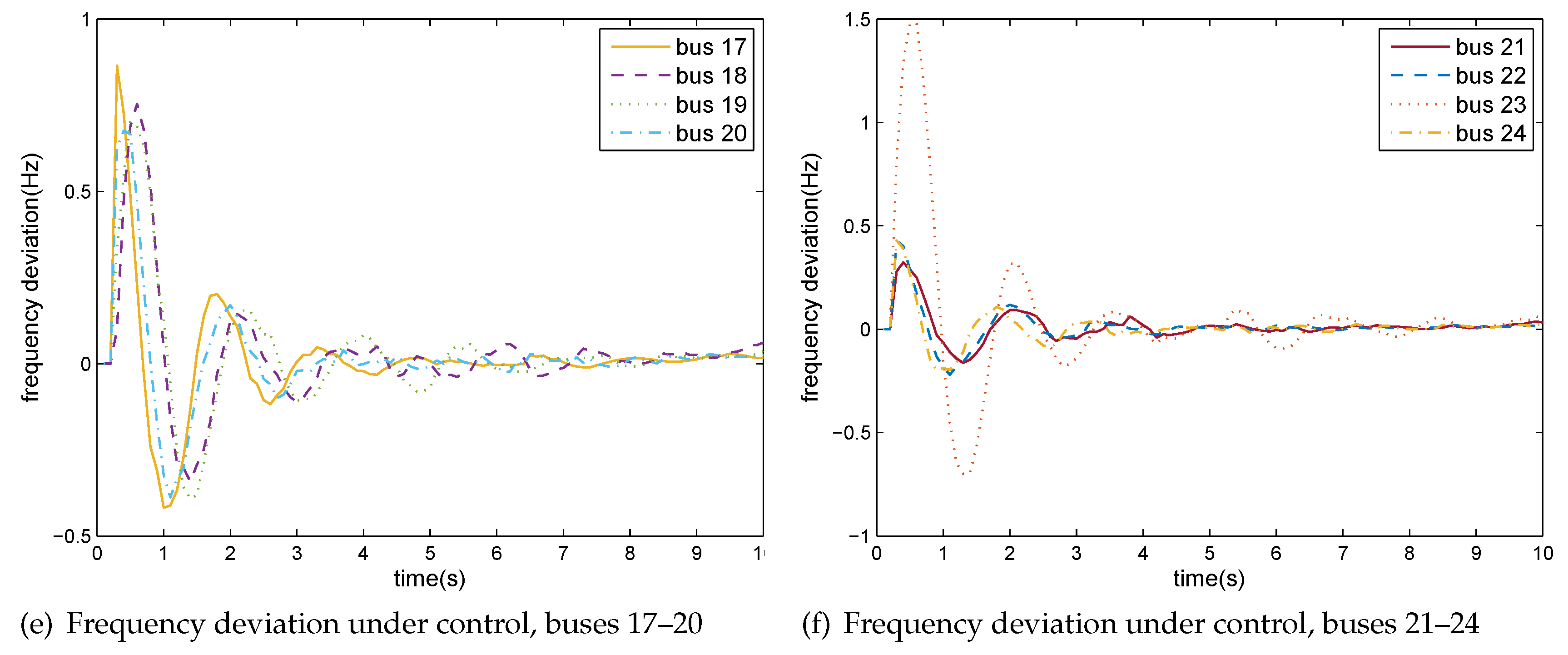
5.2. Case II: IEEE 24 Bus Test System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, P.; Li, J.; Fei, M.R. Resilient event-triggered Hinf load frequency control for networked power systems with energy-limited DoS attacks. IEEE Trans. Power Syst. 2017, 32, 4110–4118. [Google Scholar]
- Sun, J.; Zhu, Z.; Li, H.; Chai, Y.; Qi, G.; Wang, H.; Hu, Y.H. An integrated critic-actor neural network for reinforcement learning with application of DERs control in grid frequency regulation. Int. J. Electr. Power Energy Syst. 2019, 111, 286–299. [Google Scholar] [CrossRef]
- Sridhar, S.; Hahn, A.; Govindarasu, M. Cyber-Physical System Security for the Electric Power Grid. Proc. IEEE 2011, 100, 210–224. [Google Scholar] [CrossRef]
- Liang, G.; Zhao, J.; Luo, F.; Weller, S.; Dong, Z.Y. A Review of False Data Injection Attacks Against Modern Power Systems. IEEE Trans. Smart Grid 2017, 8, 1630–1638. [Google Scholar] [CrossRef]
- Yuan, Y.; Yuan, H.; Lei, G.; Yang, H.; Sun, S. Resilient Control of Networked Control System under DoS Attacks: A Unified Game Approach. IEEE Trans. Ind. Inform. 2016, 12, 1786–1794. [Google Scholar] [CrossRef]
- Srikantha, P.; Kundur, D. Denial of service attacks and mitigation for stability in cyber-enabled power grid. In Proceedings of the Innovative Smart Grid Technologies Conference, Washington, DC, USA, 18–20 February 2015. [Google Scholar]
- An, L.; Yang, G.H. Decentralized Adaptive Fuzzy Secure Control for Nonlinear Uncertain Interconnected Systems Against Intermittent DoS Attacks. IEEE Trans. Cybern. 2019, 49, 827–838. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Peng, C.; Yang, T.; Zhang, H.; He, W. Resilient control of networked control systems with stochastic denial of service attacks. Neurocomputing 2017, 270, 170–177. [Google Scholar] [CrossRef]
- Hu, S.; Yue, D.; Xie, X.; Chen, X.; Yin, X. Resilient Event-Triggered Controller Synthesis of Networked Control Systems Under Periodic DoS Jamming Attacks. IEEE Trans. Cybern. 2018. [Google Scholar] [CrossRef]
- Li, Y.; Quevedo, D.E.; Dey, S.; Ling, S. SINR-based DoS Attack on Remote State Estimation: A Game-theoretic Approach. IEEE Trans. Control Netw. Syst. 2017, 4, 632–642. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, F.; Liu, H. Resilient control of cyber-physical systems against intelligent attacker: A hierarchal stackelberg game approach. Int. J. Syst. Sci. 2016, 47, 2067–2077. [Google Scholar] [CrossRef]
- Ding, K.; Dey, S.; Quevedo, D.E.; Ling, S. Stochastic Game in Remote Estimation under DoS Attacks. IEEE Control Syst. Lett. 2017, 1, 146–151. [Google Scholar] [CrossRef]
- Ding, K.; Li, Y.; Quevedo, D.E.; Dey, S.; Ling, S. A multi-channel transmission schedule for remote state estimation under DoS attacks. Automatica 2017, 78, 194–201. [Google Scholar] [CrossRef]
- Zhu, Q.; Basar, T. Game-Theoretic Methods for Robustness, Security, and Resilience of Cyberphysical Control Systems: Games-in-Games Principle for Optimal Cross-Layer Resilient Control Systems. IEEE Control Syst. 2015, 35, 46–65. [Google Scholar]
- Atwa, Y.M.; El-Saadany, E.F. Optimal Allocation of ESS in Distribution Systems With a High Penetration of Wind Energy. IEEE Trans. Power Syst. 2010, 25, 1815–1822. [Google Scholar] [CrossRef]
- Borges, C.L.T.; Falcão, D.M. Optimal distributed generation allocation for reliability, losses, and voltage improvement. Int. J. Electr. Power Energy Syst. 2006, 28, 413–420. [Google Scholar] [CrossRef]
- Zhang, H.; Ayoub, R.; Sundaram, S. Sensor selection for Kalman filtering of linear dynamical systems: Complexity, limitations and greedy algorithms. Automatica 2017, 78, 202–210. [Google Scholar] [CrossRef]
- Gupta, V.; Chung, T.H.; Hassibi, B.; Murray, R.M. On a stochastic sensor selection algorithm with applications in sensor scheduling and sensor coverage. Automatica 2006, 42, 251–260. [Google Scholar] [CrossRef]
- Qu, C.; Chen, W.; Song, J.B.; Li, H. Distributed Data Traffic Scheduling With Awareness of Dynamics State in Cyber Physical Systems With Application in Smart Grid. IEEE Trans. Smart Grid 2015, 6, 2895–2905. [Google Scholar] [CrossRef]
- Zhu, Z.; Sun, J.; Qi, G.; Chai, Y.; Chen, Y. Frequency Regulation of Power Systems with Self-Triggered Control under the Consideration of Communication Costs. Appl. Sci. 2017, 7, 688. [Google Scholar] [CrossRef]
- Li, H. Data traffic scheduling for cyber physical systems with application in voltage control of microgrids. IEEE Syst. J. 2017, 8, 542–552. [Google Scholar] [CrossRef]
- Cambiaso, E.; Papaleo, G.; Aiello, M. Slowcomm: Design, development and performance evaluation of a new slow DoS attack. J. Inf. Secur. Appl. 2017, 35, 23–31. [Google Scholar] [CrossRef]
- Cambiaso, E.; Papaleo, G.; Giovanni, C.; Aiello, M. A Network Traffic Representation Model for Detecting Application Layer Attacks. Int. J. Archit. Comput. 2016, 5, 31–42. [Google Scholar]
- Sun, J.; Li, J. A Stable Distributed Neural Controller for Physically Coupled Networked Discrete-Time System via Online Reinforcement Learning. Complexity 2018, 2018, 5950678. [Google Scholar] [CrossRef]
- Ding, D.; Wang, Z.; Ho, D.W.; Wei, G. Observer-Based Event-Triggering Consensus Control for Multiagent Systems With Lossy Sensors and Cyber-Attacks. IEEE Trans. Cybern. 2017, 47, 1936–1947. [Google Scholar] [CrossRef] [PubMed]
- Robnik-šikonja, M. Data Generators for Learning Systems Based on RBF Networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 926–938. [Google Scholar] [CrossRef] [PubMed]
- Hansen, L.P.; Sargent, T.J. Robust Control and Model Uncertainty. Am. Econ. Rev. 2001, 91, 60–66. [Google Scholar] [CrossRef]
- Pan, C.; Liu, W.; Thompson, J.S.; Yang, C.; Jorswieck, E.A. Semi-dynamic Green Resource Management in Downlink Heterogeneous Networks by Group Sparse Power Control. IEEE J. Sel. Areas Commun. 2016, 34, 1250–1266. [Google Scholar]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Polak, E.; Yang, T.H.; Mayne, D.Q. A Method of Centers Based on Barrier Functions for Solving Optimal Control Problems with Continuum State and Control Constraints. SIAM J. Control Optim. 2006, 31, 159–179. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]


| Parameter Name | Description | Value |
|---|---|---|
| inertia constant | 0.2 | |
| damping constant | 0.26 | |
| synchronizing constant | 0.5 | |
| governor constant | 5 | |
| regulation constant | 0.5 | |
| frequency bias gain | 1 | |
| gas turbine constant | 0.2 | |
| tie-line bias control gain | 0.1 |
| Parameter Name | Description | Value |
|---|---|---|
| damping factor for cost | 0.9 | |
| N | Horizon length for cost | 10 |
| Learning rate of neural network | 0.1 | |
| Weight of group sparse regulation term | 0.012 | |
| Norm of damping parameters | 0.1 |
| Parameter Name | Description | Value |
|---|---|---|
| damping factor for cost | 0.8 | |
| N | Horizon length for cost | 10 |
| Learning rate of neural network | 1 | |
| Weight of group sparse regulation term | 0.005 | |
| Norm of damping parameters | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Qi, G.; Zhu, Z. A Sparse Neural Network Based Control Structure Optimization Game under DoS Attacks for DES Frequency Regulation of Power Grid. Appl. Sci. 2019, 9, 2217. https://doi.org/10.3390/app9112217
Sun J, Qi G, Zhu Z. A Sparse Neural Network Based Control Structure Optimization Game under DoS Attacks for DES Frequency Regulation of Power Grid. Applied Sciences. 2019; 9(11):2217. https://doi.org/10.3390/app9112217
Chicago/Turabian StyleSun, Jian, Guanqiu Qi, and Zhiqin Zhu. 2019. "A Sparse Neural Network Based Control Structure Optimization Game under DoS Attacks for DES Frequency Regulation of Power Grid" Applied Sciences 9, no. 11: 2217. https://doi.org/10.3390/app9112217
APA StyleSun, J., Qi, G., & Zhu, Z. (2019). A Sparse Neural Network Based Control Structure Optimization Game under DoS Attacks for DES Frequency Regulation of Power Grid. Applied Sciences, 9(11), 2217. https://doi.org/10.3390/app9112217







