Abstract
Engineering thermal management (ETM) is one of the critical tasks for quality control and system surveillance in many industries, and acquiring the temperature field and its evolution is a prerequisite for efficient thermal management. By harnessing the sensing data from sensor networks, an unprecedented opportunity has emerged for an accurate estimation of the temperature field. However, limited resources of sensor deployment and computation capacity pose a great challenge while modeling the spatiotemporal dynamics of the temperature field. This paper presents a novel temperature field estimation approach to describe the dynamics of a temperature field by combining a physics-specific model and a spatiotemporal Gaussian process. To reduce the computational burden while dealing with a large set of spatiotemporal data, we employ a tapering covariance function and develop an associated parameter estimation procedure. We introduce a case study of grain storage to show the effectiveness and efficiency of the proposed approach.
1. Introduction
Engineering thermal management (ETM) is one of the critical tasks for quality control and system surveillance in many industries. As a prerequisite in ETM, the temperature field distribution should be known. Generally, estimation of a temperature field is of great interest, as accurately estimating a temperature field is required in a variety of research domains, such as ecology [1,2], health care [3,4], and meteorology [5,6]. An accurate estimation of a temperature field may provide information for the guidance of the optimum design of engineering structures to reduce production cost and conserve energy [7].
Affected by a number of extrinsic factors (e.g., ambient temperature) and intrinsic factors (e.g., nature currents and moisture migration), a temperature field is often regarded as a complex system with stochastic physical dynamics and spatiotemporally varying uncertainties. For example, the temperature field in a granary (Figure 1), in which grain temperature at each location varies over time, is considered as a spatiotemporally varying thermodynamic system. However, due to the unknown inner mechanism and varying boundary conditions, accurately estimating a temperature field with spatiotemporal stochastic dynamics remains a challenging task.
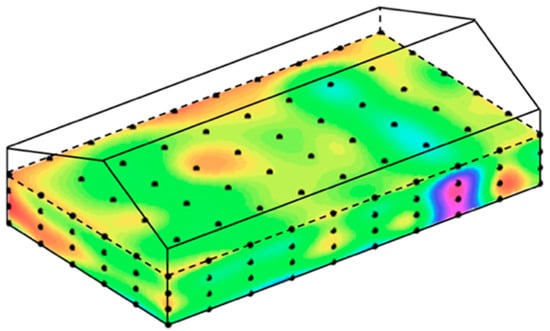
Figure 1.
A 3D grain temperature field in a granary. (Note: the cloud is the grain temperature field, and the black dots are the sensor locations).
In conventional field estimation methods, a temperature field is estimated by physics-specific models. A heat transfer model for a cubic granary was adopted by Wang and Zhang [8] and Rusinek and Kobylka [9]. Jia, Sun, and Cao [10] and Alagusundaram et al. [11] developed an unsteady heat transfer model to characterize a temperature field of a cylindrical granary. Khatchatourian and Oliveira [12] introduced a mathematical approach to model the airflow and the thermal state in a granary. For the stored grain ecosystem, a 3D transient heat, mass, and momentum transfer model was developed by Gastón et al. [13] and Jian et al. [14] to predict temperatures and moisture contents of stored grains. Jian et al. [15] and Lawrence [16] extended the Gastón’s and Jian’s work by considering a species transfer model, in which data of ambient temperature and humidity, wind speed, and solar radiation were used. Conventional methods for field estimation are mostly achieved by the simulation of physical models, in which sensing observations collected from distributed sensor networks are not considered. These methods may lead to a discrepancy between model predictions and observations because of stochastic dynamics and uncertainties in the temperature fields. For instance, excessive moisture of grain may lead to local overheating of grain, which cannot be easily captured by conventional field estimation methods.
With the development of sensor technologies, wireless sensor networks have emerged as a key tool to collect sensing data and enable the sensing data to measure the fields [17,18,19]. Many researchers have employed statistical methods for the estimation of temperature fields using sensing observations, which aim to capture stochastic dynamics and uncertainties of temperature fields. For instance, Uchiyama, Hamatani, and Higashino developed a health core temperature estimation approach using data collected from wearable sensors [20]. Yin et al. analyzed temperature fields of the stored grain in different warehouses using grain temperature sensing data [21]. Uncertainty quantification to temperature sensing data is an essential part for temperature field estimation. Some research has focused on data uncertainty quantification problems [22,23] For example, a data uncertainty quantification approach proposed by Lermusiaux is for estimating temperature fields in the ocean [24]. Sapsis and Lermusiaux employed dynamically orthogonal field equations to characterize continuous dynamical systems [25]. Some other research work has focused on tackling uncertainties using Gaussian processes. For example, Rasmussen presented the application of Gaussian processes in machine learning [26]. Krause, Singh, and Guestrin used a Gaussian process to achieve near-optimal sensor placements [27]. Sang and Huang proposed an approximation approach to covariance functions of Gaussian process for spatial data [28]. Cressie, Noel, and Wikle applied Gaussian process models to study the spatiotemporal correlation of a 2D or 3D field [29]. However, only limited sensor observations are collected, because only sparse sensors are deployed in sensor networks given the high costs of sensors and limited budget. Due to limited sensing observations and the existence of various data uncertainties, temperature field estimation purely using statistical approaches fails to achieve an accurate estimation result. Therefore, an accurate temperature field estimation requires combining appropriate physical laws and statistical approaches to finely characterize temperature distribution and associated evolution. However, few studies have addressed this issue to the best of our knowledge.
In this paper, we develop a field estimation approach to model spatiotemporal dynamics of temperature fields based on grain storage sensor networks by combining a physics-specific model and spatiotemporal stochastic processes. First, a three-dimensional thermodynamic model, that is, the 3D heat transmission model for the grain temperature field, is employed to describe the global temperature profile under ideal conditions by considering extrinsic factors. Then, we capture local temperature changes caused by intrinsic factors by a spatiotemporal Gaussian process based on the deviance of sensing observations from the global temperature profile. Directly estimating the spatiotemporal dynamics with conventional Gaussian process models will generally be computationally infeasible, as operations is required for a dataset of size . Hence, we borrow a tapering covariance function and integrate it into the Gaussian process model to reduce the computational burden. We conduct a real case of temperature fields in grain storage to validate the model performance of our field estimation method.
2. Methods
2.1. Formulation
We denote as the response variable of a temperature field at location and time , where , . We describe the temperature field by a mixed effect model framework, which contains three parts: the global temperature profile, the local variability, and the model error.
where denotes the mean function describing the global temperature profile, denotes the local variability, and ε denotes the model error. As shown in Figure 2, we use a physics specific model, that is, the thermodynamic model, to characterize the global temperature profile under ideal conditions by considering extrinsic factors. There exists a discrepancy between the global temperature profile acquired from the conventional thermodynamic model and real temperature values due to some intrinsic factors, such as the existence of nature currents and moisture migration. To deal with this issue, we model this discrepancy as the local variability. The local variability is affected by these intrinsic factors, which cannot be fully captured by the thermodynamic model. In our method, the sensing data provides us a unique chance to capture the uncertainties of the local variability caused by intrinsic factors. We adopt a spatiotemporal Gaussian process model to describe the local variability using the deviance of the sensing data from the global temperature profile. Therefore, both the effects from extrinsic and intrinsic factors, e.g., heat transfer, nature currents and moisture migration, are substantially incorporated into the mixed-effect model framework.
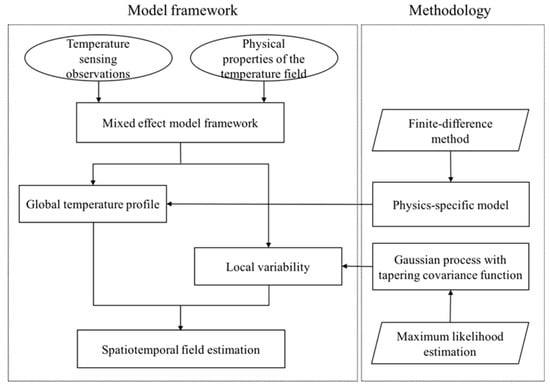
Figure 2.
The framework of our methodology.
2.2. Physics-Specific Model for the Global Temperature Profile
We employ a physics-specific model to describe the global temperature profile of a temperature field over time. To illustrate how to choose a physics-specific model for a specific temperature field, we take the grain temperature field as an example.
We consider a temperature field in a cubic granary. To describe the global temperature profile in a cubic granary, location in Equation (1) is represented by in Cartesian coordinates. We employ a 3D heat transmission in a granary as the mean function as follows:
where the parameters , , and are determined on the basis of thermal properties. For stored grains, , , and denote the thermal diffusivities of the grains in the , , and directions, respectively. Alternatively, if the thermal diffusivities of the grains are unknown, we can calculate , , and using the proposed parameter estimation approach in [30].
The finite-difference method is employed to solve Equation (2). We use an explicit marching method to calculate the global temperature profile , as shown in Equation (3), where a central difference in and directions, and a forward difference in time are considered. To be specific,
where , , , and are the indexes of locations , , and the time . , , , and are the grid spacings in the , , and directions of the space domain and time .
To satisfy a highly accurate numerical solution, this method is stable under the condition [31]:
Given the grain temperature at the initial time point and the temperature at the walls of the granary as the boundary conditions, the global temperature profiles are obtained. We adopt a Gaussian process model [26] for interpolation using the sensing data on the granary walls to obtain the boundary conditions.
2.3. Gaussian Process with a Tapering Covariance Function for Local Variability
2.3.1. Formulation of the Gaussian Process Model
Local variability of a temperature field can be affected by many intrinsic factors that cannot be fully captured by physics-specific models. For example, excessive moisture of grain leads to a quick local temperature increment, which cannot be directly characterized by conventional physical models. As shown in Figure 3, although the dynamics model is with continuous variables that consider the spatiotemporal correlation, the local variability in spatial and temporal domain caused by intrinsic factors substantially exists and exhibits with various correlation patterns. Given that the thermodynamic model is able to capture nonstationary profiles of a temperature field across the spatial and temporal domains, the local variability is assumed to be stationary. Without loss of generality, we adopt a spatiotemporal Gaussian process model to describe the spatiotemporal dependence structures of local variability using the deviance of the sensing observations from the global temperature profile in the following:
where is the covariance matrix of the Gaussian process.
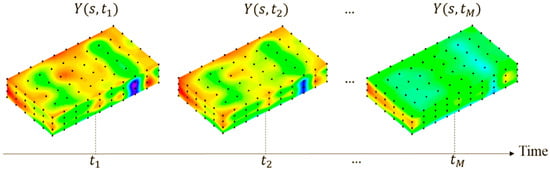
Figure 3.
Time-varying grain temperature field.
The covariance matrix of the Gaussian Process is obtained from a covariance function describing the spatial and temporal correlations. Because various thermal transmission effects exist in different directions of the granary, there are various spatial correlation patterns of local variability in different directions of the granary. Temporal evolution also exists among the time domain. Therefore, we use an anisotropic spatiotemporal covariance function to characterize spatiotemporal correlation between two different spatiotemporal locations as follows:
where is the distance metric of two locations in the spatial and temporal domains, respectively, and is the set of parameters in the covariance function. In the spatial domain, , , and are the parameters corresponding to the distance in , , and directions respectively, which capture anisotropic spatial correlation structures of a granary; in the temporal domain, a decay parameter corresponding to the time dependence effect is used to capture the temporal correlation of the local variability.
2.3.2. Covariance Tapering
Traditional Gaussian process models, which require the computational complexity of to estimate parameters with a dataset of size n [32]. In order to reduce the computational burden of Gaussian process models and satisfy the necessity in practice, we adopt a covariance tapering method to characterize the covariance function. Considered that distant pairs of temperature values are uncorrelated, the covariance tapering method aims to model a compactly supported covariance function in which the correlation of distant pairs is defined as zero. The covariance matrix of Gaussian process models obtained by the covariance tapering method is positive definite and can retain most information of the temperature field.
We adopt a tapering covariance function in the Gaussian process model by taking the product of an original covariance function and a tapering function as follows:
where is defined as an isotropic correlation function in the spatial domain that is zero whenever
where is a range parameter. We use the spherical tapering function as the tapering function in our model, which is defined by
where means that
2.3.3. Parameter Estimation for θ
We incorporate the tapering covariance function Equation (8) into the Gaussian process Equation (5). Then, the tapering covariance matrix is
where and are the covariance matrices obtained by and , respectively; the notation denotes the Schur product that is defined as the element wise matrix product. For example, two matrixes, and , have the Schur product .
We use maximum-likelihood estimation (MLE) approach to estimate . Specifically, the log-likelihood function of is as follows
where denotes the difference between the sensing observations and the global temperature profiles, and is a constant term that is uncorrelated with . Maximizing is to solve an unbiased estimating equation for , i.e., . The derivative of is equal to
Equation (11) can be used in conjunction with a numerical optimization algorithm, such as conjugate gradients, to obtain the estimation of [26].
2.3.4. Selection of Range Parameter
The choice of the range parameter in the tapering covariance function influences the accuracy of the field estimation and the computational complexity of our proposed model. Given that maximizing the likelihood function in Equation (10) is to solve an unbiased estimating equation for , it is suggested that an estimator of the sampling variability of should be estimated using the robust information criterion in [33]. To achieve a trade-off between field estimation accuracy and computational complexity, we adopt the sampling variability (SV) and the model computational time (CT) as a criterion to select an appropriate .
Let be an unbiased estimating function for . The robust information criterion for is
where is the matrix of derivatives of with respect to ,
The sampling variability is defined by the diagonal elements of , namely, the trace of .
The procedure of selecting is as follows (Figure 4): First, we obtain a pilot estimate . For example, we calculate the MLE for a small and randomly chosen subset of sensing observations. Second, we calculate the sampling variability and model computational time for an available value of . The initial value is the minimal range parameter value. Third, we repeat the second step and calculate the sampling variability and model computational time for with , where is the number of ; Finally, we select to construct a balance between the sampling variability and the model computational time , that is, smaller sampling variability and shorter model computational time.

Figure 4.
The criterion to determine the range parameter .
2.3.5. Spatiotemporal Field Estimation
When the covariance parameters are estimated and the range parameter is selected, we obtain the spatiotemporal temperature field by given environmental conditions and sensing observations. Temperature at a new location and time is estimated by
and the variance of is calculated by
where is the global temperature profile, is the vector of sensing observations, is the vector of global temperature profiles for , is the variance matrix of , is the covariance matrix between and , and is the covariance matrix of .
3. Case Study
We conducted a real case study of a grain temperature field to validate our proposed method. The sensing data in our real case were collected from the grain temperature sensor networks in a national granary in central China at least every seven days from 31 January in one year to 4 March in the second year. Figure 5 presents the grain temperature sensor network of the granary. The sensor network consisted of 240 sensors, which were uniformly distributed in a traditional granary with the volume of . The sensors were deployed at the initial positions of 0.5 m, 0.5 m, and 0.3 m in the space domain and located at 5 m intervals in the and directions and 1.8 m intervals in the direction. There were in total 17,280 sensing observations. We randomly selected training data from sensing data in the first 66 time points from 31 January in one year to 1 February in the second year, and set the remaining data as test data. The ratio of training data set to test data set was set as 3:1. To validate the prediction capability of our proposed model, we also retained the sensing data from 2 February to 4 March in the second year as the test data.
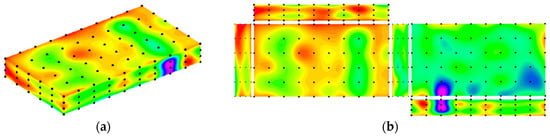
Figure 5.
Anatomy of a grain temperature sensor network; (a) full view of a grain temperature field, (b) grain temperature sensor network based on a six-view plot.
The physical properties of stored grains were given in Table 1, and the attribute values were further incorporated into the thermodynamic model. In Table 1, thermal diffusivity in the vertical directions is greater than the transverse directions due to the faster airflow enhancing the heat transfer in vertical direction.

Table 1.
Physical properties of stored grains.
The validation of the proposed field estimation approach contained three layers: modeling of the global temperature profile, parameter estimation of the proposed Gaussian process model and spatiotemporal field estimation.
3.1. Global Temperature Profile
For the global temperature profile, the parameters in the mean function are determined by the properties of grain that are listed in Table 1. Given the grain temperature sensing data in the real case, we chose = 0.5 m, = 0.5 m, = 0.5 m, and = 1 day to satisfy the stability condition of the finite-difference method in Equation (4). We acquired the sensing data of the granary walls collected by the sensors on the walls and adopted a Gaussian process model [26] for interpolation using the sensing data on the granary walls to obtain the boundary conditions of the thermodynamic model.
3.2. Parameter Estimation of the Proposed Gaussian Process Model
For the parameter estimation of the tapering covariance function in the Gaussian process, we have initially addressed the selection of the range parameter . We obtained a pilot estimate of the covariance parameters using a subset training data of size 540, which was randomly chosen from the training data set. Figure 6 shows the curves of both the sampling variability and the computational time given a series of values of . For the increasing values of , the sampling variability decreases with a substantial range when is small and tends to become flat when is large. In contrast, the computational time of field estimation rises rapidly as with the increase of . We chose = 22 as the appropriate range parameter in the spatial domain by weighting the trade-off between sampling variability and computational time. Then, we used the MLE method to acquire estimated covariance parameters , which are shown in Table 2.
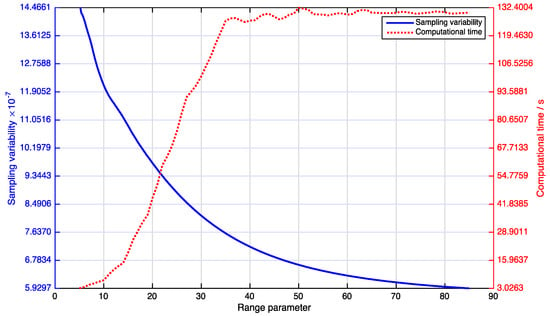
Figure 6.
Selection of the range parameter.

Table 2.
Estimated parameter values of .
3.3. Spatiotemporal Field Estimation
For the spatiotemporal field estimation, we used the mean square error (MSE) as in Equation (17) to evaluate the proposed field estimation method.
where denotes a sensing observation in the test data set, and denotes the estimated temperature value of . We tested the proposed field estimation method by estimating the grain temperature at the sensor sites of test data set by Equations (15) and (16). The MSE is equal to 0.04, which indicates the effectiveness of the estimation results using the proposed field estimation method. We show the examples of temperature profiles by the proposed field estimation method in Figure 7. The blue-star dots represent the training data, the red-plus dots represent the test data, and the blue lines denotes the estimated temperature profiles using our proposed method. The results show both interpolation and prediction capability of the proposed model with acceptable confidence intervals.
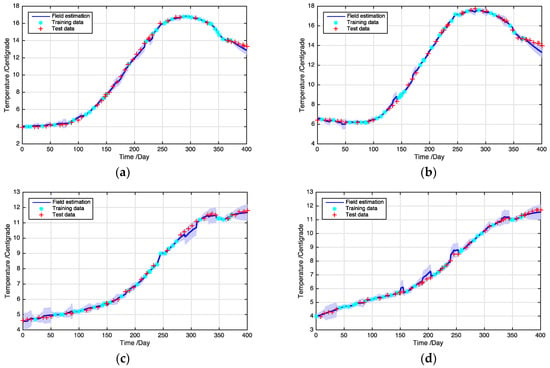
Figure 7.
Examples of estimated temperature profiles: (a) coordinate (10.5, 20.5, 3.9), (b) coordinate (15.5, 5.5, 3.9), (c) coordinate (15.5, 40.5, 2.1), (d) coordinate (20.5, 25.5, 2.1). (Note: the blue dashed area represents the 95% confidence interval).
To show the superiority of our approach, which integrates the physics-specific model and the spatiotemporal Gaussian process model, we compared it with other existing methods. In Table 3, we compared the model performance by changing mean functions proposed in the relevant literature, that is, a constant and a sinusoidal model. The result shows the superiority of the thermodynamic model as the mean function. In Table 4, our proposed method delivers a better result than the thermodynamic model and consumes less than 50% of the computational time than the conventional Gaussian process model.

Table 3.
Comparison of model performance using various mean functions.

Table 4.
Comparison of model performance using various Gaussian process models.
Figure 8 shows an example of temperature profiles at different locations estimated by the proposed field estimation method. The grain temperature field obtained by our model changes with seasonal effects. Specifically, grain temperature inside the granary varies more slowly over time and has a smaller fluctuating range than grain temperature at the outer locations. This finding is consistent with the grain temperature fields in most of the granaries in China. Moreover, it provides a new quantitative understanding of temperature field evaluation in granaries [34].
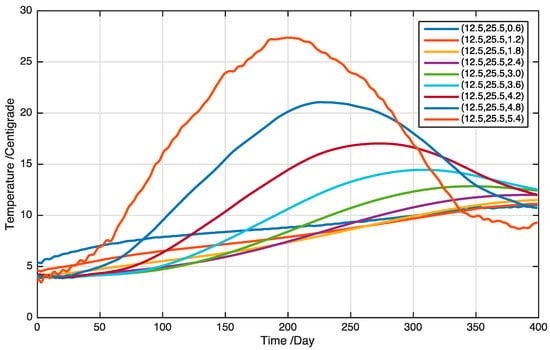
Figure 8.
Examples of temperature profiles at different locations.
4. Conclusions
This study proposes an estimation method for a 3D spatiotemporal temperature field in grain storage sensor networks. In conventional field estimation methods, a temperature field could not be estimated with high accuracy by either the pure physical or the statistical model because of the sparsity and spatiotemporal uncertainties of temperature observations. To tackle this problem, we obtain the estimation of a temperature field by combining the physics-specific model and the spatiotemporal stochastic process. First, we employ a physics-specific model to characterize the global temperature profile. Then, we adopt a spatiotemporal Gaussian process to describe the local variability using the deviance of the sensing observations from the global temperature profile. To reduce the computational burden of conventional Gaussian process models, we employ a tapering covariance function by integrating a tapering function with the original covariance function of Gaussian process model. In the case study, we validate the performance of our method by using grain temperature sensing observations collected from grain storage sensor networks. The results of the real case study deepen our understanding of the temperature field in grain storage and provide useful information for the guidance of future sensor placement designs and configurations.
In the future work, we aim to adaptively calibrate the parameters in the spatiotemporal field estimation model for precise engineering thermal management.
Author Contributions
X.Z. conceived the study and contributed to the design of the study, modeling, data interpretation, and revised the manuscript. D.W. contributed to the development of algorithms, data evaluation, data analysis, and drafted the manuscript. Both authors reviewed the manuscript.
Funding
This work was supported by the National Science Foundation of China Grants (71571003), (71771004) and (71690232).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, W.; Lü, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Automatic parameter optimization for support vector regression for land and sea surface temperature estimation from remote sensing data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 909–921. [Google Scholar] [CrossRef]
- Yao, B.; Yang, H. Physics-driven spatiotemporal regularization for high-dimensional predictive modeling: A novel approach to solve the inverse ECG problem. Sci. Rep. 2016, 6, 39012. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yang, H. Sparse modeling and recursive prediction of space-time dynamics in stochastic sensor networks. IEEE Trans. Autom. Sci. Eng. 2016, 13, 215–226. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, F.; Hsieh, H. U-Air: When urban air quality inference meets big data. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 1436–1444. [Google Scholar]
- Zhou, C.; Wang, K. Spatiotemporal divergence of the warming hiatus over land based on different definitions of mean temperature. Sci. Rep. 2016, 6, 31789. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, S.; Bergmann, N.; Jurdak, R.; Kusy, B. Time series analysis for spatial node selection in environment monitoring sensor networks. Sensors 2018, 18, 11. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, X. A prediction method for interior temperature of grain storage via dynamics model: A simulation study. In Proceedings of the IEEE International Conference on Automation Science and Engineering, Gothenburg, Sweden, 24–28 August 2015; pp. 1477–1483. [Google Scholar]
- Rusinek, R.; Kobylka, R. Experimental study and discrete element method modeling of temperature distributions in rapeseed stored in a model bin. J. Stored Prod. Res. 2014, 59, 254–259. [Google Scholar] [CrossRef]
- Jia, C.; Sun, D.; Cao, C. Finite element prediction of transient temperature distribution in a grain storage bin. J. Agric. Eng. Res. 2000, 76, 323–330. [Google Scholar] [CrossRef]
- Alagusundaram, K.; Jayas, D.S.; White, N.D.G.; Muir, W.E. Three-dimensional, finite element, heat transfer model of temperature distribution in grain storage bins. Trans. ASAE 1990, 33, 577–584. [Google Scholar] [CrossRef]
- Khatchatourian, O.A.; De Oliveira, F.A. Mathematical modeling of airflow and thermal state in large aerated grain storage. Biosyst. Eng. 2006, 95, 159–169. [Google Scholar] [CrossRef]
- Gastón, A.; Abalone, R.; Bartosik, R.E.; Rodriguez, J.C. Mathematical modelling of heat and moisture transfer of wheat stored in plastic bags (silo bags). Biosyst. Eng. 2009, 104, 72–85. [Google Scholar] [CrossRef]
- Jian, F.; Chelladurai, V.; Jayas, D.S.; White, N.D.G. Three-dimensional transient heat, mass and momentum transfer model to predict conditions of canola stored inside silo bags under Canadian Prairie conditions, Part II-model of canola bulk temperature and moisture content. Trans. ASABE 2015, 58, 1135–1144. [Google Scholar]
- Jian, F.; Jayas, D.S.; White, N.D.G.; Alagusundaram, K. A three-dimensional, asymmetric, and transient model to predict grain temperatures in grain storage bins. Trans. ASAE 2005, 48, 263–271. [Google Scholar] [CrossRef]
- Lawrence, J.; Maier, D.E.; Stroshine, L. Three-dimensional transient heat, mass, momentum and species transfer in the stored grain ecosystem: Part I. Model development and evaluation. Trans. ASABE 2013, 56, 179–188. [Google Scholar] [CrossRef]
- Ding, Y.; Elsayed, E.A.; Kumara, S.; Lu, J.; Niu, F.; Shi, J. Distributed sensing for quality and productivity improvements. IEEE Trans. Autom. Sci. Eng. 2006, 3, 344–359. [Google Scholar] [CrossRef]
- Huang, Q.; Rodriguez, K. A software framework for heterogeneous wireless sensor network towards environmental monitoring. Appl. Sci. 2019, 9, 867. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Jia, Y.; Liu, Y. Quality changes of N-3 PUFAs enriched and conventional eggs under different home storage conditions with wireless sensor network. Appl. Sci. 2017, 7, 1151. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Hamatani, T.; Higashino, T. Estimation of core temperature based on a human thermal model using a wearable sensor. In Proceedings of the IEEE 4th Global Conference on Consumer Electronics, Osaka, Japan, 27–30 October 2015; pp. 605–609. [Google Scholar]
- Yin, J.; Wu, Z.; Zhang, Z.; Wu, X.; Wu, W. Comparison and analysis of temperature field reappearance in stored grain of different warehouses. Trans. Chin. Soc. Agric. Eng. 2015, 31, 281–287. [Google Scholar]
- Eisenhower, B.; O’Neill, Z.; Fonoberovand, V.; Mezic, I. Uncertainty and sensitivity decomposition of building energy models. J. Build. Perform. Simul. 2012, 5, 171–184. [Google Scholar] [CrossRef]
- Yang, Y.; Christakos, G.; Huang, W.; Lin, C.; Fu, P.; Mei, Y. Uncertainty assessment of PM2.5 contamination mapping using spatiotemporal sequential indicator simulations and multi-temporal monitoring data. Sci. Rep. 2016, 6, 24335. [Google Scholar] [CrossRef]
- Lermusiaux, P.F.J. Uncertainty estimation and prediction for interdisciplinary ocean dynamics. J. Comput. Phys. 2006, 217, 176–199. [Google Scholar] [CrossRef]
- Sapsis, T.P.; Lermusiaux, P.F.J. Dynamically orthogonal field equations for continuous stochastic dynamical systems. Phys. D Nonlinear Phenom. 2009, 238, 2347–2360. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning in Advanced Lectures on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar]
- Krause, A.; Singh, A.; Guestrin, C. Near-optimal sensor placements in Gaussian processes: Theory, efficient algorithms and empirical studies. J. Mach. Learn. Res. 2008, 9, 235–284. [Google Scholar]
- Sang, H.; Huang, J.Z. A full-scale approximation of covariance functions for large spatial data sets. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2012, 74, 111–132. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Xun, X.; Cao, J.; Mallick, A.; Maity, A.; Carroll, R.J. Parameter estimation of partial differential equation models. J. Am. Stat. Assoc. 2013, 108, 1009–1020. [Google Scholar] [CrossRef]
- Bland, D.R. Solutions of Laplace’s Equation; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, B.; Sang, H.; Huang, J.Z.; Maity, A.; Carroll, R.J. Full-scale approximations of spatio-temporal covariance models for large datasets. Stat. Sin. 2015, 25, 99–114. [Google Scholar] [CrossRef][Green Version]
- Kaufman, G.G.; Schercish, J.M.; Nychka, D.W. Covariance tapering for likelihood-based estimation in large spatial data sets. J. Am. Stat. Assoc. 2008, 103, 1545–1555. [Google Scholar] [CrossRef]
- Yang, Z. A simulation of the quasi-static temperature field in grain storage via CFD. J. Chin. Cereals Oils Assoc. 2010, 25, 46–50. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).