A Sparse Classification Based on a Linear Regression Method for Spectral Recognition

Featured Application

The linear regression sparse classification (LRSC) algorithm is presented in this work to recognize Tegillarca granosa samples on the dataset of infrared spectral data and laser-induced breakdown spectral (LIBS), and this classification method can be extended to other spectral data for the classification of different categories. The thought of sparse representation in this classification algorithm is used to screen the useful information with less dimensions, and it can also be used to detect the outlier samples.

Abstract

This study introduces a spectral-recognition method based on sparse representation. The proposed method, the linear regression sparse classification (LRSC) algorithm, uses different classes of training samples to linearly represent the prediction samples and to further classify them according to residuals in a linear regression model. Two kinds of spectral data with completely different physical properties were used in this study. These included infrared spectral data and laser-induced breakdown spectral (LIBS) data for Tegillarca granosa samples polluted by heavy metals. LRSC algorithm was employed to recognize the two classes of data, and the results were compared with common spectral-recognition algorithms, such as partial least squares discriminant analysis (PLS-DA), soft independent modeling of class analogy (SIMCA), artificial neural network (ANN), random forest (RF), and support vector machine (SVM), in terms of recognition rate and parameter stability. The results show that LRSC algorithm is not only simple and convenient, but it also has a high recognition rate.

1. Introduction

Spectral detection methods such as infrared spectra, laser-induced breakdown spectra (LIBS), and Raman spectra are widely used in the fields of food safety [1], environmental monitoring [2], and medical diagnosis [3] as fast, convenient, and green methods. Quantitative and qualitative analyses are the two main aspects of spectral applications. Qualitative analysis involves classification and recognition of the spectra to be measured. Common recognition algorithms are mainly realized based on distance [4]. For example, the classic linear discriminant analysis (LDA) method takes the minimum within-class distance and the maximum between-class distances as criteria. However, spectral data is often a highly dimensional dataset with a small number of samples, and ordinary LDA cannot meet its classification requirements [5]. To enhance the classification characteristics, it is common practice to preprocess the data by means of a data-conversion projection, such as principal component analysis-linear discriminant analysis (PCA-LDA) [6], partial least squares discriminant analysis (PLS-DA), and soft independent modeling of class analogy (SIMCA) [7], before recognition. This projects the principal component of the data into characteristic space, thereby reducing dimensionality. In addition, support vector machine (SVM) based on kernel function [8] projects limited data into a highly dimensional space, usually resulting in a better classification.

However, a common problem with above algorithms is that it is tedious and cumbersome to select appropriate tuning parameters, such as the number of principal components in SIMCA, the number of latent variables in PLSDA, or the kernel function parameters and penalty factors in SVM, etc. Selection of these tuning parameters greatly affects the performance of the model. Apart from this, the optimal parameters vary to fit different data for different algorithms. If the optional range of optimal parameters is relatively large, the parameters will usually be dependent on the samples and the robustness of the algorithm suffers. Obviously, parameter selection by trial and error or empirical methods cannot be justified scientifically. Many algorithms, such as simple grid scanning method, genetic algorithm [9], and particle swarm algorithm [10], are available to exhaustively scan for and select the optimal parameters. However, these methods require cross-validation, which greatly affects computational efficiency. According to the principle of Occam’s razor, it is better to have a simple algorithm with general applicability to different data (spectral data in this specific case) that is independent of the performance of parameter optimization. In other words, a better method should have not only a good performance, but it must also be insensitive to parameter selection for certain types of data.

Sparse algorithms have previously been used for quantitative spectral analyses [11,12], but these studies make improvements based on the framework of common quantitative analyses, such as partial least squares or ridge regression. LRSC algorithm, introduced in our study, is applied to the field of recognition, and its framework is completely different from those of the currently available algorithms. LRSC algorithm uses a simple linear regression representation framework [13] and conducts a compressed representation of the complete training set, utilizing a testing set to select samples in a training set that are most similar to the testing set. This simple method of representation not only contains the compressed sensing ideas, but it also overcomes the difficulty of working out the sparse solutions [14] by converting the problem into a convex optimization problem, similar to lasso [15,16]. Additionally, according to the characteristics of spectral data, the algorithm’s performance will not be overly reliant on the selection of the optimal parameters. In a nutshell, the algorithm proposed in this study differs from the traditional spectral-recognition algorithms such as PLS-DA, SIMCA, SVM, and ANN. To the best of our knowledge, none of the current spectral-recognition methods use the proposed framework, which combines a sparse representation of the samples with compressed sensing for linear regression in spectral recognition and classification.

2. Theory of the LRSC Algorithm

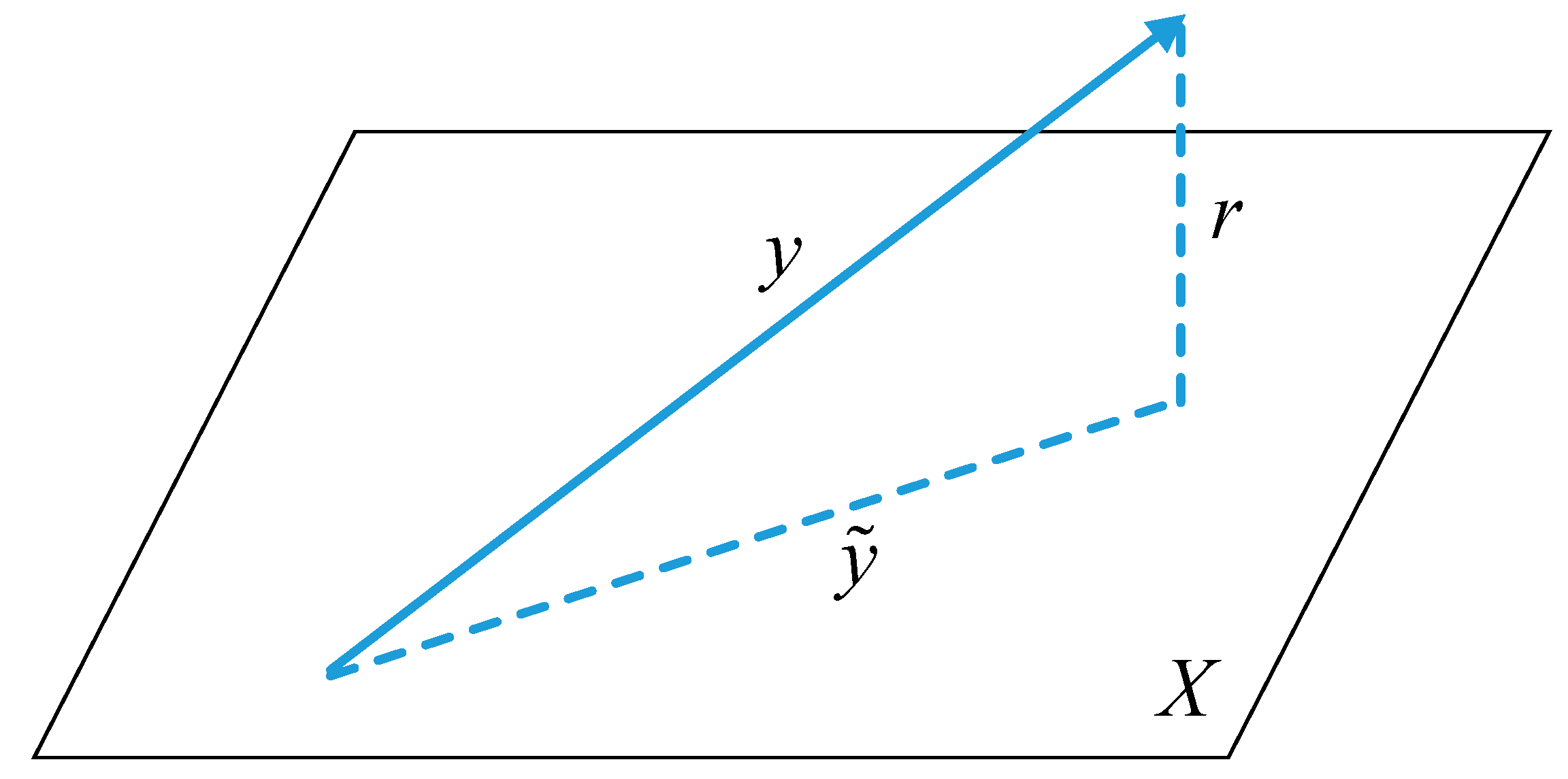
2.1. Recognition Based on Linear Regression

Unlike common linear regression models, LRSC does not use spectral data to represent label information. Instead, it conducts linear representation using the spectral data of the training samples, based on the spectra of the prediction samples. Based on the nearest neighbor (NN) method and the linear subspace of single-class objects, it then determines the linear subspace composed of single-class objects that is nearest to the prediction sample, and then performs the recognition.

As the simple three-dimensional data graph in Figure 1 shows, training sample data of the same kind can form a single-class linear subspace such as the two-dimensional plane X. If a new three-dimensional prediction sample y belongs to the class X, it can be ideally represented by the linear space of all samples in class X, i.e., $\tilde{y}$, or its distance r from this linear space should be small. When complete training samples are used for linear representation, approximate samples are selected from the training samples for linear representation using the compressed sensing approach and the sparse mode. It analyzes the linear relationships between homogeneous data from the perspective of the samples, rather than conducting regression from a variable dimensional point of view. The data can also be regressed to the label value and recognized by the least squares method. For example, in the formula $yl=X_{m\times n}\beta$, m rows are the number of the samples, n columns denote the dimension of the data (e.g., wavelength), and yl is the class label. However, for data in the form of a small number of samples with high dimensionality such as spectral data, the underdetermined equation often cannot obtain a unique solution. In this study, NN was used to select the approximate samples. The sample class with known prior information can be recognized for the spectral prediction data, and the prior information was included in the training samples.

For a specific class of target samples of spectral data, $X_i=\left[x_{i,1},x_{i,2},\dots ,x_{i,n_i}\right]\in {ℝ}^{m\times n_i}$, the spectral sample of a specific class in the training set is represented such that each sample x of data of class i is arranged in a matrix with m rows and n_i columns, where m stands for the dimensions of the spectral sample, e.g., wavelength or wavenumber, and n_i denotes the number of samples of class i. For all classes of data, all the spectral data in X can be represented as $X =\left[X_1{,X}_2{,\dots ,X}_k\right]=\left[x_{1,1}{,x}_{1,2}{,\dots ,x}_{{1,n}_1}{,x}_{2,1}{,x}_{2,2}{,\dots ,x}_{{2,n}_2}{,\dots ,x}_{{k,n}_k}\right]$. Data of class k are ordered in columns. A specific prediction sample y can then be represented by the linear framework as:

$$y={\alpha }_{1,1}{x}_{1,1}+{\alpha }_{1,2}{x}_{1,2}+\dots +{\alpha }_{k,n_k}{x}_{k,n_k}$$

(1)

where y denotes a prediction sample with m rows, one column. X denotes all the complete training samples that include all the classes, and $\alpha$ represents the regression coefficient corresponding to each training sample, which can be any real number. All samples are represented by X and all the regression coefficients are denoted by a vector ${\beta }_0$. The above expression can then be written as:

$$y=X{\beta }_0\in {ℝ}^m$$

(2)

X refers to the spectral data of information of the implicit class, and ${\beta }_0$ is the regression coefficients, expressed in the form of a vector. Theoretically, for the prediction samples, the training samples of the same class can perform linear regression, i.e., the prediction samples are in the same linear space of a certain class of training samples. There will then be a suitable solution to ${\beta }_0$. According to the sparse classification method, except for the corresponding regression coefficient of the same class, the other regression coefficients of an ideal ${\beta }_0$ are zero, i.e.,

$${\beta }_0={\left[0,\dots ,0,{\alpha }_{i,1},{\alpha }_{i,2},\dots ,{\alpha }_{i,n},0,\dots ,0\right]}^T\in {ℝ}^n$$

(3)

2.2. Sparse Solution of the Regression Coefficient

The general sparse solution mainly recognizes which class one sample belongs to on the basis of the NN or nearest subspace (NS) method. Since spectral data are typically in the form of a small number of samples of high dimensions, this linear system can be regarded as an overdetermined equation that can produce a unique but inaccurate solution, which mainly calculates the solution by the minimum $l^2$-norm:

$$\left(l^2\right):{\widehat{\beta }}_2=\mathrm{argmin}{\Vert \beta \Vert }_2 \mathrm{subject}\mathrm{to} X\beta =y$$

(4)

where ${\Vert ·\Vert }_2$ denotes the second-order norm of this vector. In case of the second-order norm, the solution of ${\widehat{\beta }}_2$ is not very sparse, which does not have a positive effect on classification recognition. To determine the sparse solution, according to the definition, the zero-order norm of the space will be minimized by solving the linear Equation (5)

$$\left(l^0\right):{\widehat{\beta }}_0=\mathrm{argmin}{\Vert \beta \Vert }_0 \mathrm{subject}\mathrm{to} X\beta =y$$

(5)

where ${\Vert ·\Vert }_0$ denotes the zero-order norm of this vector. However, there is no effective method to directly determine this zero-order sparse solution [17]. With the development of knowledge about sparse representation and compressed sensing, the minimization of the $l^1$-norm can be used to minimize the $l^0$-norm [18]. As shown in Equation (6), this problem can be transformed to a linear programming problem.

$$\left(l^1\right):{\widehat{\beta }}_1=\mathrm{argmin}{\Vert \beta \Vert }_1 \mathrm{subject}\mathrm{to} X\beta =y$$

(6)

Considering the noise of this linear system, a noise term can be added to Equation (7), transforming it to:

$$y=X{\beta }_0+e$$

(7)

where e denotes the noise of the predicted spectral data. Equation (8) tries to solve the following optimization problem for a solution of Equation (7):

$$\left(l_s^1\right):{\widehat{\beta }}_1=\mathrm{argmin}{\Vert \beta \Vert }_1 \mathrm{subject}\mathrm{to} {\Vert X\beta -y\Vert }_2\le \epsilon$$

(8)

where $\epsilon$ is a value used to represent the upper limit of fault tolerance in this linear system [18], which determines the regression of the training samples to the prediction samples under noise tolerance. As discussed above, for such highly dimensional spectral data, the linear system itself is over-determined and can have a unique solution. To determine the sparse solution to this problem, we can solve this equation by regarding it as an underdetermined equation [19], which can be solved by methods such as homotopy and proximal gradient. Here, homotopy was used to solve this optimization problem. As the noise was considered, the basis pursuit de-noising (BPDN) model was used, as shown in the following Equation (9):

$$\underset{\beta }{\min }\frac{1}{2}·{\Vert y-X\beta \Vert }_2^2+\lambda {\Vert \beta \Vert }_1$$

(9)

where λ denotes the normalized parameter, the value of which ranges from 0 to 1. This optimization problem can be transformed into a quadratic programming problem. We omit the details of the solution, which can be found in Reference [17].

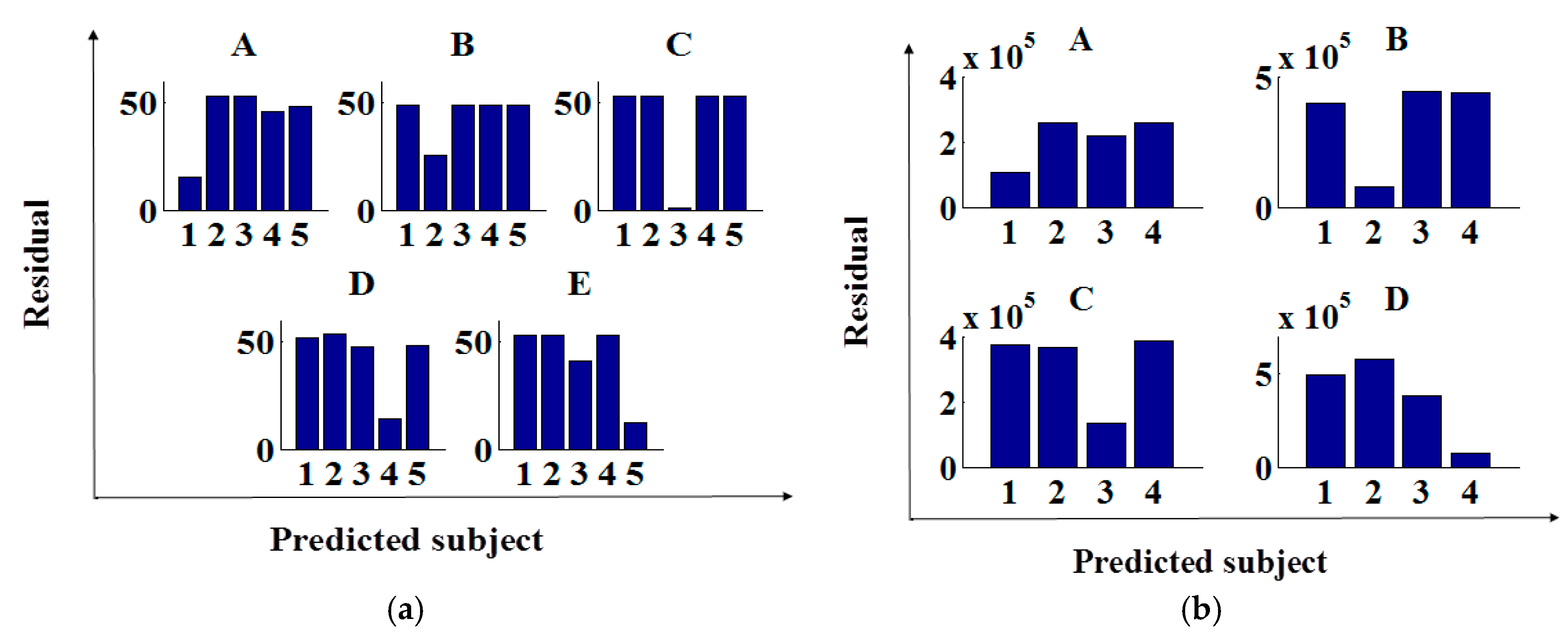
2.3. Recognition of the Prediction Samples

After the sparse solution was determined, recognition of the prediction samples was performed using a method similar to NN or NS. Specifically, it was realized by fitting the prediction samples based on the spectral data and the regression coefficient (sparse solution) that was determined:

$${\tilde{y}}_i=X{\delta }_i({\tilde{\beta }}_1)$$

(10)

As expressed in Equation (10), X denotes the spectral data of the training samples, ${\delta }_i({\tilde{\beta }}_1)$ represents the sparse regression coefficient solution, and ${\tilde{y}}_i$ denotes the prediction samples linearly estimated by one specific class of training samples. In addition, as the solution of the regression coefficient is sparse, it is possible to represent the prediction samples with training samples of the same class. The second-order norm of the residual between the estimated and actual prediction samples is calculated, and the attributes of the samples are judged according to the principle of the residual norm being the minimum, that is, the testing sample should belong to the same class label as the corresponding estimated sample giving the minimum residual norm, as shown in the following Equation (11):

$$\underset{i}{\min }{r}_i\left(y\right)={\Vert y-{\tilde{y}}_i\Vert }_2$$

(11)

As mentioned above, the LRSC algorithm first uses a linear framework to represent all the training samples, and obtains the regression coefficient by determining the sparse solution. It then estimates the prediction samples according to the regression coefficient, and outputs a final result consisting of the class with a minimum residual norm between all the estimated and real prediction samples.

The complete LRSC algorithm was calculated as follows:

(1)

Input training spectral samples and training label and a predicted sample.

(2)

Calculate the regression coefficient β₀ (sparse solution) of the predicted sample for the training samples.

(3)

Calculate estimated prediction sample ${\tilde{y}}_i$ based on each category of training data and regression coefficient β₀.

(4)

Calculate the residuals of the estimated/predicted sample from each category ri.

(5)

Output the predicted label i.

3. Data and Software

3.1. Datasets

The first dataset was the infrared spectral data, which was collected by a Tensor 27 spectrophotometer (Bruker, Inc., Ettlingen, Germany). It contained sample data for five classes of Tegillarca granosa, four of which were polluted by lead (Pb), copper (Cu), cadmium (Cd), and zinc (Zn) heavy metals in varying concentrations, and one class consisting of healthy (non-polluted) Tegillarca granosa. Each class had 30 samples. Heavy metal pollution can lead to changes in components of body tissues such as proteins, enzymes, and lipids etc. Each heavy metal can have its own unique influences and toxicological profiles, and hence it is important to recognize specific classes of heavy metal pollution [20]. Reference [20] can be referred to for specific data descriptions and further details.

The second dataset was LIBS data obtained by developed equipment (composed of a Q-switched Nd:YAG laser with a spectrometer). The LIBS data was acquired from another batch of four classes of Tegillarca granosa samples. Three of the classes comprised samples polluted by Pb, Cd, and Zn heavy metals in a certain concentration range and one class of healthy (non-polluted) samples. Each class included 30 samples. The body of a Tegillarca granosa, being a biological sample, contains a large number of organic as well as inorganic elements, and, consequently, the corresponding LIBS data contained massive amounts of information. In addition, the LIBS data also had large dimensions, reaching tens of thousands. To further increase the complexity, the same heavy metal elements in different valence states lead to many spectral lines. The LIBS data were often also affected by base-line drift [21,22], a problem commonly seen in spectral analysis, and they were susceptible to noise as well. These difficulties brought substantial challenges to the recognition algorithm in classification recognition. For specific data descriptions, please refer to Reference [23].

3.2. Software

LRSC algorithm was used in order to examine its classification performance for infrared spectral data and LIBS data, and it was compared to the performances of other classification algorithms such as PLSDA, SIMCA, ANN, RF, and SVM. The sparse solution was implemented using L1-Homotopy package [24]; SVM used libSVM 3.20 toolbox [25]; PLSDA and SIMCA were implemented with Classification_toolbox_4.2 [26]; ANN was implemented using MATLAB’s RBF neural network; and RF was implemented with the RF_MexStandalone-v0.02 toolbox [27]. All code used in the experiment was written on MATLAB 2012a.

3.3. Parameter Setting

Two thirds of the samples were randomly chosen from the two datasets as the training set, and the remaining 1/3 of the samples were used as the testing set. This data division operation was randomly executed 50 times, and the average recognition rate was taken as the final result. Algorithms like Duplex and Kennard-Stone were not used to classify the samples for training, although in this case it was possible to know the training samples as much as possible to improve the prediction samples [28]. Our only purpose was to horizontally compare the recognition effects of different algorithms, and not to improve the recognition rate. Therefore, the operation of division was randomly executed 50 times to calculate the average recognition rate.

For parameter optimization of PLSDA, the latent variables with numbers less than 20 were cross-validated with 10-fold venetian blinds, and the data were standardized using the autoscaling method (centralization and normalization), and then linearly recognized. As for SIMCA, the principal components with numbers less than 20 were cross-validated with 10-fold venetian blinds using the training set. ANN used the RBF neural network to conduct the training according to the minimum number of neurons, with the implementation target being 0 and the transfer constant being 1. RF adopted the bagging law to establish 500 trees to form the forest, with the square root of the dimension of the original data as the max features of the tree. SVM used the radial basis kernel and selected the normalized parameter c and the kernel function parameter g by optimizing in {2⁻⁵, 2⁻⁴, …2⁰, …2⁴, 2⁵}, using the grid method. To predict the classification performance, parameters with the optimal cross-validation results of the training set each time were selected to establish the model for sample prediction.

4. Results and Discussion

4.1. Parameter Selection of the LRSC Algorithm

LRSC algorithm requires two parameters while solving the sparse solution. One of these parameters is λ in Equation (9). Similarly to the normalized parameter in ridge regression, this parameter must be considered in the optimization problem. However, when it is actually applied to spectral data, there is no need to emphatically optimize it. According to the literature [29], its cross-validation error can be expressed as:

$$C\left(\lambda \right)=\frac{1}{m}{{\displaystyle \sum }}_{k=1}^K{\displaystyle \sum }_{i\in F_k}{\left(y_i-{\widehat{f}}_{\lambda }^{-k}\left(x_i\right)\right)}^2$$

(12)

where m and K denote the total number of samples and K-fold cross validation respectively, while F_k denotes the k subset. In addition, $y_i$ and ${\widehat{f}}_{\lambda }^{-k}\left(x_i\right)$ denote the one dimensional real value and estimated value modeled by dividing by the k-th subset, respectively. As can be seen from Equation (12), the selection of λ affects the value of C(λ). Here, the value of C(λ) was the average of the quadratic sum of the error of each variable. However, for the LRSC method, for spectral data with high dimensions, i.e., a large value of m (up to thousands or even tens of thousands of dimensions), the quadratic sum approaches a small value. Consequently, the C(λ) is small and selection of λ has little effect on the result. When the LRSC method is applied, the value of λ is 10⁻³, which we will discuss in Section 4.3.

The other parameter, tolerance T, represents the fault tolerance of the termination of iteration of the BPDN problem. Different from the upper limit of the fault tolerance ε in Equation (8), it shows the rate of change of the function $f$, $f=\frac{1}{2}·{\Vert y-Ax\Vert }_2^2+\lambda {\Vert x\Vert }_1$. If this rate is greater than T, the tracking process will be terminated. Figure 2 shows the sparse coefficients obtained according to different T values when the regression coefficients of the prediction samples are solved under a certain division of samples.

In Figure 2, A, B, C, and D denote the distribution of regression coefficients when T is 10⁻¹, 10⁻², 10⁻³, and 10⁻⁴ respectively. The x axis represents the training samples and the y axis stands for the regression coefficient value for each of the samples. Each regression coefficient has 100 dimensions, corresponding to the 100 training samples, and, under the condition of known prior class locations (there are in all five classes with 20 samples for each class, separated by dashed lines), the sparse distribution of the regression coefficient determines that the prediction samples are linearly represented by the training samples at the corresponding locations. The figure actually shows the optimization results of the first class of prediction samples under different fault tolerances. As can be seen, selection of different values of T had little impact on regression coefficients for the spectral data but it affected the sparseness degree of the sparse solution. In fact, for the spectral data, being highly dimensional data, as stated earlier, weakens the influence of this parameter on the performance of the algorithm to some extent. According to the definition of the rate of change of this objective function, the smaller the value of T, the smoother the convergence of the overall objective function. Here, parameter T was set to be 10⁻¹ in LRSC algorithm.

4.2. Recognition of Different Spectral Data

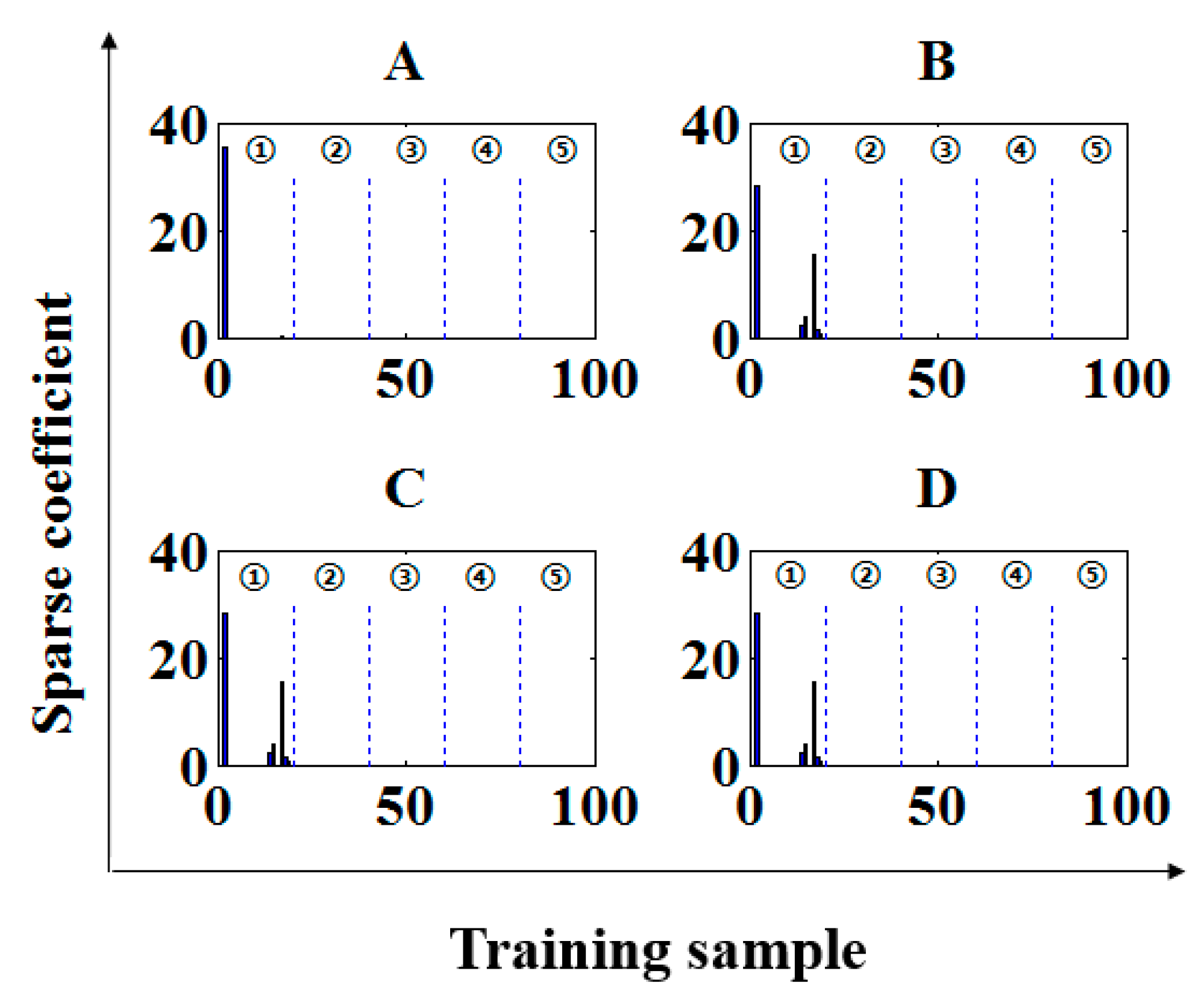
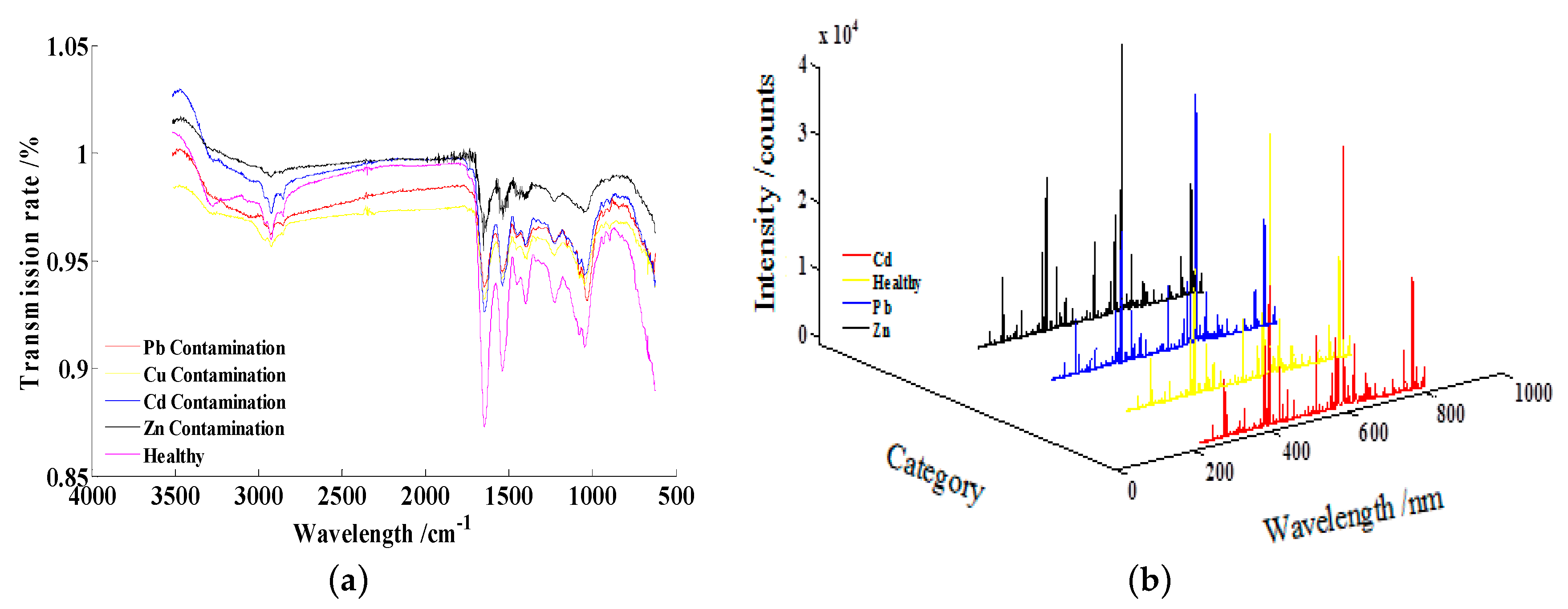
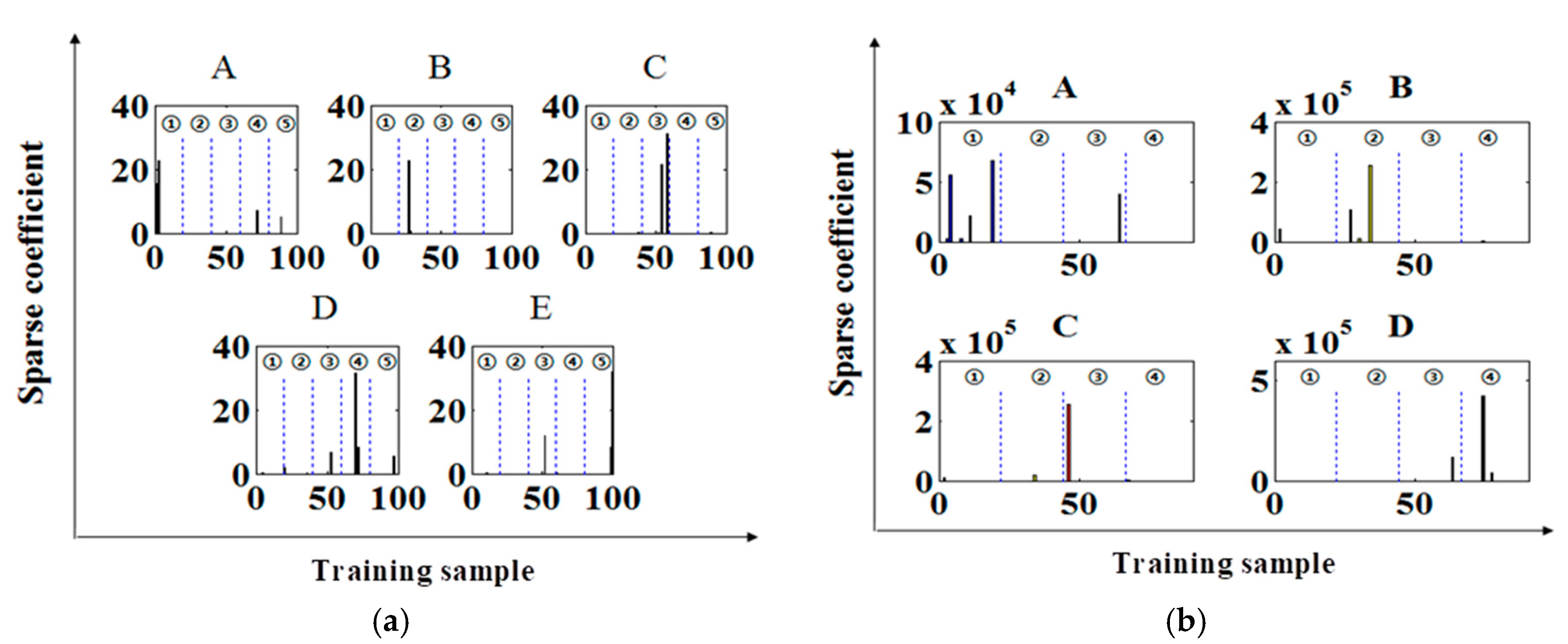
4.2.1. Infrared Spectral Data of Tegillarca Granosa Polluted by Heavy Metals

Figure 3a shows infrared spectral data for one healthy and four polluted classes of Tegillarca granosa. Figure 4a shows regression coefficients calculated for the test samples of the infrared spectral data for Tegillarca granosa polluted by heavy metals, which were taken from each of the five classes of the samples as the prediction samples to be used in the experiment. The dashed line divides each of the 20 training samples into a particular class of data (a total of five classes of data in all). According to the characteristics of the sparse algorithm, the regression coefficient reflects in the corresponding training sample sets which has a relatively large value. In other words, the size and distribution of the value reflects its degree of similarity with the modeling samples, and, on the other hand, it is also relatively sparse to the regression coefficients of other classes of samples. Even though other classes of samples might also be close to the target sample, at the time of judgment, according to Equation (11), the target with the minimum residual is selected as the prediction output. Therefore, there must be such a target class to judge which classes the prediction samples belong to according to the residual between the estimated prediction samples in some linear space and the actual prediction samples, as shown in Figure 5a. In this figure, the x axis denotes the estimated classes of the prediction samples, the y axis stands for the residuals of the prediction samples, and graphs A, B, C, D, and E represent the prediction samples that actually belong to the first through fifth classes respectively. As indicated by Figure 5a, when the actual samples of each bar graph are consistent with the prediction samples, the residual of the training samples for that class is smaller than those of other classes, i.e., the corresponding classes of different prediction samples can all be recognized by their residual values, and the estimated residuals of the prediction samples in the linear space of the target are also significantly different from those of the other four classes.

LRSC was compared with the common SIMCA, SVM, ANN, RF, and PLSDA algorithms for recognizing the data of Tegillarca granosa polluted by different heavy metals, with the results shown in

Table 1. Recognition rates of different methods using infrared spectral data and LIBS data.

Method	IR	LIBS
LRSC	0.98 ± 0.02	0.81 ± 0.05
SIMCA	0.88 ± 0.06	0.08 ± 0.06
SVM	0.80 ± 0.05	0.25 ± 0.00
ANN	0.68 ± 0.08	0.25 ± 0.00
RF	0.65 ± 0.09	0.52 ± 0.07
PLSDA	0.97 ± 0.01	0.46 ± 0.09

. All the parameters involved here were the optimal parameters of the cross-validation of the corresponding training samples, and the recognition result was the average and the corresponding variance of the testing set after a random division of the samples that was executed 50 times.

Compared with other algorithms, LRSC, SIMCA, and PLSDA showed good classification performance regarding infrared spectral data. Their average recognition rate exceeded 80%, with LRSC reaching 98% and PLSDA 97%. As there are different ways to divide the samples, the recognition rate showed some fluctuation. The recognition rates of LRSC and PLSDA were comparatively stable with a very small variance. ANOVA (analysis of variance) was used to test the differences between the recognition effects of different classification algorithms. The classification performance of LRSC was found to be significantly different from that of SIMCA, SVM, ANN, and RF. The p values of SIMCA, SVM, ANN, and RF were 0.01, 7.10 × 10⁻⁵, 3.87 × 10⁻⁵, and 4.35 × 10⁻⁵, respectively (the smaller the p value, the more significant the difference). However, the p value of both LRSC and PLSDA was 0.35, indicating no significant difference between their recognition rates. Nevertheless, a very important problem is that the recognition effect of PLSDA was achieved every time, based on the optimal parameters obtained by the cross-validation after the division of the samples, that is, the optimal parameters were almost different in each the division of the samples. Therefore, the recognition rate of PLSDA in the table is not steady, and the parameters will be discussed further in Section 4.3.

4.2.2. LIBS Data of Tegillarca granosa Polluted by Heavy Metals

Figure 3b shows the LIBS data of one class of healthy and three classes of polluted Tegillarca granosa. The LIBS data had obvious noise signals with a relatively small amplitude, and the amplitude of some noise was less than zero. This is because the organism has both organic components and inorganic components, leading to complicated information in the general LIBS data. To improve the data-processing speed, a threshold was set as the obvious noise limit. This was defined as the absolute value of the averages of the minima of each dimension. If one specific variable of all the samples was less than this threshold (12.52), then this variable was removed.

This eliminated significant noise variables and improved the algorithm’s recognition and execution rates. The original spectra had 30,267 dimensions, of which 4193 remained after significant noise was removed.

The remaining spectral variables were recognized in LRSC. Each time, one sample was selected from each of the four classes of samples as the prediction samples. Based on the sparse regression coefficients of the LIBS data of different classes of Tegillarca granosa, as shown in Figure 4b, the x axis denotes the position of the corresponding training samples, with the areas of different classes divided by the dashed line, and the y axis represents the amplitude of the corresponding regression coefficients. As the amplitude of the LIBS data was much larger than that of the infrared spectral data, the range of the corresponding regression coefficients was also relatively large. A, B, C, and D represent the four classes of actual prediction samples. It can be seen from Figure 4b that the areas where the amplitude of the estimated prediction samples was relatively high correspond well to the actual classes of prediction samples.

Figure 5b shows the residual between the estimated and actual prediction samples, where the x axis denotes the possible classes of prediction samples and the y axis stands for the residual estimate corresponding to each class of training sample. Similarly to Figure 5a, the class with the minimum residual estimate among the prediction samples was consistent with the actual class of prediction samples. However, unlike Figure 5a, the differences between classes were less significant than those of the infrared spectral data, and this is reflected in the ratio of the lowest amplitude value to the other amplitude values, so the corresponding recognition rate is lower than that of the infrared spectral data.

The second column of Table 1 shows the recognition results of other common classification methods, which were inferior to the results of IR spectral data. The average accuracy of SVM and ANN was only 25%, indicating that it is almost impossible for them to correctly recognize the data. However, the recognition rate of SIMCA was only 8%, which does not comply with statistical theories. SIMCA defined four models for the four classes. When a prediction sample is projected into the four subspaces corresponding to the training samples, if we define whether the prediction sample satisfies the training set of each subspace, the prediction sample may satisfy none of the subspaces or satisfy several classes of subspaces simultaneously. When this occurs, SIMCA can make the wrong judgment, and, therefore, its recognition rate does not meet the statistical theories. In addition, compared with infrared spectral data, LIBS data have a higher dimension and there are many characteristic spectral lines of a certain atom, making LIBS data relatively complicated. RF often needs to build a large number of trees to accomplish this task. As a result, the recognition effect of RF is not ideal. Though LIBS data are susceptible to noise and are often affected by problems such as base-line drift [21,22], the LRSC algorithm still had good accuracy, with an average accuracy of 81% over 50 times. It can also be seen that the average recognition rate of PLSDA was only 46%, and the corresponding variance was also increased due to the complexity of the LIBS data and the defects of the optimal parameter selection.

Without preprocessing, such as extracting the characteristic spectral lines, the LRSC algorithm has no greater effect in directly recognizing the LIBS data than it does with the infrared spectral data. Nevertheless, horizontally compared with other classification algorithms, the LRSC algorithm still has certain recognition advantages and has stability that other algorithms lack, for it does not depend on parameter optimization. It is obviously more difficult to recognize the full spectral data with larger dimensions, more noise, and more complex spectral lines than to recognize the infrared spectral data. Combined with other data reconstruction methods similar to the spectral changes, the present LRSC algorithm is a new idea in the field of spectral data classification.

4.3. Influences of Parameter Setting on Recognition Performance

As indicated by the parameter analysis of the LRSC algorithm in Section 4.1, being different from other algorithms, its classification process depends little on parameter optimization. Theoretically, when the sparseness degree changes because of the parameter (such as the parameter T) setting, e.g., when the sparseness degree increases, perhaps only one or two non-zero solutions can be found. The positions of these solutions recognize the training samples to which the prediction samples are most similar, and the corresponding classification labels can still be found. In the case of the infrared spectral data under one sample division, in Figure 6a, T and λ were selected as the parameters for LRSC (T: 10⁻¹, 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶; λ: 10⁻¹, 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶, 10⁻⁷, 10⁻⁸). With the grid method used to select the parameters, the recognition rates changed slightly, both reaching more than 90%. Similarly, in Figure 6b, different parameters were used, which, again, did not have a significant impact on the classification of the LIBS data. Even the value of λ made little contribution to the accuracy.

For the optimal parameters of the 50 experiments of SIMCA, the parameter optimization is similar to that of principal component analysis, except that it gives a principal component coefficient by learning each class of samples. As verified by the calculation, the optimal values of SIMCA’s five parameters varied from 2 to 10, with a relatively large variance in 50 experiments of random division samples. SIMCA’s main problem is that when the number of classes increases, there are too many parameters. When the algorithm’s parameters are uncertain, increasing the number of classes obviously increases the degrees of freedom and the uncertainty of the classification results. For example, under one specific division of IR samples, the five optimal parameters of SIMCA were 3, 6, 6, 8, and 10, respectively. The recognition rate of the prediction sample set, obtained with its optimal parameter, was 92%. If the five optimal parameters had been 3, 7, 3, 2, and 3 under the previous division of samples, then the recognition rate would only have been 78%. Therefore, parameter selection has a great influence on multi-parameter algorithms such as SIMCA, with the difference of the recognition rate exceeding 10%.

Unlike SIMCA, which learns different classes, PLSDA has only one parameter, although it is also a spatial-projection algorithm. Theoretically, a large parameter does not necessarily guarantee a good recognition effect. The known samples can be well-trained when the parameter is larger and the model is more complicated, and this is likely to cause over-fitting during prediction. As a matter of fact, for IR data, the number of optimal latent variables of PLSDA fluctuates between 7 and 11, with the average being 9.2 and the standard deviation being 1.3. Regarding LIBS data, the average number of optimal latent variables of PLSDA is 13.4 and the standard deviation is 2.6. In practice, when dealing with some prediction samples, the optimal latent variables of the prior cross-validation usually need to be selected. When the conditions are very close, the choice of number of principal components is non-negligible, which greatly affects the prediction results. Therefore, in the case of high dimensions, the larger the number of principal components, the broader the range of the optimal principal components. However, computational efficiency is drastically reduced during cross-validation to select the optimal parameters. Therefore, considering efficiency and stability, LRSC is obviously a better choice for parsimony.

Nonlinear SVM is often appropriate for spectral data, which involves selection of the kernel function and corresponding parameters. If we choose the more common RBF kernel, we must consider the two parameters c and g, where c represents the penalty coefficient that characterizes the algorithm’s nonlinear fitting ability, and g denotes the radius of the kernel function which affects its shape. The effect of SVM in Table 1 is not as good as that of other algorithms, and the problem can be found through a careful analysis of its parameter optimization process. In parameter optimization, we searched for the optimal parameters in range {2⁻⁵, 2⁻⁴, …2⁰, …2⁴, 2⁵} using the grid method, but the parameters did not reflect well the characteristics of the spectral data with high dimensionality. The optimal parameters obtained in the optimization process show that c reached the preset upper limit of the grid method, and therefore the optimal parameters were not good. However, the prior information of model parameters for data with unknown spectra is not complete, especially for highly dimensional data, so there will be more uncertainty. If the search range is expanded or the search step length is refined to optimize the parameters, the algorithm’s workload will increase. When the search range of the parameters is expanded and the optimal parameters of the infrared spectral data are worked out, namely c = 2048 and g = 0.0313 in this case, the correct recognition rate of SVM can reach more than 90%. Therefore, SVM is another algorithm that relies heavily on the parameters.

ANN and RF do not work well. RF allows the user to select large parameters (e.g., the number of trees) without concern about over-fitting. However, spectral data have relatively large dimensions. Especially for infrared spectral data, there are strong correlations between dimensions. Therefore, a large amount of sample data is required. The data dimensions must be reduced to achieve better performance at classifying the spectral data [30]. A major drawback of ANN is its inability to interpret its inference process. It converts the inference process to numerical computation, and it can give no prior information for uncertain samples. For example, the fault-tolerant terminal conditions of iteration [31] can lead to over-fitting of the prediction samples. In addition, for highly dimensional spectral data, the regression into a class label in the form of a simple integer can cause larger errors. In conclusion, LRSC has a weaker dependence than other algorithms on the parameters. LRSC can be fairly ideal for highly dimensional data such as spectral data.

5. Conclusions and Prospects

This study introduced a sparse representation recognition algorithm based on linear regression for spectral data recognition. This classification method does not require spatial changes or feature selection of spectral data to preprocess the data, nor does it require precise parameter optimization for parsimony. The LRSC algorithm achieved satisfactory results in classifying the actual spectral data of Tegillarca granosa samples polluted by heavy metals, both for infrared spectral data and LIBS data. LRSC provides a new idea for spectral recognition, compared with the common spectral recognition algorithms.