1. Introduction
In the context of collision check and path planning in robotics and game AI, the Distance Map (DM) has been widely used as a consistent model to encode the search space [
1,
2,
3,
4,
5]. In a grid-based environment with regions of blocked cells, a corresponding DM can be constructed to provide each cell a maximal clearance value, which registers the distance from itself to the nearest obstacle. Thus, a DM can help an agent (e.g., a Non-Player Character (NPC) in the video game or a robot in the real world) with a certain safety radius to efficiently search out collision-free paths and to avoid obstacles in motion.
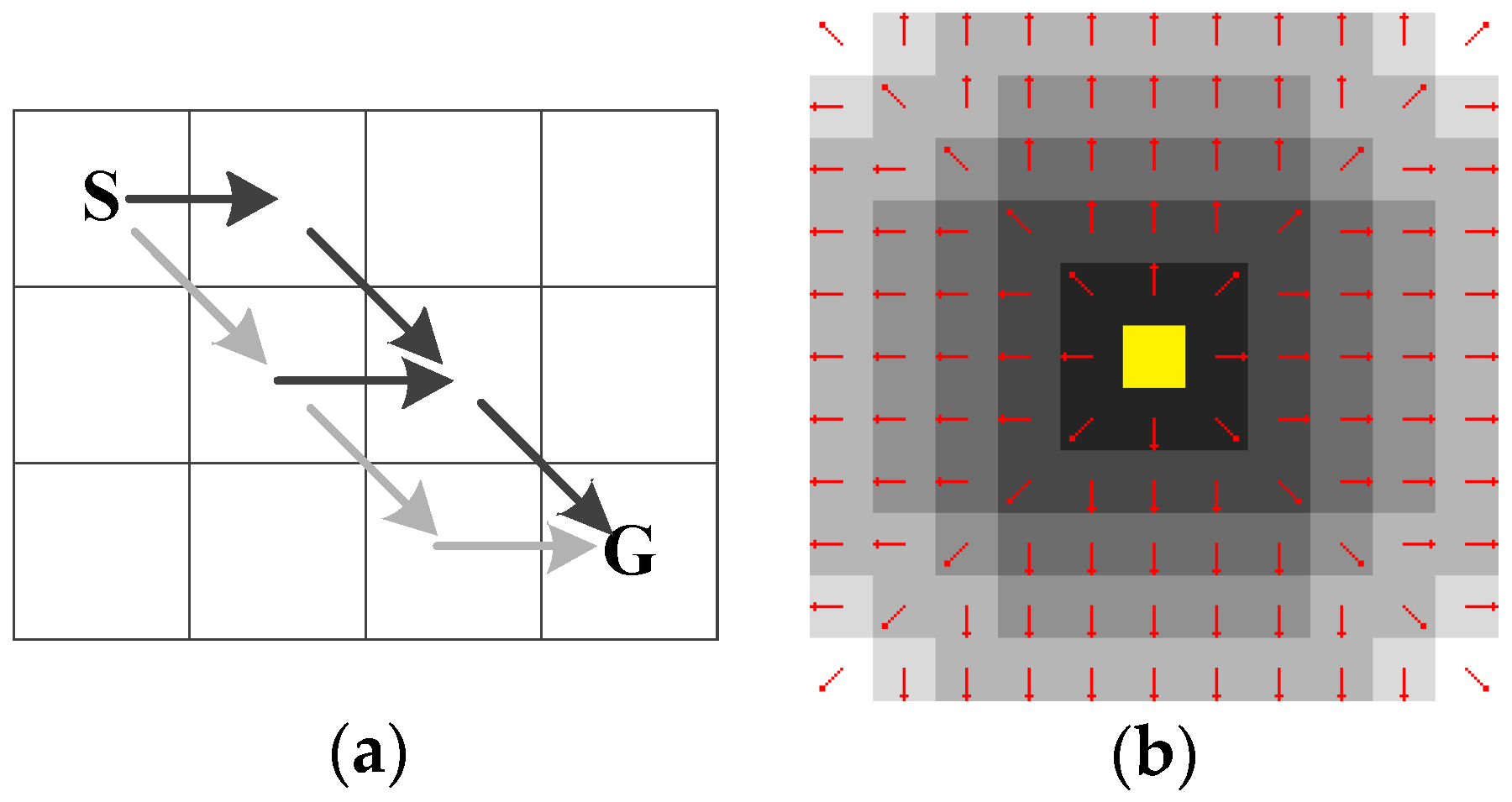
Figure 1 presents a DM constructed in an indoor environment.
In many practical applications, the underlying environments that an agent maneuvers in are often dynamic; therefore, it is necessary to reconstruct their corresponding DMs whenever changes of cell states are observed (e.g., an obstacle is inserted, removed, reshaped, or transferred). Since such changes usually occur within a relatively neighboring area around the agent, only portions of the previously constructed DM need repair. To make use of this localized feature, existing algorithms such as Dynamic Brushfire [
6] and its subsequent variants [
7,
8] aim to speed up the reconstruction by launching a wavefront from the source of the state changes to incrementally repair the distance values, rather than reconstructing the whole DM from scratch. With such a localized mechanism, only those cells that are actually affected by the wavefront need to be handled; thus, in most cases, the computation costs can be efficiently reduced.
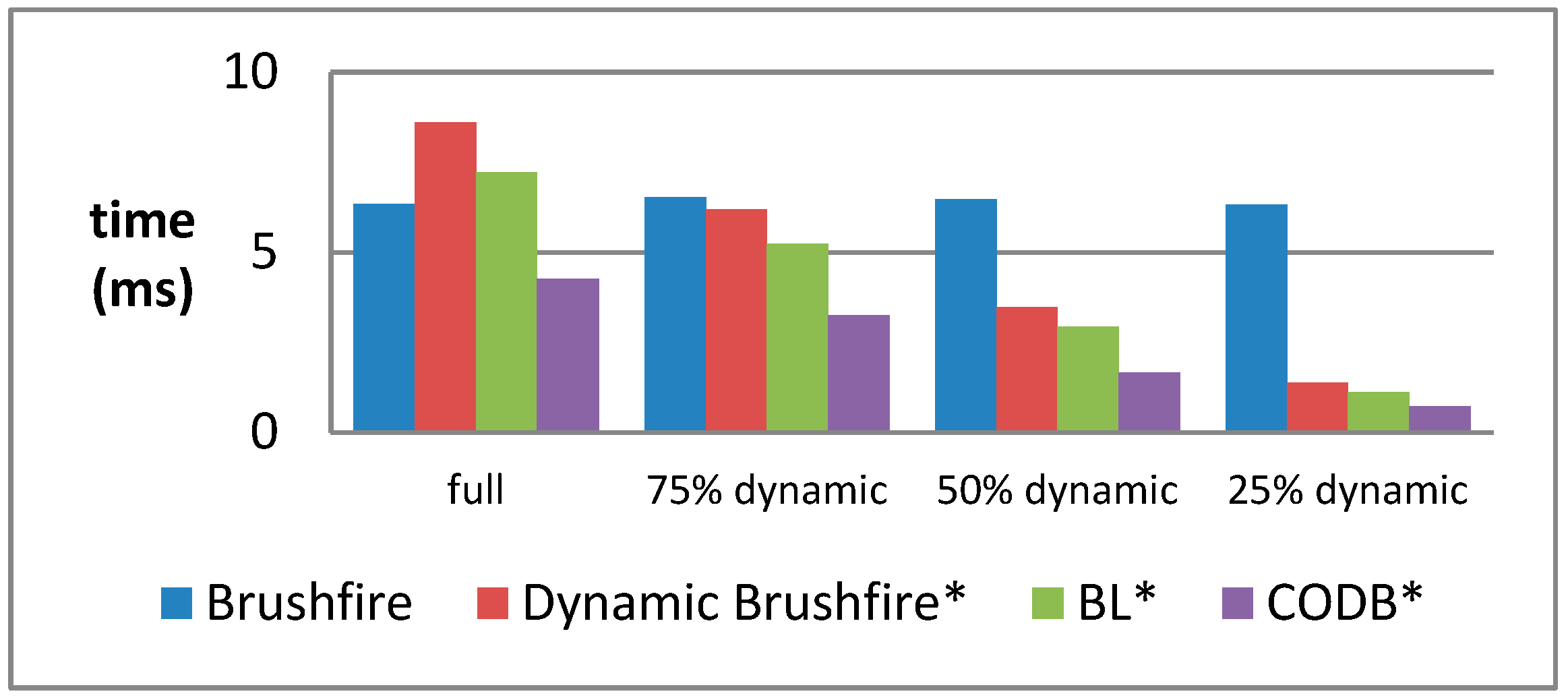
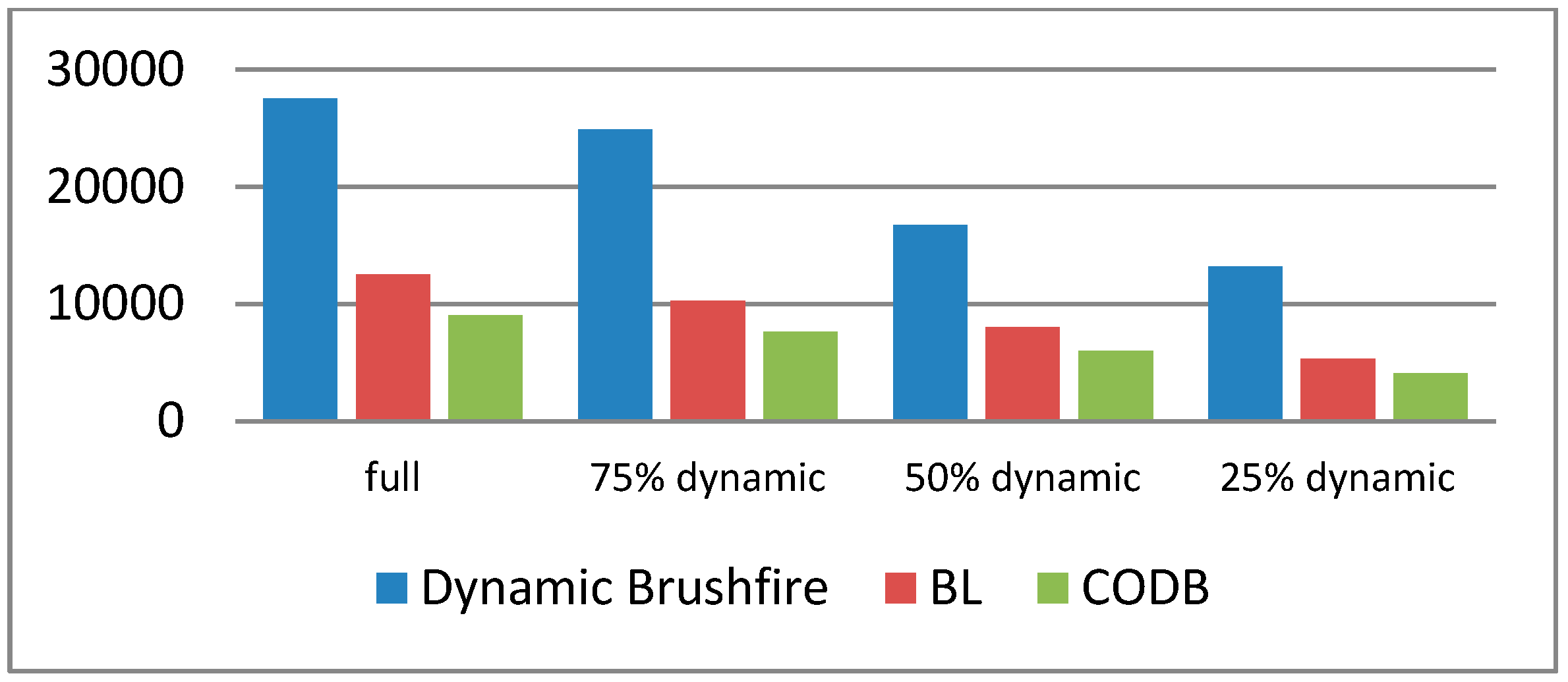
However, for all of the previously proposed algorithms, the propagation of the wavefronts simply expands all the neighbors of a processed cell without preference, and then inserts the newly affected neighbors into a priority queue, so as to prepare for the next round propagation. Such indiscriminate expansion results in a much longer priority queue and thus becomes an efficiency bottleneck. In order to reduce the number of elements which need to be sorted by the priority queue, a searching strategy, Canonical Ordering, is introduced by us to systematically choose a single route from the equivalent propagation paths.
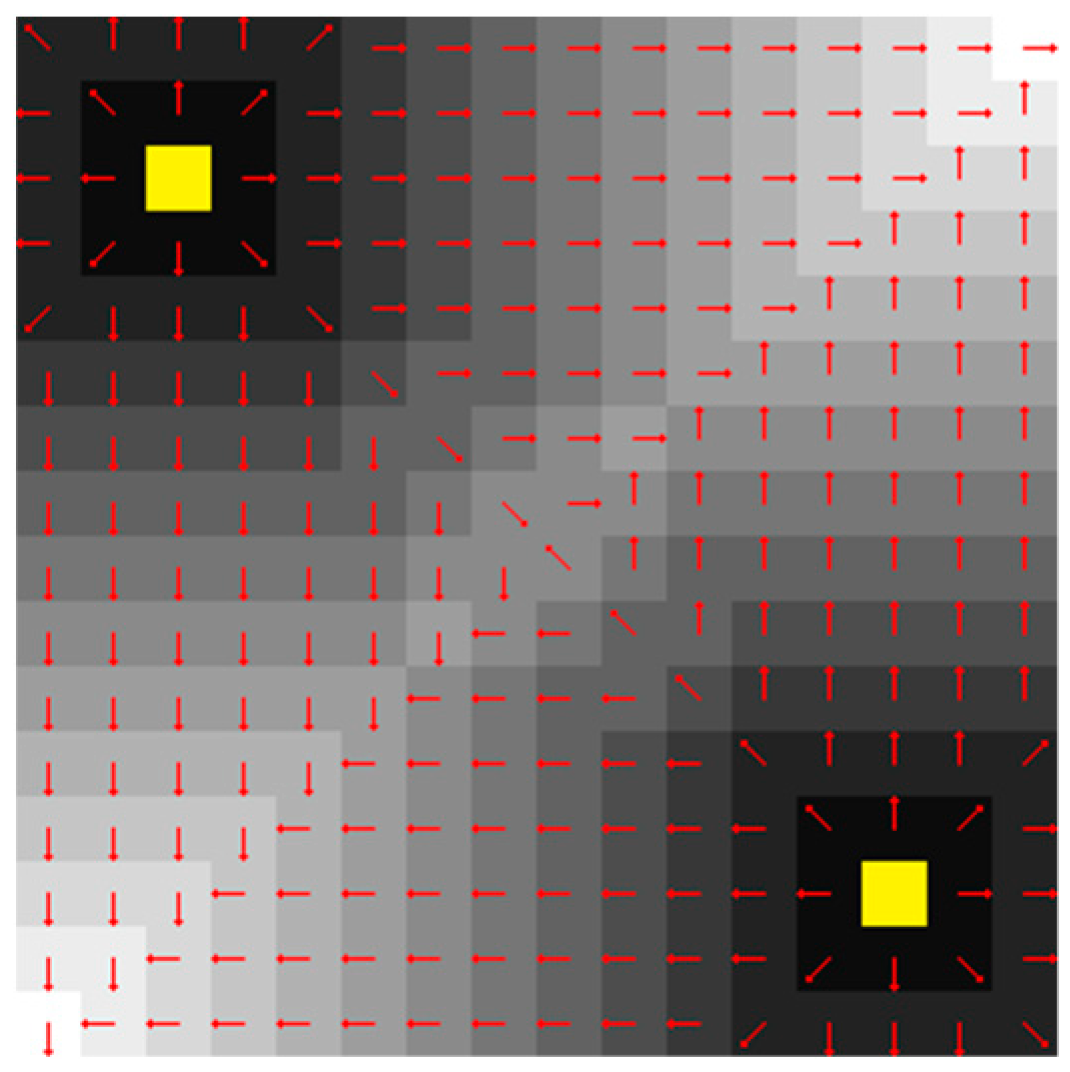
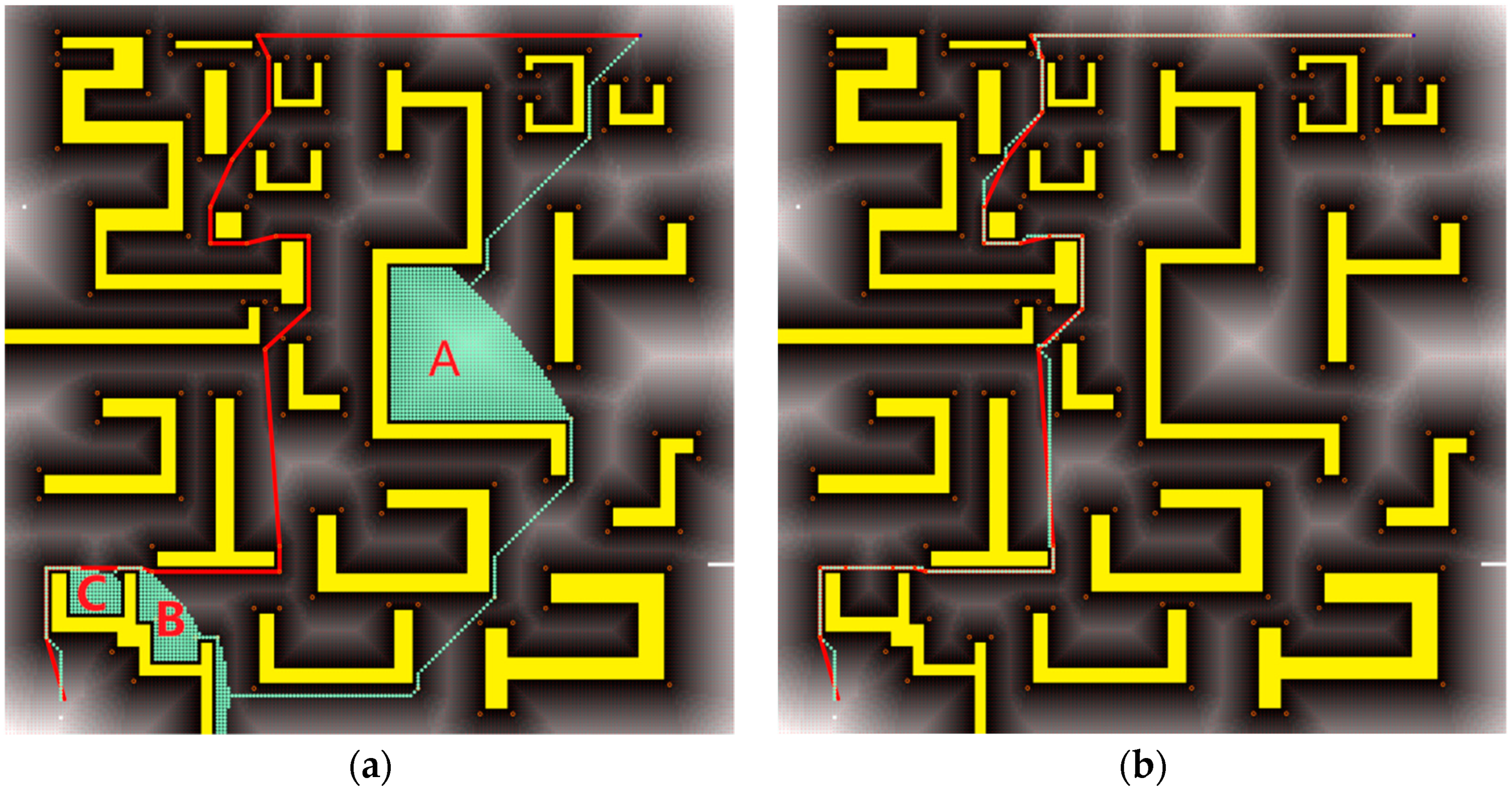
Figure 2 shows how our algorithm propagates the wavefront form the source blocked cell (denoted as yellow tiles), visiting each affected cell only once (where the red arrows denotes the propagation directions of the wavefronts). We choose the successors of an expanded cell,
s, by following two basic rules described in Nathan R. Sturtevant and Steve Rabin’s paper [
9]. That is, for a cell
s, with the propagation direction
c that was previously used to reach
s, (1) If
c to arrive at
s is one of the four cardinal directions, the only legal direction at
s for the next round propagation is
c; (2) If the
c to arrive at
s is one of the four diagonal directions which can be decomposed into two perpendicular cardinal components
c1 and
c2, the legal directions at
s for the next round propagation are
c,
c1, and
c2. We name our algorithm Canonical Ordering Dynamic Brushfire (abbreviated to CODB in the rest of this paper).
Since a DM stores the maximal clearance for each traversable cell to its nearest obstacle, operations such as collision checks can be simplified to instant look-up queries (As shown in Equation (1)). For instance, if an agent with safety radius
R> 0 is located on cell
s, then the result of the collision check is determined by Equation (1) as below (where 1 denotes collision detected and 0 denotes collision-free):
To make better use of this feature, we furthermore propose algorithms to construct DM-based subgoal graphs. The resulting subgoal graphs are sparse but adequate high-level roadmaps to enable agents who possess safety radius to search out collision-free paths in real time. In order to reduce the possibility of replanning caused by dynamic terrain changes, we introduce Learning Real Time A* (LRTA*) [
10], an algorithm for planning immediate moves at runtime, to drive the agents between subgoals connected by the high-level paths. Since each segment of the high-level paths is proved to be direct h-reachable, irrational behaviors such as trapping in local minima can be eliminated when LRTA* is iteratively applied between the direct-h-reachable subgoals (see the definition of direct h-reachable in
Section 4.1.3).
There is another space representation; i.e., grid-based Voronoi diagrams can be used as a sparse model to help agents to maximize its distance to the obstacle cells. Actually, current algorithms for building grid-based Voronoi graphs can also obtain a corresponding distance map in which each cells keeps the distance to its nearest obstacle cell [
11,
12,
13]. Although a Voronoi diagram can provide an agent with a sparser search space, its drawback is also prominent. For instance, in Multi-Agent Pathfinding Problems (MAPF) [
14,
15,
16,
17,
18,
19], a group of coordinated agents share the same Voronoi edges as their search space, thus a dense cluster of conflicts may occur, which needs to resolve during the planning process. Different from grid-based Voronoi Diagram, DM-based subgoal graphs don’t conservatively compress the search space in unnecessary narrow channels. Furthermore, the search space between each pair of the direct-h-reachable subgoals commonly reserve more spaces than Voronoi edges for a group of coordinated agents to resolve conflicts.
We provide three main contributions in this paper. Firstly, we present an algorithm, Canonical Ordering Dynamic Brushfire (CODB), to speed up the incremental update of grid-based Distance Maps (DMs). Secondly, we propose algorithms to compute DM-based subgoal graphs which are used to provide high-level, collision-free roadmaps for agents with certain safety radius. Thirdly, we verify that under the guidance of the subgoal graphs, real-time search algorithms such as LRTA* can effectively avoid local minima; therefore, the resulting trajectories can successfully coincide with the optimal solutions searched by A*. We present our algorithms both intuitively and through pseudocode, compare them to current approaches on typical scenarios, and demonstrate their usefulness for fast path planning tasks.
The outline of this paper is as follow:
Section 2 discusses related studies on DMs, Canonical Ordering, and subgoal graphs;
Section 3 gives preliminaries and notations;
Section 4 presents our algorithms both intuitively and through pseudocode;
Section 5 compares CODB to other algorithms and tests the usefulness of DM-based subgoal graph for fast path planning tasks. This paper ends with conclusions in
Section 6.
3. Preliminaries and Notation
All the algorithms studied in this paper work in planar, eight-connected grid maps with regions of obstacles consisting of blocked cells. A wavefront launched by a cell state change can propagate from one cell to its neighbor in any cardinal or diagonal directions, and the length of the cardinal and diagonal moves are 1 and
, respectively. We follow the definition of octile distance to compute the heuristic distance between any two cells in a grid map, i.e., the distance between cells
s and
s’ is computed by following Equation (2):
In Equation (2),
dx and
dy denote the differences of the 2D coordinates of cell
s and
s’. For each cell
s,
obsts maintains coordinates of the obstacle cell
so to which
s is currently closest, and
dists maintains the distance between
s and
so. The notation
dirs maintains the direction along with which s would propagate the wavefront. The options of
dirs include four cardinal directions (denoted as left = 1, up = 3, right = 5, and down = 7), four diagonal directions (denoted as up-left = 2, up-right = 4, down-right = 6, and down-left = 8), and full directions (denoted as full-dir = 0, declaring that
s is the source of the wavefront; thus, all the eight directions need to be considered in the next round propagation). The notation
raises shows if the wavefront on
s is a raise wavefront or a lower one (the differences between raise and lower wavefronts are explained in
Section 4.1.1). Given a cell
s, a direction
d, and an integer
k, the notation s’ =
s +
kd denotes a cell
s’ that is reached from
s by moving
k steps along
d. For two perpendicular directions
c1 and
c2, we have
d=
c1+
c2 to denote that the sum of
c1 and
c2 results in their corresponding diagonal direction
d.