Research on Scene Classification Method of High-Resolution Remote Sensing Images Based on RFPNet
Abstract
:1. Introduction
- (1)
- The paper proposes a multi-view scaling strategy, which is a data amplification strategy, aiming to solve the problem of the limited number of images in the current high-resolution remote sensing image datasets. The difference between the multi-view scaling strategy and other dataset amplification methods is that different parts of the labeled boxes can be cropped randomly, and four interpolation algorithms are selected randomly to stretch the scale of the image, so as to serve as the input of the neural network. This method can not only enlarge the number of datasets, but also introduce noise through interpolation, thus improving the generalization ability of the convolutional neural network constructed.
- (2)
- This paper proposes the structure of RFPNet to learn high-level visual features of high-resolution remote sensing images for scene classification. The main characteristic of the RFPNet structure is to adopt the residual block, so that the accuracy will not reduce when adding more layers to the model constructed; The fusion strategy of pooling layer feature maps is proposed to ensure the integrity of information by solving the problem of information loss in the process of pooling. In order to further improve the accuracy of the model, the paper also uses the optimization methods of Dropout, parameter norm penalty, and the moving average model, to avoid the overfitting problem caused by the limited data in the existing high-resolution remote sensing image datasets.
2. Related Work
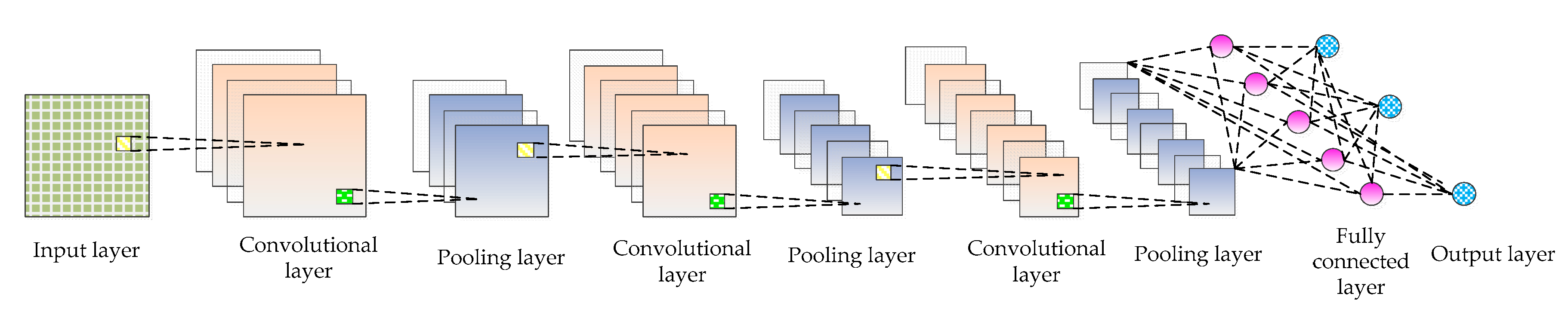
2.1. Convolutional Neural Network
- Input layer: The input layer is the input of the whole CNN. In the neural network of image processing, it generally represents the pixel matrix of the image.
- Convolutional layer: The convolutional layer is used to extract image features. Low-level convolutional layer extracts shallow features (such as edges, lines, and corners). High-level convolutional layer further learns abstract features through the input of low-level features. The convolutional layer obtains multiple feature activation maps by convolving the convolution kernel of a specific size with the previous layer, as shown in Equation (1).where represents the input image set, represents the jth feature map of the l layer, “*” represents the operation of convolution, is the ith feature map of the l-1 layer, represents the filter connecting the jth feature map of the l layer and the ith feature map of the l-1 layer, is the bias, represents the nonlinear activation function that can solve problems that cannot be solved by linear models. The activation functions commonly used include sigmoid, tanh, ReLU, etc. The calculation equation is as follows:
- Pooling layer: The introduction of a pooling layer is to reduce dimension and abstract the input image by imitating the human visual system. By sampling the convolved feature maps, the useful information of the image is preserved and the redundant data is removed, thus effectively preventing the overfitting problem and speeding up the computation speed. What’s more, the pooling layer has feature invariance which can make the model more concerned with the presence of certain features rather than the specific location of the features and tolerate some small displacement of features. There are generally two kinds of operations: maximum pooling and average pooling. The calculation equation of pooling layer is as follows:where is a sub-sampling function, represents the sub-sampling coefficient, represents the jth feature map in the l layer, is the ith feature map in the l-1 layer, is the bias, and represents the nonlinear activation function.
- Fully connected layer: The fully connected layer is usually used in the last layers of the network, which can combine the information transmitted in the former layers to achieve the explicit expression of classification.
- Output layer: CNN’s input image is passed over the layers of a convolutional layer, pooling layer, and fully connected layer, and it is finally passed through the classifier in the form of a category or probability. The logistic regression model is commonly used for binary classification problems, while the Softmax classifier is commonly used for multi-classification problems. The Softmax classifier is essentially a normalized exponential function. Assuming that the training set is composed of m tag samples , where . Supposing that the input data x is given, the probability value of j of each category needs to be estimated by using the hypothesis function whose equation is as follows:where is the parameter and the expression plays the role of normalization and ensures that the sum of probabilities of all categories is 1. The loss function of the whole system iswhere the function is defined as: , , . The gradient equation of the loss function is as follows:The parameter is updated by Equation (9), and the probability that x is classified as j is determined by Equation (10).
2.2. The Application of Convolution Neural Network in Remote Sensing Image Scene Classification
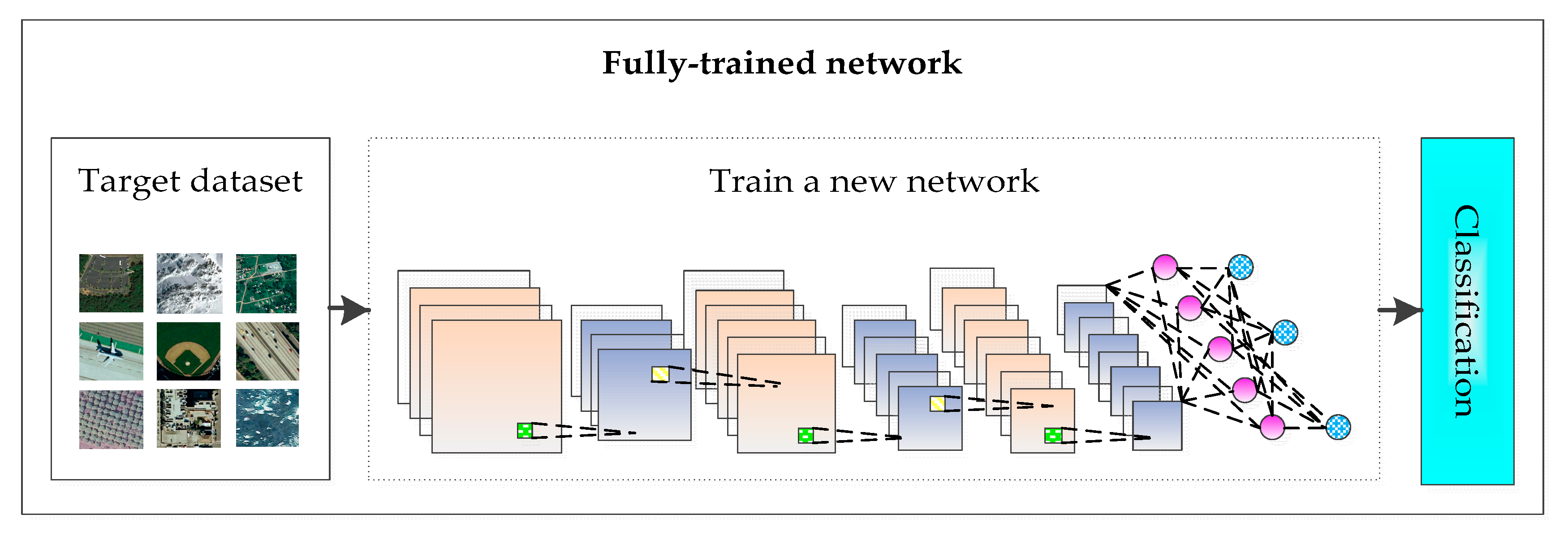
- Full-trained network: A new CNN is designed and trained based on the currently shared remote sensing image scene dataset, as shown in Figure 2.
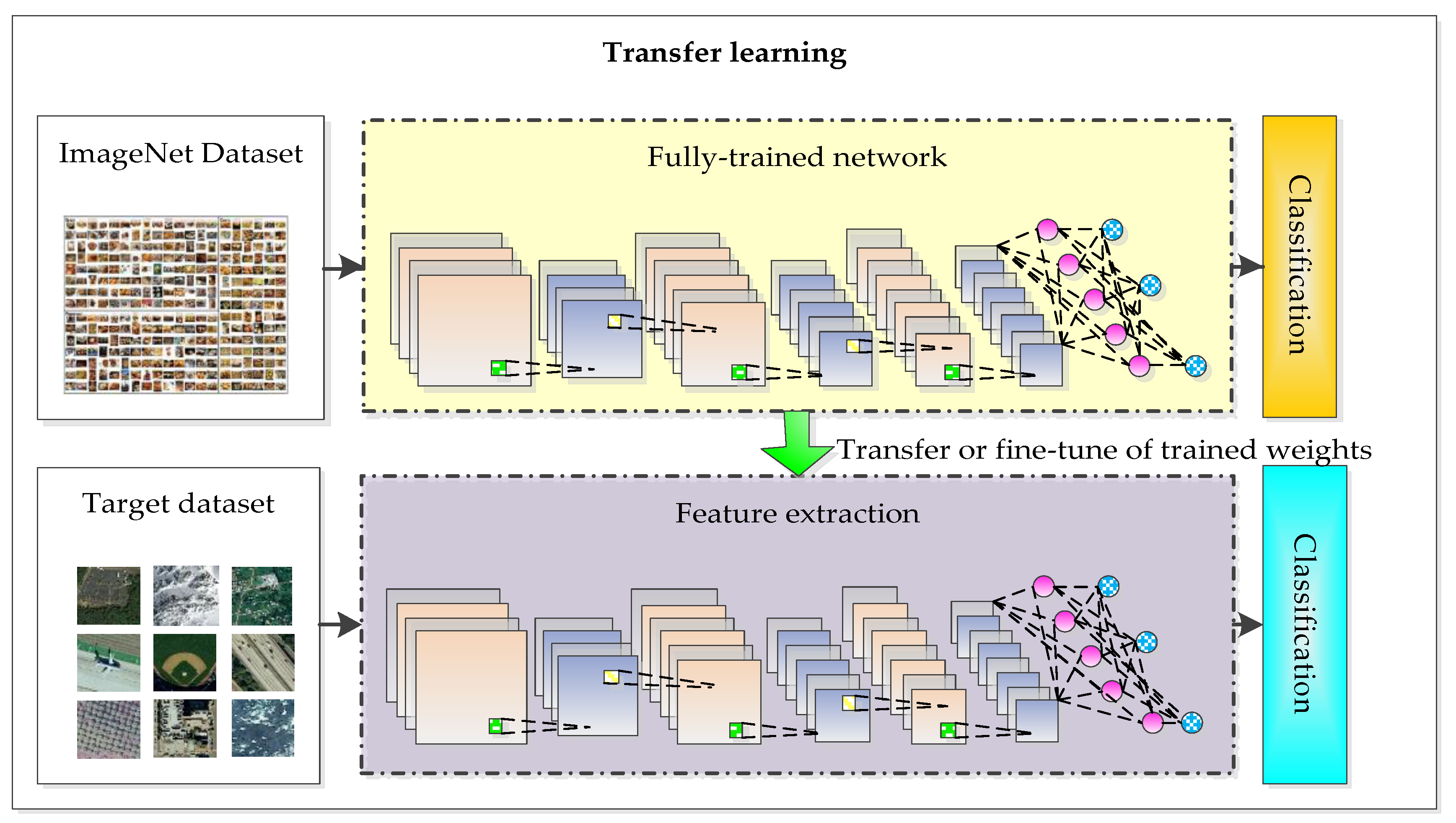
- Transfer learning: The deep convolutional neural network model based on the large-scale image dataset is applied to remote sensing image scene classification directly or by fine-tuning, as shown in Figure 3.
3. Proposed Method
3.1. Multi-View Scaling Strategy
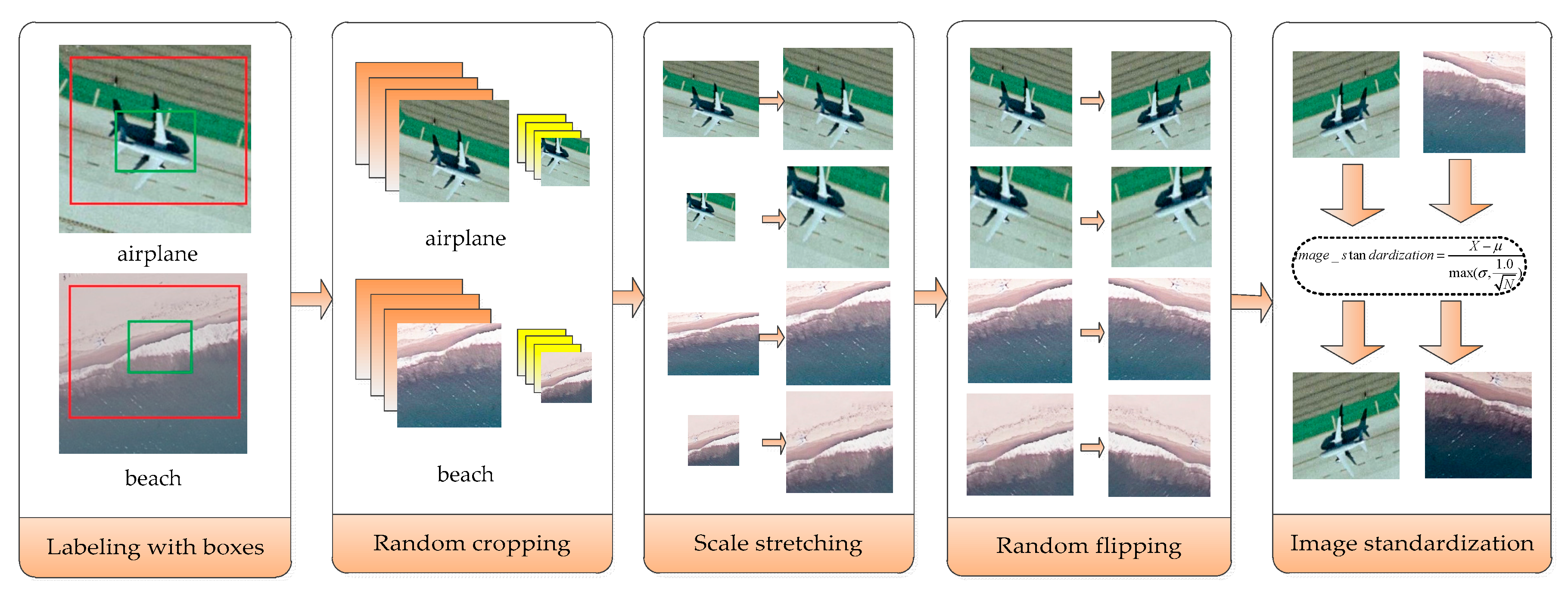
- Labeling with boxes: In order to extract different information from different perspectives, high-resolution remote sensing images are labeled with two boxes.
- Random cropping: Different parts of the labeled boxes are cropped randomly and get different pictures each time.
- Scale stretching: Four different size adjustment algorithms, including bilinear interpolation, nearest neighbor interpolation, bicubic interpolation, and area interpolation method, are used to stretch the intercepted image, so that the stretched image is the size of the input layer of the constructed convolutional neural network.
- Random flipping: Flip the image randomly with a certain probability.
- Image standardization: Normalize the image, so that the mean brightness value becomes 0 and the variance becomes 1, as shown in Equation (11).where represents the image matrix, represents the mean value of the image, represents the standard variance and represents the number of pixels in the image.
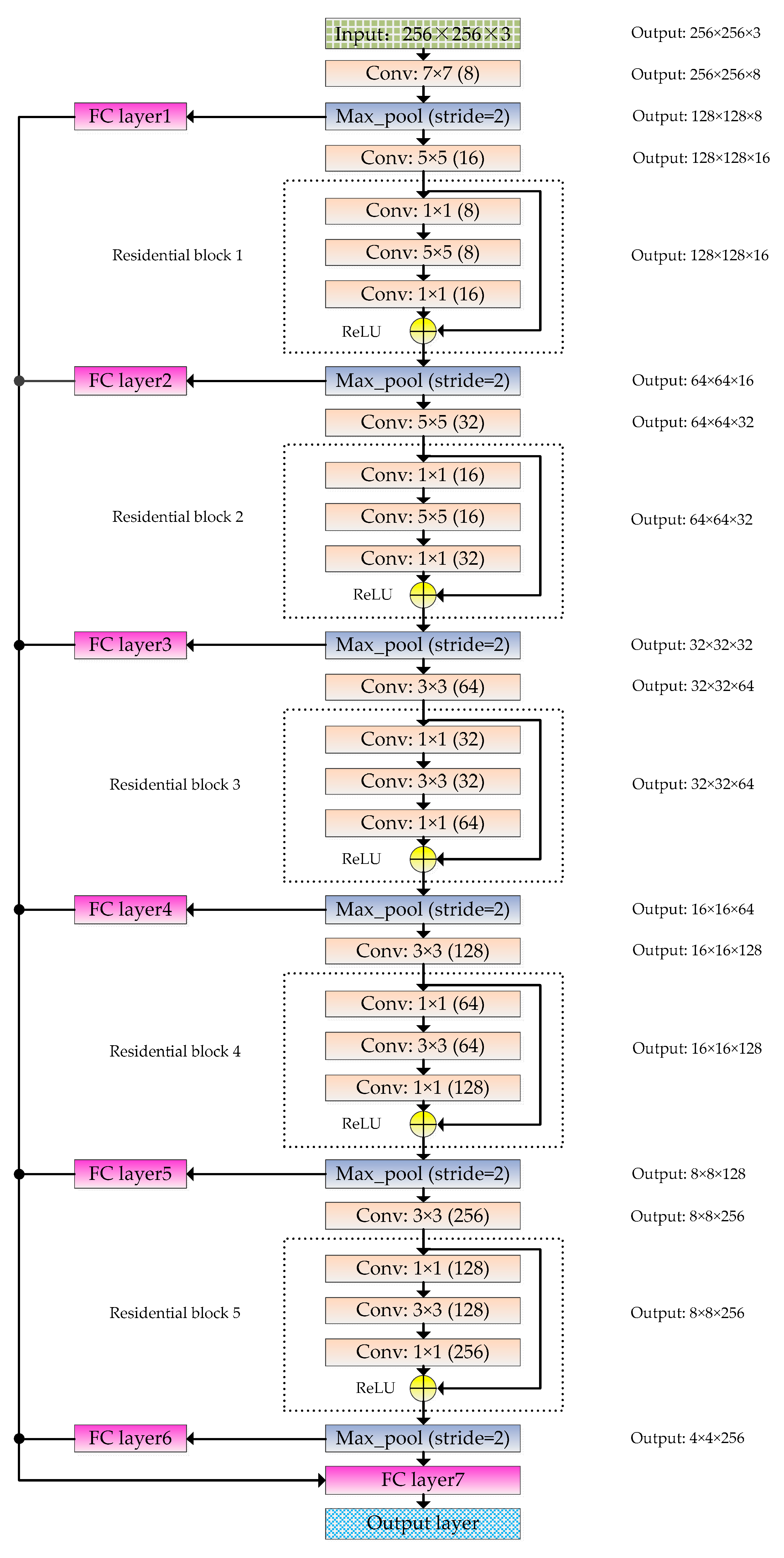
3.2. The Structure of RFPNet
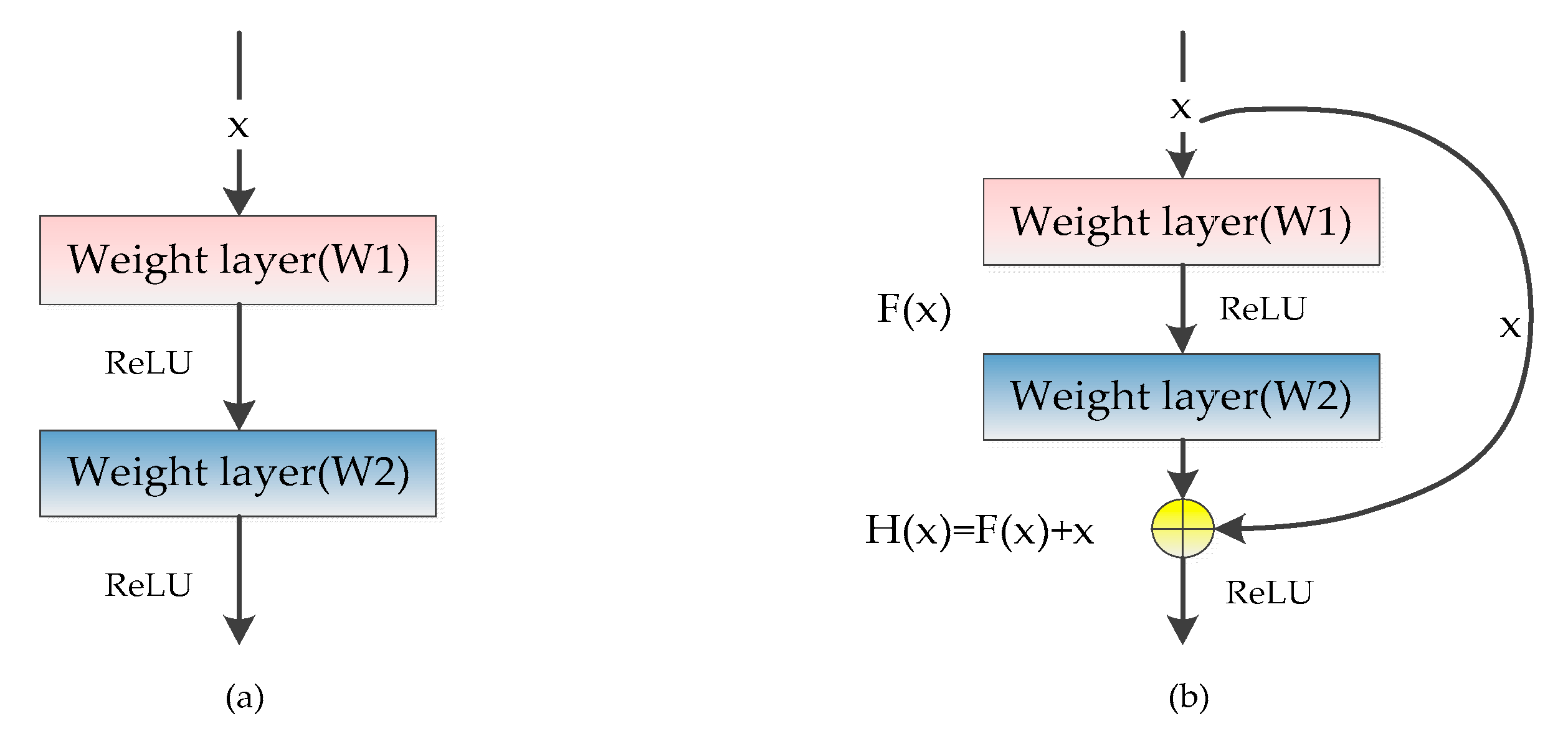
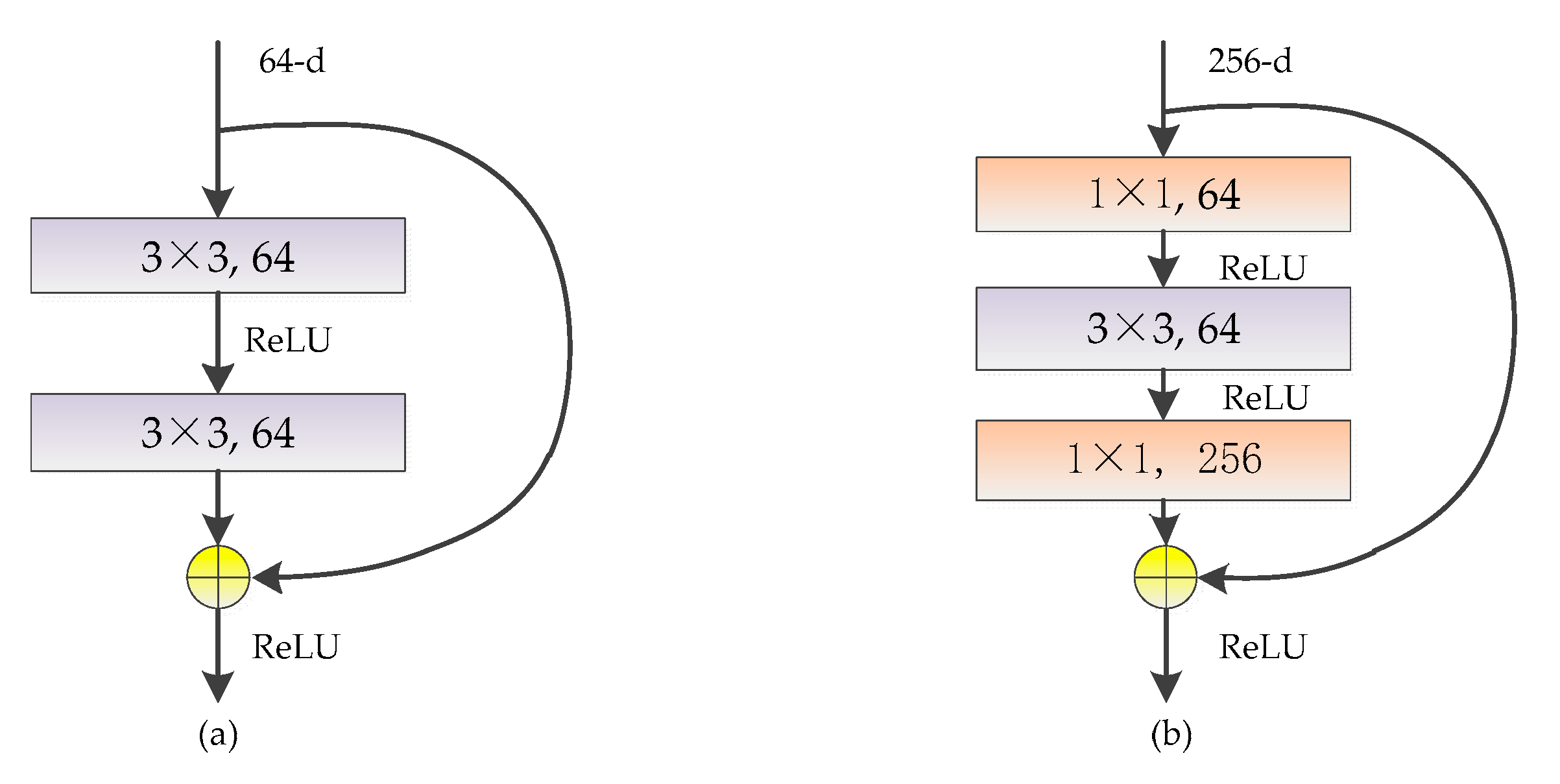
3.2.1. The Residual Block
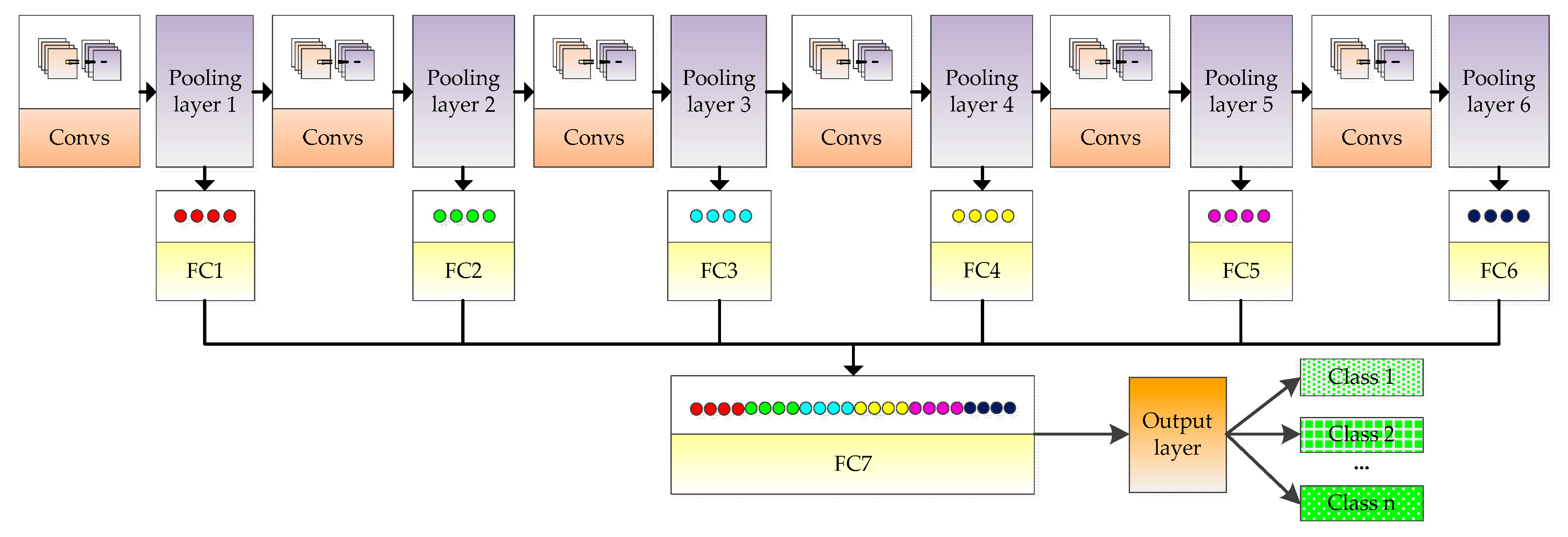
3.2.2. Fusion Strategy of Pooling Layer Feature Maps
3.3. Optimization Methods
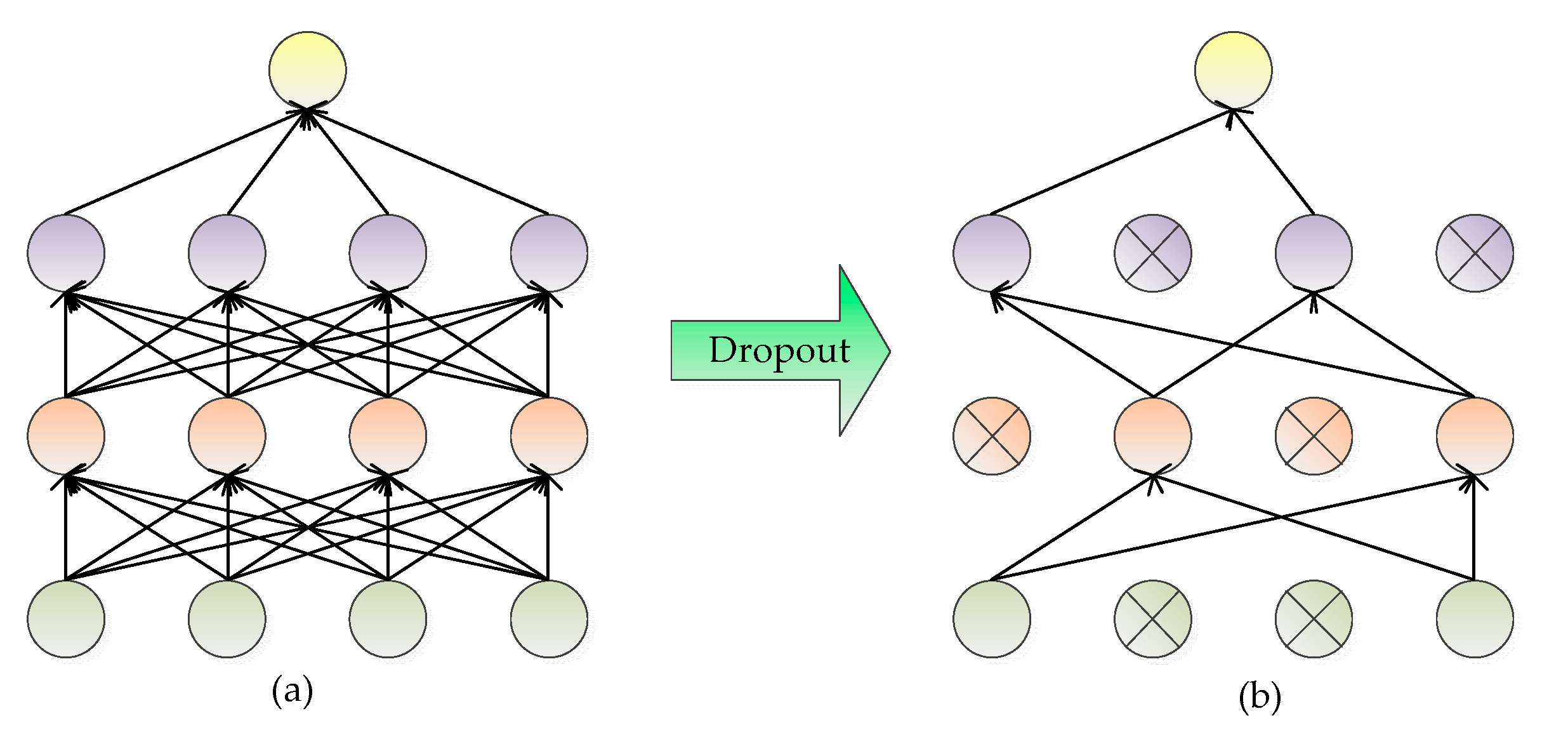
3.3.1. Dropout
3.3.2. Parameter Norm Penalty
3.3.3. Moving Average Model
4. Results
4.1. Experiment Settings
4.2. Evaluation Indicators
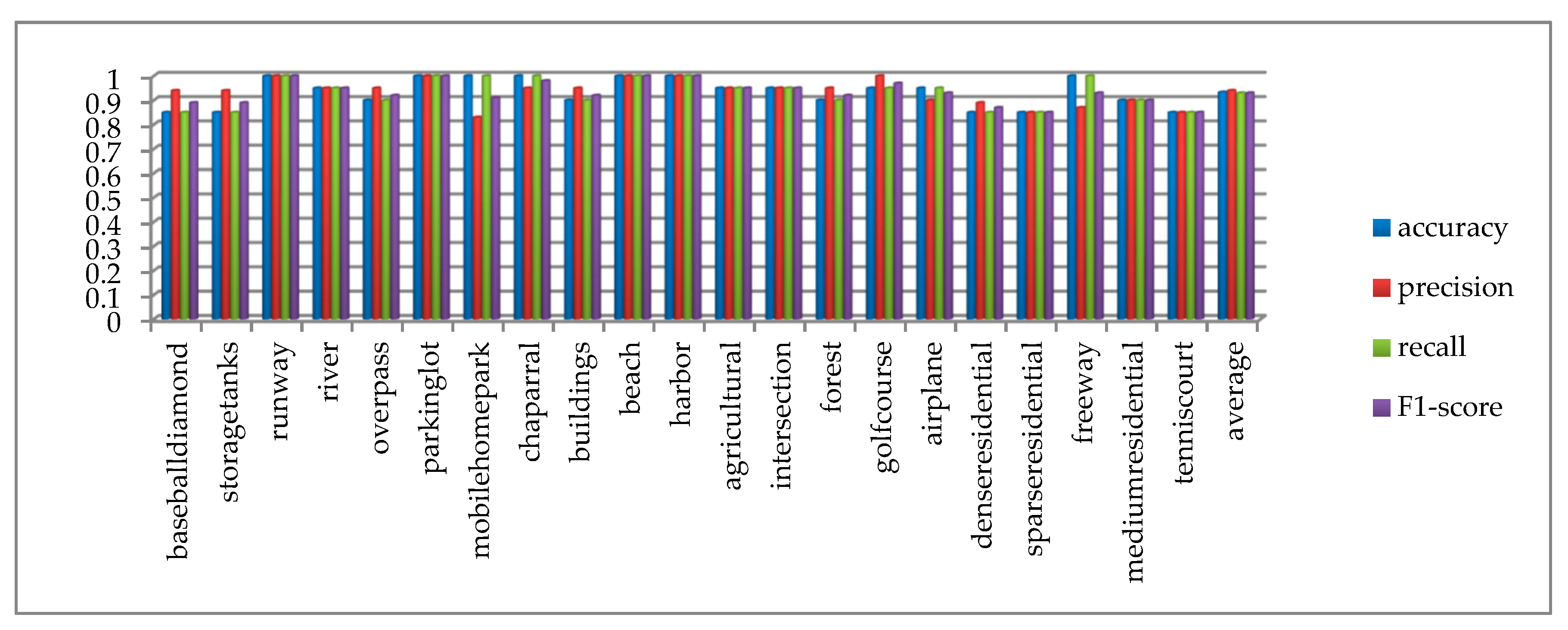
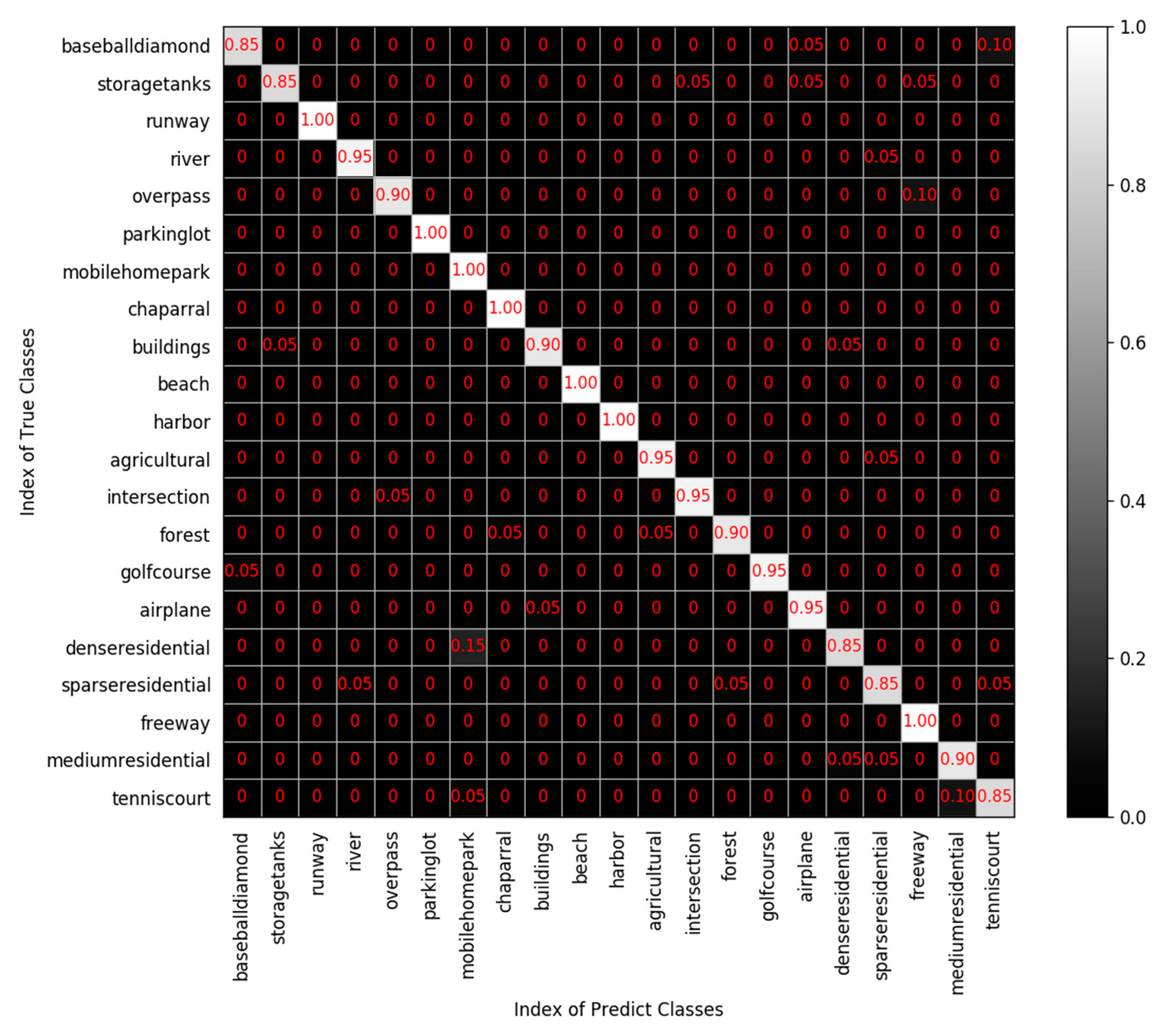
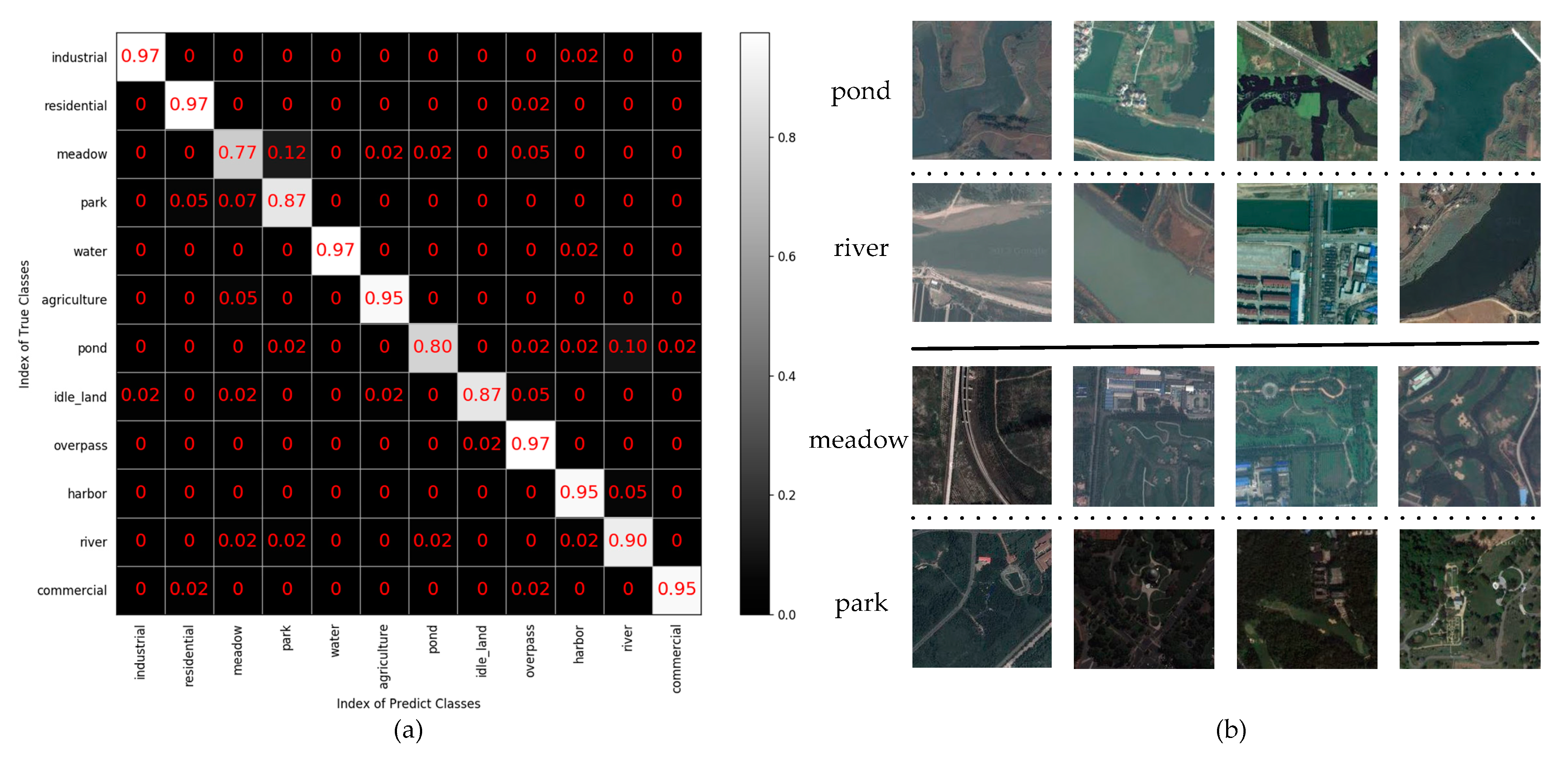
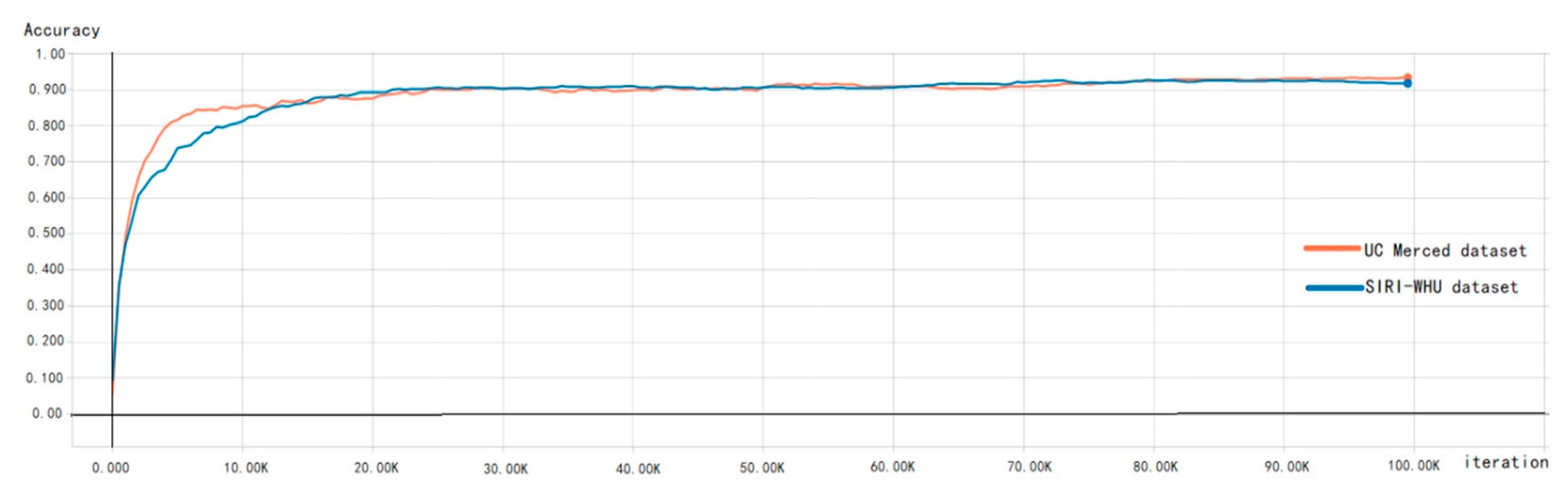
4.3. The Analysis of Test Results on the UC Merced Dataset
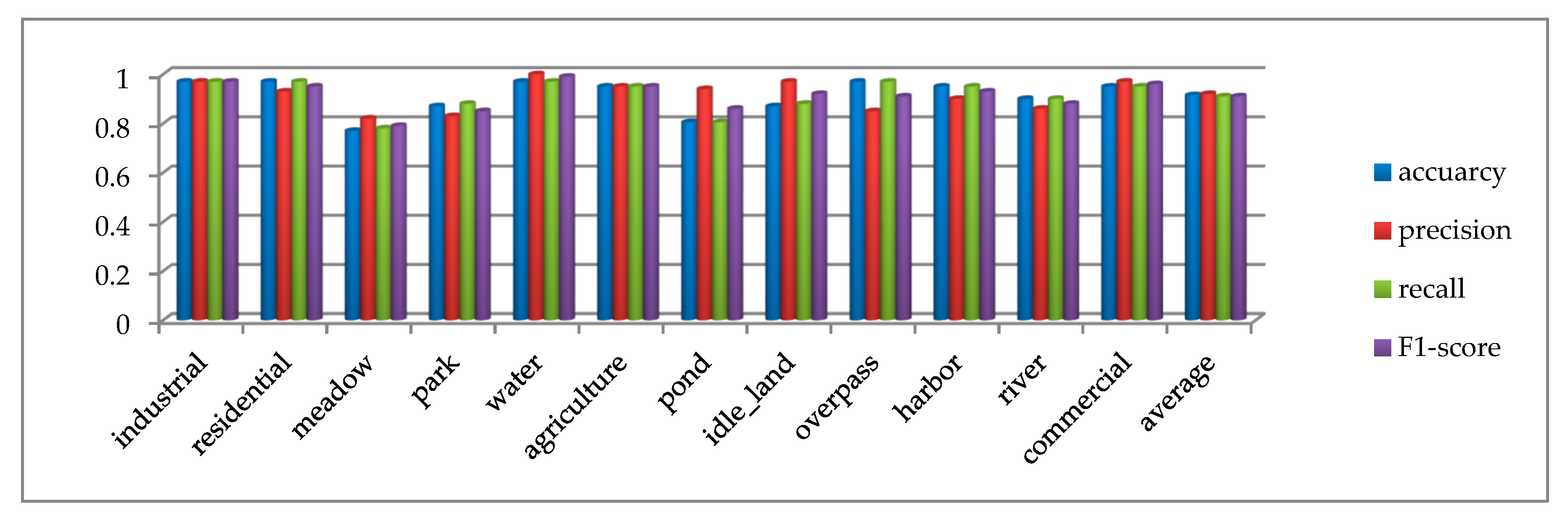
4.4. The Analysis of Test Result on the SIRI-WHU Dataset
5. Discussion
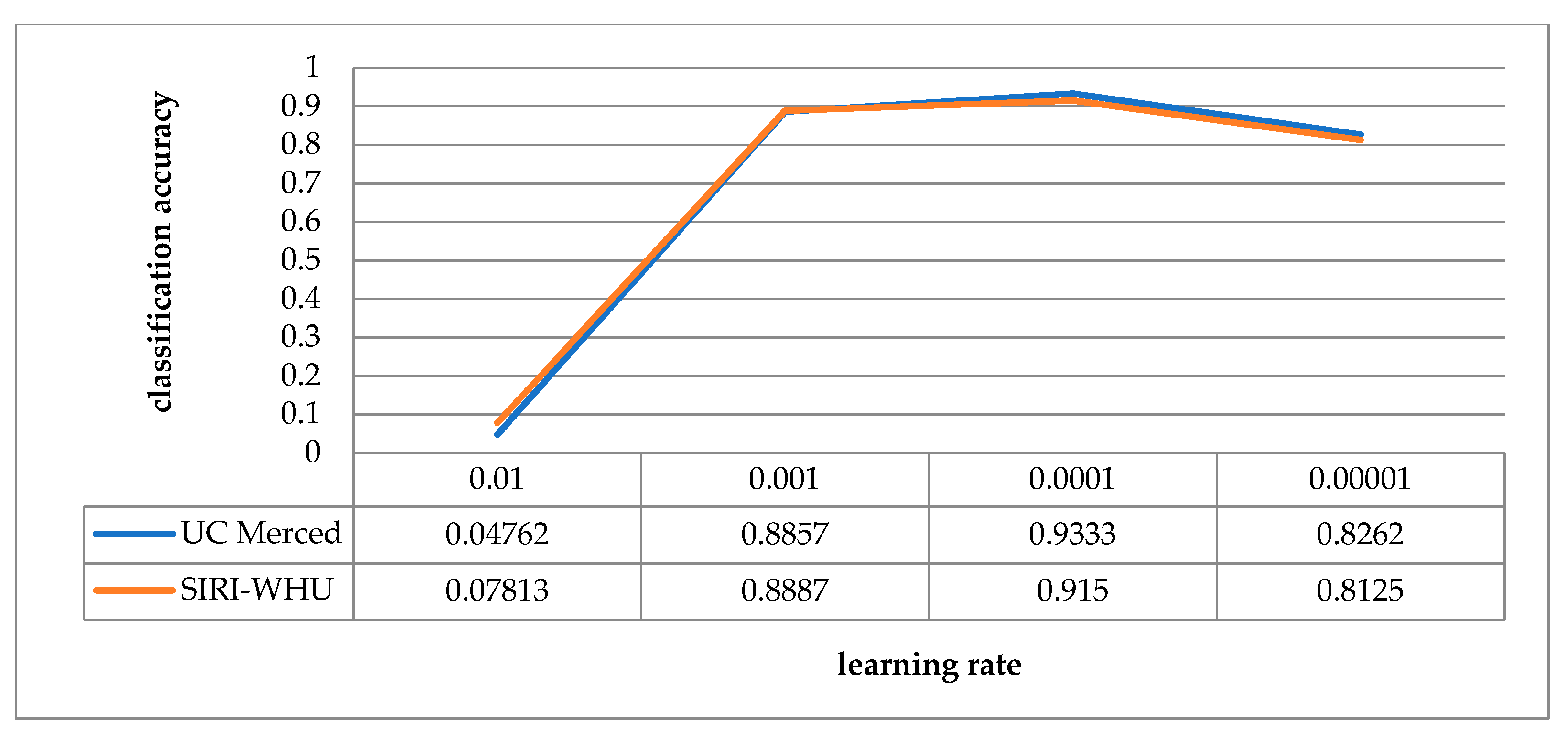
5.1. Analysis in Relation to Learning Rate
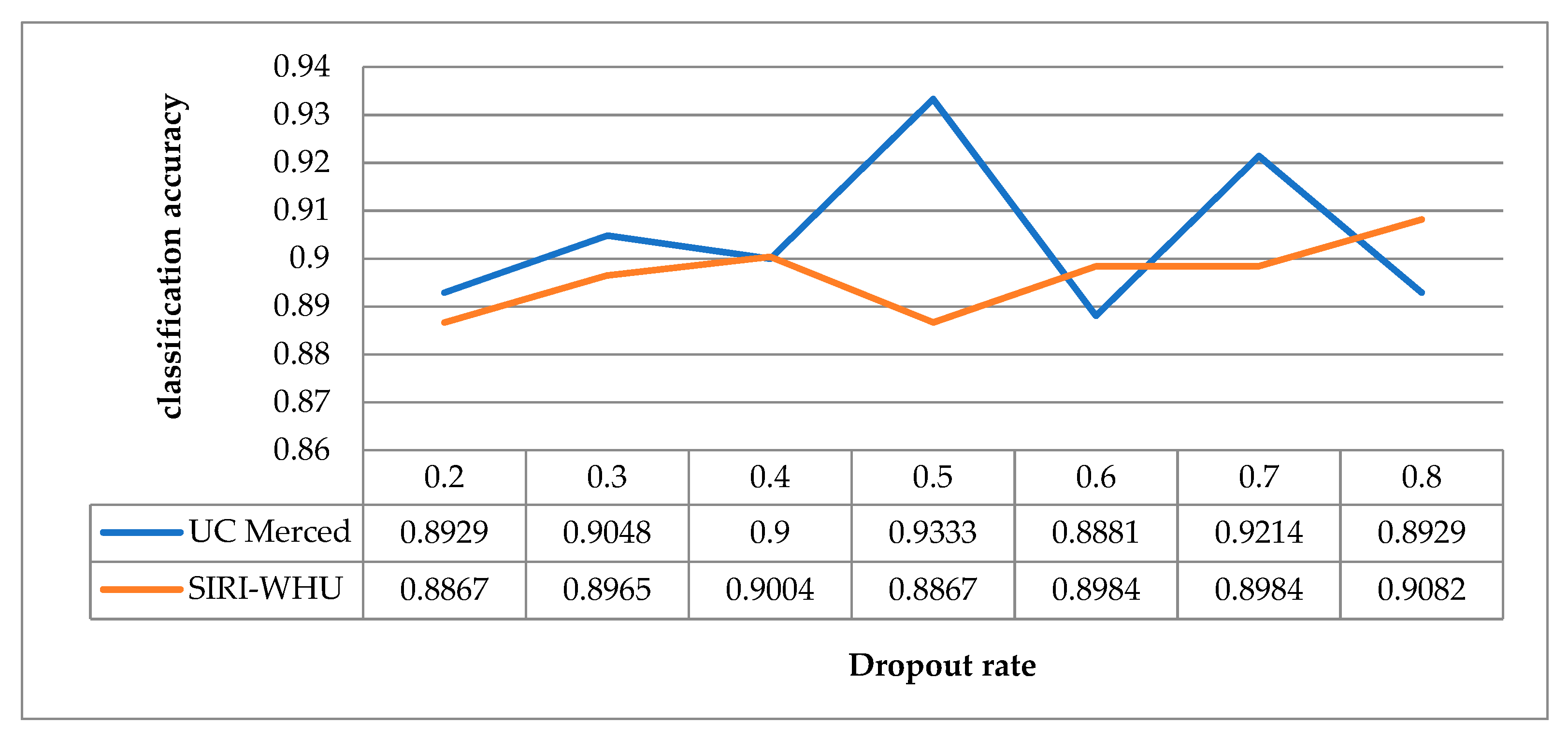
5.2. Analysis in Relation to Dropout Rate
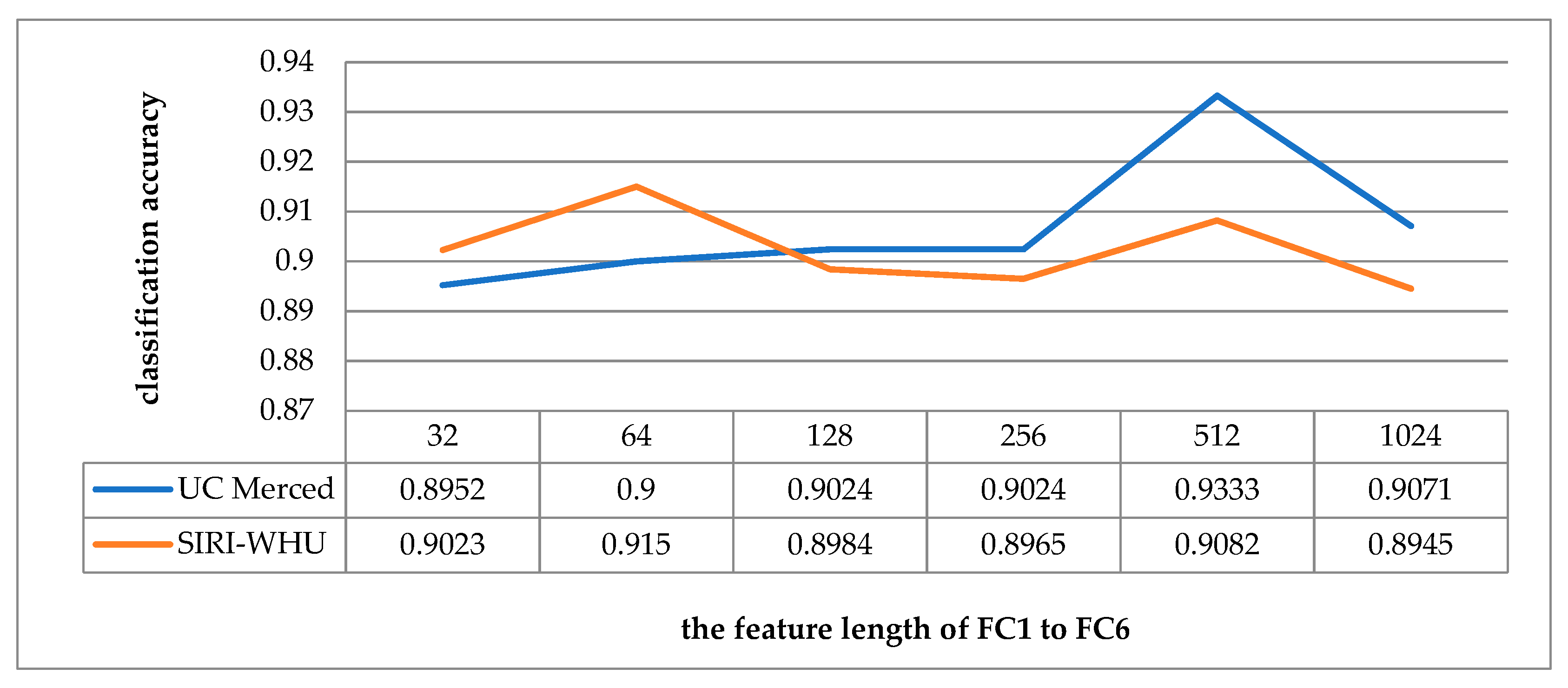
5.3. Analysis in Relation to the Feature Length of the Fully Connected Layer
5.4. Analysis in Relation to the Training Iterations
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Zhang, F.; Du, B.; Zhang, L. Scene Classification via a Gradient Boosting Random Convolutional Network Framework. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1793–1802. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Tao, C.; Zhu, H. Content-Based High-Resolution Remote Sensing Image Retrieval via Unsupervised Feature Learning and Collaborative Affinity Metric Fusion. Remote Sens. 2016, 8, 709. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Tong, X.; Zhang, L.; Zhang, Z.; Liu, H.; Xing, X.; Mathiopoulos, P.T. A Three-Layered Graph-Based Learning Approach for Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6020–6034. [Google Scholar] [CrossRef]
- Zhang, D.; Han, J.; Cheng, G.; Liu, Z.; Bu, S.; Guo, L. Weakly Supervised Learning for Target Detection in Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 701–705. [Google Scholar] [CrossRef]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks. arXiv 2015, arXiv:1508.00092. [Google Scholar]
- Janssen, L.L.F.; Middelkoop, H. Knowledge-based crop classification of a Landsat thematic mapper image. Int. J. Remote Sens. 1992, 13, 2827–2837. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE. 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Cheng, G.; Ma, C.; Zhou, P.; Yao, X.; Han, J. Scene classification of high resolution remote sensing images using convolutional neural networks. In Proceedings of the International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 767–770. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. Modeling the Shape of the Scene: A Holistic Representation of the Spatial Envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; pp. 886–893. [Google Scholar]
- Bahmanyar, R.; Cui, S.; Datcu, M. A Comparative Study of Bag-of-Words and Bag-of-Topics Models of EO Image Patches. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1357–1361. [Google Scholar] [CrossRef]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 2169–2178. [Google Scholar]
- Hu, F.; Yang, W.; Chen, J.; Sun, H. Tile-Level Annotation of Satellite Images Using Multi-Level Max-Margin Discriminative Random Field. Remote Sens. 2013, 5, 2275–2291. [Google Scholar] [CrossRef]
- Zou, J.; Wei, L.; Chen, C.; Qian, D. Scene Classification Using Local and Global Features with Collaborative Representation Fusion. Inf. Sci. 2016, 348, 209–226. [Google Scholar] [CrossRef]
- Lienou, M.; Maitre, H.; Datcu, M. Semantic Annotation of Satellite Images Using Latent Dirichlet Allocation. IEEE Geosci. Remote Sens. Lett. 2010, 7, 28–32. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Olshausen, B.A.; Field, D.J. Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Salakhutdinov, R.; Hinton, G.E. An efficient learning procedure for deep boltzmann machines. Neural Comput. 2012, 24, 1967–2006. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Donahue, J.; Jia, Y.; Vinyals, O.; Hoffman, J.; Zhang, N.; Tzeng, E.; Darrell, T. DeCAF: A Deep Convolutional Activation Feature for Generic Visual Recognition. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 647–655. [Google Scholar]
- Fukushima, K. Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Lecun, Y.; Boser, B.E.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Shen, Y.; He, X.; Gao, J.; Deng, L.; Mesnil, G. Learning semantic representations using convolutional neural networks for web search. In Proceedings of the Proceedings of the 23rd International Conference on World Wide Web, Seoul, Korea, 7–11 April 2014. [Google Scholar]
- Liu, Y.; Racah, E.; Prabhat; Correa, J.; Khosrowshahi, A.; Lavers, D.A.; Kunkel, K.E.; Wehner, M.F.; Collins, W.D. Application of Deep Convolutional Neural Networks for Detecting Extreme Weather in Climate Datasets. arXiv 2016, arXiv:1605.01156. [Google Scholar]
- Rivenson, Y.; Liu, T.; Wei, Z.; Zhang, Y.; De Haan, K.; Ozcan, A. PhaseStain: The digital staining of label-free quantitative phase microscopy images using deep learning. Light-Sci. Appl. 2018, 8, 23. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, B.; Loterie, D.; Konstantinou, G.; Psaltis, D.; Moser, C. Multimode optical fiber transmission with a deep learning network. Light-Sci. Appl. 2018, 7, 69. [Google Scholar] [CrossRef]
- Rivenson, Y.; Zhang, Y.; Gunaydin, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light-Sci. Appl. 2018, 7, 17141. [Google Scholar] [CrossRef]
- Clark, C.A.; Storkey, A.J. Training Deep Convolutional Neural Networks to Play Go. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1766–1774. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; Lecun, Y. OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks. In Proceedings of the 2nd International Conference on Learning Representations (ICLR2014), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2015, Boston, MA, USA, 8–10 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. In Proceedings of the European Conference on Computer Vision, Zürich, Switzerland, 6–12 September 2014; pp. 346–361. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the European Conference on Computer Vision 2014, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Huang, G.; Liu, Z.; Der Maaten, L.V.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Luus, F.P.S.; Salmon, B.P.; Den Bergh, F.V.; Maharaj, B.T. Multiview Deep Learning for Land-Use Classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2448–2452. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; Dibiano, R.; Karki, M.; Nemani, R. DeepSat—A Learning framework for Satellite Imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; pp. 1–10. [Google Scholar]
- Liu, Y.; Fei, F.; Zhu, Q. Scene Classification Based on a Deep Random-Scale Stretched Convolutional Neural Network. Remote Sens. 2018, 10, 444. [Google Scholar] [CrossRef]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep Learning Earth Observation Classification Using ImageNet Pretrained Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 105–109. [Google Scholar] [CrossRef]
- Nogueira, K.; Penatti, O.A.B.; Santos, J.A.D. Towards better exploiting convolutional neural networks for remote sensing scene classification. Pattern Recognit. 2017, 61, 539–556. [Google Scholar] [CrossRef]
- Liu, X.; Chi, M.; Zhang, Y.; Qin, Y. Classifying High Resolution Remote Sensing Images by Fine-Tuned VGG Deep Networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Yang, Y.; Newsam, S.D. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Yi, Y.; Newsam, S. Spatial pyramid co-occurrence for image classification. In Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Jiang, Y.; Yuan, J.; Gang, Y. Randomized Spatial Partition for Scene Recognition; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fan, H.; Xia, G.S.; Wang, Z.; Zhang, L.; Hong, S. Unsupervised feature coding on local patch manifold for satellite image scene classification. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Chen, S.; Tian, Y.L. Pyramid of Spatial Relatons for Scene-Level Land Use Classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1947–1957. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhong, Y.; Zhang, L. Multi-feature probability topic scene classifier for high spatial resolution remote sensing imagery. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Cheriyadat, A.M. Unsupervised Feature Learning for Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 439–451. [Google Scholar] [CrossRef]
- Gueguen, L. Classifying Compound Structures in Satellite Images: A Compressed Representation for Fast Queries. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1803–1818. [Google Scholar] [CrossRef]
- Gong, C.; Han, J.; Lei, G.; Liu, Z.; Bu, S.; Ren, J. Effective and Efficient Midlevel Visual Elements-Oriented Land-Use Classification Using VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4238–4249. [Google Scholar]
- Zhong, Y.; Fei, F.; Zhang, L. Large patch convolutional neural networks for the scene classification of high spatial resolution imagery. J. Appl. Remote Sens. 2016, 10, 025006. [Google Scholar] [CrossRef]
- Zhao, B.; Zhong, Y.; Xia, G.; Zhang, L. Dirichlet-Derived Multiple Topic Scene Classification Model for High Spatial Resolution Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2108–2123. [Google Scholar] [CrossRef]
- Bosch, A.; Zisserman, A.; Muoz, X. Scene Classification Using a Hybrid Generative/Discriminative Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 712–727. [Google Scholar] [CrossRef]
- Fan, Z.; Bo, D.; Zhang, L. Saliency-Guided Unsupervised Feature Learning for Scene Classification. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2175–2184. [Google Scholar]
- Csurka, G.; Dance, C.R.; Fan, L.; Willamowski, J.; Bray, C. Visual Categorization with Bags of Keypoints. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 15 May 2004. [Google Scholar]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. Mach. Learn. 2004, 45, 157–176. [Google Scholar]
- Wang, X.; Xiong, X.; Ning, C.; Shi, A.; Lv, G. Integration of heterogeneous features for remote sensing scene classification. J. Appl. Remote Sens. 2018, 12, 015023. [Google Scholar] [CrossRef]


| Name | Multi-View Scaling Strategy | The Residual Block | Fusion Strategy | Dropout | Parameter Norm Penalty | Moving Average Model |
|---|---|---|---|---|---|---|
| WMS-RFPNet | √ | √ | √ | √ | √ | |
| MFPNet | √ | √ | √ | √ | √ | |
| MRNet | √ | √ | √ | √ | √ | |
| WD-RFPNet | √ | √ | √ | √ | √ | |
| WPNP-RFPNet | √ | √ | √ | √ | √ | |
| WWAM-RFPNet | √ | √ | √ | √ | √ | |
| RFPNet | √ | √ | √ | √ | √ | √ |
| Attribute | Method | Accuracy (%) |
|---|---|---|
| Traditional methods | SPCK [51] | 73.14 |
| BOVW [50] | 76.81 | |
| BRSK [52] | 77.80 | |
| SPMK [14] | 75.29 | |
| Bag-of-SIFT [53] | 85.37±1.56 | |
| SPM [54] | 86.8 | |
| SAL-LDA [55] | 88.33 | |
| UFL [56] | 81.67 | |
| MinTree+KD-Tree [57] | 83.1±1.2 | |
| Partlets [58] | 88.76 | |
| Deep learning methods | LPCNN [59] | 89.9 |
| CNN with Overfeat feature [47] | 92.4 | |
| WMS-RFPNet | 61.67 | |
| MFPNet | 88.81 | |
| MRNet | 87.38 | |
| WD-RFPNet | 87.38 | |
| WPNP-RFPNet | 90.95 | |
| WMAM-RFPNet | 89.05 | |
| RFPNet | 93.33 |
| Attribute | Method | Accuracy (%) |
|---|---|---|
| Traditional methods | SPM [14] | 77.69±1.01 |
| LDA [17] | 60.32±1.20 | |
| PLSA [61] | 89.60±0.89 | |
| S-UFL [62] | 74.84 | |
| SIFT+BoVW [63] | 75.63 | |
| RF [64] | 89.29 | |
| Features integration [65] | 88.64 | |
| Deep learning methods | LPCNN [59] | 89.88 |
| WMS-RFPNet | 83.2 | |
| MFPNet | 86.52 | |
| MRNet | 88.67 | |
| WD-RFPNet | 88 | |
| WPNP-RFPNet | 90.63 | |
| WMAM-RFPNet | 90.43 | |
| RFPNet | 91.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, Y.; Zhang, N.; Xu, D.; Chen, B. Research on Scene Classification Method of High-Resolution Remote Sensing Images Based on RFPNet. Appl. Sci. 2019, 9, 2028. https://doi.org/10.3390/app9102028
Zhang X, Wang Y, Zhang N, Xu D, Chen B. Research on Scene Classification Method of High-Resolution Remote Sensing Images Based on RFPNet. Applied Sciences. 2019; 9(10):2028. https://doi.org/10.3390/app9102028
Chicago/Turabian StyleZhang, Xin, Yongcheng Wang, Ning Zhang, Dongdong Xu, and Bo Chen. 2019. "Research on Scene Classification Method of High-Resolution Remote Sensing Images Based on RFPNet" Applied Sciences 9, no. 10: 2028. https://doi.org/10.3390/app9102028
APA StyleZhang, X., Wang, Y., Zhang, N., Xu, D., & Chen, B. (2019). Research on Scene Classification Method of High-Resolution Remote Sensing Images Based on RFPNet. Applied Sciences, 9(10), 2028. https://doi.org/10.3390/app9102028





