A New Approach to Border Irregularity Assessment with Application in Skin Pathology
Abstract
:1. Introduction
- we propose a new border irregularity assessment method which can be used in different applications, and
- we present an accurate algorithm for the detection of individual projections and for measuring their morphometry.
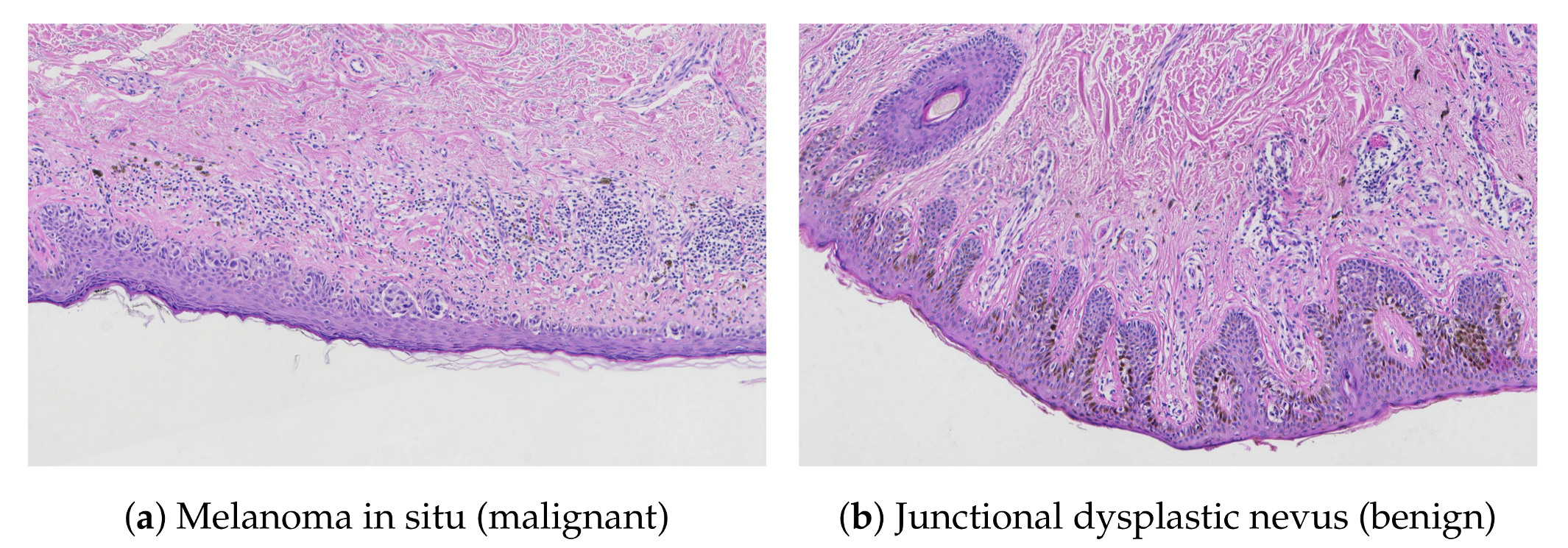
Related Works
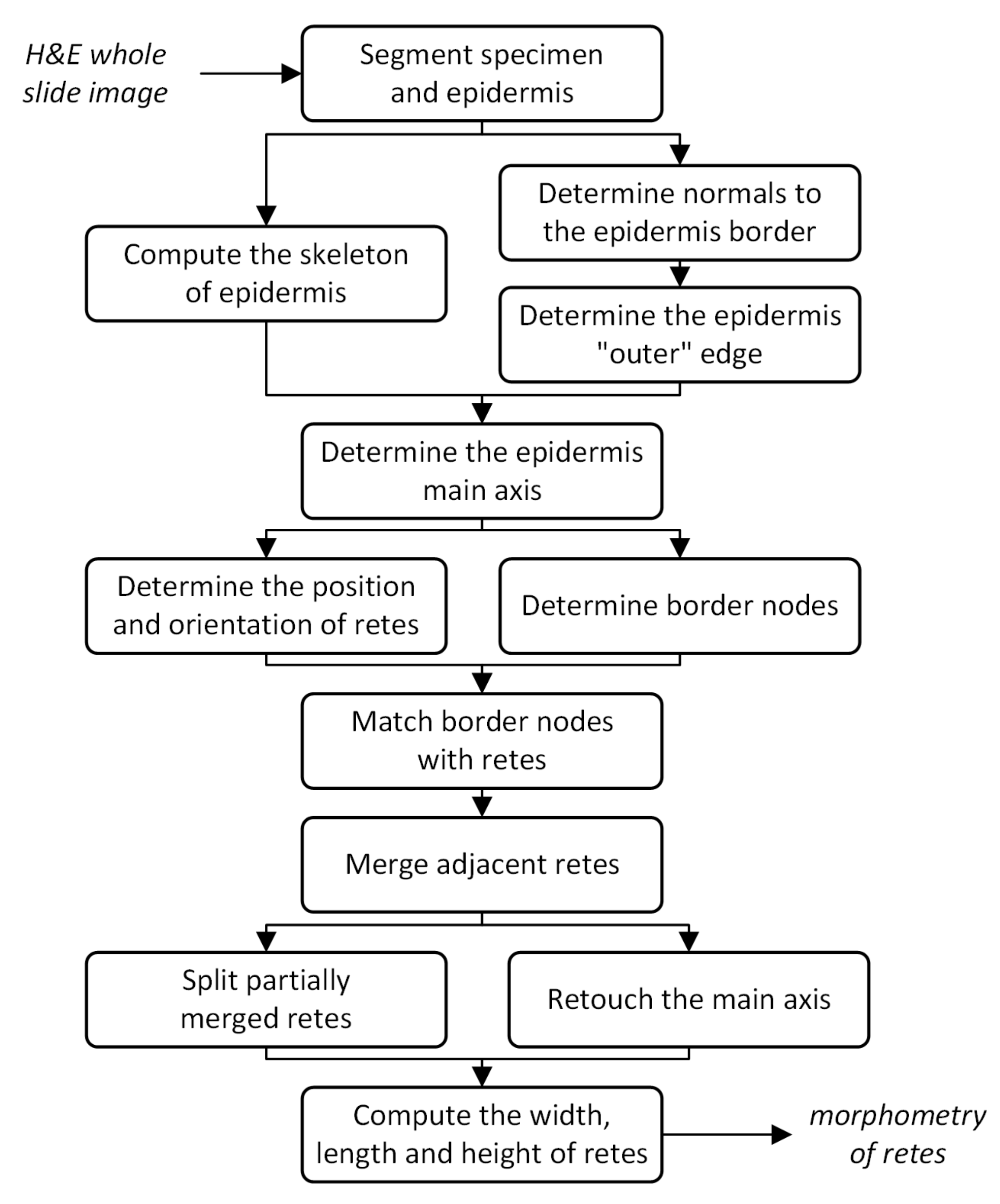
2. Material and Methods
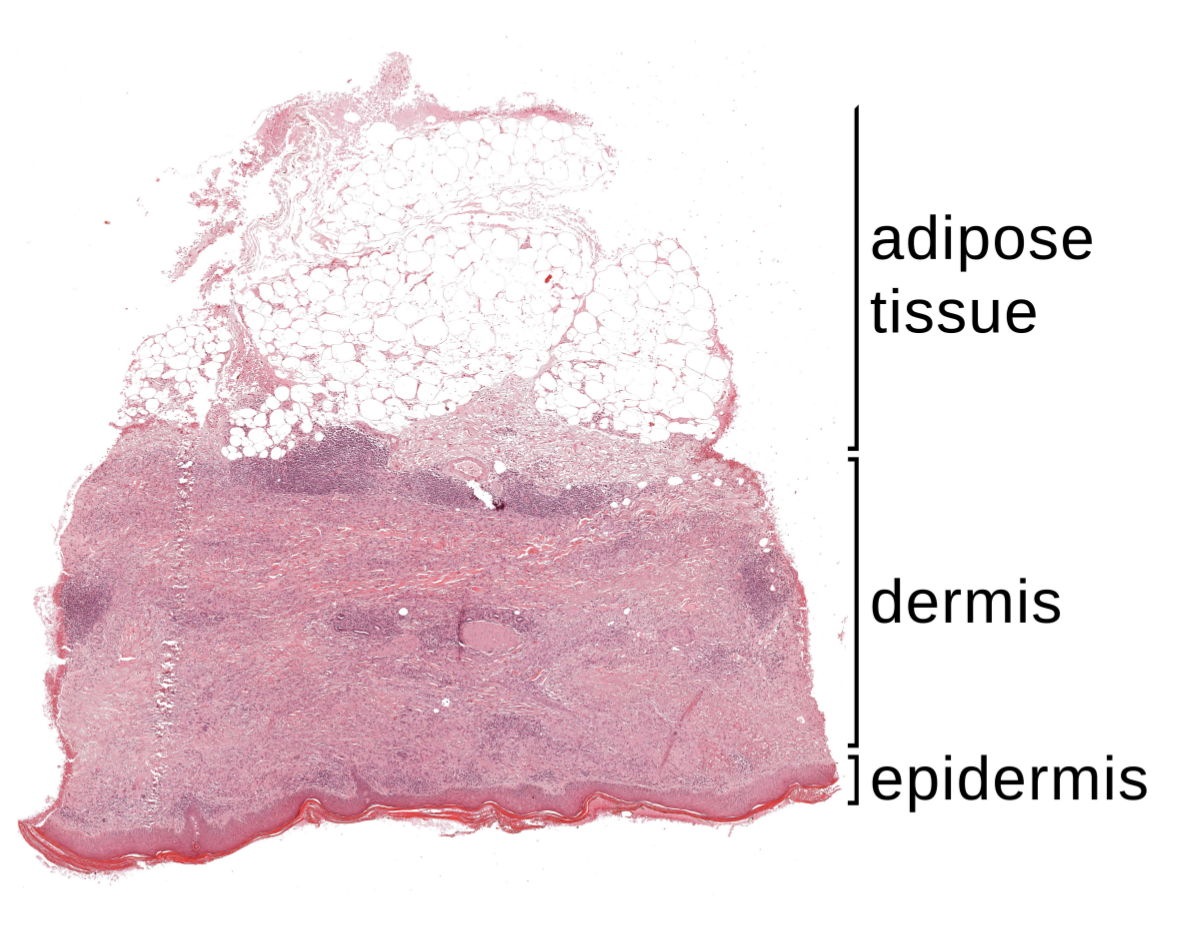
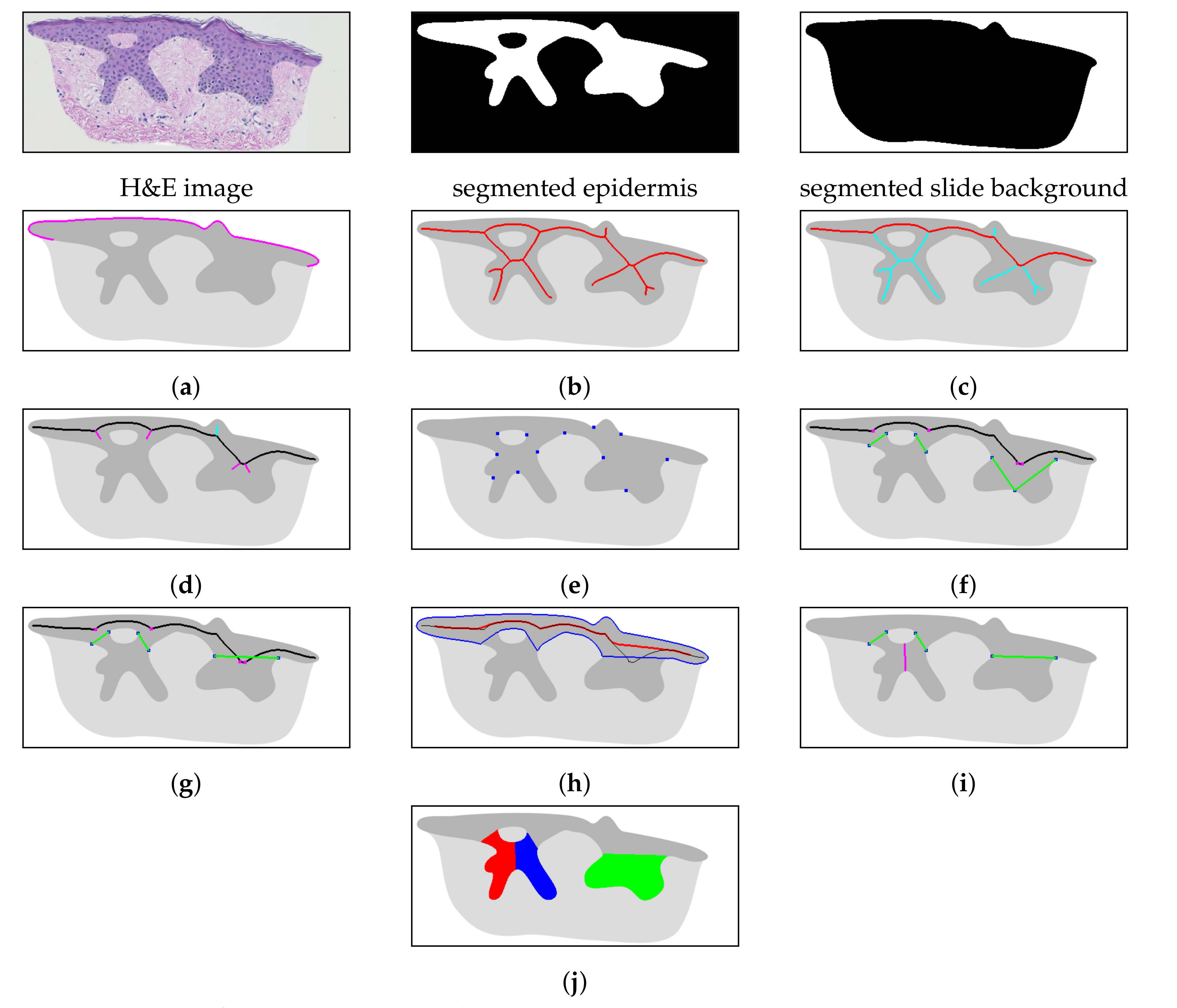
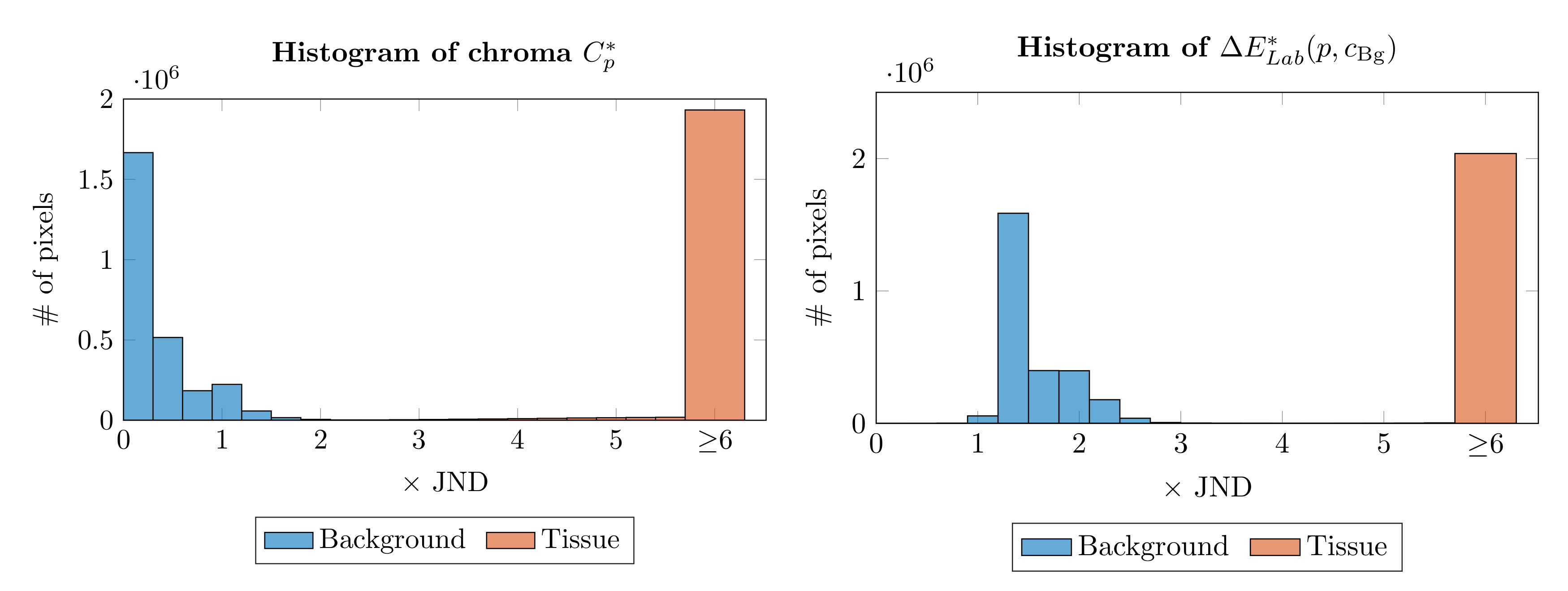
2.1. Specimen Segmentation
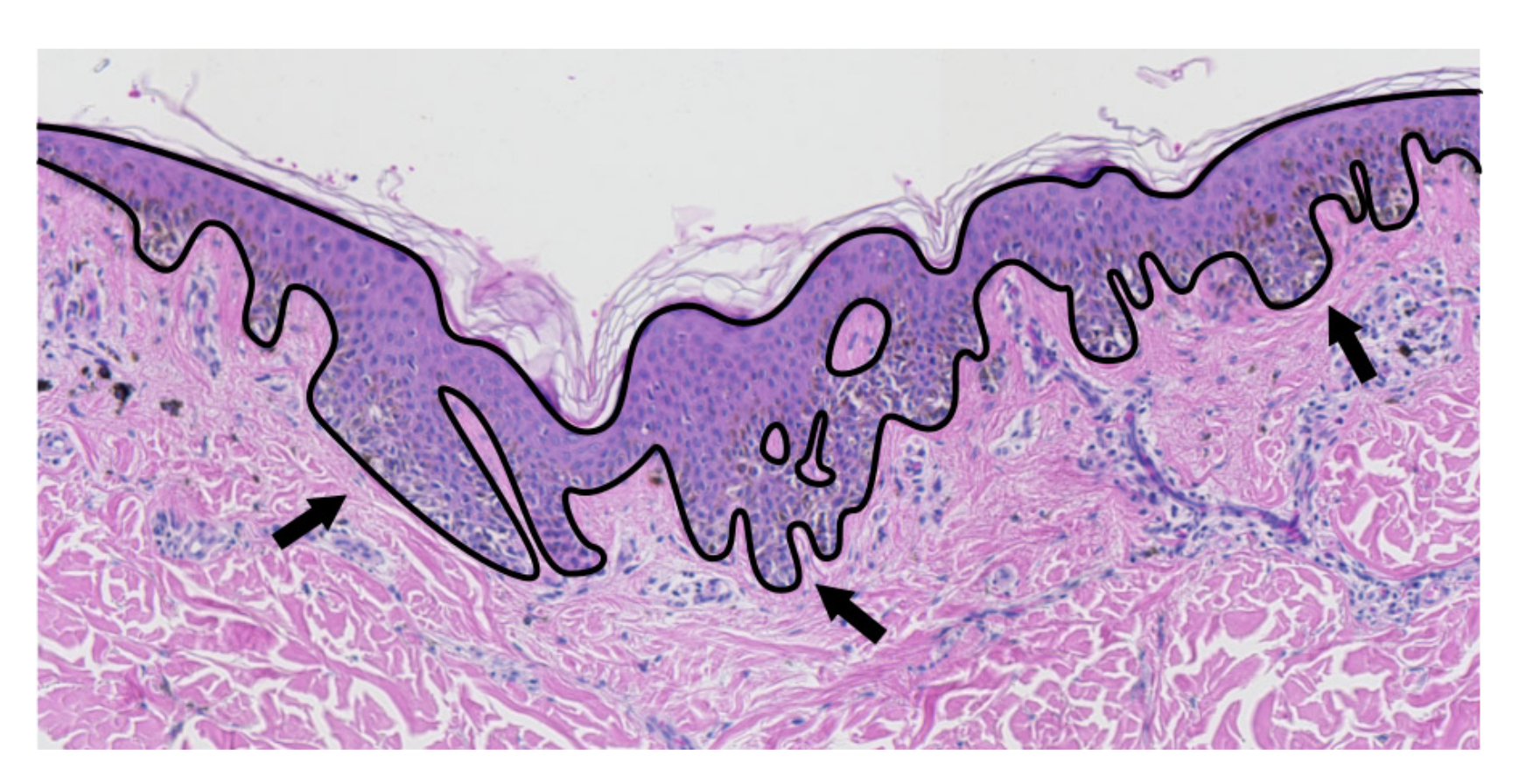
2.2. Epidermis Segmentation
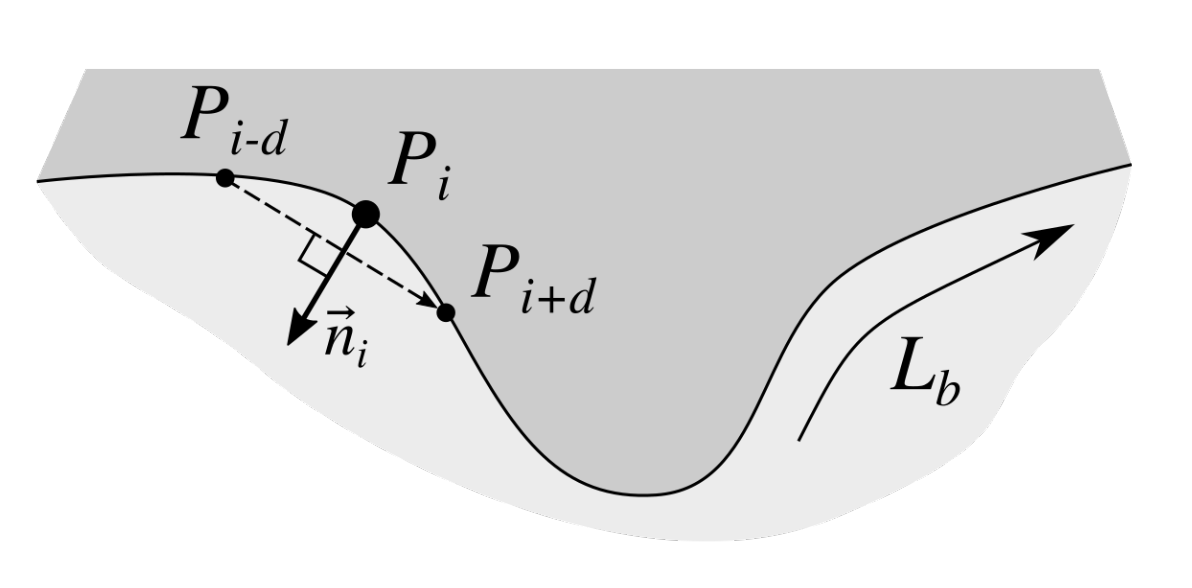
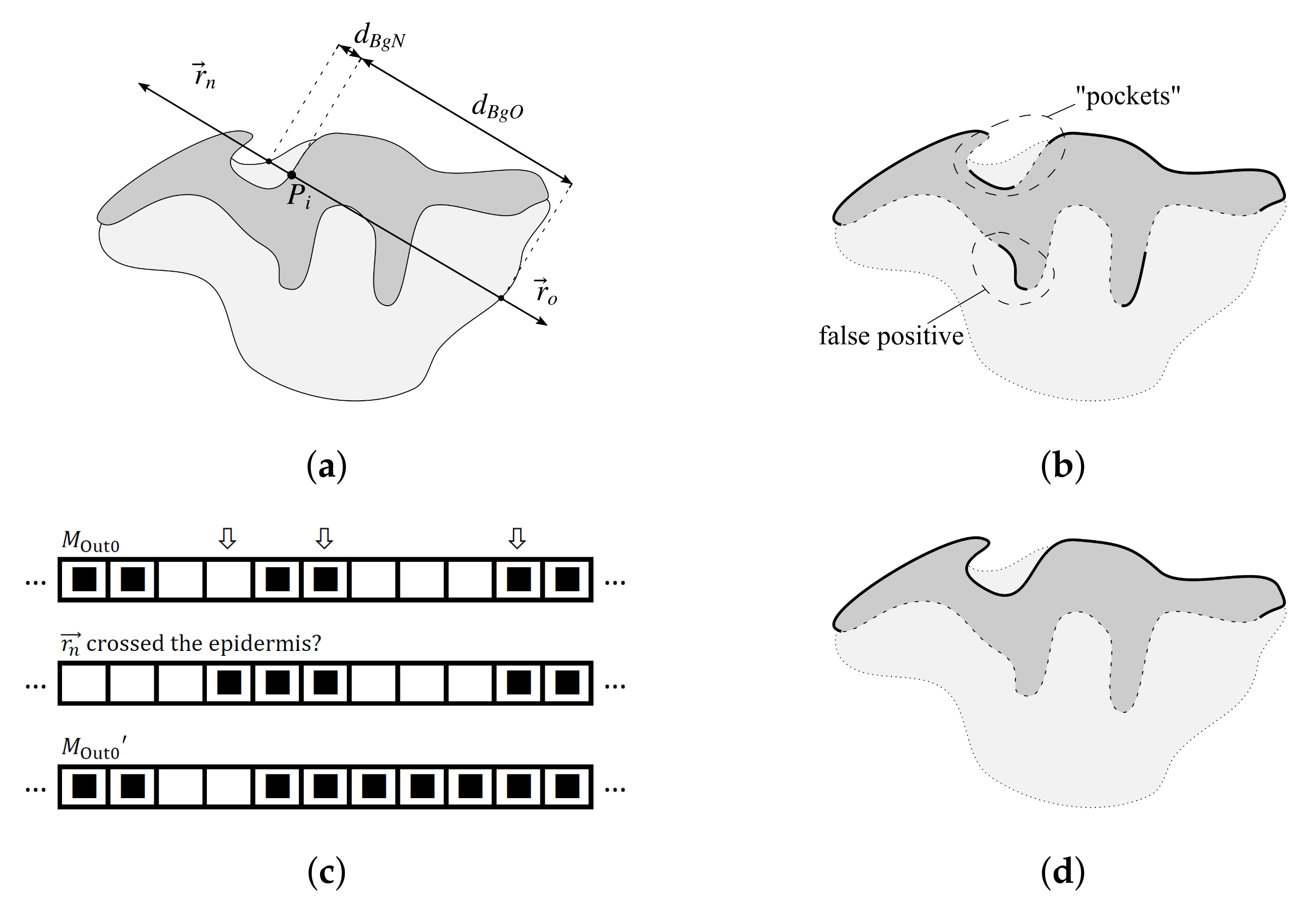
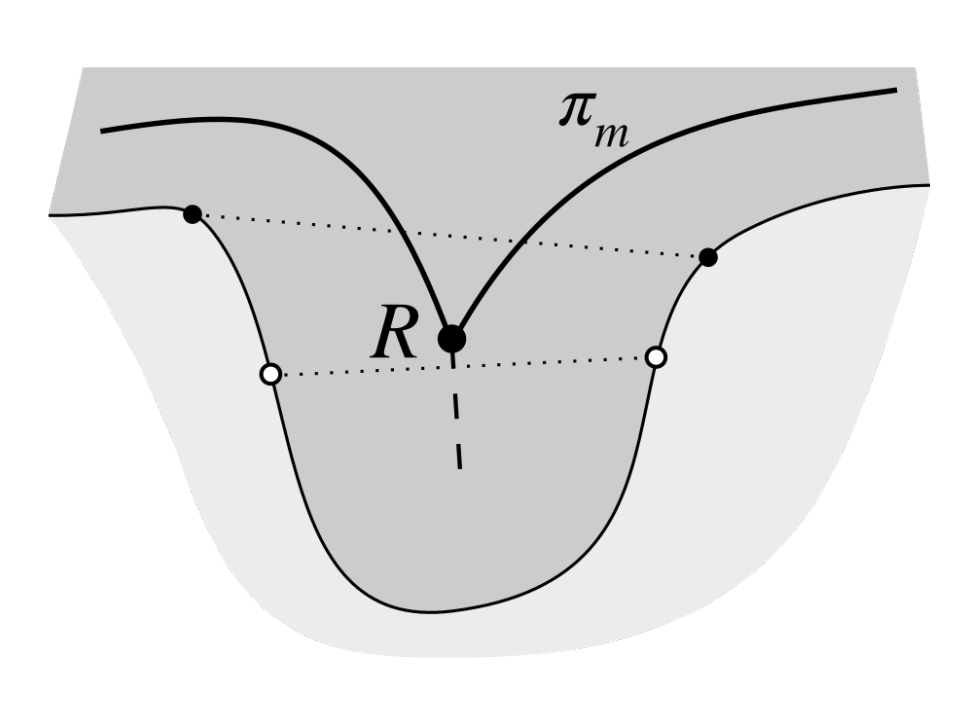
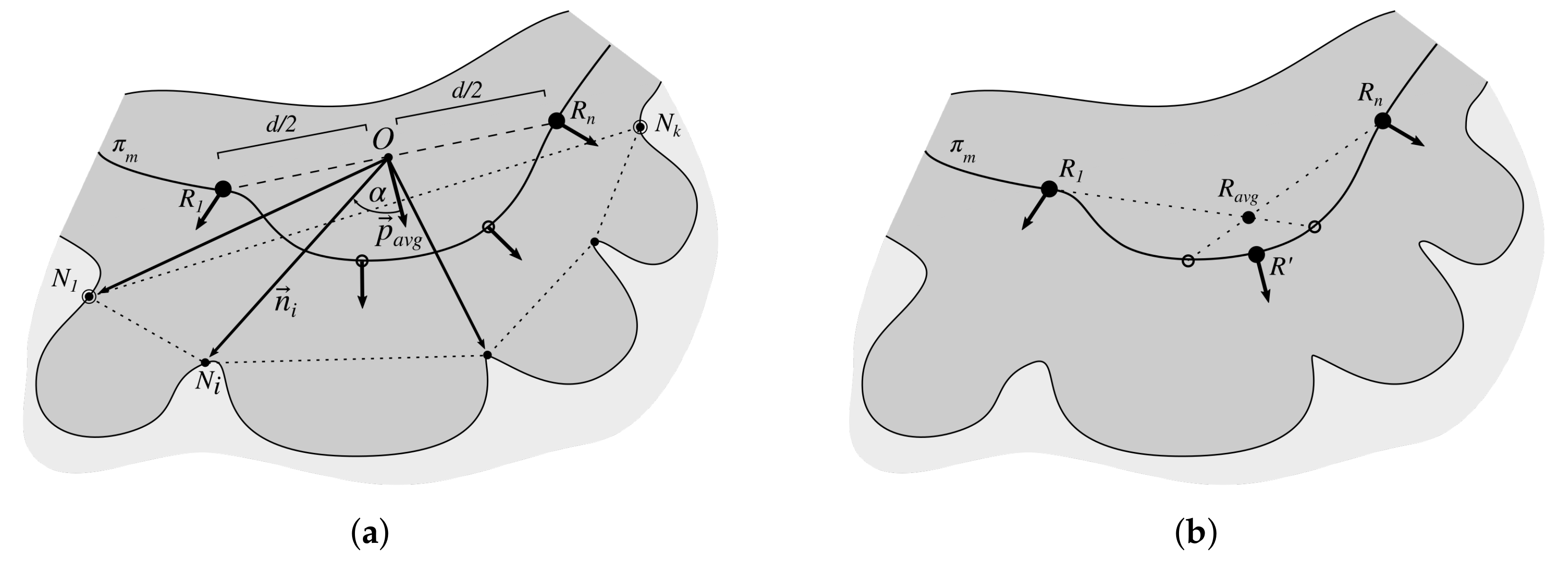
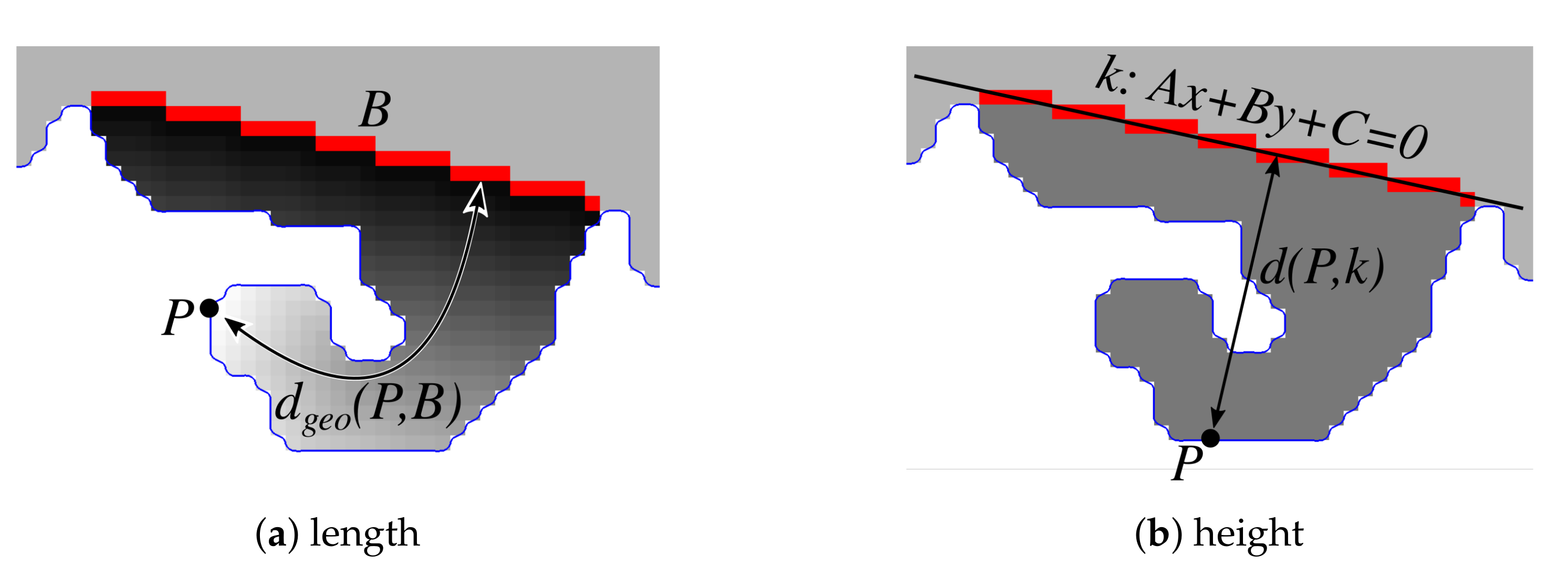
2.3. Determining Normals to the Epidermis Border
2.4. Determining the Epidermis “Outer” Edge
2.5. Computing the Epidermis Skeleton
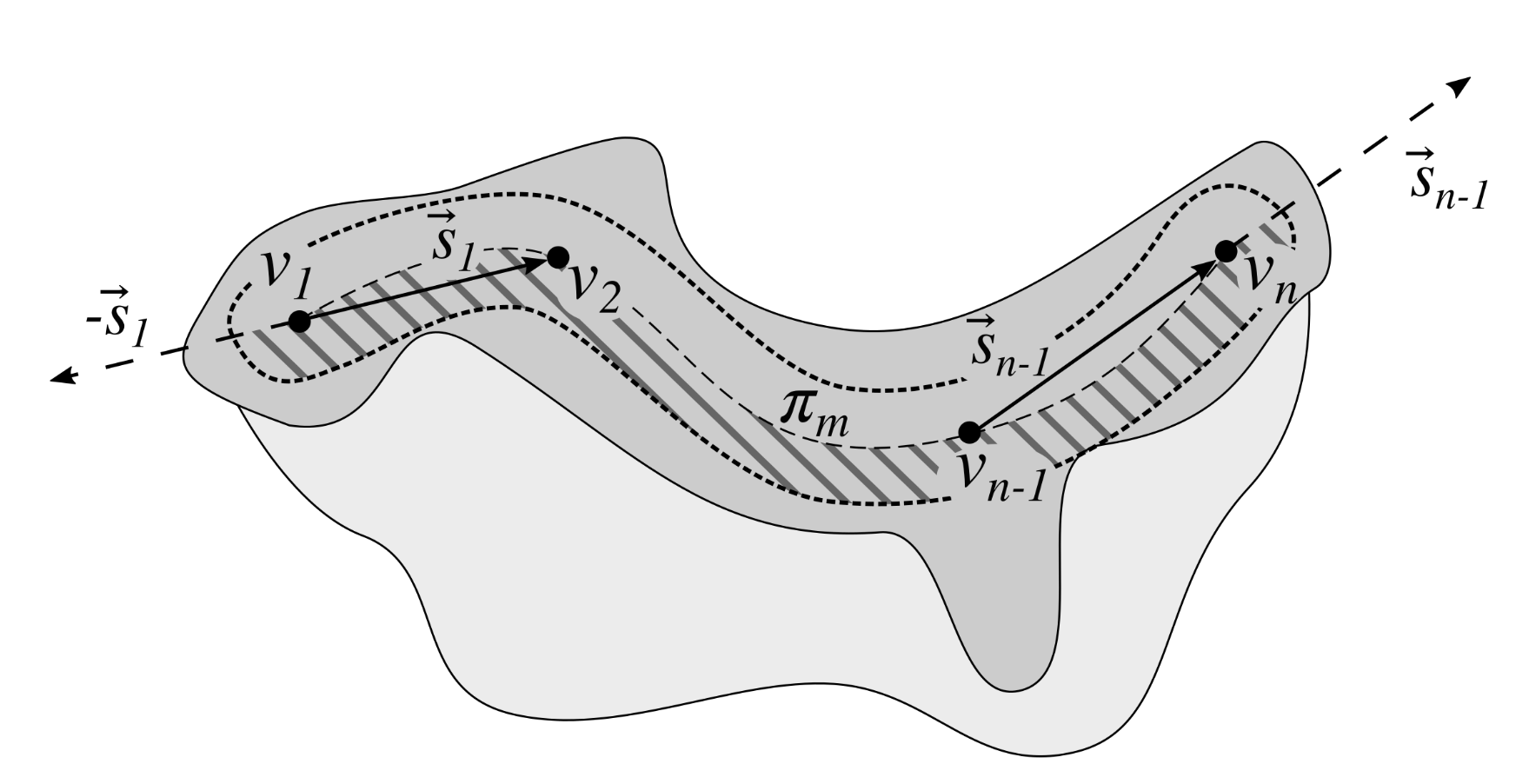
2.6. Determining the Epidermis Main Axis
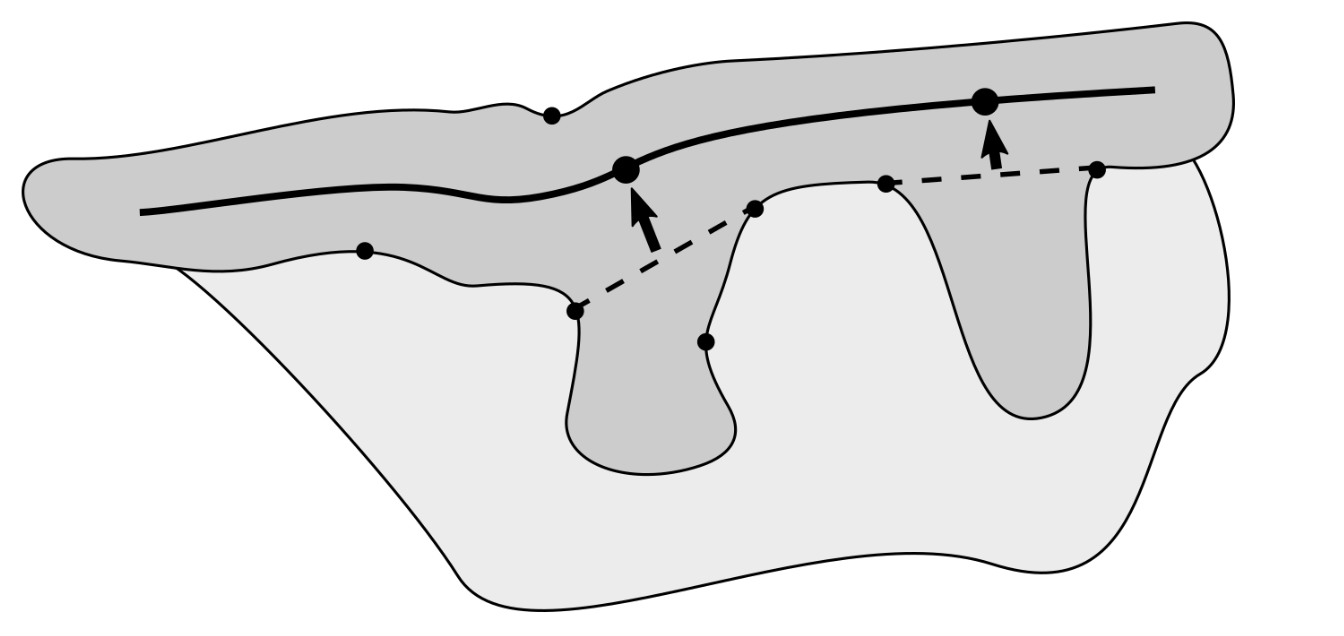
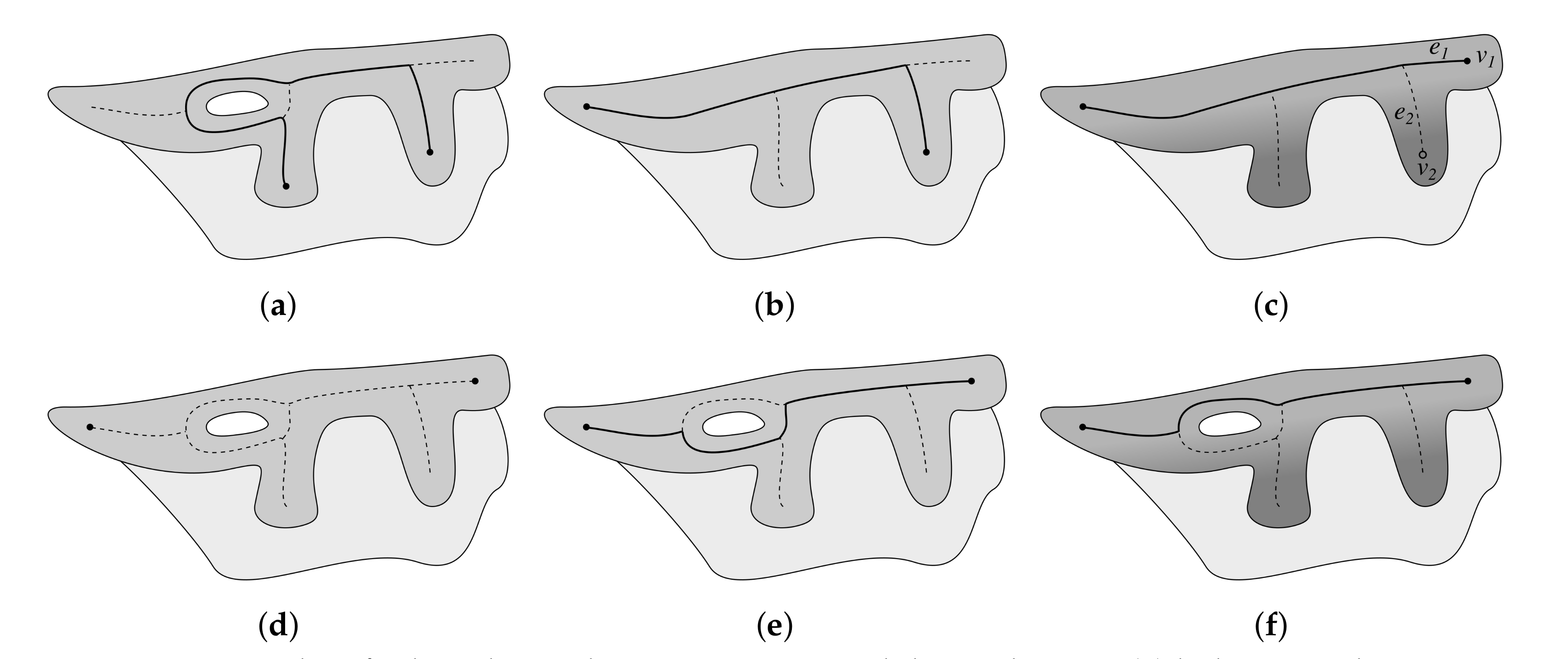
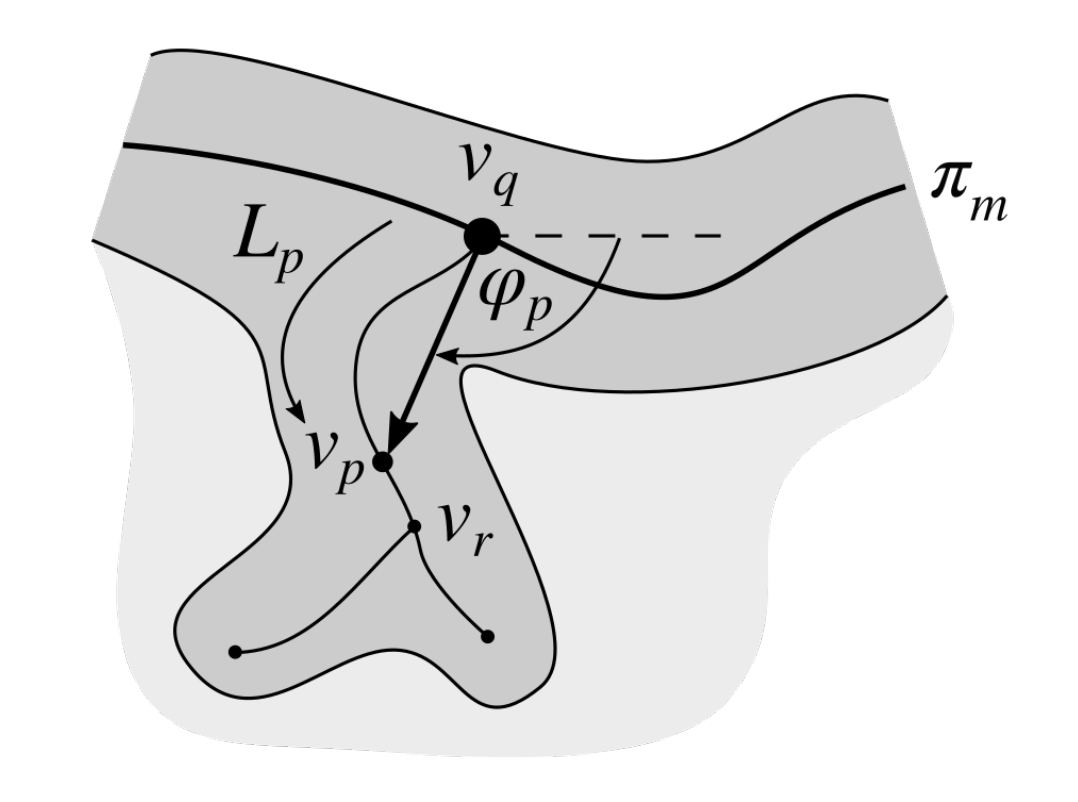
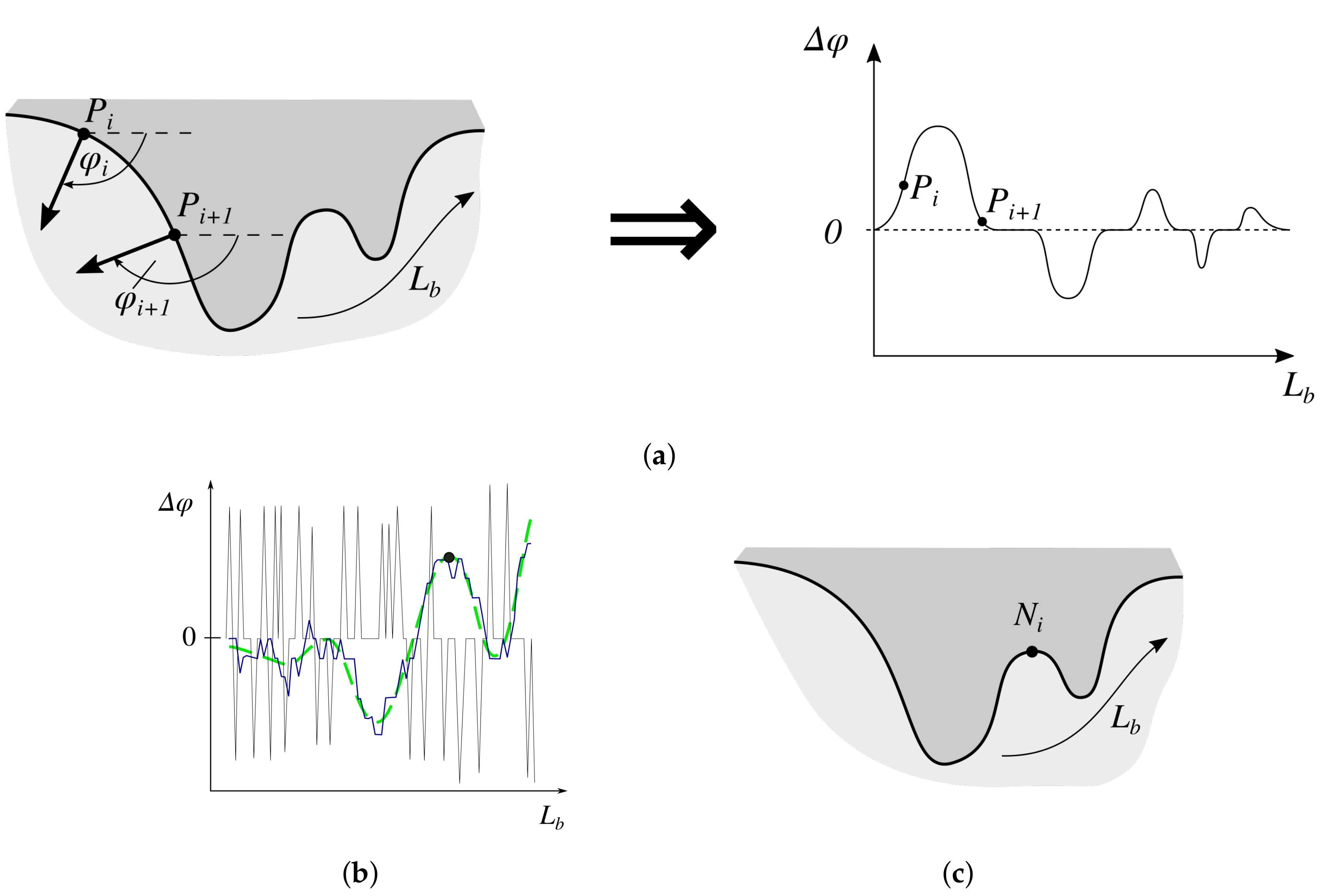
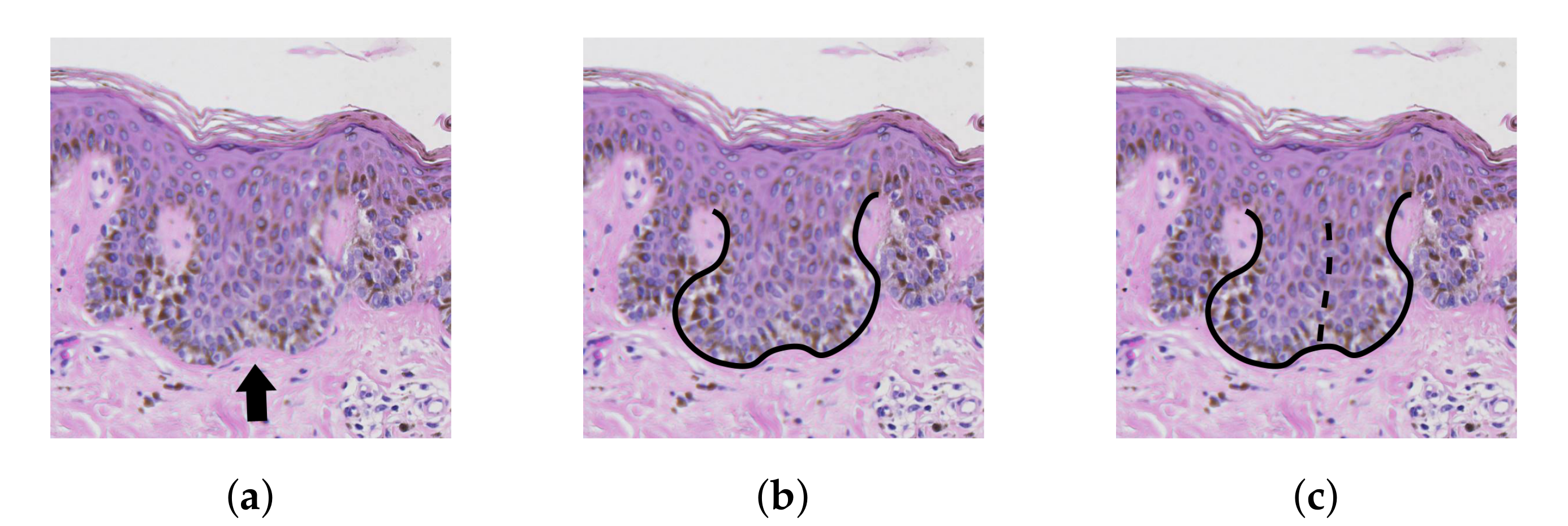
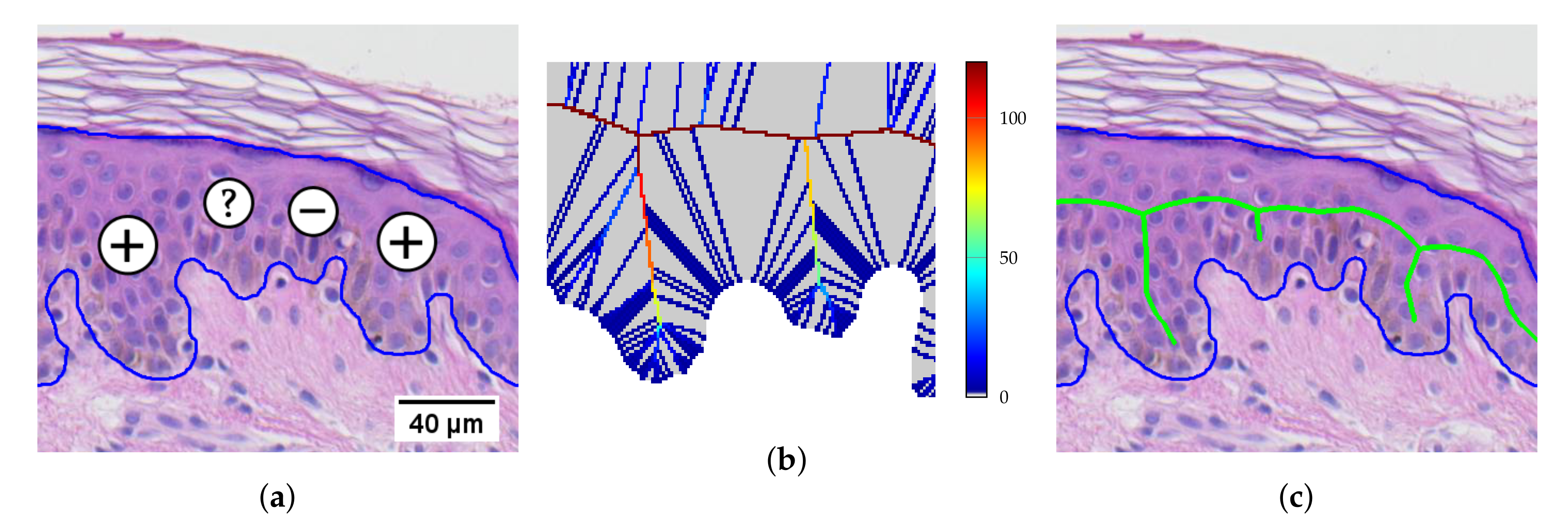
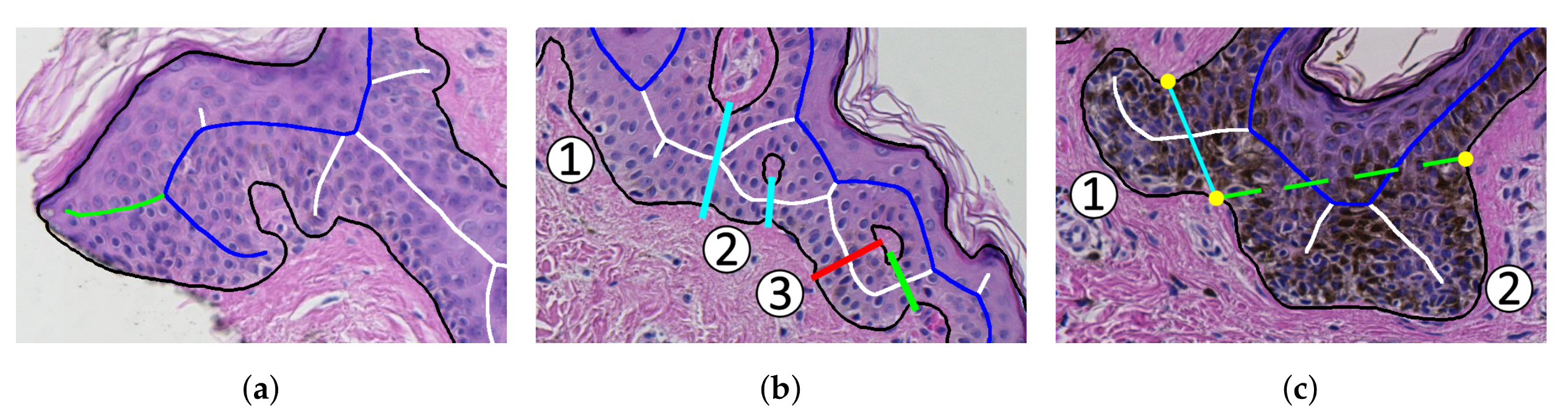
2.7. Determining the Position and Orientation of Retes
2.8. Determining Border Nodes
2.9. Matching Border Nodes with Retes
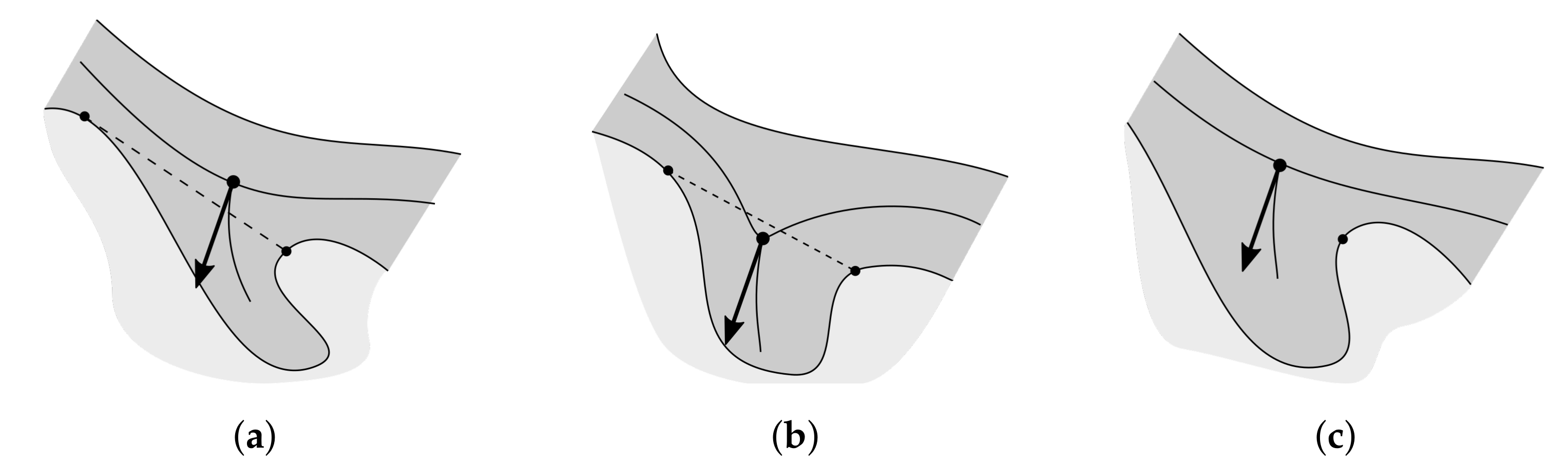
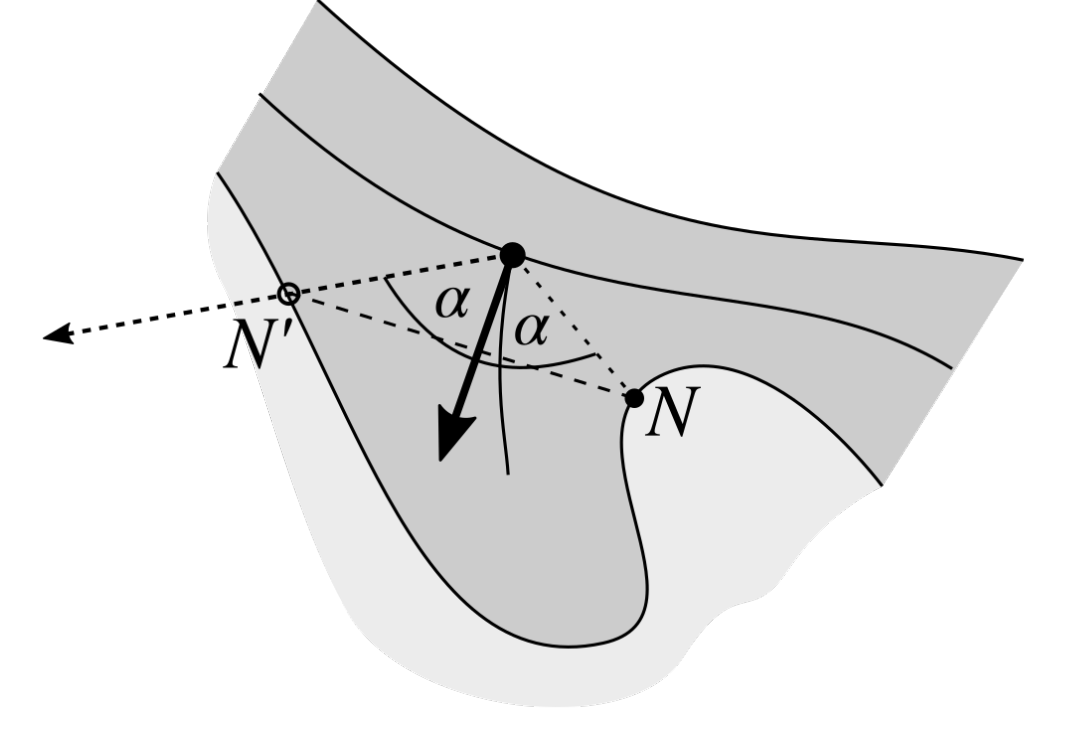
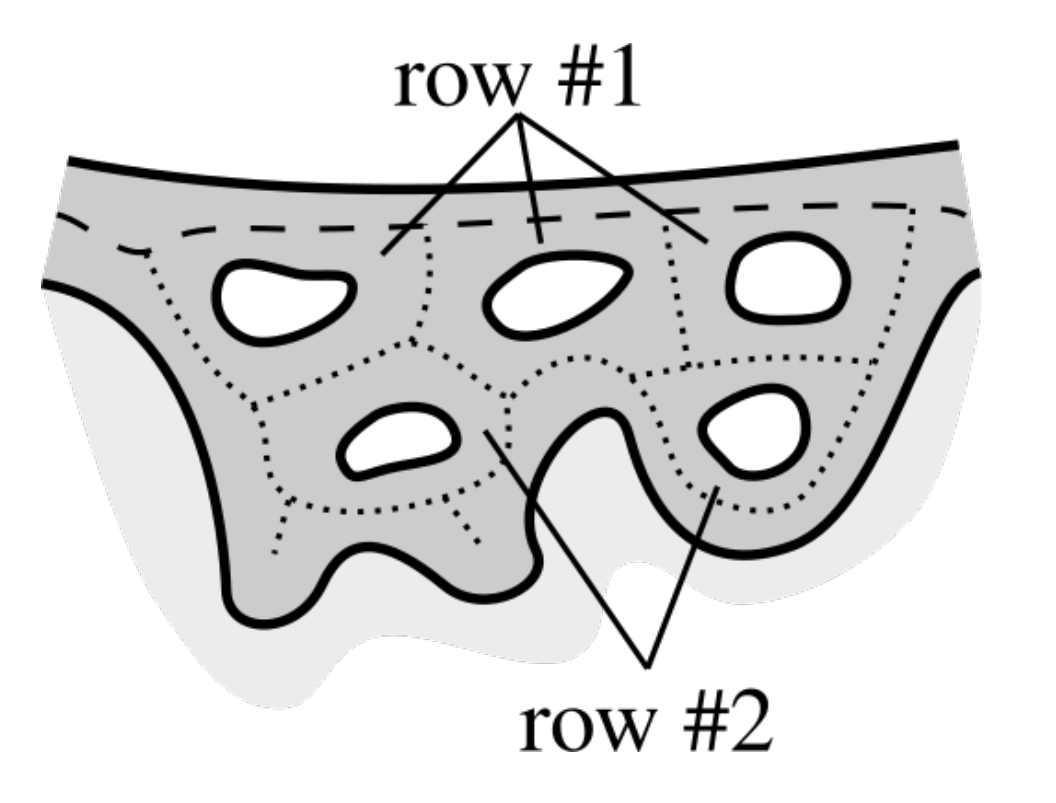
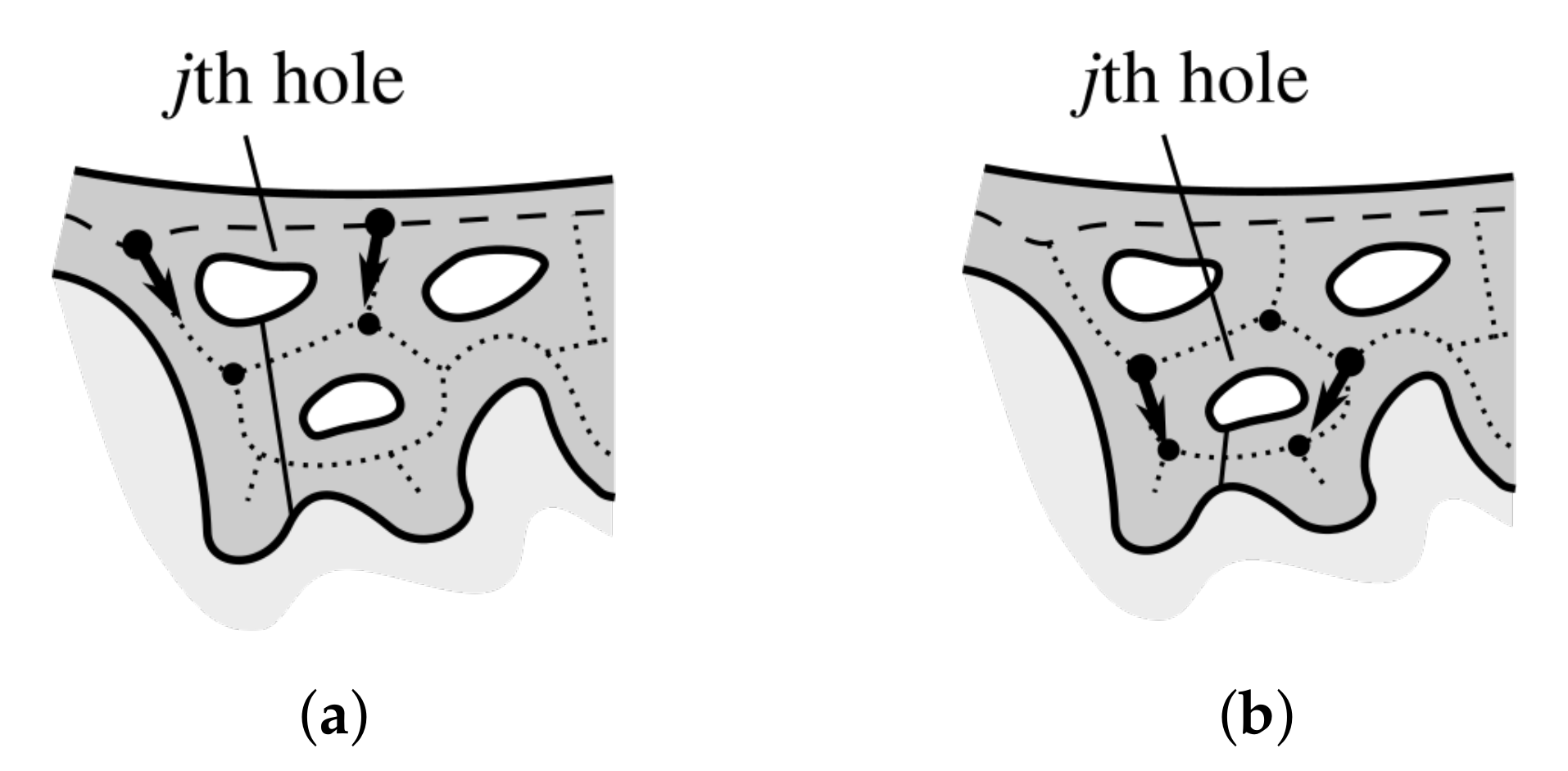
2.10. Merging Adjacent Retes
2.11. Retouching the Main Axis
2.12. Splitting Partially Merged Retes
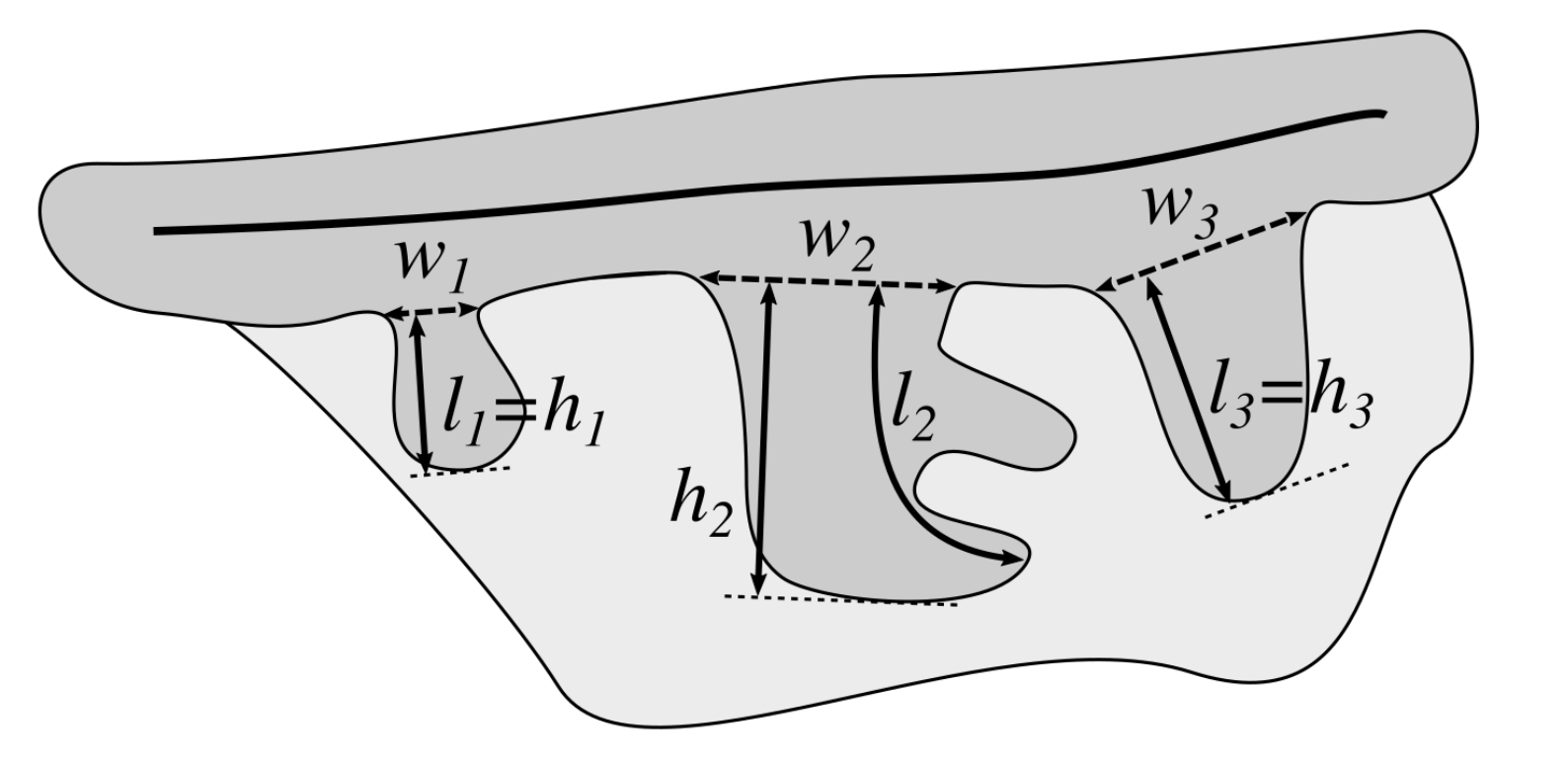
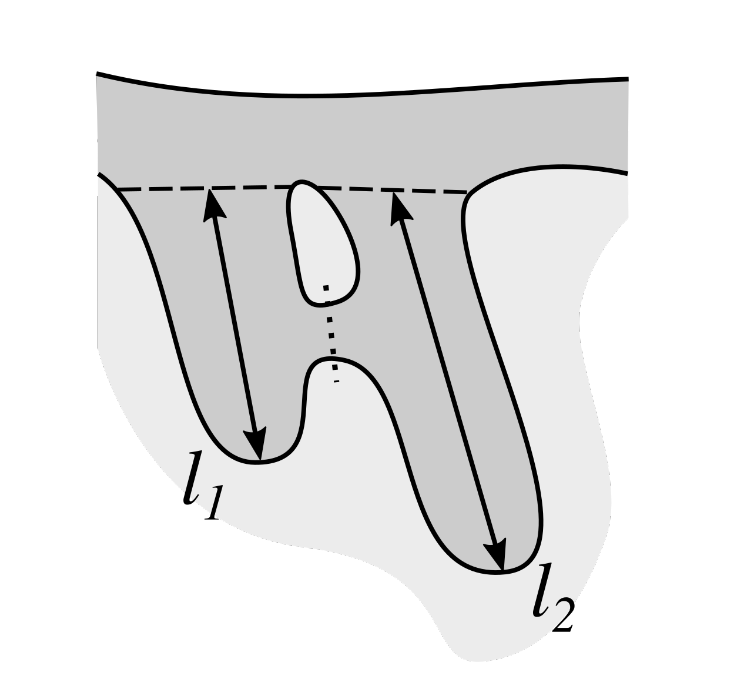
2.13. Computing the Morphometry of Retes
3. Results
3.1. Image Dataset
3.2. Evaluation Metrics
3.3. Parameter Selection
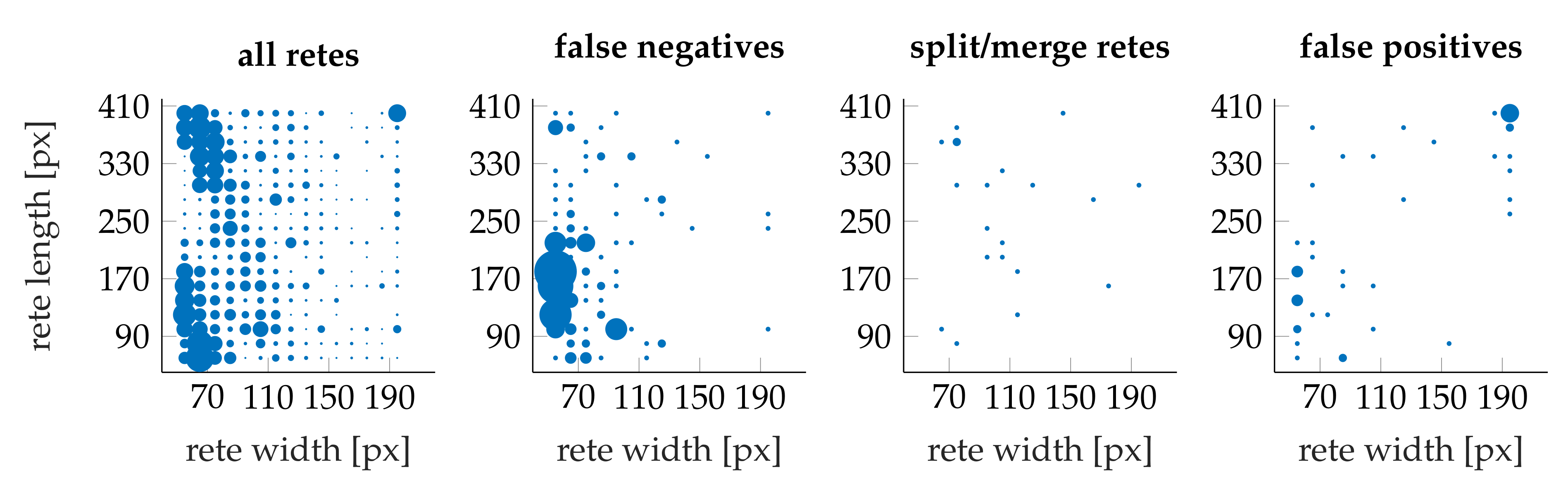
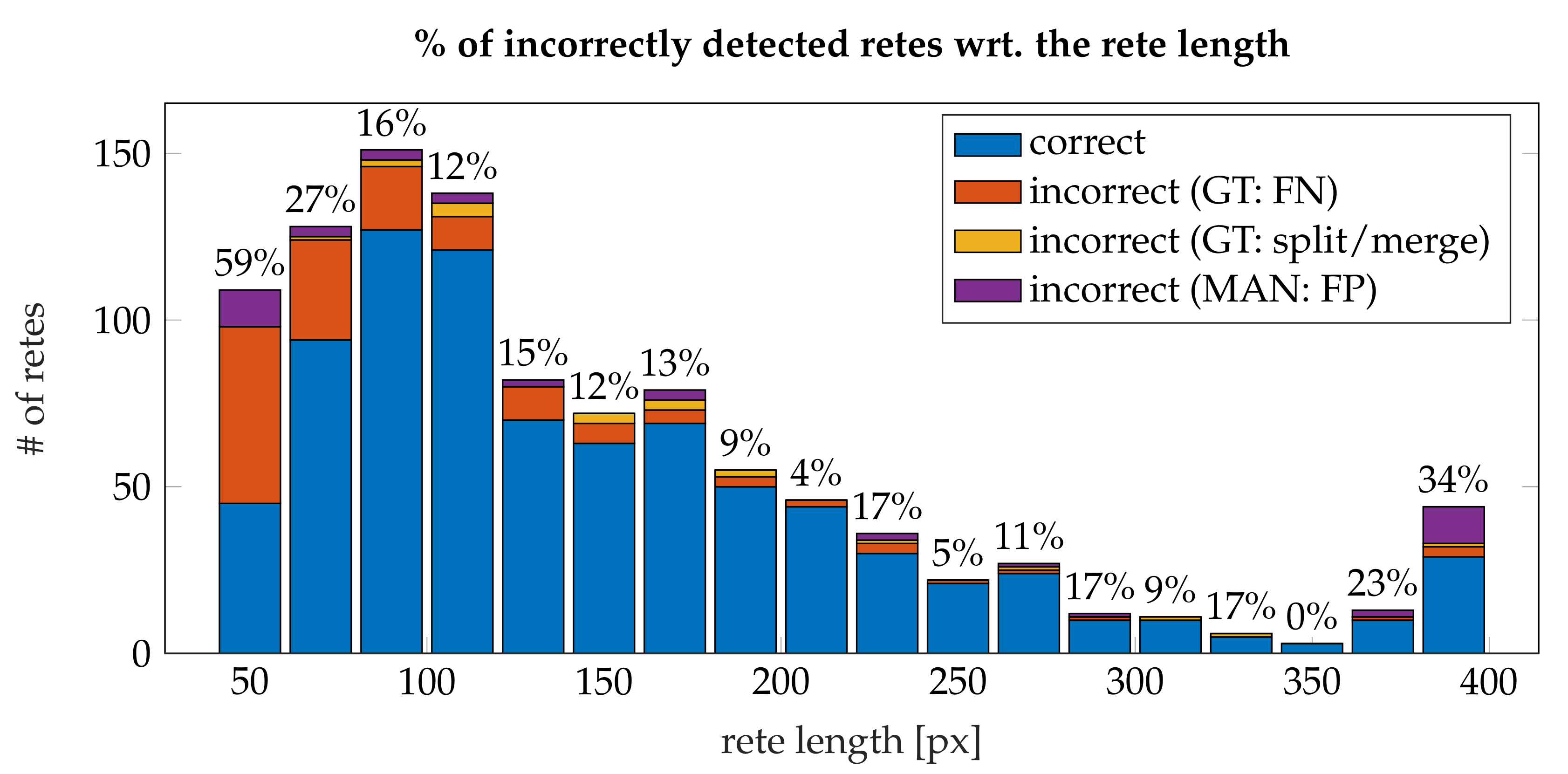
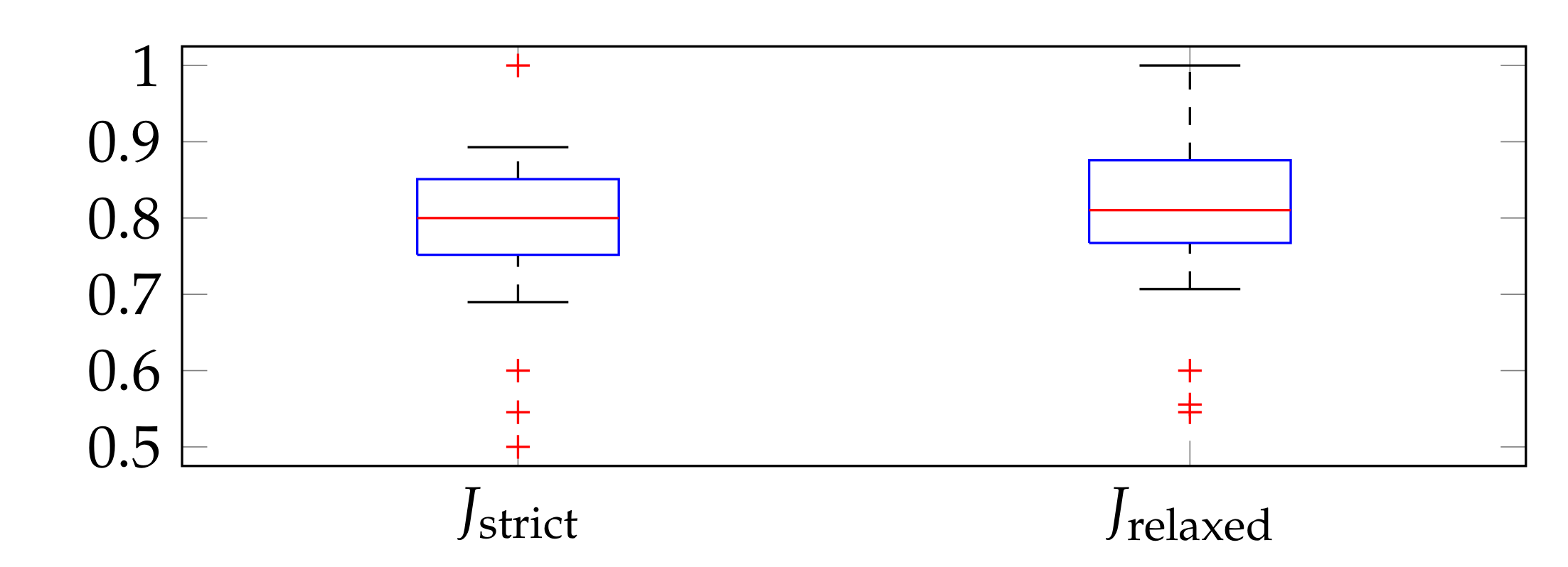
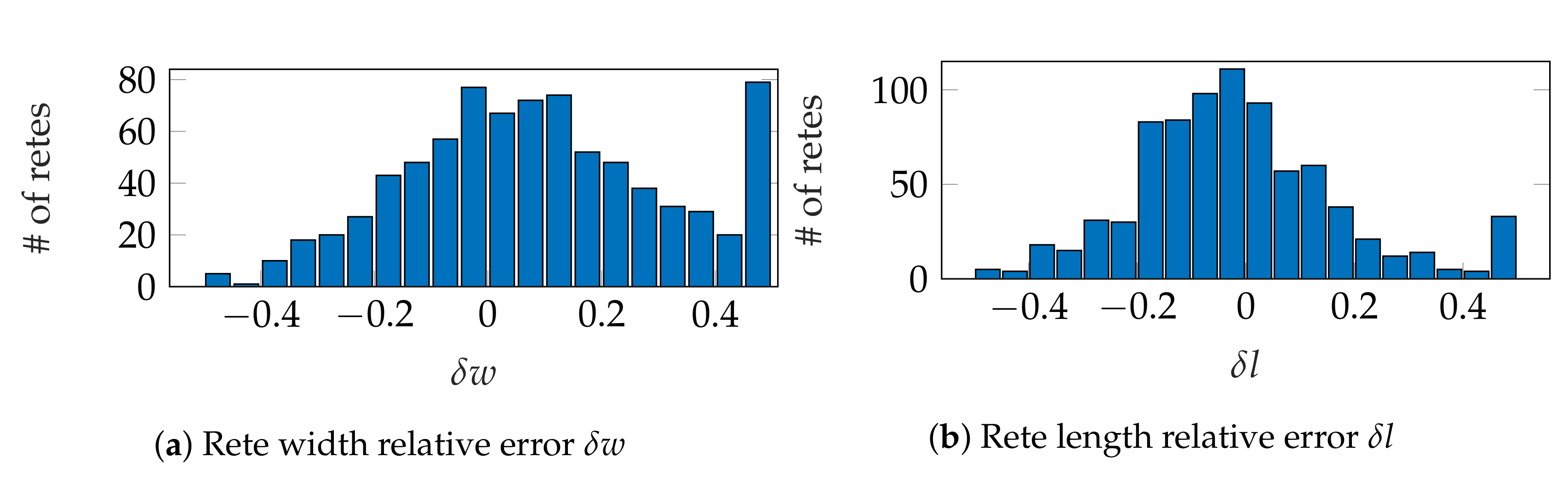
3.4. Performance
- the algorithm incorrectly takes long retes at the end of the lesion as part of the main axis (since usually such a rete is close to the lesion boundary, it is difficult to distinguish a short “tip” of the epidermal plate from a rete);
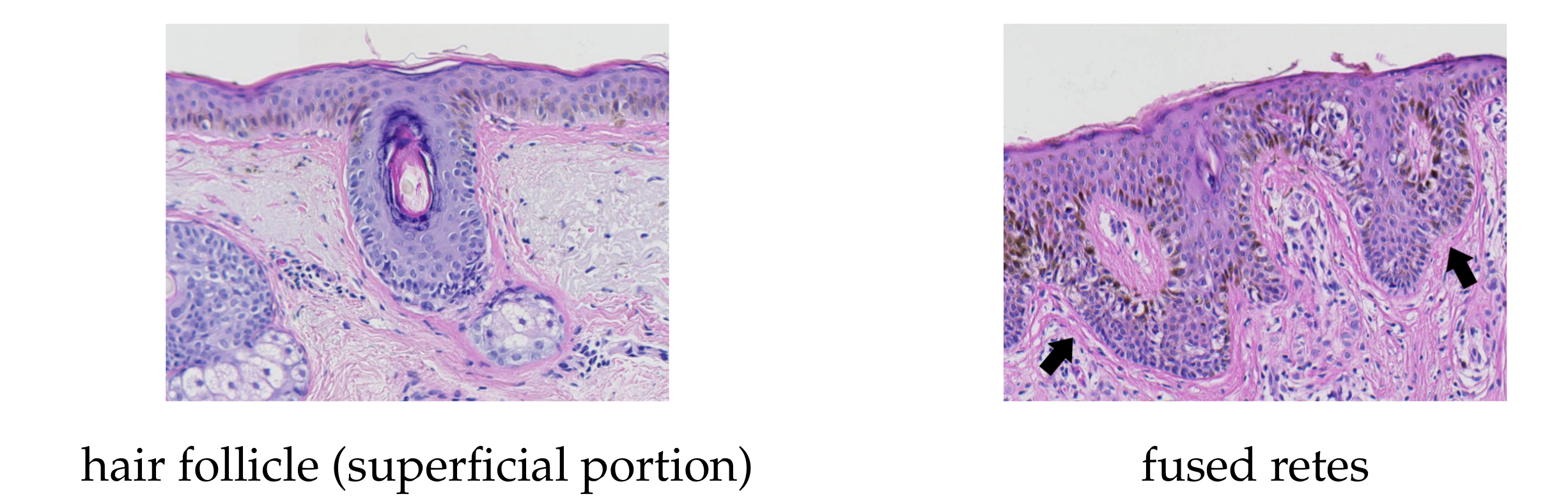
- long retes which do not grow approximately perpendicularly into dermis, but rather are joined with the epidermal plate in multiple places along their boundary, will usually be split by the algorithm as if they were series of short retes fused together;
- our method fails to identify the rete base for a group retes fused near the epidermal plate if total width of such a group is too large.
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Garbe, C.; Leiter, U. Melanoma epidemiology and trends. Clin. Dermatol. 2009, 27, 3–9. [Google Scholar] [CrossRef]
- Cancer Facts & Figures 2016. Available online: http://www.cancer.org/research/cancerfactsstatistics/cancerfactsfigures2016/index (accessed on 15 January 2019).
- Australian Bureau of Statistics. 3303.0 Causes of death, Australia 2015. 2016. Available online: http://www.abs.gov.au/Causes-of-Death (accessed on 21 January 2019).
- Argenziano, G.; Soyer, P.H.; Giorgio, V.D.; Piccolo, D.; Carli, P.; Delfino, M.; Ferrari, A.; Hofmann-Wellenhof, R.; Massi, D.; Mazzocchetti, G.; et al. Interactive Atlas of Dermoscopy; Edra Medical Publishing and New Media: Milan, Italy, 2000. [Google Scholar]
- Braun, R.P.; Gutkowicz-Krusin, D.; Rabinovitz, H.; Cognetta, A.; Hofmann-Wellenhof, R.; Ahlgrimm-Siess, V.; Polsky, D.; Oliviero, M.; Kolm, I.; Googe, P.; et al. Agreement of dermatopathologists in the evaluation of clinically difficult melanocytic lesions: How golden is the ‘gold standard’? Dermatology 2012, 224, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Storm, C.A.; Elder, D.E. Skin. In Rubin’s Pathology: Clinicopathologic Foundations of Medicine, 6th ed.; Rubin, R., Strayer, D.S., Rubin, E., Eds.; Lippincott Williams & Wilkins: Baltimore, Philadelphia, PA, USA, 2011; Chapter 24; pp. 1111–1168. [Google Scholar]
- Massi, G.; LeBoit, P.E. Histological Diagnosis of Nevi and Melanoma; Springer-Verlag: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Barnhill, R.L.; Lugassy, C.; Taylor, E.; Zussman, J. Cutaneous Melanoma. In Pathology of Melanocytic Nevi and Melanoma; Barnhill, R.L., Piepkorn, M., Busam, K.J., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2014; Chapter 10; pp. 331–488. [Google Scholar]
- Lodha, S.; Saggar, S.; Celebi, J.; Silvers, D. Discordance in the histopathologic diagnosis of difficult melanocytic neoplasms in the clinical setting. J. Cutan. Pathol. 2008, 35, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Mar, V.; McLean, C.; Wolfe, R.; Kelly, J. Diagnostic accuracy of malignant melanoma according to subtype. Australas. J. Dermatol. 2013, 55, 35–42. [Google Scholar] [CrossRef]
- Ogiela, L.; Tadeusiewicz, R.; Ogiela, M.R. Cognitive Analysis in Diagnostic DSS-Type IT Systems. In Artificial Intelligence and Soft Computing—ICAISC 2006; Rutkowski, L., Tadeusiewicz, R., Zadeh, L.A., Żurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 962–971. [Google Scholar]
- Tadeusiewicz, R.; Ogiela, L.; Ogiela, M.R. Cognitive Analysis Techniques in Business Planning and Decision Support Systems. In Artificial Intelligence and Soft Computing—ICAISC 2006; Rutkowski, L., Tadeusiewicz, R., Zadeh, L.A., Żurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1027–1039. [Google Scholar]
- Jaworek-Korjakowska, J.; Kłeczek, P. Automatic Classification of Specific Melanocytic Lesions Using Artificial Intelligence. BioMed Res. Int. 2016, 2016, 1–17. [Google Scholar]
- Papadogiorgaki, M.; Mezaris, V.; Chatzizisis, Y.S.; Giannoglou, G.D.; Kompatsiaris, I. Image Analysis Techniques for Automated IVUS Contour Detection. Ultrasound Med. Biol. 2008, 34, 1482–1498. [Google Scholar] [CrossRef] [PubMed]
- Ino, Y.; Kubo, T.; Matsuo, Y.; Yamaguchi, T.; Shiono, Y.; Shimamura, K.; Katayama, Y.; Nakamura, T.; Aoki, H.; Taruya, A.; et al. Optical Coherence Tomography Predictors for Edge Restenosis After Everolimus-Eluting Stent Implantation. Circ. Cardiovasc. Interv. 2016, 9, 1–9. [Google Scholar] [CrossRef]
- Ahmed, J.M.; Mintz, G.S.; Waksman, R.; Lansky, A.J.; Mehran, R.; Wu, H.; Weissman, N.J.; Pichard, A.D.; Satler, L.F.; Kent, K.M.; et al. Serial intravascular ultrasound analysis of edge recurrence after intracoronary gamma radiation treatment of native artery in-stent restenosis lesions. Am. J. Cardiol. 2001, 87, 1145–1149. [Google Scholar] [CrossRef]
- Pociask, E.; Malinowski, K.P.; Ślęzak, M.; Jaworek-Korjakowska, J.; Wojakowski, W.; Roleder, T. Fully Automated Lumen Segmentation Method for Intracoronary Optical Coherence Tomography. J. Healthc. Eng. 2018, 1–13. [Google Scholar] [CrossRef]
- Athanasiou, L.; Nezami, F.R.; Galon, M.Z.; Lopes, A.C.; Lemos, P.A.; de la Torre Hernandez, J.M.; Ben-Assa, E.; Edelman, E.R. Optimized Computer-Aided Segmentation and Three-Dimensional Reconstruction Using Intracoronary Optical Coherence Tomography. IEEE J. Biomed. Health Inform. 2018, 22, 1168–1176. [Google Scholar] [CrossRef]
- Kłeczek, P.; Dyduch, G.; Jaworek-Korjakowska, J.; Tadeusiewicz, R. Automated epidermis segmentation in histopathological images of human skin stained with hematoxylin and eosin. Proc. SPIE 2017, 10140. [Google Scholar] [CrossRef]
- Haggerty, J.; Wang, X.; Dickinson, A.; O’Malley, C.; Martin, E. Segmentation of epidermal tissue with histopathological damage in images of haematoxylin and eosin stained human skin. BMC Med. Imaging 2014, 14, 1–21. [Google Scholar] [CrossRef]
- Lu, C.; Mandal, M. Automated segmentation and analysis of the epidermis area in skin histopathological images. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 5355–5359. [Google Scholar]
- Xu, H.; Mandal, M. Epidermis segmentation in skin histopathological images based on thickness measurement and k-means algorithm. EURASIP J. Image Video Process. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Mokhtari, M.; Rezaeian, M.; Gharibzadeh, S.; Malekian, V. Computer aided measurement of melanoma depth of invasion in microscopic images. Micron 2014, 61, 40–48. [Google Scholar] [CrossRef]
- Noroozi, N.; Zakerolhosseini, A. Computerized measurement of melanocytic tumor depth in skin histopathological images. Micron 2015, 77, 44–56. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Mahmood, M.; Jha, N.; Mandal, M. Automated Segmentation of the Melanocytes in Skin Histopathological Images. IEEE J. Biomed. Health Inform. 2013, 17, 284–296. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Lu, C.; Berendt, R.; Jha, N.; Mandal, M.K. Automated analysis and classification of melanocytic tumor on skin whole slide images. Comput. Med Imaging Graph. Off. J. Comput. Med Imaging Soc. 2018, 66, 124–134. [Google Scholar] [CrossRef] [PubMed]
- Olsen, T.G.; Jackson, B.; Feeser, T.A.; Kent, M.N.; Moad, J.C.; Krishnamurthy, S.; Lunsford, D.D.; Soans, R.E. Diagnostic performance of deep learning algorithms applied to three common diagnoses in dermatopathology. J. Pathol. Inform. 2018, 9, 32. [Google Scholar] [CrossRef] [PubMed]
- Noroozi, N.; Zakerolhosseini, A. Differential diagnosis of squamous cell carcinoma in situ using skin histopathological images. Comput. Biol. Med. 2016, 70, 23–39. [Google Scholar] [CrossRef]
- Filho, M.; Ma, Z.; Tavares, J.A.M. A Review of the Quantification and Classification of Pigmented Skin Lesions: From Dedicated to Hand-Held Devices. J. Med. Syst. 2015, 39, 1–12. [Google Scholar] [CrossRef]
- Oliveira, R.B.; Filho, M.E.; Ma, Z.; Papa, J.P.; Pereira, A.S.; Tavares, J.M.R. Computational methods for the image segmentation of pigmented skin lesions: A review. Comput. Methods Programs Biomed. 2016, 131, 127–141. [Google Scholar] [CrossRef]
- Oliveira, R.B.; Papa, J.A.P.; Pereira, A.S.; Tavares, J.A.M. Computational Methods for Pigmented Skin Lesion Classification in Images: Review and Future Trends. Neural Comput. Appl. 2018, 29, 613–636. [Google Scholar] [CrossRef]
- Yuan, Y.; Chao, M.; Lo, Y. Automatic Skin Lesion Segmentation Using Deep Fully Convolutional Networks With Jaccard Distance. IEEE Trans. Med Imaging 2017, 36, 1876–1886. [Google Scholar] [CrossRef]
- Jafari, M.H.; Karimi, N.; Nasr-Esfahani, E.; Samavi, S.; Soroushmehr, S.M.R.; Ward, K.; Najarian, K. Skin lesion segmentation in clinical images using deep learning. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Brisbane, Australia, 16–20 August 2016; pp. 337–342. [Google Scholar] [CrossRef]
- Li, Y.; Shen, L. Skin Lesion Analysis towards Melanoma Detection Using Deep Learning Network. Sensors 2018, 18, 556. [Google Scholar] [CrossRef]
- Ma, Z.; Tavares, J.; Natal Jorge, R. A Review on the Current Segmentation Algorithms for Medical Images. In Proceedings of the 1st International Conference on Computer Imaging Theory and Applications (IMAGAPP 2009), Lisboa, Portugal, 5–8 February 2009; pp. 135–140. [Google Scholar]
- Gonçalves, P.; Tavares, J.; Natal Jorge, R. Segmentation and Simulation of Objects Represented in Images using Physical Principles. Comput. Model. Eng. Sci. 2008, 32. [Google Scholar] [CrossRef]
- Ma, Z.; Tavares, J.M.R.; Jorge, R.N.; Mascarenhas, T. A review of algorithms for medical image segmentation and their applications to the female pelvic cavity. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 235–246. [Google Scholar] [CrossRef]
- Mahy, M.; van Eycken, L.; Oosterlinck, A. Evaluation of Uniform Color Spaces Developed after the Adoption of CIELAB and CIELUV. Color Res. Appl. 1994, 19, 105–121. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Telea, A.; van Wijk, J.J. An augmented Fast Marching Method for computing skeletons and centerlines. In Proceedings of the Symposium on Data Visualisation 2002 (VISSYM ’02), Barcelona, Spain, 27–29 May 2002; pp. 251–260. [Google Scholar]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Bresenham, J.E. Algorithm for computer control of a digital plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
- University of Michigan Virtual Slide Box. 2013. Available online: https://www.pathology.med.umich.edu/slides/search.php?collection=Andea&dxview=show (accessed on 5 February 2019).
- UBC Virtual Slidebox. 2005. Available online: http://histo.anat.ubc.ca/PATHOLOGY/Anatomical%20Pathology/DermPath/ (accessed on 6 February 2019).
- Huzaira, M.; Rius, F.; Rajadhyaksha, M.; Anderson, R.R.; Gonzaález, S. Topographic Variations in Normal Skin, as Viewed by In Vivo Reflectance Confocal Microscopy. J. Investig. Dermatol. 2001, 116, 846–852. [Google Scholar] [CrossRef]
- Sandby-Möller, J.; Poulsen, T.; Wulf, H.C. Epidermal Thickness at Different Body Sites: Relationship to Age, Gender, Pigmentation, Blood Content, Skin Type and Smoking Habits. Acta Derm. Venereol. 2003, 83, 410–413. [Google Scholar] [CrossRef] [PubMed]
- Watt, F.M.; Green, H. Involucrin Synthesis Is Correlated with Cell Size in Human Epidermal Cultures. Involucrin Synth. Is Correl. Cell Size Hum. Epidermal Cult. 1981, 90, 738–742. [Google Scholar] [CrossRef] [PubMed]
| Set | Mag. | μm/px | Image Format | Device | Laboratory |
|---|---|---|---|---|---|
| 1 | 0.345 | TIFF | Olympus BX51 + Pike F505C VC50 | Jagiellonian Univ. MC | |
| 2 | 0.44 | TIFF | Axio Scan.Z1 | Jagiellonian Univ. MC | |
| 3 | 0.25 | JPEG2000 q70 | Aperio AT2 | Univ. of Michigan [43] | |
| 4 | 0.25 | JPEG q30 | Aperio ScanScope CS2 | Univ. of British Columbia [44] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleczek, P.; Dyduch, G.; Graczyk-Jarzynka, A.; Jaworek-Korjakowska, J. A New Approach to Border Irregularity Assessment with Application in Skin Pathology. Appl. Sci. 2019, 9, 2022. https://doi.org/10.3390/app9102022
Kleczek P, Dyduch G, Graczyk-Jarzynka A, Jaworek-Korjakowska J. A New Approach to Border Irregularity Assessment with Application in Skin Pathology. Applied Sciences. 2019; 9(10):2022. https://doi.org/10.3390/app9102022
Chicago/Turabian StyleKleczek, Pawel, Grzegorz Dyduch, Agnieszka Graczyk-Jarzynka, and Joanna Jaworek-Korjakowska. 2019. "A New Approach to Border Irregularity Assessment with Application in Skin Pathology" Applied Sciences 9, no. 10: 2022. https://doi.org/10.3390/app9102022
APA StyleKleczek, P., Dyduch, G., Graczyk-Jarzynka, A., & Jaworek-Korjakowska, J. (2019). A New Approach to Border Irregularity Assessment with Application in Skin Pathology. Applied Sciences, 9(10), 2022. https://doi.org/10.3390/app9102022






