A Comparative Study of Multiphase Lattice Boltzmann Methods for Bubble-Dendrite Interaction during Solidification of Alloys
Abstract
1. Introduction
- Shan-Chen (pseudopotential) model [34];
2. Cellular Automaton Model for Dendritic Growth
3. Single Phase Lattice Boltzmann Equation
4. The Original Shan-Chen Model for Multiphase Flow
5. Improvements to the Original Shan-Chen Model
5.1. Realistic Equation of State
5.2. Force with a Higher Order of Isotropy (E8 Force Scheme) and Middle-Range Repulsion Force
6. Phase Field Lattice Boltzmann Method
6.1. Solving the Cahn-Hillard Equation for Interface Capturing with the WENO Scheme
6.2. Phase Field LB for the Flow Field
7. Results
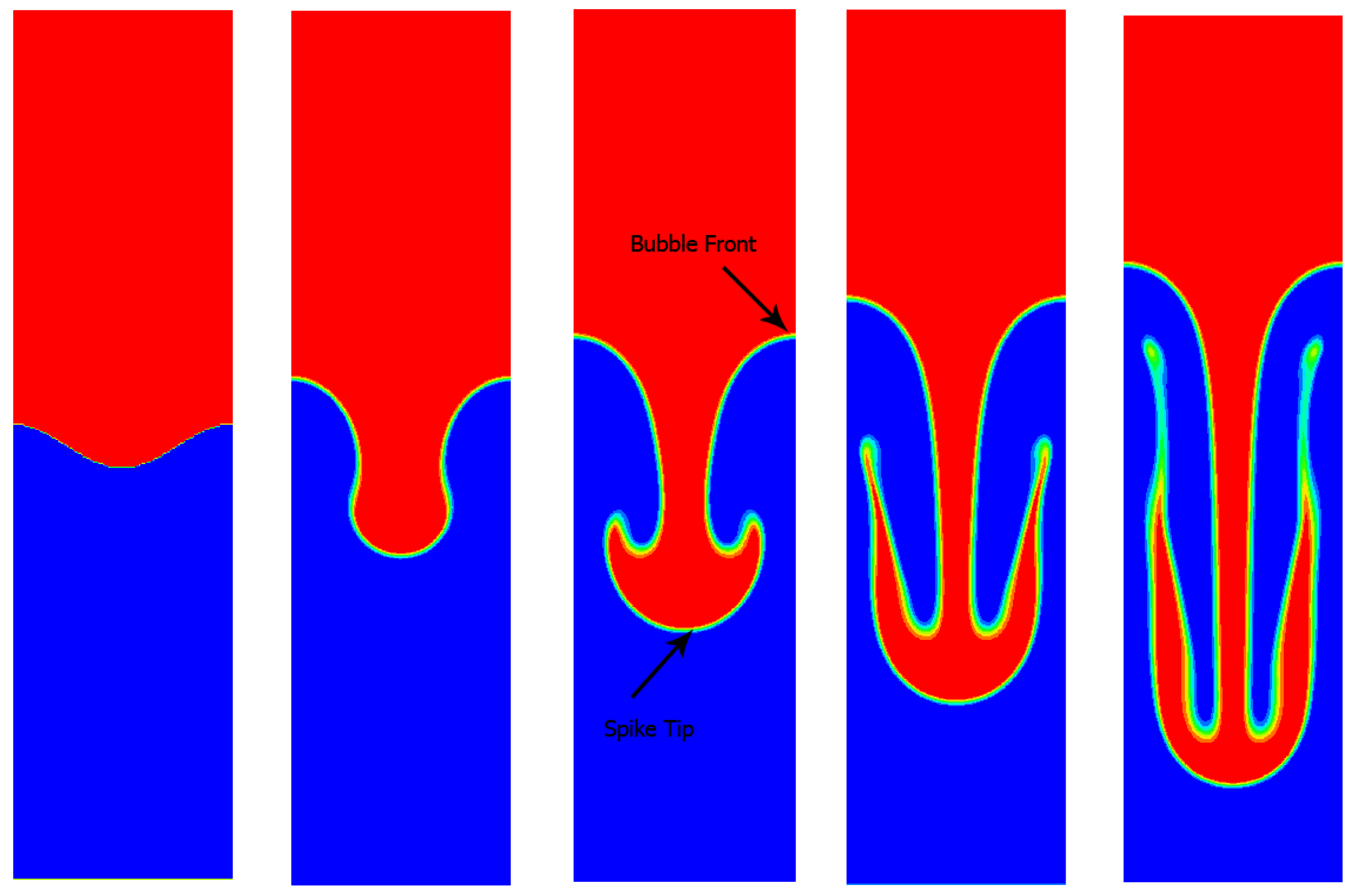
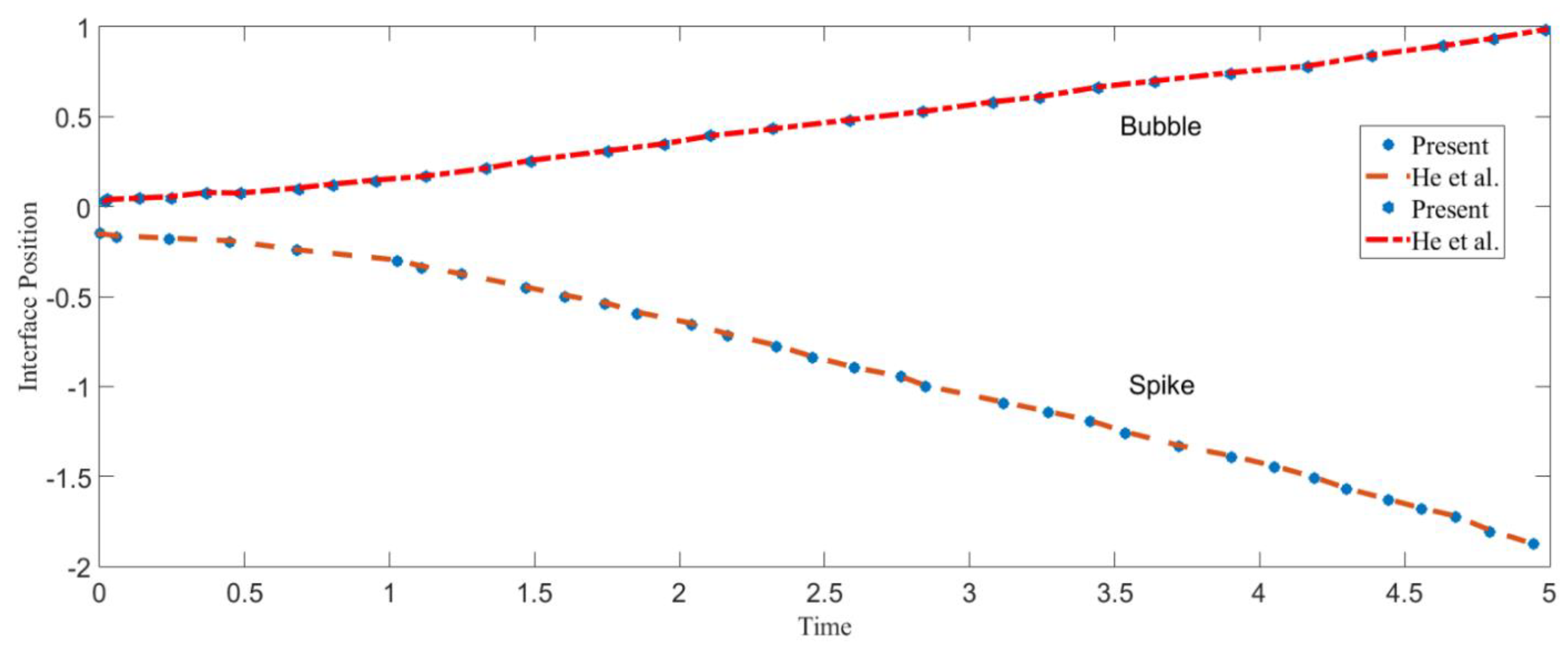
7.1. Rayleigh Instability
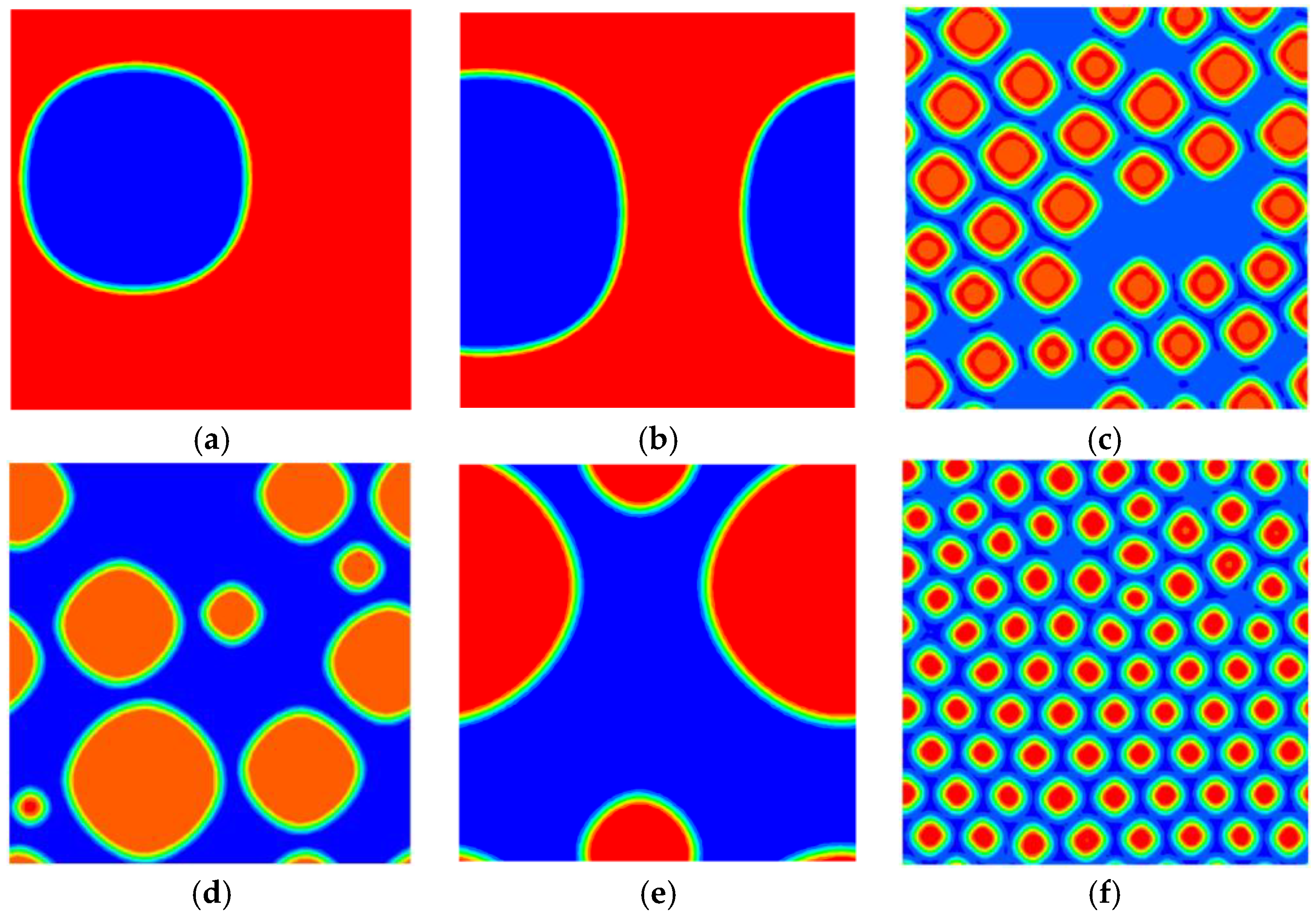
7.2. The Phase Separation Problem with the Enhanced Model
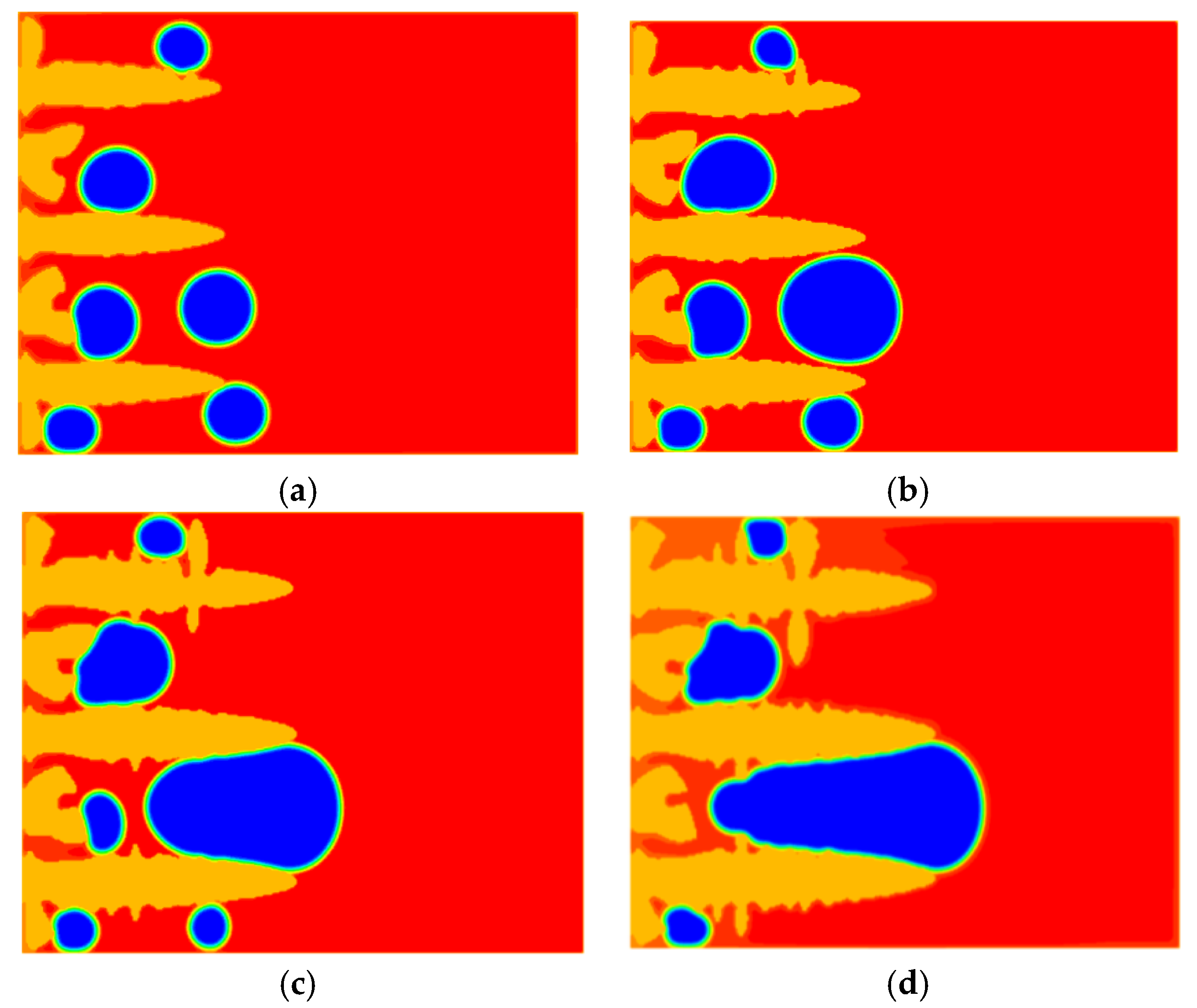
7.3. Columnar Dendritic Growth with Original Shan-Chen Model
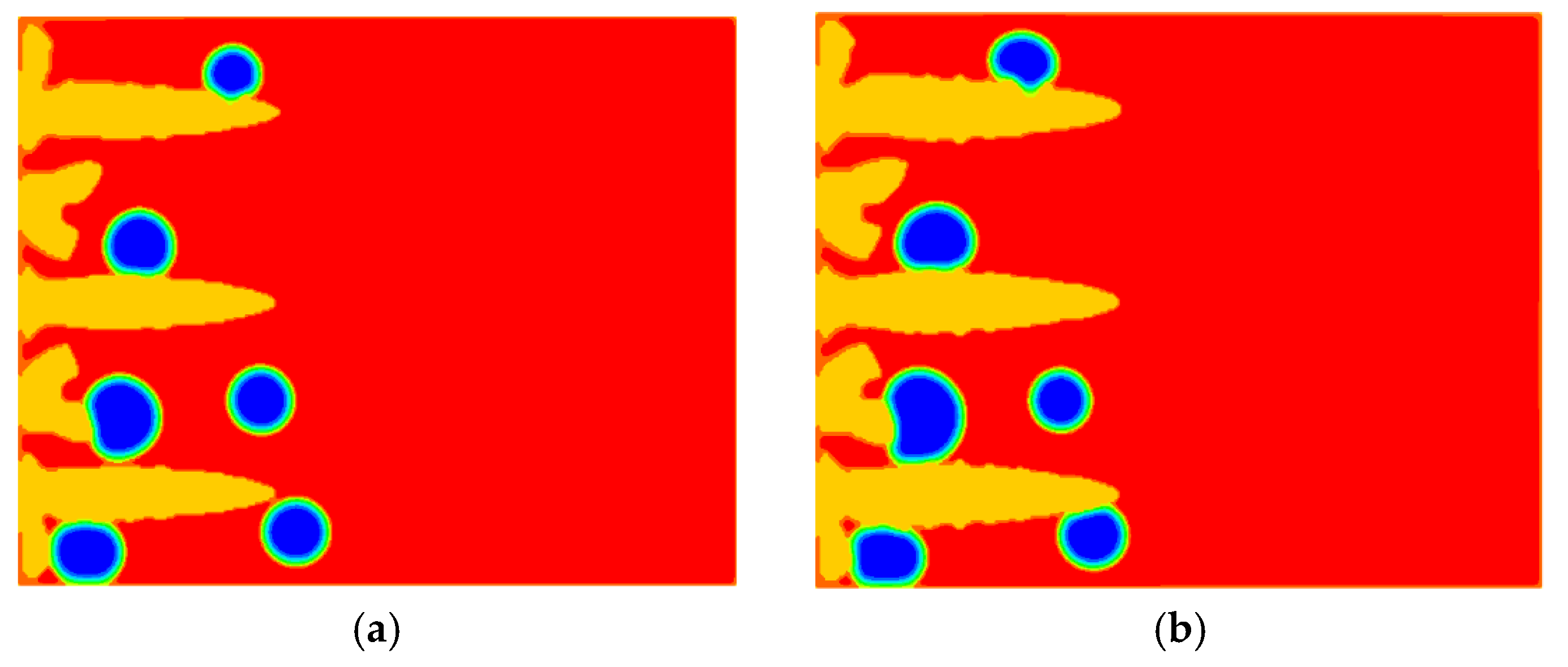
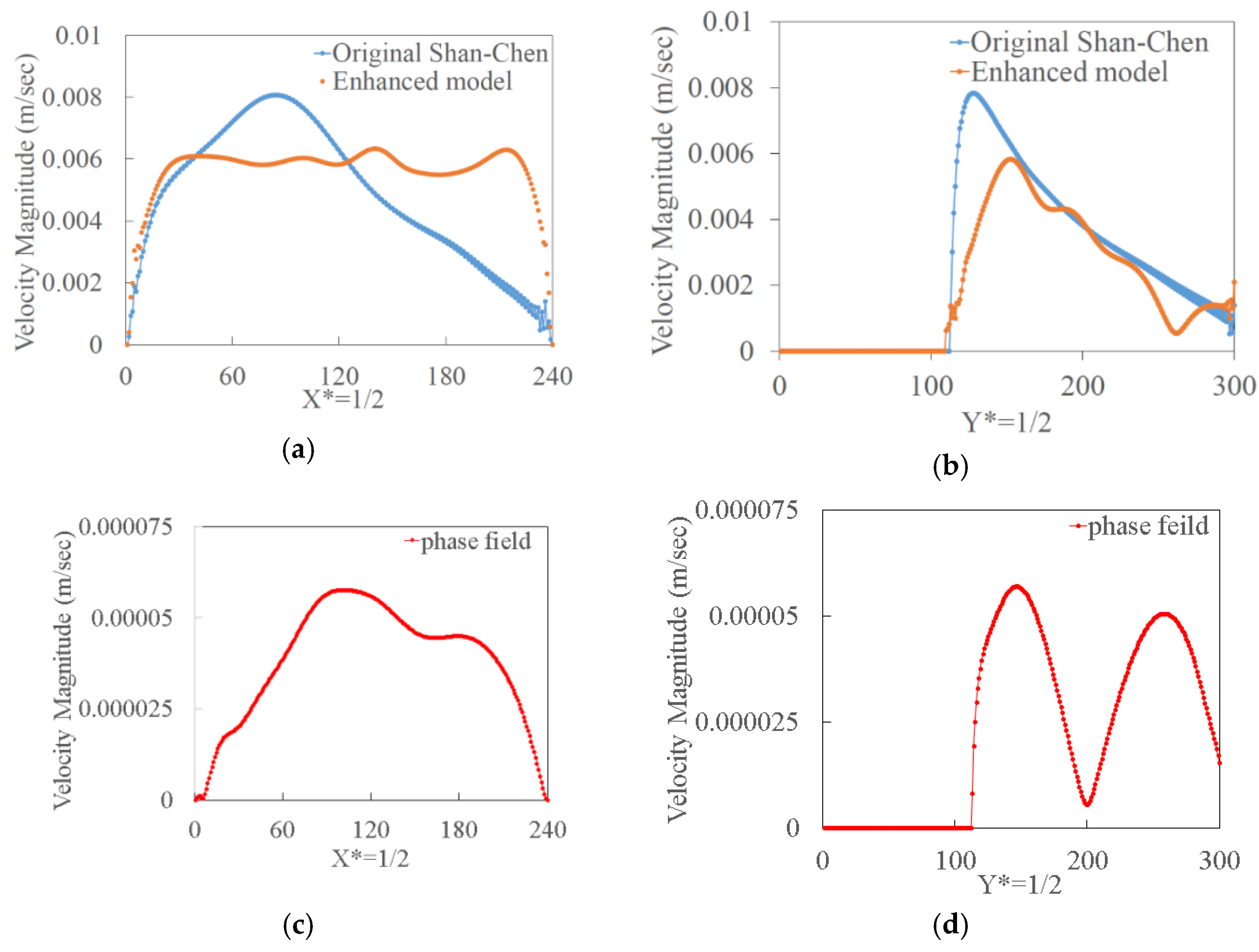
7.4. Dendritic Growth with the Enhanced Shan-Chen Model
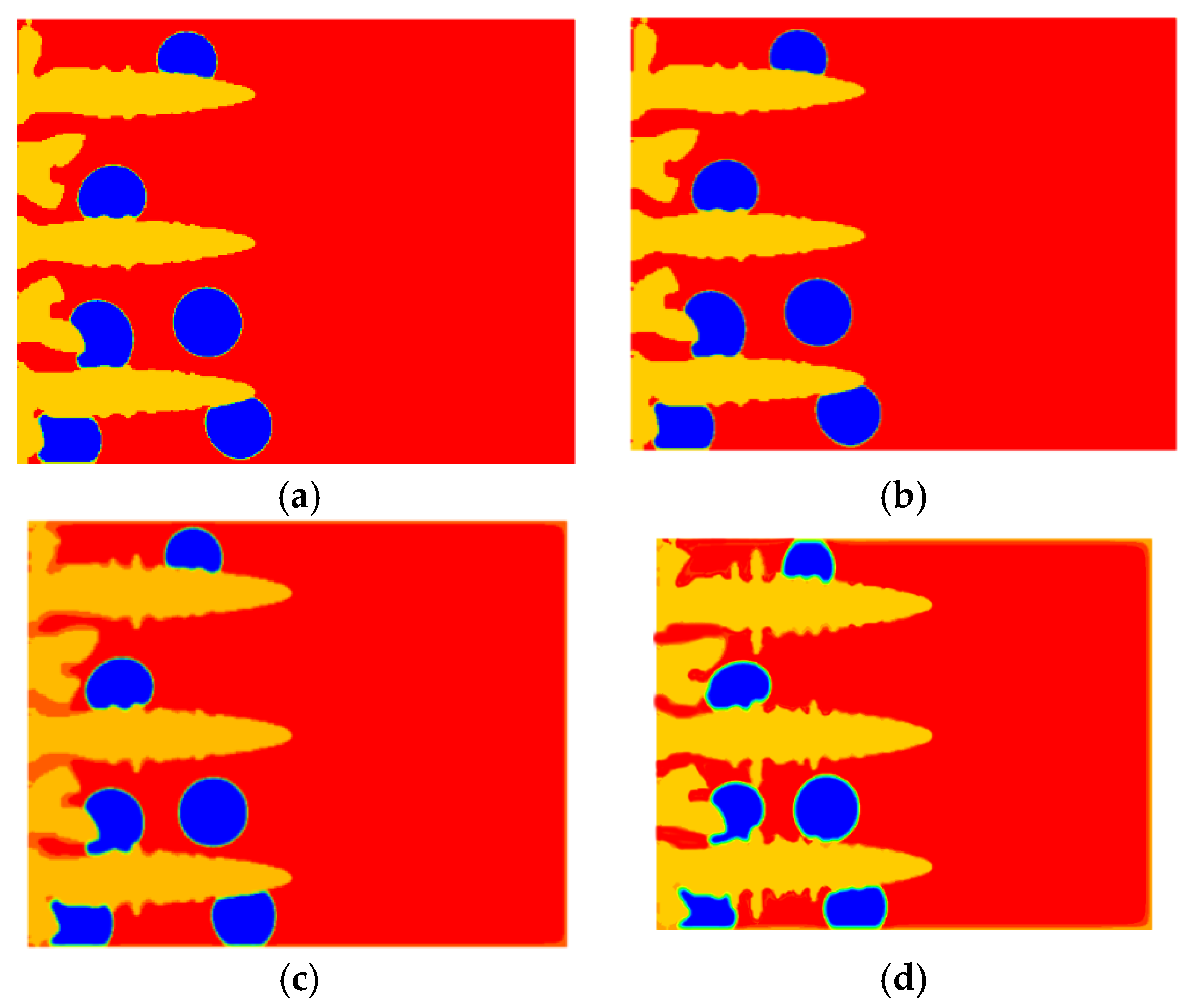
7.5. Dendritic Growth with the Phase Field Model
8. Comparison with PFMI Experiments
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| local interface equilibrium solute concentration | |
| local actual solute concentration | |
| D | solute diffusivity |
| increase in the solid fraction | |
| K | interface curvature |
| distribution function | |
| relaxation time | |
| kinematic viscosity in LB | |
| discrete lattice velocity in direction α | |
| first belt weight coefficient | |
| effective mass | |
| p | pressure |
| W | Width of the interface |
| Chemical potential | |
| temperature | |
| Equilibrium liquidus temperature | |
| Gibbs–Thomson coefficient | |
| anisotropy coefficient | |
| k | partitioning coefficient |
| R | gas constant |
| initial concentration | |
| G1 | first belt cohesion force parameter |
| G2 | s belt cohesion force parameter |
| second belt weight coefficient | |
| discrete lattice velocity in direction γ | |
| preferential orientation | |
| liquidus slope | |
| Greek symbol | |
| growth angle | |
| ρ | density |
| local order parameter | |
| mobility | |
| Subscripts | |
| cr | critical |
| s | solid |
| l | liquid |
| g | gas |
References
- Rudy, J.; Rupert, E. Effects of porosity on mechanical properties of aluminum welds. Weld. J. 1970, 49, 322. [Google Scholar]
- Wang, Q.; Apelian, D.; Lados, D. Fatigue behavior of A356-T6 aluminum cast alloys. Part I. Effect of casting defects. J. Light Met. 2001, 1, 73–84. [Google Scholar] [CrossRef]
- Ammar, H.R.; Samuel, A.M.; Samuel, F.H. Porosity and the fatigue behavior of hypoeutectic and hypereutectic aluminum–silicon casting alloys. Int. J. Fatigue 2008, 30, 1024–1035. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, G.; Xiao, C.; Lee, T.L.; Han, B.; Li, Z.; Daisenberger, D.; Mi, J. The interdendritic-melt solidification control (IMSC) and its effects on the porosity and phase change of a Ni-based superalloy. Scr. Mater. 2014, 74, 84–87. [Google Scholar] [CrossRef]
- Lee, S.G.; Gokhale, A.M. Formation of gas induced shrinkage porosity in Mg-alloy high-pressure die-castings. Scr. Mater. 2006, 55, 387–390. [Google Scholar] [CrossRef]
- Jie, Z.; Zhang, J.; Huang, T.; Su, H.; Li, Y.; Liu, L.; Yang, W.; Fu, H. Enhanced Grain Refinement and Porosity Control of the Polycrystalline Superalloy by a Modified Thermally Controlled Solidification. Adv. Eng. Mater. 2016, 18, 1785–1791. [Google Scholar] [CrossRef]
- Sun, D.; Zhu, M.; Wang, J.; Sun, B. Lattice Boltzmann modeling of bubble formation and dendritic growth in solidification of binary alloys. Int. J. Heat Mass Transf. 2016, 94, 474–487. [Google Scholar] [CrossRef]
- Carte, A. Air bubbles in ice. Proc. Phys. Soc. 1961, 77, 757. [Google Scholar] [CrossRef]
- Han, Q. Motion of bubbles in the mushy zone. Scr. Mater. 2006, 55, 871–874. [Google Scholar] [CrossRef]
- Lee, P.; Hunt, J. Hydrogen porosity in directional solidified aluminium-copper alloys: In situ observation. Acta Mater. 1997, 45, 4155–4169. [Google Scholar] [CrossRef]
- Lei, Z.; Hengcheng, L.; Ye, P.; Qigui, W.; Guoxiong, S. In-situ observation of porosity formation during directional solidification of Al-Si Casting Alloys. Res. Dev. 2011. [Google Scholar]
- Lee, P.D.; Hunt, J.D. Measuring the nucleation of hydrogen porosity during the solidification of aluminium-copper alloys. Scr. Mater. 1997, 36, 399–404. [Google Scholar] [CrossRef]
- Eshraghi, M.; Jelinek, B.; Felicelli, S.D. Large-scale three-dimensional simulation of dendritic solidification using lattice Boltzmann method. JOM 2015, 67, 1786–1792. [Google Scholar] [CrossRef]
- Karagadde, S.; Sundarraj, S.; Dutta, P. A model for growth and engulfment of gas microporosity during aluminum alloy solidification process. Comput. Mater. Sci. 2012, 65, 383–394. [Google Scholar] [CrossRef]
- Tiedje, N.S.; Taylor, J.A.; Easton, M.A. A new multi-zone model for porosity distribution in Al–Si alloy castings. Acta Mater. 2013, 61, 3037–3049. [Google Scholar] [CrossRef]
- Du, L.; Wang, L.; Zheng, B.; Du, H. Phase-field modeling of microstructure evolution during solidification in presence of gas bubble. Comput. Mater. Sci. 2016, 114, 94–98. [Google Scholar] [CrossRef]
- Hou, T.Y.; Lowengrub, J.S.; Shelley, M.J. Boundary Integral Methods for Multicomponent Fluids and Multiphase Materials. J. Comput. Phys. 2001, 169, 302–362. [Google Scholar] [CrossRef]
- Souli, M.h.; Benson, D.J. Arbitrary Lagrangian Eulerian and Fluid-Structure Interaction: Numerical Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- She, D.; Kaufman, R.; Lim, H.; Melvin, J.; Hsu, A.; Glimm, J. Front-Tracking Methods. Handb. Numer. Anal. 2016, 17, 383–402. [Google Scholar] [CrossRef]
- Muradoglu, M.; Tasoglu, S. A front-tracking method for computational modeling of impact and spreading of viscous droplets on solid walls. Comput. Fluids 2010, 39, 615–625. [Google Scholar] [CrossRef]
- Terashima, H.; Tryggvason, G. A front-tracking method with projected interface conditions for compressible multi-fluid flows. Comput. Fluids 2010, 39, 1804–1814. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.-J. A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Zhu, M.; Stefanescu, D. Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys. Acta Mater. 2007, 55, 1741–1755. [Google Scholar] [CrossRef]
- Uzgoren, E.; Sim, J.; Shyy, W. Marker-based, 3-D adaptive Cartesian grid method for multiphase flow around irregular geometries. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 1239. [Google Scholar]
- van Wachem, B.G.M.; Almstedt, A.E. Methods for multiphase computational fluid dynamics. Chem. Eng. J. 2003, 96, 81–98. [Google Scholar] [CrossRef]
- Wörner, M. Numerical modeling of multiphase flows in microfluidics and micro process engineering: A review of methods and applications. Microfluid. Nanofluidics 2012, 12, 841–886. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.-L.; Tao, W.-Q. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Huang, H.; Sukop, M.; Lu, X. Multiphase Lattice Boltzmann Methods: Theory and Application; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Huang, J.J.; Shu, C.; Feng, J.J.; Chew, Y.T. A Phase-Field-Based Hybrid Lattice-Boltzmann Finite-Volume Method and Its Application to Simulate Droplet Motion under Electrowetting Control. J. Adhes. Sci. Technol. 2012, 26, 1825–1851. [Google Scholar] [CrossRef]
- Connington, K.; Lee, T. A review of spurious currents in the lattice Boltzmann method for multiphase flows. J. Mech. Sci. Technol. 2012, 26, 3857–3863. [Google Scholar] [CrossRef]
- Rothman, D.H.; Keller, J.M. Immiscible cellular-automaton fluids. J. Stat. Phys. 1988, 52, 1119–1127. [Google Scholar] [CrossRef]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Swift, M.R.; Orlandini, E.; Osborn, W.; Yeomans, J. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 1996, 54, 5041. [Google Scholar] [CrossRef]
- Inamuro, T.; Ogata, T.; Tajima, S.; Konishi, N. A lattice Boltzmann method for incompressible two-phase flows with large density differences. J. Comput. Phys. 2004, 198, 628–644. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A Lattice Boltzmann Scheme for Incompressible Multiphase Flow and Its Application in Simulation of Rayleigh–Taylor Instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Lee, T.; Liu, L. Lattice Boltzmann simulations of micron-scale drop impact on dry surfaces. J. Comput. Phys. 2010, 229, 8045–8063. [Google Scholar] [CrossRef]
- Huang, H.; Huang, J.-J.; Lu, X.-Y. A mass-conserving axisymmetric multiphase lattice Boltzmann method and its application in simulation of bubble rising. J. Comput. Phys. 2014, 269, 386–402. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.-L. A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ratio. J. Comput. Phys. 2005, 206, 16–47. [Google Scholar] [CrossRef]
- Shao, J.Y.; Shu, C. A hybrid phase field multiple relaxation time lattice Boltzmann method for the incompressible multiphase flow with large density contrast. Int. J. Numer. Methods Fluids 2015, 77, 526–543. [Google Scholar] [CrossRef]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18, 042101. [Google Scholar] [CrossRef]
- Shan, X. Analysis and reduction of the spurious current in a class of multiphase lattice Boltzmann models. Phys. Rev. E 2006, 73, 047701. [Google Scholar] [CrossRef]
- Chibbaro, S.; Falcucci, G.; Chiatti, G.; Chen, H.; Shan, X.; Succi, S. Lattice Boltzmann models for nonideal fluids with arrested phase-separation. Phys. Rev. E 2008, 77, 036705. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhang, Y.; Valocchi, A.J. Modeling and simulation of thermocapillary flows using lattice Boltzmann method. J. Comput. Phys. 2012, 231, 4433–4453. [Google Scholar] [CrossRef]
- Zu, Y.Q.; He, S. Phase-field-based lattice Boltzmann model for incompressible binary fluid systems with density and viscosity contrasts. Phys. Rev. E 2013, 87, 043301. [Google Scholar] [CrossRef] [PubMed]
- Safari, H.; Rahimian, M.H.; Krafczyk, M. Consistent simulation of droplet evaporation based on the phase-field multiphase lattice Boltzmann method. Phys. Rev. E 2014, 90, 033305. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Valocchi, A.J.; Zhang, Y.; Kang, Q. Lattice Boltzmann phase-field modeling of thermocapillary flows in a confined microchannel. J. Comput. Phys. 2014, 256, 334–356. [Google Scholar] [CrossRef]
- Tiribocchi, A.; Stella, N.; Gonnella, G.; Lamura, A. Hybrid lattice Boltzmann model for binary fluid mixtures. Phys. Rev. E 2009, 80, 026701. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Zhu, M.F.; Sun, D.K.; Dai, T.; Han, Q.Y.; Raabe, D. Modelling of dendritic growth and bubble formation. Iop Conf. Ser. Mater. Sci. Eng. 2012, 33, 012103. [Google Scholar] [CrossRef]
- Yin, H.; Felicelli, S.D.; Wang, L. Simulation of a dendritic microstructure with the lattice Boltzmann and cellular automaton methods. Acta Mater. 2011, 59, 3124–3136. [Google Scholar] [CrossRef]
- Eshraghi, M.; Felicelli, S.D.; Jelinek, B. Three dimensional simulation of solutal dendrite growth using lattice Boltzmann and cellular automaton methods. J. Cryst. Growth 2012, 354, 129–134. [Google Scholar] [CrossRef]
- Jelinek, B.; Eshraghi, M.; Felicelli, S.; Peters, J.F. Large-scale parallel lattice Boltzmann–cellular automaton model of two-dimensional dendritic growth. Comput. Phys. Commun. 2014, 185, 939–947. [Google Scholar] [CrossRef]
- Qian, Y.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. EPL (Europhys. Lett.) 1992, 17, 479. [Google Scholar] [CrossRef]
- Benzi, R.; Biferale, L.; Sbragaglia, M.; Succi, S.; Toschi, F. Mesoscopic modeling of a two-phase flow in the presence of boundaries: The contact angle. Phys. Rev. E 2006, 74, 021509. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.Y.; Shu, C.; Huang, H.B.; Chew, Y.T. Free-energy-based lattice Boltzmann model for the simulation of multiphase flows with density contrast. Phys. Rev. E 2014, 89, 033309. [Google Scholar] [CrossRef] [PubMed]
- Shu, C.-W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Gottlieb, S.; Mullen, J.S.; Ruuth, S.J. A Fifth Order Flux Implicit WENO Method. J. Sci. Comput. 2006, 27, 271–287. [Google Scholar] [CrossRef]
- Zheng, L.; Zheng, S.; Zhai, Q. Continuous surface force based lattice Boltzmann equation method for simulating thermocapillary flow. Phys. Lett. A 2016, 380, 596–603. [Google Scholar] [CrossRef]
- Wei, P.S.; Huang, C.C.; Wang, Z.P.; Chen, K.Y.; Lin, C.H. Growths of bubble/pore sizes in solid during solidification—An in situ measurement and analysis. J. Cryst. Growth 2004, 270, 662–673. [Google Scholar] [CrossRef]
- Grugel, R.N.; Brush, L.N.; Anilkumar, A.V. Disruption of an Aligned Dendritic Network by Bubbles During Re-melting in a Microgravity Environment. Microgravity Sci. Technol. 2012, 24, 93–101. [Google Scholar] [CrossRef]
- Arnberg, L.; Mathiesen, R.H. The real-time, high-resolution X-ray video microscopy of solidification in aluminum alloys. JOM 2007, 59, 20–26. [Google Scholar] [CrossRef]






| G1 | G2 | ||
|---|---|---|---|
| Case1 | −1.4 | 1.00 | 0.20 |
| Case2 | −1.4 | 1.00 | 0.170 |
| Case3 | −1.4 | 1.00 | 0.130 |
| Case4 | −1.4 | 0.95 | 0.130 |
| Case5 | −1.4 | 0.90 | 0.130 |
| Case6 | −1.4 | 1.00 | 0.117 |
| Spurious Current | Normalized Total CPU Time | |
|---|---|---|
| Original Shan-Chen | 0.03 | 1 |
| The enhanced model | 0.005 | 2.49 |
| Gibbs Thomson Coefficient (G) | 0.00000024 m K |
|---|---|
| Domain size | |
| Contact Angle | |
| Kinematic Viscosity | 5.6566 × 10−8 m2/s |
| Solute Diffusivity | 3 × 10−9 m2/s |
| Thermal Diffusivity | 2.4210−5 m2/s |
| Liquidus Slope (ml) | −2.6 (K/wt%) |
| Partitioning Coefficient | 0.17 |
| Maximum Spurious Velocity (mm/s) | Density Ratio | CPU-Time (s) | |
|---|---|---|---|
| Original Shan-Chen model | 5 | 4 | 1527 |
| The enhanced model | 3.5 | 40 | 2351 |
| The phase field model | 0.03 | 40 | 35,861 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nabavizadeh, S.A.; Eshraghi, M.; Felicelli, S.D. A Comparative Study of Multiphase Lattice Boltzmann Methods for Bubble-Dendrite Interaction during Solidification of Alloys. Appl. Sci. 2019, 9, 57. https://doi.org/10.3390/app9010057
Nabavizadeh SA, Eshraghi M, Felicelli SD. A Comparative Study of Multiphase Lattice Boltzmann Methods for Bubble-Dendrite Interaction during Solidification of Alloys. Applied Sciences. 2019; 9(1):57. https://doi.org/10.3390/app9010057
Chicago/Turabian StyleNabavizadeh, Seyed Amin, Mohsen Eshraghi, and Sergio D. Felicelli. 2019. "A Comparative Study of Multiphase Lattice Boltzmann Methods for Bubble-Dendrite Interaction during Solidification of Alloys" Applied Sciences 9, no. 1: 57. https://doi.org/10.3390/app9010057
APA StyleNabavizadeh, S. A., Eshraghi, M., & Felicelli, S. D. (2019). A Comparative Study of Multiphase Lattice Boltzmann Methods for Bubble-Dendrite Interaction during Solidification of Alloys. Applied Sciences, 9(1), 57. https://doi.org/10.3390/app9010057






