Featured Application
Simulation of fuel cell systems.
Abstract
Because of their fuel flexibility, Solid Oxide Fuel Cells (SOFCs) are promising candidates to coach the energy transition. Yet, SOFC performance are markedly affected by fuel composition and operative parameters. In order to optimize SOFC operation and to provide a prompt regulation, reliable performance simulation tools are required. Given the high variability ascribed to the fuel in the wide range of SOFC applications and the high non-linearity of electrochemical systems, the implementation of artificial intelligence techniques, like Artificial Neural Networks (ANNs), is sound. In this paper, several network architectures based on a feedforward-backpropagation algorithm are proposed and trained on experimental data-set issued from tests on commercial NiYSZ/8YSZ/LSCF anode supported planar button cells. The best simulator obtained is a 3-hidden layer ANN (25/22/18 neurons per layer, hyperbolic tangent sigmoid as transfer function, obtained with a gradient descent with adaptive learning rate backpropagation). This shows high accuracy (RMS = 0.67% in the testing phase) and successful application in the forecast of SOFC polarization behaviour in two additional experiments (RMS in the order of 3% is scored, yet it is reduced to about 2% if only the typical operating current density range of real application is considered, from 300 to 500 mA·cm−2). Therefore, the neural tool is suitable for system simulation codes/software whether SOFC operating parameters agree with the input ranges (anode feeding composition 0–48%vol H2, 0–38%vol CO, 0–45%vol CH4, 9–32%vol CO2, 0–54%vol N2, specific equivalent hydrogen flow-rate per unit cell active area 10.8–23.6 mL·min−1·cm−2, current density 0–1300 mA·cm−2 and temperature 700–800 °C).
1. Introduction
Nowadays, artificial intelligence are widely used for the dynamic management of complex systems. Spanning the last two decades, among the most successful artificial intelligence techniques, artificial neural networks (ANNs) certainly deserve attention, for their simplicity of implementation and wide possibility of application [1,2]. ANNs’ strong point is the ability to predict the evolution of a system when non-linear phenomena are occurring [3]: for that reason, they are claimed particularly interesting for control engineering and fault diagnosis matters. Hence, in the field of energy systems, scientific literature shows a plethora of recent advancements, addressing forecast and simulation of system based on unpredictable power sources such as sun and wind [4], along with algorithms for load management in sub-grids [5,6,7], where dynamic and self-learning codes are useful to customize the system management (i.e., demand-side response programs). Beside management issues, with regard to energy conversion systems, ANNs exhibit a great relevance to the matters of performance mapping and fault diagnosis (e.g., related to gas-turbines [8,9,10] heat exchangers [11], internal combustion engines [12,13,14], cogeneration units [15]). With regard to the present energy roadmap, electrochemical energy systems—like batteries and fuel cells—are increasingly attracting attention, because of their high efficiency and eco-friendliness [16,17]. Whilst electrochemistry and catalysis are complex non-linear processes, ANNs can easily handle performance variation and faults prediction of such systems. For this reason, they are a particularly suitable technique to foster the integration of electrochemical devices in energy systems and facilitate their management, coping with the variability of operating conditions. To this end, other researchers already investigated the topic of artificial intelligence applications in electrochemical energy systems. For example, the authors of [18] applied ANNs to fault diagnosis of batteries for electric vehicles, while in Reference [19] the topic was addressed in the outlook of energy management in hybrid configuration. Yet, ANNs significantly lower computational times and their application specific to fuel cells have been studied in several papers [20,21]. In many of them, this method is applied to go through the integration of the fuel cell in a complex system, as in Reference [22] regarding the development and control of a Polymer Electrolyte Fuel Cell-based (PEFC) electric power train for bicycles. Also Reference [23] shows a study to improve the integration of fuel cells in grid-connected power plants. Finally, in others, artificial intelligence is used to gain insight within the fuel cell itself, being a sophisticated component and subcomponent-level modelling approach. For instance, the authors of Reference [24] applied ANNs to improve the power density of low temperature PEFCs. Similarly, high temperature fuel cells like Solid Oxide Fuel Cells (SOFCs) are particularly interesting, since the implementation of ANN in the system modelling and control allows by-passing a detailed characterization required because of complex chemistry on the fuel cell surface. SOFCs show high flexibility with regard to the fuel, yet their performances might be sensitive to the variation of fuel composition and operative conditions. For example, a change in temperature impacts on the electrolyte conductivity, as well as it affects chemical kinetics of internal reforming and gas shift reactions. Then, as the anode feeding total flow rate decreases, the gas residence time at the active sites of the cells increases, driving equilibrium-driven internal processes. Detailed modelling approaches take into account non-linear phenomena (viz. gas diffusivity, kinetics), which require the knowledge of many parameters that are hard to collect experimentally. Moreover, any model stands upon the superimposition of some hypothesis, introducing a loss of knowledge due to a certain level of simplification. Minimizing this source of error implies high computational times to get reliable results. Conversely, the implementation of artificial intelligence techniques [20,21] such as ANNs, overlooks them.
SOFCs fast and reliable simulation is of interest of a bunch of different applications. First, at component level, they are called in 3D-CFD models, to improve significantly computational times and to approach the problem of transient simulation [25]. Second, at system level, a consistent simulation tool is necessary to forecast the SOFC performance when the system asks for operating conditions modification, to further optimize its working point and to provide a prompt regulation. In this framework, in the scientific literature there are a few examples of ANNs applications to SOFC simulation. In References [26,27] the problem of internal multiple reforming is studied, in References [28,29] the complex composition of the fuel is taken up, while in Reference [30] fault diagnosis in SOFC is deeply investigated. In detail, in Reference [28], the effect of anode and cathode feeding composition on the polarization curve of a SOFC is addressed. In that paper, the ANN algorithm is developed on the experimental evidence from test benches described in References [31,32] and shows both good simulation performances and a lean architecture (after the first hidden layer, a linear transfer function is applied). Yet, its applicability is valid for SOFC operation at 800 °C (common parameter among all the tests used for the training/validation procedure) and to a rather limited fuel composition range. In addition, the problem of internal reforming of methane is not considered. Moreover, the original input parameters come from two different works and there is no mention about the anode materials used for the experiments. The material and the cell geometry determine electric and catalytic properties of the SOFC, hence they are one fundamental to assess the applicability of an ANN simulator. An improved ANN model for SOFC performance simulation is presented in Reference [26], where three levels of operative temperature (700–750–800 °C) are accounted for. However, since the paper aims at investigating multiple reforming mechanisms occurring in direct-biogas fuel cells, only the operation on humidified CH4/CO2 gas mixtures is taken into account. Whilst that study provides thorough insight on complex competitive reactions (steam and dry reforming), its applicability is limited to a narrow range of fuels and does not consider other gas species. Regarding some promising SOFC applications, the fuel gas (hydrocarbon reformate, coal and biomass syngas) has non-negligible amounts of H2 and CO. This substantially modifies the reaction rates associated to methane decomposition. A slightly more complex fuel mixture (28.1% CH4, 56.7% H2O, 0.5% CO, 12% H2 and 2.7% CO2) is considered in Reference [27]. Nonetheless, in that paper, gas components fractions do not vary in the data-set used to develop the ANN. Again, the results obtained do not show a high generalization capability with regard to any operative conditions.
For the sake of generalization and the reduction of computational time, an ANN simulator based on a broader application framework and state-of-the-art SOFC materials is the topic addressed in this work. Hence, this simulator is able to handle variable temperature conditions and a wider range of anode feeding compositions, considering the co-occurrence of CH4, H2, CO and CO2 and it predicts voltage losses from a few input parameters (temperature, fuel main components partial flow rates, electric load). Such algorithm is suitable to calculate quickly the SOFC electric power output in a wide range of applications, resulting flexible for many system integration designs, which show promising potentialities (e.g., biogas-fed small-scale SOFC units [33], integrated-gasifier fuel cell systems [34] etc.). The data-set for the network training are collected experimentally on SOFC materials representing the current state-of-the-art, regarding thickness and material composition.
2. Materials and Methods
Section 2 aims at providing details concerning the network architecture and training methodology (Section 2.1), as well as material and methods used in the experiments performed to retrieve data-set for the network development (Section 2.2).
2.1. Artificial Neural Network Development
2.1.1. Architecture Definition
A number of different feedforward-backpropagation network configurations (as depicted in the scheme at Figure 1) are trained and tested.
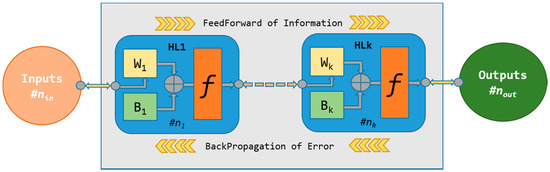
Figure 1.
Feedforward-backpropagation ANN structure: in each HL a number #nk of artificial neurons are connected and correlated through the weight matrix (Wk) and the bias matrix (Bk).
As detailed in Table 1, each one features a few distinctive parameters: number hidden layers (HL), number of neurons in each hidden layer, training algorithm and transfer function. During the training phase, all of them are processed, in order to define the most performing ones. For all tested architectures, the number of neurons in the input and output layers are equal to the number of input (#nin) and output parameters (#nout) respectively. As Table 1 reports, two transfer functions are implemented: the log-sigmoid (Logsig) and the hyperbolic tangent sigmoid (Tansig). At the beginning, the learning rate (LR) is initialized to 0.01, then it is varied dynamically to find the best value, since great values favour convergence speed, yet they can also lead to instabilities in the convergence itself (Rumelhart relation [35]).

Table 1.
Network configurations: architecture, number of neurons per hidden layers and functions.
2.1.2. Training
Once the architecture is defined, the neural network is trained, validated and tested upon the experimental data-set made of the primary input signals from the system. In detail, for each network configuration, the training process is carried out dividing the experimental results into three subsets of samples, randomly assorted:
- The first subset (70% of samples) is used for the training itself and it is fed to the network algorithm in order to calculate the values associated to the weight and bias matrix elements;
- The second subset (15% of samples) is used as validation basis. This is employed to measure the generalization capability of the network and to abort the training process early if the network performance on this subset does not improve. (i.e., before the target value for the error function is reached). The validation subset does not influence the network generalization capabilities.
- The third subset (15% of samples) is used for the test, that is to say for a further generalization capability check having no effect on the training phase.
As reported in Table 1, two kinds of algorithms are considered to train the networks. First, the Gradient descent with momentum backpropagation (TrainGDM). It updates weights and bias values according to gradient descent with momentum (momentum acts like a low-pass filter and allows ignoring small errors in the error surface). Second, the Gradient descent with adaptive learning rate backpropagation (TrainGDA). It uses a gradient descent with adaptive learning rate. Specifically, for each training iteration (either referred to as epoch), whether performances decrease, the learning rate is updated based on learning rate increasing ratio, LRinc. During training, if the nth-step error is less than (n − 1)th-step error, the learning rate is increased. Otherwise, in the event of abnormal performance enhancement, the learning rate is decreased by the learning rate decreasing ratio, LRdec. If the nth-step error exceeds the error calculated at the preceding iteration, the learning rate is decreased accordingly. With regard to the network training, Table 2 shows the value assigned to the main parameters of the process, managing learning speed and aborting the process when needed. The other parameters in Table 2 are: “minimum performance gradient” represents the minimum accepted value of performance improvement; “maximum validation failures” is the maximum number of failures allowed along the network improvement and “performance goal” is the target of the performance function. During the training phase, simulation performances are checked on the Mean Squared normalized Error (MSE, Equation (1)) and Root Mean squared Error (RMS, Equation (2)), both based on the sum of squared errors (the difference between the ANN output θann,i and the corresponding experimental results θexp,i).

Table 2.
Training settings.
The training phase ends when any of these conditions occurs: (i) either maximum epochs or maximum calculation time is reached; (ii) the performance goal (i.e., MSE) scores target value; (iii) the performance gradient falls below the minimum allowed, or, (iv) the network performances upon the validation set increase more than maximum validation failures.
2.2. Experimental Data Collection
2.2.1. Materials and Experimental Set-Up
Commercial anode-supported NiYSZ/8YSZ/LSCF button cells are used (outer diameter: 30 mm, active area: 3.14 cm2, thickness anode/electrolyte/cathode: 240/8/50 μm). The sealing used is Aremco Ceramabond® 552. The test rig and related equipment are fully described in Reference [36]. The cell is connected to an electronic load, simulating the user. Raw data are sampled at 1 Hz and processed with an average filter to remove measurement noise (on a 120-sample basis).
2.2.2. Design of Experiments
The experimental data-set used as physical input is based on 45 tests, resulting from all the possible different combinations of the main process variables. Namely, process variables considered are: temperature, current density, anode gas composition and flow rate, like Table 3 summarizes. In detail, temperature is varied according to three levels: 700, 750 and 800 °C. The anode feeding is changed simulating five syngas mixtures resulting from different processes (“synA” from wood air-gasification, “synB” from sewage sludge air-gasification, “synC” from wood oxy-gasification, “synD” from steam methane reforming and “synE” from the anaerobic digestion of organic waste). Since syngas are heterogeneous gas mixtures made of H2, CO2, CH4, CO and N2, the total flow rate is expressed with an auxiliary variable, defined as “equivalent hydrogen” (definition given at Equation (3). Equivalent hydrogen flowrate is set to three levels and expressed per unit cell active area (10.8, 14.7, 23.2 mL·min−1·cm−2) to vary the fuel utilization (see the relation between the fuel utilization coefficient Uf and the flowrate of equivalent hydrogen at Equation (4).

Table 3.
Design of experiments set-points for process decision variables.
As unique feature for each single test, the fuel total indicator is assumed and it will be shown while presenting experimental results. is calculated according to Equation (5), as the ratio between Uf and the fuel mixture dilution fraction (DF, see Equation (6).
2.2.3. Tests Execution: Methods
The button cell is started up with a standard procedure, until the desired operative temperature is reached. Hence, it undergoes reduction and it is firstly validated with a polarization test under pure hydrogen. Then, SOFC anode feeding is varied, according to the specification discussed in Section 2.2.2. All of the tests are performed on the same SOFC specimen in order to eliminate any other source of error. In each test condition, a polarization curve is measured, performing tests at variable current. In the polarization test, starting operative load is 0 A (open circuit voltage, OCV), then current is increased by constant-amplitude steps, so that the SOFC performances are mapped with a current density (j) resolution of 50 mA·cm−2. The waiting time between two consecutive tests is reduced to the minimum duration (average 2 h), to lower the likelihood of cumulative damage and to sort a consistent data-set, suitable for the ANN training.
3. Results
3.1. Experimental
Time-average experimental results are summarized in a 1260-row matrix, used as input for the ANN development. Hence, from each test, on the input section, the test matrix includes: current load, temperature, H2, CO2, CH4, CO and N2 volume flowrates. As output section, the matrix shows voltage outputs related to each combination of the previous parameters. Hereinafter, Figure 2 presents a couple of examples regarding SOFC performance maps obtained experimentally. In detail, performances maps are represented for two load conditions, 100 mA·cm−2 and 250 mA·cm−2. On the y-axis, measured voltage is shown, while on the primary and secondary x-axis the fuel total indicator (Equation (5)) and the temperature are shown. As explained above, the fuel total indicator is a useful dimensionless parameter to sum up the information relative to the kind of fuel mixture and the way it is employed (that is to say the current load and the anode feeding flow rate).
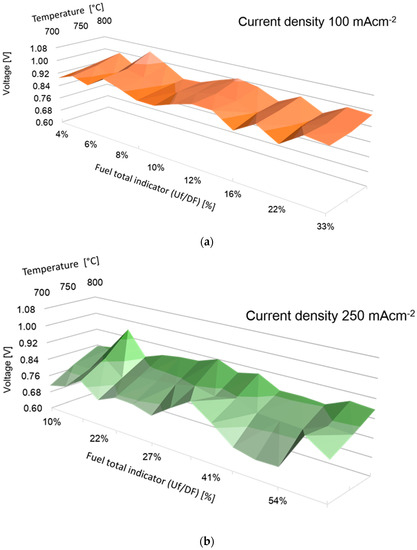
Figure 2.
Performances maps at constant current load: 100 mA·cm−2 (a) and 250 mA·cm−2 (b).
3.2. Neural Network Development
For all the network configurations discussed hereinabove, performance indexes are summarized in Table 4. L1 architecture yields poor results. ANN1, ANN2 and ANN3 show a high RMS over a 1000-sample population. On the contrary, for all the other networks configurations featuring either L2 (3 HLs) or L3 architecture (4 HLs), RMS is in the neighbourhood of 1%. The increase up to 4 HLs does not produce any further performance enhancement. Among the investigated ANN configurations with 3 HLs, the sensitivity analysis performed on neurons number ends in the identification of ANN5 as most performing network (0.67% RMS in the test). For this reason, ANN5 is chosen to build the final simulation tool for SOFC performance. On the other hand, ANN4 scores the worst performance (1.21% RMS in the test) among the 3-HL configurations. ANN4 and ANN5 error dispersion during the last epoch training phase is shown in Figure 3b and Figure 3c, respectively).

Table 4.
Artificial neural networks performances.
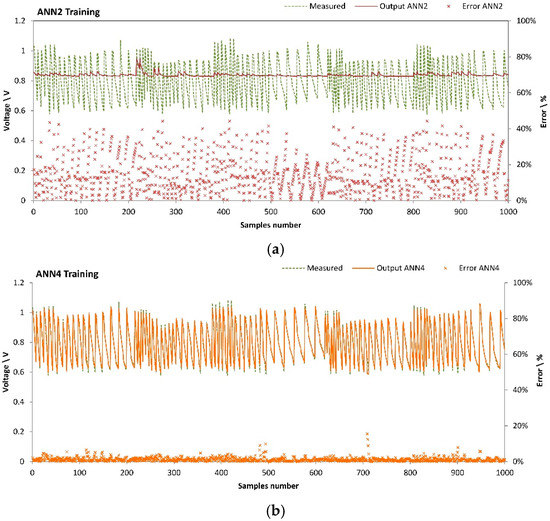
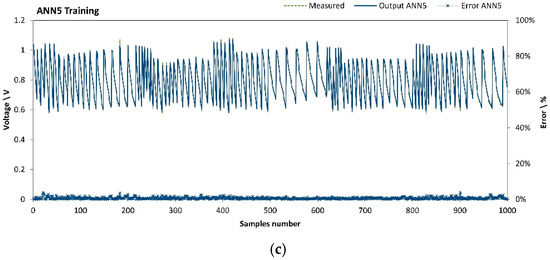
Figure 3.
Training of ANN2 (a), ANN4 (b) and ANN5 (c): error dispersion.
With regard the validation data-set of the algorithm, more interesting comments can be made. The error dispersion obtained throughout the validation phase is plotted in Figure 4a for ANN2, Figure 4b for ANN4 and Figure 4c for ANN5.With regard to the simulated and experimental voltage data, it is clear as ANN2 is not able to reproduce the SOFC performance varying all the operating conditions input of the developed model. Moreover, observing the error dispersion trend the better generalization capability of ANN5 with respect to ANN4 is evident.
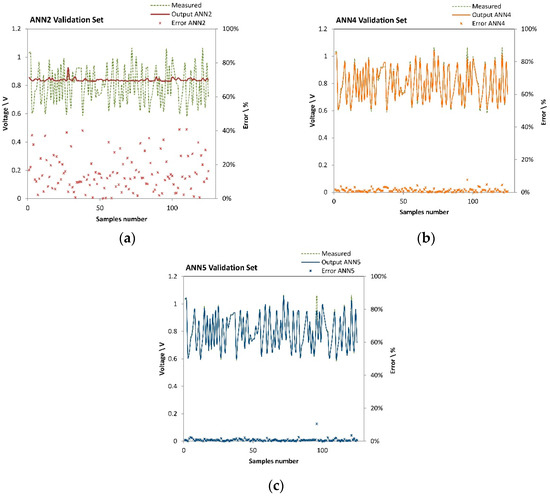
Figure 4.
Validation of ANN2 (a), ANN4 (b) and ANN5 (c): error dispersion.
Finally, on the basis of an independent data-subset excluded from the training and validation phase, the simulation performances of the neural network under investigation are test. Once again, simple configuration with just 2 HLs produced output results affected with high error, ANN5 shows the lowest RMS (0.67%). Figure 5 depicts the error dispersion for ANN2, ANN4 and ANN5 highlighting the best performance of ANN5 in reproducing the SOFC behaviour.
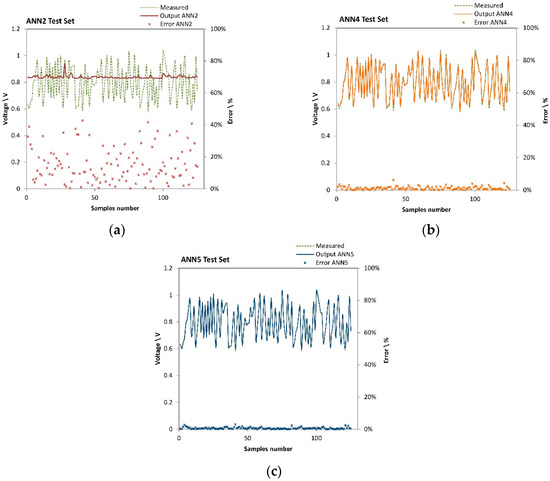
Figure 5.
Test of ANN2 (a), ANN4 (b) and ANN5 (c) test: error dispersion.
3.3. Neural Network Application
The best network sorted from the previous section, namely ANN5, is finally applied to simulate the performance of SOFCs based on state-of-art materials. Hence, a couple of additional experimental data-set are used to check the generalization capability of ANN5. The first data-set regards a polarization test performed on a different SOFC specimen with the same features of the one used for the previous experiments and tested on the same test bench (as discussed in Section 2).
Then, aiming at validating ANN5 generalization capability over different SOFC single cell set-ups, the second one is related to a polarization experiment performed on another test bench, implementing cells with a slightly different geometry, yet featuring the same material composition (as reported in Reference [42]). Table 5 summarizes the experiments input variables regarding both of them—for the further, see column “Exp synF”, while for the latter column “Exp synG”. All of process input variables fall in the input ranges used to develop ANN5.

Table 5.
Validation experiments input data.
Figure 6 shows simulation results obtained with ANN5. On the left side, the experiment related to “Exp synF”is reported. The blue dotted line shows the ANN5 simulation output, while the red-diamond series depicts the experimental evidence, that is to say, the validation target of the simulation tool. There is a good agreement between the two curves, as also confirmed by the calculation of RMS (2.23% on the entire current density range observed 0–500 mA·cm−2).
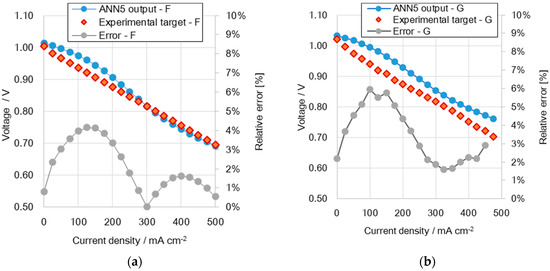
Figure 6.
ANN5 application: comparison of simulated and experimental polarization curves (a) under Exp synF and (b) Exp synG operating conditions.
Likewise, on the right side of Figure 6, results regarding experiment Exp synG are shown. In this case, being the forecast accuracy still acceptable, the simulation through ANN5 is not as good as in the previous example. However, this issue was anticipated by the fact that Exp synG experimental results regard a different SOFC specimen tested on a different test bench. Nonetheless, RMS is still low (3.17%, considering the entire current density range simulated 0–500 mA·cm−2 ) and the ANN5 tool can be used with a good approximation also to predict results related to the operation of SOFC cells as in Reference [42]. In addition to that, it is worth highlighting the distribution of forecast error in the current density range observed (grey dotted lines in Figure 6). Both simulated curves fit well the real voltage at open circuit and in a current density range, which recalls real applications. In fact, the relative error on the single measurement is significantly lower (<2% Exp synF, <3% Exp synG) at 0 mA·cm−2 and in the current density range 300–500 mA·cm−2. In terms of RMS, the result scored is 0.93% and 1.6% for the Exp synF curve simulation and Exp synF curve simulation respectively.
4. Conclusions
This paper aimed at the development of a simulation tool for SOFC performances based on a feed-forward backpropagation neural network algorithm. The neural network approach was chosen in order to get a lean and quick simulator that can be implemented in any computational code/system simulation software, without getting computational time slower because of the complexity due to a deterministic set of detailed modelling equations.
As a result, a 3-hidden layer network (featuring 25, 22 and 18 neurons and a transfer function Tansig) is the best configuration to fit the experimental data collected for the purpose, by means of thorough test campaign on state-of-the-art SOFC materials. The accuracy of the developed model is very high, implying low forecast errors in reproducing SOFC output voltage fed with fuels with a variable hydrogen concentration, as well as variable amount of non-reformed light hydrocarbons (in this study, methane was considered as model compound for this category). Furthermore, the variation of the fuel utilization, as well as the operating temperature of the cell, are considered to build the application framework of the model. The last two features make this neural network simulator advanced with respect to other already presented and provide the additional value when it comes to SOFC operation in integrated systems.
In detail, considering the error between experimental results and data-set used for the development, RMS on forecast is 0.67%, while it is slightly higher 2% and 3% respectively in the simulation of a polarization curve obtained in a different experiment with the same SOFC type and in reproducing the performance of a SOFC cell with different geometry. However, RMS shrinks to about 1%, whether the typical current density range for SOFC operation (300–500 mA·cm−2) is observed.
For the features of the experimental data-set used as training basis and the interpolation capability of the algorithm verified through the final validation data-set, the model can be applied whether the SOFC operating variables fall into the neural network input range. In other words, whether the SOFC is run on fuel mixtures exhibiting a composition in the range 0–48%vol H2, 0–38%vol CO, 0–45%vol CH4, 9–32%vol CO2, 0–54%vol N2, with an equivalent hydrogen area-specific flow-rate between 10.8 and 23.2 mL·min−1·cm−2 and temperature from 700 °C to 800 °C.
Since the input range contains the operating conditions occurring in many relevant system designs, this algorithm shows useful impacts in the simulation of a number of applications of technical interest.
Author Contributions
Methodology, investigation, validation, data collection, writing and original draft preparation, A.B.; conceptualization, review and editing L.B.; software, F.B.; formal analysis and data curation, F.C.I.; supervision, G.B.
Funding
This research was funded by EUROPEAN UNION’S HORIZON 2020 research and innovation program under project Net-Tools, Grant Agreement-736648.
Acknowledgments
F.C.I. acknowledges the Erasmus+ program for Mobility for Traineeship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Suzuki, K. Industrial and Control Engineering Applications. In Artificial Neural Networks; InTechOpen, 2011; p. 490. Available online: https://www.intechopen.com/books/artificial-neural-networks-industrial-and-control-engineering-applications (accessed on 20 November 2017). [CrossRef]
- Deng, J.; Stobart, R.; Maass, B. The Applications of Artificial Neural Networks to Engines. In Artificial Neural Networks—Industrial and Control Engineering Applications; Loughborough University: Loughborough, UK, 2012; p. 450. [Google Scholar]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. Demand forecast of PV integrated bioclimatic buildings using ensemble framework. Appl. Energy 2017, 208, 1626–1638. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Dore, J.; Sproul, A.B. Recent advances in the analysis of residential electricity consumption and applications of smart meter data. Appl. Energy 2017, 208, 402–427. [Google Scholar] [CrossRef]
- Ma, W.; Fang, S.; Liu, G.; Zhou, R. Modeling of district load forecasting for distributed energy system. Appl. Energy 2017, 204, 181–205. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, S.; Chung, D.H. Analysis of energy and control efficiencies of fuzzy logic and artificial neural network technologies in the heating energy supply system responding to the changes of user demands. Appl. Energy 2017, 190, 222–231. [Google Scholar] [CrossRef]
- Sadough Vanini, Z.N.; Khorasani, K.; Meskin, N. Fault detection and isolation of a dual spool gas turbine engine using dynamic neural networks and multiple model approach. Inf. Sci. 2014, 259, 234–251. [Google Scholar] [CrossRef]
- Talaat, M.; Gobran, M.H.; Wasfi, M. A hybrid model of an artificial neural network with thermodynamic model for system diagnosis of electrical power plant gas turbine. Eng. Appl. Artif. Intell. 2018, 68, 222–235. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Abdul Karim, Z.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Davoudi, E.; Vaferi, B. Applying artificial neural networks for systematic estimation of degree of fouling in heat exchangers. Chem. Eng. Res. Des. 2018, 130, 138–153. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Bonucci, F. Diagnosis methodology for the turbocharger groups installed on a 1 MW internal combustion engine. Appl. Energy 2009, 86, 2721–2730. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Bonucci, F. Development of the regulation mapping of 1 MW internal combustion engine for diagnostic scopes. Appl. Energy 2009, 86, 1087–1104. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Bonucci, F. Diagnosis of a turbocharging system of 1 MW internal combustion engine. Energy Convers. Manag. 2013, 68, 28–39. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G. Design of the measurements validation procedure and the expert system architecture for a cogeneration internal combustion engine. Appl. Therm. Eng. 2005, 25, 2698–2714. [Google Scholar] [CrossRef]
- European Commission. Communication from the Commission to the European Parliament, The Council, The European Economic and Social Committee, The Committee of the Regions and the European Investment Bank—Clean Energy for All Europeans; EU: Bruxelles, Belgium, 2017; Volume 14. [Google Scholar]
- IEA. Technology Roadmap: Energy Storage; International Energy Agency: Paris, France, 2014. [Google Scholar]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Xiang, C.; Ding, F.; Wang, W.; He, W. Energy management of a dual-mode power-split hybrid electric vehicle based on velocity prediction and nonlinear model predictive control. Appl. Energy 2017, 189, 640–653. [Google Scholar] [CrossRef]
- Daud, W.R.W.; Rosli, R.E.; Majlan, E.H.; Hamid, S.A.A.; Mohamed, R.; Husaini, T. PEM fuel cell system control: A review. Renew. Energy 2017, 113, 620–638. [Google Scholar] [CrossRef]
- Almeida, P.E.M.; Simões, M.G. Neural optimal control of PEM fuel cells with parametric CMAC networks. IEEE Trans. Ind. Appl. 2005, 41, 237–245. [Google Scholar] [CrossRef]
- Kheirandish, A.; Motlagh, F.; Shafiabady, N.; Dahari, M.; Khairi Abdul Wahab, A. Dynamic fuzzy cognitive network approach for modelling and control of PEM fuel cell for power electric bicycle system. Appl. Energy 2017, 202, 20–31. [Google Scholar] [CrossRef]
- Wu, G.; Sun, L.; Lee, K.Y. Disturbance rejection control of a fuel cell power plant in a grid-connected system. Control Eng. Pract. 2017, 60, 183–192. [Google Scholar] [CrossRef]
- Cheng, S.J.; Miao, J.M.; Wu, S.J. Use of metamodeling optimal approach promotes the performance of proton exchange membrane fuel cell (PEMFC). Appl. Energy 2013, 105, 161–169. [Google Scholar] [CrossRef]
- Madani, O.; Das, T. Feedforward based transient control in solid oxide fuel cells. Control Eng. Pract. 2016, 56, 86–91. [Google Scholar] [CrossRef]
- Tran, D.L.; Tran, Q.T.; Sakamoto, M.; Sasaki, K.; Shiratori, Y. Modelling of CH4 multiple-reforming within the Ni-YSZ anode of a solid oxide fuel cell. J. Power Sources 2017, 359, 507–519. [Google Scholar] [CrossRef]
- Chaichana, K.; Patcharavorachot, Y.; Chutichai, B.; Saebea, D.; Assabumrungrat, S.; Arpornwichanop, A. Neural network hybrid model of a direct internal reforming solid oxide fuel cell. Int. J. Hydrogen Energy 2012, 37, 2498–2508. [Google Scholar] [CrossRef]
- Milewski, J.; Świrski, K. Artificial Neural Network-Based Model for Calculating the Flow Composition Influence of Solid Oxide Fuel Cell. J. Fuel Cell Sci. Technol. 2013, 11, 021001. [Google Scholar] [CrossRef]
- Milewski, J.; Świrski, K. Modelling the SOFC behaviours by artificial neural network. Int. J. Hydrogen Energy 2009, 34, 5546–5553. [Google Scholar] [CrossRef]
- Wu, X.; Gao, D. Fault tolerance control of SOFC systems based on nonlinear model predictive control. Int. J. Hydrogen Energy 2017, 42, 2288–2308. [Google Scholar] [CrossRef]
- Jiang, Y.; Virkar, A.V. Fuel Composition and Diluent Effect on Gas Transport and Performance of Anode-Supported SOFCs. J. Electrochem. Soc. 2003, 150, A942–A951. [Google Scholar] [CrossRef]
- Virkar, A.V. Low Temperature Anode-Supported High Power Density Solid Oxide Fuel Cells with Nanostructured Electrodes; University of Utah: Salt Lake City, UT, USA, 2003. [Google Scholar] [CrossRef]
- Tjaden, B.; Gandiglio, M.; Lanzini, A.; Santarelli, M.; Ja, M. Small-Scale Biogas-SOFC Plant: Technical Analysis and Assessment of Di ff erent Fuel Reforming Options. Energy Fuels 2014, 28, 4216–4232. [Google Scholar] [CrossRef]
- Baldinelli, A.; Cinti, G.; Desideri, U.; Fantozzi, F. Biomass Integrated Gasifier-Fuel Cells: Experimental investigation on wood-syngas tars impact on SOFC anode materials. In Proceedings of the 11th EUROPEAN SOFC & SOE FORUM (EFCF Luzern), Lucerne, Switzerland, 1–4 July 2014. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Data Process; Rumelhart, D.E., McClelland, J.L., Eds.; The MIT Press: Cambridge, MA, USA, 1986; pp. 318–362. [Google Scholar]
- Baldinelli, A.; Barelli, L.; Bidini, G.; Di Michele, A.; Vivani, R. SOFC direct fuelling with high-methane gases: Optimal strategies for fuel dilution and upgrade to avoid quick degradation. Energy Convers. Manag. 2016, 124, 492–503. [Google Scholar] [CrossRef]
- Baldinelli, A.; Cinti, G.; Desideri, U.; Fantozzi, F. Biomass integrated gasifier-fuel cells: Experimental investigation on wood syngas tars impact on NiYSZ-anode Solid Oxide Fuel Cells. Energy Convers. Manag. 2016, 128, 361–370. [Google Scholar] [CrossRef]
- Marie-Rose, S.C.; Perinet, A.L.; Lavoie, J. Conversion of Non-Homogeneous Biomass to Ultraclean Syngas and Catalytic Conversion to Ethanol. In Biofuel’s Engineering Process Technology; InTechOpen, 2008; Available online: https://www.intechopen.com/books/biofuel-s-engineering-process-technology/conversion-of-non-homogeneous-biomass-to-ultraclean-syngas-and-catalytic-conversion-to-ethanol/ (accessed on 12 November 2017).
- Baldinelli, A.; Barelli, L.; Bidini, G. Performance characterization and modelling of syngas-fed SOFCs (solid oxide fuel cells) varying fuel composition. Energy 2015, 90, 2070–2084. [Google Scholar] [CrossRef]
- Matsuka, M.; Shigedomi, K.; Ishihara, T. Comparative study of propane steam reforming in vanadium based catalytic membrane reactor with nickel-based catalysts. Int. J. Hydrogen Energy 2014, 39, 14792–14799. [Google Scholar] [CrossRef]
- The Biogas. Available online: http://www.biogas-renewable-energy.info/biogas_composition.html (accessed on 5 November 2017).
- Subotic, V.; Baldinelli, A.; Barelli, L.; Scharler, R. Optimization of an integrated biomass gasifier-fuel cell system: An experimental study on the cell response to process variations. In Proceedings of the Energy Procedia—10th International Conference on Applied Energy (ICAE2018), Hong Kong, China, 22–25 August 2018; pp. 22–25. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).