Stability and Heat Input Controllability of Two Different Modulations for Double-Pulse MIG Welding
Abstract
:1. Introduction
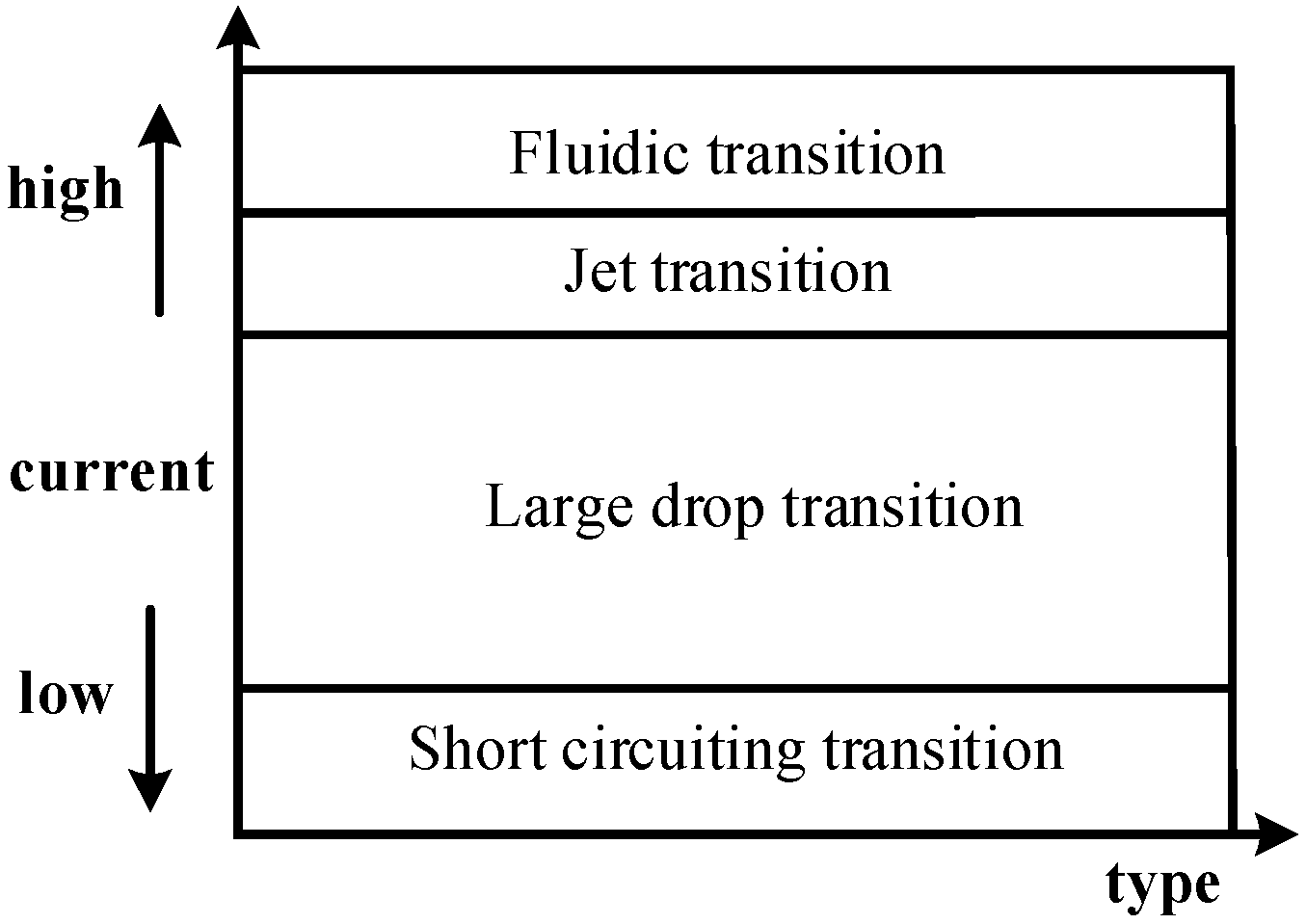
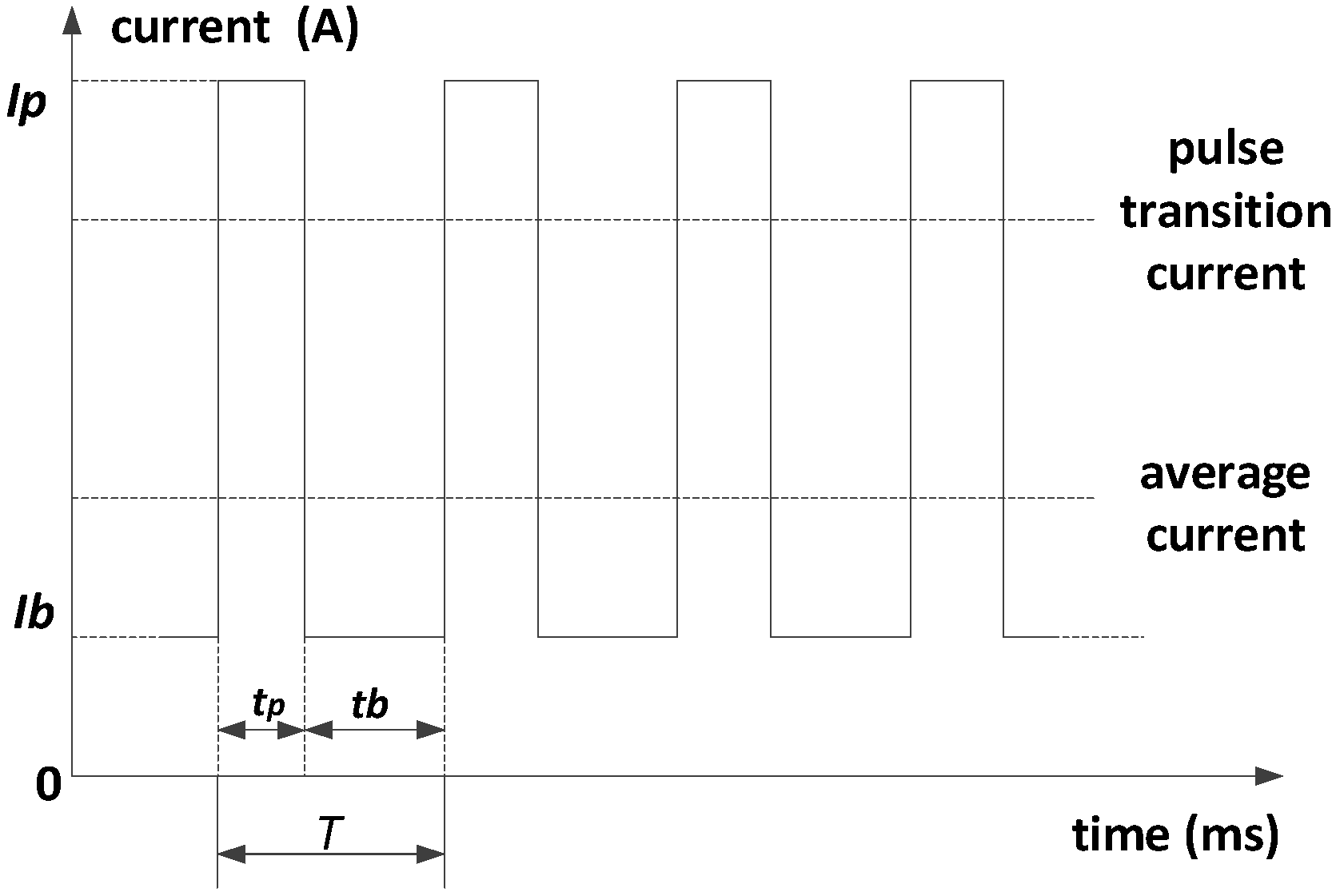
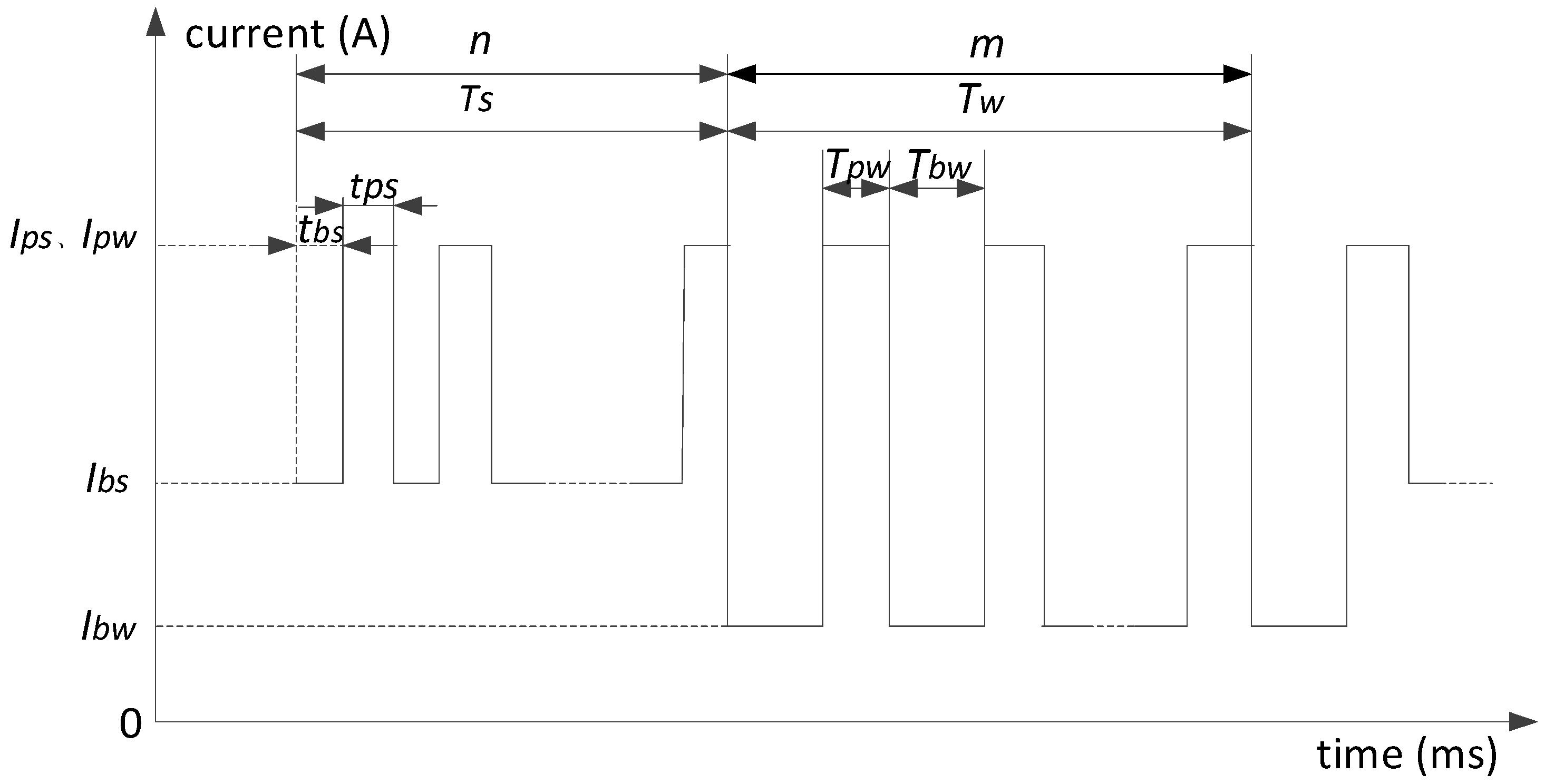
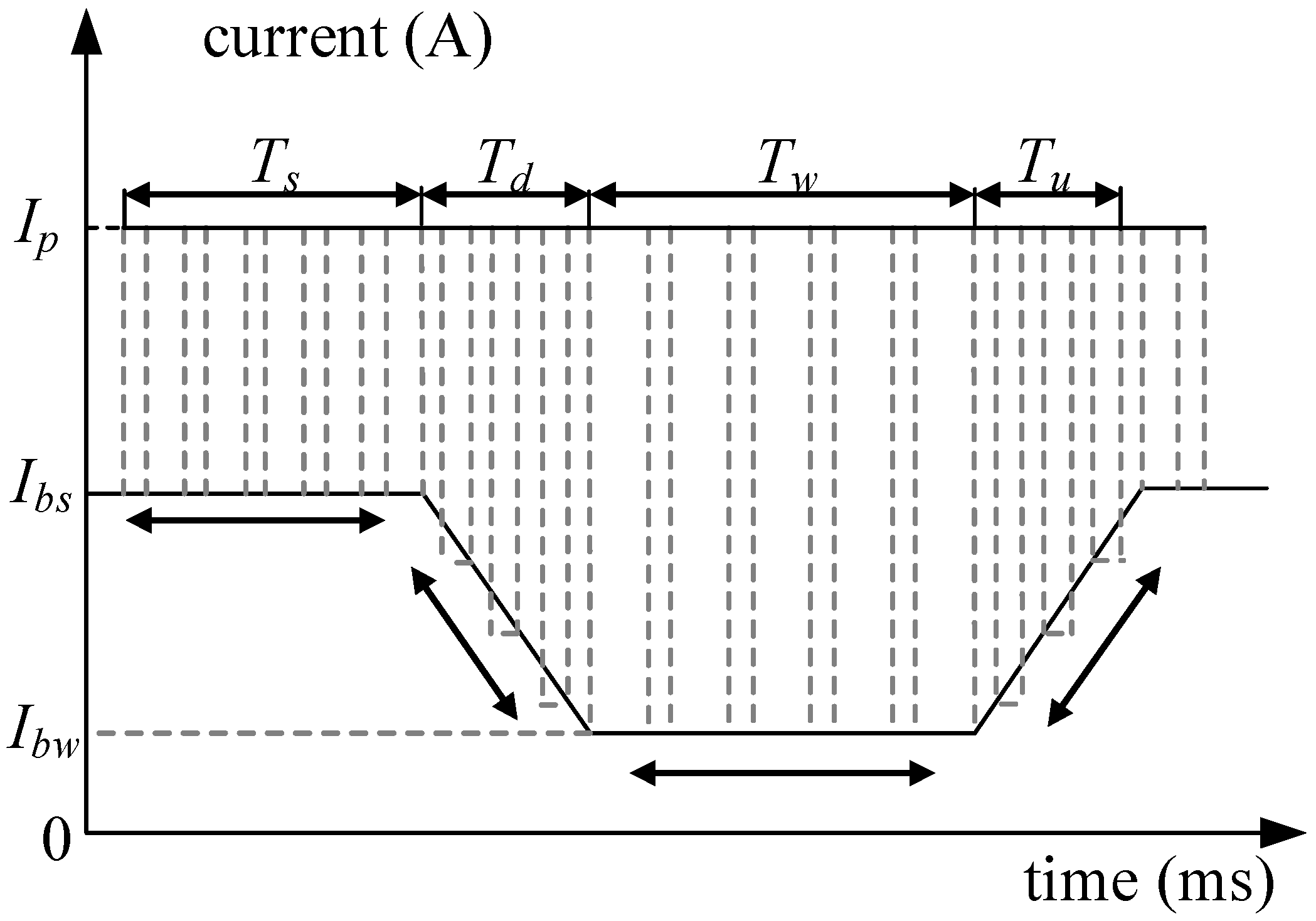
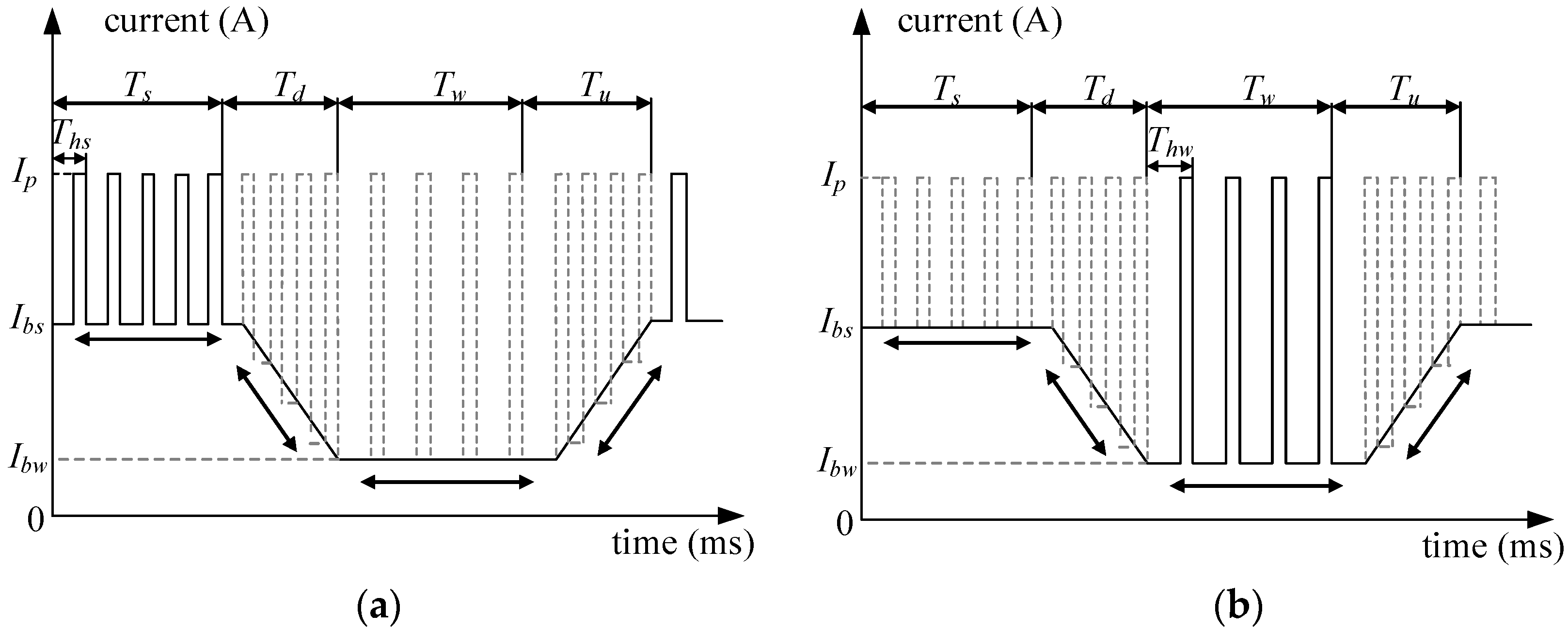
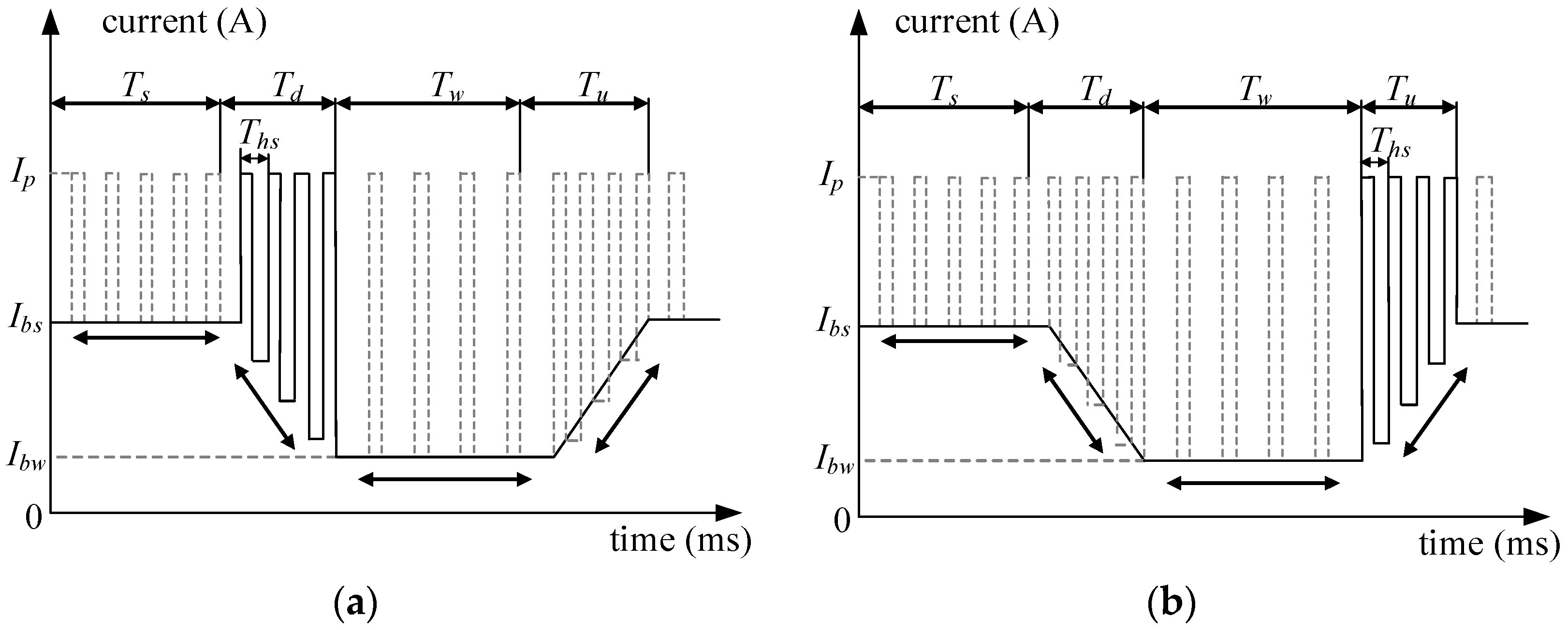
2. Design of Current Waveform Parameters for Double-Pulse MIG Welding with Two Different Modulations
3. Comparison of Stabilities of DP-MIG Welding and TP-MIG Welding
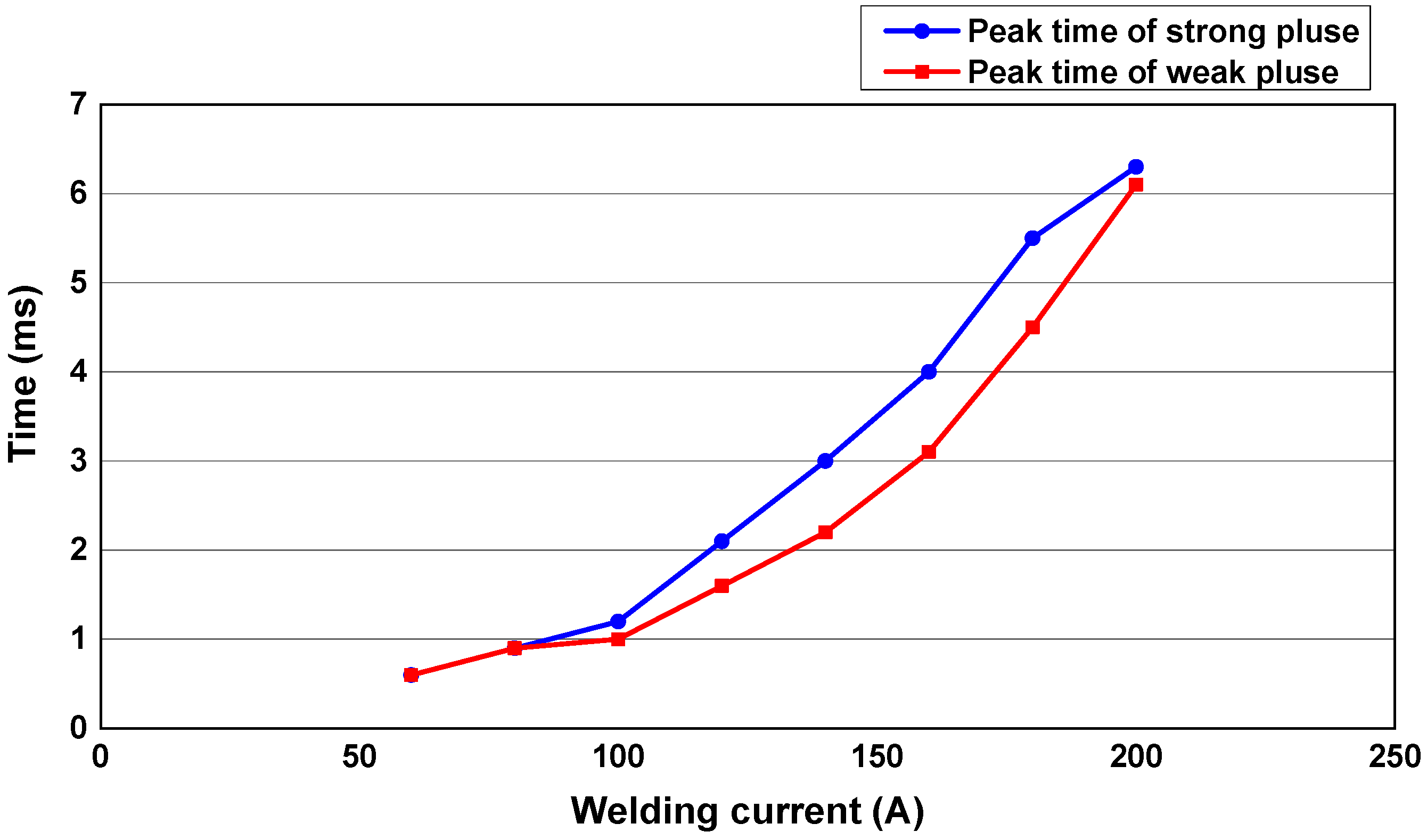
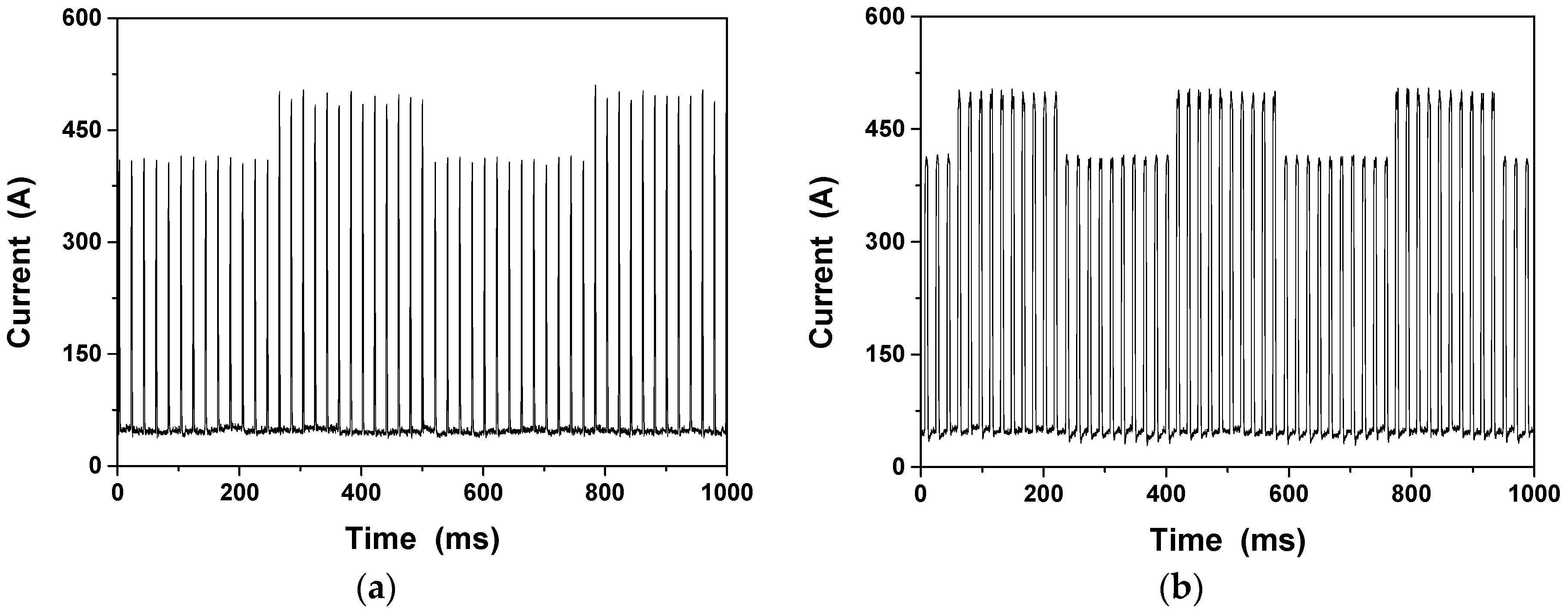
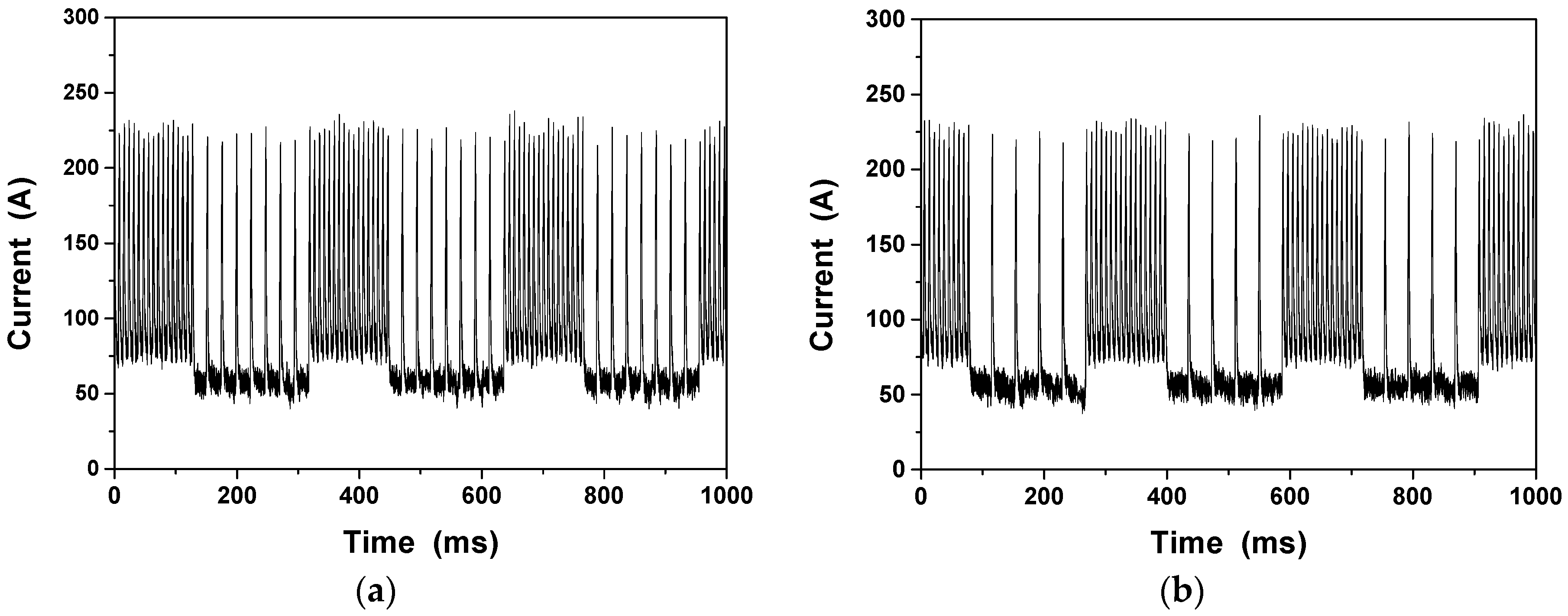
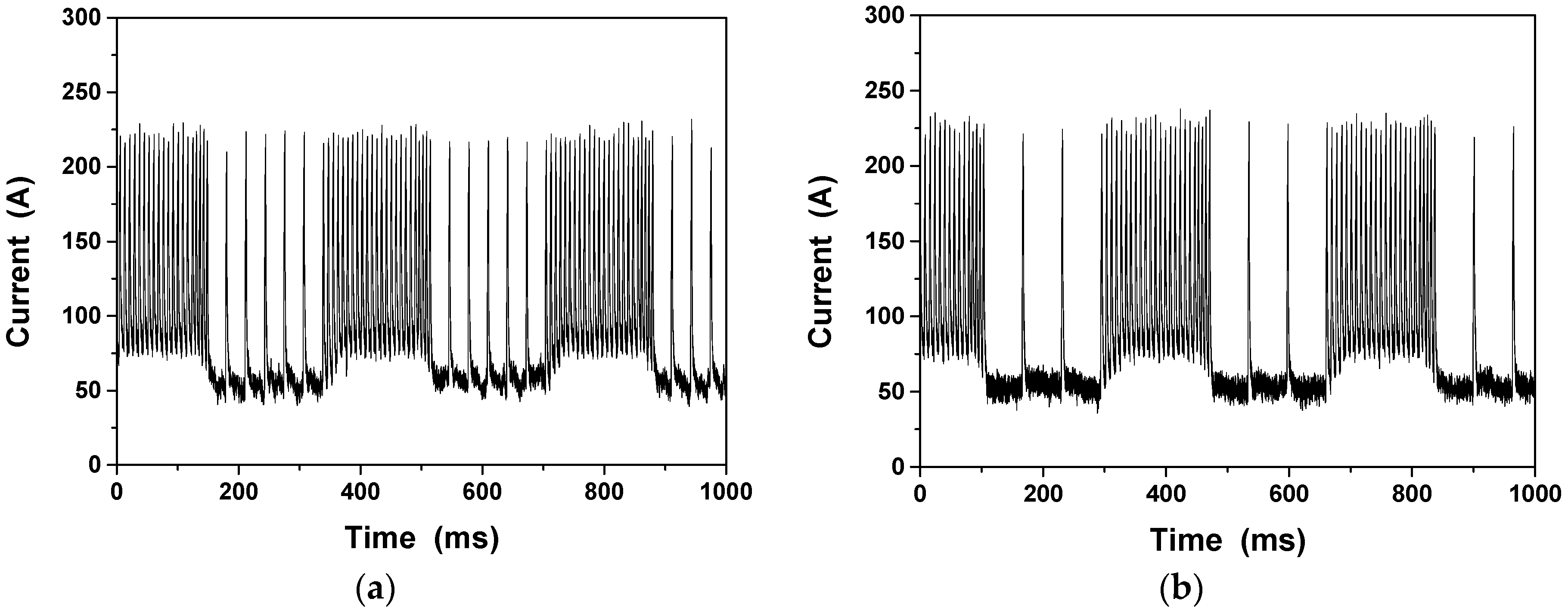
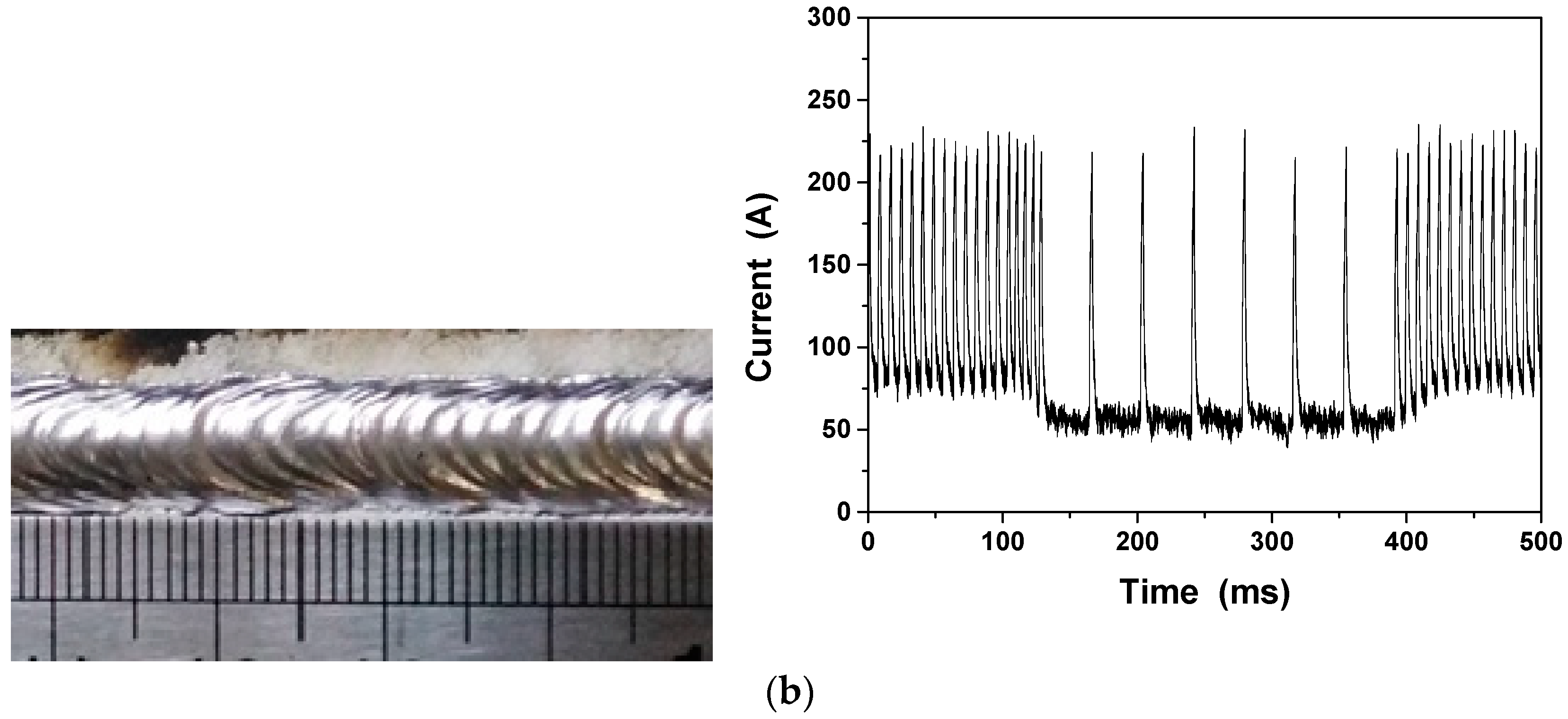
3.1. Process Stability of DP-MIG Welding
3.2. Process Stability of TP-MIG Welding
4. Process Control Experiment on Reduction of Heat Input in TP-MIG Welding and DP-MIG Welding
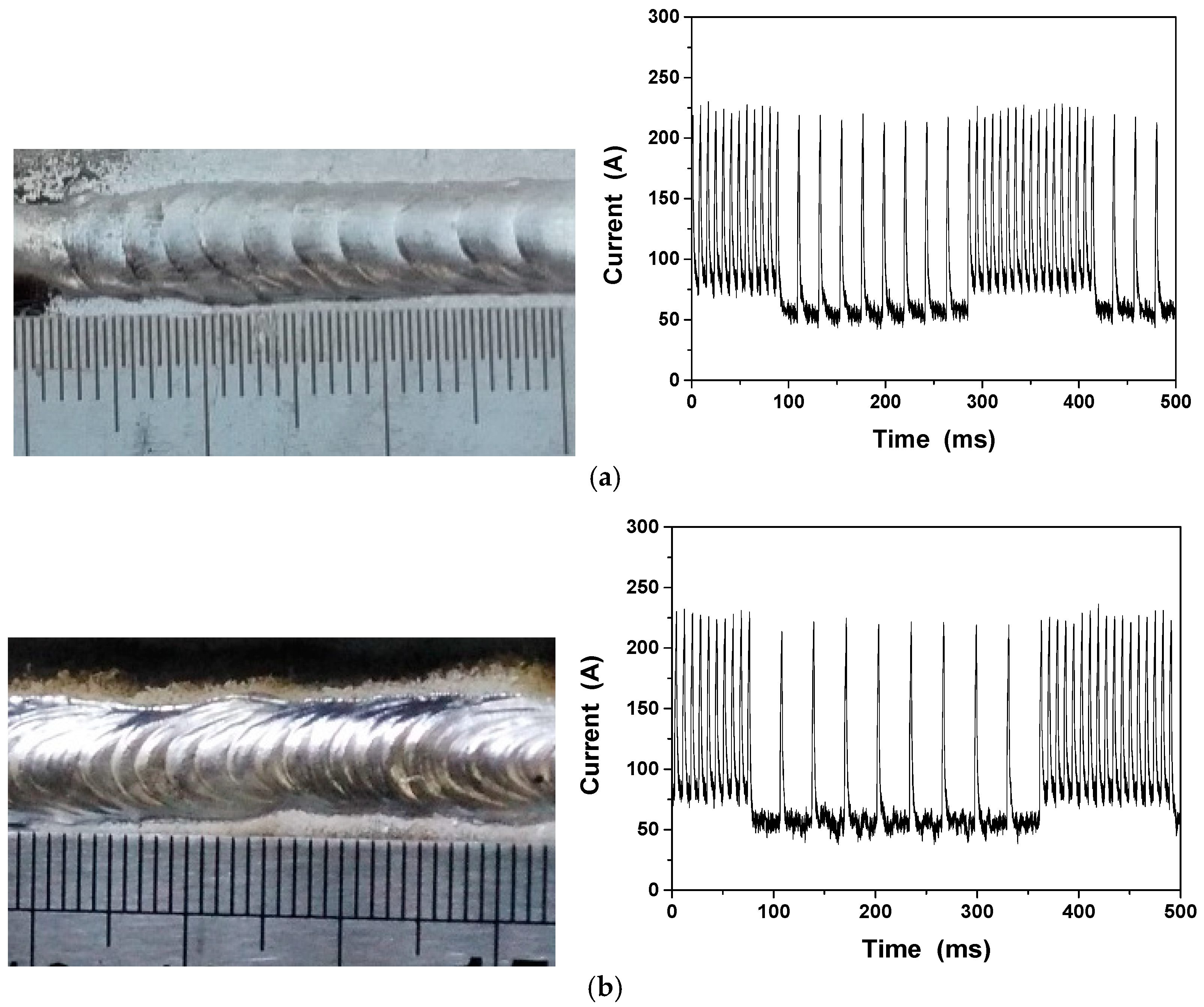
4.1. Reducing Heat Input by Varying Base Time by Adjusting the Number of Pulses in the Low-Energy Pulse Train
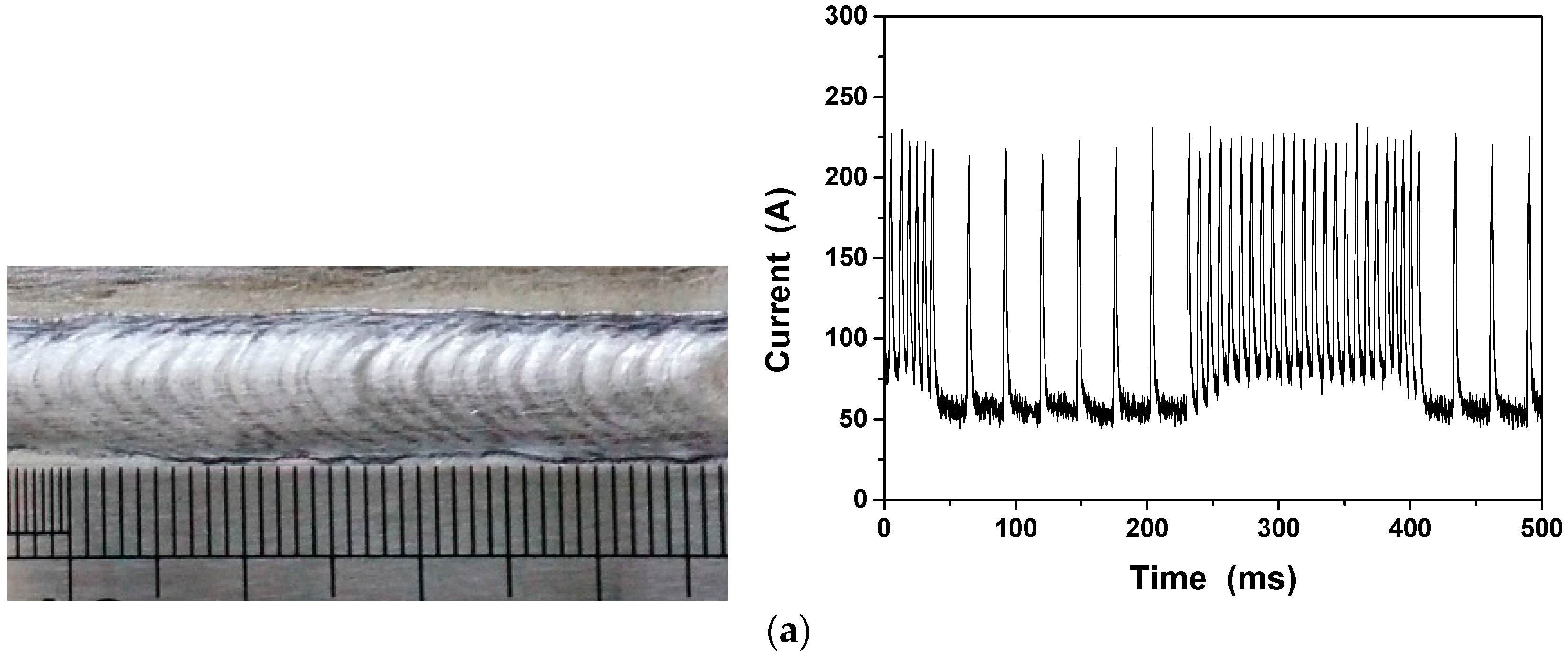
4.2. Reducing Heat Input by Adjusting the Frequency of Low-Energy Pulse Train to Vary the Base Time
4.3. Effects of Welding Speed on Input Energy
5. Conclusions
- Owing to abrupt changes in current induced by pulse train transitions in DP-MIG welding, the welding arc makes a sharp sound. In addition, the probabilities of welder burn-back and the formation of screw-like wires during long welding operations are higher in DP-MIG welding than in TP-MIG welding. In TP-MIG welding, the presence of transitional pulses in the pulse train transitions helps stabilize the welding process and soften the sound of the welding arc. The weld formed by TP-MIG welding has a high level of aesthetic quality.
- The input energy can be reduced by adjusting the number of pulses in the low-energy pulse train or the base time of the pulses. It was found that varying the number of pulses can reduce the current by 8 A and the input energy by approximately 14%. The welds formed by TP-MIG welding have finer grain sizes than those formed by DP-MIG welding. Under the same conditions, the input energy can be reduced by 12% by adjusting the base time of the pulses. In addition, the density of the fish scales increases as the frequency decreases.
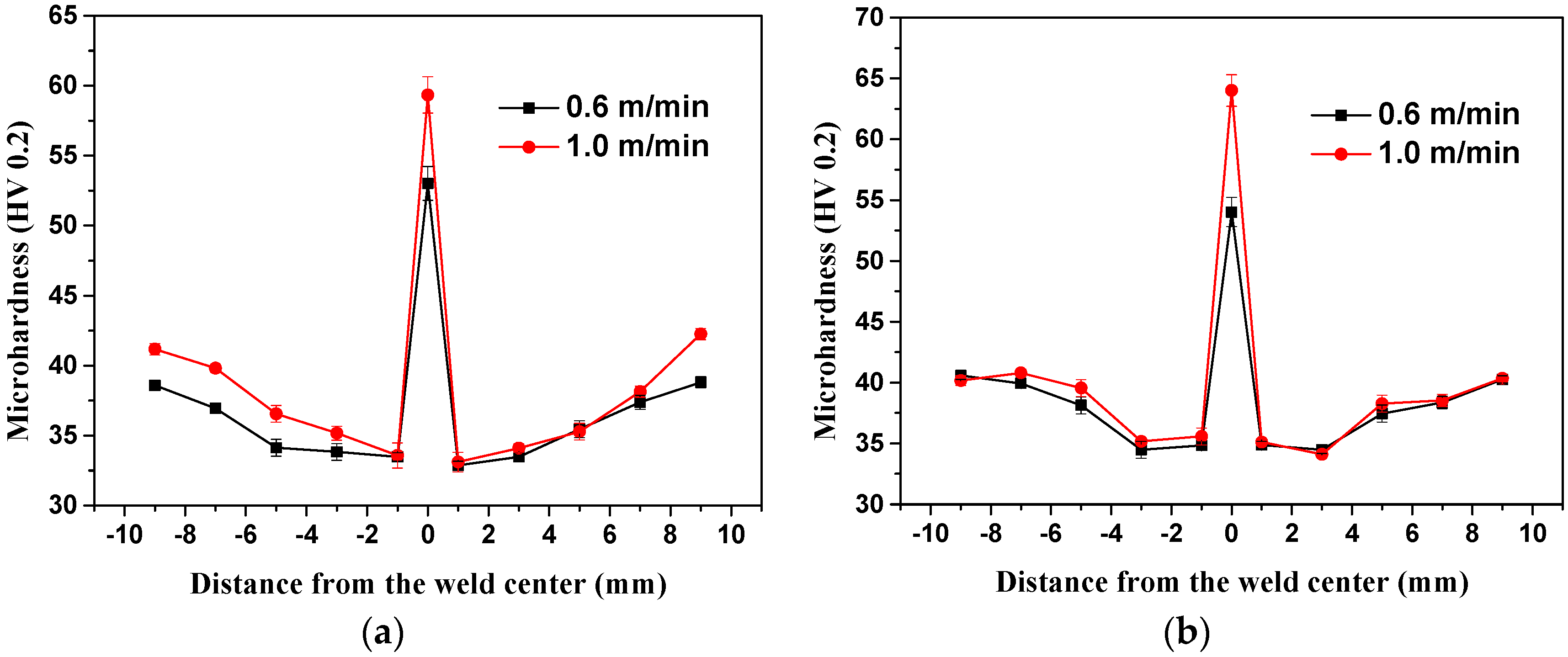
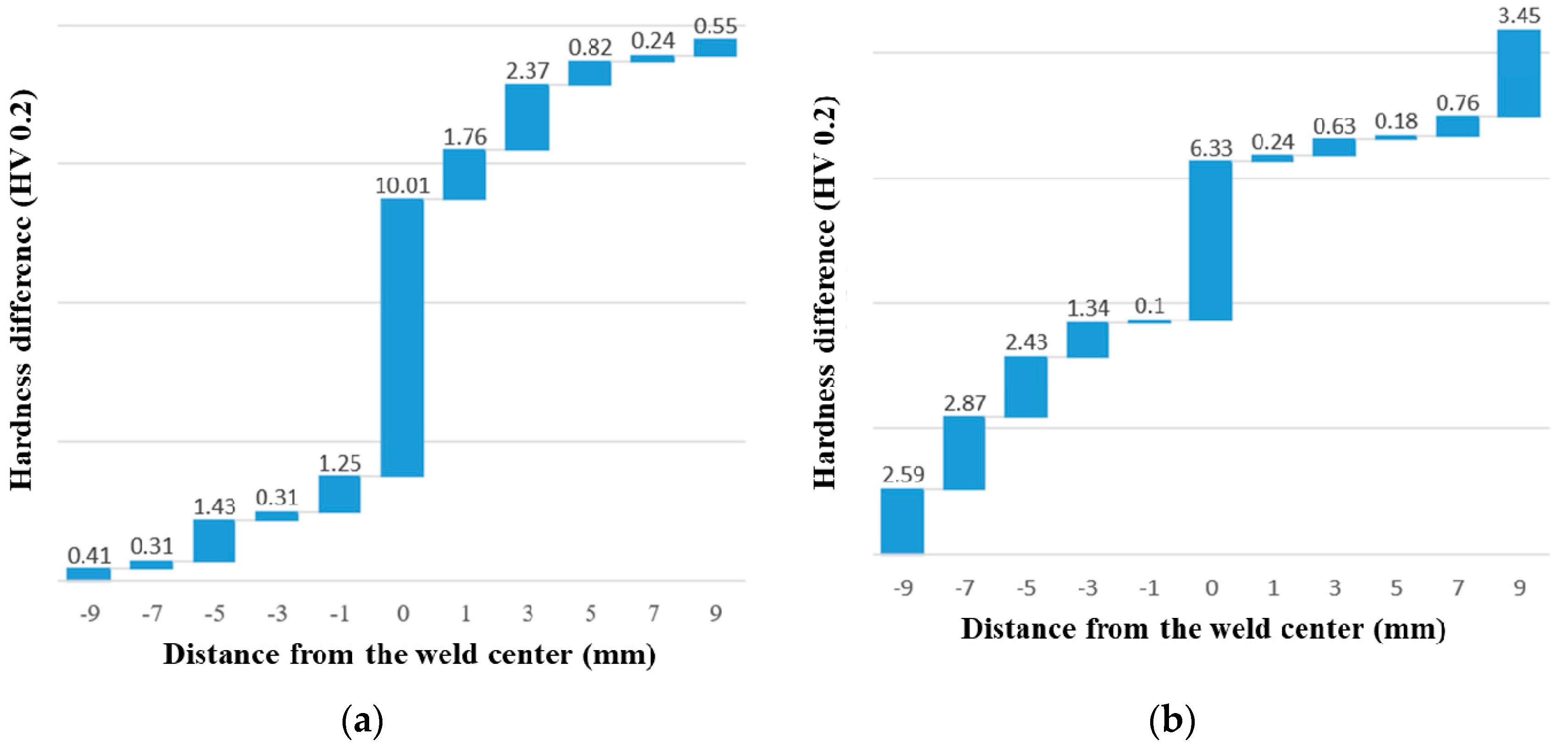
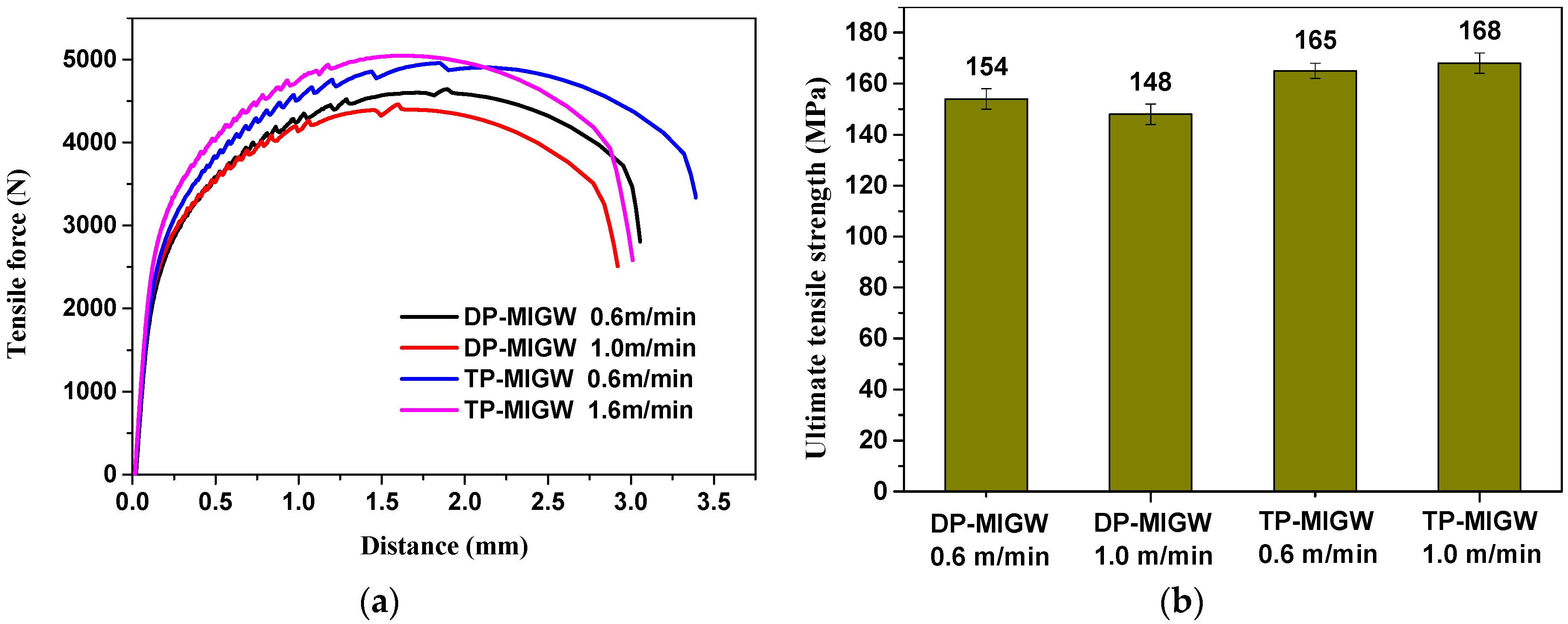
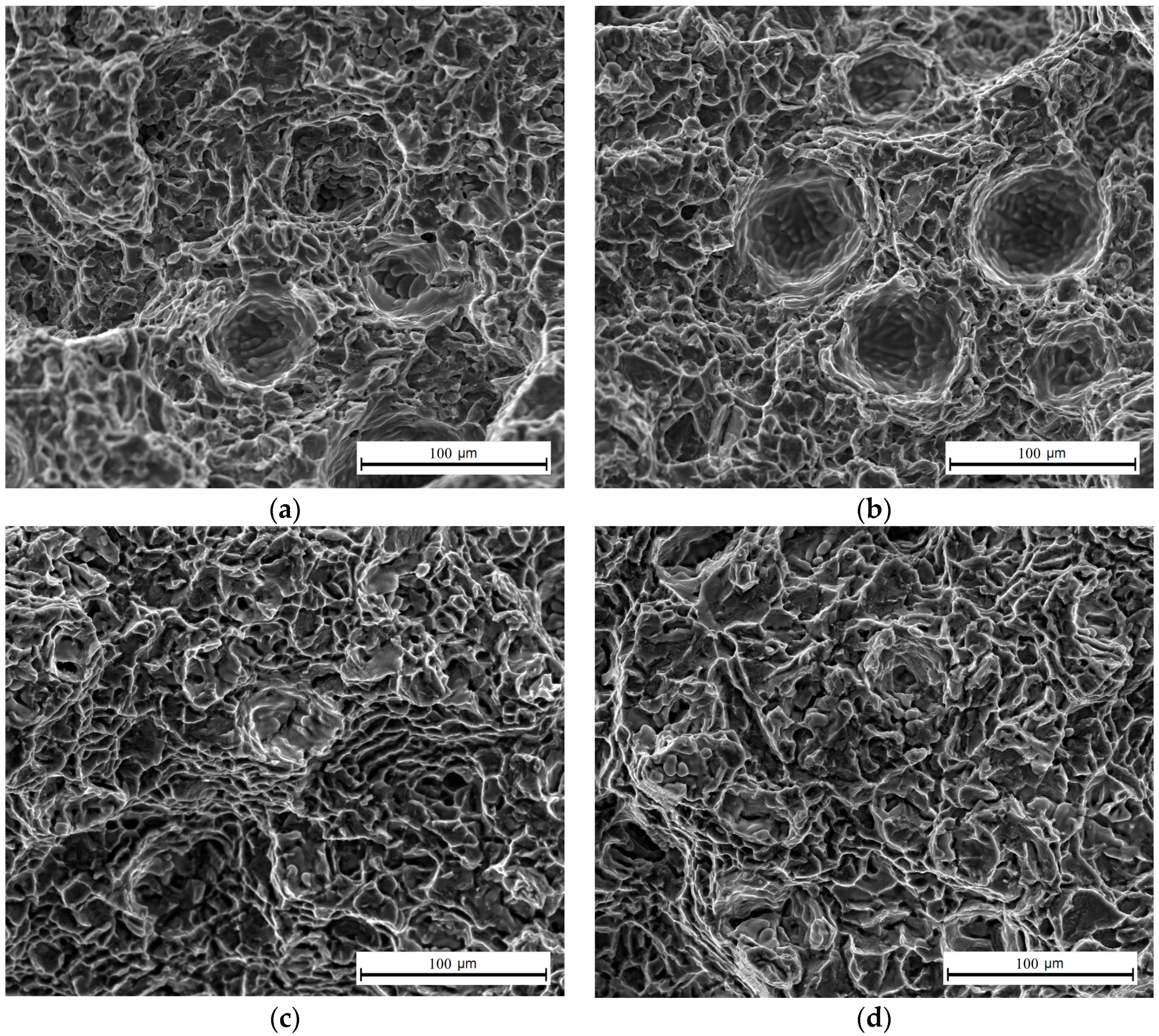
- The energies produced by TP-MIG welding and DP-MIG welding decrease as the welding speed increases. An increase in the welding speed from 0.6 m/min to 1.0 m/min decreases the area of the softened zone by 21% and 27% in DP-MIG welding and TP-MIG welding, respectively. In addition, the joint formed by TP-MIG welding is harder than the joint formed by DP-MIG welding. Additionally, the joint formed by TP-MIG welding has better tensile properties than the joint formed by DP-MIG welding. Therefore, TP-MIG welding is a superior technique in terms of its efficacy in reducing welding energy input.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Wu, C.S.; Gao, J.Q. Suppression of humping bead in high speed GMAW with external magnetic field. Sci. Technol. Weld. Join. 2016, 21, 139–141. [Google Scholar] [CrossRef]
- Li, Y.; Wu, C.S.; Wang, L.; Gao, J.K. Analysis of additional electromagnetic force for mitigating the humping bead in high-speed gas metal arc welding. J. Mater. Process. Technol. 2015, 229, 207–215. [Google Scholar] [CrossRef]
- Choi, H.W.; Farson, D.F.; Cho, M.H. Using a Hybrid Laser Plus GMAW Process for Controlling the Bead Humping Defect. Weld. J. 2006, 174-s–179-s. [Google Scholar] [CrossRef]
- Rosado, T.; Almeida, P.; Pires, I.; Miranda, R.; Quintino, L. Innovations in arc welding. In Proceedings of the 5th Congresso Luso-Moc, ambicano de Engenharia, Maputo, Mozambique, 2–4 September 2008. [Google Scholar]
- Liu, A.; Tang, X.; Lu, F. Arc profile characteristics of Al alloy in double-pulsed GMAW. Int. J. Adv. Manuf. Technol. 2013, 65, 1–7. [Google Scholar] [CrossRef]
- Gery, D.; Long, H.; Maropoulos, P. Effects of welding speed, energy input and heat source distribution on temperature variations in butt joint welding. J. Mater. Process. Technol. 2005, 167, 393–401. [Google Scholar] [CrossRef]
- Hang, Z.; Wu, D.; Zou, Y. Effect of bypass coupling on droplet transfer in twin-wire indirect arc welding. J. Mater. Process. Technol. 2018, 262, 123–130. [Google Scholar]
- Wen, C.; Wang, Z.; Deng, X.; Wang, G.; Misra, R.D.K. Effect of heat input on the microstructure and mechanical properties of low alloy ultra-high strength structural steel welded joint. Steel Res. Int. 2018, 89, 1700500. [Google Scholar] [CrossRef]
- Reis, R.P.; Scotti, A.; Norrish, J.; Cuiuri, D. Investigation on welding arc interruptions in the presence of magnetic fields: Arc length, torch angle and current pulsing frequency influence. IEEE Tran. Plasma Sci. 2013, 41, 133–139. [Google Scholar] [CrossRef]
- Armentani, E.; Esposito, R.; Sepe, R. The influence of thermal properties and preheating on residual stresses in welding. Int. J. Comput. Mater. Sci. Surf. Eng. 2007, 1, 146–162. [Google Scholar] [CrossRef]
- Hazvinloo, H.R.; Honarbakhsh Raouf, A. Effect of gas-shielded flux cored arc welding parameters on weld width and tensile properties of weld metal in a low carbon steel. J. Appl. Sci. 2010, 10, 658–663. [Google Scholar]
- Armentani, E.; Pozzi, A.; Sepe, R. Finite-element simulation of temperature fields and residual stresses in butt welded joints and comparison with experimental measurements. In Proceedings of the ASME 2014 12th Biennial Conference on Engineering Systems Design and Analysis, ESDA 2014, Copenhagen, Denmark, 25–27 June 2014. [Google Scholar]
- Somashekara, M.A.; Naveenkumar, M.; Kumar, A.; Viswanath, C.; Simhambhatla, S. Investigations into effect of weld-deposition pattern on residual stress evolution for metallic additive manufacturing. Int. J. Adv. Manuf. Technol. 2017, 90, 2009–2025. [Google Scholar] [CrossRef]
- Wang, L.L.; Jin, L.; Huang, W.J.; Xue, J. Effect of Thermal Frequency on AA6061 Aluminum Alloy Double Pulsed Gas Metal Arc Welding. Mater. Manuf. Process. 2015, 31, 2152–2157. [Google Scholar] [CrossRef]
- Pépe, N.; Egerland, S.; Colegrove, P.A.; Yapp, D.; Leonhartsberger, A.; Scotti, A. Measuring the process efficiency of controlled gas metal arc welding processes. Sci. Technol. Weld. Join. 2013, 16, 412–417. [Google Scholar] [CrossRef]
- Kah, P.; Suoranta, R.; Martikainen, J. Advanced gas metal arc welding processes. Int. J. Adv. Manuf. Technol. 2013, 67, 655–674. [Google Scholar] [CrossRef]
- Cruz, J.G.; Torres, E.M.; Alfaro, S.C.A. A methodology for modeling and control of weld bead width in the GMAW process. J. Braz. Soc. Mech. Sci. 2015, 37, 1529–1541. [Google Scholar] [CrossRef]
- Jin, L.; Xue, J.X.; Hu, Y.; Zhang, Z. Effects of Thermal Frequency on Microstructures, Mechanical and Corrosion Properties of AA6061 Joints. Appl. Sci. (Basel) 2018, 8, 540. [Google Scholar] [CrossRef]
- Mvola, B. Adaptive Gas Metal Arc Welding Control and Optimization of Welding Parameters Output: Influence on Welded Joints. Int. Rev. Mech. Eng. 2016, 10, 67–72. [Google Scholar] [CrossRef]
- Yi, L.; Yan, Z.; Xie, X.; Yang, Z. Effect of welding heat input to metal droplet transfer characterized by structure-borne acoustic emission signals detected in GMAW. Measurement 2015, 70, 75–82. [Google Scholar] [CrossRef]
- Narendra, K.S.; Annaswamy, A.M. Robust Adaptive Control; Springer: London, UK, 2015. [Google Scholar]
- Miao, B.; Li, T. A novel neural network-based adaptive control for a class of uncertain nonlinear systems in strict-feedback form. Nonlinear Dyn. 2015, 79, 1005–1013. [Google Scholar] [CrossRef]
- Huang, S.; Gu, X.; Jiao, X.; Zhang, Y. Effects of pulse current on droplet transfer in hyperbaric pulsed MIG welding. Trans. China Weld. Inst. 2015, 36, 25–29. [Google Scholar]







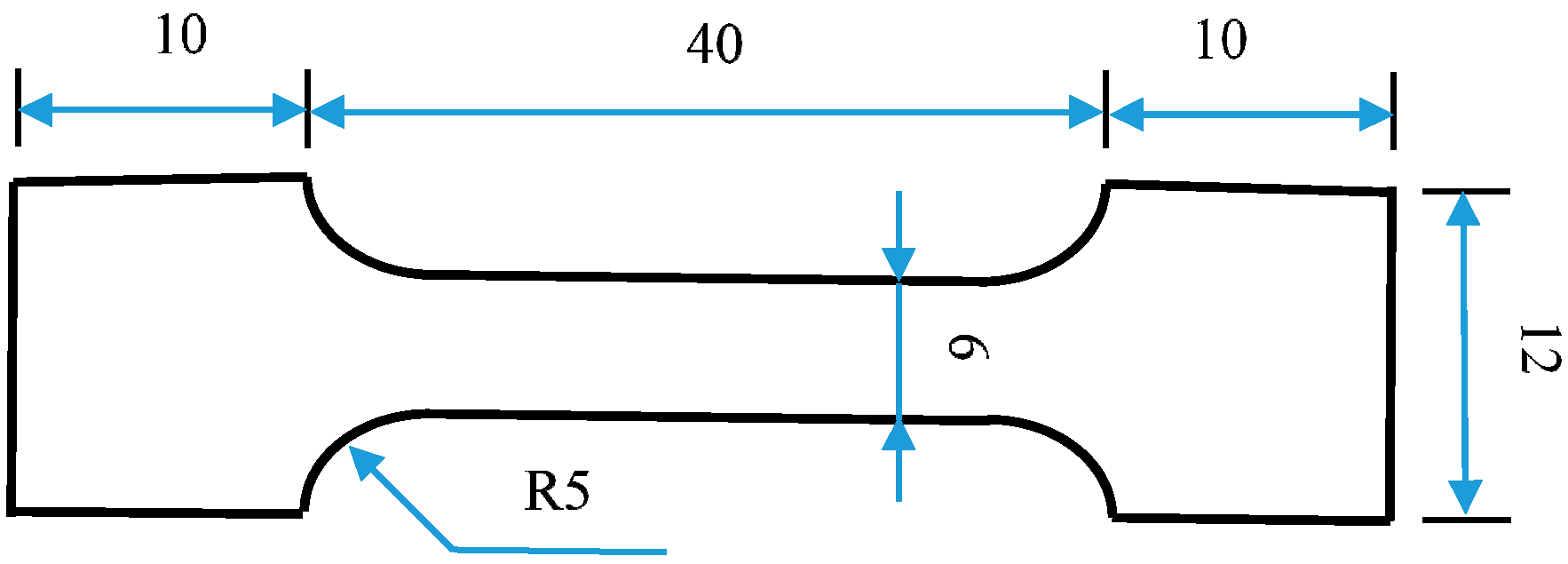



| Material | Mg | Si | Fe | Cu | Mn | Ti | Al |
|---|---|---|---|---|---|---|---|
| AA6061 | 0.80~1.2 | 0.4~0.8 | 0.7 | 0.15~0.40 | 0.15 | 0.15 | Bal. |
| ER4043 | 0.05 | 5.60 | 0.80 | 0.30 | 0.05 | – | Bal. |
| Ips (A) | tps (ms) | Ibs (A) | tbs (ms) | n (number) | Ipw (A) | tpw (ms) | Ibw (A) | tbw (ms) | m (number) | Average Current (A) | Average Voltage (V) | Input Energy (J) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 210 | 2 | 72 | 6 | 16 | 210 | 2 | 48 | 15 | 8 | 88 | 22 | 135,520 |
| 210 | 2 | 72 | 6 | 16 | 210 | 2 | 48 | 26 | 5 | 80 | 21 | 117,600 |
| Ips, Ipsw, Ipw, Ipws (A) | tps, tpsw, tpw, tpws (ms) | Ibs (A) | tbs (ms) | n | Ibw (A) | tbw (ms) | m | nsw | nws | Average Current (A) | Average Voltage (V) | Input Energy (J) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 210 | 2 | 72 | 6 | 15 | 48 | 25 | 6 | 4 | 4 | 88 | 22 | 135,520 |
| 210 | 2 | 72 | 6 | 15 | 48 | 50 | 3 | 4 | 4 | 80 | 21 | 117,600 |
| Ips (A) | tps (ms) | Ibs (A) | tbs (ms) | n | Ipw (A) | tpw (ms) | Ibw (A) | tbw (ms) | m | Average Current (A) | Average Voltage (V) | Input Energy (J) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 210 | 2 | 77 | 6 | 16 | 210 | 2 | 50 | 13 | 9 | 90 | 22 | 138,600 |
| 210 | 2 | 77 | 6 | 16 | 210 | 2 | 50 | 22 | 9 | 80 | 22 | 123,200 |
| Ips, Ipsw, Ipw, Ipws (A) | tps, tpsw, tpw, tpws (ms) | Ibs (A) | tbs (ms) | n | Ibw (A) | tbw (ms) | m | nsw | nws | Average Current (A) | Average Voltage (V) | Input Energy (J) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 210 | 2 | 77 | 6 | 15 | 50 | 20 | 7 | 4 | 4 | 90 | 22 | 138,600 |
| 210 | 2 | 77 | 6 | 15 | 50 | 30 | 7 | 4 | 4 | 80 | 22 | 123,200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Xu, M.; Huang, W.; Zhang, Z.; Wu, W.; Jin, L. Stability and Heat Input Controllability of Two Different Modulations for Double-Pulse MIG Welding. Appl. Sci. 2019, 9, 127. https://doi.org/10.3390/app9010127
Xue J, Xu M, Huang W, Zhang Z, Wu W, Jin L. Stability and Heat Input Controllability of Two Different Modulations for Double-Pulse MIG Welding. Applied Sciences. 2019; 9(1):127. https://doi.org/10.3390/app9010127
Chicago/Turabian StyleXue, Jiaxiang, Min Xu, Wenjin Huang, Zhanhui Zhang, Wei Wu, and Li Jin. 2019. "Stability and Heat Input Controllability of Two Different Modulations for Double-Pulse MIG Welding" Applied Sciences 9, no. 1: 127. https://doi.org/10.3390/app9010127
APA StyleXue, J., Xu, M., Huang, W., Zhang, Z., Wu, W., & Jin, L. (2019). Stability and Heat Input Controllability of Two Different Modulations for Double-Pulse MIG Welding. Applied Sciences, 9(1), 127. https://doi.org/10.3390/app9010127





