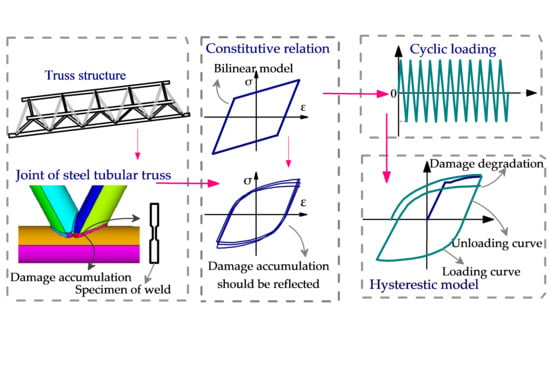
Study on Hysteresis Model of Welding Material in Unstiffened Welded Joints of Steel Tubular Truss Structure
Abstract
Featured Application
Abstract
1. Introduction
2. Experimental Study
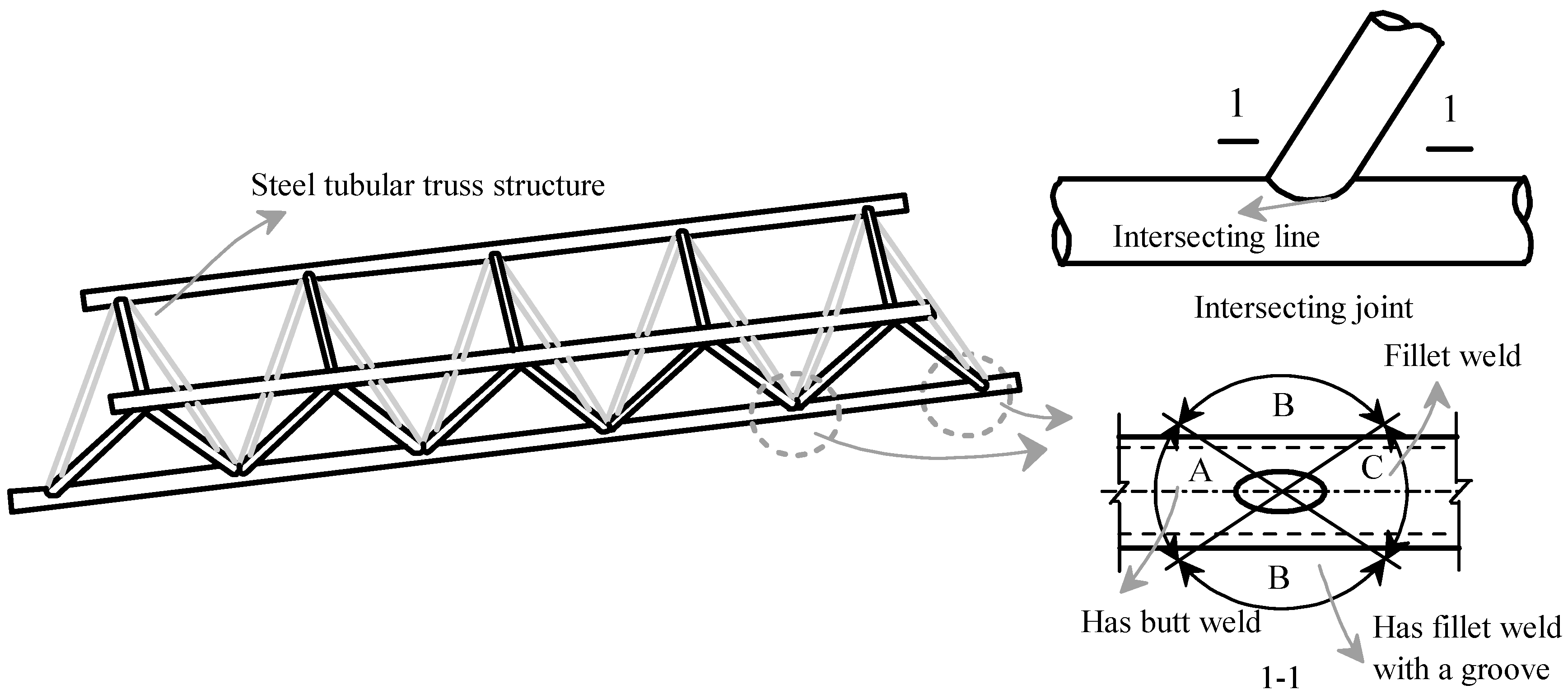
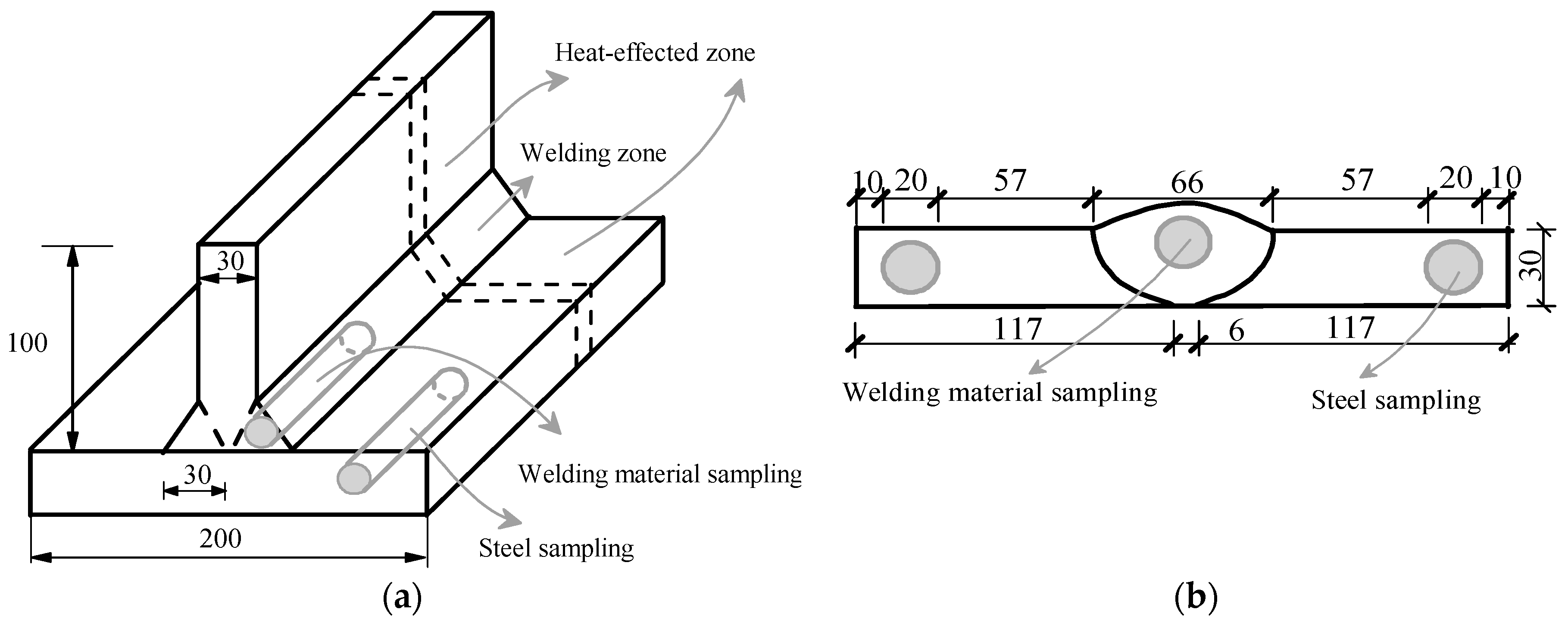
2.1. Specimen Design
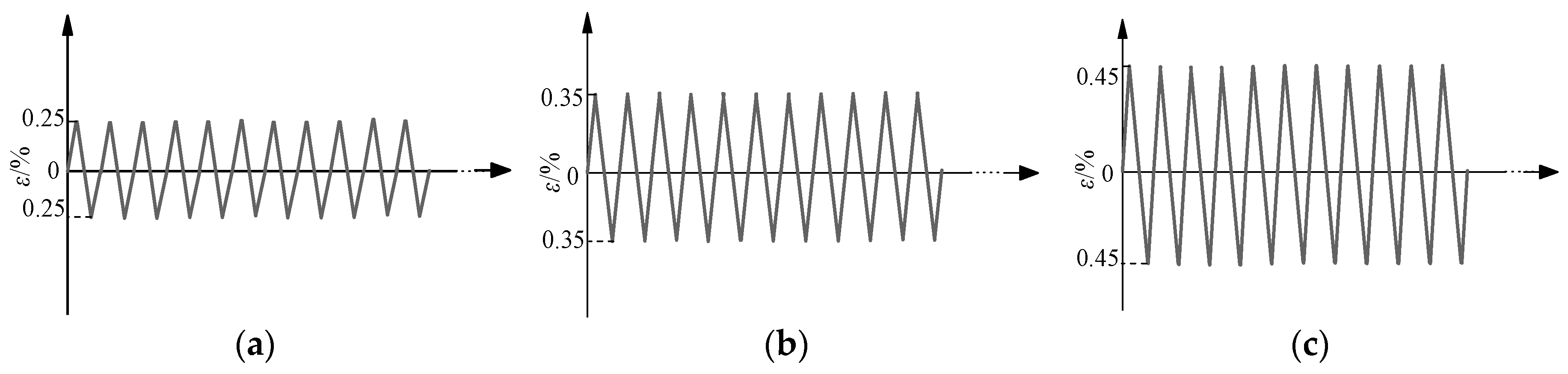
2.2. Test Procedure
3. The Test Results and Discussion
3.1. Failure Model and Damage Processes
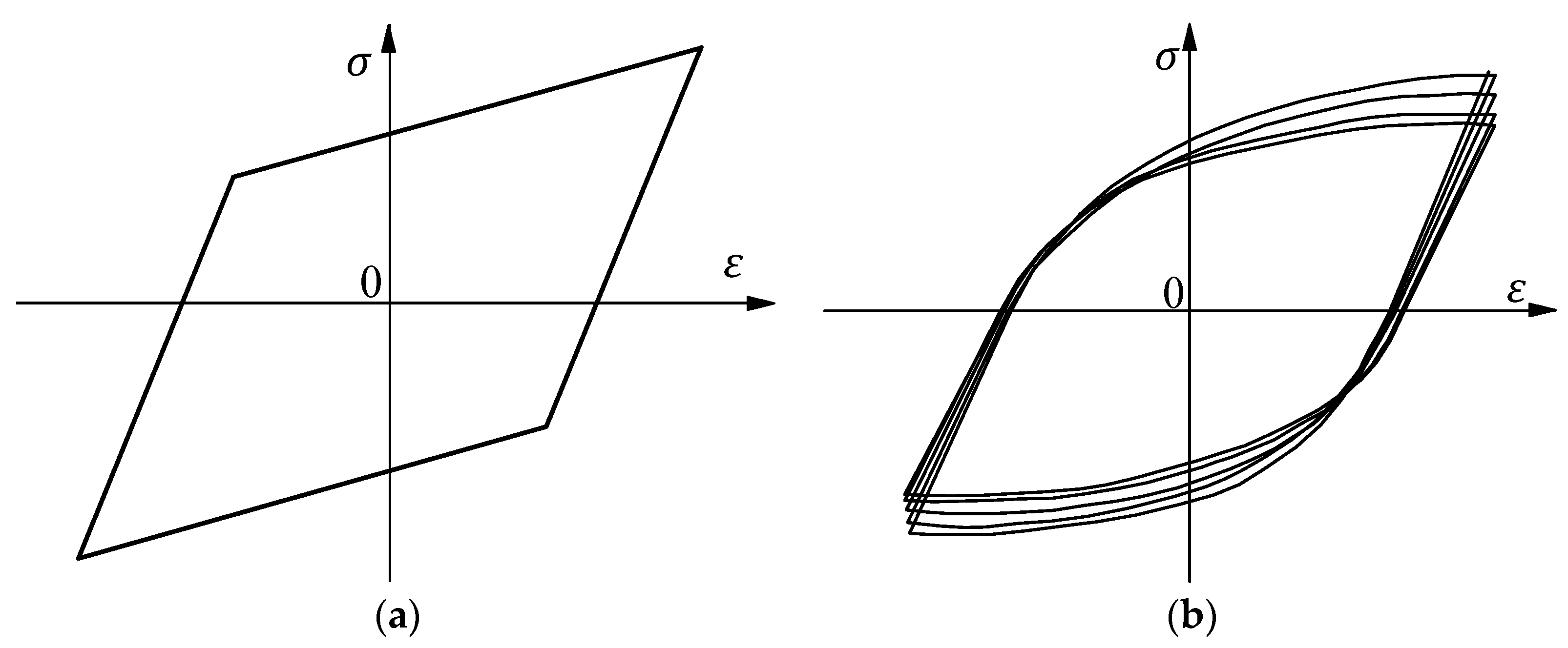
3.2. Cyclic Behavior and Damage Analysis
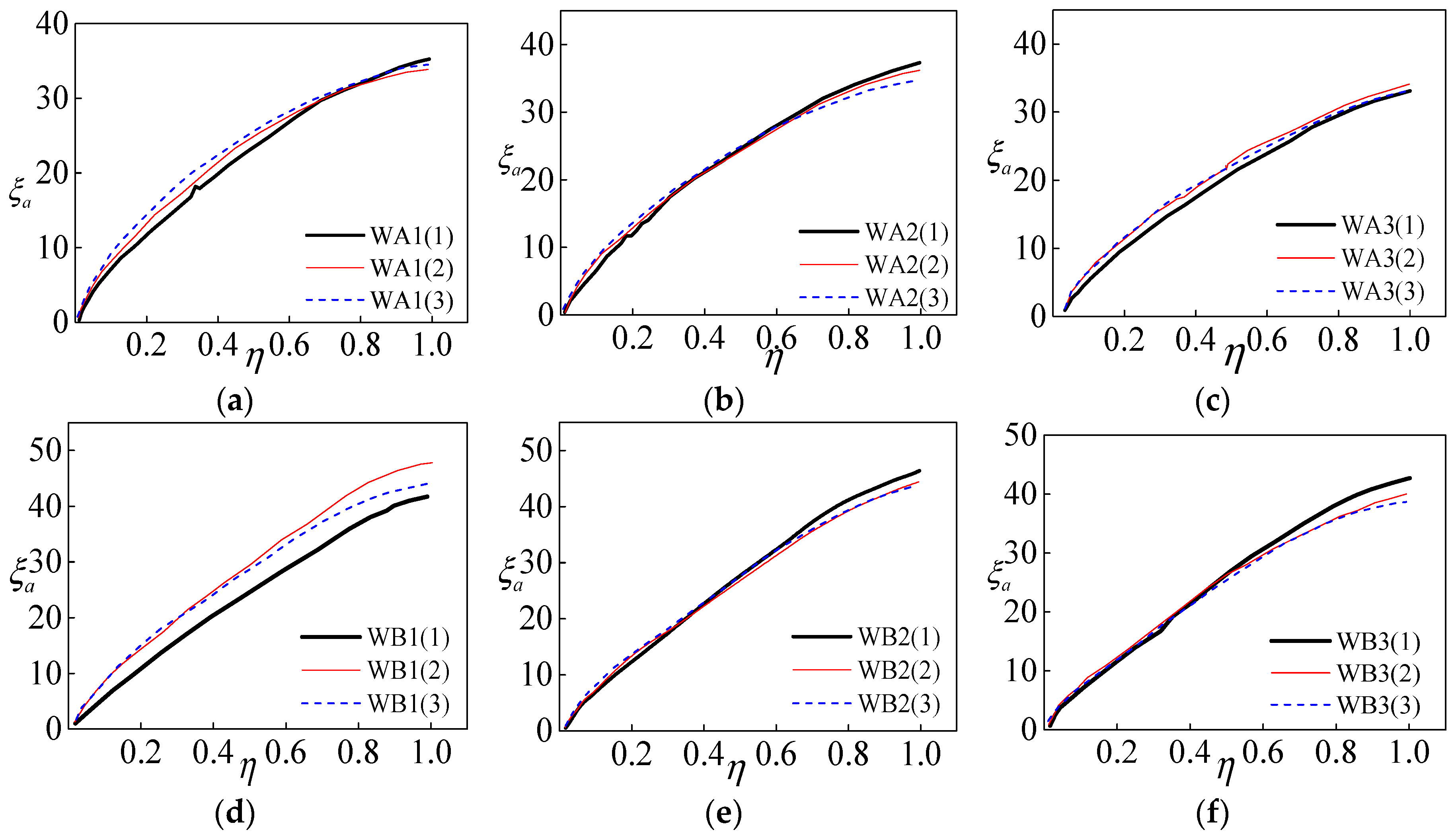
3.3. Variation of Cyclic Stress Amplitude
3.4. EnergyDissipation Behavior
4. An Evolution Equation of Damage Accumulation for Welding Materials
5. A Hysteresis Model with Damage Accumulation of Welding Materials
5.1. Basic Requirements of the Model
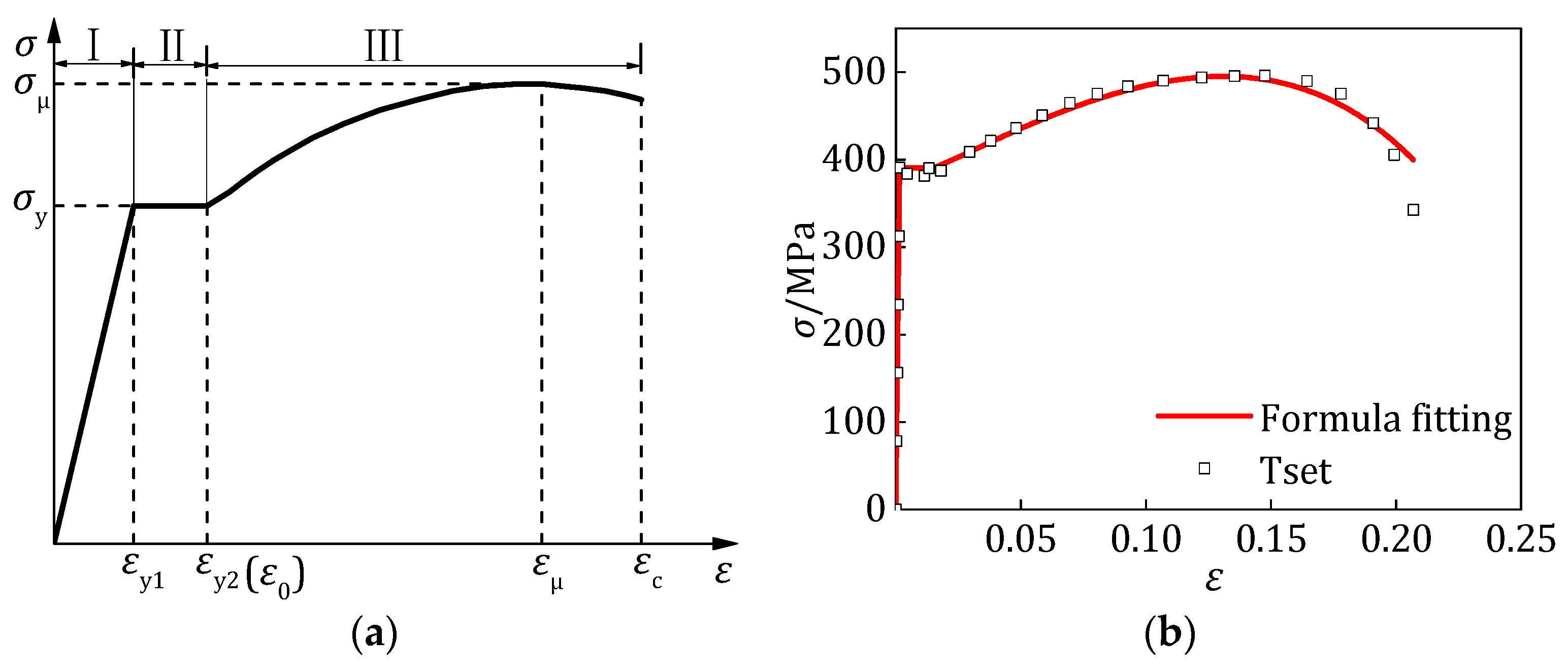
5.2. Initial Loading Curve
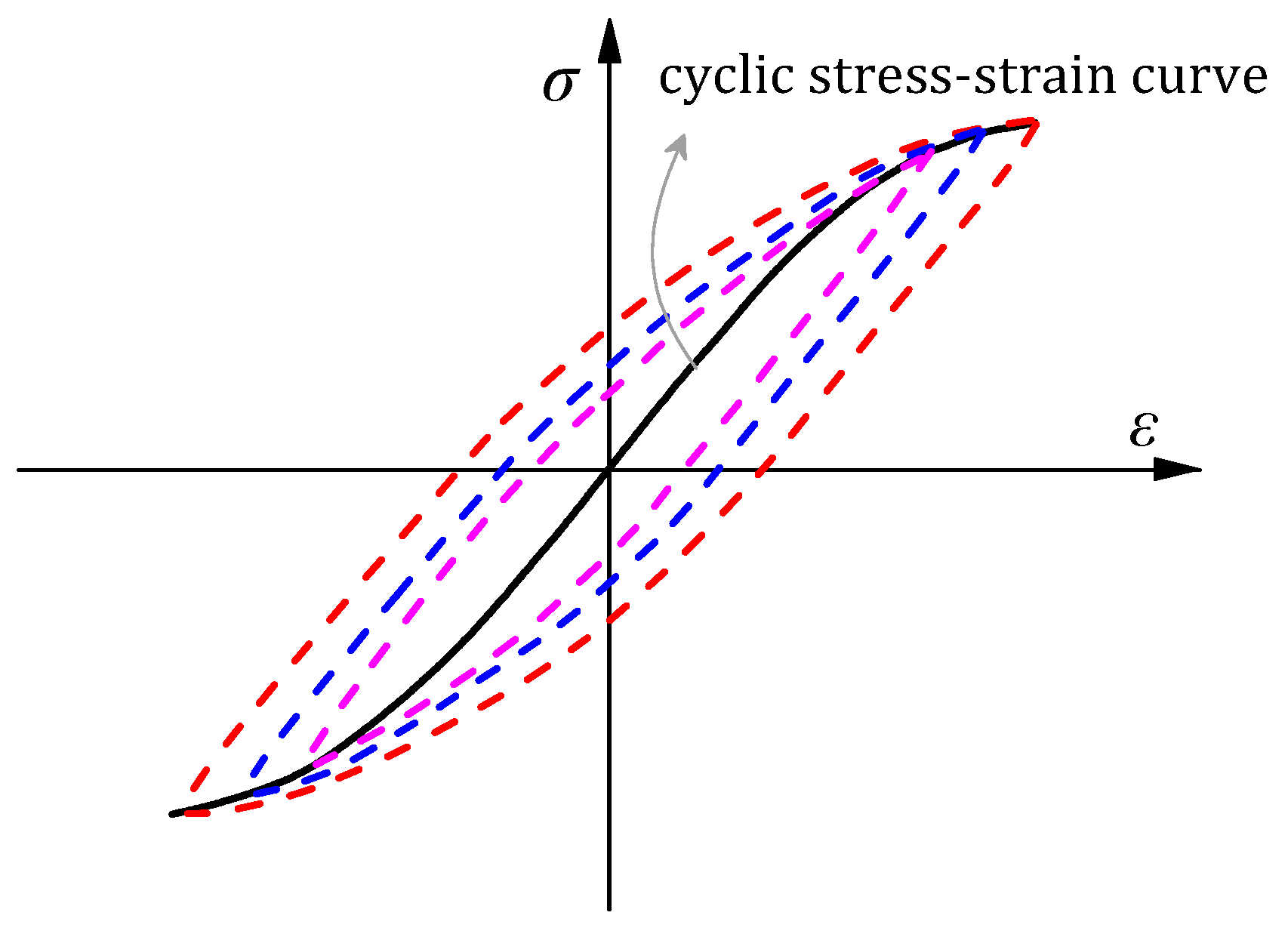
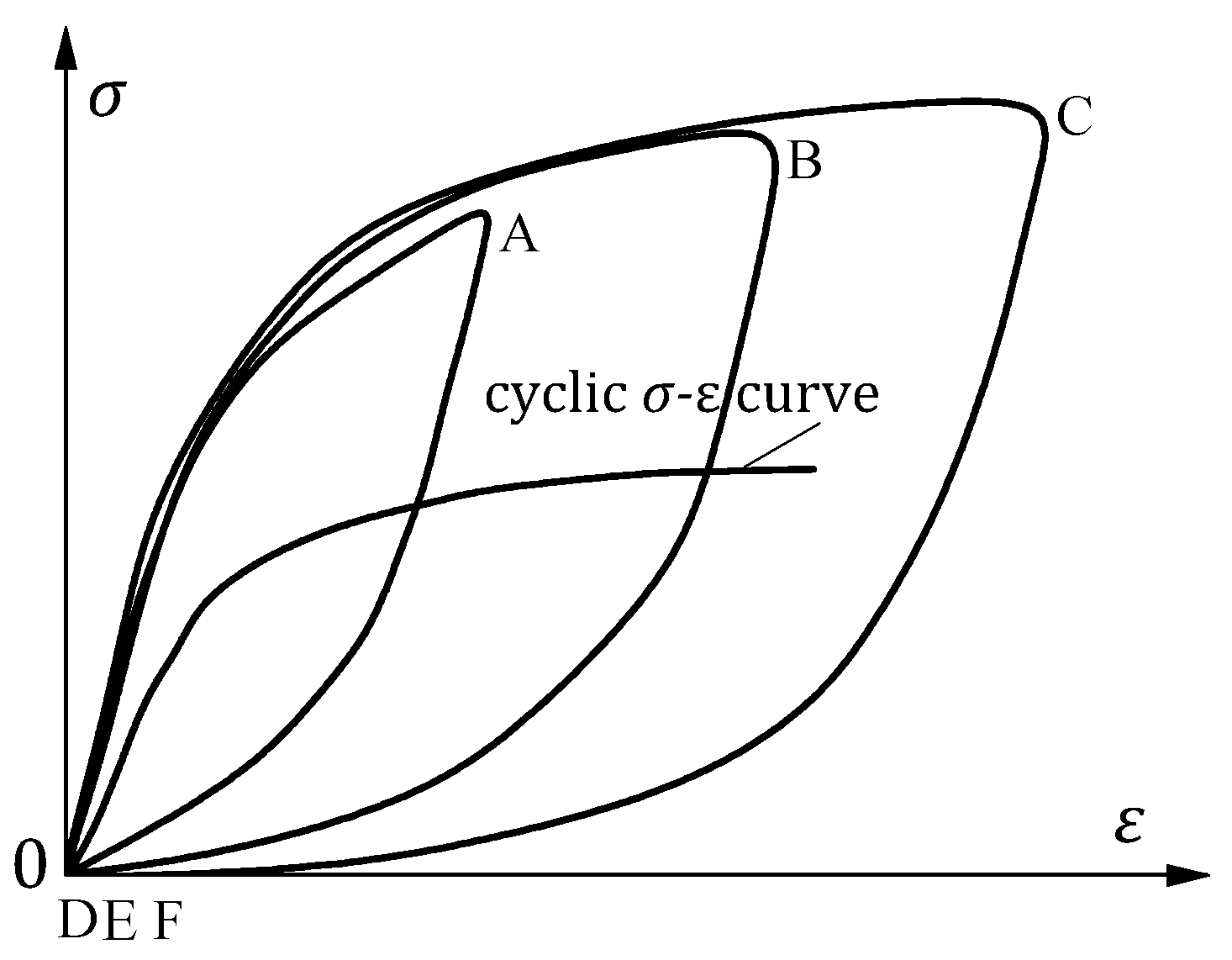
5.3. Cyclic Stress-Strain Curve Based on Ramberg–Osgood Model
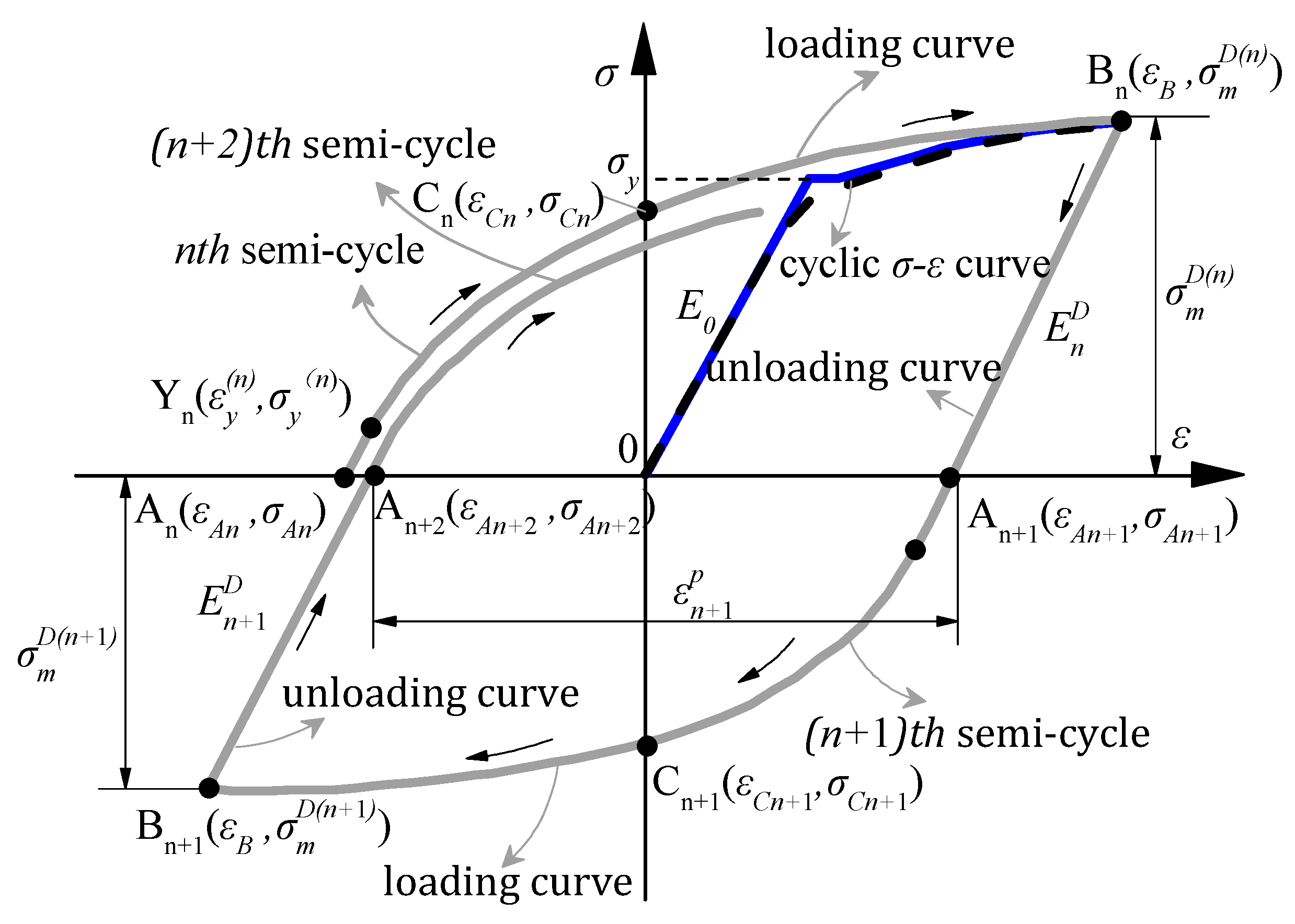
5.4. A Model of Hysteretic Curve with Damage Accumulation
- (1)
- unloading curve (Linear)
- (2)
- loading curve (nonlinear)
5.5. Parameter Fitting of the Model
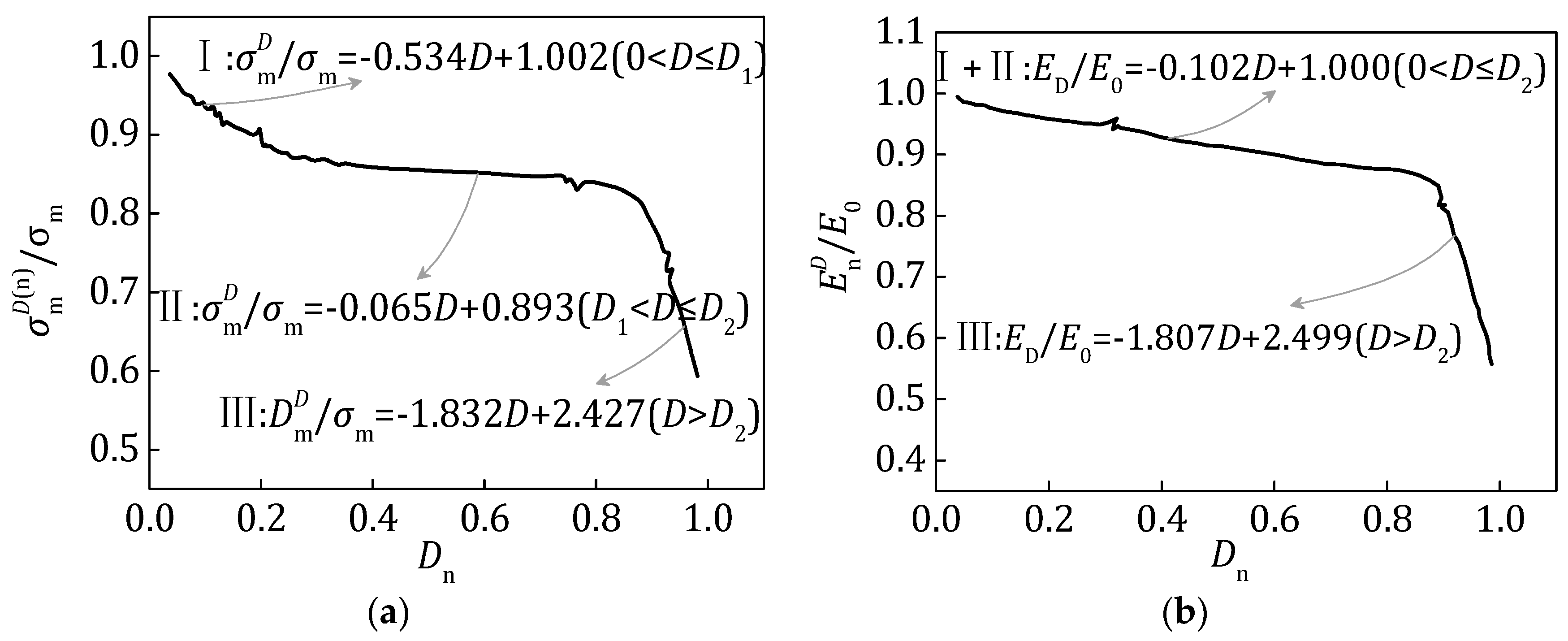
5.5.1. The Parameter λ of EvolutionEquation of Damage Accumulation
5.5.2. The Parameters η, ξ, g, h, K’ and n’
- (1)
- Damage Parameters η, ξ, g, h
- (2)
- K’ and n’
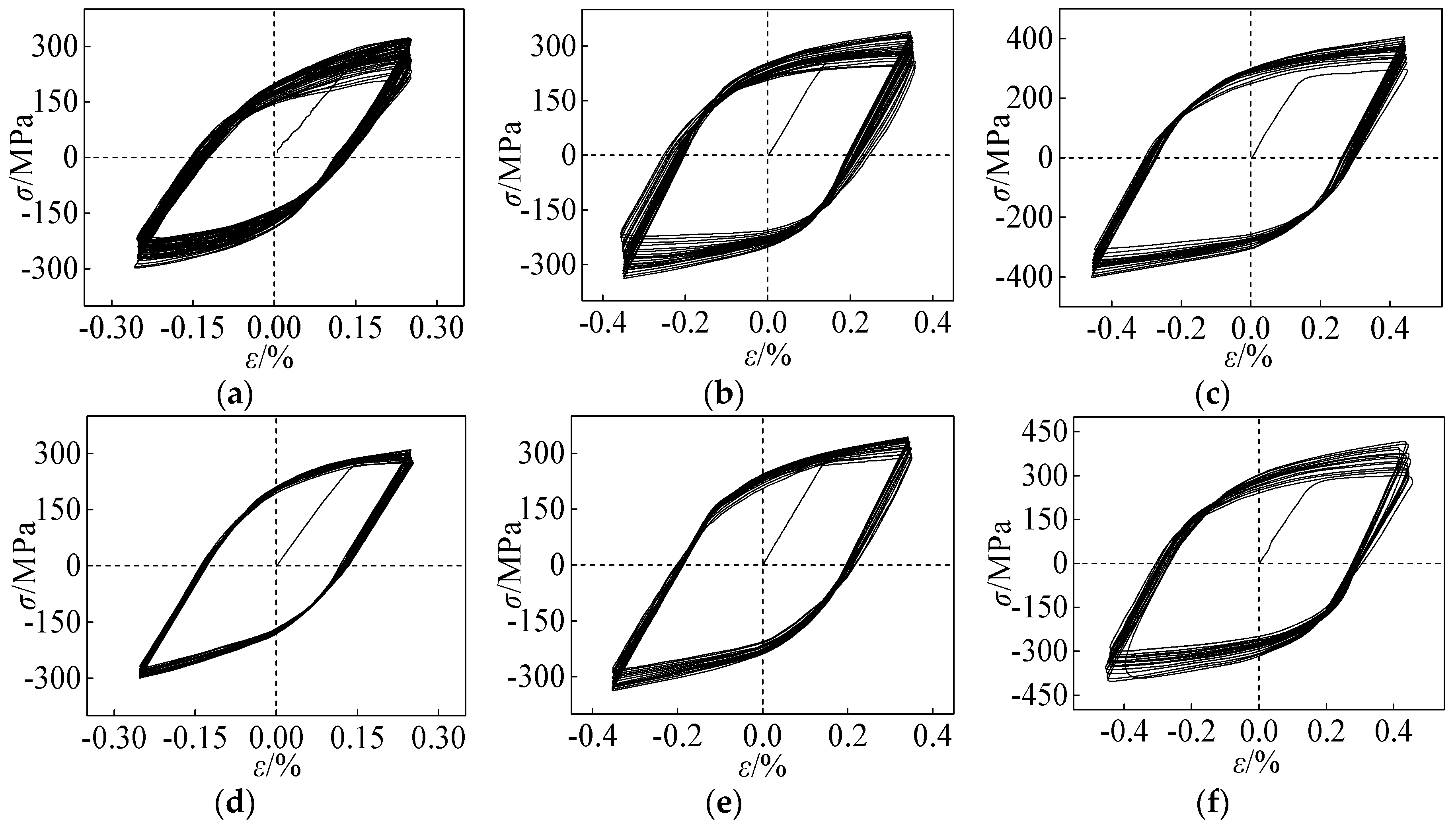
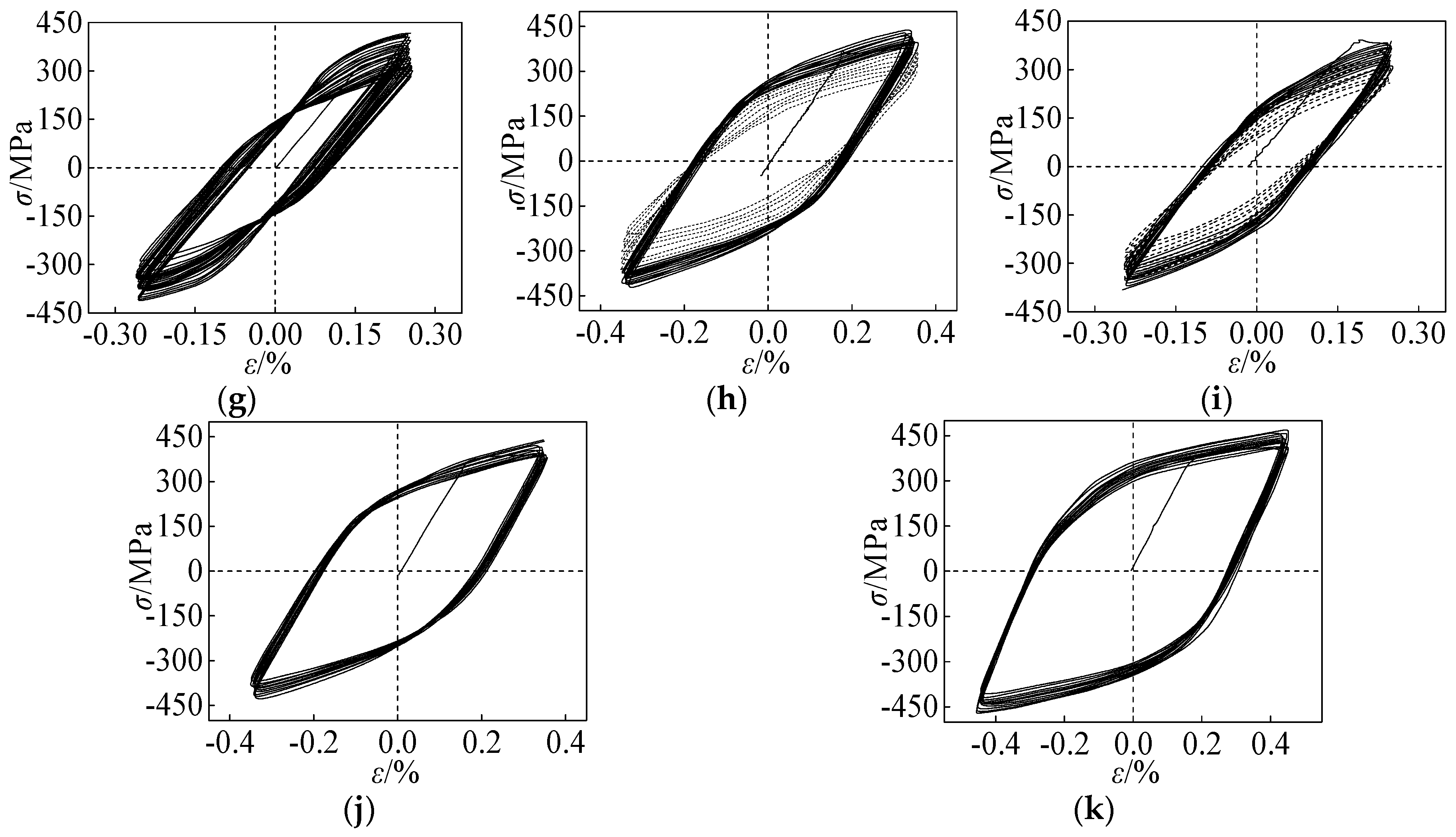
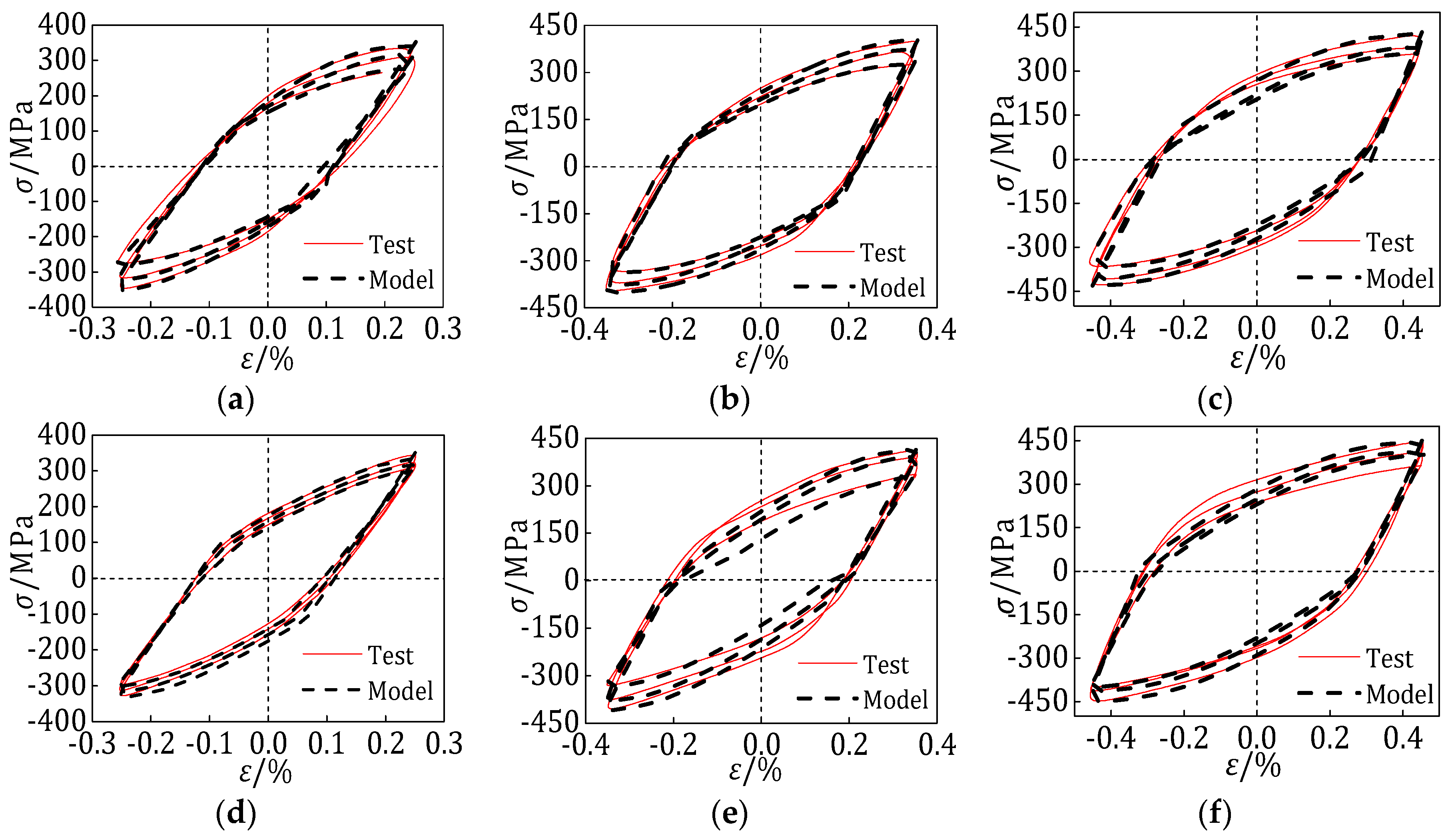
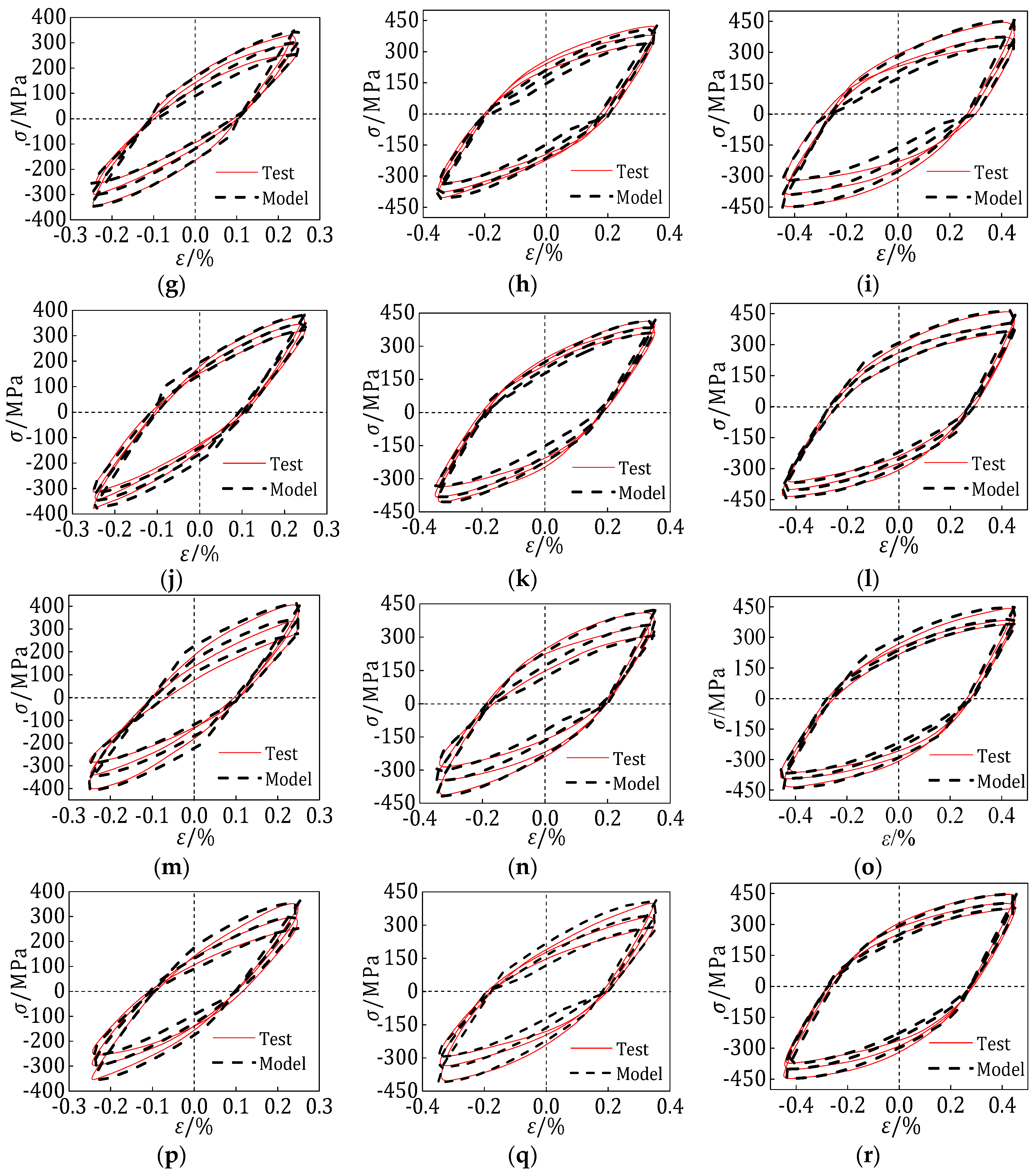
5.6. Comparison between the Test Results and Results Calculated by the Proposal Model
6. Conclusions
- (1)
- The cumulative damage process of welding materials can be divided into three stages, which are presented as the stage of crack initiation, the stage of crack propagation, and the stage the specimenis fractured, and when the specimensare destroyed along the maximum main crack.
- (2)
- As the imposed displacement cycles increased, the cyclic softening behavior of the welding materials of the welded joints in a tubular truss structureis apparent, and the steel hardening behavior is shown. Furthermore, with the increase of cyclic cycles, the effect of damage accumulation on the welding materials is obvious, that is, the cyclic stress amplitude, unloading stiffness, and energy dissipation capacity of the weldingmaterials degenerate gradually. Furthermore, the larger the controlled loading strain amplitude, the faster the rate of damage accumulation. The amplitude of the loading strain has a greater effect on the welding material of base metal Q235 than that of base metal Q345.
- (3)
- Based on the test results and Park–Ang model, an evolutionequation of damage accumulation for welding materials is established considering both energy and deformation comprehensively, in which the energy part is no longer confined to the perfect elastic-plastic condition. Then, the value of parameter λ is fitted by the test data.
- (4)
- It is revealed by the experimental research that the cyclic characteristic and constitutive behavior of the welding material is quite different from the base metal, and the constitutive model used for monotonic loading cannot simulate the damage degradation behavior of the welding materials under cyclic loading. Therefore, a hysteresismodel with damage accumulation of welding materials is constructed based on the Ramberg–Osgood model and the experimental results, which includedthe initial loading curve, cyclic stress-strain curve, and a model of the hysteretic curve. The model can reveal the effects of damage accumulation and the nonlinear constitutive relation of the plasticstage.
- (5)
- The damage parameters and model parameters η, ξ, g, h, K’ and n’ are fitted by the test results. The hysteretic curves calculated by the hysteretic model are compared with the test results, which show that the model has good applicability and the cumulative damage evolution law of the welding materials reflected by the model is basically consistent with the test results.
Author Contributions
Funding
Conflicts of Interest
References
- Wardenier, J.; Packer, J.A.; Zhao, X.L.; Vegte, G.J.V.D. Hollow Sections in Structural Applications; Bouwen Met Staal: Rotterdam, The Netherlands, 2010. [Google Scholar]
- Khademi, F. Load Rating of Railway Bridges by Analysis and Testing. Master’s Thesis, Illinois Institute of Technology, Chicago, IL, USA, 2015. [Google Scholar]
- Khademi, F. Enhancing Load Rating of Railway Truss Bridges through a Hybrid Structural Analysis and instrumentation Procedure. Ph.D. Thesis, Illinois Institute of Technology, Chicago, IL, USA, 2017. [Google Scholar]
- Chen, Y.; Feng, R.; Gao, S.W. Experimental study of concrete-filled multiplanar circular hollow section tubular trusses. Thin-Walled Struct. 2015, 94, 199–213. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, Q.H.; Bao, Y.; Kang, J.P.; Bu, Y.Z. Fatigue performance and evaluation of welded joints in steel truss bridges. J. Constr. Steel Res. 2018, 148, 450–456. [Google Scholar] [CrossRef]
- Gillman, A.; Fuchi, K.; Buskohl, P.R. Truss-based nonlinear mechanical analysis for origami structures exhibiting bifurcation and limit point instabilities. Int. J. Solids Struct. 2018, 147, 80–93. [Google Scholar] [CrossRef]
- Huang, W.J.; Fenu, L.G.; Chen, B.C.; Briseghella, B. Experimental study on joint resistance and failure modes of concrete filled steel tubular (cfst) truss girders. J. Constr. Steel Res. 2018, 141, 241–250. [Google Scholar] [CrossRef]
- Ozyurt, E.; Wang, Y.C. Effects of non-uniform temperature distribution on critical member temperature of steel tubular truss. Eng. Struct. 2016, 116, 95–106. [Google Scholar] [CrossRef]
- Tiainen, T.; Mela, K.; Jokinen, T.; Heinisuo, M. The effect of steel grade on weight and cost of warren-type welded tubular trusses. Proc. Inst. Civ. Eng. Struct. Build. 2017, 170, 855–873. [Google Scholar] [CrossRef]
- Van Der Kooi, K.; Hoult, N.A.; Le, H. Monitoring an in-service railway bridge with a distributed fiber optic strain sensing system. J. Bridge Eng. 2018, 23, 05018007. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, Y.; Wang, K.; Han, S.; Galarza, F.P. Experimental research on circular concrete filled stainless steel tubular truss. Thin-Walled Struct. 2017, 117, 224–238. [Google Scholar] [CrossRef]
- Yang, W.W.; Wang, X.L.; Wang, D.D. Design of long-span and wave-shaped steel canopy structure of ningxia helan mountain stadium. Adv. Mater. Res. 2011, 243–249, 72–78. [Google Scholar] [CrossRef]
- Cui, W.; Wang, F. Damage Accumulation. In Encyclopedia of Tribology, 2013 Edition; Wang, Q.J., Chung, Y.-W., Eds.; Springer: Boston, MA, USA, 2013; pp. 706–709. [Google Scholar]
- Diel, S.; Huber, O. A continuum damage mechanics model for the static and cyclic fatigue of cellular composites. Materials 2017, 10, 951. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.H.; Jia, X.X.; Munstermann, S.; Bleck, W. A generalized damage model accounting for instability and ductile fracture for sheet metals. Key Eng. Mater. 2014, 611–612, 106–110. [Google Scholar] [CrossRef]
- Möller, B.; Baumgartner, J.; Wagener, R.; Kaufmann, H.; Melz, T. Low cycle fatigue life assessment of welded high-strength structural steels based on nominal and local design concepts. Int. J. Fatigue 2017, 101, 192–208. [Google Scholar] [CrossRef]
- Nie, G.B.; Fan, F.; Zhi, X.D. A constitutive model for circular steel pipe by spatial hysteretic test. Adv. Struct. Eng. 2012, 15, 1279–1290. [Google Scholar] [CrossRef]
- Rong, J.; Kyriakides, S. Ratcheting, wrinkling and collapse of tubes under axial cycling. Int. J. Solids Struct. 2009, 46, 2856–2870. [Google Scholar]
- Whittaker, M.T.; Wilshire, B. Creep and creep fracture of 2.25cr–1.6w steels (grade 23). Mater. Sci. Eng. A 2010, 527, 4932–4938. [Google Scholar] [CrossRef]
- Du, G.F.; Huo, L.S.; Kong, Q.Z.; Song, G.B. Damage detection of pipeline multiple cracks using piezoceramic transducers. J. Vibroeng. 2016, 18, 2828–2838. [Google Scholar] [CrossRef]
- Feng, Q.; Kong, Q.Z.; Song, G.B. Damage detection of concrete piles subject to typical damage types based on stress wave measurement using embedded smart aggregates transducers. Measurement 2016, 88, 345–352. [Google Scholar] [CrossRef]
- Feng, Q.; Xiao, H.; Kong, Q.Z.; Liang, Y.B.; Song, G.B. Damage detection of concrete piles subject to typical damages using piezoceramic based passive sensing approach. J. Vibroeng. 2016, 18, 801–812. [Google Scholar]
- Ling, Y.B.; Li, D.S.; Song, G.B.; Zhan, C. Damage detection of shear buildings through structural mass-stiffness distribution. Smart Struct. Syst. 2017, 19, 11–20. [Google Scholar] [CrossRef]
- Lu, G.T.; Li, Y.R.; Wang, T.; Xiao, H.; Huo, L.S.; Song, G.B. A multi-delay-and-sum imaging algorithm for damage detection using piezoceramic transducers. J. Intell. Mater. Syst. Struct. 2017, 28, 1150–1159. [Google Scholar] [CrossRef]
- Guo, Y.L.; Zhou, P.; Wang, M.Z.; Pi, Y.L.; Bradford, M.A. Numerical studies of cyclic behavior and design suggestions on triple-truss-confined buckling-restrained braces. Eng. Struct. 2017, 146, 1–17. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, B.; Wu, L.; Han, Q. Experimental research on hysteretic behavior of unstiffened tubular n-joints. J. Build. Struct. 2008, 29, 69–74. [Google Scholar]
- Yang, W.; Wang, X. Experimental research on seismic behavior of unstiffened overlapped chs k-joints. J. Build. Struct. 2013, 34, 85–92. [Google Scholar]
- Yang, W.; Wang, X. Numerical analysis of hysteretic behavior of unstiffened overlapped chs k-joints in steel pipe structures by finite element method. J. Lanzhou Univ. Technol. 2012, 33, 009. [Google Scholar]
- Wang, H.; Jing, H.; Zhao, L.; Han, Y.; Lv, X.; Xu, L. Dislocation structure evolution in 304l stainless steel and weld joint during cyclic plastic deformation. Mater. Sci. Eng. A 2017, 690, 16–31. [Google Scholar] [CrossRef]
- Shen, Z.; Wu, A. Seismic analysis of steel structures considering damage cumulation. Front. Arch. Civ. Eng. China 2007, 1, 1–11. [Google Scholar] [CrossRef]
- Shen, Z.Y. A cumulative damage model for the analysis of steel frames under seismic actions. In Proceedings of the Advances in Steel Structures, Hong Kong, China, 15–17 December 1999; pp. 13–24. [Google Scholar]
- Sun, Z.; Wang, X. Postbuckling investigations of piezoelectric microdevices considering damage effects. Sensors 2014, 14, 4876. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Wang, M.; Wang, Y. Experimental and constitutive model study of structural steel under cyclic loading. J. Constr. Steel Res. 2011, 67, 1185–1197. [Google Scholar] [CrossRef]
- Do, V.N.V.; Lee, C.H.; Chang, K.H. A constitutive model for uniaxial/multiaxial ratcheting behavior of a duplex stainless steel. Mater. Des. 2015, 65, 1161–1171. [Google Scholar]
- Wang, M.; Fahnestock, L.A.; Qian, F.; Yang, W. Experimental cyclic behavior and constitutive modeling of low yield point steels. Constr. Build. Mater. 2017, 131, 696–712. [Google Scholar] [CrossRef]
- Nip, K.H.; Gardner, L.; Davies, C.M.; Elghazouli, A.Y. Extremely low cycle fatigue tests on structural carbon steel and stainless steel. J. Constr. Steel Res. 2009, 66, 96–110. [Google Scholar] [CrossRef]
- Basan, R.; Franulović, M.; Prebil, I.; Kunc, R. Study on ramberg-osgood and chaboche models for 42crmo4 steel and some approximations. J. Constr. Steel Res. 2017, 136, 65–74. [Google Scholar] [CrossRef]
- Dundu, M. Evolution of stress-strain models of stainless steel in structural engineering applications. Constr. Build. Mater. 2018, 165, 413–423. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Elchalakani, M.; Karrech, A.; Patel, V.I.; Yang, B. Behaviour of concrete-filled double-skin short columns under compression through finite element modelling: Shs outer and shs inner tubes. Structures 2018, 14, 358–375. [Google Scholar] [CrossRef]
- Marohnic, T.; Basan, R.; Franulovic, M. Evaluation of methods for estimation of cyclic stress-strain parameters from monotonic properties of steels. Metals 2017, 7, 15. [Google Scholar] [CrossRef]
- Szymczak, C.; Kujawa, M. Torsional buckling and post-buckling of columns made of aluminium alloy. Appl. Math. Model. 2018, 60, 711–720. [Google Scholar] [CrossRef]
- Zappalorto, M.; Maragoni, L. Nonlinear mode iii crack stress fields for materials obeying a modified ramberg-osgood law. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 708–714. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Technical Note; NationalAdvisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Corigliano, P.; Crupi, V.; Fricke, W.; Friedrich, N.; Guglielmino, E. Experimental and numerical analysis of fillet-welded joints under low-cycle fatigue loading by means of full-field techniques. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1327–1338. [Google Scholar] [CrossRef]
- Aucott, L.; Huang, D.; Dong, H.B.; Wen, S.W.; Marsden, J.; Rack, A.; Cocks, A.C.F. A three-stage mechanistic model for solidification cracking during welding of steel. Met. Mater. Trans. A Phys. Met. Mater. Sci. 2018, 49A, 1674–1682. [Google Scholar] [CrossRef]
- Borgesen, P.; Wentlent, L.; Khasawneh, S.; Shirazi, S.; Schmitz, D.; Alghoul, T.; Greene, C.; Yin, L. A mechanistic thermal fatigue model for snagcu solder joints. J. Electron. Mater. 2018, 47, 2526–2544. [Google Scholar] [CrossRef]
- Mac Ardghail, P.; Harrison, N.; Leen, S.B. A through-process, thermomechanical model for predicting welding-induced microstructure evolution and post-weld high-temperature fatigue response. Int. J. Fatigue 2018, 112, 216–232. [Google Scholar] [CrossRef]
- Markiewicz, E.; Langrand, B.; Notta-Cuvier, D. A review of characterisation and parameters identification of materials constitutive and damage models: From normalised direct approach to most advanced inverse problem resolution. Int. J. Impact Eng. 2017, 110, 371–381. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, C.; Gan, J.; Dong, J. Determination of the local constitutive properties of the welded steel joints using digital image correlation method. Constr. Build. Mater. 2018, 171, 485–492. [Google Scholar] [CrossRef]
- Wang, X.L.; Yang, W.W.; Zou, L. Finite element analysis for unstiffened overlapped chs kk-joints welded in different ways. Adv. Mater. Res. 2011, 163–167, 299–306. [Google Scholar] [CrossRef]
- Brünig, M.; Gerke, S. Simulation of damage evolution in ductile metals undergoing dynamic loading conditions. Int. J. Plast. 2011, 27, 1598–1617. [Google Scholar] [CrossRef]
- Cheng, C.; Li, X. Cyclic experimental studies on damage evolution behaviors of shale dependent on structural orientations and confining pressures. Energies 2018, 11, 160. [Google Scholar] [CrossRef]
- Ku-Herrera, J.; Pacheco-Salazar, O.; Ríos-Soberanis, C.; Domínguez-Rodríguez, G.; Avilés, F. Self-sensing of damage progression in unidirectional multiscale hierarchical composites subjected to cyclic tensile loading. Sensors 2016, 16, 400. [Google Scholar] [CrossRef] [PubMed]
- Mielke, A. Complete-damage evolution based on energies and stresses. Discret. Contin. Dyn. Syst. Ser. S (DCDS-S) 2012, 4, 423–439. [Google Scholar]
- Murakami, S.; Kamiya, K. Constitutive and damage evolution equations of elastic-brittle materials based on irreversible thermodynamics. Int. J. Mech. Sci. 1997, 39, 473–486. [Google Scholar] [CrossRef]
- Chinese Code. Gb/700-2006 Carbon Structural Steel; Standards Press of China: Beijing, China, 2006. [Google Scholar]
- Chinese Code. Jgj81-2002 Technical Specification for Welding of Steel Structure of Building; Standards Press of China: Beijing, China, 2003. [Google Scholar]
- Park, Y.J.; Ang, H.S. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Krajcinovic, D. Damage Mechanics; Elsevier: New York, NY, USA, 1996; pp. 117–197. [Google Scholar]
- Shi, G.; Gao, Y.; Wang, X.; Zhang, Y. Mechanical properties and constitutive models of low yield point steels. Constr. Build. Mater. 2018, 175, 570–587. [Google Scholar] [CrossRef]
- Shi, G.; Wang, M.; Bai, Y.; Wang, F.; Shi, Y.; Wang, Y. Experimental and modeling study of high-strength structural steel under cyclic loading. Eng. Struct. 2012, 37, 1–13. [Google Scholar] [CrossRef]
- Christ, H.J.; Mughrabi, H. Cyclic stress-strain response and microstructure under variable amplitude loading. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 335–348. [Google Scholar] [CrossRef]
- Mayer, T.; Mazza, E.; Holdsworth, S.R. Parameter evolution in a continuous masing approach for cyclic plasticity and its physical interpretation. Mech. Mater. 2013, 57, 86–96. [Google Scholar] [CrossRef]
- Segalman, D.J.; Starr, M.J. Inversion of masing models via continuous iwan systems. Int. J. Non-Linear Mech. 2007, 43, 74–80. [Google Scholar] [CrossRef]
- Siddiquee, M.S.A. A pressure-sensitive kinematic hardening model incorporating masing’s law. Acta Geotech. 2015, 10, 623–642. [Google Scholar] [CrossRef]


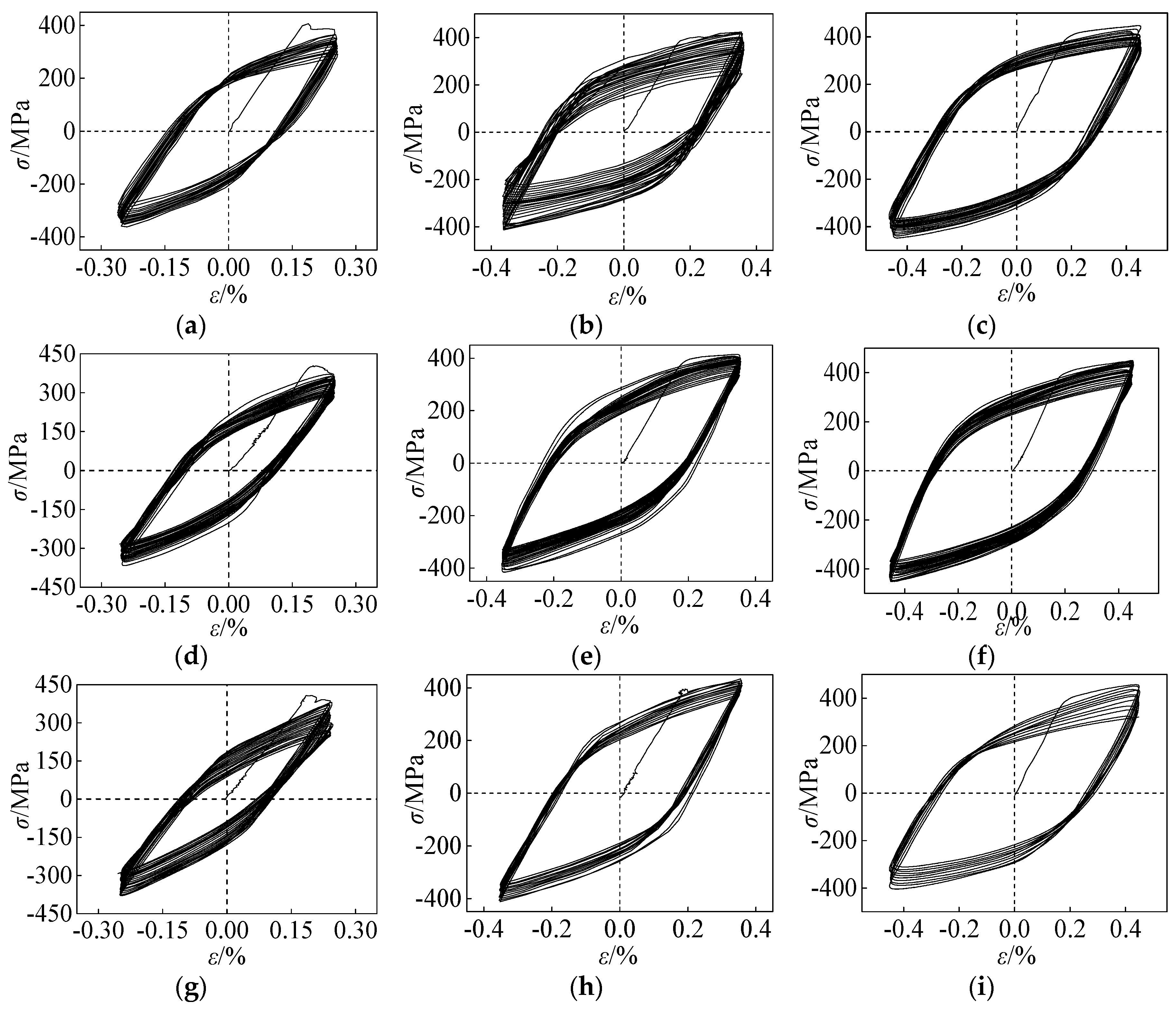
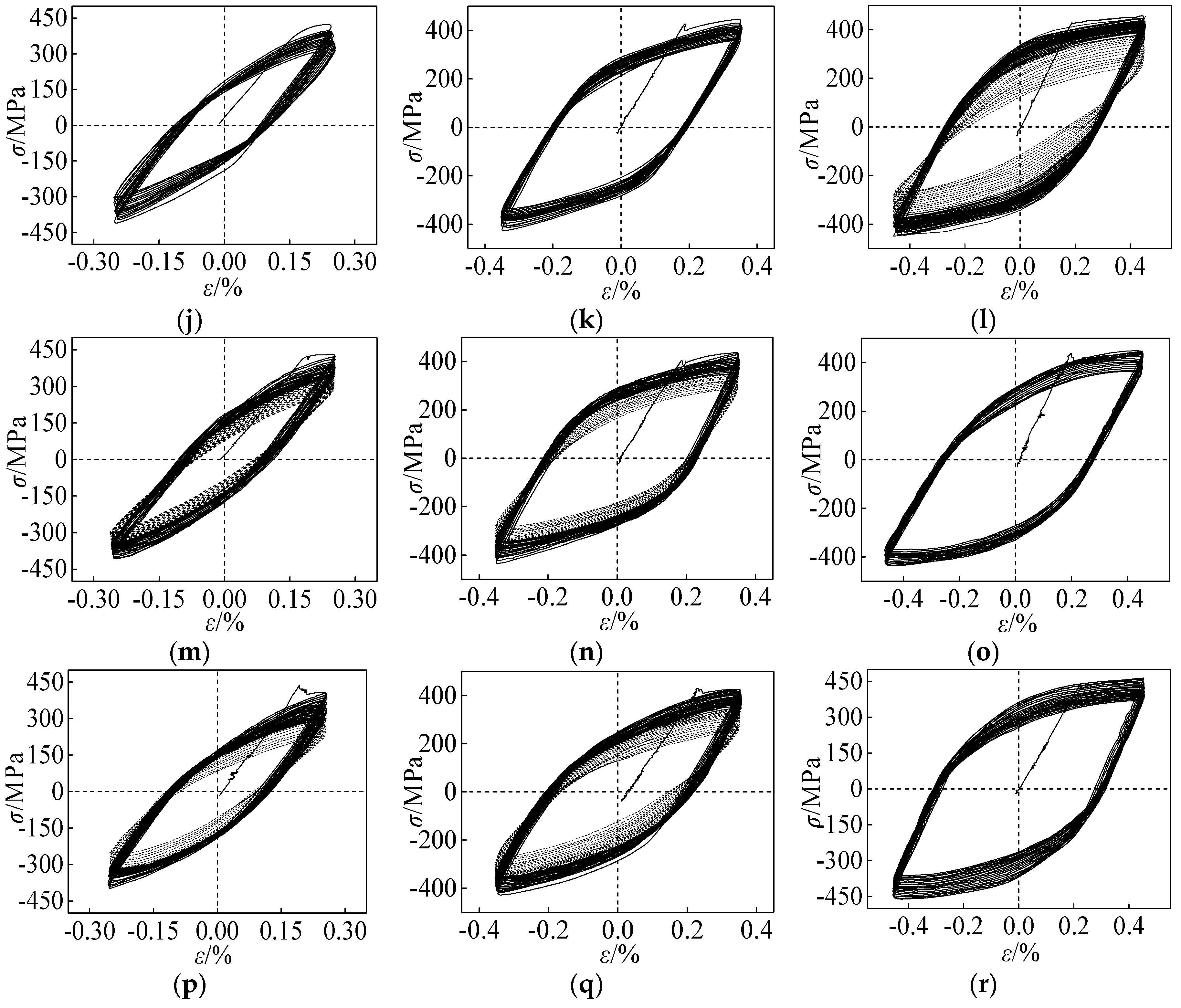

| Type for Base Metal | Steel Specimen before Welding | Welding Material | Steel of Heat-Effected Zone | |||||
|---|---|---|---|---|---|---|---|---|
| Parallel Rolling Direction | Vertical Rolling Direction | Butt Weld | Fillet Weld of T Type | Butt Weld | Fillet Weld of T Type | |||
| Left | Right | Left | Right | |||||
| Q235 | SA1 | SA2 | WA1 | WA2 | WA3 | HA1 | HA2 | HA3 |
| (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | |
| Q345 | SB1 | SB2 | WB1 | WB2 | WB3 | HB1 | HB2 | HB3 |
| (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | (1)–(3) | |
| Specimens | fy/MPa | fu/MPa | εy/% | εu/% | E/GPa |
|---|---|---|---|---|---|
| SA1 | 268.8 | 430.1 | 0.15 | 16.3 | 207.1 |
| SA2 | 268.1 | 429.7 | 0.15 | 16.4 | 195.7 |
| WA1 | 391.7 | 497.6 | 0.16 | 13.0 | 239.7 |
| WA2 | 401.6 | 486.8 | 0.17 | 12.7 | 233.6 |
| WA3 | 402.3 | 497.8 | 0.17 | 11.8 | 213.0 |
| HA1 | 254.7 | 433.5 | 0.13 | 15.8 | 223.3 |
| HA2 | 259.2 | 423.6 | 0.13 | 15.5 | 203.6 |
| HA3 | 255.4 | 422.9 | 0.13 | 15.6 | 204.5 |
| SB1 | 365.6 | 532.6 | 0.16 | 16.0 | 216.1 |
| SB2 | 385.1 | 540.1 | 0.15 | 15.2 | 217.9 |
| WB1 | 420.1 | 498.1 | 0.15 | 12.7 | 235.5 |
| WB2 | 426.3 | 508.5 | 0.17 | 11.7 | 251.0 |
| WB3 | 431.5 | 525.4 | 0.17 | 11.3 | 217.6 |
| HB1 | 365.2 | 531.0 | 0.16 | 16.0 | 235.0 |
| HB2 | 357.8 | 530.5 | 0.15 | 15.3 | 225.1 |
| HB3 | 358.5 | 527.6 | 0.16 | 15.2 | 218.3 |
| Specimens | Welded Specimens | Steel Specimens | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| WA1 | WA2 | WA3 | WB1 | WB2 | WB3 | SA1 | SA2 | SB1 | SB2 | |
| (1) (0.25%) | 3091 | 3810 | 3430 | 4351 | 4205 | 4293 | 4321 | 3789 | 4766 | 4703 |
| (2) (0.35%) | 1865 | 1801 | 1831 | 2223 | 1992 | 1973 | 2109 | 1983 | 2525 | 2607 |
| (3) (0.45%) | 1089 | 994 | 977 | 1559 | 1165 | 1106 | 1301 | 976 | 1639 | |
| Base Metal | Welding Material | E/Gpa | σy/MPa | K/Gpa | m | εy1/% | εy2(ε0)/% | εc/% | b | DC/% |
|---|---|---|---|---|---|---|---|---|---|---|
| Q235 | Butt weld | 239.70 | 391.70 | 2.73 | 0.77 | 0.16 | 1.50 | 21.25 | 0.065 | 59.24 |
| Fillet weld | 223.30 | 401.94 | 1.82 | 0.54 | 0.18 | 1.50 | 21.34 | 0.046 | 50.03 | |
| Q345 | Butt weld | 247.71 | 420.07 | 2.52 | 0.65 | 0.17 | 1.70 | 17.71 | 0.052 | 57.64 |
| Fillet weld | 241.07 | 433.92 | 2.17 | 0.60 | 0.18 | 1.70 | 16.97 | 0.044 | 53.11 |
| With Q235 Base Metal | With Q345 Base Metal | ||||||
|---|---|---|---|---|---|---|---|
| Specimens | E0/GPa | K0/MPa | n0 | Specimens | E0/GPa | K0/MPa | n0 |
| WA1 | 239.700 | 1266 | 4.784 | WB1 | 247.710 | 953 | 8.099 |
| WA2 | 223.000 | 1331 | 5.531 | WB2 | 241.070 | 939 | 8.610 |
| WA3 | 223.000 | 1466 | 6.203 | WB3 | 241.070 | 885 | 9.272 |
| Specimens | Welding Material of Q235 Steel | Welding Material of Q345 Steel | ||||
|---|---|---|---|---|---|---|
| Butt Weld | Fillet Weld | Butt Weld | Fillet Weld | |||
| WA1 | WA2 | WA3 | WB1 | WB2 | WB3 | |
| (1) | 0.02529 | 0.02609 | 0.02871 | 0.02311 | 0.02156 | 0.02176 |
| (2) | 0.02233 | 0.02538 | 0.02613 | 0.01905 | 0.01909 | 0.02433 |
| (3) | 0.02905 | 0.03043 | 0.03280 | 0.02071 | 0.02326 | 0.02230 |
| Model Parameters | 0.0256 | 0.0273 | 0.0294 | 0.0209 | 0.02130 | 0.0227 |
| Specimens | I | II | III | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ξ1 | η1 | D1 | ξ2 | η2 | D2 | ξ3 | η3 | ||
| Butt weld of Q235 steel | WA1(1) | 0.509 | 0.961 | 0.228 | 0.099 | 0.873 | 0.897 | 1.799 | 2.350 |
| WA1(2) | 0.475 | 0.998 | 0.239 | 0.105 | 0.875 | 0.866 | 1.879 | 2.355 | |
| WA1(3) | 0.485 | 1.001 | 0.231 | 0.087 | 0.897 | 0.860 | 1.770 | 2.362 | |
| Model Parameters | 0.489 | 0.986 | 0.233 | 0.097 | 0.882 | 0.874 | 1.816 | 2.356 | |
| Left fillet weld of Q235 steel | WA2(1) | 0.530 | 1.001 | 0.247 | 0.057 | 0.858 | 0.883 | 1.191 | 1.871 |
| WA2(2) | 0.455 | 0.997 | 0.241 | 0.058 | 0.901 | 0.886 | 2.158 | 2.790 | |
| WA2(3) | 0.456 | 0.998 | 0.226 | 0.059 | 0.899 | 0.859 | 2.157 | 2.788 | |
| Model Parameters | 0.480 | 0.999 | 0.238 | 0.058 | 0.886 | 0.876 | 1.825 | 2.483 | |
| Right fillet weld of Q235 steel | WA3(1) | 0.445 | 1.002 | 0.251 | 0.086 | 0.887 | 0.863 | 1.167 | 1.843 |
| WA3(2) | 0.500 | 1.000 | 0.243 | 0.045 | 0.889 | 0.858 | 2.078 | 2.678 | |
| WA3(3) | 0.525 | 0.999 | 0.229 | 0.077 | 0.896 | 0.886 | 1.996 | 2.675 | |
| Model Parameters | 0.490 | 1.000 | 0.241 | 0.069 | 0.891 | 0.869 | 1.747 | 2.399 | |
| Butt weld of Q345 steel | WB1(1) | 0.468 | 0.999 | 0.235 | 0.058 | 0.902 | 0.899 | 2.551 | 3.151 |
| WB1(2) | 0.534 | 1.002 | 0.228 | 0.065 | 0.893 | 0.869 | 1.832 | 2.427 | |
| WB1(3) | 0.508 | 0.989 | 0.236 | 0.075 | 0.887 | 0.889 | 2.235 | 2.912 | |
| Model Parameters | 0.503 | 0.997 | 0.233 | 0.066 | 0.894 | 0.885 | 2.206 | 2.830 | |
| Left fillet weld of Q345 steel | WB2(1) | 0.535 | 0.998 | 0.233 | 0.068 | 0.889 | 0.865 | 1.622 | 2.233 |
| WB2(2) | 0.625 | 1.002 | 0.241 | 0.077 | 0.868 | 0.887 | 1.620 | 2.237 | |
| WB2(3) | 0.612 | 1.000 | 0.231 | 0.095 | 0.881 | 0.859 | 1.634 | 2.210 | |
| Model Parameters | 0.592 | 1.000 | 0.235 | 0.080 | 0.879 | 0.865 | 1.625 | 2.227 | |
| Right fillet weld of Q345 steel | WB3(1) | 0.505 | 0.998 | 0.219 | 0.064 | 0.902 | 0.875 | 2.279 | 2.841 |
| WB3(2) | 0.446 | 0.997 | 0.241 | 0.048 | 0.901 | 0.887 | 2.587 | 3.153 | |
| WB3(3) | 0.455 | 0.998 | 0.246 | 0.063 | 0.902 | 0.878 | 2.284 | 2.854 | |
| Model Parameters | 0.469 | 0.998 | 0.235 | 0.058 | 0.902 | 0.880 | 2.383 | 2.949 | |
| Specimens | I + II | III | ||||
|---|---|---|---|---|---|---|
| h2 | g2 | D2 | h3 | g3 | ||
| Butt weld of Q235 steel | WA1(1) | 0.045 | 0.991 | 0. 889 | 2.083 | 2.466 |
| WA1(2) | 0.024 | 0.982 | 0. 881 | 1.694 | 2.433 | |
| WA1(3) | 0.024 | 0.989 | 0. 879 | 1.668 | 2.453 | |
| Model Parameters | 0.031 | 0.987 | 0. 883 | 1.815 | 2.446 | |
| Left fillet weld of Q235 steel | WA2(1) | 0.020 | 0.997 | 0. 875 | 1.751 | 2.553 |
| WA2(2) | 0.021 | 0.998 | 0. 882 | 1.751 | 2.503 | |
| WA2(3) | 0.020 | 0.997 | 0. 879 | 1.709 | 2.513 | |
| Model Parameters | 0.020 | 0.997 | 0. 879 | 1.737 | 2.523 | |
| Right fillet weld of Q235 steel | WA3(1) | 0.056 | 1.000 | 0.887 | 1.345 | 2.134 |
| WA3(2) | 0.020 | 0.997 | 0.886 | 1.384 | 2.196 | |
| WA3(3) | 0.113 | 1.000 | 0.886 | 0.981 | 1.796 | |
| Model Parameters | 0.063 | 0.999 | 0.886 | 1.225 | 2.044 | |
| Butt weld of Q345 steel | WB1(1) | 0.109 | 0.999 | 0.890 | 1.519 | 2.269 |
| WB1(2) | 0.111 | 1.000 | 0.882 | 1.807 | 2.499 | |
| WB1(3) | 0.103 | 1.002 | 0.886 | 1.445 | 2.196 | |
| Model Parameters | 0.107 | 1.000 | 0.886 | 1.509 | 2.321 | |
| Left fillet weld of Q345 steel | WB2(1) | 0.113 | 0.997 | 0.879 | 1.005 | 1.825 |
| WB2(2) | 0.094 | 0.999 | 0.881 | 1.083 | 1.878 | |
| WB2(3) | 0.104 | 1.001 | 0.877 | 1.054 | 1.883 | |
| Model Parameters | 0.104 | 0.999 | 0.879 | 1.047 | 1.862 | |
| Right fillet weld of Q345 steel | WB3(1) | 0.083 | 0.999 | 0.857 | 1.198 | 1.956 |
| WB3(2) | 0.057 | 1.000 | 0.887 | 2.365 | 3.043 | |
| WB3(3) | 0.089 | 0.999 | 0.890 | 1.789 | 2.513 | |
| Model Parameters | 0.076 | 0.999 | 0.878 | 1.784 | 2.504 | |
| Specimens | εB/% | K’ | n’ | |
|---|---|---|---|---|
| WA1 | WA1(1) | 0.25 | 2.26 × 107 | 0.546 |
| WA1(2) | 0.35 | 2.65 × 107 | 0.499 | |
| WA1(3) | 0.45 | 3.05 × 107 | 0.459 | |
| Model Parameters | ||||
| WA2 | WA2(1) | 0.25 | 2.23 × 107 | 0.547 |
| WA2(2) | 0.35 | 2.64 × 107 | 0.504 | |
| WA2(3) | 0.45 | 3.05 × 107 | 0.461 | |
| Model Parameters | ||||
| WA3 | WA3(1) | 0.25 | 2.24 × 107 | 0.546 |
| WA3(2) | 0.35 | 2.64 × 107 | 0.505 | |
| WA3(3) | 0.45 | 3.04 × 107 | 0.464 | |
| Model Parameters | ||||
| WB1 | WB1(1) | 0.25 | 1.40 × 107 | 0.567 |
| WB1(2) | 0.35 | 1.63 × 107 | 0.521 | |
| WB1(3) | 0.45 | 1.86 × 107 | 0.475 | |
| Model Parameters | ||||
| WB2 | WB2(1) | 0.25 | 1.41 × 107 | 0.566 |
| WB2(2) | 0.35 | 1.63 × 107 | 0.521 | |
| WB2(3) | 0.45 | 1.85 × 107 | 0.476 | |
| Model Parameters | ||||
| WB3 | WB3(1) | 0.25 | 1.40 × 107 | 0.566 |
| WB3(2) | 0.35 | 1.64 × 107 | 0.520 | |
| WB3(3) | 0.45 | 1.86 × 107 | 0.475 | |
| Model Parameters | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suo, Y.; Yang, W.; Chen, P. Study on Hysteresis Model of Welding Material in Unstiffened Welded Joints of Steel Tubular Truss Structure. Appl. Sci. 2018, 8, 1701. https://doi.org/10.3390/app8091701
Suo Y, Yang W, Chen P. Study on Hysteresis Model of Welding Material in Unstiffened Welded Joints of Steel Tubular Truss Structure. Applied Sciences. 2018; 8(9):1701. https://doi.org/10.3390/app8091701
Chicago/Turabian StyleSuo, Yaqi, Wenwei Yang, and Peng Chen. 2018. "Study on Hysteresis Model of Welding Material in Unstiffened Welded Joints of Steel Tubular Truss Structure" Applied Sciences 8, no. 9: 1701. https://doi.org/10.3390/app8091701
APA StyleSuo, Y., Yang, W., & Chen, P. (2018). Study on Hysteresis Model of Welding Material in Unstiffened Welded Joints of Steel Tubular Truss Structure. Applied Sciences, 8(9), 1701. https://doi.org/10.3390/app8091701