Optimal Robust Control of Path Following and Rudder Roll Reduction for a Container Ship in Heavy Waves
Abstract
1. Introduction
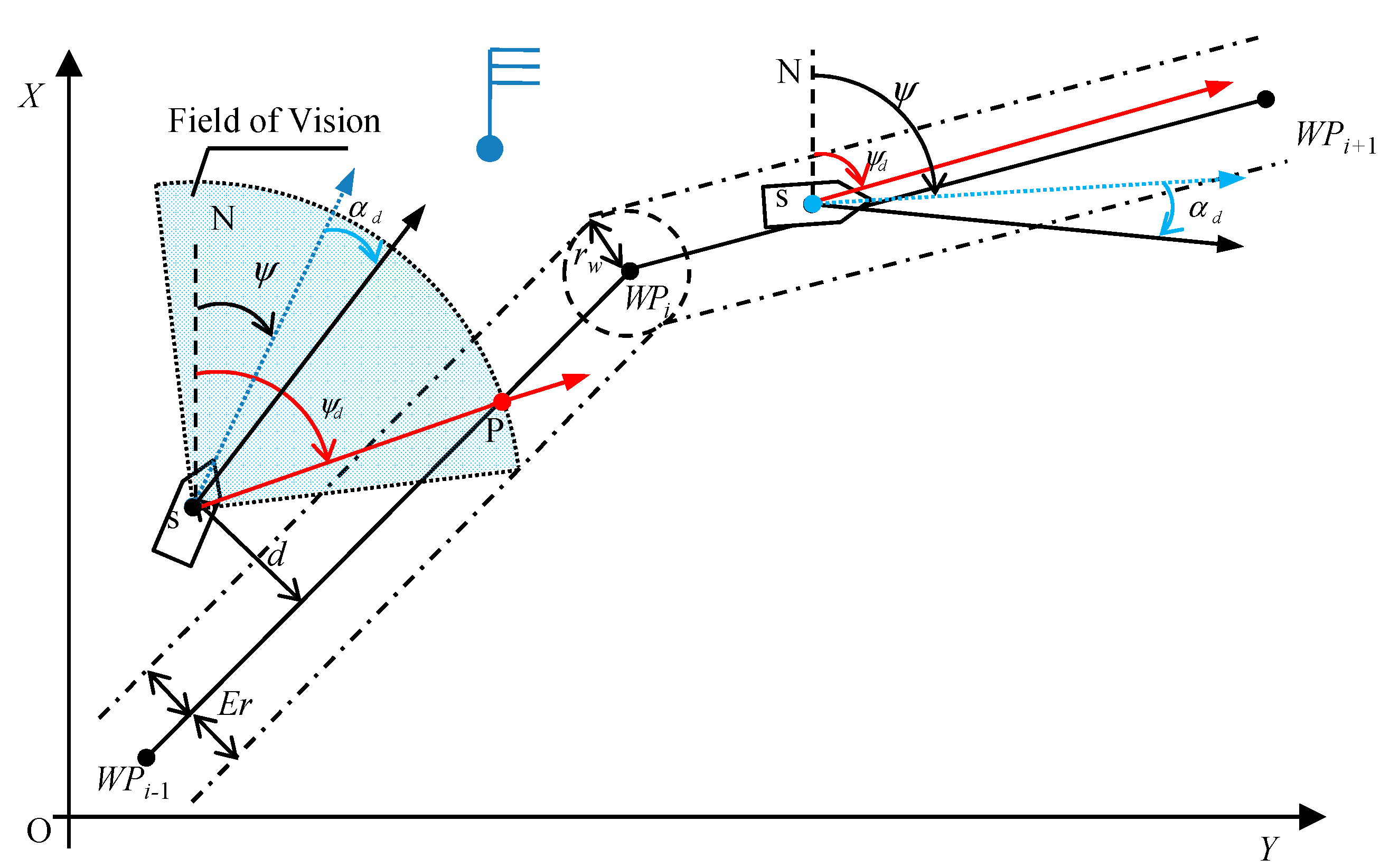
- An improved line of sight (LOS) principle with course-keeping in track belt (LOS-CT) is firstly proposed to guide the ship in field of marine practice, which can reduce the rudder movements greatly by keeping the ship in track-belt rather than following the exact route.
- The uniform asymptotic stability proofs of the developed concise robust control design for the course and roll are given. The control parameters have obvious physical significance and can be determined easily.
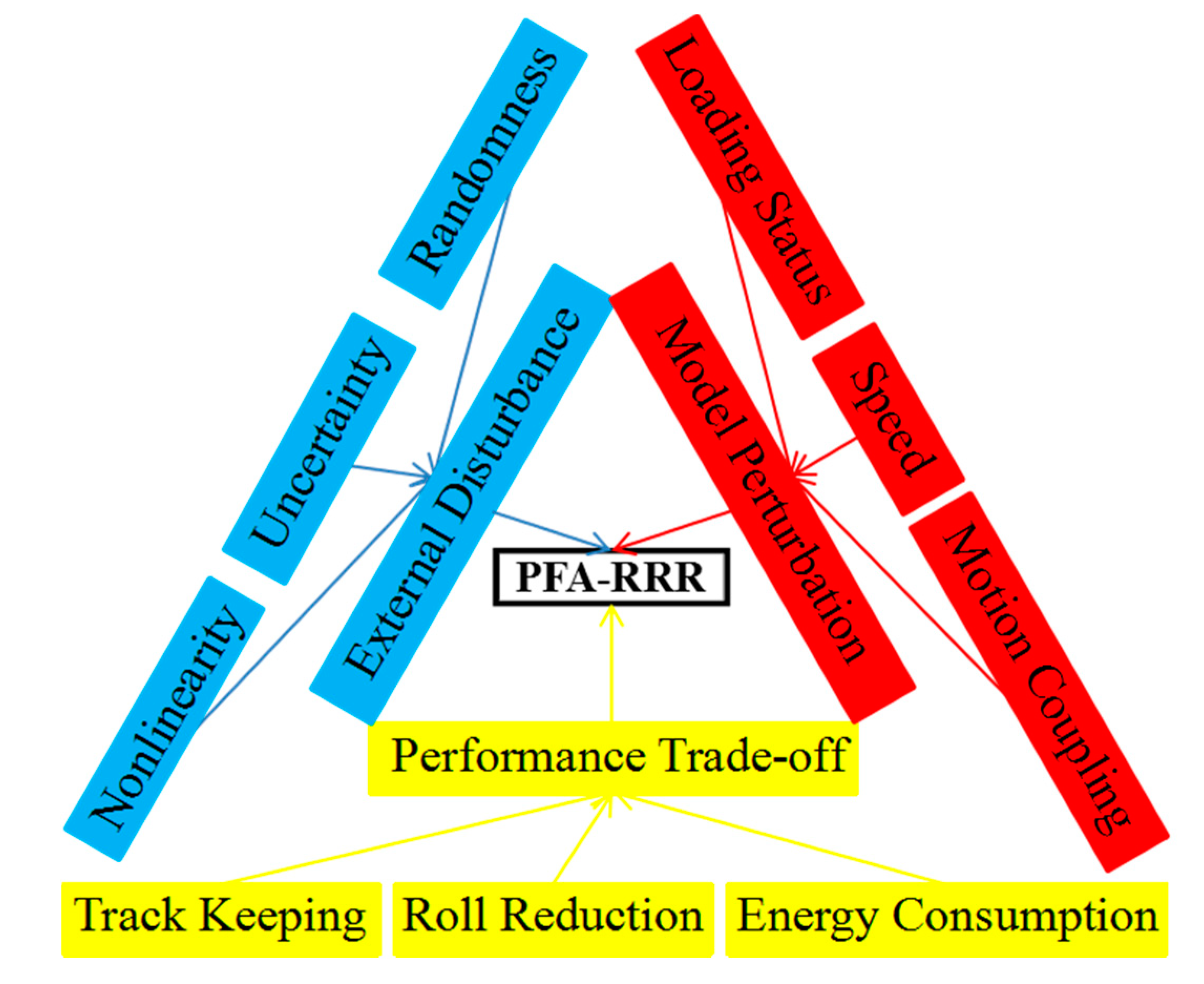
- NSGA-II is recommended to solve the restrictions caused by the model perturbation, external disturbance and the performance trade-off for optimal control solution.
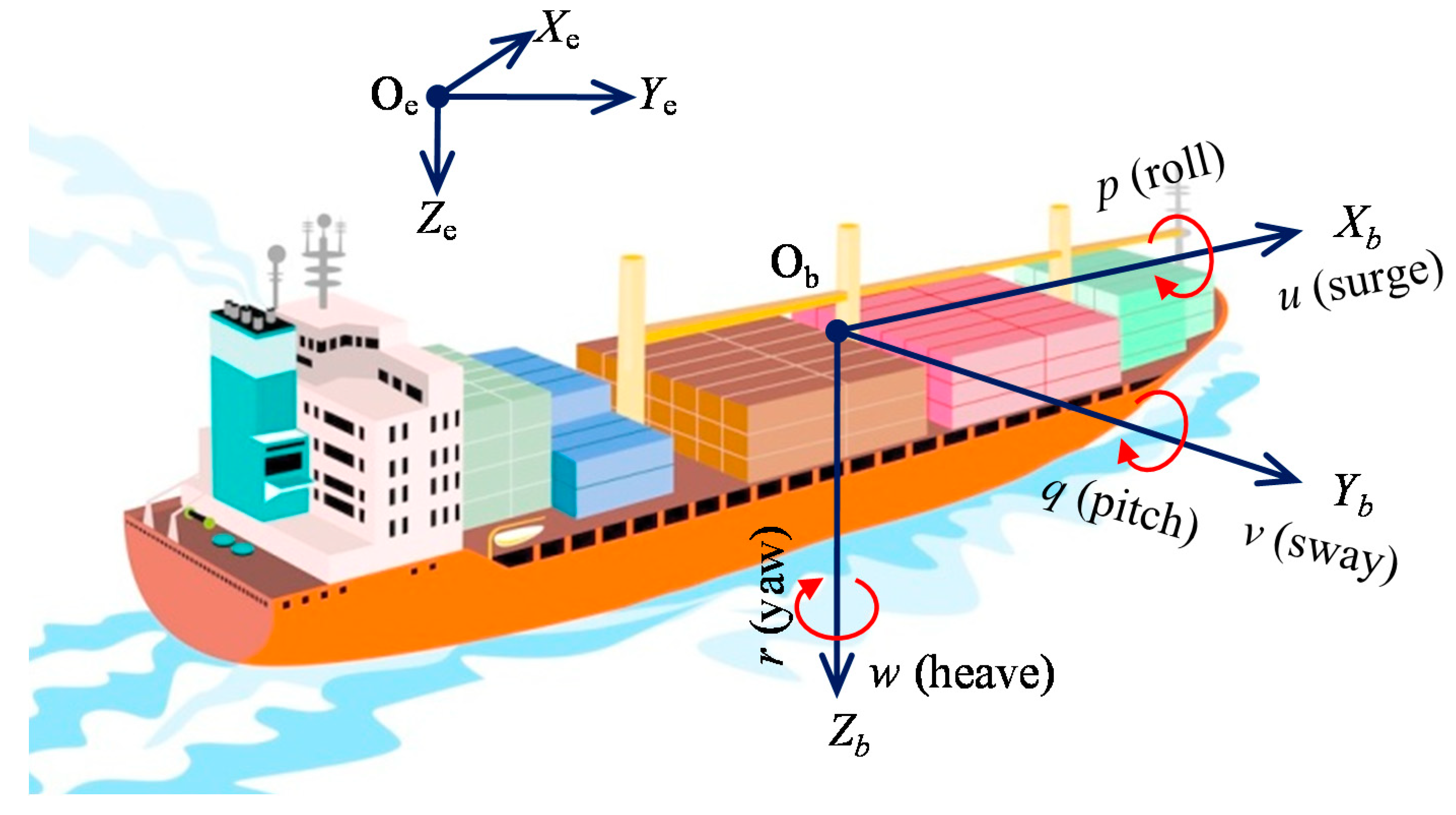
2. Analysis of Mathematical Model
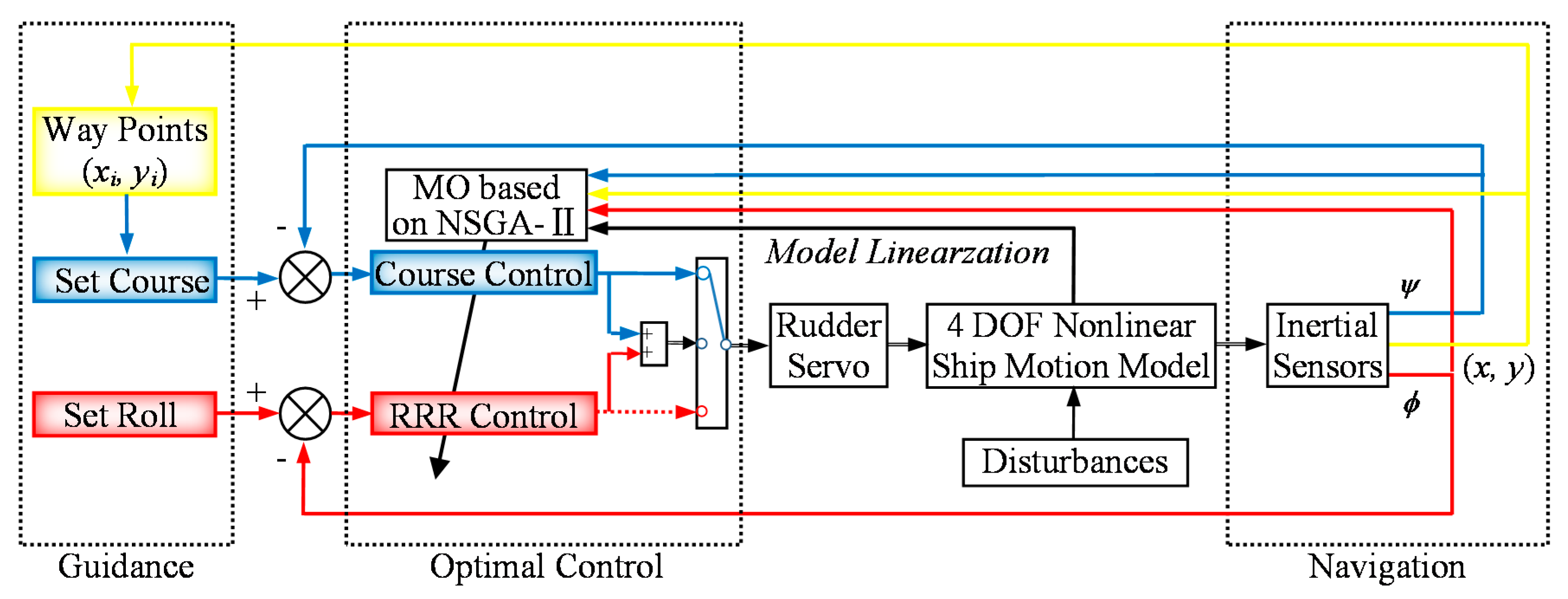
3. Design of Concise Robust Path-Following Control with RRR
3.1. Guidance System for Underactuated Ships
3.2. Control Design
3.2.1. Concise Course Control Based on Backstepping
3.2.2. Concise RRR Control Based on Backstepping
3.2.3. Control Parameters Determining
4. Multi-Objective Optimization Based on NSGA-II
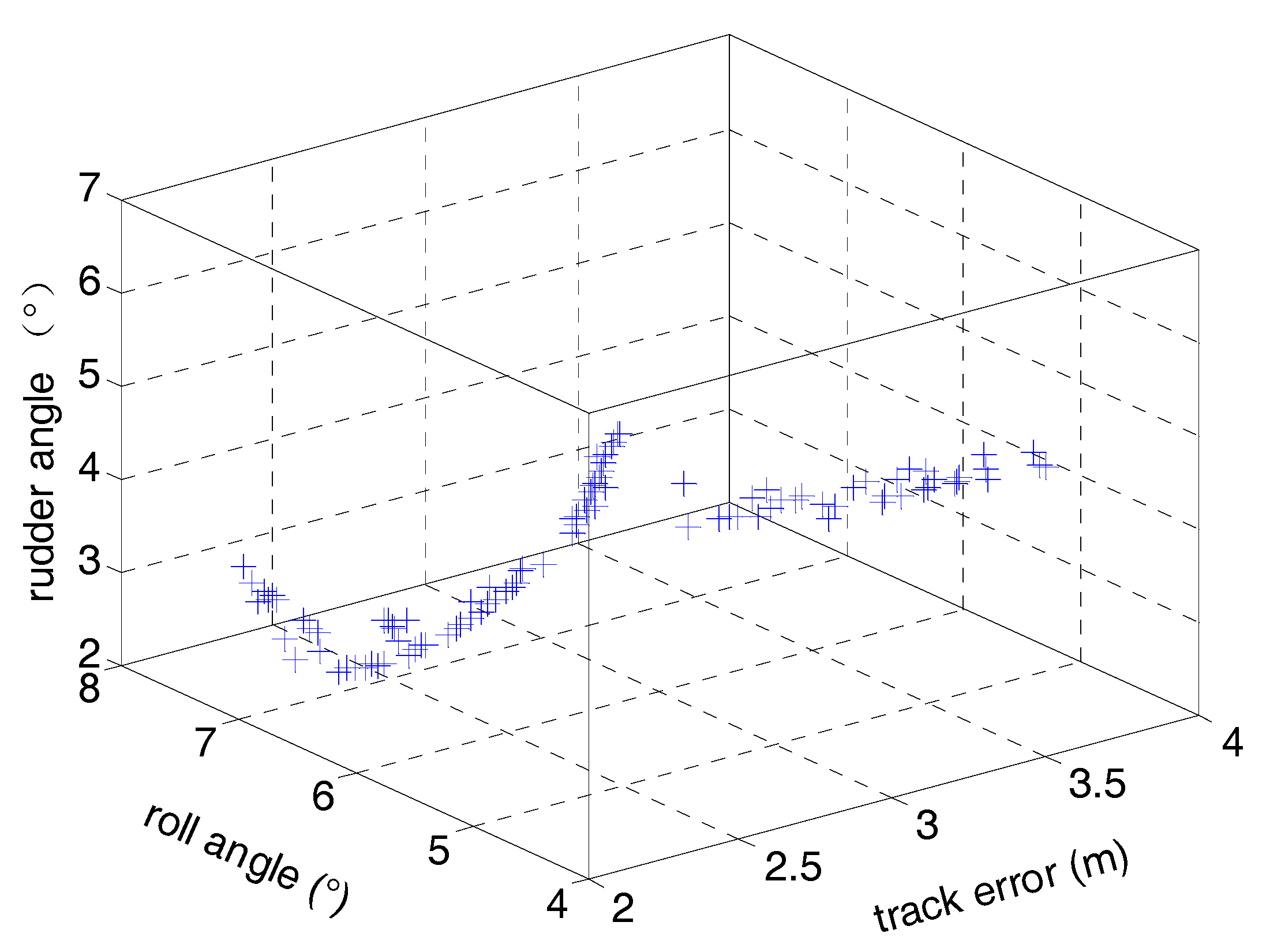
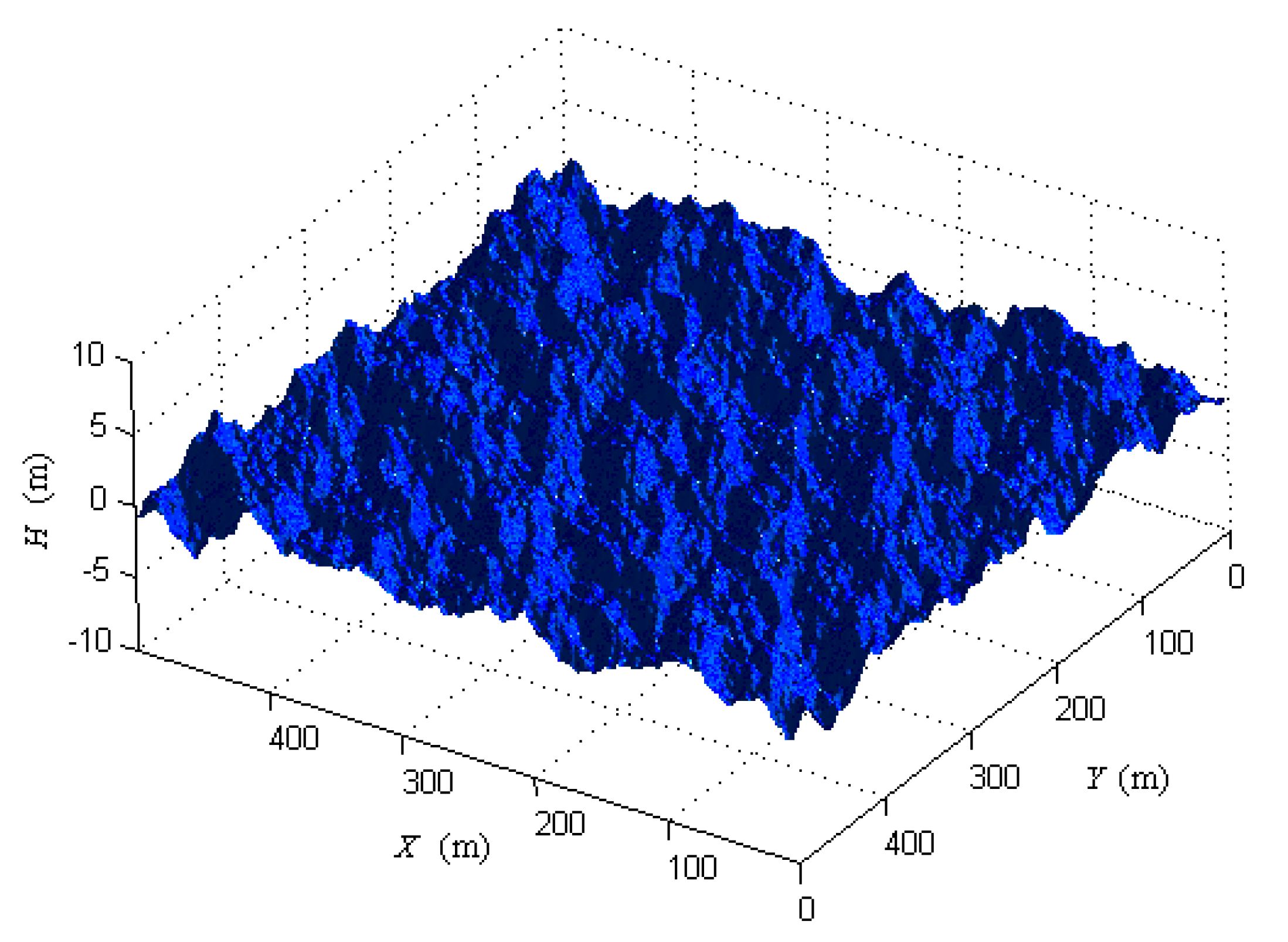
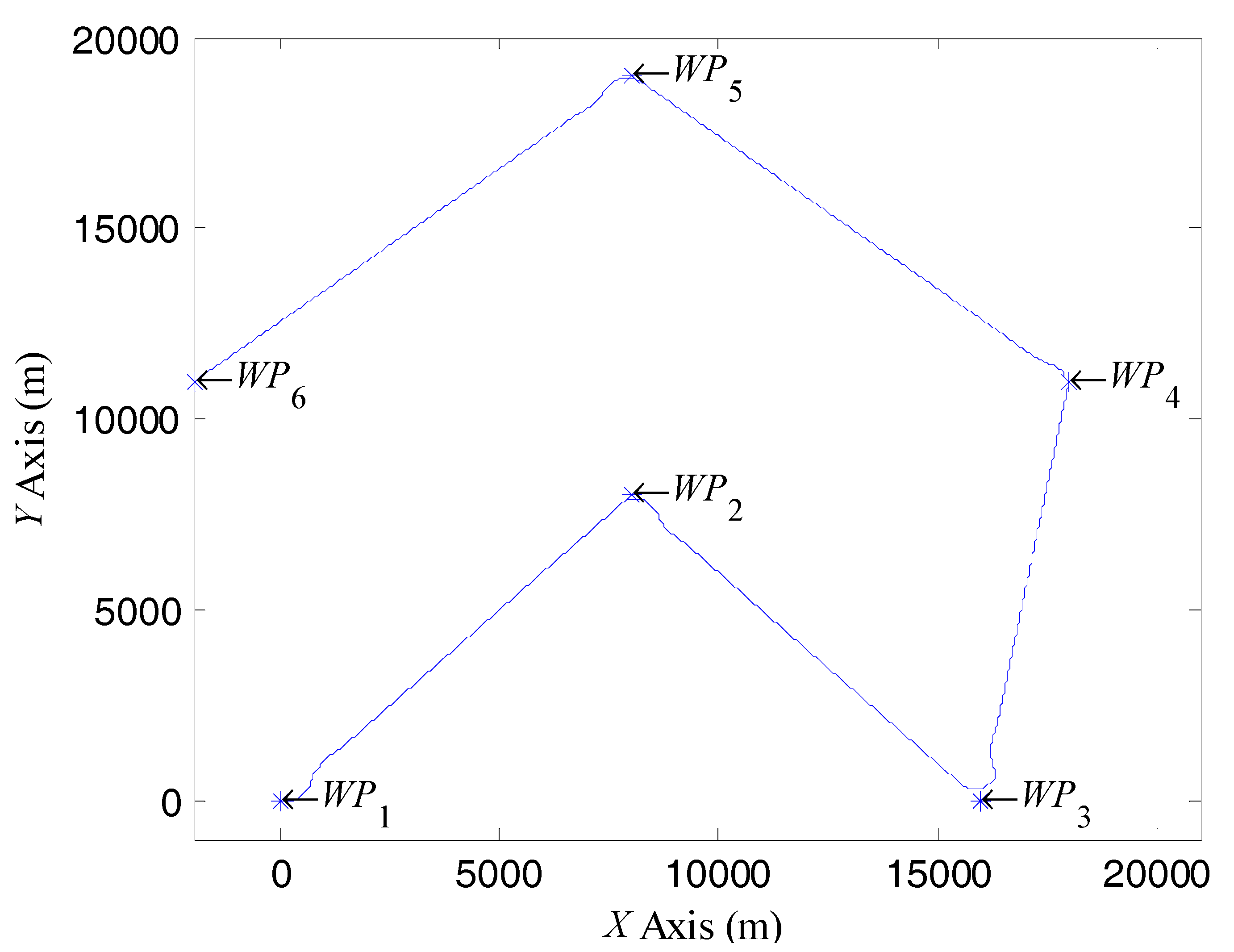
5. Simulation Examples
5.1. Configurations
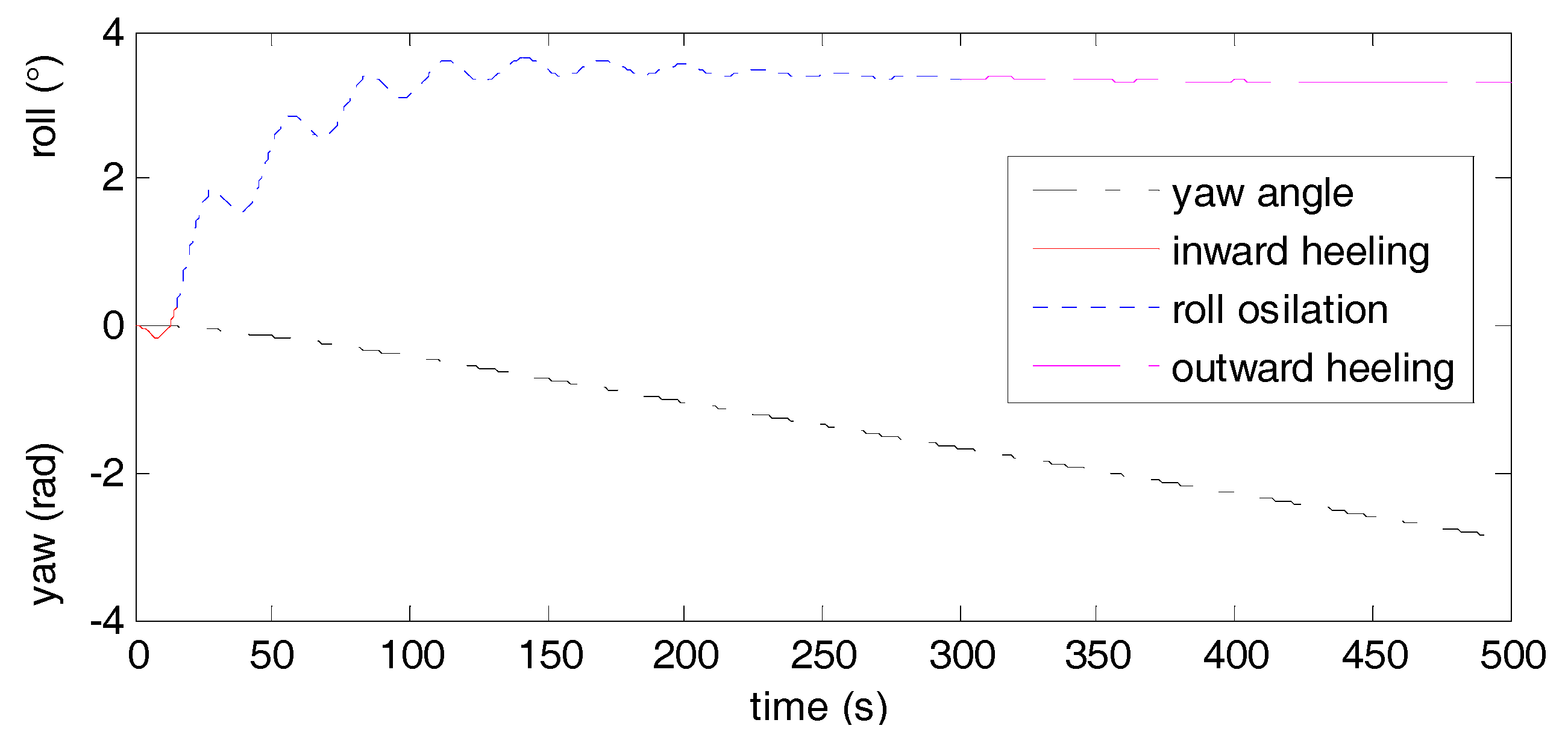
5.2. Simulation Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PHA | path following autopilot |
| CGSA | closed-loop gain shaping algorithm |
| RRR | rudder roll reduction |
| MO | multi-objective optimization |
| LOS | line of sight |
| DOF | degree of freedom |
| CT | track belt |
| PM | Pierson–Moskowitz |
| RMS | root mean square |
| STD | standard deviation |
| ship mass | |
| ship displacement weight | |
| ship’s length | |
| rudder angle of RRR control | |
| ship’s width | |
| rudder angle of course control | |
| ship’s displacement | |
| roll reduction rate | |
| mean draft | |
| STD of wave-induced roll motions | |
| time constants | |
| STD of roll motions with RRR | |
| damping ratio | |
| wave encountering frequency | |
| rolling natural frequency | |
| direction from to | |
| leeway drift coefficient | |
| set course by LOS guidance | |
| equivalent rudder angle | |
| from point S to point P | |
| denotes the wind speed | |
| radius of the visual field | |
| relative wind angle | |
| natural frequency of the control loop | |
| way points | |
| natural frequency of course loop | |
| wave strength factor | |
| natural frequency of RRR loop | |
| turning-ability index | |
| added mass of inertia about x, y | |
| turning-lag index | |
| added moments of inertia about x, z | |
| range of track-belt | |
| moment of inertia about x, z | |
| set course | |
| z-coordinates of the centers of | |
| drift angle | |
| deviation of course and roll | |
| block coefficient | |
| positive design parameters | |
| propeller revolutions | |
| positive design parameters | |
| forward speed | |
| linear robust controllers | |
| current speed | |
| set course and set roll angle | |
| current direction | |
| yaw and roll angle | |
| significant wave height | |
| constant coefficients | |
| turning radius | |
| constant coefficients | |
| maximum of roll angle | |
| sample values of | |
| sample number | |
| surge, sway, yaw and roll velocities | |
| rudder angle | |
| hydrodynamic forces and moments | |
| speed-related gains in roll | |
| control inputs | |
| speed-related gains in yaw | |
| RMS values of | |
| metacentric height | |
| ship’s position S coordinates | |
| x-coordinate of center | |
| cross position P coordinates of the planned route and the vision field arc |
References
- Perez, T.; Blanke, M. Ship roll damping control. Annu. Rev. Control 2012, 36, 129–147. [Google Scholar] [CrossRef]
- Liu, C.; Sun, J.; Zou, Z. Integrated Line of Sight and Model Predictive Control for Path Following and Roll Motion Control Using Rudder. J. Ship Res. 2015, 59, 99–112. [Google Scholar] [CrossRef]
- Perez, T. Ship Motion Control: Course Keeping and Roll Stabilization Using Rudder and Fins; Springer: Berlin, Germany, 2005. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Brockett, R.; Millman, R.; Sussman, H. Differential Geometric Control Theory; Birkhauser: Boston, MA, USA, 1983. [Google Scholar]
- Ghommam, J.; Mnif, F.; Derbel, N. Global stabilization and tracking control of underactuated surface vessels. IET Control Theory Appl. 2010, 4, 71–88. [Google Scholar] [CrossRef]
- Oh, S.-R.; Sun, J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control. Ocean Eng. 2010, 37, 289–295. [Google Scholar] [CrossRef]
- Khaled, N.; Chalhoub, N.G. A self-tuning guidance and control system for marine surface vessels. Nonlinear Dyn. 2013, 73, 897–906. [Google Scholar] [CrossRef]
- Fossen, T. Guidance and Control of Ocean Vehicles; John Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Wang, L.; Wang, S.; Liu, J.; Han, J. Robust PID control of course-keeping with RRS and its MCO based on NSGA-II. ICIC Express Lett. 2015, 9, 3113–3119. [Google Scholar]
- Zhang, X.K.; Yang, G.; Zhang, Q.; Zhang, G.; Zhang, Y. Improved Concise Backstepping Control of Course Keeping for Ships Using Nonlinear Feedback Technique. J. Navig. 2017, 70, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.K.; Zhang, Q.; Ren, H.X.; Yang, G.P. Linear reduction of backstepping algorithm based on nonlinear decoration for ship course-keeping control system. Ocean Eng. 2018, 147, 1–8. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Zheng, Y. Adaptive neural path-following control for underactuated ships in fields of marine practice. Ocean Eng. 2015, 104, 558–567. [Google Scholar] [CrossRef]
- Fang, M.C.; Luo, J.H. On the track keeping and roll reduction of the ship in random waves using different sliding mode controllers. Ocean Eng. 2007, 34, 479–488. [Google Scholar] [CrossRef]
- Fang, M.C.; Lin, Y.H.; Wang, B.J. Applying the PD controller on the roll reduction and track keeping for the ship advancing in waves. Ocean Eng. 2012, 54, 13–25. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S. Course-keeping Autopilot with RRD Based on GA-PD Adaptive Optimization. Lect. Notes Electr. Eng. 2013, 210, 695–702. [Google Scholar]
- Ren, R.; Zou, Z.; Wang, X. A two-time scale control law based on singular perturbations used in rudder roll stabilization of ships. Ocean Eng. 2014, 88, 488–498. [Google Scholar] [CrossRef]
- Bingul, Z. Adaptive genetic algorithms applied to dynamic multiobjective problems. Appl. Soft Comput. 2007, 7, 791–799. [Google Scholar] [CrossRef]
- Liu, T.; Gao, X.; Wang, L. Multi-objective optimization method using an improved NSGA-II algorithm for oil–gas production process. J. Taiwan Inst. Chem. Eng. 2015, 57, 42–53. [Google Scholar] [CrossRef]
- Chaine, S.; Tripathy, M.; Satpathy, S. NSGA-II based optimal control scheme of wind thermal power system for improvement of frequency regulation characteristics. Ain Shams Eng. J. 2015, 6, 851–863. [Google Scholar] [CrossRef]
- Kalaivani, L.; Subburaj, P.; Iruthayarajan, M.W. Speed control of switched reluctance motor with torque ripple reduction using non-dominated sorting genetic algorithm (NSGA-II). Int. J. Electr. Power Energy Syst. 2013, 53, 69–77. [Google Scholar] [CrossRef]
- Kashani, H.N.; Rafiei, S.M.R. Optimal Control of Active Power Filters using Fractional Order Controllers Based on NSGA-II Optimization Method. Int. J. Electr. Power Energy Syst. 2014, 63, 1008–1014. [Google Scholar] [CrossRef]
- Zamanifar, M.; Fani, B.; Golshan, M.E.H.; Karshenas, H.R. Dynamic modeling and optimal control of DFIG wind energy systems using DFT and NSGA-II. Electr. Power Syst. Res. 2014, 108, 50–58. [Google Scholar] [CrossRef]
- Son, K.; Nomoto, K. On the Coupled Motion of Steering and Rolling of a High Speed Container Ship. J. Jpn. Soc. Nav. Archit. Ocean Eng. 1981, 150, 232–244. [Google Scholar] [CrossRef]
- Son, K.H.; Nomoto, K. On the Coupled Motion of Steering and Rolling of a Ship in Following Seas. J. Jpn. Soc. Nav. Archit. Ocean Eng. 1982, 152, 180–191. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G. Stabilization of pure unstable delay systems by the mirror mapping technique. J. Process Control 2013, 23, 1465–1470. [Google Scholar] [CrossRef]
- Wang, L. Determining robust parameters in stabilizing set of backstepping based nonlinear controller for ship course keeping comment. Int. J. Marit. Eng. 2016, 158, A275–A276. [Google Scholar]
- Wang, L.; Zhang, X. Improved closed-loop gain shaping algorithm and its application in RRS. ICIC Express Lett. 2011, 5, 4215–4220. [Google Scholar]
- Arab Tehrani, K.; Amirahmadi, A.; Rafiei, S.M.R.; Griva, G.; Barrandon, L.; Hamzaoui, M.; Rasoanarivo, I.; Sargos, F.M. Design of fractional order PID controller for boost converter based on multi-objective optimization. In Proceedings of the 14th International Power Electronics and Motion Control Conference (EPE-PEMC), Ohrid, Macedonia, 6–8 September 2010. [Google Scholar]
- Wang, L.; Wang, S. High Degree Cubature Federated Filter for Multisensor Information Fusion with Correlated Noises. Math. Probl. Eng. 2016, 2016, 5252487. [Google Scholar] [CrossRef]
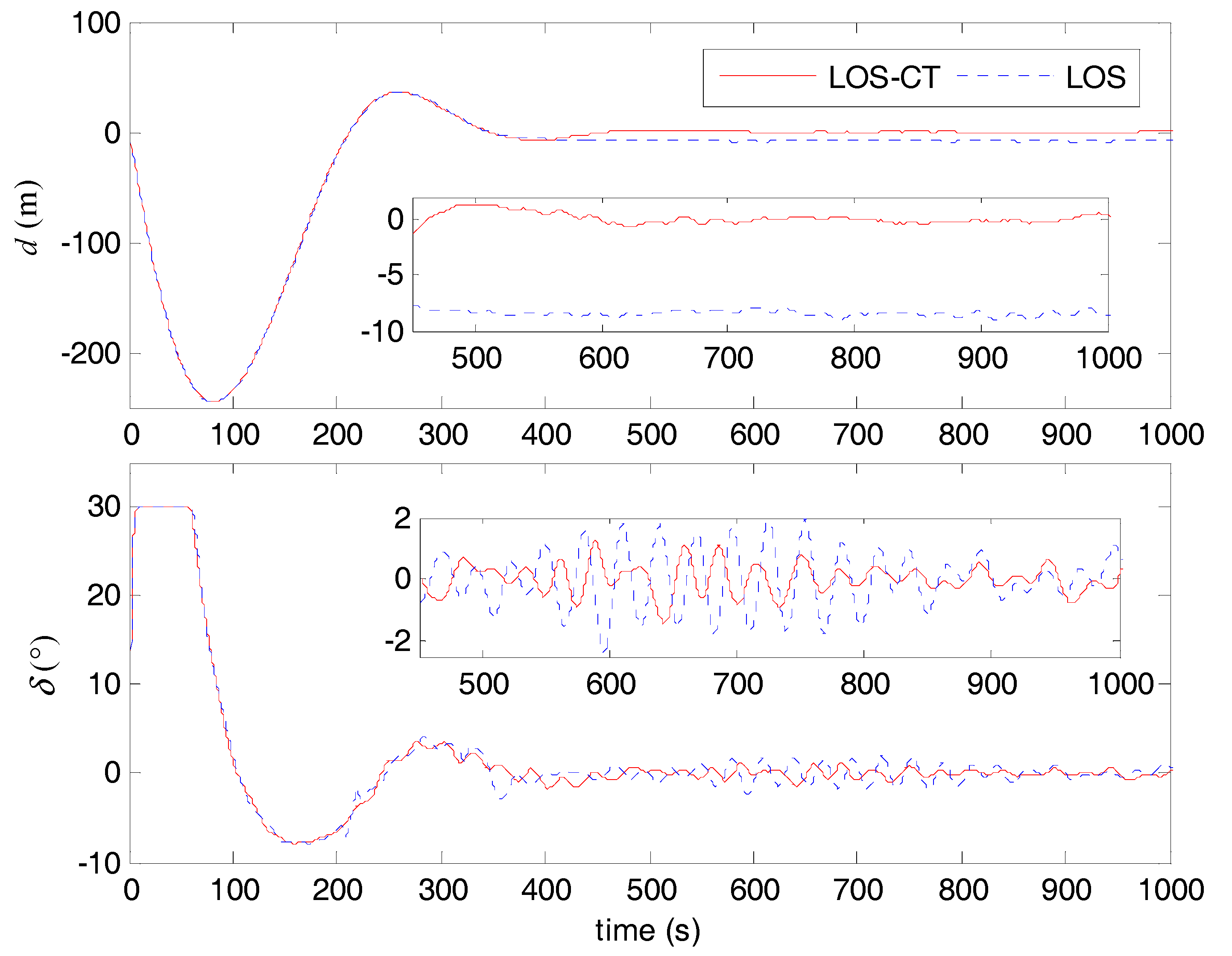
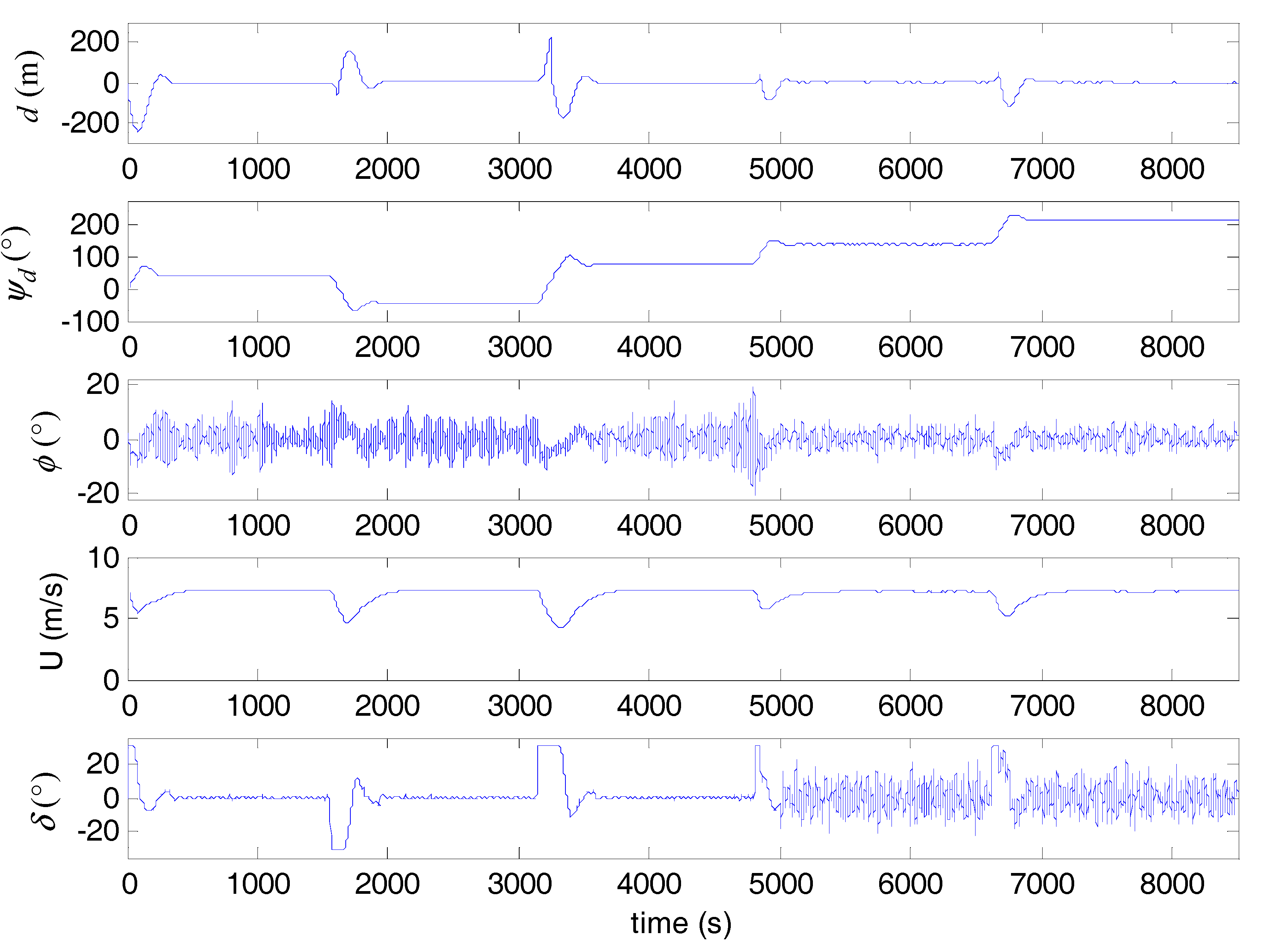
| Autopilot | Path Following | Waypoint Turning | ||||||
|---|---|---|---|---|---|---|---|---|
| (m) | (°) | (°) | (°) | (m) | (°) | (°) | (°) | |
| RRR-OFF | 0.47 | 0.22 | 5.69 | 0.65 | 86.32 | 3.13 | 4.64 | 14.03 |
| RRR-ON | 2.12 ↑ | 0.90↑ | 2.93↓ | 7.61↑ | 45.24↓ | 0.16↓ | 4.61↓ | 13.81↓ |
| Sea State | (°) | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 |
| (°) | 3.9 | 5.2 | 6.8 | 7.7 | 9.8 | 10.3 | |
| (m) | 1.4 | 1.9 | 2.6 | 2.9 | 3.3 | 5.9 | |
| (%) | 40.9 | 44.7 | 49.2 | 50.5 | 57.0 | 43.8 | |
| (°) | 6.0 | 7.3 | 8.5 | 9.3 | 10.3 | 13.8 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, L.; Qiao, Z.; Li, F. Optimal Robust Control of Path Following and Rudder Roll Reduction for a Container Ship in Heavy Waves. Appl. Sci. 2018, 8, 1631. https://doi.org/10.3390/app8091631
Wang S, Wang L, Qiao Z, Li F. Optimal Robust Control of Path Following and Rudder Roll Reduction for a Container Ship in Heavy Waves. Applied Sciences. 2018; 8(9):1631. https://doi.org/10.3390/app8091631
Chicago/Turabian StyleWang, Sisi, Lijun Wang, Zixuan Qiao, and Fengshan Li. 2018. "Optimal Robust Control of Path Following and Rudder Roll Reduction for a Container Ship in Heavy Waves" Applied Sciences 8, no. 9: 1631. https://doi.org/10.3390/app8091631
APA StyleWang, S., Wang, L., Qiao, Z., & Li, F. (2018). Optimal Robust Control of Path Following and Rudder Roll Reduction for a Container Ship in Heavy Waves. Applied Sciences, 8(9), 1631. https://doi.org/10.3390/app8091631





