Multiple Signal Classification-Based Impact Localization in Composite Structures Using Optimized Ensemble Empirical Mode Decomposition

Abstract

Multiple signal classification (MUSIC) algorithm-based structural health monitoring technology is a promising method because of its directional scanning ability and easy arrangement of the sensor array. However, in previous MUSIC-based impact location methods, the narrowband signals at a particular central frequency had to be extracted from the wideband Lamb waves induced by each impact using a wavelet transform. Additionally, the specific center frequency had to be obtained after carefully analyzing the impact signal, which is time consuming. Aiming at solving this problem, this paper presents an improved approach that combines the optimized ensemble empirical mode decomposition (EEMD) and two-dimensional multiple signal classification (2D-MUSIC) algorithm for real-time impact localization on composite structures. Firstly, the impact signal at an unknown position is obtained using a unified linear sensor array. Secondly, the fast Hilbert Huang transform (HHT) with an optimized EEMD algorithm is introduced to extract intrinsic mode functions (IMFs) from impact signals. Then, all IMFs in the whole frequency domain are directly used as the input vector of the 2D-MUSIC model separately to locate the impact source. Experimental data collected from a cross-ply glass fiber reinforced composite plate are used to validate the proposed approach. The results show that the use of optimized EEMD and 2D-MUSIC is suitable for real-time impact localization of composite structures.

1. Introduction

Composite structures have been increasingly used in various aircraft structures due to their superior stiffness and weight characteristics. However, composite structures are susceptible to low velocity impacts, which can cause internal damage that will lead to a significant reduction of the local structural strength [1]. Therefore, impact monitoring has become an important task of structural health monitoring (SHM) to ensure the safety of these applications.

Recently, sensor array signal processing-based methods have emerged as a set of new promising SHM methods. Yin et al. constructed two Z-shaped clusters at different positions for acoustic source localization in anisotropic plates [2]. Xiao et al. proposed an acoustic emission source localization approach based on beamforming with two uniform linear arrays [3]. He developed a method for localizing two acoustic emission sources simultaneously based on beamforming and singular value decomposition. Agarwal and Macháň proposed a statistical super-resolution technique called the multiple signal classification (MUSIC) algorithm published in Nature Communications, and demonstrated that the MUSIC algorithm had a comparable or better performance in comparison with other localization techniques [4]. Because it has such advantages, the MUSIC algorithm was developed for the impact monitoring of plate-like structures. By processing the whole sensor array outputs using the MUSIC algorithm, the transfer function and material properties of the structure are not needed [5]. Since the MUSIC algorithm belongs to an eigen-structure and sub-space approach, it can effectively extract the key features of signals received and successfully detect the source signal under a low signal-to-noise ratio [6]. Some developments have been published by applying this method to process the sensor array signals in the structural health monitoring area. Stepinski and Engholm [7] presented a far-field MUSIC algorithm-based method to estimate the direction of arrival (DOA) of single elastic waves on an aluminum plate using a uniform circular array. Yang et al. [8] employed the far-field MUSIC algorithm to estimate the DOA of one impact on an aluminum plate. Yuan et al. presented a single frequency component-based re-estimated MUSIC algorithm to reduce the localization error caused by the anisotropy of the complex composite structure [9]. To deal with the near-field monitoring problem, the authors in previous work proposed the near-field 2D-MUSIC algorithm-based impact localization method for a composite plate using Gabor wavelet transform [10,11]. However, in previous MUSIC-based impact location methods, the narrowband signals at a particular central frequency had to be extracted from the wideband Lamb waves induced by each impact, and the specific center frequency had to be obtained after carefully analyzing the impact signal, which is time consuming.

EMD is a new time–frequency analysis technique which can decompose the complicated signal into a set of complete and almost orthogonal components named intrinsic mode functions (IMFs) [12]. The IMFs represent the natural oscillatory mode embedded in the signal and work as the basis functions, which are determined by the signal itself [13]. Thus, it is a self-adaptive signal processing method that can be applied to a nonlinear and non-stationary process to decompose it into stationary signals. Generally, EMD cannot accurately extract fault features because of the mode mixing phenomena. Wu and Huang proposed a new ensemble EMD (EEMD) method to reduce mode mixing [14]. However, the EMD and its improved version EEMD are computation intensive methods, which are not suitable for on-line detection. A noise-assisted approach in conjunction with a multivariate empirical mode decomposition (MEMD) algorithm has been proposed for the computation of EMD, in order to produce localized frequency estimates at the accuracy level of instantaneous frequency [15,16,17]. Leo developed Bivariate EMD to detect defective areas in composite materials [18]. Wang et al. [19] proposed a fast HHT with an optimized EEMD algorithm to speed up the computational efficiency by 1000 times. They also proved that the computational complexity of the EMD is equivalent to fast Fourier transform (FFT). Hence, the optimized EEMD method might be a good choice to be applied to the real-time impact localization of composite structures.

This paper presents an improved approach that combines the optimized EEMD and 2D-MUSIC algorithm for the on-line impact localization on composite structures without selecting the center frequency. The layout of the paper is structured as follows: In Section 2, an optimized EEMD-based 2D-MUSIC method for impact monitoring is presented. An impact monitoring experiment on a cross-ply glass fiber reinforced composite plate is performed in Section 3 to verify the proposed method. Finally, the conclusion and future works are given in Section 4.

2. Optimized EEMD Based 2D-MUSIC Method

2.1. 2D-MUSIC Algorithm for Impact Localization

In this section, the 2D-MUSIC algorithm in [10,11] is briefly introduced. As seen in Figure 1, a uniform linear array (ULA) consists of M piezoelectric (PZT) sensors on the structure, which are arranged uniformly along the x axis and asymmetric with the y axis. The distance between two sensors is d.

$A(r,\theta )$ is defined as the array steering vector

$$A(r,\theta )=[a_1(r,\theta ),a_2(r,\theta ),\cdots ,a_M(r,\theta )]$$

(1)

where

$$\begin{gathered} a_i(r,\theta )=\frac{r}{r_i}\exp (-j{\omega }_0{\tau }_i) \\ {\tau }_i=\frac{(-d\sin \theta )}{c_{AV}}(i-1)+(-\frac{d^2}{c_{AV}r}{\cos }^2\theta ){(i-1)}^2 \end{gathered}$$

r is defined as the distance between the impact source and the ULSA, which is the distance from the source to the reference sensor labeled as 1 in the sensor array. $\theta$ denotes the wave propagating direction caused by the impact with respect to the coordinate y axis. $c_{AV}$ is the average velocity of the Lamb wave.

The basic idea of the MUSIC algorithm is to obtain the signal subspace and noise subspace through eigenvalue decomposition of the signal covariance matrix, and then to estimate the signal parameter using the orthogonality of two spaces. To describe the orthogonality between the signal subspace and noise subspace, the spatial spectrum is used, which can be calculated by

$$P_{\mathrm{MUSIC}}(r,\theta )=\frac{1}{A^{\mathrm{H}}(r,\theta )U_{\mathrm{N}}{U}_{\mathrm{N}}{}^{\mathrm{H}}A(r,\theta )}$$

(2)

where $U_{\mathrm{N}}$ denotes the noise subspace spanned by the eigenvector matrix corresponding to those small eigenvalues. Based on Equation (2), by varying r and $\theta$ to realize a scanning process, $A(r,\theta )$ is steered to scan the whole structure area. The peak point on the spatial spectrum corresponds to the impact source point. Both the distance and direction of the impact source can be obtained.

2.2. Fast EEMD for Impact Signal Extraction

In 1998, Huang et al. introduced the EMD, which is able to adaptively and effectively decompose a complicated signal into a collection of stationary IMFs [12]. Therefore, it has often been used in nonlinear and non-stationary signal processing. In the EMD method, the data $x(t)$ is decomposed in terms of IMFs $c_j$ as

$$x(t)={\displaystyle \sum _{j=1}^n{c}_j}+r_n$$

(3)

where $r_n$ is the residual of data $x(t)$, after n number of IMFs are extracted. IMFs are simple oscillatory functions that have the following two properties:

• Throughout the whole length of a single IMF, the number of extrema $N_e$ (maxima and minima) and the number of zero-crossings $N_Z$ must either be equal or differ at most by one, i.e.,

  $$(N_z-1)\le N_e\le (N_z+1)$$

  (4)
• At any time point $t_i$, the mean value of the envelope $f_{\max }^{}(t_i)$ and $f_{\min }^{}(t_i)$ respectively defined by the local maxima and the local minima are zero, i.e.,

  $$\left[f_{\max }^{}(t_i)+f_{\min }^{}(t_i)\right]/2=0t_i\in [t_a,t_b]$$

  (5)

  where $[t_a,t_b]$ is the time interval.

In practice, the EMD decomposition procedures (sifting procedure) are as follows:

• Identify all the local maxima and minima and connect all of them using a cubic spline as the upper and lower envelope $f_{\max }^{}(t)$ and $f_{\min }^{}(t)$, respectively. Then, calculate the mean value $m(t)$ of $f_{\max }^{}(t)$ and $f_{\min }^{}(t)$ as

  $$m(t)=\left[f_{\max }^{}(t)+f_{\min }^{}(t)\right]/2$$

  (6)
• Obtain the first component $h_1$ by taking the difference between the data $x(t)$ and the local mean $m(t)$ as

  $$h_1(t)=x(t)-m(t)$$

  (7)
• Treat $h_1(t)$ as the data and repeat steps 1 and 2 as many times as is required until the two properties of IMF as shown in Equations (4) and (5) are satisfied. Then, the final $h_1(t)$ is designated as an IMF $c_1(t)$.
• Treat $r_i(t)=x(t)-c_i(t)$, ($i=1,2,\cdots ,n-1$) as the data and repeat steps 1–3. Finally, we obtain additional IMFs $c_2(t),c_3(t),\cdots c_n(t)$ and the final residual $r_n(t)$, which are represented by Equation (3).

Generally, the stop criterion of the sifting procedure is restrained by

$$S_d={\displaystyle \sum _{t=0}^T\frac{{\left|h_{k-1}(t)-h_k(t)\right|}^2}{h_k^2(t)}}$$

(8)

where T is the signal length; $h_{k-1}(t)$ and $h_k(t)$ are the neighbor components in sifting procedures for one IMF; and $S_d$ is the standard deviation, which is suggested to be 0.2–0.3.

However, mode mixing appears to be the most significant drawback of EMD [19]. Therefore, in 2009, a new artificial noise-excited EMD method was proposed by Wu and Huang, which was called EEMD [19]. The procedures are similar to EMD, except only one series of white noise with a finite amplitude are added into the original signals and the procedures are summarized as follows:

• Add a white noise $n_i(t)$ series (noise level is N_l) to the targeted data and decompose the data with added white noise into IMFs as

  $$x(t)+n_i(t)={\displaystyle \sum _{j=1}^n{c}_j^i(t)}+r_n^i(t)$$

  (9)

  where $i=1,2,\cdots ,q$ and q is the average time (ensemble number).
• Repeat step1 q times with different white noise series $n_i(t)$.
• Obtain the (ensemble) means of corresponding IMFs of the decompositions as the final result, that is

  $$x(t)+n_i(t)=\frac{1}{q}{\displaystyle \sum _{i=1}^q{\displaystyle \sum _{j=1}^n{c}_j^i}}(t)+\frac{1}{q}{\displaystyle \sum _{i=1}^q{r}_n^i}(t)={\displaystyle \sum _{j=1}^n{d}_j^{}}(t)+r_n(t)$$

  (10)

  where $d_j(t)$ is the jth IMFs of EEMD decomposition as

  $$d_j(t)=\frac{1}{q}{\displaystyle \sum _{i=1}^q{c}_j^i}(t)$$

  (11)

  and $r_n(t)$ is the final residual of EEMD decomposition as

  $$r_n(t)=\frac{1}{q}{\displaystyle \sum _{i=1}^q{r}_n^i}(t)$$

  (12)

2.3. Impact Localiaztion Process

The implementing process of the impact location method based on the proposed method is shown in Figure 2. The fast HHT with an optimized EEMD algorithm is introduced to extract IMFs from impact signals. The spatial spectrum $P_{\mathrm{MUSIC}}$ of each IMF is evaluated versus all ($r,\theta$) in the $r-\theta$ plane to find the steering vector $A(r,\theta )$ which matches the actual impact signal vectors. When the right steering vector is found, the denominator of Equation (2) approaches zero due to the orthogonal properties, resulting in a peak in the spatial spectrum which corresponds to the estimated impact position.

3. Experimental Investigations

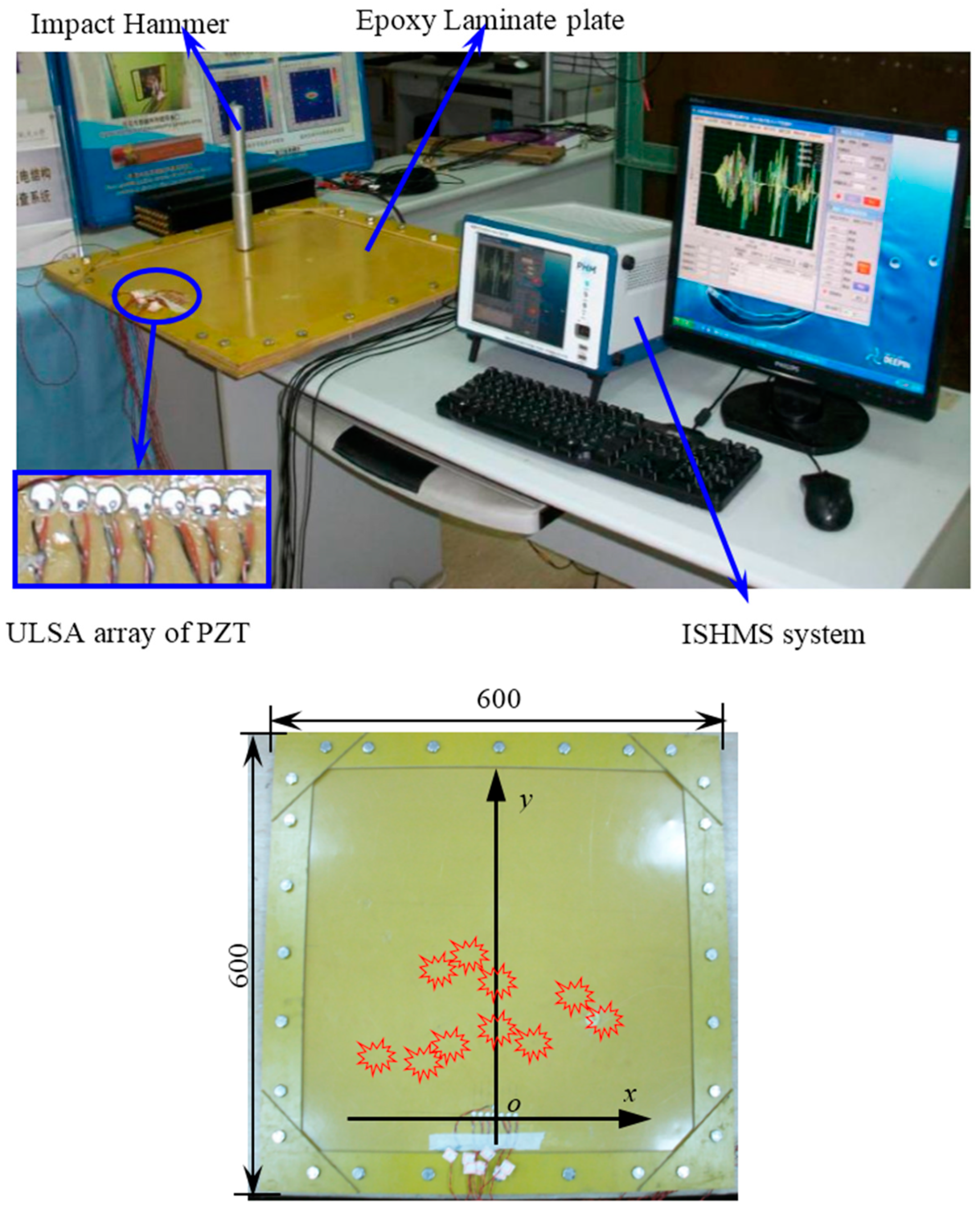
3.1. Experiment Setup

The experiment setup is shown in Figure 3, including a 600 mm × 600 mm × 2 mm cross-ply glass fiber reinforced composite plate with unknown material properties. The thickness of each ply is 0.125 mm and the ply sequence is [0₂/90₄/0₂]_S. The integrated structural health monitoring scanning system (ISHMS) is adopted as the monitoring system. This system is developed to control the excitation and sensing of the PZT sensor array. As seen in Figure 3, the array used in the experiment is a ULSA bonded on the structure surface with seven PZT sensors. The diameter of the PZT sensor is 8 mm. These sensors are arranged with a space of 10 mm and are labeled as PZT1–7, respectively, from the left to the right, where the length of the sensor array $L$ is 60 mm.

Ten low-velocity impacts with a 2 J energy are performed at various positions on the structure shown in Figure 3. These impacts are induced by an impact hammer. The sampling rate is set to be 2 MHz and the trigger voltage is set to 3 V in the experiments. The sampling length is 10,000, including 2000 pre-trigger samples.

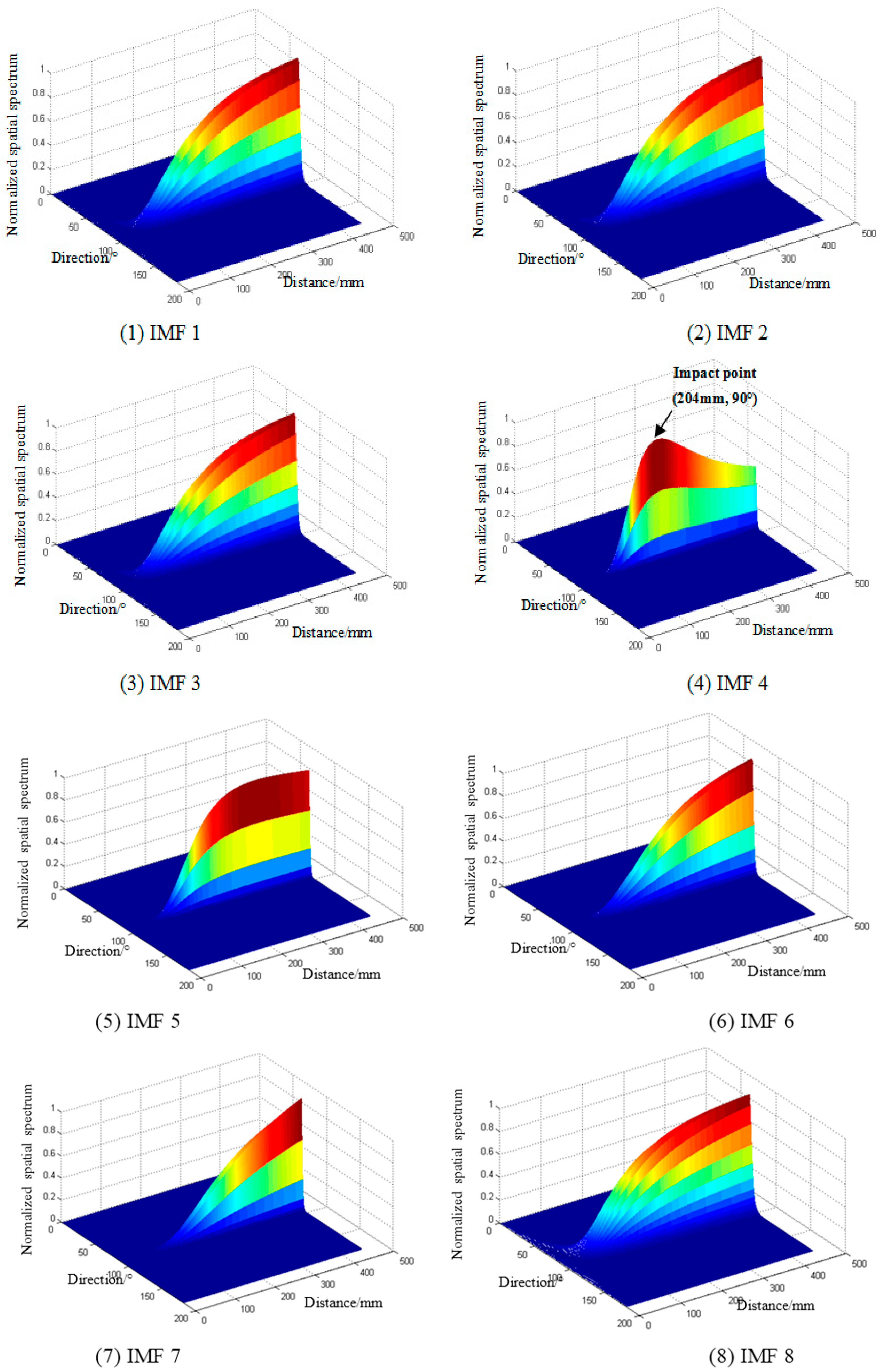
3.2. Impact Localization Results

A near-field impact at the point (200 mm, 90°) is chosen as a typical case to be analyzed first. The impact signals extracted from each sensor of each IMF are shown in Figure 4. From Figure 4, the wave fronts cannot been seen in the high frequency region, including IMF1, IMF2, and IMF3. Additionally, much more noise signal, boundary reflection, and pattern aliasing appear in the IMF5, IMF6, IMF7, and IMF8. Only the wave fronts of impact signals can be easily found in the IMF4.

All the IMFs extracted from the impact signals are used to form the input vector of the near-field 2D-MUSIC model. The measured average velocity on this plate is 1154 m/s [11]. According to the structure dimension, the scanned area is set to be the distance from 0 to 450 mm and the direction from 0° to 180°, and the scanning step length of the distance and direction is 1 mm and 1°, respectively. The near-field impact obtained at the point (200 mm, 90°) spatial spectrum $P_{\mathrm{MUSIC}}(r,\theta )$ is shown in Figure 5. The figure represents the spatial spectrum magnitudes of each scanned point $(r,\theta )$, and the highest pixel point of the figure represents the impact point localized by the presented 2D-MUSIC algorithm. Seen from Figure 5, the spatial spectrum of IMF4 located the impact source, and the direction and distance error are 0° and 0.4 cm, respectively.

Ten estimated results of impact points and the errors compared with actual impact points are listed in

Table 1. The localization results.

	Parameter	Actual Positions		Estimated Positions		Errors
Impacts		r/mm	θ/°	IMF4	IMF5	r/mm	θ/°
1		150	45	(135,43)	-	15	2
2		200	56	(208,54)	-	8	2
3		124	75	(109,76)	-	15	1
4		150	90	(155,90)	-	5	0
5		200	90	(194,90)	-	6	0
6		255	100	-	(242,100)	13	0
7		255	110	-	(245,112)	10	2
8		150	124	(140,123)	-	10	1
9		150	135	(146,133)	-	4	2
10		255	150	-	(235,147)	20	3

, including seven located results at the spatial spectrum of IMF4, and three located results at the spatial spectrum of IMF5. It shows that ten near-field impacts are in good agreement with the actual impacts. The maximum error is at the impact position (255 mm, 150°), whose direction and distance error are 3°and 2 cm, respectively.

4. Conclusions

This paper presents an improved approach that combines the EEMD and 2D-MUSIC algorithm for the real-time impact localization on composite structures. The fast Hilbert Huang transform with an optimized EEMD algorithm is introduced to extract IMFs from impact signals in the whole frequency domain. Then, all IMFs in the whole frequency domain are directly used as the input vector of the 2D-MUSIC model separately to locate the impact source. The main advantage of the proposed method is its computational efficiency, which requires less time in comparison to the previous MUSIC-based impact location method, in order to achieve the same location accuracy. From experimental results on a cross-ply glass fiber reinforced composite plate, the wave fronts of impact signals can be easily found in the IMF4 or IMF5, and the corresponding spatial spectrum peak also easily located the impact source. Ten near-field impacts are in good agreement with the actual impacts. The maximum direction and distance error are 3° and 2 cm, respectively. The experiment on a cross-ply glass fiber reinforced composite plate proved that the use of the 2D-MUSIC algorithm improved by EEMD is a suitable approach for the real-time impact localization of composite structures.