Numerical Study on the Absorption Characteristics of Subwavelength Metallic Gratings Covered with a Lossy Dielectric Layer
Abstract
1. Introduction
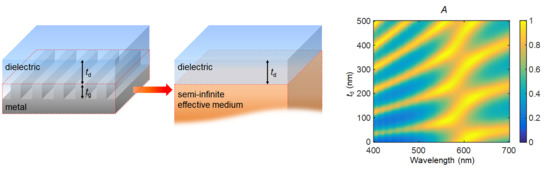
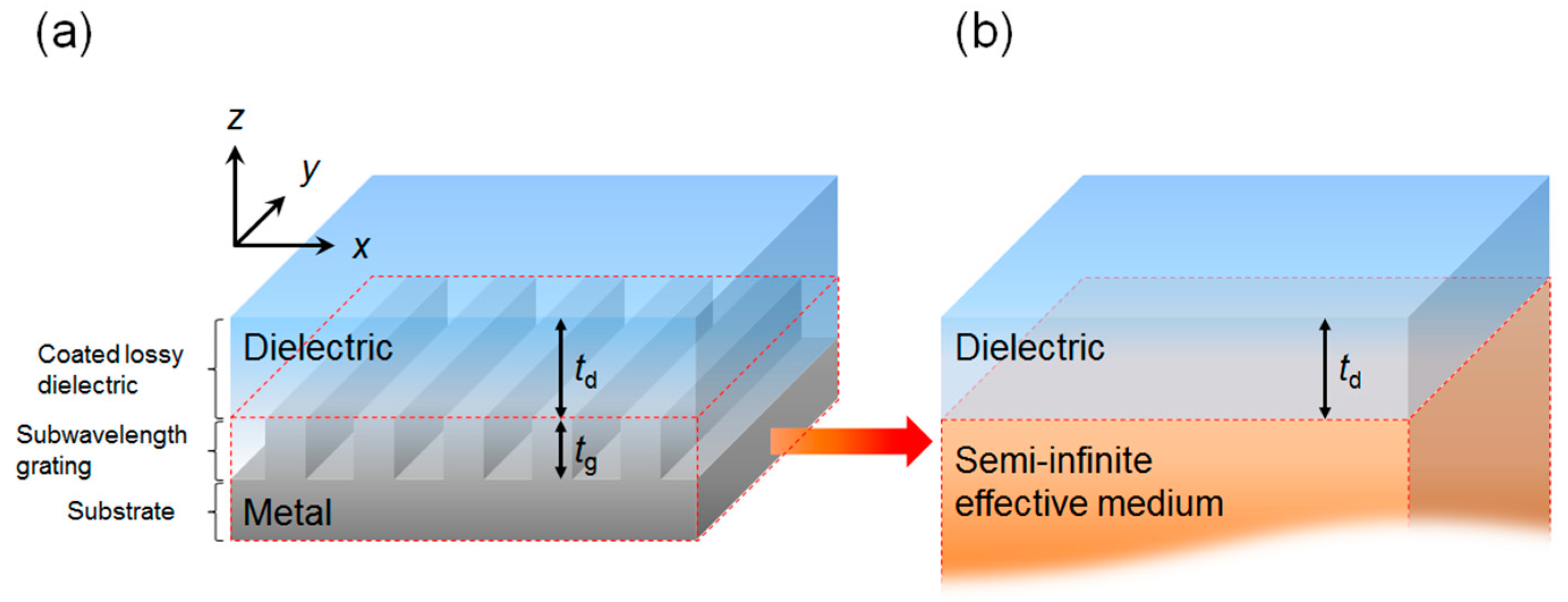
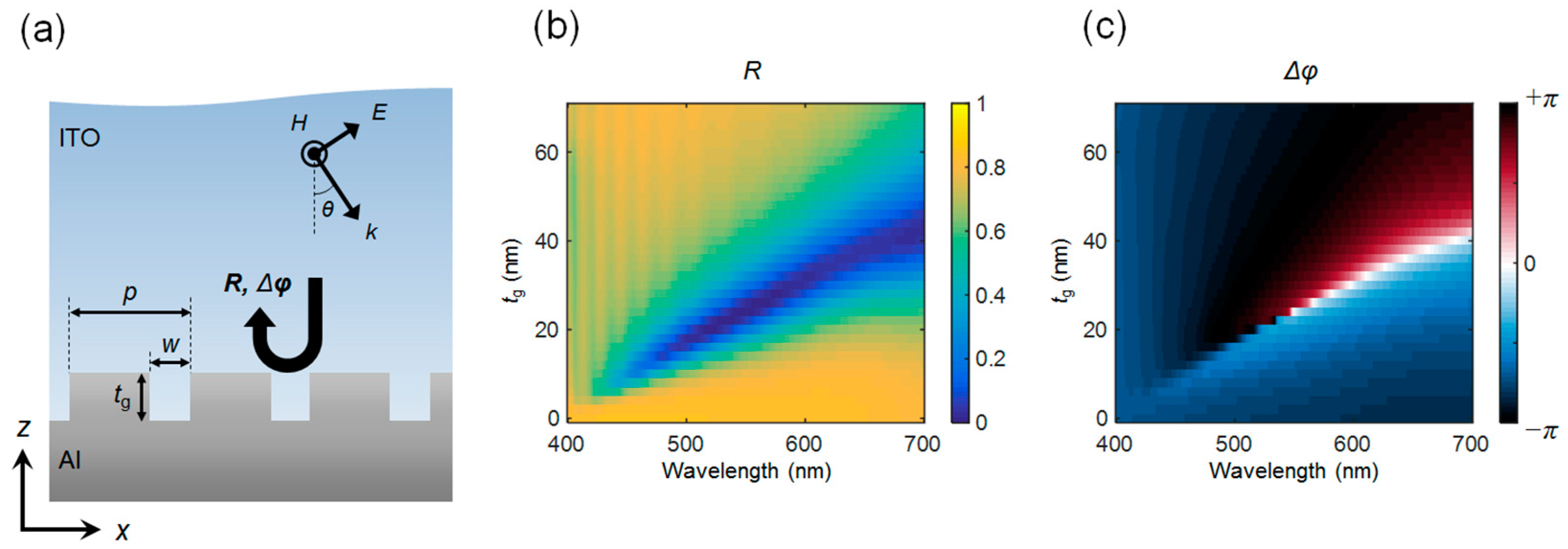
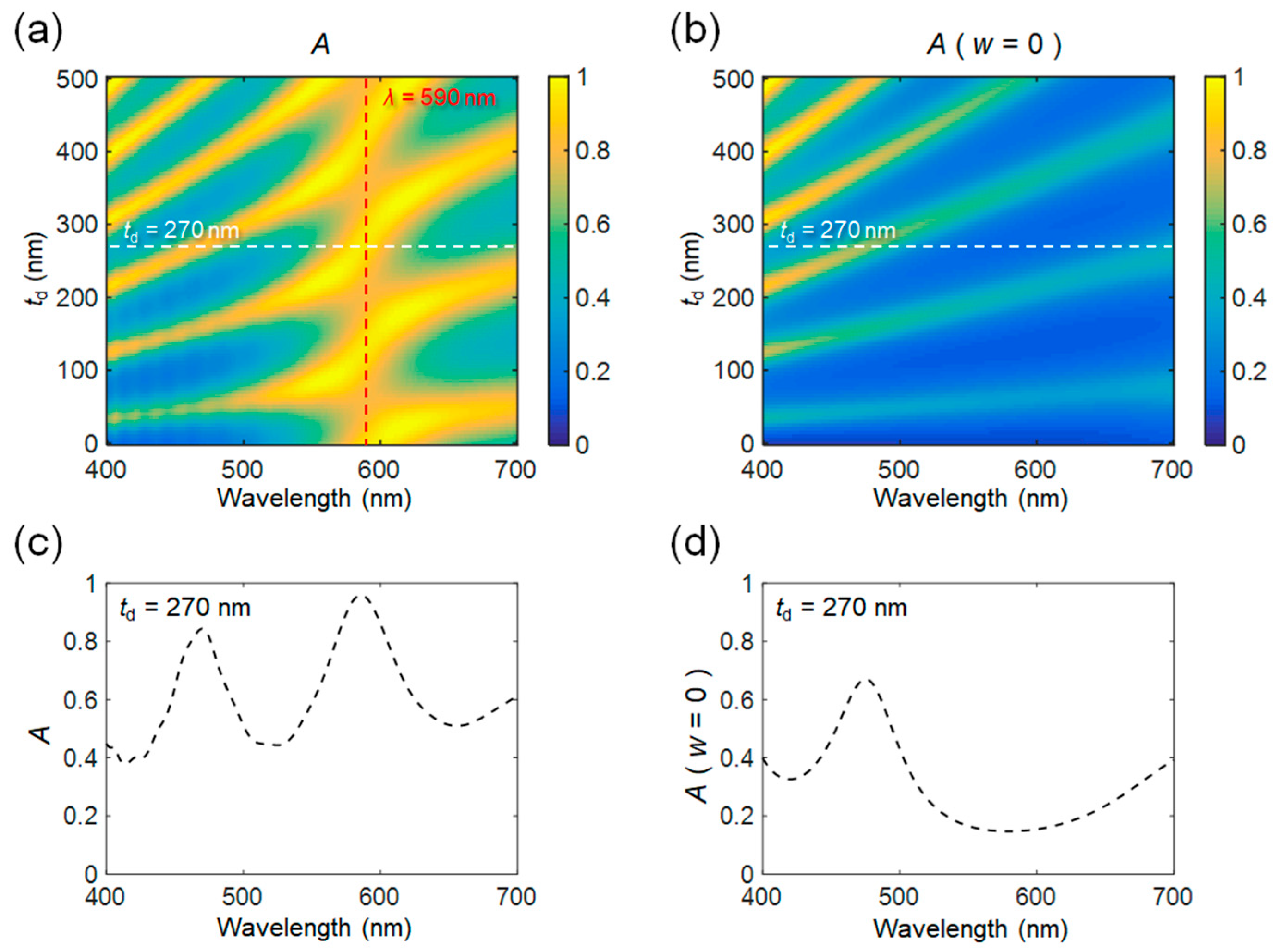
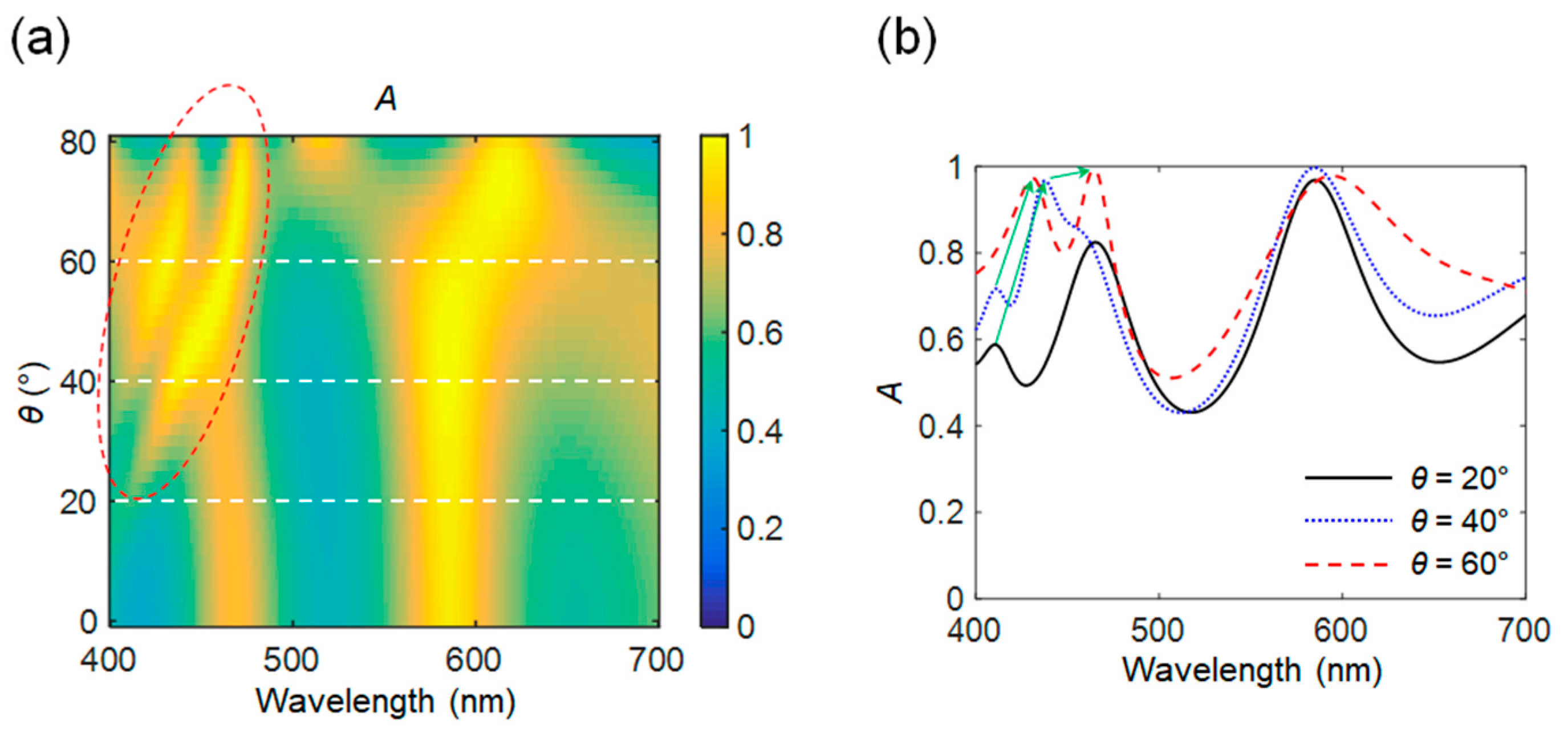
2. Absorption Characteristics of a Subwavelength Metallic Grating Covered with a Lossy Dielectric Layer
3. Conditions for Complete Optical Absorption by Critical Coupling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cui, Y.; He, Y.; Jin, Y.; Ding, F.; Yang, L.; Ye, Y.; Zhong, S.; Lin, Y.; He, S. Plasmonic and metamaterial structures as electromagnetic absorbers. Laser Photonics Rev. 2014, 8, 495–520. [Google Scholar] [CrossRef]
- Hedayati, M.K.; Faupel, F.; Elbahri, M. Review of plasmonic nanocomposite metamaterial absorber. Materials 2014, 7, 1221–1248. [Google Scholar] [CrossRef] [PubMed]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 2012, 24, OP98–OP120. [Google Scholar] [CrossRef] [PubMed]
- Alaee, R.; Albooyeh, M.; Rockstuhl, C. Theory of metasurface based perfect absorbers. J. Phys. D. 2017, 50, 503002. [Google Scholar] [CrossRef]
- Kats, M.A.; Capasso, F. Optical absorbers based on strong interference in ultra-thin films. Laser Photonics Rev. 2016, 10, 735–749. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.F.; Sun, T.; Cao, F.; Liu, Q.; Ren, Z. Metallic nanostructures for light trapping in energy-harvesting devices. Light Sci. Appl. 2014, 3, e161. [Google Scholar]
- Sergeant, N.P.; Agrawal, M.; Peumans, P. High performance solar-selective absorbers using coated subwavelength gratings. Opt. Express 2010, 18, 5525–5540. [Google Scholar] [CrossRef] [PubMed]
- Azad, A.K.; Kort-Kamp, W.J.M.; Sykora, M.; Weisse-Bernstein, N.R.; Luk, T.S.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H.T. Metasurface Broadband Solar Absorber. Sci. Rep. 2016, 6, 20347. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.T.; Seo, S.; Guo, L.J. High-color-purity subtractive color filters with a wide viewing angle based on plasmonic perfect absorbers. Adv. Mater. 2015, 3, 347–352. [Google Scholar] [CrossRef]
- Kats, M.A.; Blanchard, R.; Genevet, P.; Capasso, F. Nanometre optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 2012, 12, 20–24. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Butun, S.; Aydin, K. Large-area, lithography-free super absorbers and color filters at visible frequencies using ultrathin metallic films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Hwang, C.Y.; Yi, Y.; Choi, C.G. Reflection-type spatial amplitude modulation of visible light based on a sub-wavelength plasmonic absorber. Opt. Lett. 2016, 41, 990–993. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.Y.; Lee, S.Y.; Kim, Y.H.; Kim, T.Y.; Kim, G.H.; Yang, J.H.; Pi, J.E.; Choi, J.H.; Choi, K.; Kim, H.O.; et al. Switchable subwavelength plasmonic structures with phase-change materials for reflection-type active metasurfaces in the visible region. Appl. Phys. Lett. 2017, 10, 122201. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
- Dhawan, A.; Canva, M.; Vo-Dinh, T. Narrow groove plasmonic nano-gratings for surface plasmon resonance sensing. Opt. Express 2011, 19, 787–813. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Li, K.; Song, C.; Hao, P.; Chi, M.; Yu, M.; Wu, Y. Polarization-independent and omnidirectional nearly perfect absorber with ultra-thin 2D subwavelength metal grating in the visible region. Opt. Express 2015, 23, A413–A418. [Google Scholar] [CrossRef] [PubMed]
- Suen, J.Y.; Fan, K.; Montoya, J.; Bingham, C.; Stenger, V.; Sriram, S.; Padilla, W.J. Multifunctional metamaterial pyroelectric infrared detectors. Optica 2017, 4, 276–279. [Google Scholar] [CrossRef]
- Hao, J.M.; Wang, J.; Liu, X.L.; Padilla, W.J.; Zhou, L.; Qiu, M. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 2010, 96, 251104. [Google Scholar] [CrossRef]
- Aydin, K.; Ferry, V.E.; Briggs, R.M.; Atwater, H.A. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2011, 2, 517. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Li, Z.; Stan, L.; Rosenmann, D.; Czaplewski, D.; Gao, J.; Yang, X. Broadband perfect absorber based on one ultrathin layer of refractory metal. Opt. Lett. 2015, 40, 2592–2595. [Google Scholar] [CrossRef] [PubMed]
- Shu, S.; Li, Z.; Li, Y.Y. Triple-layer Fabry-Perot absorber with near-perfect absorption in visible and near-infrared regime. Opt. Express 2013, 21, 25307–25315. [Google Scholar] [CrossRef] [PubMed]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared Spatial and Frequency Selective Metamaterial with Near-Unity Absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Hendrickson, J.; Guo, J. Multispectral near-perfect metamaterial absorbers using spatially multiplexed plasmon resonance metal square structures. J. Opt. Soc. Am. B 2013, 30, 656–662. [Google Scholar] [CrossRef]
- Sun, J.; Liu, L.; Dong, G.; Zhou, J. An extremely broad band metamaterial absorber based on destructive interference. Opt. Express 2011, 19, 21155–21162. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T. Interference theory of metamaterial perfect absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Zhou, L.; Qiu, M. Nearly total absorption of light and heat generation by plasmonic metamaterials. Phys. Rev. B 2011, 83, 165107. [Google Scholar] [CrossRef]
- Guo, W.; Liu, Y.; Han, T. Ultra-broadband infrared metasurface absorber. Opt. Express 2016, 24, 20586–20592. [Google Scholar] [CrossRef] [PubMed]
- Kats, M.A.; Sharma, D.; Lin, J.; Genevet, P.; Blanchard, R.; Yang, Z.; Qazilbash, M.M.; Basov, D.N.; Ramanathan, S.; Capasso, F. Ultra-thin perfect absorber employing a tunable phase change material. Appl. Phys. Lett. 2012, 101, 221101. [Google Scholar] [CrossRef]
- Long, Y.; Su, R.; Wang, Q.; Shen, L.; Li, B.; Zheng, W. Deducing critical coupling condition to achieve perfect absorption for thin-film absorbers and identifying key characteristics of absorbing materials needed for perfect absorption. Appl. Phys. Lett. 2014, 104, 091109. [Google Scholar] [CrossRef]
- Le Perchec, J.; Quémerais, P.; Barbara, A.; López-Ríos, T. Why metallic surfaces with grooves a few nanometers deep and wide may strongly absorb visible light. Phys. Rev. Lett. 2008, 100, 066408. [Google Scholar] [CrossRef] [PubMed]
- Chern, R.L.; Chen, Y.T.; Lin, H.Y. Anomalous optical absorption in metallic gratings with subwavelength slits. Opt. Express 2010, 18, 19510–19521. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Y.; Chen, G.; Xu, J.; Qi, Z.; Li, X.; Wang, Q. Multiple-band perfect absorbers based on the combination of Fabry–Perot resonance and the gap plasmon resonance. Opt. Commun. 2017, 399, 28–33. [Google Scholar] [CrossRef]
- Lin, C.H.; Chern, R.L.; Lin, H.Y. Polarization-independent broad-band nearly perfect absorbers in the visible regime. Opt. Express 2011, 19, 415–424. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Lai, J.; Wang, S.; Li, X.; Huang, Y. UV-visible broadband wide-angle polarization-insensitive absorber based on metal groove structures with multiple depths. Appl. Opt. 2017, 56, 5844–5848. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, H.T.; Kurokawa, Y. Squeezing visible light waves into a 3-nm-thick and 55-nm-long plasmon cavity. Phys. Rev. Lett. 2006, 96, 097401. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, Y.; Miyazaki, H.T. Metal-insulator-metal plasmon nanocavities: Analysis of optical properties. Phys. Rev. B 2007, 75, 035411. [Google Scholar] [CrossRef]
- Genet, G.; Ebbesen, T.W. Light in tiny holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Vidal, F.J.; Martin-Moreno, L.; Ebbesen, T.W.; Kuipers, L. Light passing through subwavelength apertures. Rev. Mod. Phys. 2010, 82, 729–787. [Google Scholar] [CrossRef]
- Porto, J.A.; Garcia-Vidal, F.J.; Pendry, J.B. Transmission resonances on metallic gratings with very narrow slits. Phys. Rev. Lett. 1999, 83, 2845–2848. [Google Scholar] [CrossRef]
- Neutens, P.; Van Dorpe, P.; De Vlaminck, I.; Lagae, L.; Borghs, G. Electrical detection of confined gap plasmons in metal–insulator–metal waveguides. Nat. Photonics 2009, 3, 283–286. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- White, J.S.; Veronis, G.; Yu, Z.; Barnard, E.S.; Chandran, A.; Fan, S.; Brongersma, M.L. Extraordinary optical absorption through subwavelength slits. Opt. Lett. 2009, 34, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, G.; Wong, W.; Pun, E.Y.B.; Cheah, K.K. Sharp plasmonic resonance on gold gratings in amplitude and phase domains. Appl. Opt. 2012, 51, 8563–8566. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, K.; Miyazaki, H.T.; Kasaya, T.; Yamamoto, K.; Inoue, Y.; Fujimura, K.; Kanakugi, T.; Okada, M.; Hatade, K.; Kitagawa, S. Controlled thermal emission of polarized infrared waves from arrayed plasmon nanocavities. Appl. Phys. Lett. 2008, 92, 021117. [Google Scholar] [CrossRef]
- Miyazaki, H.T.; Ikeda, K.; Kasaya, T.; Yamamoto, K.; Inoue, Y.; Fujimura, K.; Kanakugi, T.; Okada, M.; Hatade, K.; Kitagawa, S. Thermal emission of two-color polarized infrared waves from integrated plasmon cavities. Appl. Phys. Lett. 2008, 92, 141114. [Google Scholar] [CrossRef]
- Bouchon, P.; Pardo, F.; Portier, B.; Ferlazzo, L.; Ghenuche, P.; Dagher, G.; Dupuis, C.; Bardou, N.; Haïdar, R.; Pelouard, J. Total funneling of light in high aspect ratio plasmonic nanoresonators. Appl. Phys. Lett. 2011, 98, 191109. [Google Scholar] [CrossRef]
- Ogawa, S.; Kimata, M. Direct fabrication and characterization of high-aspect-ratio plasmonic nanogratings using tapered-sidewall molds. Opt. Mater. Express 2017, 7, 633–640. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Lee, B. Fourier Modal Method and Its Applications in Computational Nanophotonics, 1st ed.; CRC Press: Boca Raton, Florida, USA, 2012. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, C.-Y.; Kim, Y.-H.; Choi, J.H.; Kim, G.H.; Yang, J.-H.; Pi, J.-E.; Kim, H.-O.; Hwang, C.-S. Numerical Study on the Absorption Characteristics of Subwavelength Metallic Gratings Covered with a Lossy Dielectric Layer. Appl. Sci. 2018, 8, 1445. https://doi.org/10.3390/app8091445
Hwang C-Y, Kim Y-H, Choi JH, Kim GH, Yang J-H, Pi J-E, Kim H-O, Hwang C-S. Numerical Study on the Absorption Characteristics of Subwavelength Metallic Gratings Covered with a Lossy Dielectric Layer. Applied Sciences. 2018; 8(9):1445. https://doi.org/10.3390/app8091445
Chicago/Turabian StyleHwang, Chi-Young, Yong-Hae Kim, Ji Hun Choi, Gi Heon Kim, Jong-Heon Yang, Jae-Eun Pi, Hee-Ok Kim, and Chi-Sun Hwang. 2018. "Numerical Study on the Absorption Characteristics of Subwavelength Metallic Gratings Covered with a Lossy Dielectric Layer" Applied Sciences 8, no. 9: 1445. https://doi.org/10.3390/app8091445
APA StyleHwang, C.-Y., Kim, Y.-H., Choi, J. H., Kim, G. H., Yang, J.-H., Pi, J.-E., Kim, H.-O., & Hwang, C.-S. (2018). Numerical Study on the Absorption Characteristics of Subwavelength Metallic Gratings Covered with a Lossy Dielectric Layer. Applied Sciences, 8(9), 1445. https://doi.org/10.3390/app8091445