Relay-Enabled Task Offloading Management for Wireless Body Area Networks
Abstract
:1. Introduction
2. Related Work
3. System Model
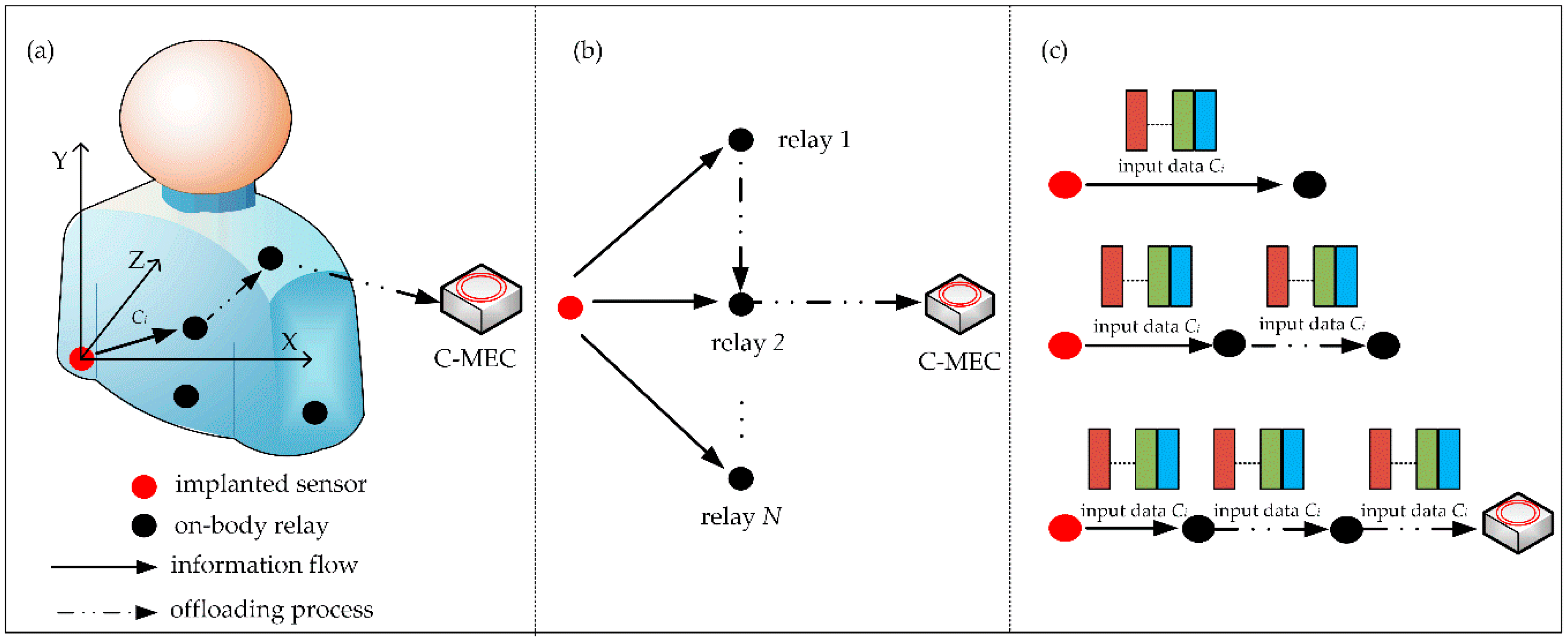
3.1. System Architecture
3.2. Computation Model
3.3. Channel Characterization
4. Proposed Resource Management Solution
4.1. Network Initialization Phase
4.2. Local Decision Process
| Algorithm 1. Proposed Iterative Relay Selection Method |
| The relay and implanted sensor sets are denoted as and . Initialization: each relay is assigned a unique ID; select the x-th relay as the target to connect; for a specific implanted sensor ; current round r; current residual energy status ; For do calculate the distance between the implanted sensor and the i-th relay: calculate the relay’s residual energy: ; If then //do nothing, x is still the best choice so far; Else x = i;//i-th relay becomes a better choice; End if End for establish a link between the implanted sensor and the x-th relay; Update , |
4.3. Data Offloading Process
| Algorithm 2. Proposed Iterative Task Offloading Strategy |
| Initialize,, The task with a size of received according to Algorithm 1; Update according to Equation (3); If or Then execute the task locally according to Equations (5)–(8) Else with a minimal value is selected according to Equation (25); offload task to relay j according to Equations (9)–(12); End if While do execute the task on j-th relay according to Equations (5)–(8); Else offload task to the C-MEC according to Equations (9)–(12); End while |
4.4. Scheduling and Data Transmission
5. Results and Discussion
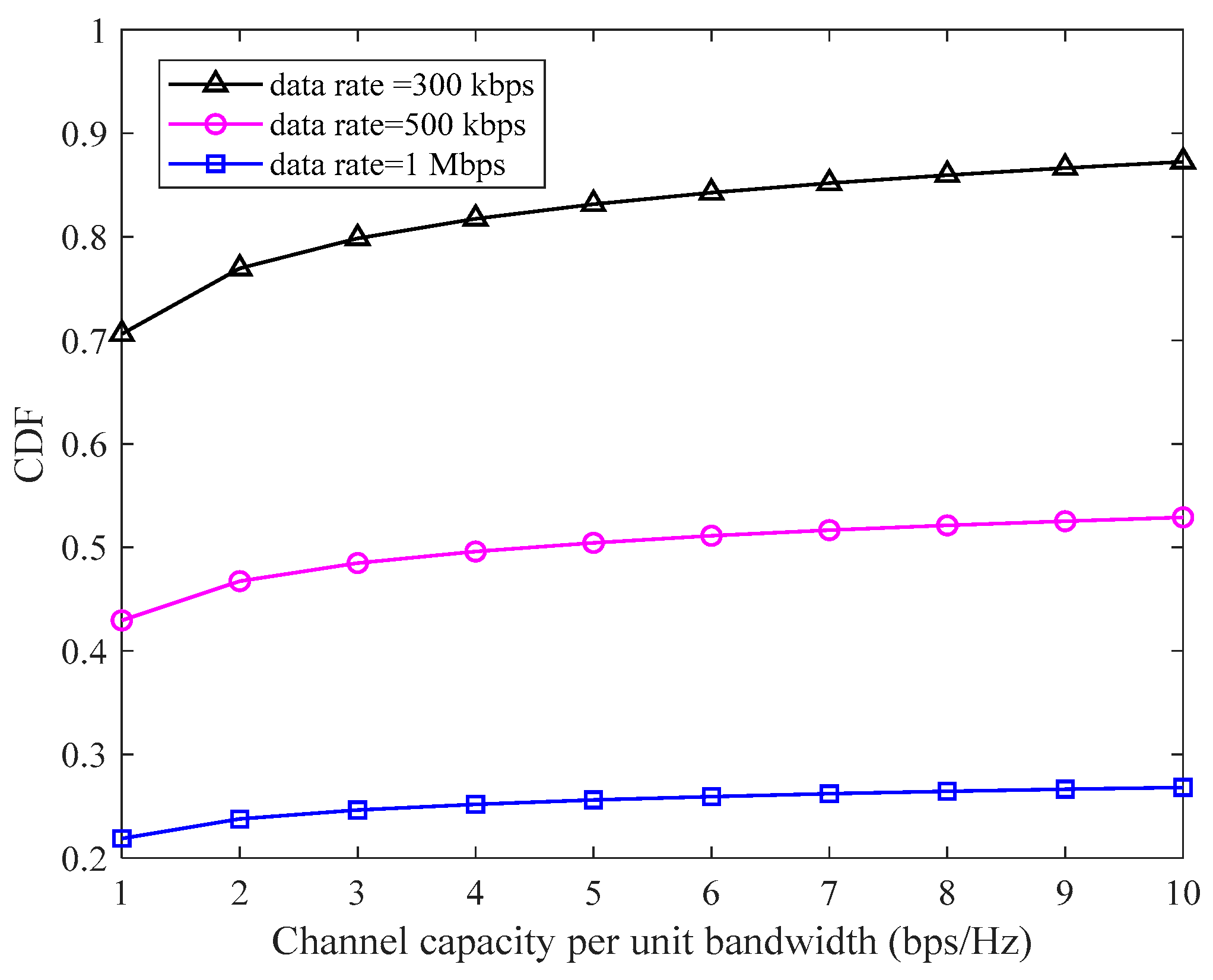
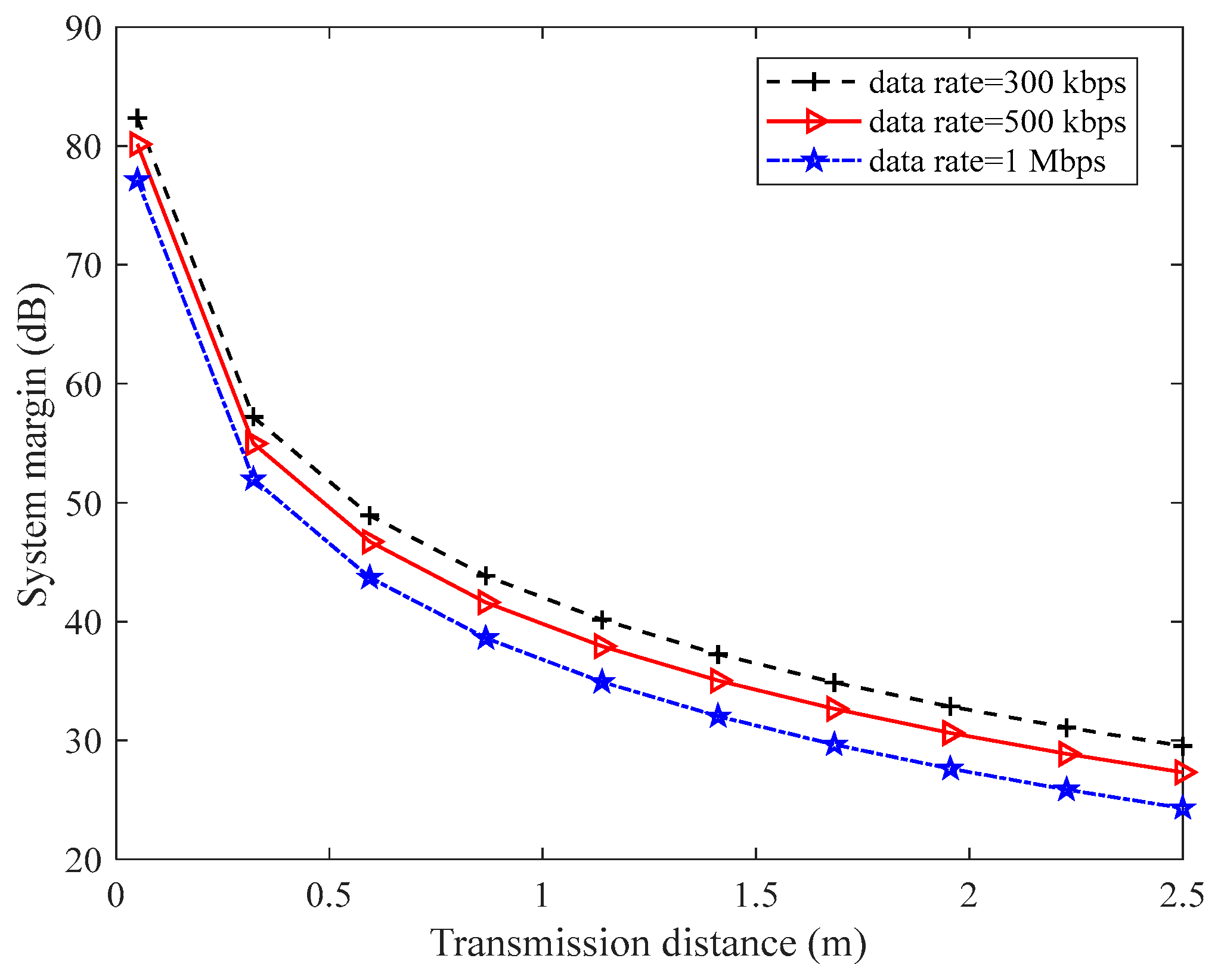
5.1. Link Quality Analysis
5.2. Network Topology
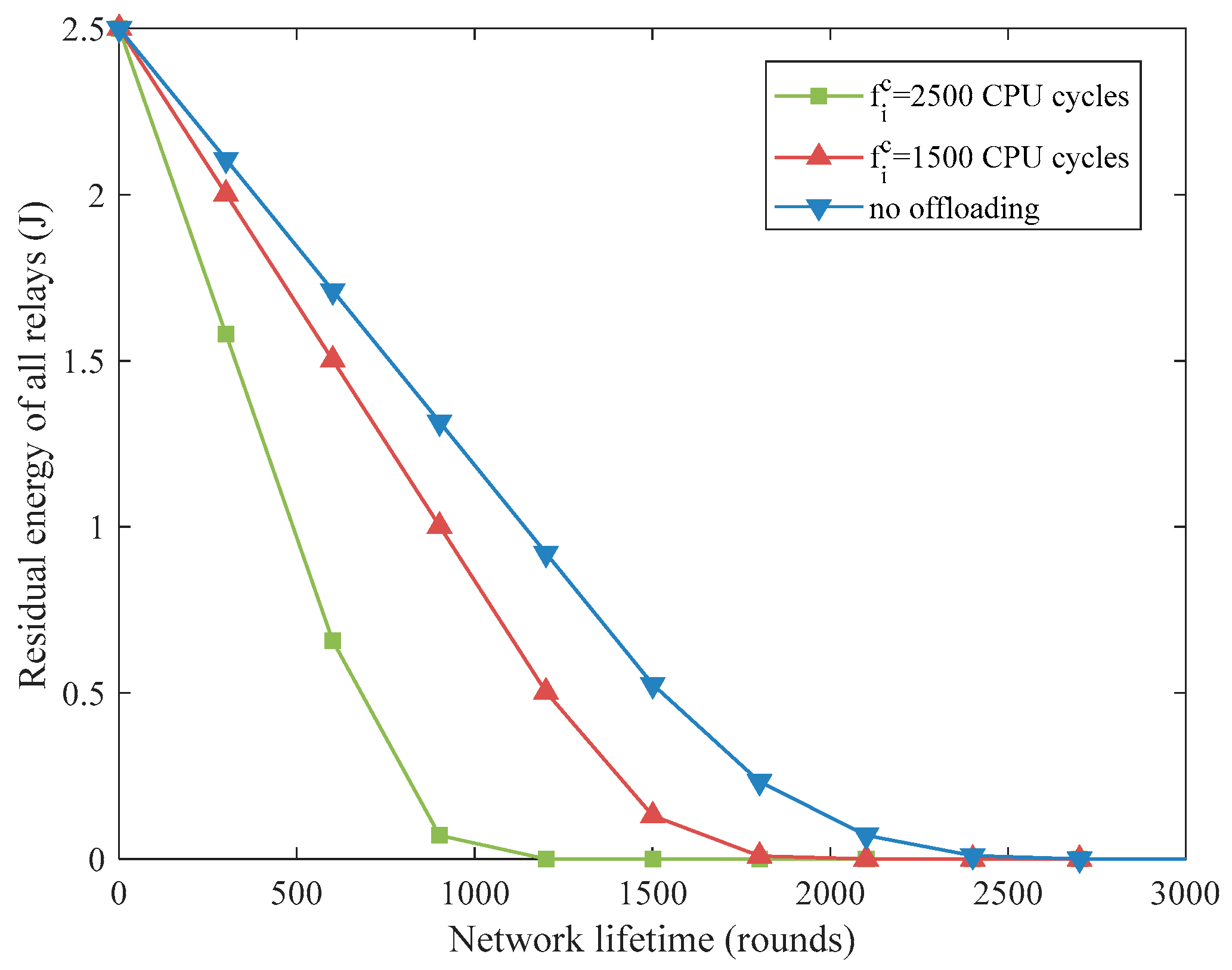
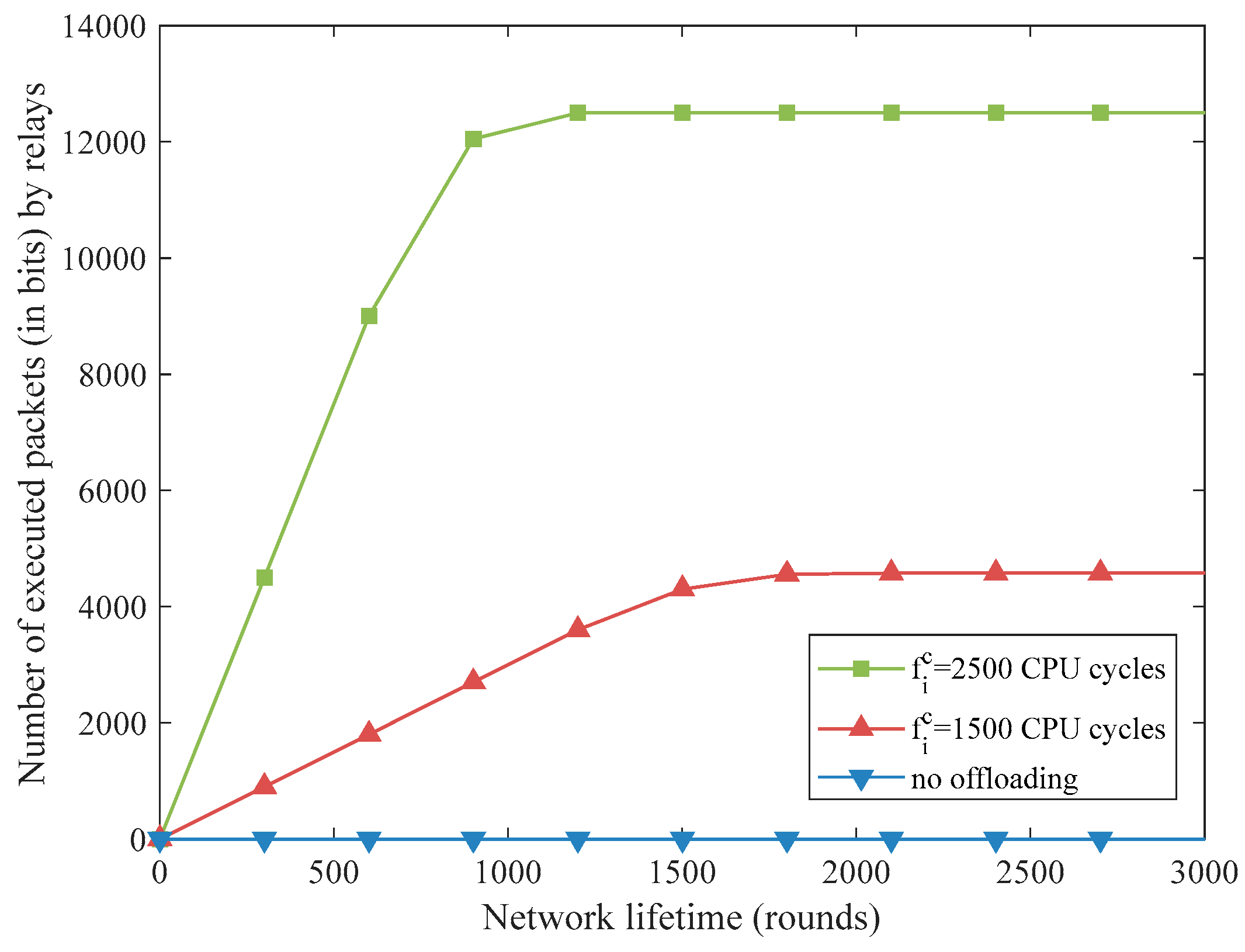
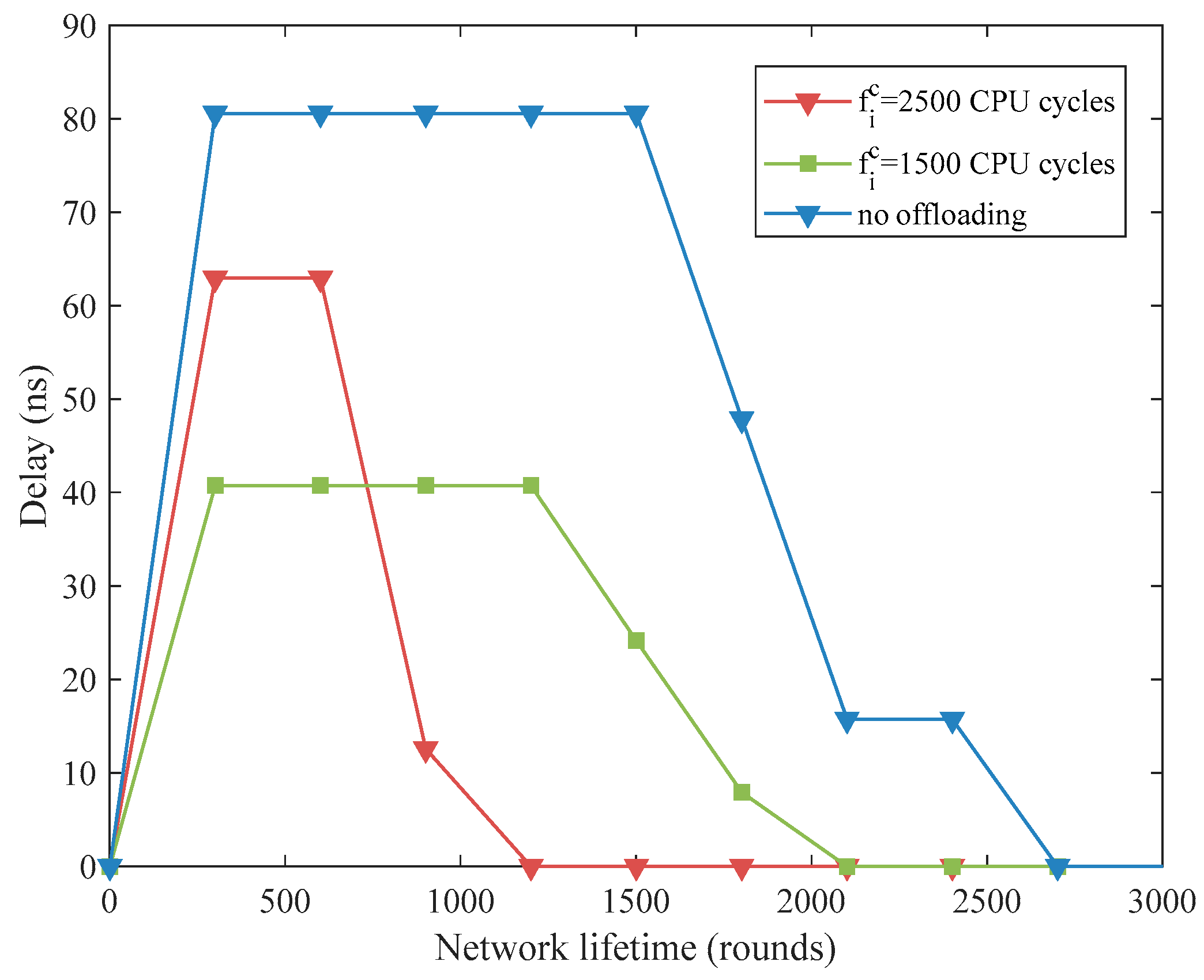
5.3. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, F.; Liu, X.; Shao, M.; Sui, D.; Wang, L. Wireless energy and information transfer in WBAN: An overview. IEEE Netw. 2017, 31, 90–96. [Google Scholar] [CrossRef]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless body area networks: A survey. IEEE Commun. Surv. Tutor. 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Salayma, M.; Al-Dubai, A.; Romdhani, I.; Nasser, Y. Wireless body area network (WBAN): A survey on reliability, fault tolerance, and technologies coexistence. ACM Comput. Surv. 2017, 50, 3. [Google Scholar] [CrossRef]
- Qi, X.; Wang, K.; Huang, A.; Hu, H.; Han, G. MAC protocol in wireless body area network for mobile health: A survey and an architecture design. Int. J. Distrib. Sens. Netw. 2015, 11, 289404. [Google Scholar] [CrossRef]
- Cavallari, R.; Martelli, F.; Rosini, R.; Buratti, C.; Verdone, R. A survey on wireless body area networks: Technologies and design challenges. IEEE Commun. Surv. Tutor. 2014, 16, 1635–1657. [Google Scholar] [CrossRef]
- Tran, T.X.; Hajisami, A.; Pandey, P.; Pompili, D. Collaborative mobile edge computing in 5G networks: New paradigms, scenarios, and challenges. IEEE Commun. Mag. 2017, 55, 54–61. [Google Scholar] [CrossRef]
- Jararweh, Y.; Doulat, A.; AlQudah, O.; Ahmed, E.; Al-Ayyoub, M.; Benkhelifa, E. The future of mobile cloud computing: Integrating cloudlets and mobile edge computing. In Proceedings of the 23rd International Conference on Telecommunications (ICT), Thessaloniki, Greece, 16–18 May 2016. [Google Scholar]
- Deepak, K.S.; Babu, A.V. Improving energy efficiency of incremental relay based cooperative communications in wireless body area networks. Int. J. Commun. Syst. 2015, 28, 91–111. [Google Scholar] [CrossRef]
- Sawand, A.; Djahel, S.; Zhang, Z.; Naït-Abdesselam, F. Multidisciplinary approaches to achieving efficient and trustworthy eHealth monitoring systems. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Shanghai, China, 13–15 October 2014. [Google Scholar]
- Maskooki, A.; Soh, C.B.; Gunawan, E.; Low, K.S. Opportunistic routing for body area network. In Proceedings of the IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2011. [Google Scholar]
- Gai, K.; Qiu, M.; Zhao, H.; Tao, L.; Zong, Z. Dynamic energy-aware cloudlet-based mobile cloud computing model for green computing. J. Netw. Comput. Appl. 2016, 59, 46–54. [Google Scholar] [CrossRef]
- Yang, L.; Cao, J.; Yuan, Y.; Li, T.; Han, A.; Chan, A. A framework for partitioning and execution of data stream applications in mobile cloud computing. ACM SIGMETRICS Perform. Eval. Rev. 2013, 40, 23–32. [Google Scholar] [CrossRef]
- Dinh, H.T.; Lee, C.; Niyato, D.; Wang, P. A survey of mobile cloud computing: Architecture, applications, and approaches. Wirel. Commun. Mob. Comput. 2013, 13, 1587–1611. [Google Scholar] [CrossRef]
- Rahimi, M.R.; Ren, J.; Liu, C.H.; Vasilakos, A.V.; Venkatasubramanian, N. Mobile cloud computing: A survey, state of art and future directions. Mob. Netw. Appl. 2014, 19, 133–143. [Google Scholar] [CrossRef]
- Wang, K.; Yang, K.; Pan, C.; Wang, J. Joint offloading framework to support communication and computation cooperation. arXiv. 2017. Available online: https://arxiv.org/abs/1705.10384 (accessed on 20 July 2018).
- Bello, O.; Zeadally, S.; Badra, M. Network layer inter-operation of device-to-device communication technologies in Internet of Things (IoT). Ad Hoc Netw. 2017, 57, 52–62. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, S.; Chen, Y.; Wang, S.; Chu, X.; Niu, Z. Simultaneous information and energy flow for IoT relay systems with crowd harvesting. IEEE Commun. Mag. 2016, 54, 143–149. [Google Scholar] [CrossRef]
- Nakamura, T.; Nagata, S.; Benjebbour, A.; Kishiyama, Y.; Hai, T.; Xiaodong, S.; Nan, L. Trends in small cell enhancements in LTE advanced. IEEE Commun. Mag. 2013, 51, 98–105. [Google Scholar] [CrossRef]
- Liao, Y.; Leeson, M.S.; Cai, Q.; Ai, Q.; Liu, Q. Mutual-information-based incremental relaying communications for wireless biomedical implant systems. Sensors 2018, 18, 515. [Google Scholar] [CrossRef] [PubMed]
- Yi, C.; Wang, L.; Li, Y. Energy efficient transmission approach for WBAN based on threshold distance. IEEE Sens. J. 2015, 15, 5133–5141. [Google Scholar] [CrossRef]
- Liao, Y.; Leeson, M.S.; Higgins, M.D.; Bai, C. Analysis of in-to-out wireless body area network systems: Towards QoS-aware health internet of things applications. Electronics 2016, 5, 38. [Google Scholar] [CrossRef]
- Javaid, N.; Ahmad, A.; Khan, Y.; Khan, Z.A.; Alghamdi, T.A. A relay based routing protocol for wireless in-body sensor networks. Wirel. Pers. Commun. 2015, 80, 1063–1078. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Y.; Alouini, M.S.; Xu, F. BER and optimal power allocation for amplify-and-forward relaying using pilot-aided maximum likelihood estimation. IEEE Trans. Commun. 2014, 62, 3462–3475. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Y.; Di Renzo, M. Outage probability of dual-hop selective AF with randomly distributed and fixed interferers. IEEE Trans. Veh. Technol. 2015, 64, 4603–4616. [Google Scholar] [CrossRef]
- Kim, S. Nested game-based computation offloading scheme for mobile cloud IoT systems. EURASIP J. Wirel. Commun. Netw. 2015, 1, 229. [Google Scholar] [CrossRef]
- Chen, M.; Hao, Y.; Qiu, M.; Song, J.; Wu, D.; Humar, I. Mobility-aware caching and computation offloading in 5G ultra-dense cellular networks. Sensors 2016, 16, 974. [Google Scholar] [CrossRef] [PubMed]
- Javaid, N.; Ahmad, A.; Nadeem, Q.; Imran, M.; Haider, N. iM-SIMPLE: IMproved stable increased-throughput multi-hop link efficient routing protocol for wireless body area networks. Comput. Hum. Behav. 2015, 15, 1003–1011. [Google Scholar] [CrossRef]
- Ahmed, S.; Javaid, N.; Yousaf, S.; Ahmad, A.; Sandhu, M.M.; Imran, M.; Khan, Z.A.; Alrajeh, N. Co-LAEEBA: Cooperative link aware and energy efficient protocol for wireless body area networks. Comput. Hum. Behav. 2015, 51, 1205–1215. [Google Scholar] [CrossRef]
- Magurawalage, C.M.S.; Yang, K.; Hu, L.; Zhang, J. Energy-efficient and network-aware offloading algorithm for mobile cloud computing. Comput. Netw. 2014, 74, 22–33. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Le Long, B. Joint computation offloading and resource allocation in cloud based wireless HetNets. In Proceedings of the IEEE Global Communications Conference, Singapore, 4–8 December 2017. [Google Scholar]
- Cheffena, M. Performance evaluation of wireless body sensors in the presence of slow and fast fading effects. IEEE Sens. J. 2015, 15, 5518–5526. [Google Scholar] [CrossRef]
- Zhang, L.; Leeson, M.S.; Liao, Y.; Higgins, M.D. Performance evaluation of reliable communications for wireless in-body sensor networks. In Proceedings of the 2017 International Conference on Computer, Information and Telecommunication Systems (CITS), Dalian, China, 21–23 July 2017. [Google Scholar]
- Al Ameen, M.; Hong, C.S. An on-demand emergency packet transmission scheme for wireless body area networks. Sensors 2015, 15, 30584–30616. [Google Scholar] [CrossRef] [PubMed]
- Akbar, M.S.; Yu, H.; Cang, S. Delay, reliability, and throughput based QoS profile: A MAC layer performance optimization mechanism for biomedical applications in wireless body area sensor networks. J. Sens. 2016, 2016, 7170943. [Google Scholar] [CrossRef]
- Kim, T.Y.; Youm, S.; Jung, J.J.; Kim, E.J. Multi-hop WBAN construction for healthcare IoT systems. In Proceedings of the 2015 International Conference on Platform Technology and Service (PlatCon), Jeju, Korea, 26–28 January 2015. [Google Scholar]
- Fouad, H. Continuous health-monitoring for early detection of patient by Web telemedicine system. In Proceedings of the International Conference on Circuits, Systems and Signal Processing, St. Petersburg, Russia, 23–25 September 2014. [Google Scholar]
- Pham, Q.V.; Hwang, W.J. Fairness-aware spectral and energy efficiency in spectrum-sharing wireless networks. IEEE Trans. Veh. Technol. 2017, 66, 10207–10219. [Google Scholar] [CrossRef]
- Ngo, D.T.; Khakurel, S.; Le-Ngoc, T. Joint subchannel assignment and power allocation for OFDMA femtocell networks. IEEE Trans. Wirel. Commun. 2014, 13, 342–355. [Google Scholar] [CrossRef]

| Type | Node ID | X-Coordinate | Y-Coordinate |
|---|---|---|---|
| On-body relay | 1 | 0.2 | 1.65 |
| 2 | 0.1 | 1.5 | |
| 3 | 0.65 | 1.5 | |
| 4 | 0.25 | 0.8 | |
| 5 | 0.7 | 1 | |
| Implanted sensor | − | 0.4 | 0.85 |
| C-MEC | − | 2.5 | 2.5 |
| Parameter | Value (Unit) |
|---|---|
| 1500 bits | |
| 1000 bits | |
| c | 3 × 108 ms−1 |
| 300 kHz | |
| 10−11 | |
| 2 | |
| 1.97 nJ (bit)−1 | |
| 0.12 × 10−9 nJ (bit)−1 | |
| 0.3064 nJ (bit)−1 | |
| 16.7 nJ (bit)−1 | |
| 36.1 nJ (bit)−1 | |
| 17 dB | |
| 10−3 | |
| 4.15 dB | |
| 48.4 dB | |
| PL exponent n | 5.9 |
| Initial power | 0.5 J |
| Number of relays | 5 |
| Bandwidth B | 300 kHz |
| Boltzmann constant v | 1.38 × 10−23 |
| Environment temperature | 290 K |
| Transmission power | −12 dBm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Yu, Q.; Han, Y.; Leeson, M.S. Relay-Enabled Task Offloading Management for Wireless Body Area Networks. Appl. Sci. 2018, 8, 1409. https://doi.org/10.3390/app8081409
Liao Y, Yu Q, Han Y, Leeson MS. Relay-Enabled Task Offloading Management for Wireless Body Area Networks. Applied Sciences. 2018; 8(8):1409. https://doi.org/10.3390/app8081409
Chicago/Turabian StyleLiao, Yangzhe, Quan Yu, Yi Han, and Mark S. Leeson. 2018. "Relay-Enabled Task Offloading Management for Wireless Body Area Networks" Applied Sciences 8, no. 8: 1409. https://doi.org/10.3390/app8081409






