A New Method for Active Cancellation of Engine Order Noise in a Passenger Car
Abstract
:Featured Application
Abstract
1. Introduction
2. Development of Novel Algorithm for Control of Amplitude of Order Sound
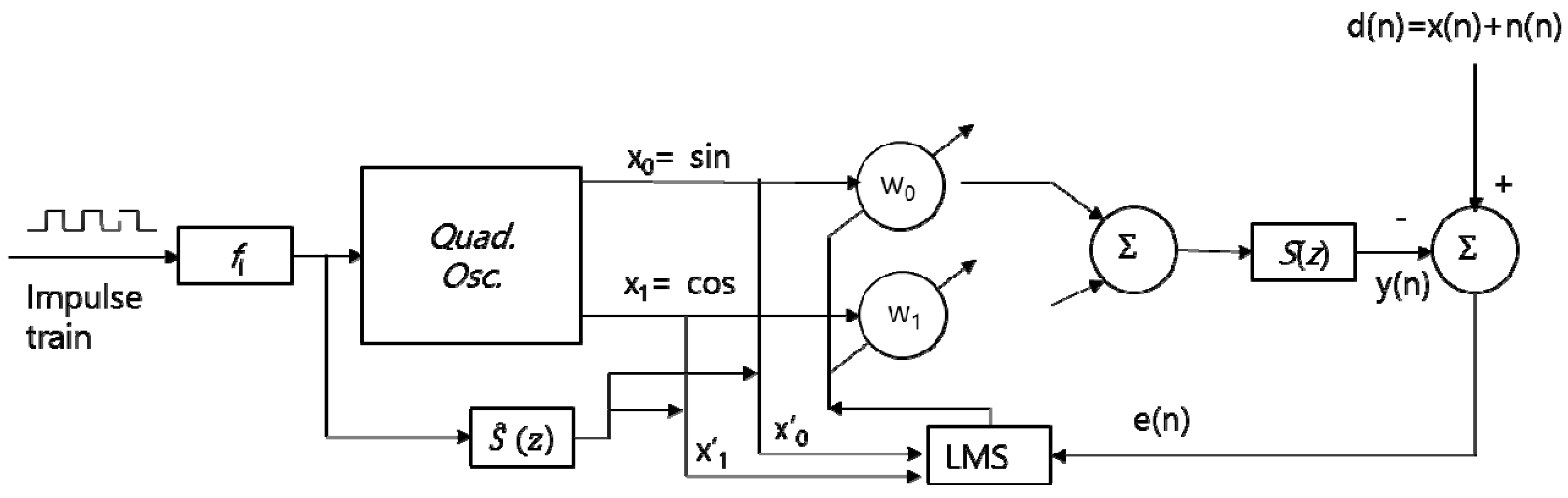
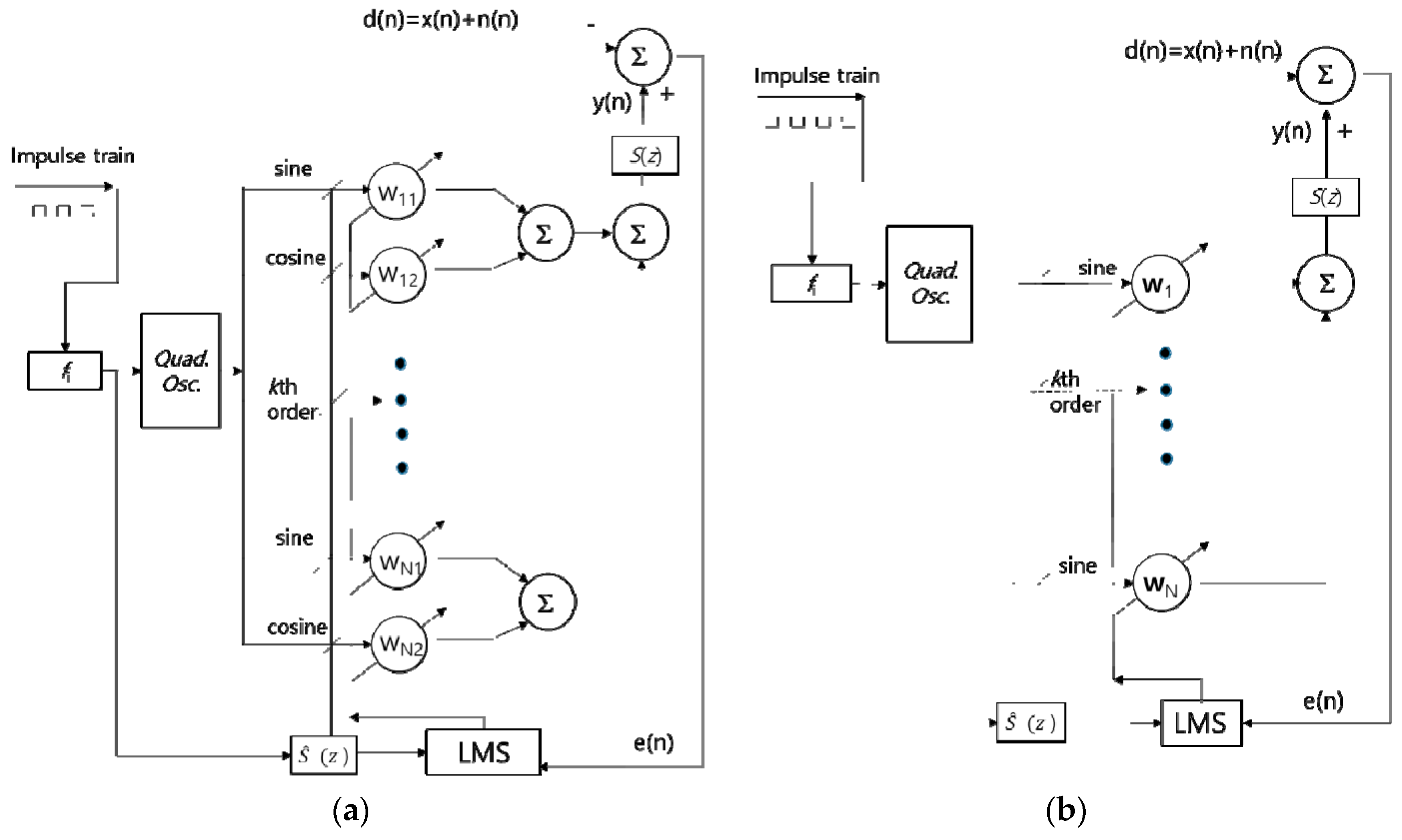
2.1. Conventional Method for ANC of Engine Noise
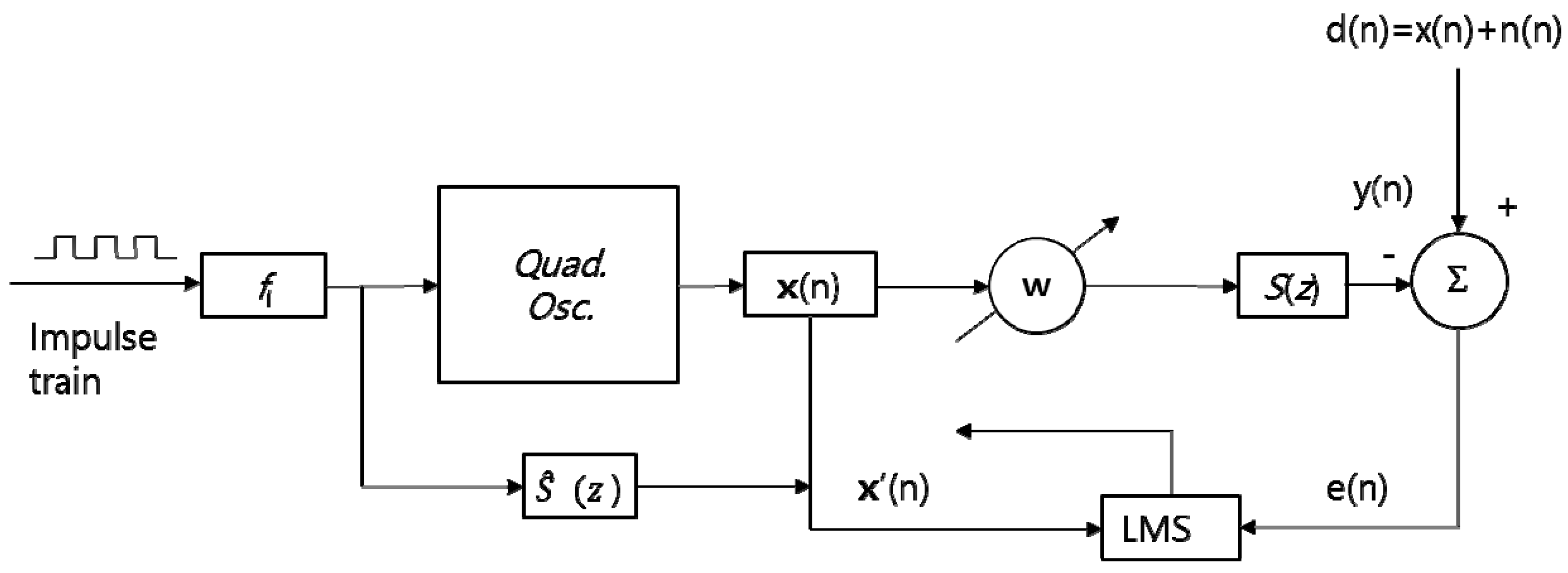
2.2. Novel Optimized Weights-LMS Algorithm: OW-FxLMS
3. Simulation and Validation of the Proposed Algorithm
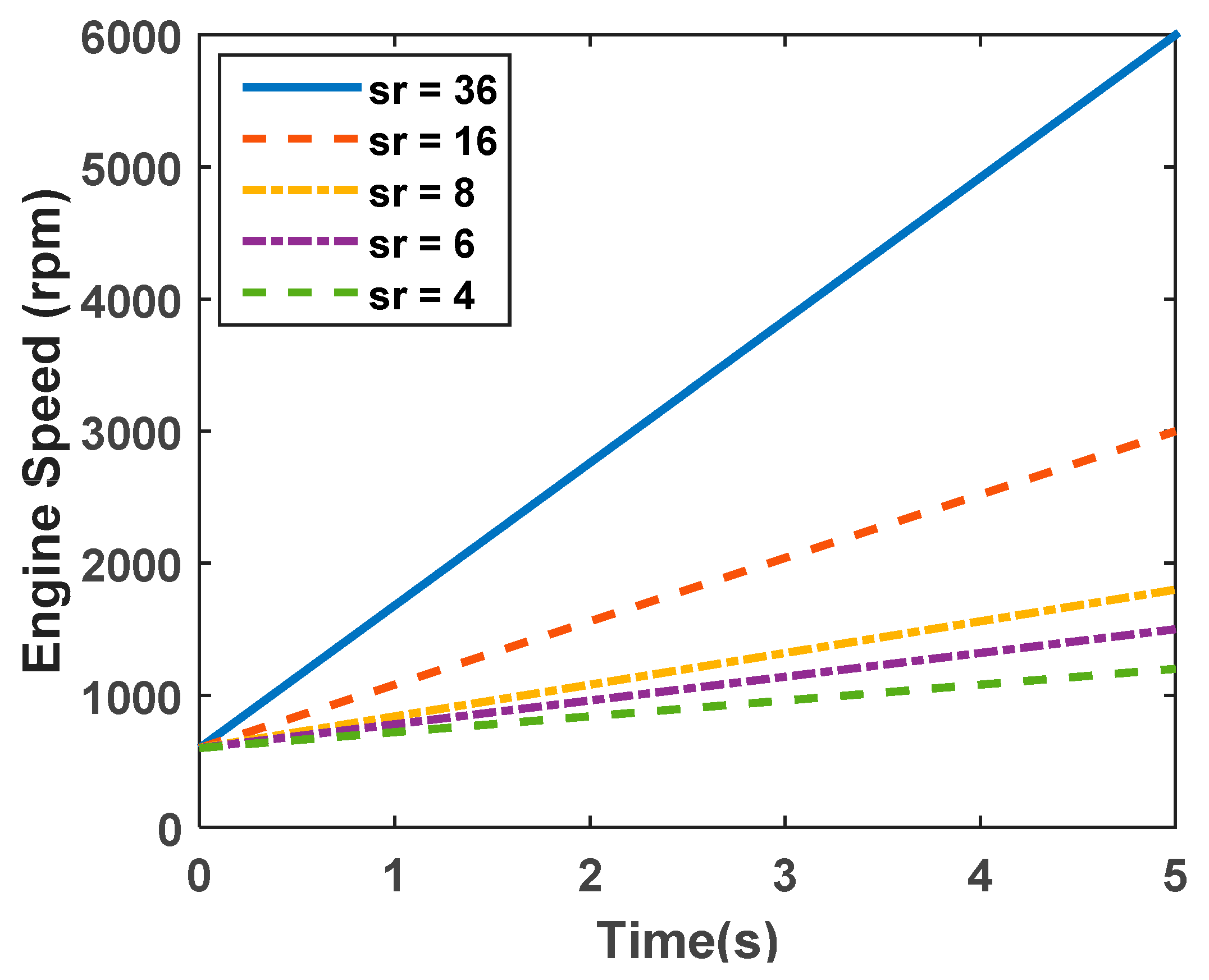
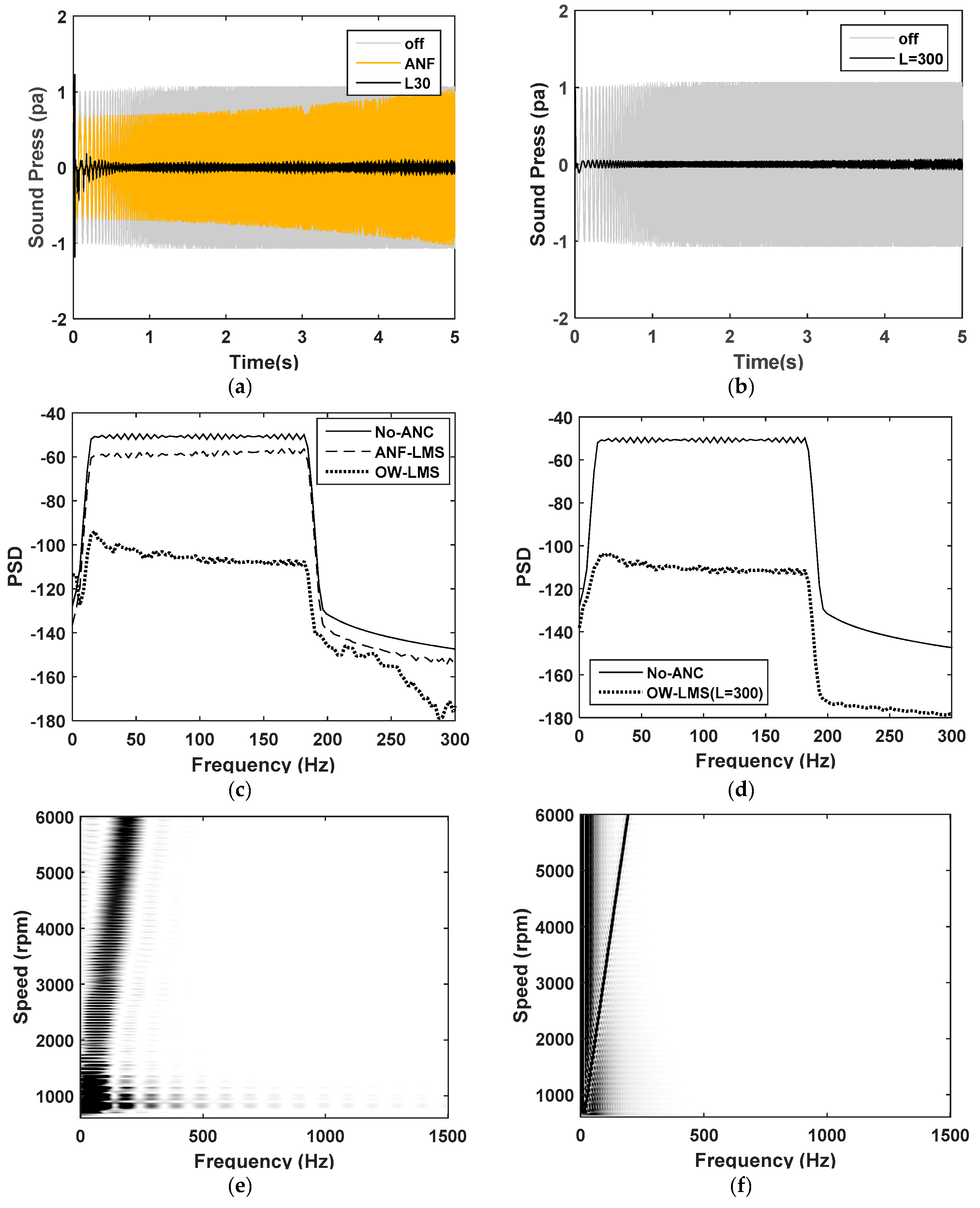
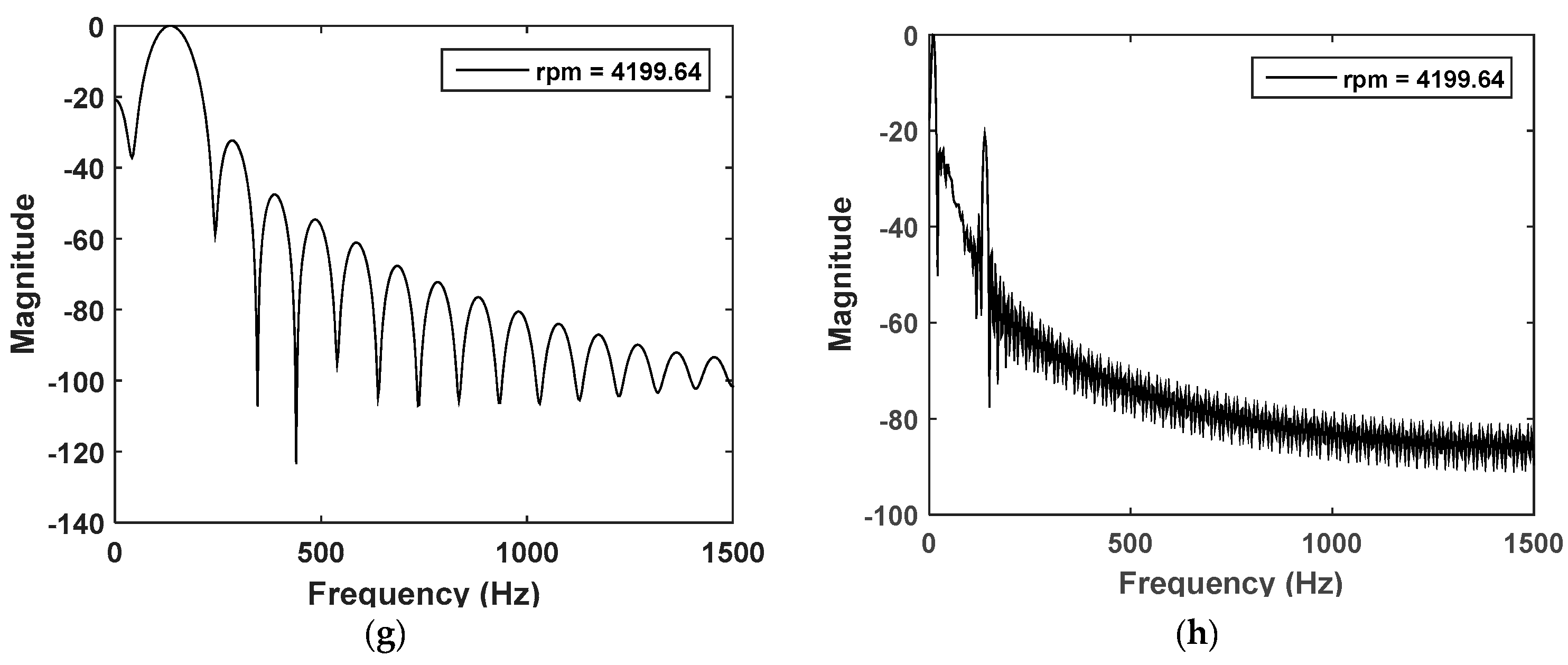
3.1. Synthesizing the Engine Noise Signal Inside a Car Cabin
3.2. Validation of the Proposed Algorithm
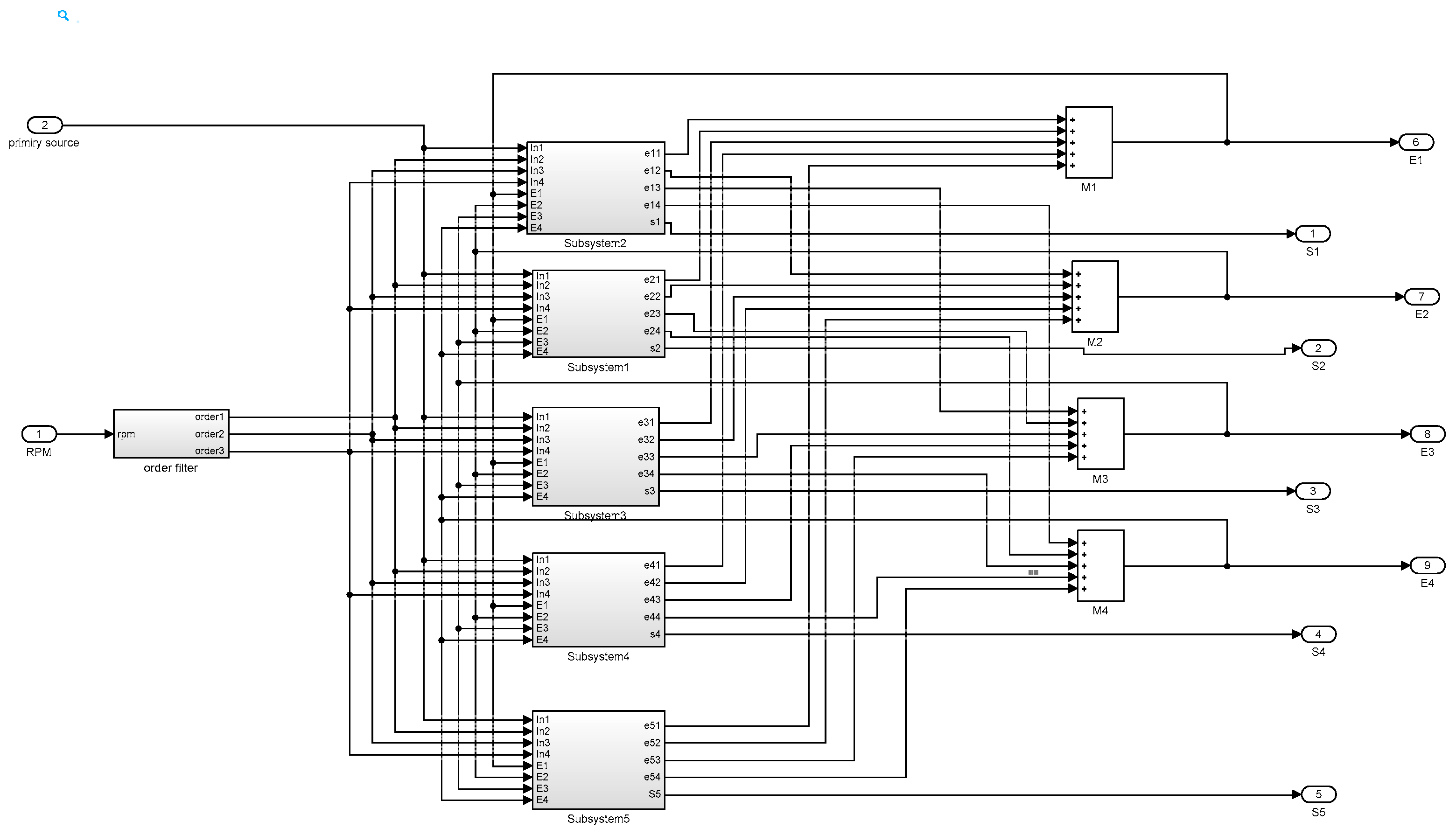
4. OW-FxLMS Algorithm for ANC of Engine Noise
5. Application of the OW-Fxlms Algorithm to ANC of Interior Noise
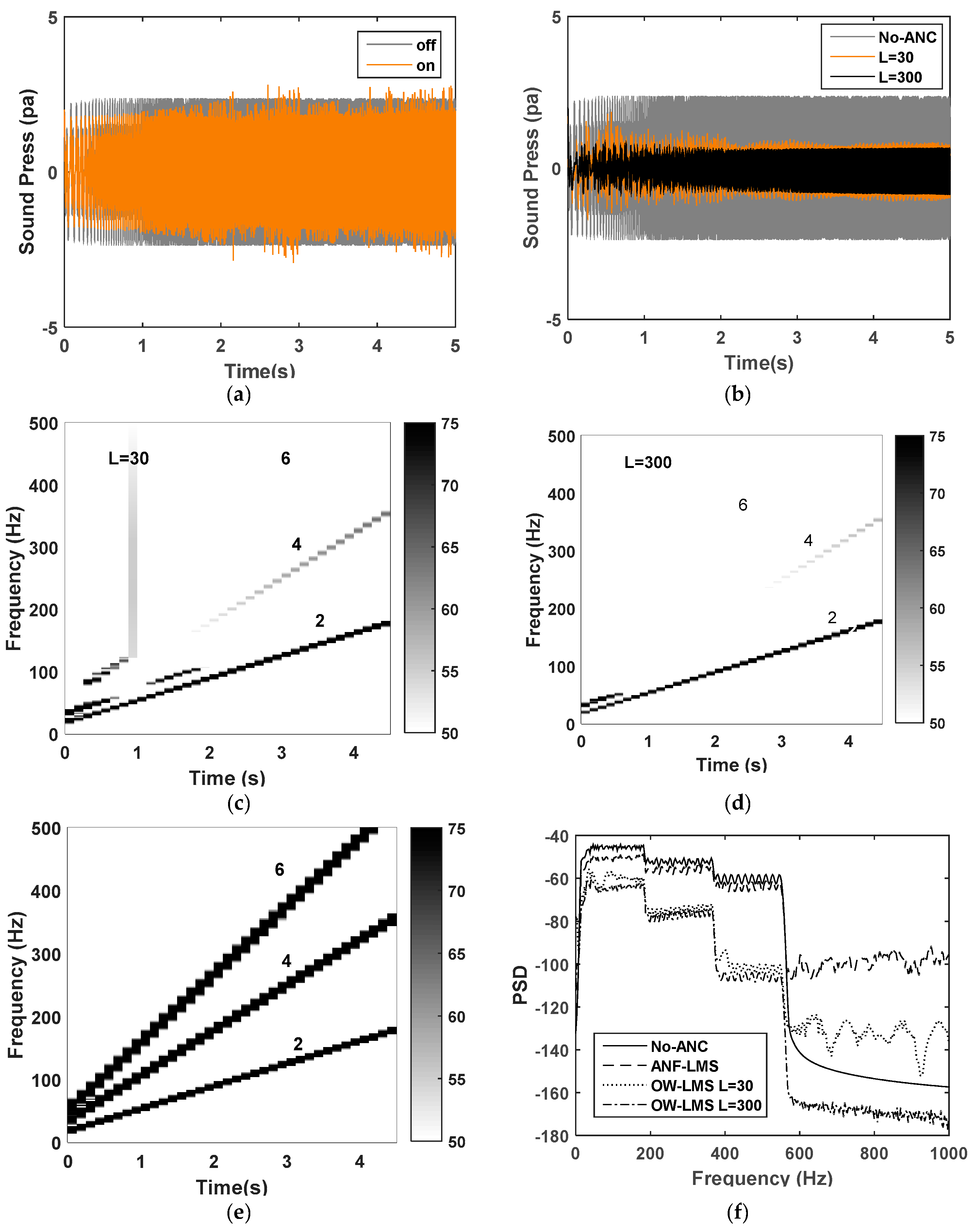
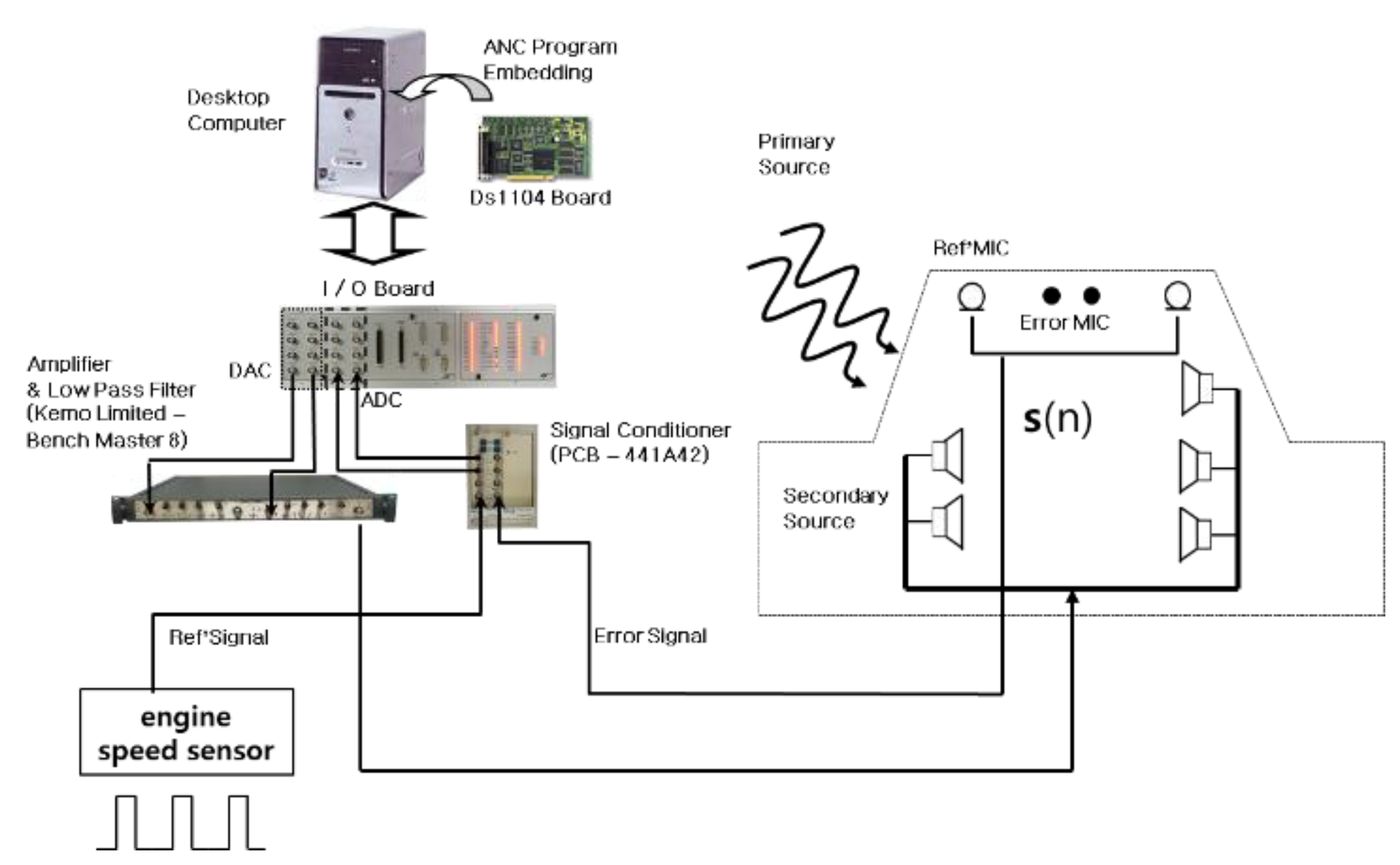
5.1. Experimental Setup and Procedure
5.2. Measurement of the Impulse Response of the Secondary Path
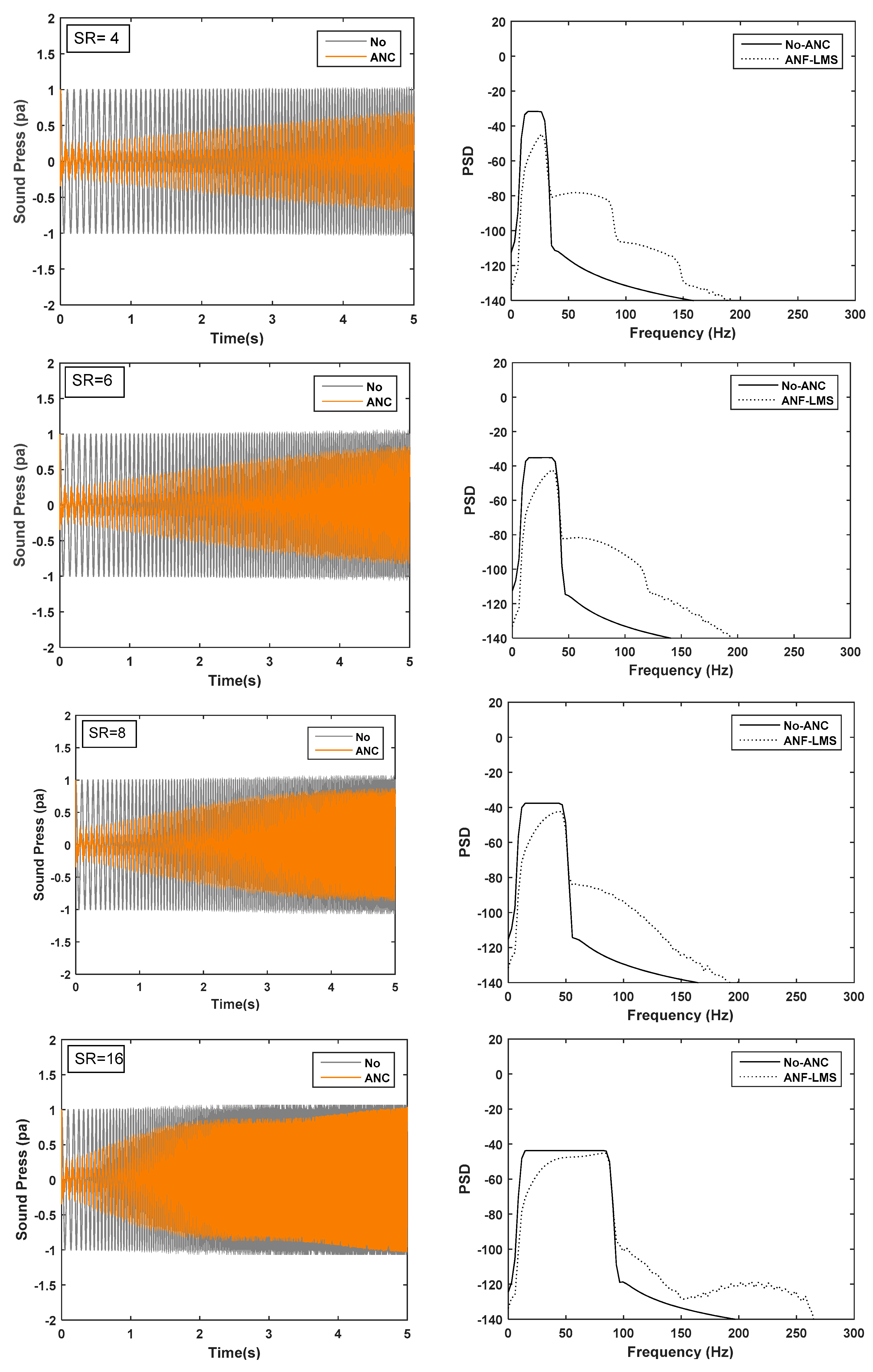
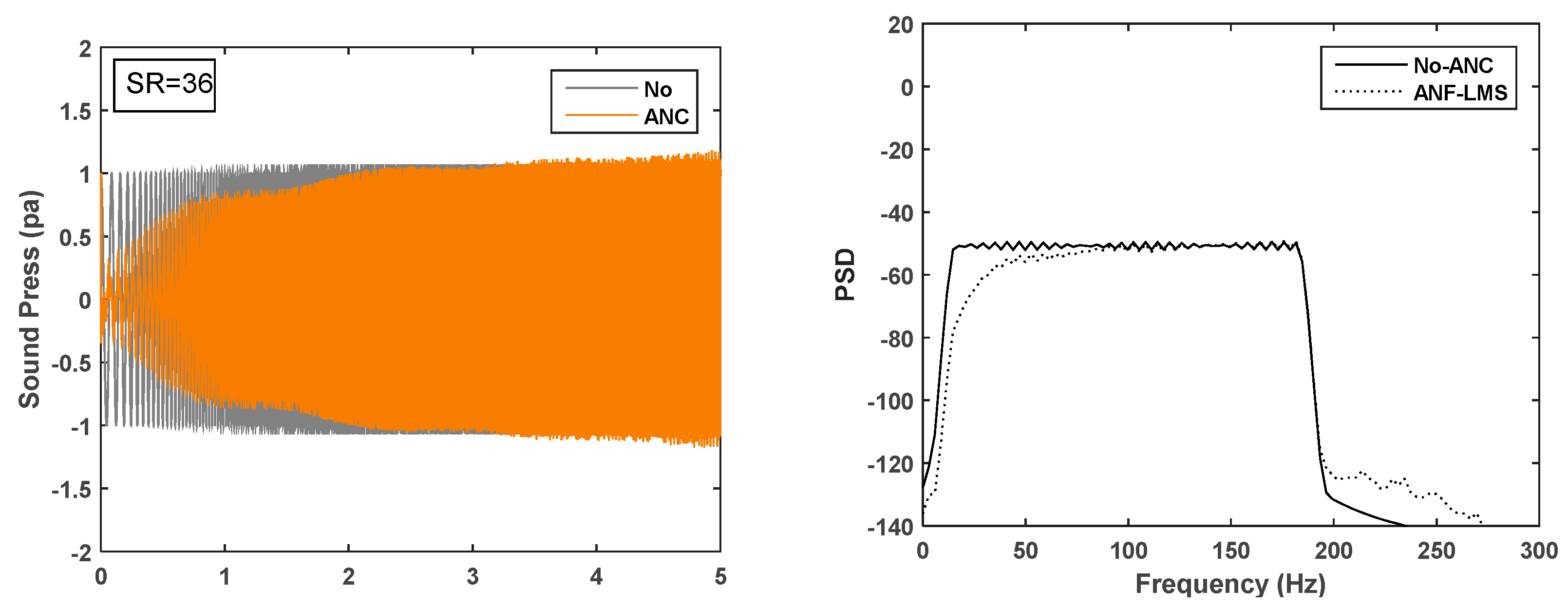
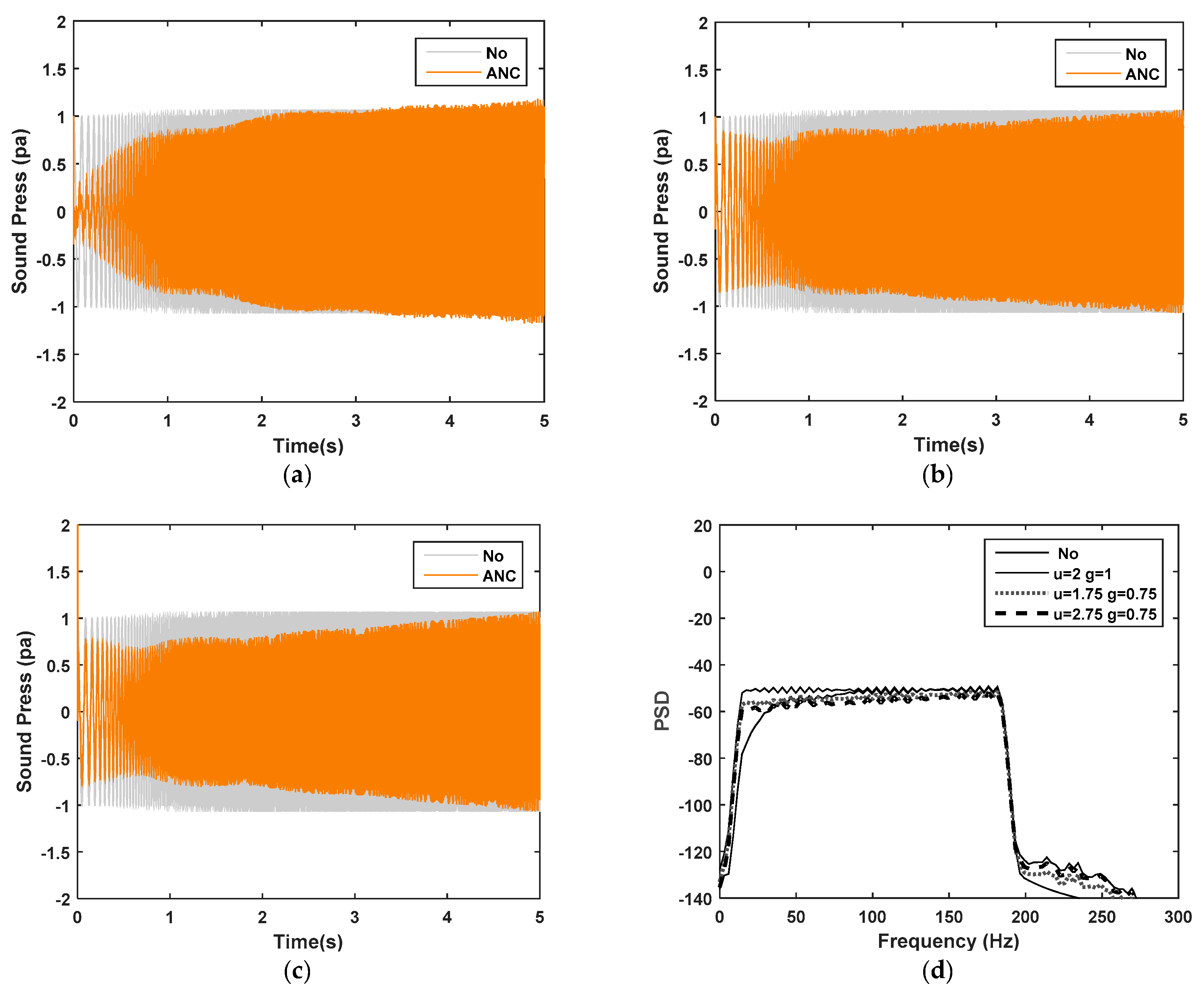
5.3. Application of Adaptive Algorithms to ANC for Interior Noise
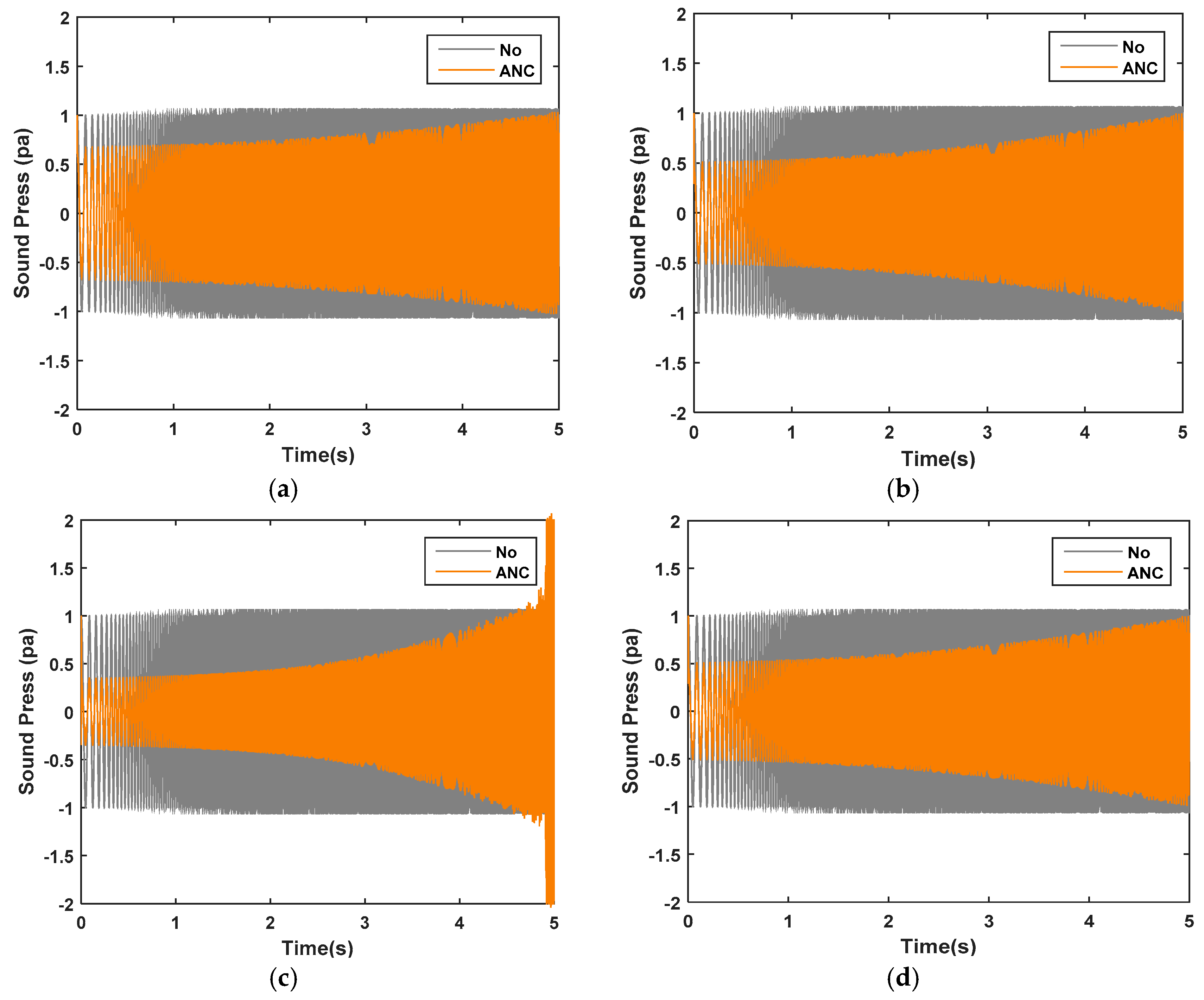
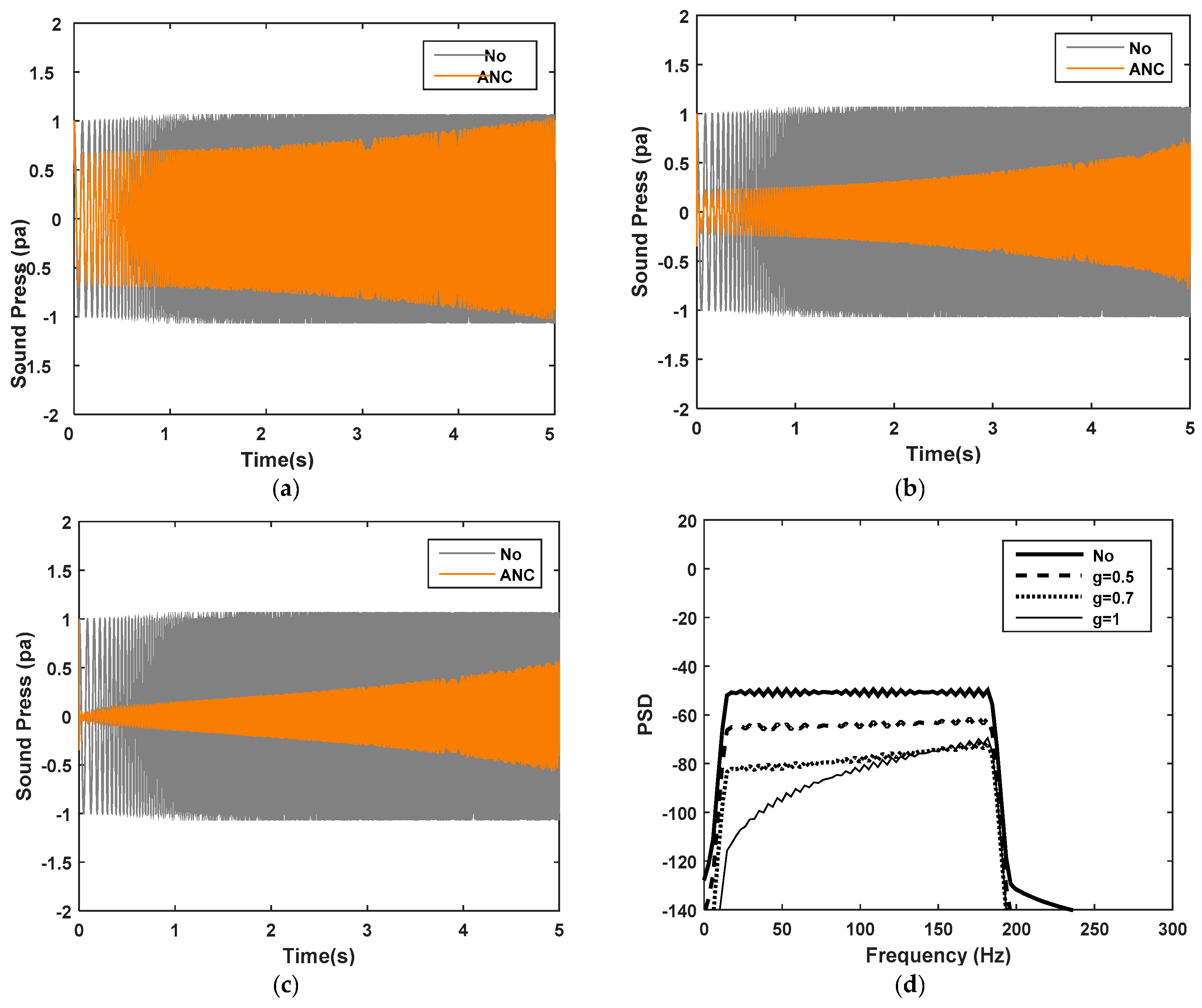
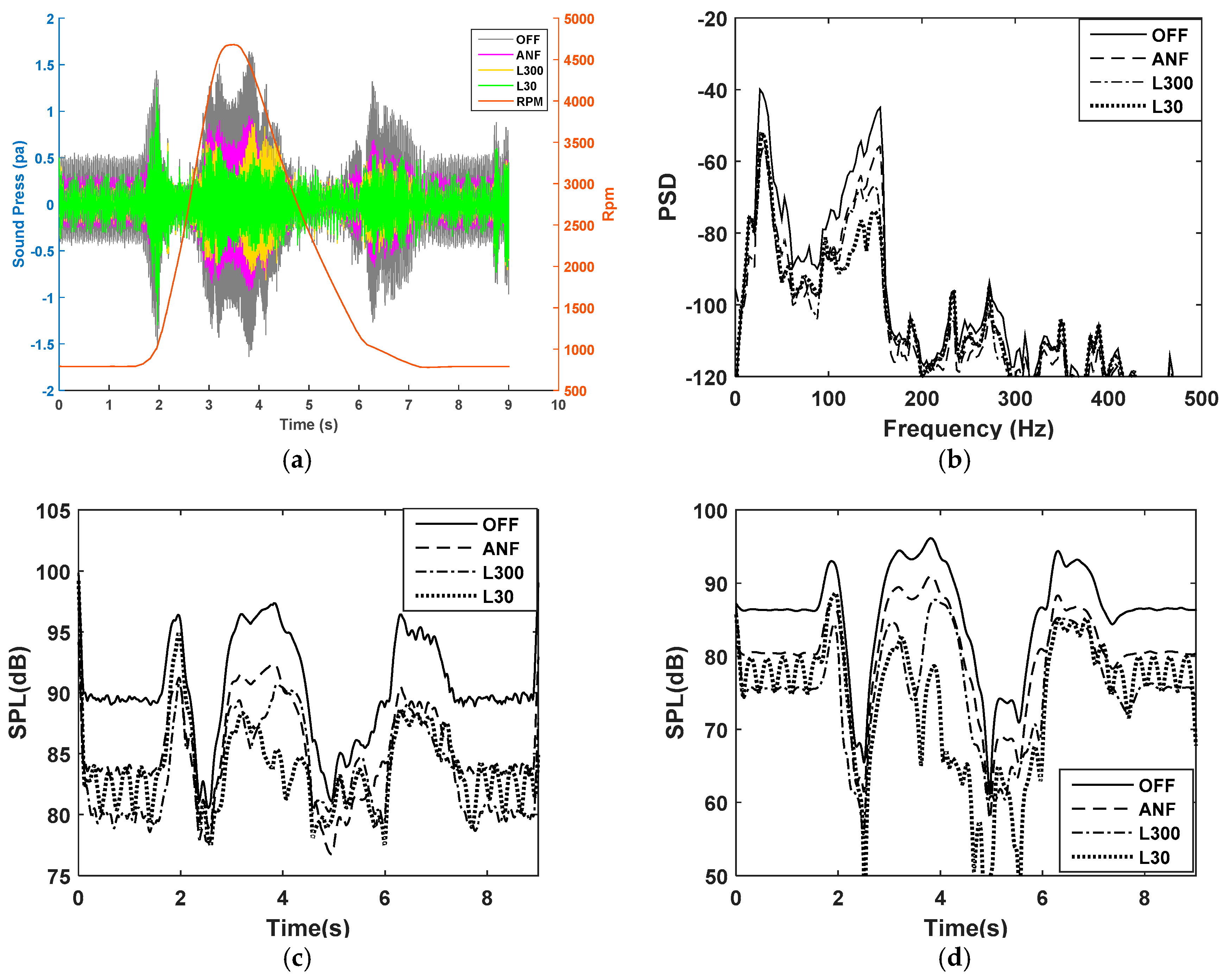
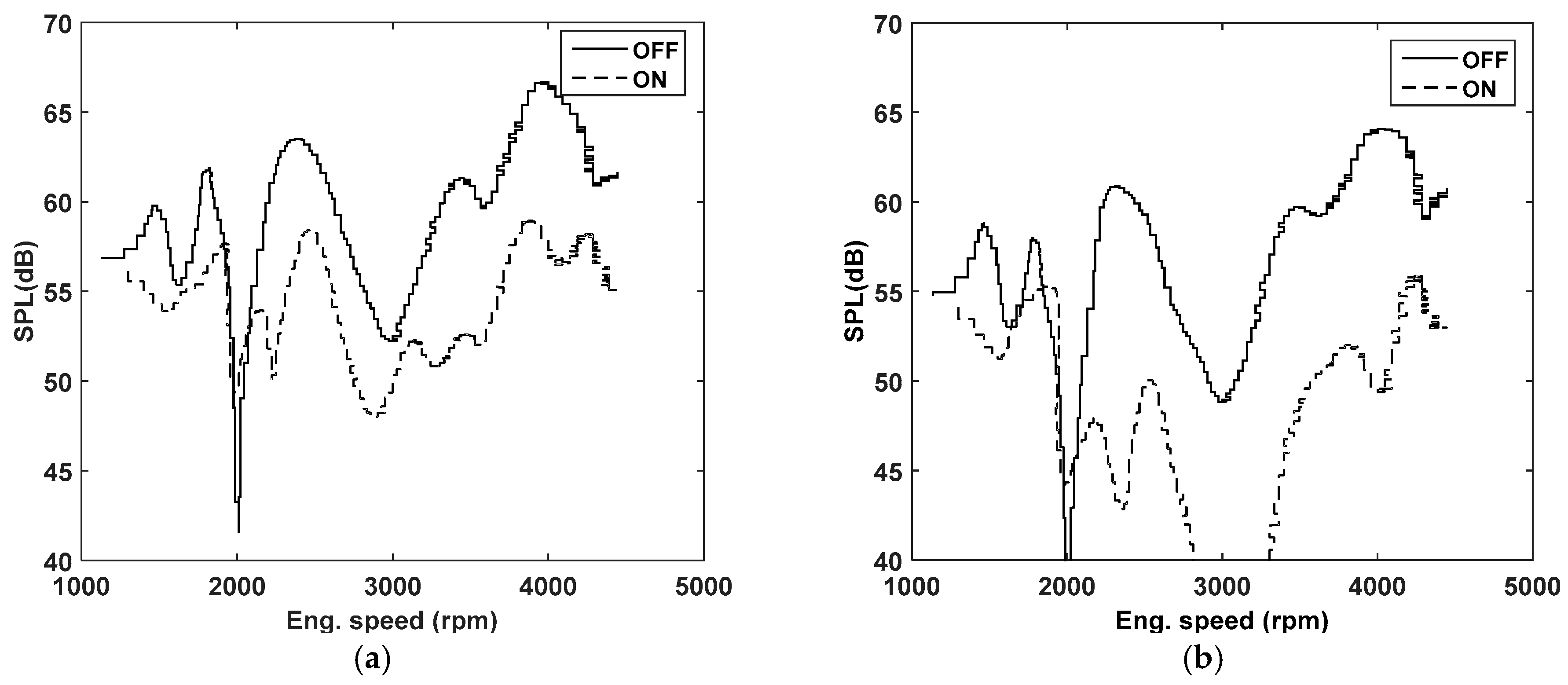
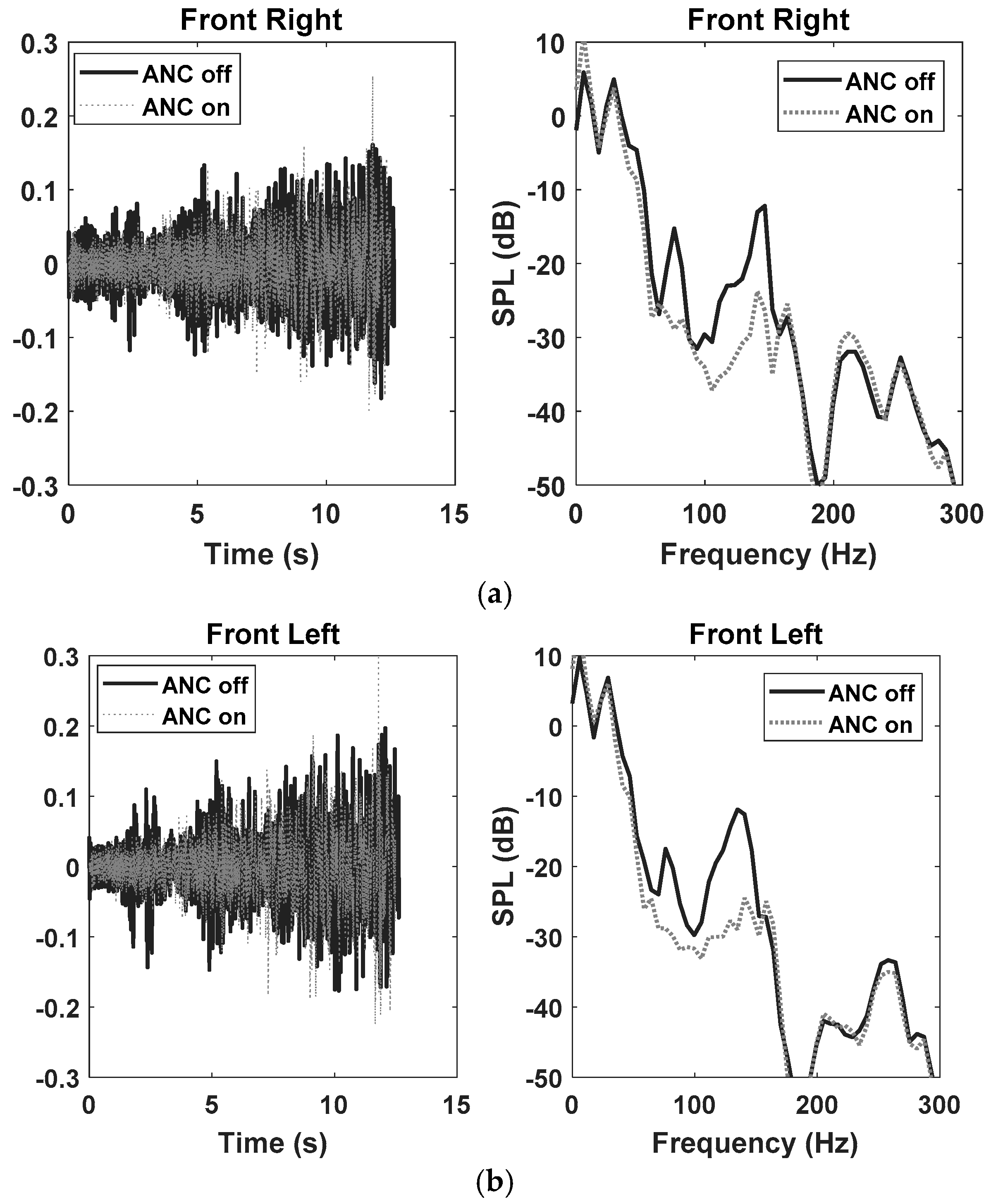
5.4. Performance of the ANC System with OW-FxLMS
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, T.G.; Lee, S.K.; Lee, H.H. Characterization and quantification of luxury sound quality in premium-class passenger cars. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2009, 223, 343–353. [Google Scholar] [CrossRef]
- Lee, H.H.; Lee, S.K. Objective evaluation of interior noise booming in a passenger car based on sound metrics and artificial neural networks. Appl. Ergon. 2009, 40, 860–869. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.K. Objective Evaluation of Interior Sound Quality in Passenger Cars during Acceleration. J. Sound Vib. 2008, 310, 149–168. [Google Scholar] [CrossRef]
- Elliott, S.J. A Review of Active Noise and Vibration Control in Road Vehicles; Technical Memorandum, No. 981; ISVR, University of Southampton: Southampton, UK, 2008. [Google Scholar]
- Samarasinghe, P.N.; Zhang, W.; Abhayapala, T.D. Recent Advances in Active Noise Control inside Automobile Cabins: Toward quieter cars. IEEE Signal Process. Mag. 2016, 33, 61–73. [Google Scholar] [CrossRef]
- Elliott, S.J. Signal Processing for Active Control; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Kuo, S.M.; Morgan, D.R. Active Noise Control Systems Algorithms and DSP Implementations; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Lee, S.K. Adaptive Signal Processing and Higher Order Time Frequency Analysis for Acoustic and Vibration Signatures in Condition Monitoring. Ph.D. Thesis, ISVR, University of Southampton, Southampton, UK, 1998. [Google Scholar]
- Hykin, S. Adaptive Filter Theory, 5th ed.; Pearson: Boston, MA, USA, 2014. [Google Scholar]
- Pritzker, Z.; Feuer, A. Variable length stochastic gradient algorithm. IEEE Trans. Signal Process. 1991, 997, 1001. [Google Scholar] [CrossRef]
- Bilcu, R.C.; Kuosmanen, P.; Egiazarian, K. A new variable length LMS algorithm: Theoretical analysis and implementations. In Proceedings of the 9th International Conference on Electronics, Circuits and Systems, Dubrovnik, Croatia, 15–18 September 2002. [Google Scholar]
- Nascimento, V.H. Improving the initial convergence of adaptive filters: Variable-length LMS algorithms. In Proceedings of the 14th International Conference on Digital Signal Processing, DSP 2002, Santorini, Greece, 1–3 July 2002. [Google Scholar]
- Li, C.Y.; Chu, S.I.; Tsai, S.H. Improved Variable Step-Size Partial Update LMS Algorithm Green Technology and Sustainable Development (GTSD). In Proceedings of the International Conference on Green Technology and Sustainable Development, Kaohsiung, Taiwan, 24–25 November 2016. [Google Scholar]
- Widrow, B. Adaptive Signal Processing, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Kim, E.Y.; Kim, B.H.; Lee, S.K. Active Noise Control in a Duct System Based on a Frequency-estimation Algorithm and The FX-LMS Algorithm. Int. J. Autom. Technol. 2013, 14, 291–299. [Google Scholar] [CrossRef]
- Sun, X.; Liu, N.; Meng, G. Adaptive frequency tuner for active narrowband noise control systems. Mech. Syst. Signal Process. 2009, 23, 845–854. [Google Scholar] [CrossRef]
- Bismor, D.; Czyz, K.; Ogonowski, Z. Review and Comparison of Variable Step-Size LMS Algorithms. Int. J. Acoust. Vib. 2016, 21, 24–39. [Google Scholar]
- Oliveira, P.R.L.; Stallaert, B.; Janssens, K.; Auweraer, H.V. NEX-LMS: A novel adaptive control scheme for harmonic sound quality control. Mech. Syst. Signal Process. 2010, 24, 1727–1738. [Google Scholar] [CrossRef]
- Kim, H.W.; Park, H.S.; Lee, S.K.; Shin, K. Modified-Filtered-u LMS Algorithm for Active Noise Control and Its Application to a Short Acoustic Duct. Mech. Syst. Signal Process. 2011, 25, 475–484. [Google Scholar] [CrossRef]
- Lee, S.K.; Lee, S.M.; Kang, I.D.; Shin, T. Active Sound Design for a Passenger Car Based on Adaptive Order Filter. In Proceedings of the Internoise 2014, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Lee, S.M.; Lee, S.K.; Park, D.C.; Kim, S. A Novel Method for Objective Evaluation of Interior Sound in a Passenger Car and Its Application to the Design of Interior Sound in a Luxury Passenger Car. In Proceedings of the NoiseCon 2017, Grand Rapids, MI, USA, 12–14 June 2017. [Google Scholar]
- Kraus, R.; Millitzer, J.; Hansmann, J.; Wolter, S.; Jackel, M. Experimental study on active noise and active vibration control for a passenger car using novel piezoelectric engine mounts and electrodynamic inertial mass actuators. In Proceedings of the 25th International Conference on Adaptive Structure and Technologies (ICAST2014), Hague, The Netherlands, 6–8 October 2014. [Google Scholar]
- Bismor, D.; Pawelczyk, M. Stability Conditions for the Leaky LMS Algorithm Based on Control Theory Analysis. Arch. Acoust. 2016, 41, 731–739. [Google Scholar] [CrossRef] [Green Version]
- Turner, C.L. Recursive Discrete-time Sinusoidal Oscillators. IEEE Signal Process. Mag. 2003, 20, 103–111. [Google Scholar] [CrossRef]
- Righam, E. Fast Fourier Transform and Its Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Kim, S.J.; Lee, S.K. Prediction of structure-borne noise caused by the powertrain on the basis of the hybrid transfer path. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2009, 223, 485–502. [Google Scholar] [CrossRef]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal—Part 1: Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]



| Parameters: | Lo = Number of Taps | |
|---|---|---|
| Initial condition: | w (0) = 0 | Use Equation (16) |
| Data | ||
| (a) Given: | (n); Lo-by-1 tap input vector | |
| : Normalized sinusoidal signal | ||
| d(n): desired response at time n | : Measured impulse response of the 2nd path of the system includes electric part. | |
| Note: ⊗ means convolution | ||
| (b) To be computed: | w(n + 1) = estimate of tap-weight vector at time n + 1 | |
| Computation: | n = 0, 1, 2, … | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-K.; Lee, S.; Back, J.; Shin, T. A New Method for Active Cancellation of Engine Order Noise in a Passenger Car. Appl. Sci. 2018, 8, 1394. https://doi.org/10.3390/app8081394
Lee S-K, Lee S, Back J, Shin T. A New Method for Active Cancellation of Engine Order Noise in a Passenger Car. Applied Sciences. 2018; 8(8):1394. https://doi.org/10.3390/app8081394
Chicago/Turabian StyleLee, Sang-Kwon, Seungmin Lee, Jiseon Back, and Taejin Shin. 2018. "A New Method for Active Cancellation of Engine Order Noise in a Passenger Car" Applied Sciences 8, no. 8: 1394. https://doi.org/10.3390/app8081394





