Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids
Abstract
1. Introduction
2. Theoretical Behavior of Distributed versus Concentrated Volt/var Local Control Strategy
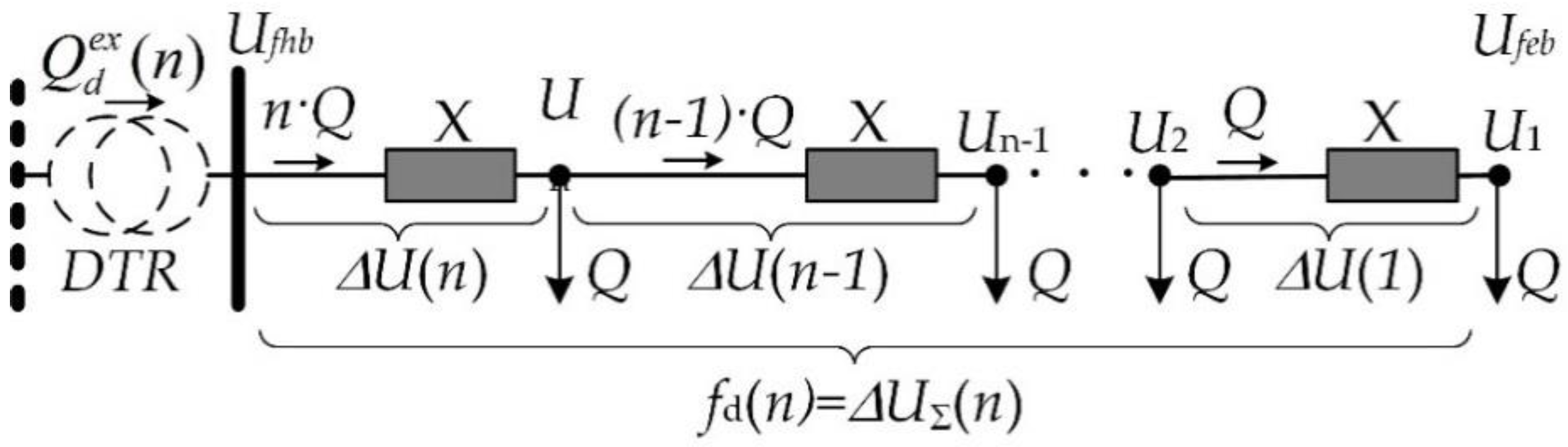
2.1. Definitions
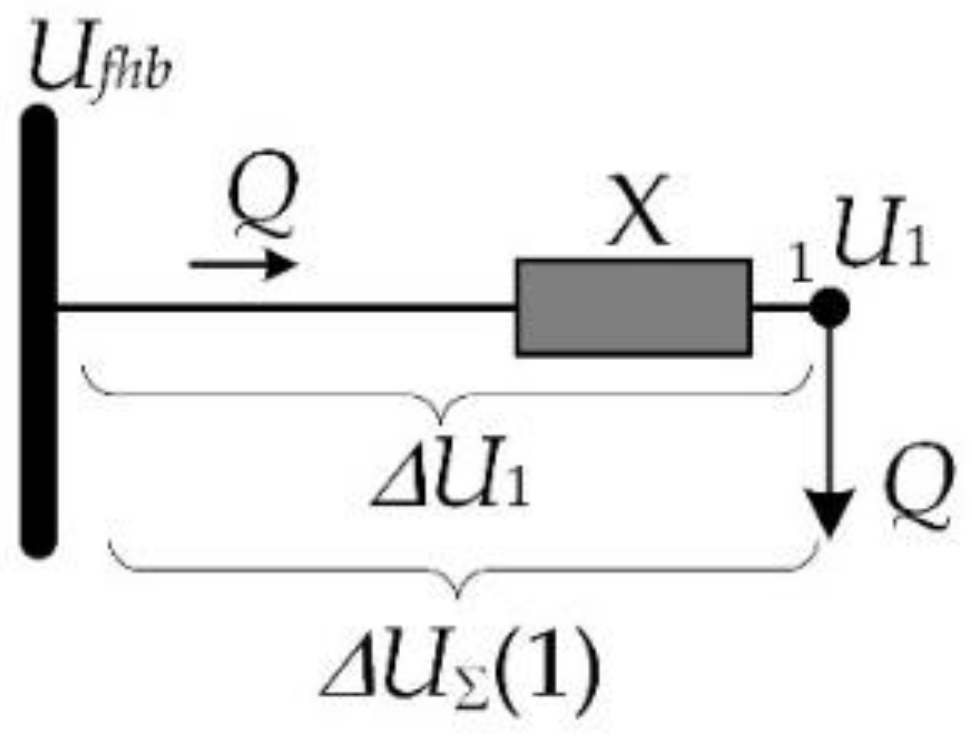
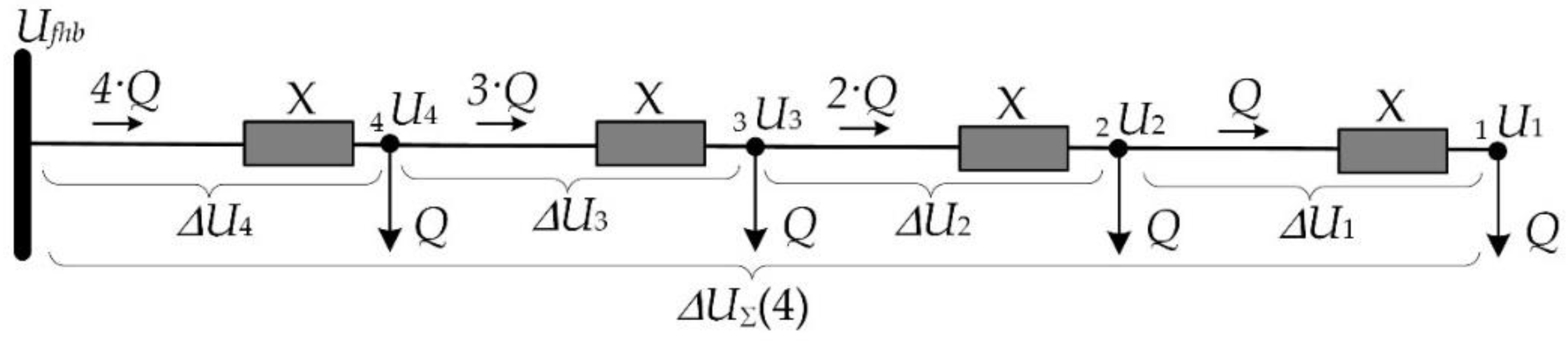
2.2. Theoretical Background
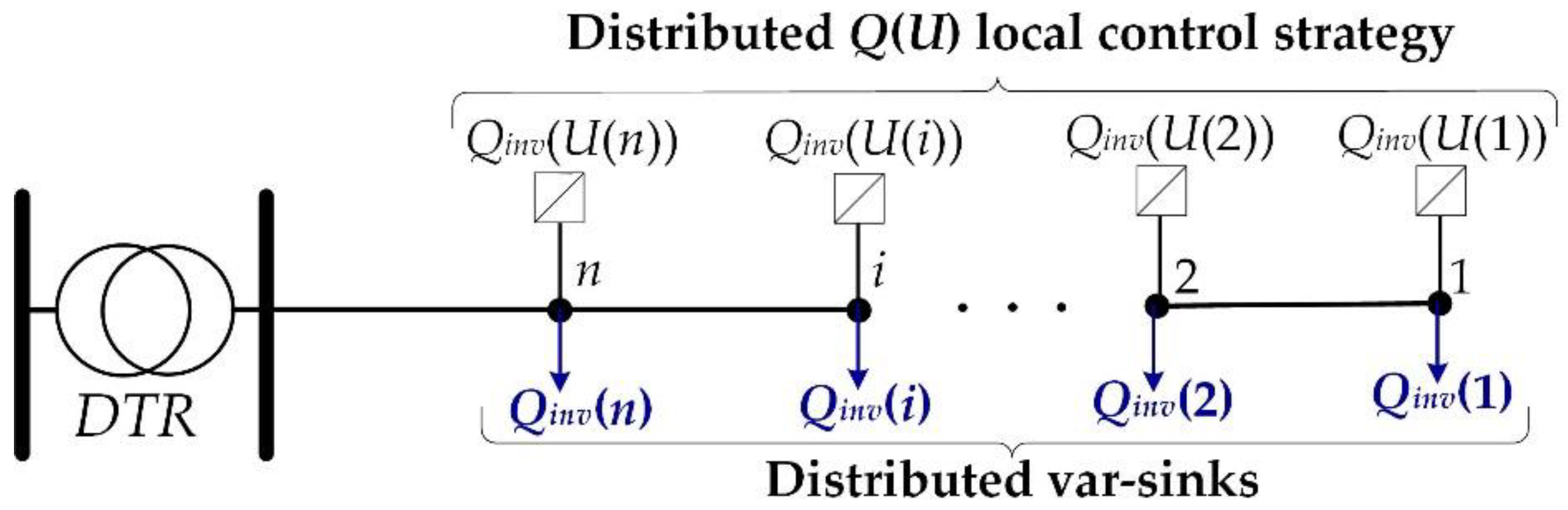
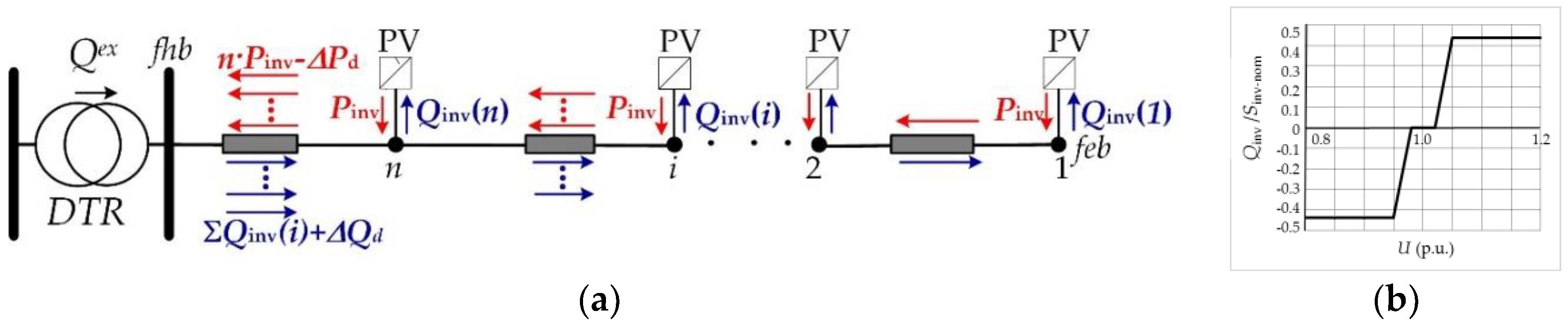
2.3. Distributed Var-Sinks
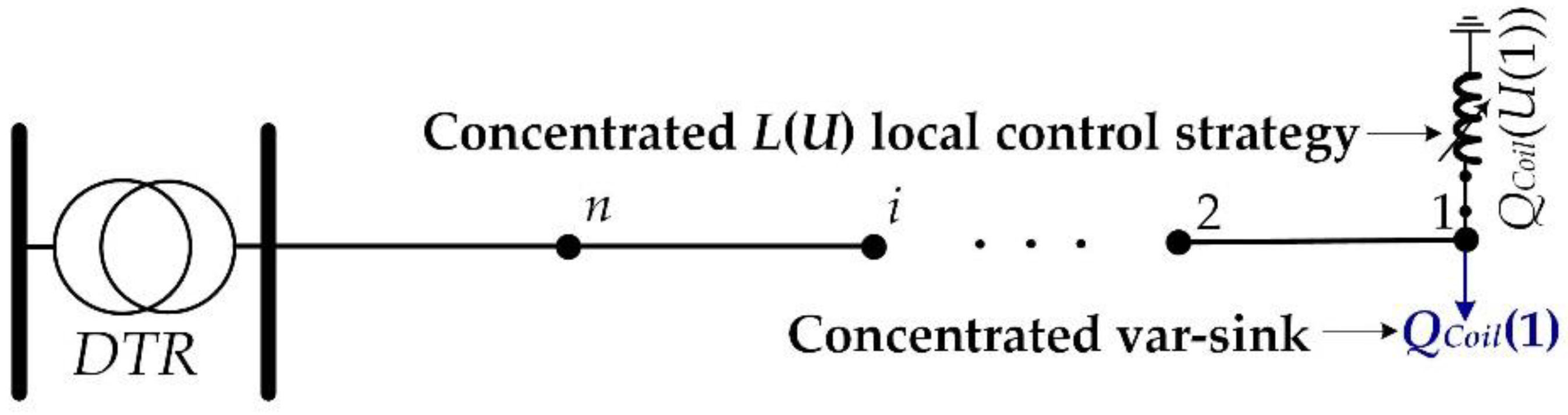
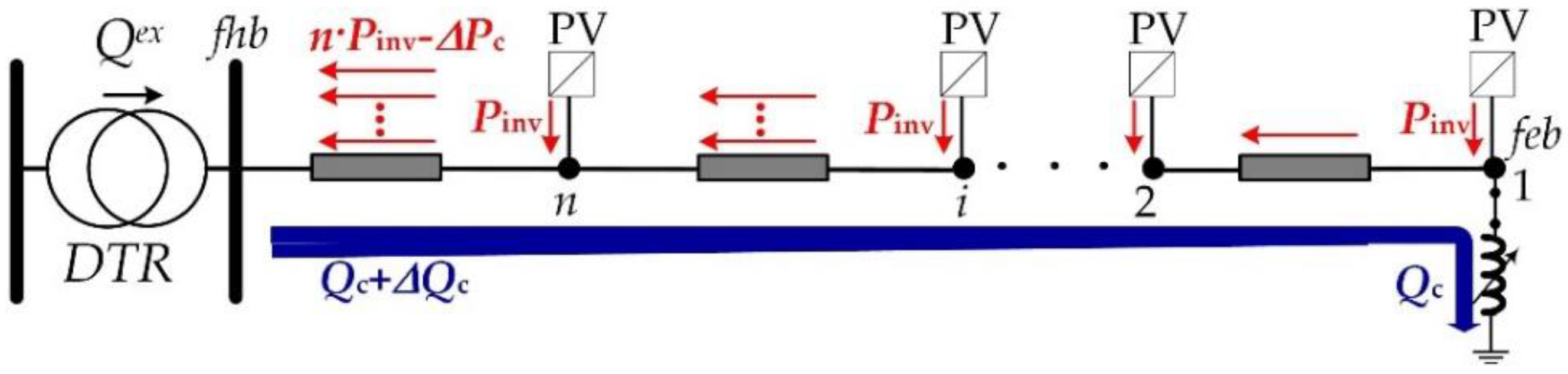
2.4. Concentrated Var-Sink
2.5. Distributed versus Concentrated Var-Sinks
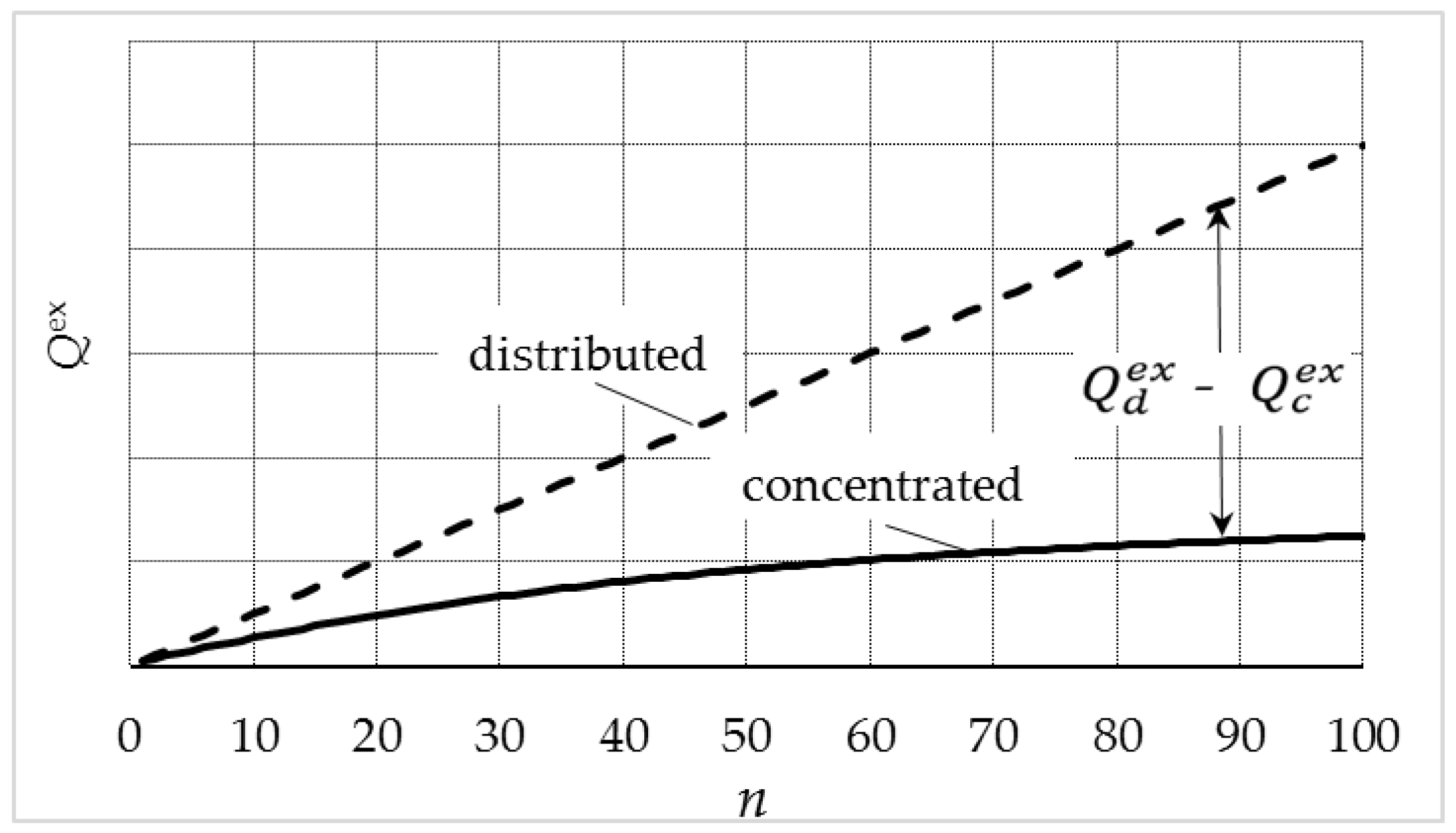
- the reactive power exchange, Qex,
- the voltage drop behavior, and
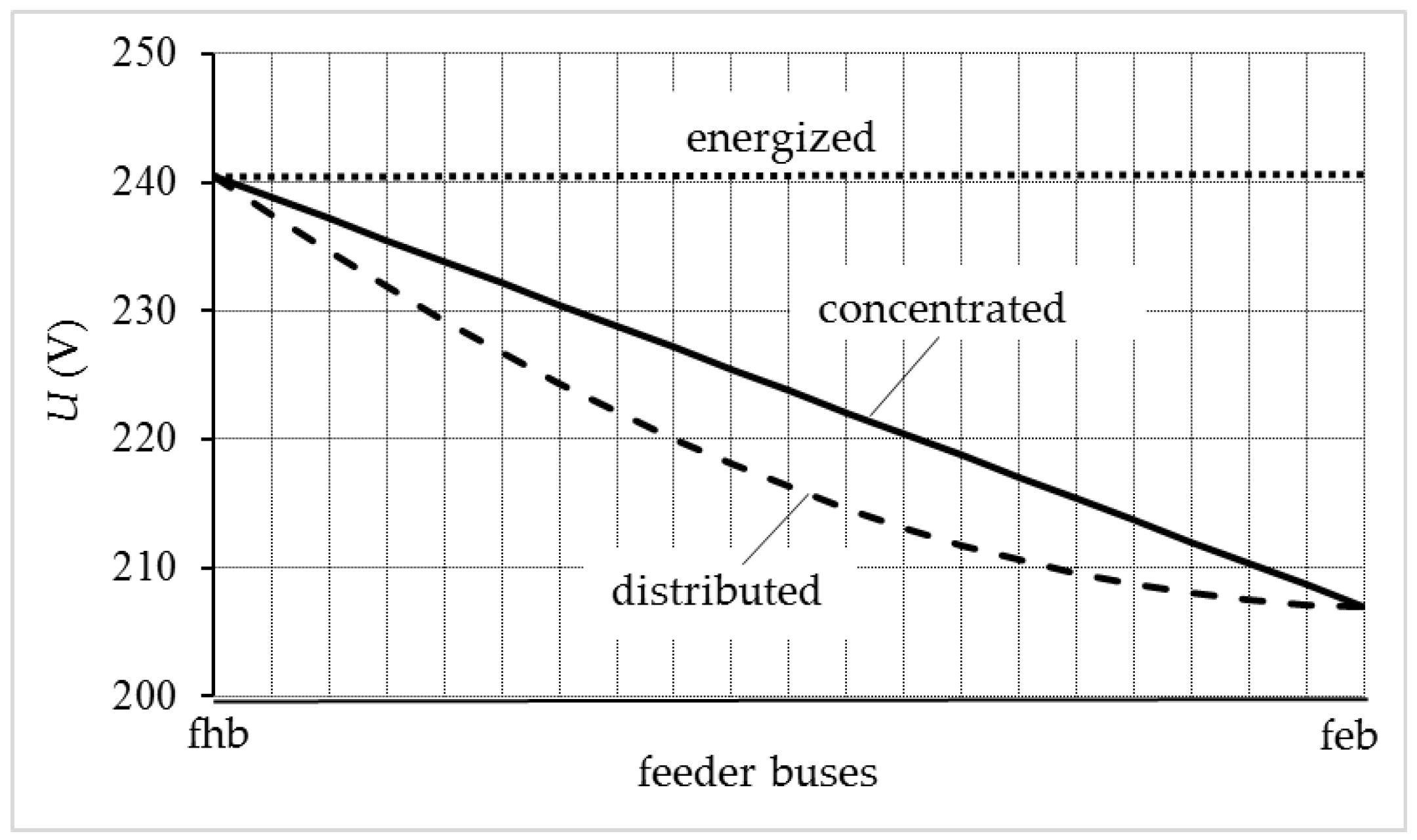
- the voltage profile.
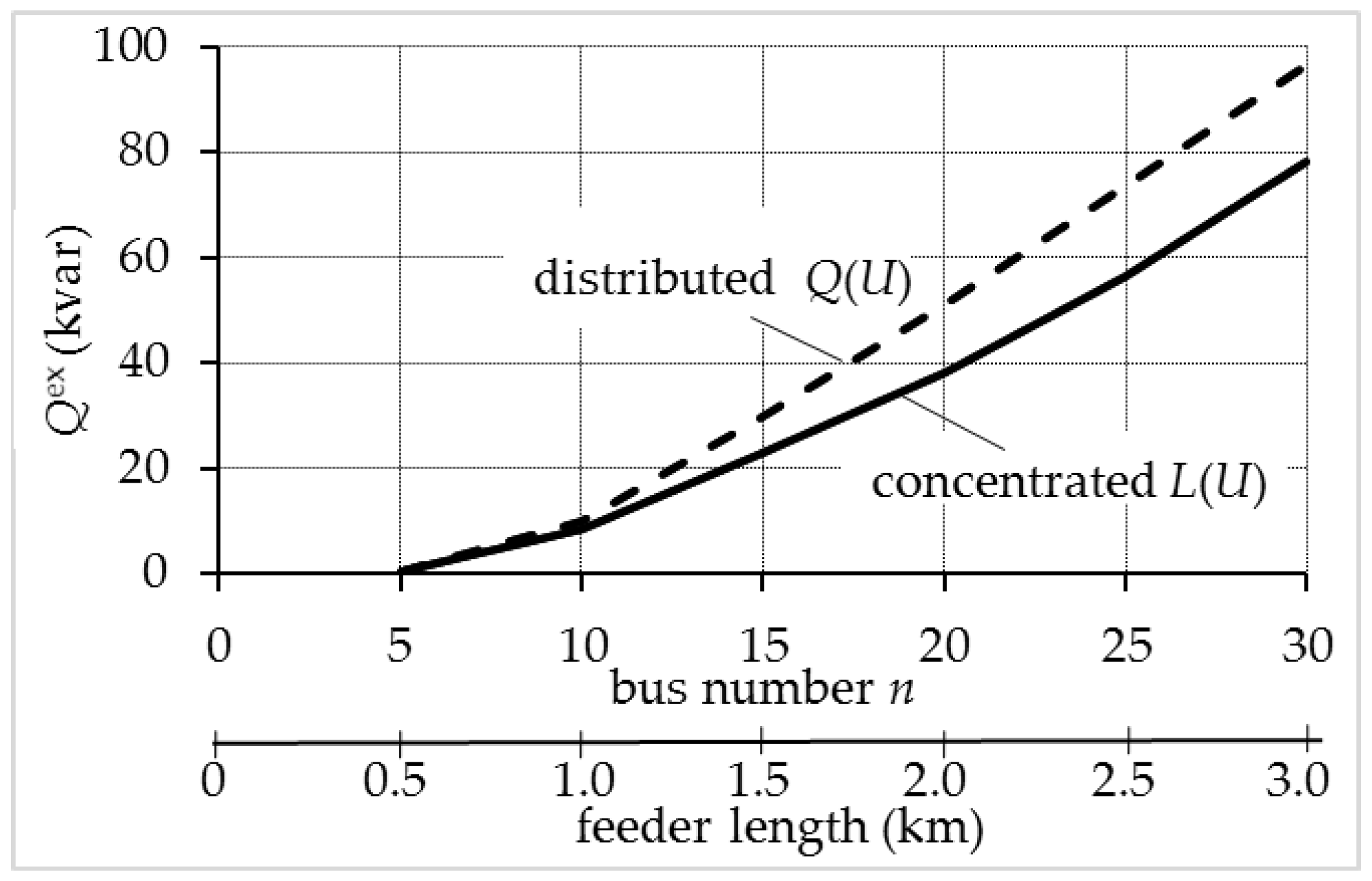
2.5.1. Reactive Power Exchange
2.5.2. Voltage Drop Behavior
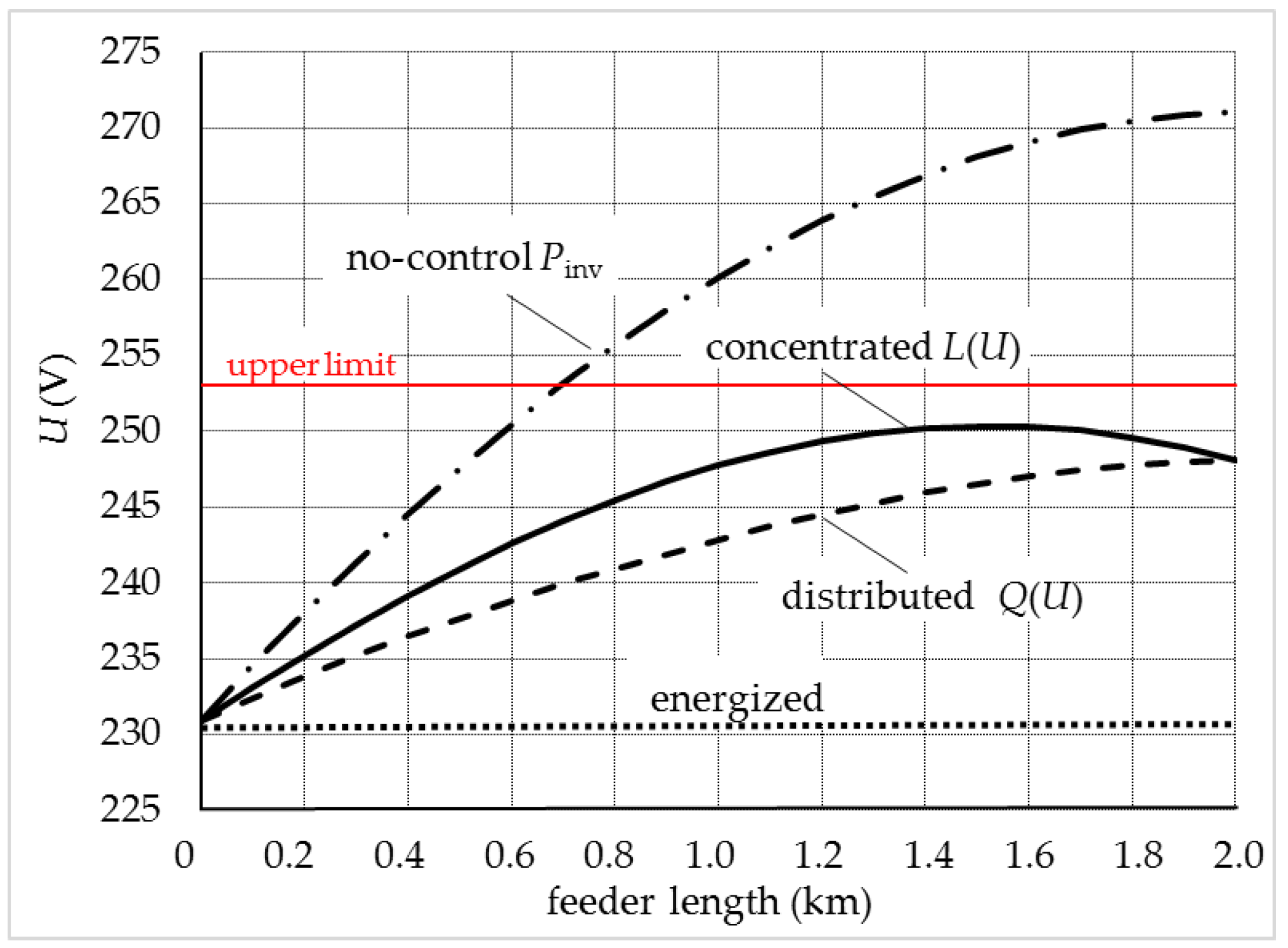
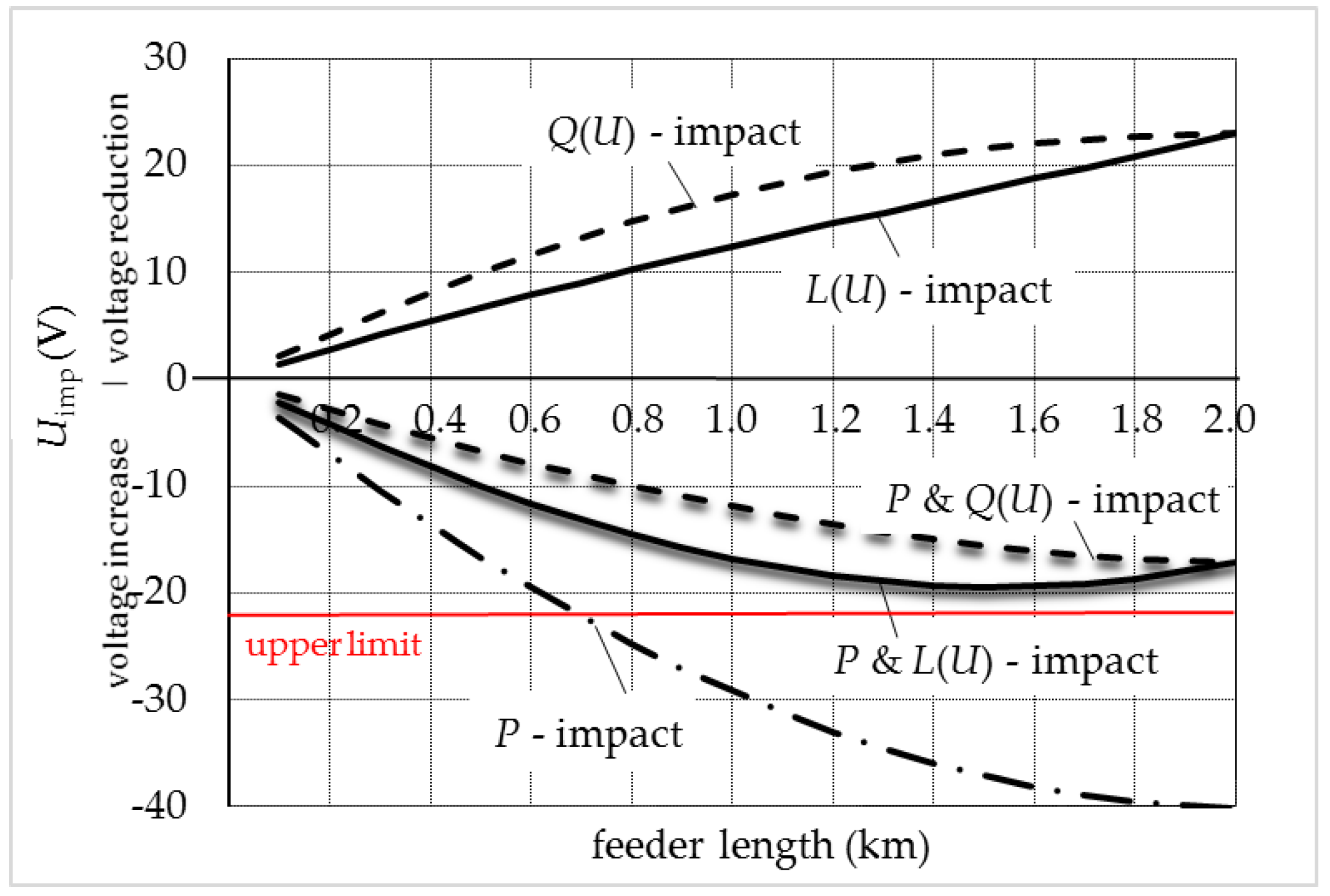
2.5.3. Voltage Profile
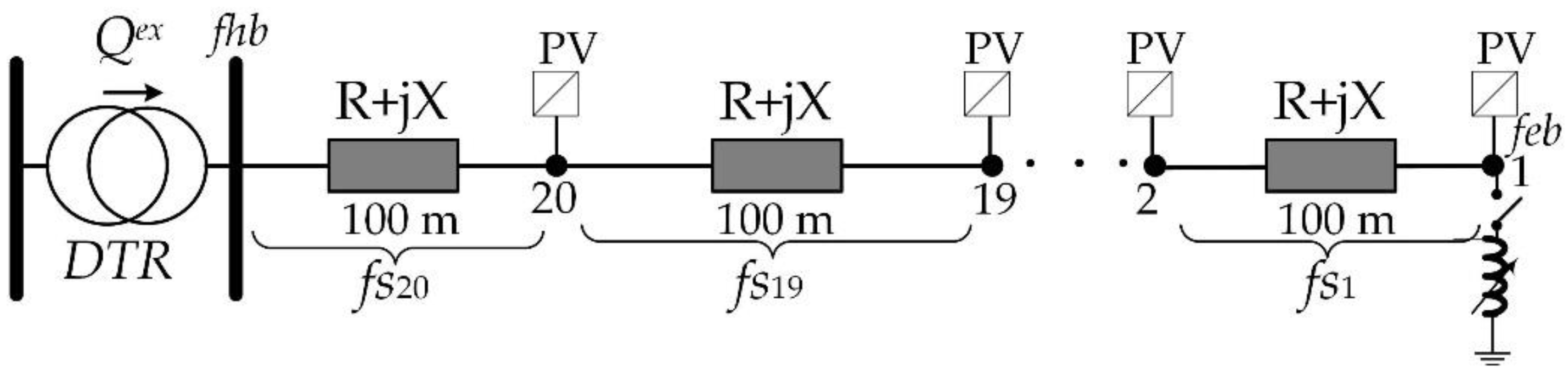
3. Comparison of Different Control Strategies in a Test Feeder
4. Behavior of Distributed versus Concentrated Local Control Strategy in Different Real Grids
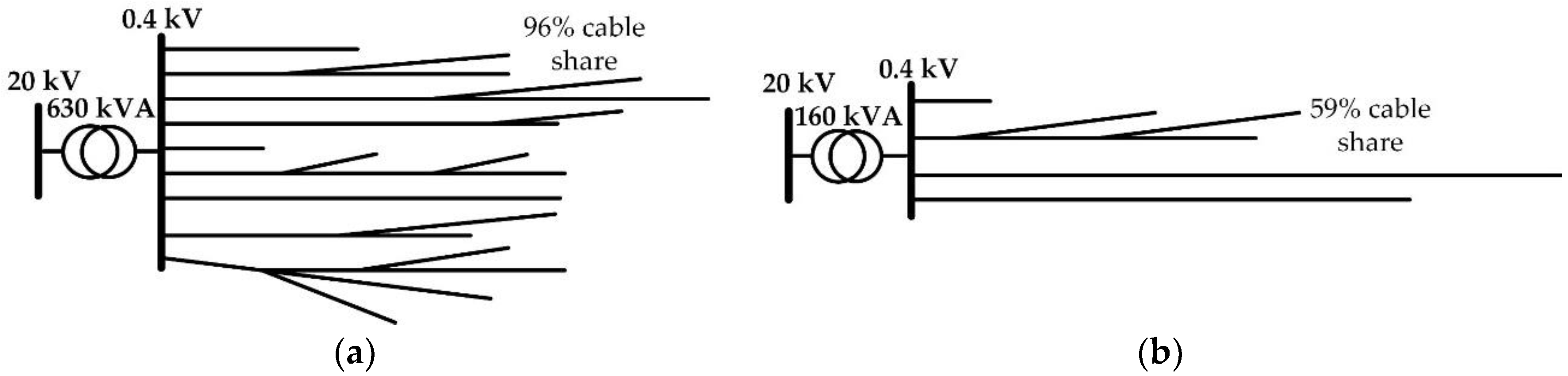
4.1. Description of the Real Grids
4.2. Local Control Strategies
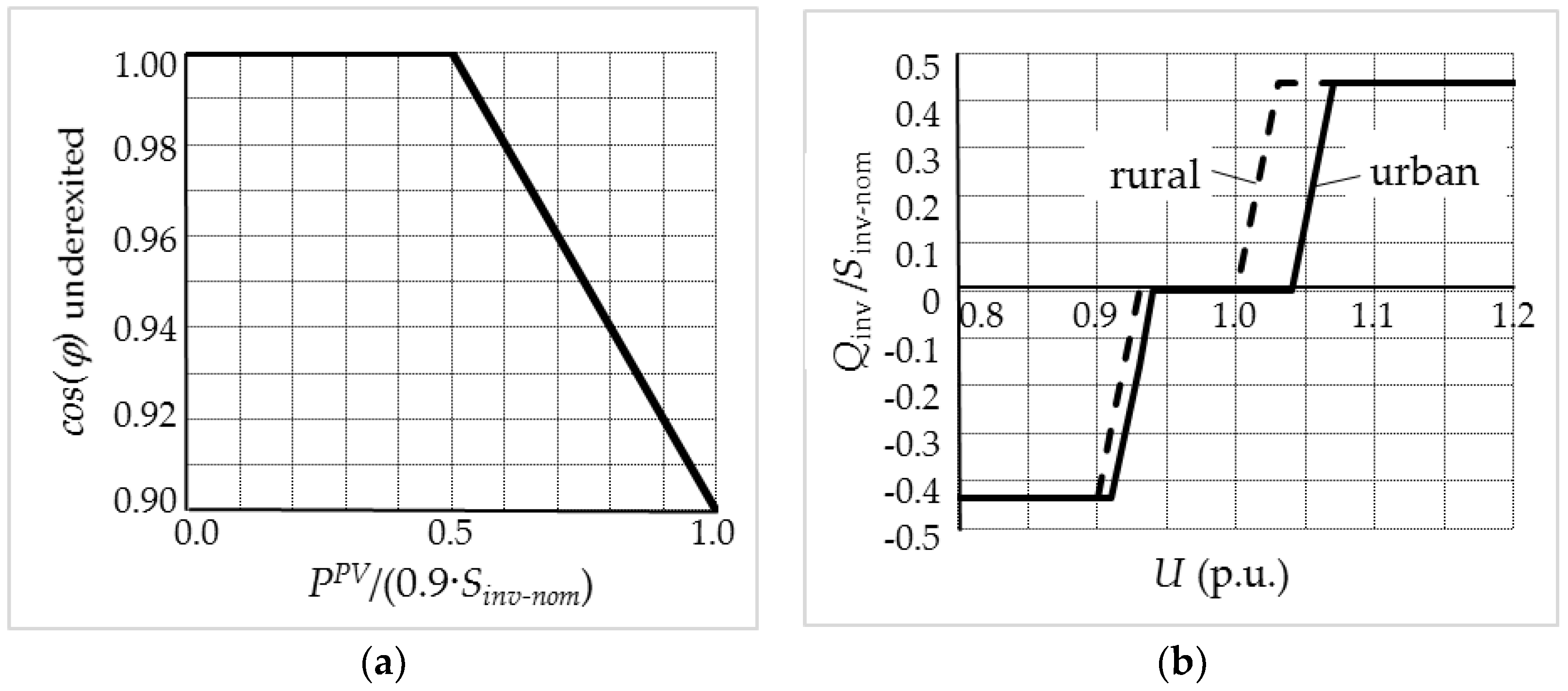
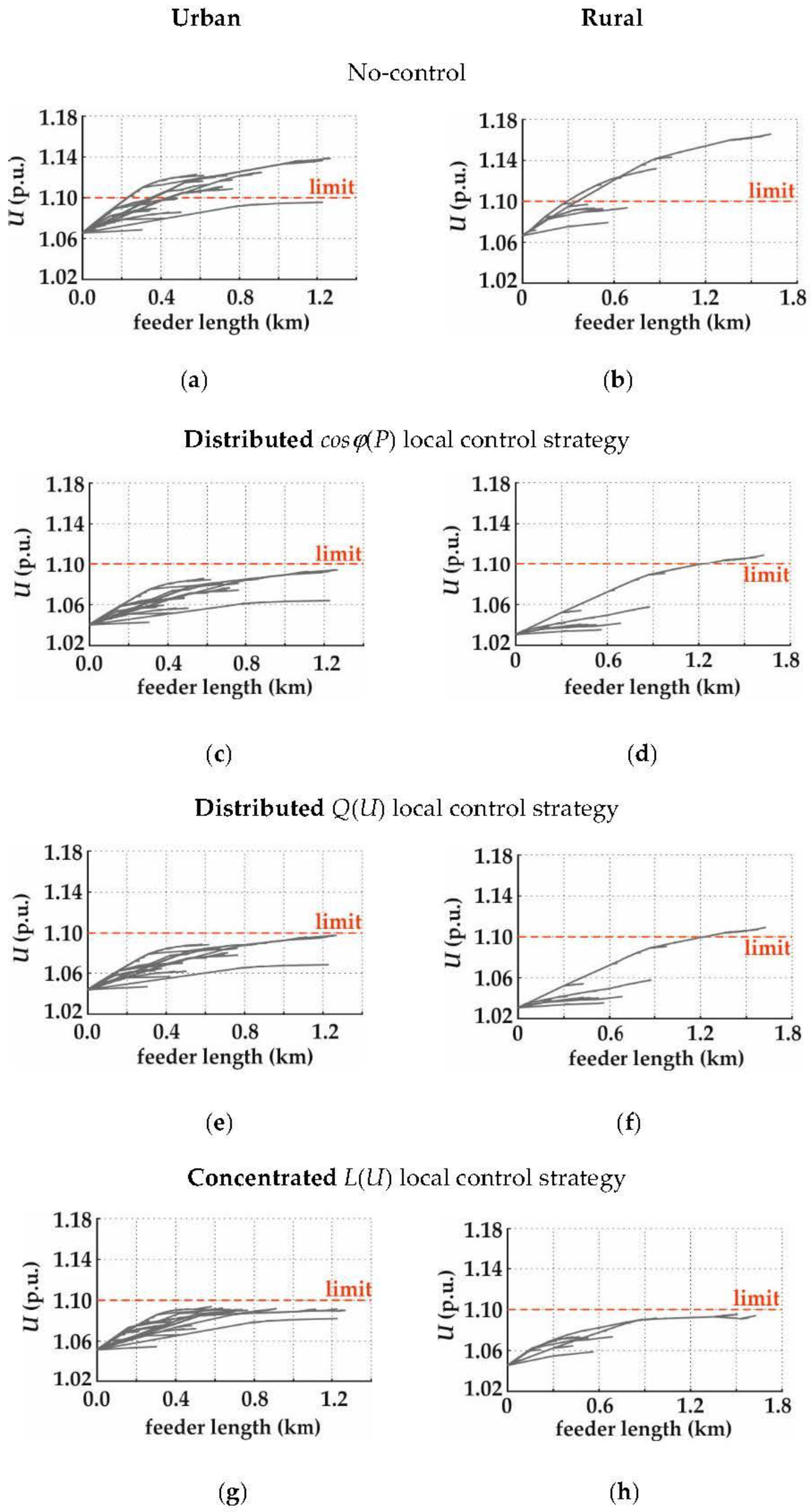
4.2.1. Distributed
- cosφ(P)—it is assumed that all of the prosumers have the same weather conditions. That means that all of the prosumers inject the maximal real power with a cos(φ) = 0.9 as given from the inverter characteristic shown in Figure 19a.
4.2.2. Concentrated
4.3. Behavior of Concentrated versus Distributed Control Strategy
5. Impact of the Control Strategies in the Reciprocal Behavior between MVG and LVGs
5.1. Combined Medium and Low-Voltage Grid Modeling
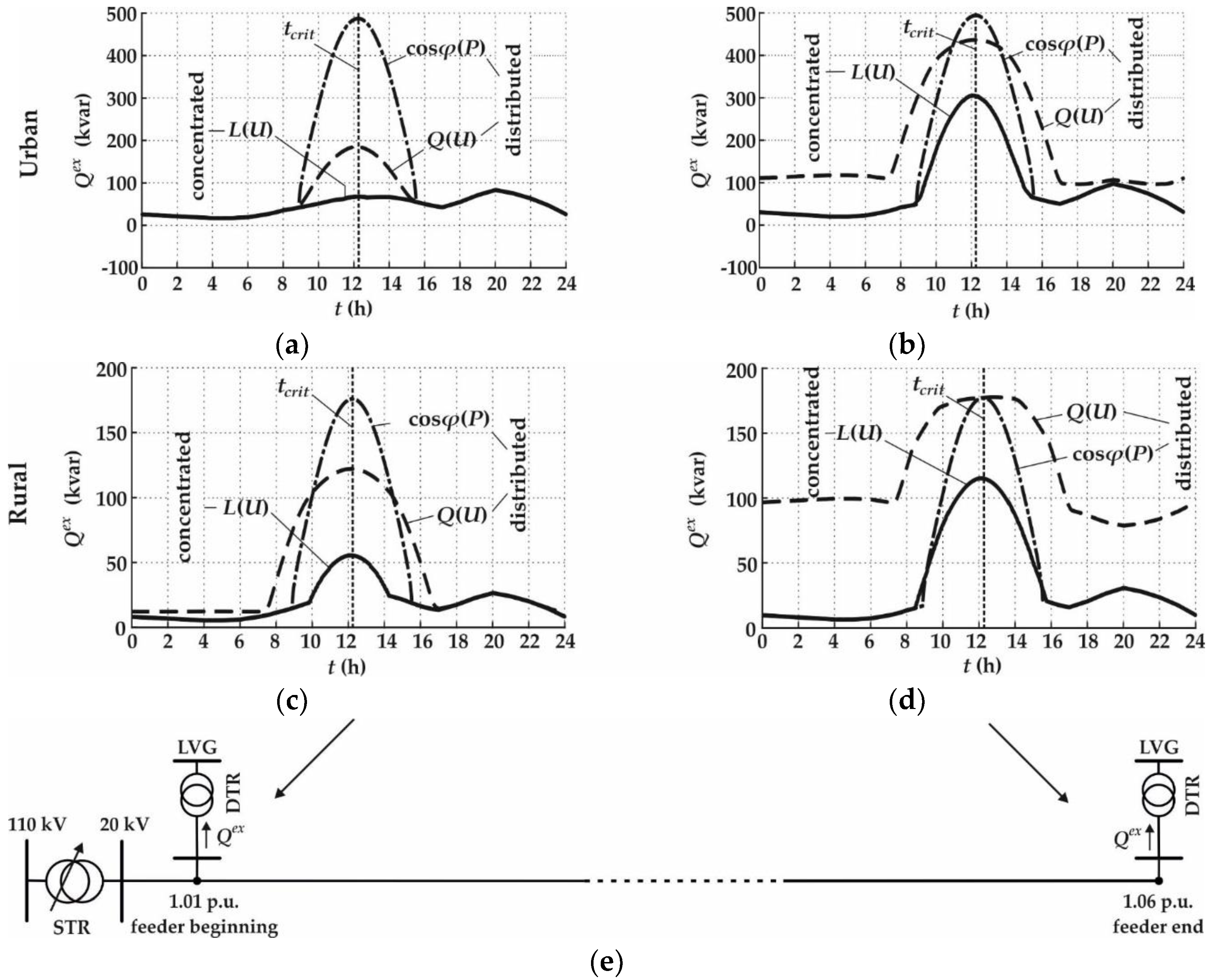
5.2. Impact of Different Control Strategies on the Behavior of MVG
5.2.1. Influence of the DTR Connection Point on Qex
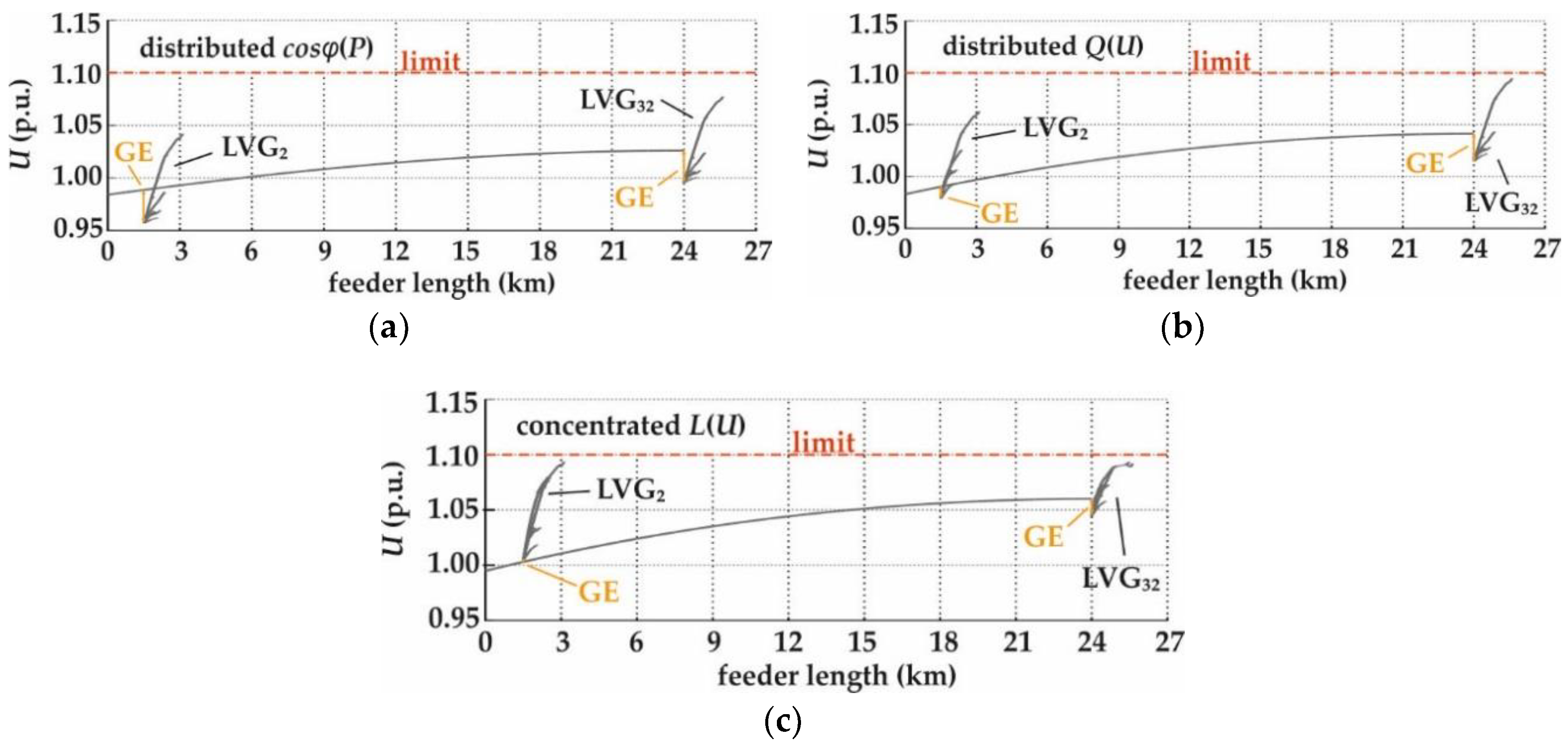
5.2.2. Influence of the Concentrated versus Distributed Control Strategy on the Voltage Profile in MVG
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


References
- Witzmann, R.; Esslinger, P.; Grass, N.; Girstl, S.; Keck, R.; Adelmann, A. Improving power quality and capacity in low voltage grids with decentral power generation using intelligent inverters. In Proceedings of the IETG Congress, Würzburg, Germany, 8–9 November 2011. [Google Scholar]
- Bertani, A.; Borghetti, A.; Bossi, C.; de Biase, L.; Lamquet, O.; Massucco, S.; Morini, A.; Nucci, C.A.; Paolone, M.; Quaia, E.; et al. Management of low voltage grids with high penetration of distributed generation: Concepts, implementations and experiments. In Proceedings of the CIGRE Session, Paris, France, 27 August–1 September 2006; pp. 1–13. [Google Scholar]
- Taljan, G.; Krasnitzer, M.; Strempfl, F.; Jarz, A. Spannungsregelung im 30 kV Netz UW Judenburg/West Lösungsansätze mit Smart Grids. In Proceedings of the Symposium Energieinnovation, Graz, Austria, 15–17 February 2012. [Google Scholar]
- Procházka, K.; Vaculík, P.; Kysnar, F.; Novotny, J.; Mezera, D. Voltage quality and reactive power flow solution in distribution networks with a high share of renewable energy sources. In Proceedings of the CIRED, Stockholm, Sweden, 10–13 June 2013; pp. 1–5. [Google Scholar]
- Elbs, C. Netzeinsparungsmöglichkeiten und Erfahrungen einer realen Q(U)-Einführung bei PV Wechselrichtern im Bundesland. In Proceedings of the Smart Grid Week, Graz, Austria, 19–23 May 2014. [Google Scholar]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for control of reactive power by distributed photovoltaic generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- Malekpour, A.R.; Pahwa, A. Reactive Power and Voltage Control in Distribution Systems with Photovoltaic Generation; North American Power Symposium (NAPS): Champaign, IL, USA, 2012; pp. 1–6. [Google Scholar]
- Bollen, M.H.J.; Sannino, A. Voltage control with inverter-based distributed generation. IEEE Trans. Power Deliv. 2005, 20, 519–520. [Google Scholar] [CrossRef]
- Bolognani, S.; Zampieri, S. A distributed control strategy for reactive power compensation in smart Microgrids. IEEE Trans. Autom. Control 2013, 58, 2818–2833. [Google Scholar] [CrossRef]
- Caldon, R.; Coppo, M.; Turri, R. Distributed voltage control strategy for LV networks with inverter-interfaced generators. Electr. Power Syst. Res. 2014, 107, 85–92. [Google Scholar] [CrossRef]
- Neal, R. The of AMI meters and solar PV inverters in advanced Volt/var control system on a distributed circuit. In Proceedings of the IEEE PES Transmission and Distribution Conference and Exposition, New Orleans, LA, USA, 19–22 April 2010; pp. 1–4. [Google Scholar]
- Guideline for Generating Plants’ Connection to and Parallel Operation with the Medium-Voltage Network. Available online: http://electrical-engineering-portal.com/res2/Generating-Plants-Connected-to-the-Medium-Voltage-Network.pdf (accessed on 23 July 2018).
- IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003); IEEE: Piscataway, NJ, USA, 2018; pp. 1–138. [CrossRef]
- Demirok, E.; González, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovol. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Smith, J.W.; Sunderman, W.; Dugan, R.; Seal, B. Smart inverter volt/var control functions for high penetration of PV on distribution systems. In Proceedings of the IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6. [Google Scholar]
- Zhang, F.; Guo, X.; Chang, X.; Fan, G.; Chen, L.; Wang, Q.; Tang, Y.; Dai, J. The reactive power voltage control strategy of PV systems in low-voltage string lines. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Winter, C.; Schwalbe, R.; Heidl, M.; Prüggler, W. Harnessing PV inverter controls for increased hosting capacities of smart low voltage grids: Recent results from Austrian research and demonstration projects. In Proceedings of the 4th International Workshop on Integration of Solar Power into Power Systems, Berlin, Germany, 10–11 November 2014. [Google Scholar]
- Karthikeyan, N.; Pokhrel, B.R.; Pillai, J.R.; Bak-Jensen, B. Coordinated voltage control of distributed PV inverters for voltage regulation in low voltage distribution networks. In Proceedings of the IEEE PES Innovative Smart Grid Technol. Conf. Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Demirok, E.; Gonzalez, P.C.; Fredriksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorecu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovolt. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Jahangiri, P.; Aliprantis, D.C. Distributed volt/var control by PV inverters. IEEE Trans. Power Syst. 2013, 28, 3429–3439. [Google Scholar] [CrossRef]
- Marggraf, O.; Laudahn, S.; Engel, B.; Lindner, M.; Aigner, C.; Witzmann, R.; Schoeneberger, M.; Patzack, S.; Vennegeerts, H.; Cremer, M.; et al. U-Control—Analysis of distributed and automated voltage control in current and future distribution grids. In Proceedings of the International ETG Congress, Bonn, Germany, 28–29 November 2017; pp. 1–6. [Google Scholar]
- Hashemi, S.; Østergaard, J. Methods and strategies for overvoltage prevention in low voltage distribution systems with PV. IET Renew. Power Gener. 2017, 11, 205–214. [Google Scholar] [CrossRef]
- Bletterie, B.; Kadam, S.; Bolgaryn, R.; Zegers, A. Voltage control with PV inverters in low voltage networks—In depth analysis of different concepts and parameterization criteria. IEEE Trans. Power Syst. 2017, 32, 177–185. [Google Scholar] [CrossRef]
- Schultis, D.-L.; Ilo, A.; Schirmer, C. Evaluation of different local var control strategies in low voltage grids. In Proceedings of the CIRED Workshop, Ljubljana, Slovenia, 7–8 June 2018; pp. 1–4. [Google Scholar]
- Schultis, D.-L.; Ilo, A.; Schirmer, C. Overall performance evaluation of reactive power control strategies in low voltage grids with high prosumer share. Electr. Power Syst. Res. 2018. under review. [Google Scholar]
- Ilo, A. Effects of the reactive power injection on the grid-The rise of the Volt/var interaction chain. Smart Grid Renew. Energy 2016, 7, 217–232. [Google Scholar] [CrossRef]





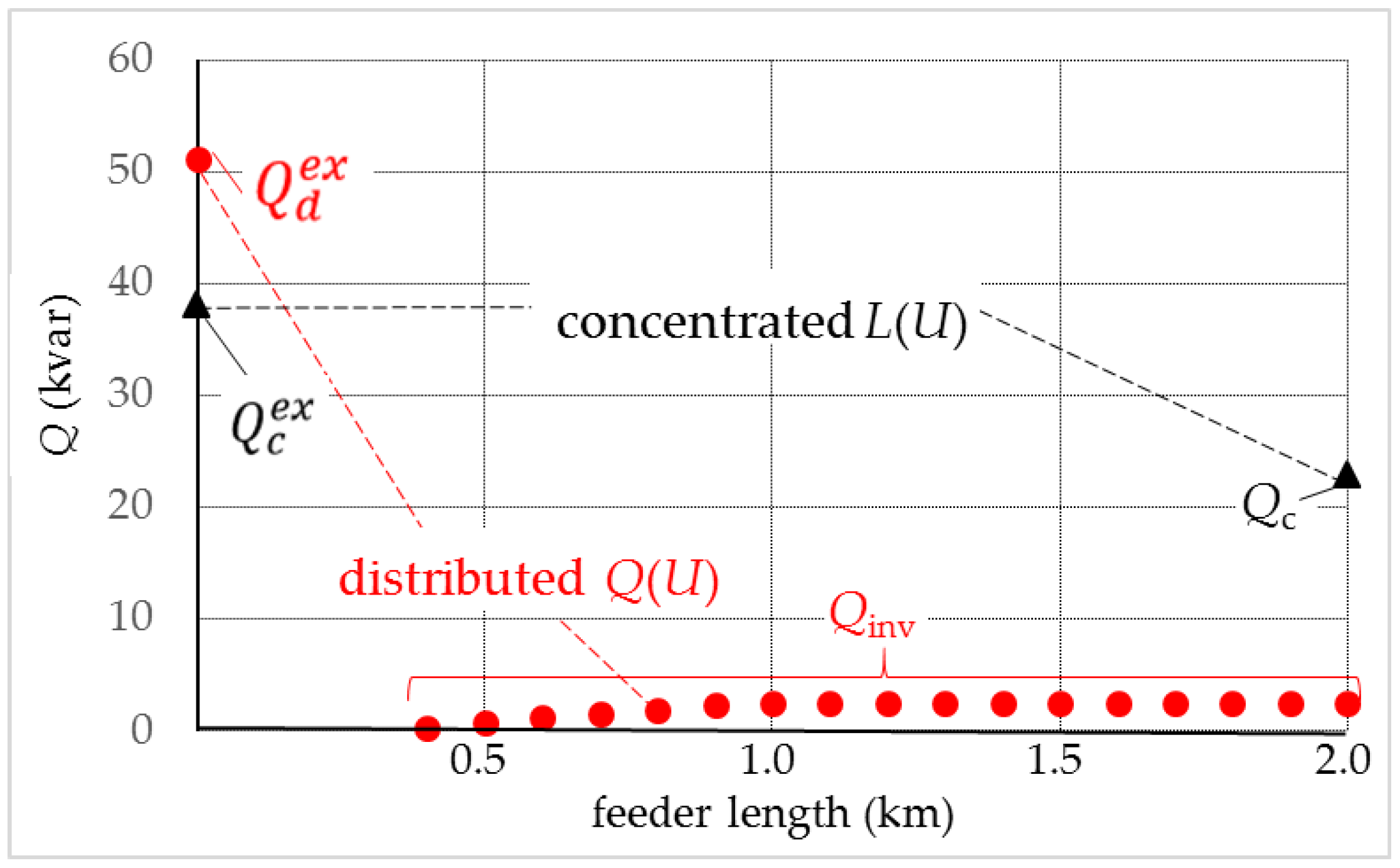


| ΣQinv or Qc (kvar) | Q-Loss (kvar) | Qex (kvar) | |
|---|---|---|---|
| distributed Q(U) | 34.52 | 16.55 | 51.07 |
| concentrated L(U) | 22.77 | 15.29 | 38.06 |
| Distributed | Concentrated | |||||
|---|---|---|---|---|---|---|
| cosφ(P) | Q(U) | L(U) | ||||
| Qex (kvar) | TrL (%) | Qex (kvar) | TrL (%) | Qex (kvar) | TrL (%) | |
| Urban | 491.68 | 130.00 | 436.03 | 125.11 | 305.02 | 114.52 |
| Rural | 176.44 | 181.65 | 176.44 | 181.65 | 115.15 | 158.38 |
| OLTC Position Change | GE (p.u) | ||||
|---|---|---|---|---|---|
| DTR2 | DTR32 | ||||
| distributed | cosφ(P) | 11.493 | 13→15 | −0.0318 | −0.0305 |
| Q(U) | 8.118 | none | −0.0113 | −0.0267 | |
| concentrated | L(U) | 5.452 | none | +0.0014 | −0.0151 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilo, A.; Schultis, D.-L.; Schirmer, C. Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids. Appl. Sci. 2018, 8, 1382. https://doi.org/10.3390/app8081382
Ilo A, Schultis D-L, Schirmer C. Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids. Applied Sciences. 2018; 8(8):1382. https://doi.org/10.3390/app8081382
Chicago/Turabian StyleIlo, Albana, Daniel-Leon Schultis, and Christian Schirmer. 2018. "Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids" Applied Sciences 8, no. 8: 1382. https://doi.org/10.3390/app8081382
APA StyleIlo, A., Schultis, D.-L., & Schirmer, C. (2018). Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids. Applied Sciences, 8(8), 1382. https://doi.org/10.3390/app8081382







