Ultraviolet Transient Absorption Spectrometer with Sub-20-fs Time Resolution
Abstract
1. Introduction
- (i)
- the generation of few-optical-cycle pulses in the UV is difficult, due to the lack of suitable broadband gain media, either linear or nonlinear, in this frequency range;
- (ii)
- standard methods for the temporal characterization of ultrashort pulses, based on nonlinear frequency up-conversion processes such as second harmonic generation (SHG), cannot be applied to the UV, and more complex techniques are required;
- (iii)
- due to the proximity with the onset of electronic transitions, all transparent materials in the UV display a strong dispersion, causing a frequency chirp; this calls for a careful design of the spectroscopic system to minimize the number and the thickness of refractive optical elements and prevent the loss of temporal resolution.
2. UV Pulse Generation and Characterization
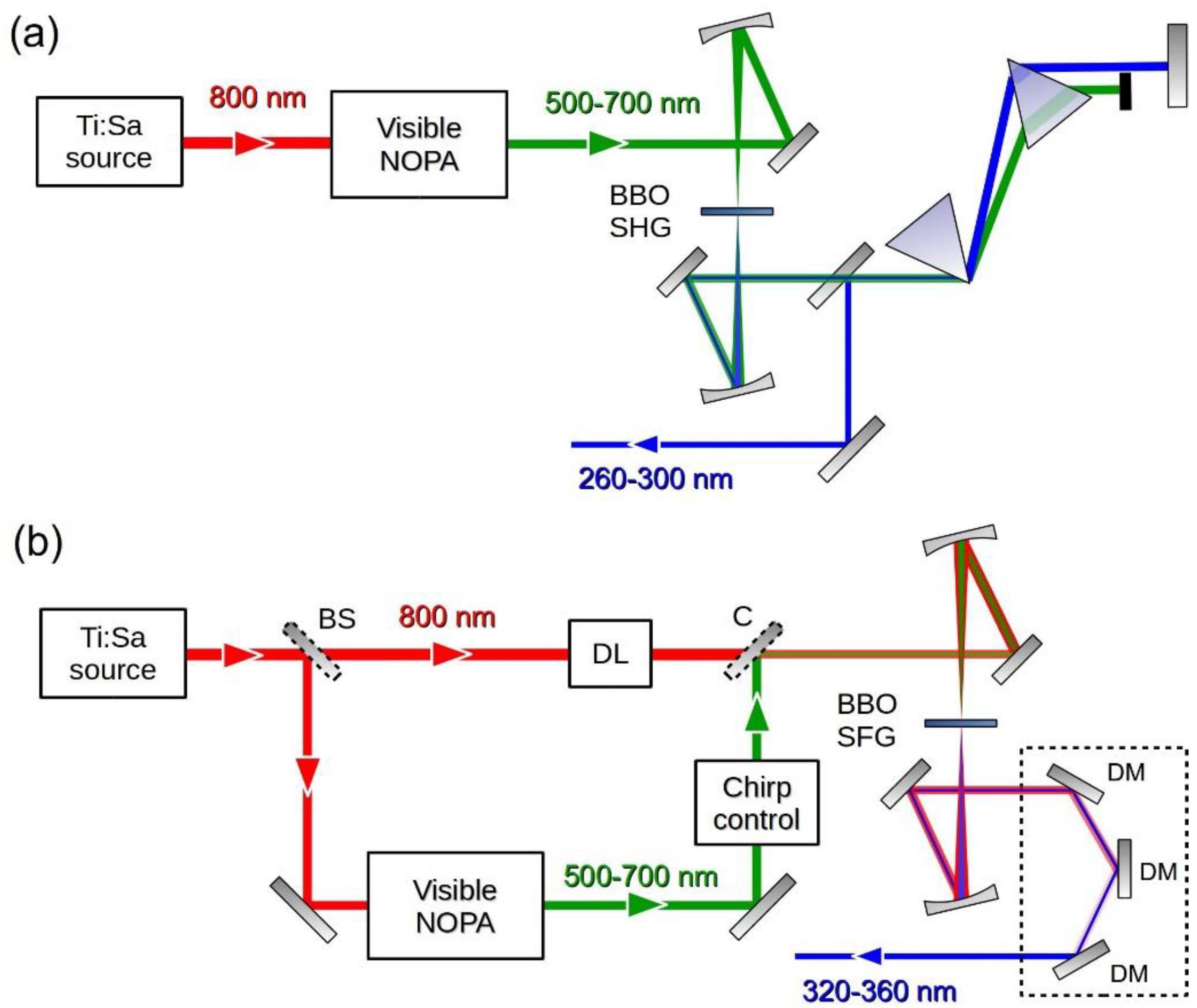
2.1. Pulse Generation
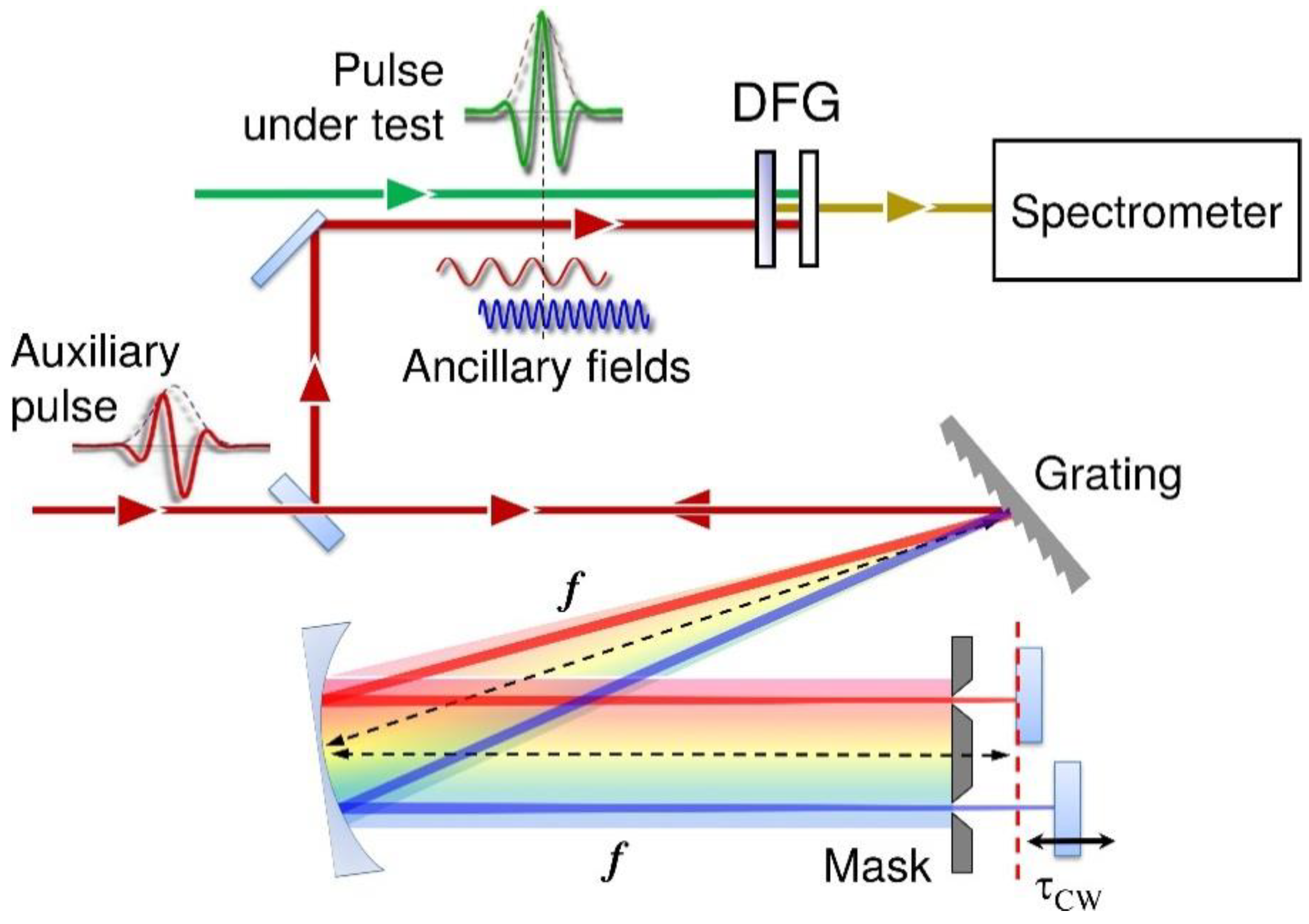
2.2. Pulse Characterization
3. Experimental Setup
3.1. UV Pump Pulse Generation
3.2. UV Pulse Characterization
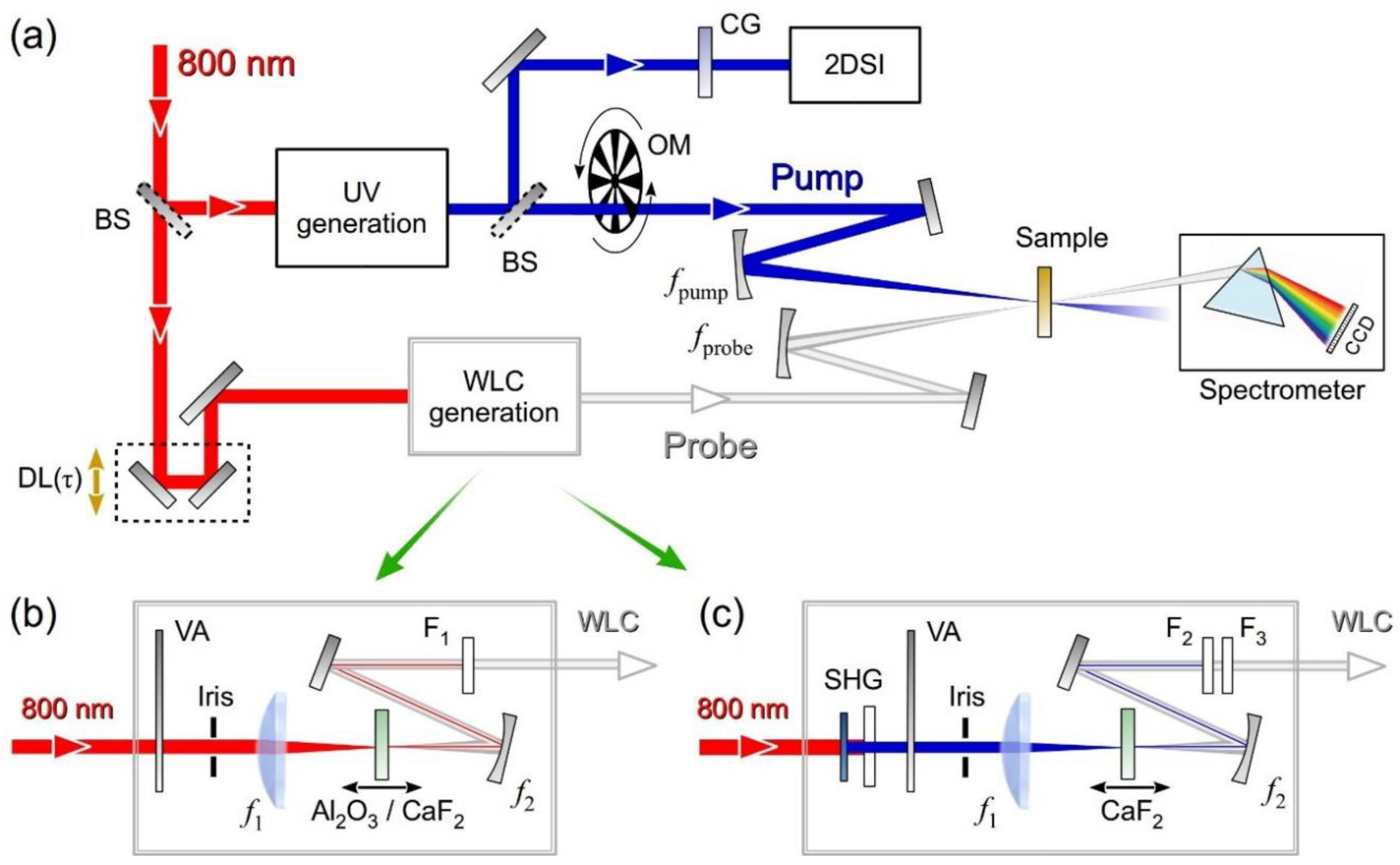
3.3. Broadband TA Spectrometer
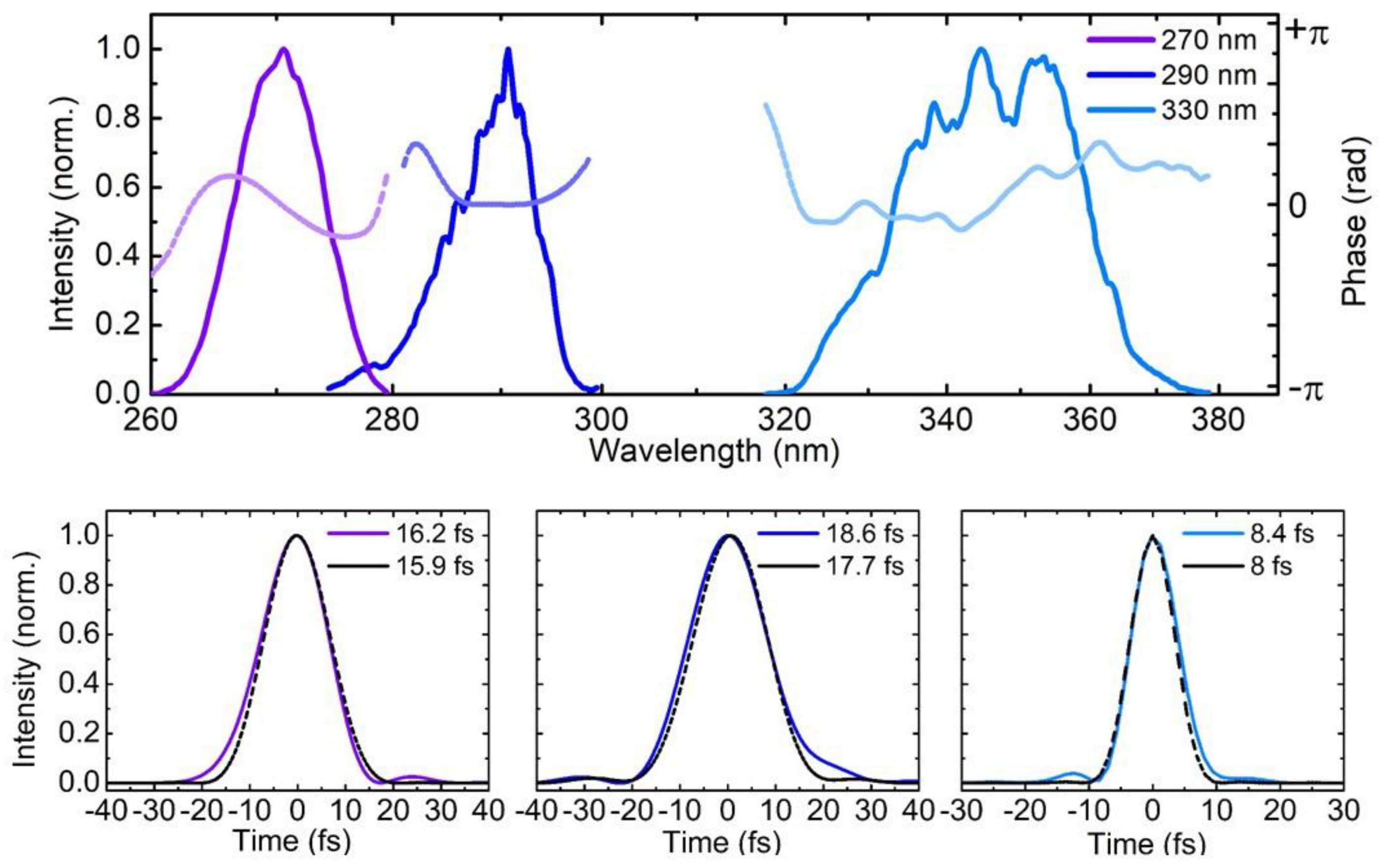
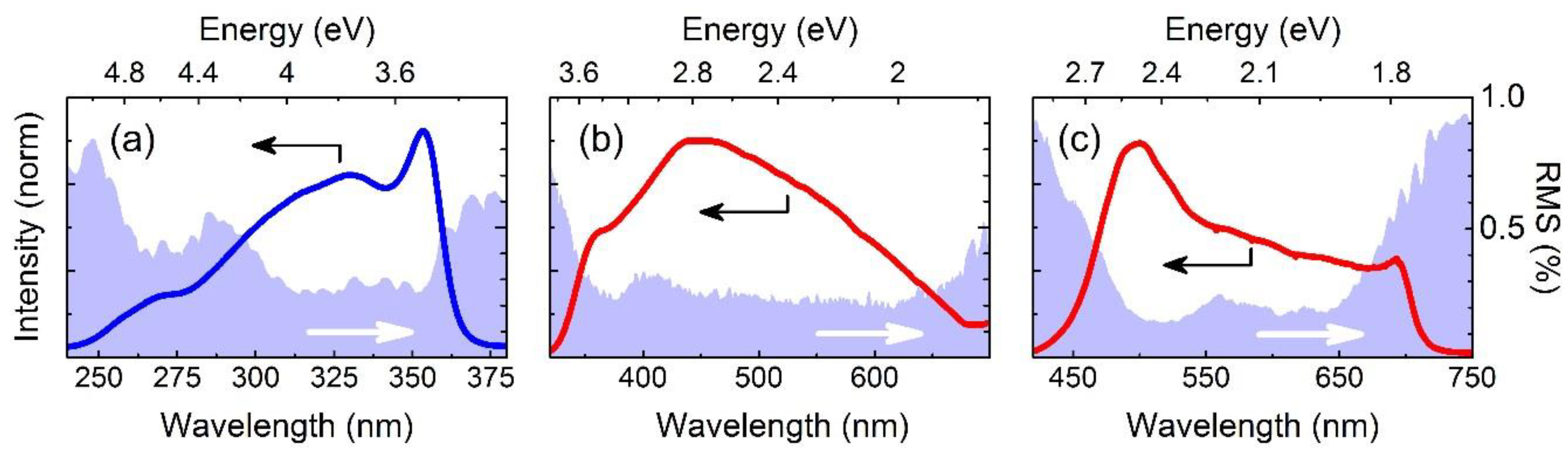
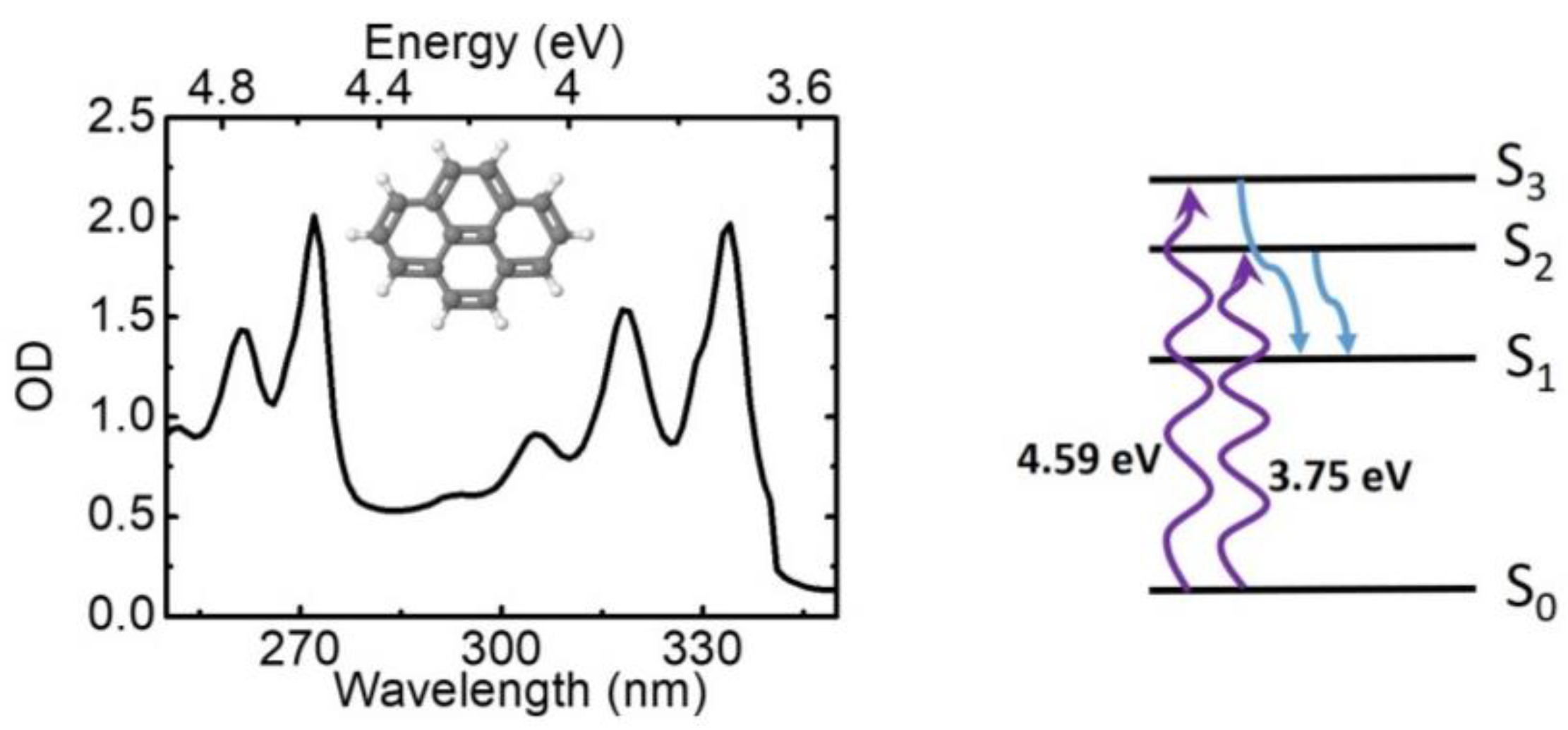
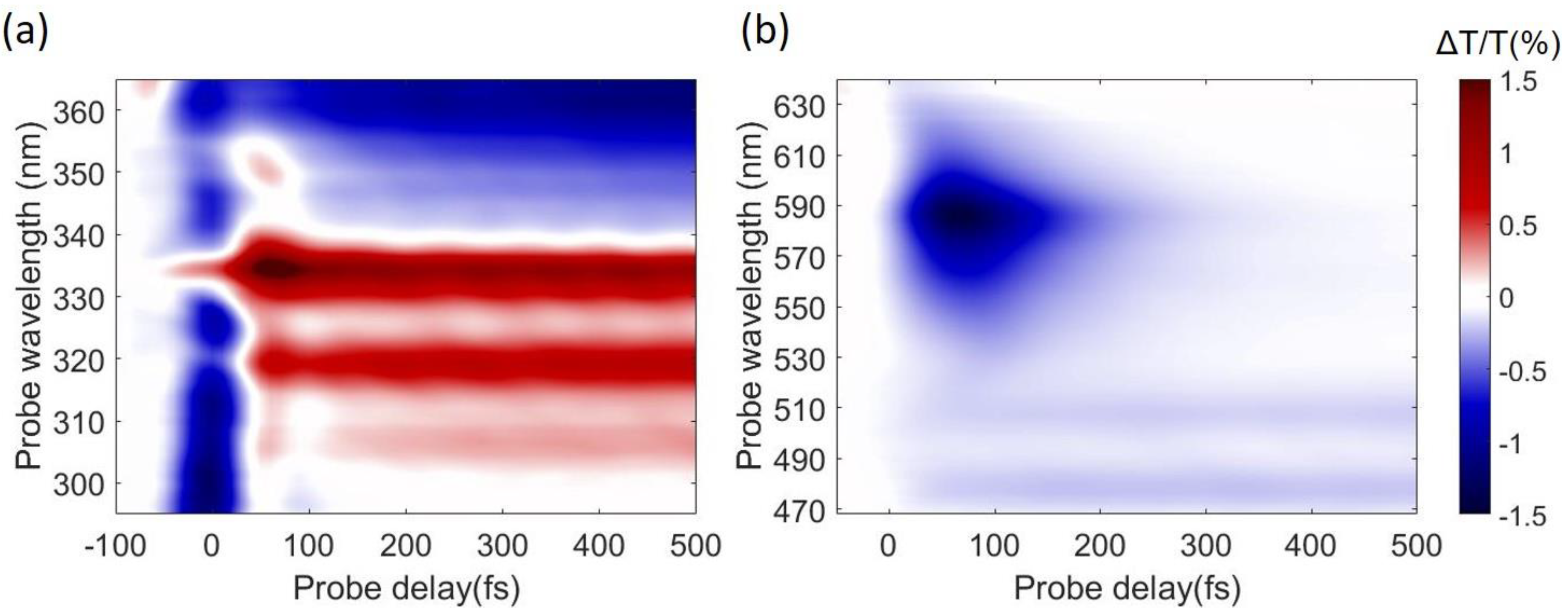
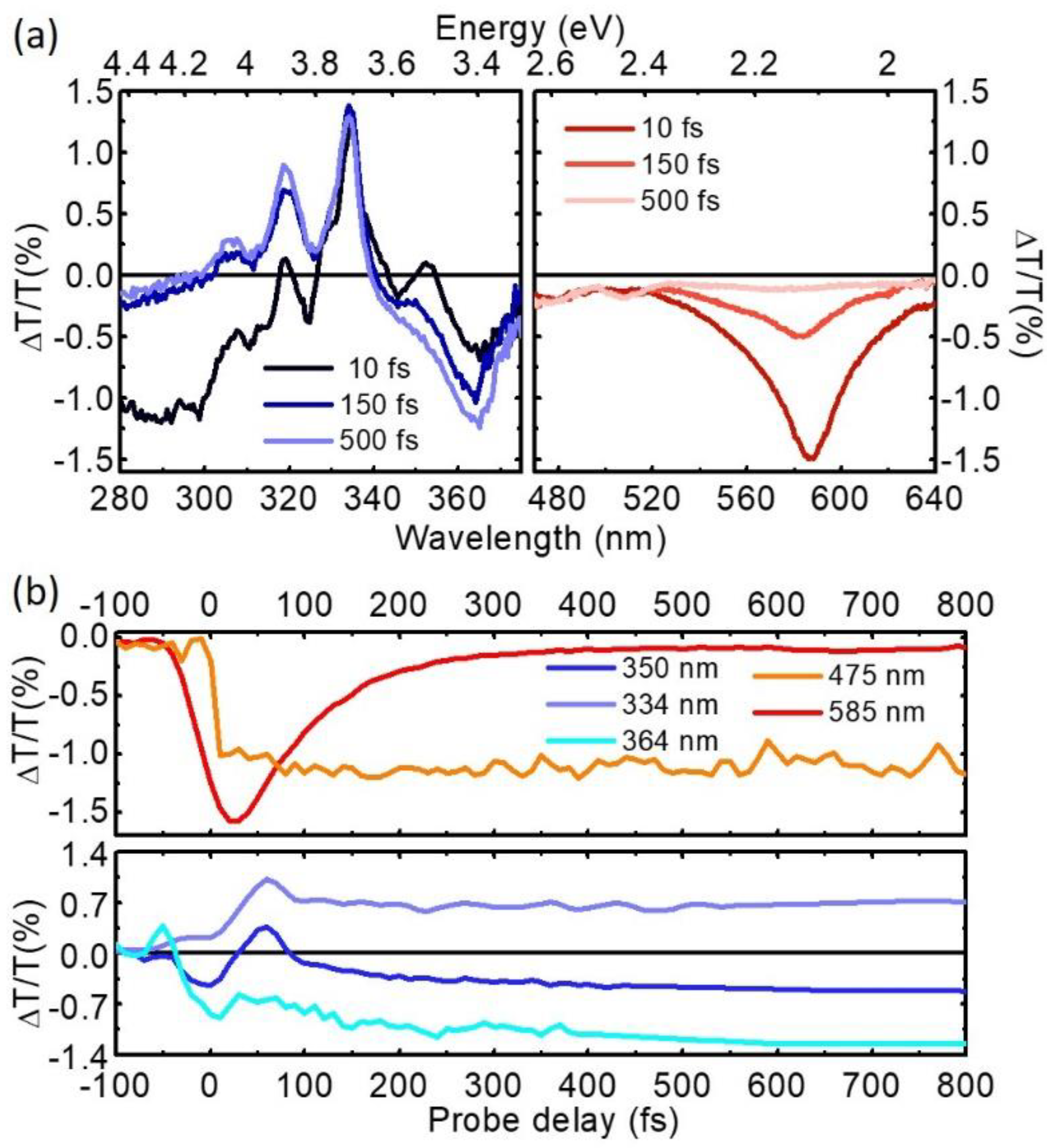
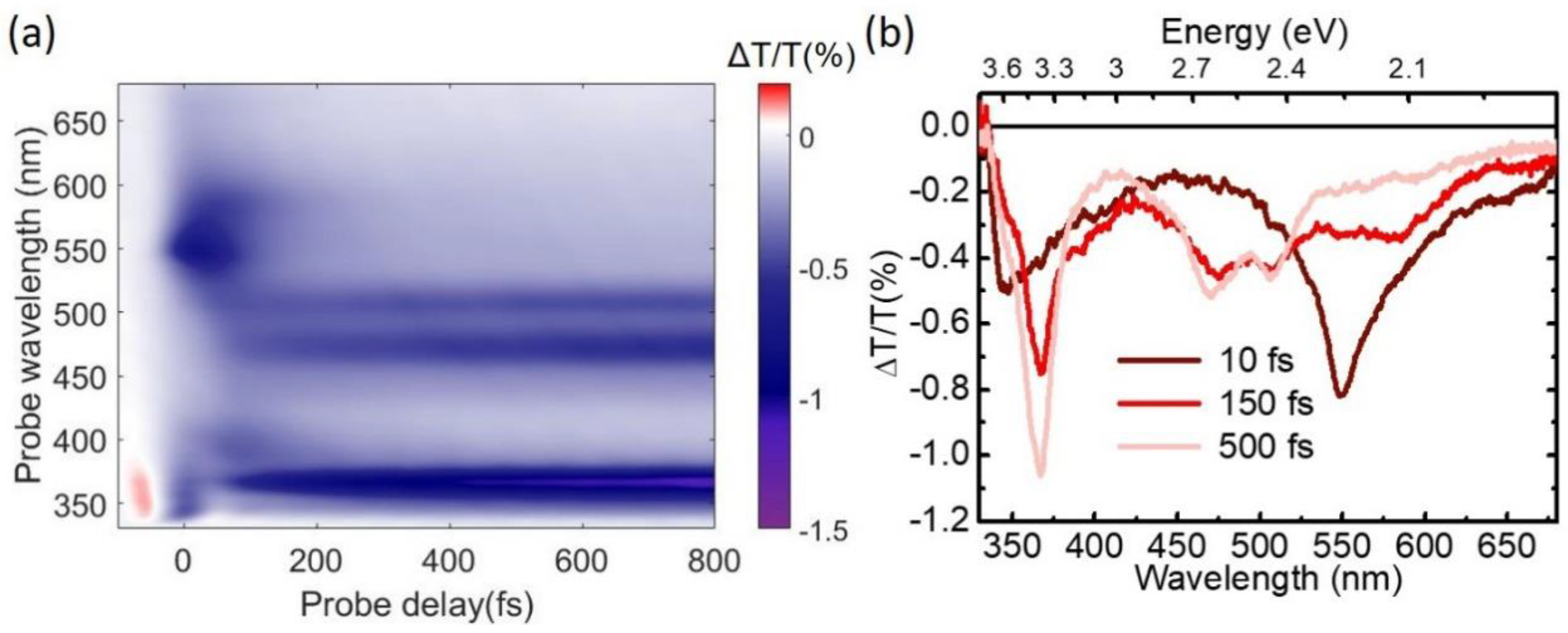
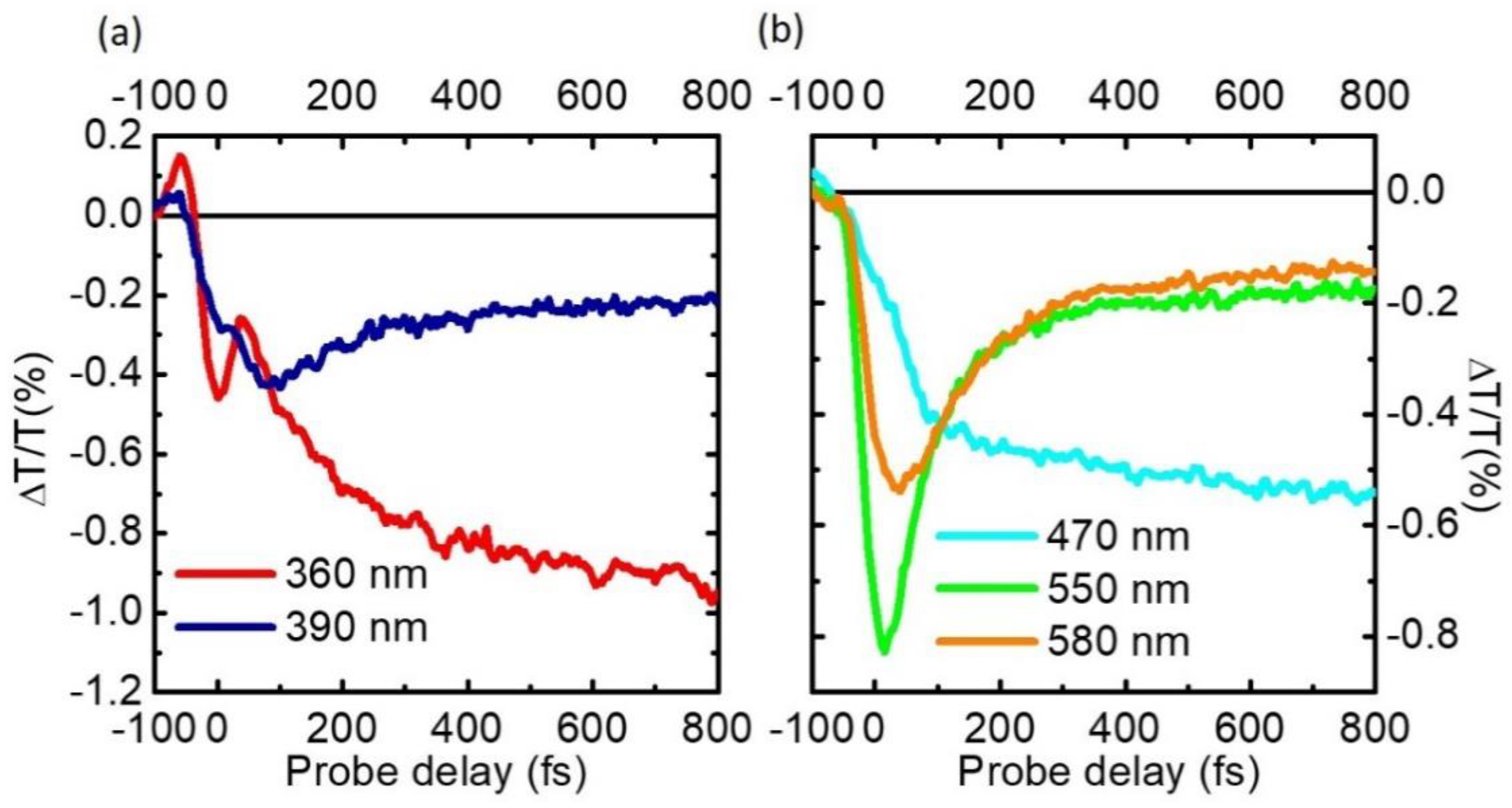
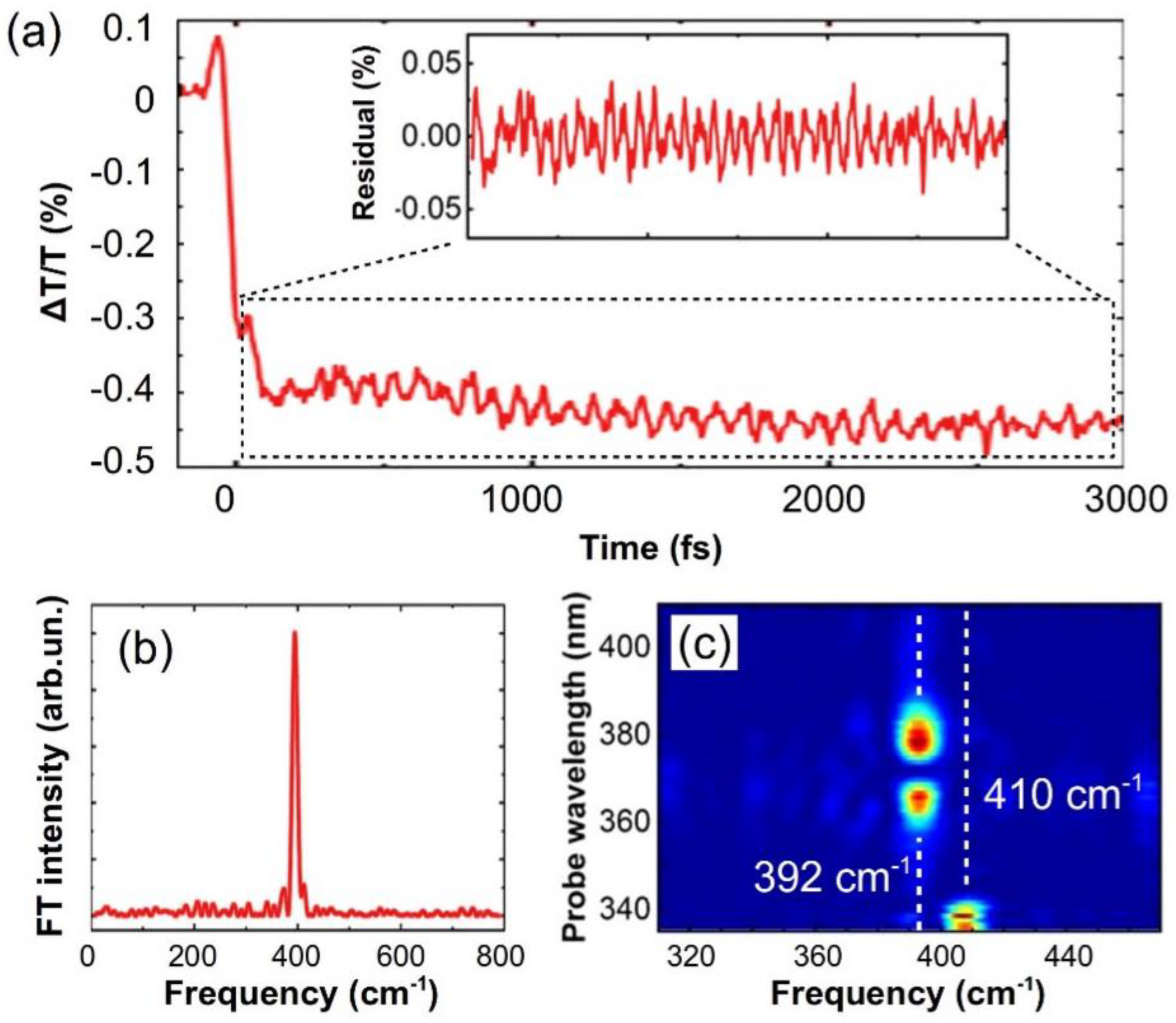
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Steinmeyer, G.; Sutter, D.; Gallmann, L.; Matuschek, N.; Keller, U. Frontiers in Ultrashort Pulse Generation: Pushing the Limits in Linear and Nonlinear Optics. Science 1999, 286, 1507–1512. [Google Scholar] [CrossRef] [PubMed]
- Zewail, A.H. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar] [CrossRef]
- Sundström, V. Femtobiology. Annu. Rev. Phys. Chem. 2008, 59, 53–77. [Google Scholar] [CrossRef] [PubMed]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press on Demand: Oxford, UK, 1999. [Google Scholar]
- Fuller, F.D.; Ogilvie, J.P. Experimental Implementations of Two-Dimensional Fourier Transform Electronic Spectroscopy. Annu. Rev. Phys. Chem. 2015, 66, 667–690. [Google Scholar] [CrossRef] [PubMed]
- Cerullo, G.; Manzoni, C.; Lüer, L.; Polli, D. Time-resolved methods in biophysics. 4. Broadband pump–probe spectroscopy system with sub-20 fs temporal resolution for the study of energy transfer processes in photosynthesis. Photochem. Photobiol. Sci. 2007, 6, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Polli, D.; Lüer, L.; Cerullo, G. High-time-resolution pump-probe system with broadband detection for the study of time-domain vibrational dynamics. Rev. Sci. Instrum. 2007, 78. [Google Scholar] [CrossRef] [PubMed]
- Megerle, U.; Pugliesi, I.; Schriever, C.; Sailer, C.F.; Riedle, E. Sub-50 fs broadband absorption spectroscopy with tunable excitation: Putting the analysis of ultrafast molecular dynamics on solid ground. Appl. Phys. B 2009, 96, 215–231. [Google Scholar] [CrossRef]
- Riedle, E.; Bradler, M.; Wenninger, M.; Sailer, C.F.; Pugliesi, I. Electronic transient spectroscopy from the deep UV to the NIR: Unambiguous disentanglement of complex processes. Faraday Discuss. 2013, 163, 139–158. [Google Scholar] [CrossRef] [PubMed]
- Vardeny, Z.; Tauc, J. Picosecond coherence coupling in the pump and probe technique. Opt. Commun. 1981, 39, 396–400. [Google Scholar] [CrossRef]
- Polli, D.; Brida, D.; Mukamel, S.; Lanzani, G.; Cerullo, G. Effective temporal resolution in pump-probe spectroscopy with strongly chirped pulses. Phys. Rev. A 2010, 82, 53809. [Google Scholar] [CrossRef]
- Kovalenko, S.A.; Dobryakov, A.L.; Ruthmann, J.; Ernsting, N.P. Femtosecond spectroscopy of condensed phases with chirped supercontinuum probing. Phys. Rev. A 1999, 59, 2369–2384. [Google Scholar] [CrossRef]
- Few-Cycle Laser Pulse Generation and Its Applications; Kärtner, F.X., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 95, Topics in Applied Physics; ISBN 978-3-540-20115-1. [Google Scholar]
- Brixner, T.; Stenger, J.; Vaswani, H.M.; Cho, M.; Blankenship, R.E.; Fleming, G.R. Two-dimensional spectroscopy of electronic couplings in photosynthesis. Nature 2005, 434, 625–628. [Google Scholar] [CrossRef] [PubMed]
- Polli, D.; Altoè, P.; Weingart, O.; Spillane, K.M.; Manzoni, C.; Brida, D.; Tomasello, G.; Orlandi, G.; Kukura, P.; Mathies, R.A.; et al. Conical intersection dynamics of the primary photoisomerization event in vision. Nature 2010, 467, 440–443. [Google Scholar] [CrossRef] [PubMed]
- De Vivie-Riedle, R.; De Waele, V.; Kurtz, L.; Riedle, E. Ultrafast Excited-State Proton Transfer of 2-(2′-Hydroxyphenyl)benzothiazole: Theoretical Analysis of the Skeletal Deformations and the Active Vibrational Modes. J. Phys. Chem. A 2003, 107, 10591–10599. [Google Scholar] [CrossRef]
- Nenov, A.; Borrego-Varillas, R.; Oriana, A.; Ganzer, L.; Segatta, F.; Conti, I.; Segarra-Marti, J.; Omachi, J.; Dapor, M.; Taioli, S.; et al. UV-Light-Induced Vibrational Coherences: The Key to Understand Kasha Rule Violation in trans -Azobenzene. J. Phys. Chem. Lett. 2018, 9, 1534–1541. [Google Scholar] [CrossRef] [PubMed]
- Crespo-Hernández, C.E.; Cohen, B.; Hare, P.M.; Kohler, B. Ultrafast excited-state dynamics in nucleic acids. Chem. Rev. 2004, 104, 1977–2019. [Google Scholar] [CrossRef] [PubMed]
- Markovitsi, D. UV-induced DNA Damage: The Role of Electronic Excited States. Photochem. Photobiol. 2016, 92, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Middleton, C.T.; de La Harpe, K.; Su, C.; Law, Y.K.; Crespo-Hernández, C.E.; Kohler, B. DNA Excited-State Dynamics: From Single Bases to the Double Helix. Annu. Rev. Phys. Chem. 2009, 60, 217–239. [Google Scholar] [CrossRef] [PubMed]
- Improta, R.; Santoro, F.; Blancafort, L. Quantum Mechanical Studies on the Photophysics and the Photochemistry of Nucleic Acids and Nucleobases. Chem. Rev. 2016, 116, 3540–3593. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Mukamel, S. Two-Dimensional Ultraviolet (2DUV) Spectroscopic Tools for Identifying Fibrillation Propensity of Protein Residue Sequences. Angew. Chem. Int. Ed. 2010, 49, 9666–9669. [Google Scholar] [CrossRef] [PubMed]
- Nenov, A.; Rivalta, I.; Cerullo, G.; Mukamel, S.; Garavelli, M. Disentangling Peptide Configurations via Two-Dimensional Electronic Spectroscopy: Ab Initio Simulations beyond the Frenkel Exciton Hamiltonian. J. Phys. Chem. Lett. 2014, 5, 767–771. [Google Scholar] [CrossRef] [PubMed]
- Ell, R.; Morgner, U.; Kärtner, F.X.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T.; Lederer, M.J.; Boiko, A.; et al. Generation of 5-fs pulses and octave-spanning spectra directly from a Ti:sapphire laser. Opt. Lett. 2001, 26, 373. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, M.; De Silvestri, S.; Svelto, O.; Szipöcs, R.; Ferencz, K.; Spielmann, C.; Sartania, S.; Krausz, F. Compression of high-energy laser pulses below 5 fs. Opt. Lett. 1997, 22, 522. [Google Scholar] [CrossRef] [PubMed]
- Baltuška, A.; Wei, Z.; Pshenichnikov, M.S.; Wiersma, D.A. Optical pulse compression to 5 fs at a 1-MHz repetition rate. Opt. Lett. 1997, 22, 102. [Google Scholar] [CrossRef] [PubMed]
- Brida, D.; Manzoni, C.; Cirmi, G.; Marangoni, M.; Bonora, S.; Villoresi, P.; De Silvestri, S.; Cerullo, G. Few-optical-cycle pulses tunable from the visible to the mid-infrared by optical parametric amplifiers. J. Opt. 2010, 12, 13001. [Google Scholar] [CrossRef]
- Baltuška, A.; Fuji, T.; Kobayashi, T. Visible pulse compression to 4 fs by optical parametric amplification and programmable dispersion control. Opt. Lett. 2002, 27, 306. [Google Scholar] [CrossRef] [PubMed]
- Szatmári, S. High-brightness ultraviolet excimer lasers. Appl. Phys. B Laser Opt. 1994, 58, 211–223. [Google Scholar] [CrossRef]
- Nagy, T.; Simon, P. Generation of 200-μJ, sub-25-fs deep-UV pulses using a noble-gas-filled hollow fiber. Opt. Lett. 2009, 34, 2300. [Google Scholar] [CrossRef] [PubMed]
- Tzankov, P.; Fiebig, T.; Buchvarov, I. Tunable femtosecond pulses in the near-ultraviolet from ultrabroadband parametric amplification. Appl. Phys. Lett. 2003, 82, 517–519. [Google Scholar] [CrossRef]
- Backus, S.; Peatross, J.; Zeek, Z.; Rundquist, A.; Taft, G.; Murnane, M.M.; Kapteyn, H.C. 16-fs, 1-μJ ultraviolet pulses generated by third-harmonic conversion in air. Opt. Lett. 1996, 21, 665. [Google Scholar] [CrossRef] [PubMed]
- Graf, U.; Fiess, M.; Schultze, M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Intense few-cycle light pulses in the deep ultraviolet. Opt. Express 2008, 16, 18956–18963. [Google Scholar] [CrossRef] [PubMed]
- Reiter, F.; Graf, U.; Schultze, M.; Schweinberger, W.; Schröder, H.; Karpowicz, N.; Azzeer, A.M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Generation of sub-3 fs pulses in the deep ultraviolet. Opt. Lett. 2010, 35, 2248–2250. [Google Scholar] [CrossRef] [PubMed]
- Kosma, K.; Trushin, S.A.; Schmid, W.E.; Fuss, W. Vacuum ultraviolet pulses of 11 fs from fifth-harmonic generation of a Ti:sapphire laser. Opt. Lett. 2008, 33, 723–725. [Google Scholar] [CrossRef] [PubMed]
- Durfee, C.G., III; Backus, S.; Murnane, M.M.; Kapteyn, H.C. Ultrabroadband phase-matched optical parametric generation in the ultraviolet by use of guided waves. Opt. Lett. 1997, 22, 1565–1567. [Google Scholar] [CrossRef]
- Durfee, C.G.; Backus, S.; Kapteyn, H.C.; Murnane, M.M.; Durfee, C.G., III; Backus, S.; Kapteyn, H.C.; Murnane, M.M.; Durfee, C.G.; Backus, S.; et al. Intense 8-fs pulse generation in the deep ultraviolet. Opt. Lett. 1999, 24, 697–699. [Google Scholar] [CrossRef] [PubMed]
- Beutler, M.; Ghotbi, M.; Noack, F. Generation of intense sub-20-fs vacuum ultraviolet pulses compressed by material dispersion. Opt. Lett. 2011, 36, 3726. [Google Scholar] [CrossRef] [PubMed]
- Kida, Y.; Liu, J.; Kobayashi, T. Single 10-fs deep-ultraviolet pulses generated by broadband four-wave mixing and high-order dispersion compensation. Appl. Phys. B Lasers Opt. 2011, 105, 675–679. [Google Scholar] [CrossRef]
- Kida, Y.; Okamura, K.; Liu, J.; Kobayashi, T. Sub-10-fs deep-ultraviolet light source with stable power and spectrum. Appl. Opt. 2012, 51, 6403–6410. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhao, B.; Sueda, K.; Miyanaga, N.; Kobayashi, T. Tunable sub-40 fs ultraviolet pulses from non-collinear four-wave mixing in CaF2 crystal. Chin. Opt. Lett. 2011, 9, s10604. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kida, Y. Ultrafast spectroscopy with sub-10 fs deep-ultraviolet pulses. Phys. Chem. Chem. Phys. 2012, 14, 6200–6210. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Yabushita, A.; Kobayashi, T. Ultrafast dynamics of uracil and thymine studied using a sub-10 fs deep ultraviolet laser. Phys. Chem. Chem. Phys. 2016, 18, 17044–17053. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yabushita, A.; Taniguchi, S.; Chosrowjan, H.; Imamoto, Y.; Sueda, K.; Miyanaga, N.; Kobayashi, T. Ultrafast time-resolved pump-probe spectroscopy of PYP by a sub-8 fs pulse laser at 400 nm. J. Phys. Chem. B 2013, 117, 4818–4826. [Google Scholar] [CrossRef] [PubMed]
- Horio, T.; Spesyvtsev, R.; Suzuki, T. Generation of sub-17 fs vacuum ultraviolet pulses at 133 nm using cascaded four-wave mixing through filamentation in Ne. Opt. Lett. 2014, 39, 6021. [Google Scholar] [CrossRef] [PubMed]
- Marangoni, M.; Brida, D.; Quintavalle, M.; Cirmi, G.; Pigozzo, F.M.; Manzoni, C.; Baronio, F.; Capobianco, A.D.; Cerullo, G. Narrow-bandwidth picosecond pulses by spectral compression of femtosecond pulses in a second-order nonlinear crystal. Opt. Express 2007, 15, 174–180. [Google Scholar] [CrossRef]
- Beutler, M.; Ghotbi, M.; Noack, F.; Brida, D.; Manzoni, C.; Cerullo, G. Generation of high-energy sub-20 fs pulses tunable in the 250–310 nm region by frequency doubling of a high-power noncollinear optical parametric amplifier. Opt. Lett. 2009, 34, 710–712. [Google Scholar] [CrossRef] [PubMed]
- Szabó, G.; Bor, Z. Broadband frequency doubler for femtosecond pulses. Appl. Phys. B Photophys. Laser Chem. 1990, 50, 51–54. [Google Scholar] [CrossRef]
- Martinez, O.E. Achromatic phase matching for second harmonic generation of femtosecond pulses. IEEE J. Quantum Electron. 1989, 25, 2464–2468. [Google Scholar] [CrossRef]
- Baum, P.; Lochbrunner, S.; Riedle, E. Generation of tunable 7-fs ultraviolet pulses: Achromatic phase matching and chirp management. Appl. Phys. B Lasers Opt. 2004, 79, 1027–1032. [Google Scholar] [CrossRef]
- Baum, P.; Lochbrunner, S.; Riedle, E. Tunable sub-10-fs ultraviolet pulses generated by achromatic frequency doubling. Opt. Lett. 2004, 29, 1686–1688. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Jiang, Y.; Sueda, K.; Miyanaga, N.; Kobayashi, T. Sub-15fs ultraviolet pulses generated by achromatic phase-matching sum-frequency mixing. Opt. Express 2009, 17, 17711–17714. [Google Scholar] [CrossRef] [PubMed]
- Varillas, R.B.; Candeo, A.; Viola, D.; Garavelli, M.; De Silvestri, S.; Cerullo, G.; Manzoni, C.; De Silvestri, S.; Cerullo, G.; Manzoni, C. Microjoule-level, tunable sub-10 fs UV pulses by broadband sum-frequency generation. Opt. Lett. 2014, 39, 3849–3852. [Google Scholar] [CrossRef] [PubMed]
- Walmsley, I.A.; Dorrer, C. Characterization of ultrashort electromagnetic pulses. Adv. Opt. Photonics 2009, 1, 308. [Google Scholar] [CrossRef]
- Streltsov, A.M.; Ranka, J.K.; Gaeta, A.L. Femtosecond ultraviolet autocorrelation measurements based on two-photon conductivity in fused silica. Opt. Lett. 1998, 23, 798–800. [Google Scholar] [CrossRef] [PubMed]
- Takagi, Y. Simple autocorrelator for ultraviolet pulse-width measurements based on the nonlinear photoelectric effect. Appl. Opt. 1994, 33, 6328. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, M.H.R.; McIntyre, I.A.; Gibson, G.N.; Rhodes, C.K. Measurement of 248-nm, subpicosecond pulse durations by two-photon fluorescence of xenon excimers. Opt. Lett. 1987, 12, 102. [Google Scholar] [CrossRef] [PubMed]
- Trushin, S.A.; Fuss, W.; Kosma, K.; Schmid, W.E. Widely tunable ultraviolet sub-30-fs pulses from supercontinuum for transient spectroscopy. Appl. Phys. B 2006, 85, 1–5. [Google Scholar] [CrossRef]
- Homann, C.; Krebs, N.; Riedle, E. Convenient pulse length measurement of sub-20-fs pulses down to the deep UV via two-photon absorption in bulk material. Appl. Phys. B 2011, 104, 783–791. [Google Scholar] [CrossRef]
- Reuther, A.; Laubereau, A.; Nikogosyan, D.N. A simple method for the in situ analysis of femtosecond UV pulses in the pump-probe spectroscopy of solutions. Opt. Commun. 1997, 141, 180–184. [Google Scholar] [CrossRef]
- Dadap, J.I.; Focht, G.B.; Reitze, D.H.; Downer, M.C. Two-photon absorption in diamond and its application to ultraviolet femtosecond pulse-width measurement. Opt. Lett. 1991, 16, 499. [Google Scholar] [CrossRef] [PubMed]
- Jailaubekov, A.E.; Bradforth, S.E. Tunable 30-femtosecond pulses across the deep ultraviolet. Appl. Phys. Lett. 2005, 87, 21107. [Google Scholar] [CrossRef]
- Möhring, J.; Buckup, T.; Motzkus, M. Shaper-assisted ultraviolet cross correlator. Opt. Lett. 2010, 35, 1816. [Google Scholar] [CrossRef] [PubMed]
- Kane, D.J.; Trebino, R. Characterization of Arbitrary Femtosecond Pulses Using Frequency-Resolved Optical Gating. IEEE J. Quantum Electron. 1993, 29, 571–579. [Google Scholar] [CrossRef]
- Kane, D.J.; Trebino, R. Single-shot measurement of the intensity and phase of an arbitrary ultrashort pulse by using frequency-resolved optical gating. Opt. Lett. 1993, 18, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Linden, S.; Giessen, H.; Kuhl, J. XFROG—A New Method for Amplitude and Phase Characterization of Weak Ultrashort Pulses. Phys. Status Solidi 1998, 206, 119–124. [Google Scholar] [CrossRef]
- Seidel, M.T.; Zhang, Z.Y.; Yan, S.X.; Wells, K.L.; Tan, H.S. Characterization of polarization shaped ultraviolet femtosecond laser pulses. J. Opt. Soc. Am. B Opt. Phys. 2011, 28, 2718–2725. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Feng, Y.; Chen, C.; Pan, H.; Wu, J.; Zeng, H. Temporal and phase measurements of ultraviolet femtosecond pulses at 200 nm by molecular alignment based frequency resolved optical gating. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
- Kacprowicz, M.; Wasilewski, W.; Banaszek, K. Complete characterization of weak ultra-short near-UV pulses by spectral interferometry. Appl. Phys. B Lasers Opt. 2008, 91, 283–286. [Google Scholar] [CrossRef]
- Iaconis, C.; Walmsley, I. Self-referencing spectral interferometry for measuring ultrashortoptical pulses. IEEE J. Quantum Electron. 1999, 35, 501–509. [Google Scholar] [CrossRef]
- Shirakawa, A.; Sakane, I.; Kobayashi, T. Pulse-front-matched optical parametric amplification for sub-10-fs pulse generation tunable in the visible and near infrared. Opt. Lett. 1998, 23, 1292. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T.; Piel, J.; Riedle, E. Sub-20-fs pulses tunable across the visible from a blue-pumped single-pass noncollinear parametric converter. Opt. Lett. 1997, 22, 1494. [Google Scholar] [CrossRef] [PubMed]
- Cerullo, G.; Nisoli, M.; De Silvestri, S. Generation of 11 fs pulses tunable across the visible by optical parametric amplification. Appl. Phys. Lett. 1997, 71, 3616–3618. [Google Scholar] [CrossRef]
- Zavelani-Rossi, M.; Cerullo, G.; De Silvestri, S.; Gallmann, L.; Matuschek, N.; Steinmeyer, G.; Keller, U.; Angelow, G.; Scheuer, V.; Tschudi, T. Pulse compression over a 170-THz bandwidth in the visible by use of only chirped mirrors. Opt. Lett. 2001, 26, 1155. [Google Scholar] [CrossRef] [PubMed]
- Borrego-Varillas, R.R.; Oriana, A.; Branchi, F.; De Silvestri, S.; Cerullo, G.; Manzoni, C. Optimized ancillae generation for ultra-broadband two-dimensional spectral-shearing interferometry. J. Opt. Soc. Am. B 2015, 32, 1851–1855. [Google Scholar] [CrossRef]
- Birge, J.R.; Crespo, H.M.; Kärtner, F.X. Theory and design of two-dimensional spectral shearing interferometry for few-cycle pulse measurement. J. Opt. Soc. Am. B 2010, 27, 1165. [Google Scholar] [CrossRef]
- Birge, J.R.; Ell, R.; Kärtner, F.X. Two-dimensional spectral shearing interferometry for few-cycle pulse characterization and optimization. In Ultrafast Phenomena XV, Proceedings of the 15th International Conference, Pacific Grove, USA, 30 July–4 August 2006; Springer Series in Chemical Physics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 88, pp. 160–162. [Google Scholar]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Huber, R.; Satzger, H.; Zinth, W.; Wachtveitl, J. Noncollinear optical parametric amplifiers with output parameters improved by the application of a white light continuum generated in CaF2. Opt. Commun. 2001, 194, 443–448. [Google Scholar] [CrossRef]
- Pecourt, J.-M.L.; Peon, J.; Kohler, B. DNA Excited-State Dynamics: Ultrafast Internal Conversion and Vibrational Cooling in a Series of Nucleosides. J. Am. Chem. Soc. 2001, 123, 10370–10378. [Google Scholar] [CrossRef] [PubMed]
- Jou, F.-Y.; Freeman, G.R. Temperature and isotope effects on the shape of the optical absorption spectrum of solvated electrons in water. J. Phys. Chem. 1979, 83, 2383–2387. [Google Scholar] [CrossRef]
- Baba, M.; Saitoh, M.; Kowaka, Y.; Taguma, K.; Yoshida, K.; Semba, Y.; Kasahara, S.; Yamanaka, T.; Ohshima, Y.; Hsu, Y.C.; et al. Vibrational and rotational structure and excited-state dynamics of pyrene. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef] [PubMed]
- Foggi, P.; Pettini, L.; Santa, I.; Righini, R.; Califano, S. Transient absorption and vibrational relaxation dynamics of the lowest excited singlet state of pyrene in solution. J. Phys. Chem. 1995, 99, 7439–7445. [Google Scholar] [CrossRef]
- Neuwahl, F.V.R.; Foggi, P. Direct Observation of S2–S1 Internal Conversion in Pyrene by Femtosecond Transient Absorption. Laser Chem. 1999, 19, 375–379. [Google Scholar] [CrossRef]
- Raytchev, M.; Pandurski, E.; Buchvarov, I.; Modrakowski, C.; Fiebig, T. Bichromophoric interactions and time-dependent excited state mixing in pyrene derivatives. A femtosecond broad-band pump-probe study. J. Phys. Chem. A 2003, 107, 4592–4600. [Google Scholar] [CrossRef]
- Shinohara, H.; Yamakita, Y.; Ohno, K. Raman spectra of polycyclic aromatic hydrocarbons. Comparison of calculated Raman intensity distributions with observed spectra for naphthalene, anthracene, pyrene, and perylene. J. Mol. Struct. 1998, 442, 221–234. [Google Scholar] [CrossRef]
- Wang, Q.; Schoenlein, R.; Peteanu, L.; Mathies, R.; Shank, C. Vibrationally coherent photochemistry in the femtosecond primary event of vision. Science 1994, 266, 422–424. [Google Scholar] [CrossRef] [PubMed]
- Pugliesi, I.; Krebs, N.; Riedle, E. Coherent internal conversion of pyrene revealed by pump-probe and ultrabroad 2D-UV spectroscopy. In Proceedings of the 2013 Conference on Lasers & Electro-Optics Europe & International Quantum Electronics Conference CLEO EUROPE/IQEC, Munich, Germany, 12–16 May 2013; Volume 782, p. 1. [Google Scholar]
- Borisevich, N.A.; Kazberuk, D.A.; Mel’nichuk, S.V.; Tikhomirov, S.A.; Tolstorozhev, G.B. Picosecond dynamics of intramolecular charge transfer in benzophenone amino derivatives. J. Appl. Spectrosc. 1995, 62, 441–446. [Google Scholar] [CrossRef]
- Zhang, J.; Han, F.; Kong, W. Zero Kinetic Energy Photoelectron Spectroscopy of Pyrene. J. Phys. Chem. A 2010, 114, 11117–11124. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borrego-Varillas, R.; Ganzer, L.; Cerullo, G.; Manzoni, C. Ultraviolet Transient Absorption Spectrometer with Sub-20-fs Time Resolution. Appl. Sci. 2018, 8, 989. https://doi.org/10.3390/app8060989
Borrego-Varillas R, Ganzer L, Cerullo G, Manzoni C. Ultraviolet Transient Absorption Spectrometer with Sub-20-fs Time Resolution. Applied Sciences. 2018; 8(6):989. https://doi.org/10.3390/app8060989
Chicago/Turabian StyleBorrego-Varillas, Rocío, Lucia Ganzer, Giulio Cerullo, and Cristian Manzoni. 2018. "Ultraviolet Transient Absorption Spectrometer with Sub-20-fs Time Resolution" Applied Sciences 8, no. 6: 989. https://doi.org/10.3390/app8060989
APA StyleBorrego-Varillas, R., Ganzer, L., Cerullo, G., & Manzoni, C. (2018). Ultraviolet Transient Absorption Spectrometer with Sub-20-fs Time Resolution. Applied Sciences, 8(6), 989. https://doi.org/10.3390/app8060989





