1. Introduction
Because of globalization and environmental regulations, chemical process industries are constantly examining all aspects of their processes in an effort to improve their operations to ensure that they remain competitive. In particular, process optimization has been at the forefront of this undertaking. Optimizing process operations in chemical plants involves developing a sufficiently accurate phenomenological, or empirical, model to assist in finding the optimal operating points. In recent years, multiobjective optimization, instead of the minimization of an aggregate objective function used in traditional optimization, has increased in popularity. Indeed, traditional optimization techniques have resolved multiple objectives by combining them into a single objective comprising the weighted sum of the individual objectives, or by considering one objective while treating the others as constraints. Even though single objective optimization is sufficient in many situations, multiobjective optimization provides additional information on the underlying relationships between various objectives.
In multiobjective optimization, all objectives are initially considered equally important and the concept of domination serves to circumscribe the Pareto domain using a representative process model. Most often, some of the objective functions conflict such that one objective cannot be improved without deteriorating another. The Pareto domain, comprising nondominated solutions, is obtained without any bias with respect to all objectives and is commonly approximated with a large number of solutions. When the Pareto domain has been obtained, all nondominated solutions are ranked using some preferences expressed by an expert or decision-maker, and the optimal solution is identified. The optimal solution, which is obtained using process models, is then validated on the actual process.
Often the solution of the process or plant models used to circumscribe the Pareto domain is computationally expensive, such that determining a sufficiently large number of Pareto-optimal solutions may require an impractically long time. For example, optimization of an ethanol batch fermentation process integrated with a continuous vacuum separation unit performed by combining a Visual Basic for Applications (VBA) code with a Honeywell UniSim
® Design R430 process flowsheet took a few days to obtain one Pareto domain [
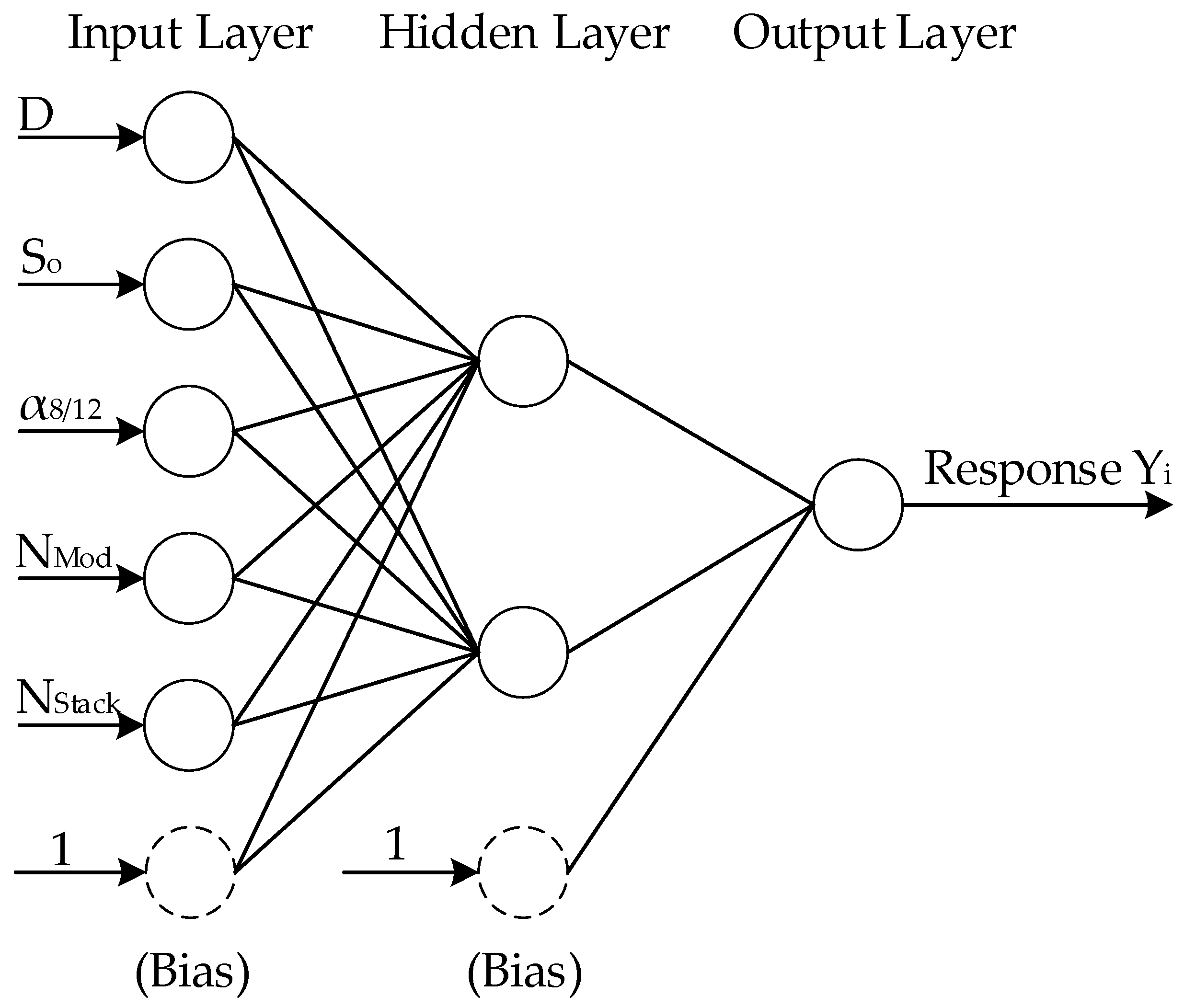
1]. One alternative is to use a metamodel, or a surrogate model, where complete or partial operation of the chemical process is modelled with a representative model, often empirical, for which the computational cost would be significantly reduced. One such model is an artificial neural network (ANN), which is a computational network that attempts to mimic the functionality of neurons within the biological central nervous system. In an ANN, adaptable nodes store experiential knowledge acquired via learning algorithms, allowing the network to recognize and predict patterns with no knowledge of the underlying governing equations. This allows ANNs to be used as black-box tools where no prior knowledge about the system is required, thereby achieving high accuracy in multifactorial and nonlinear analysis of complex processes such as fermentation. However, training a neural network requires a good number of representative solutions, which may counteract efforts to reduce the computation time. Strategies to develop effective neural network models for smaller sets of data using a combination of experimental design and stacked neural networks have been previously proposed [
2,
3]. In an effort to maximize process information given a small set of data, it is possible to use experimental design. Numerous optimization problems could benefit from such a strategy.
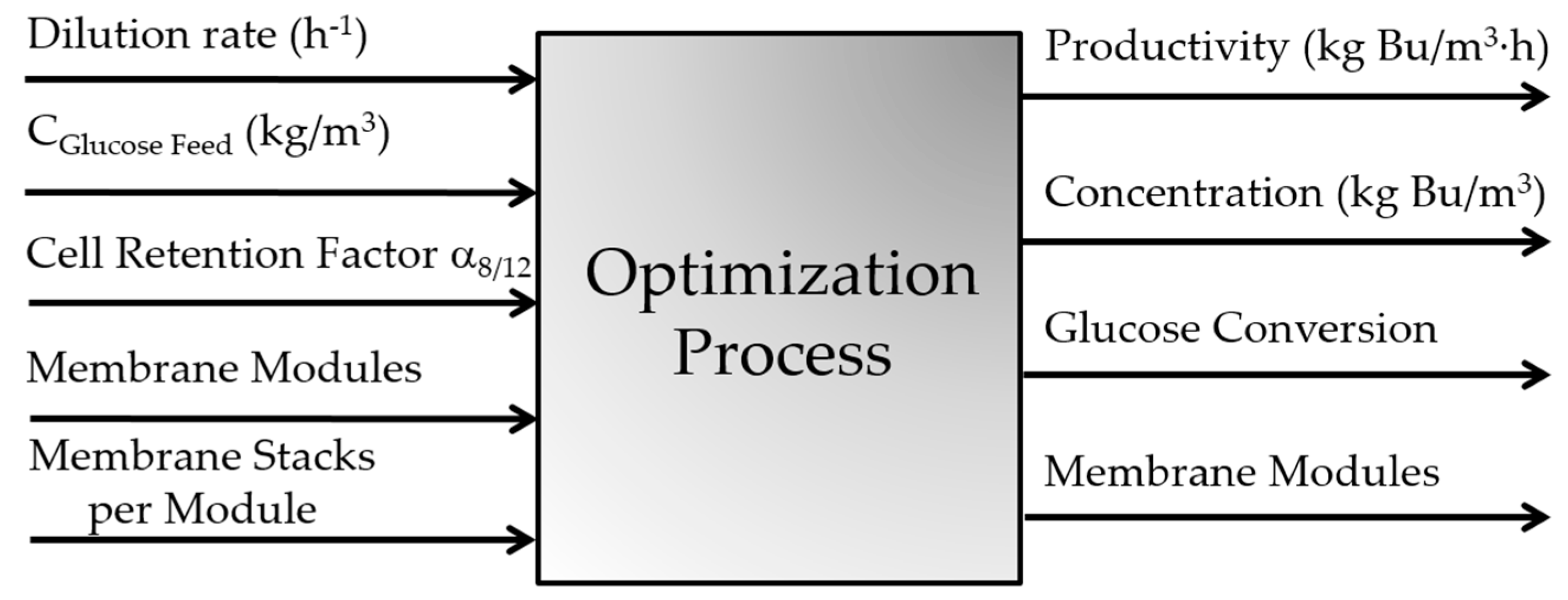
In this paper, metamodels are used in the multiobjective optimization of a continuous biobutanol production process where the fermentation system is integrated with a membrane pervaporation unit to selectively remove solvents from the fermentation broth to enhance the productivity and overall effluent concentration of butanol. This paper is divided as follows. The process to be optimized is first described. Next, the strategy used to develop the ANN metamodels to assist in the computationally effective determination of the Pareto domain is discussed. Finally, results are presented and discussed, prior to presenting the concluding remarks.
2. Description of the Integrated ABE Fermentation–Membrane Pervaporation Process
The process considered in this investigation is the biochemical production of butanol via acetone–butanol–ethanol (ABE) fermentation. ABE fermentation is a biphasic biological production involving acidogenesis and solventogenesis. Acidic metabolites accumulate during the former phase and are subsequently assimilated into industrial relevant solvents such as butanol. Butanol is an important chemical precursor and is currently being produced commercially via the hydroformylation of propylene. ABE fermentation can potentially be used for commercial production of butanol instead of the aforementioned petrochemical-based process. This interest in the development of bio-based processing alternatives is motivated by the enviable characteristic of biobutanol as a renewable liquid fuel.
The ABE fermentation process suffers from low butanol yield and productivity because of the co-production of acetone, ethanol, and organic acids. Moreover, the concentration of butanol in the final fermentation broth is limited to very low concentrations (typically <13 g/L) due to butanol toxicity to the producing bacteria [
4]. Consequently, the recovery of ABE solvents is energy-intensive and costly. At such low concentrations, the energy requirement for product recovery is greater than the energy content of the product itself [
5]. Significant experimental efforts have been made to optimize ABE fermentation for improved butanol yields. One such method is extractive fermentation, a continuous process in which fermentation and solvent separation are integrated, thereby partly alleviating product inhibition, reducing downtime associated with batch processing, and increasing overall butanol concentration.
Researchers have proposed various mathematical models describing cell growth and variations in the concentration of metabolites over time, by accounting for their rates of production and consumption in the biochemical reaction pathway to adequately represent the experimental observations [
6,
7]. These mathematical models of ABE fermentation provide cost- and time-effective simulations for fermentation design and optimization studies. Therefore, extractive fermentation can be adequately modelled, allowing researchers to further generate new testable hypotheses and proposals, which can significantly improve the overall process and identify optimal operating conditions.
For the continuous integrated fermentation process, pervaporation is an attractive separation method that can be used to continuously recover butanol from the ABE fermentation broth [
8]. Pervaporation is a membrane-based separation process of binary or multicomponent liquid mixtures, and, as its name implies, it involves permeation through a dense hydrophobic membrane and evaporation on the permeate side. The permeating vapor is then recovered by condensation. Polydimethylsiloxane (PDMS) membrane is regarded as a promising candidate for butanol separation, as it exhibits high and stable performance in butanol recovery from ABE solvents via pervaporation [
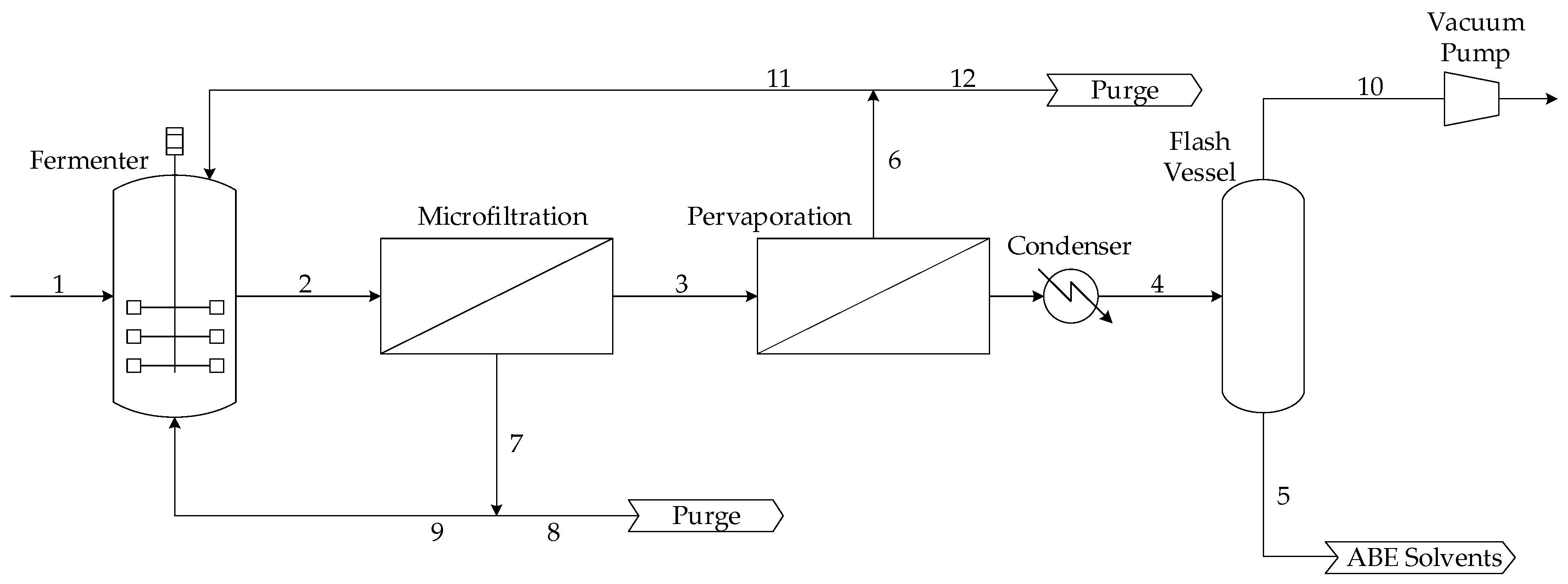
9]. The continuous integrated fermentation-membrane pervaporation process that was optimized in this work is presented schematically in
Figure 1. This process mainly consists of a continuous fermenter, a microfiltration unit, and a membrane pervaporation system. For a set of input operating conditions of the overall process, the dynamic mass balance of each individual component of the process is solved with time until a steady state is achieved. The main input variables of the process, i.e., the decision variables in the optimization problem, are the fermenter dilution rate, the inlet sugar concentration, the cell retention factor, and the membrane area of the pervaporation unit as dictated by the number of membrane modules and the number of membrane stacks per module. Mass balances for the main species of the fermentation broth, namely acetone, acetic acid, butanol, butyric acid, ethanol, microorganism, glucose, and water, were considered in this work. The detailed set of mass balances and process equations can be found in [
10].
In this process, a solution of glucose is continuously fed to a 400 m
3 fermenter with a constant flow rate and sugar concentration. Initial species concentrations in the fermenter are assumed. The set of kinetic reactions as described by Mulchandani and Volesky [
11], accounting for the production of solvents (acetone, butanol, and ethanol), intermediate products (acetic acid and butyric acid), and microbial cells as well as the consumption of glucose in the fermentation broth was used. This model is still the most commonly used in the literature, because it accounts for the carbon substrate limitation in addition to the inhibition of butanol and butyric acid. Other models were recently proposed in the literature and were tested in this investigation. Shinto et al. [
12] presented a kinetic model that considers numerous intermediates in the metabolic pathway as well as product and glucose inhibition. However, this model could not be used, as it leads to unrealistically high butanol concentration, far beyond the inhibitory concentration levels. The dynamic model of Buehler and Mesbah [
13] initially seemed interesting, as it accounts for the pH of the fermentation broth, but some dynamic model constants are extremely high, therefore the system of ordinary differential equations cannot be solved with a practical step size in terms of time.
To achieve steady state for a set of input conditions, the overall mass balance is satisfied by removing the same quantity of material through Streams 5, 8, 10 and 12 as the one entering into the process in Stream 1. In a continuous operation, Stream 2 is sent to the microfiltration membrane unit to give the permeate cell-free Stream 3 and the retentate Stream 7 containing all the microbial cells of Stream 2. A large proportion of Stream 7 is returned to the fermenter through Stream 9. Stream 8 is purged and sent to the separation train. Purge Stream 8 is adjusted to maintain an optimal steady-state concentration of microbial cells in the fermenter and provides an exit for other metabolites [
14]. Stream 3 flows through the membrane pervaporation unit, where a fraction permeates through the membrane and is subsequently cooled in the condenser to form Stream 4. The permeate side of the membrane is maintained under high vacuum. The rate of permeation depends on the membrane area and permeability as well as stream temperature and composition [
10]. Stream 4 is separated to give Streams 5 and 10, assumed to be 99% and 1% of Stream 4, respectively. Stream 5, which has a much higher concentration of ABE solvents than Stream 3, is sent to the separation train. Retentate Stream 6 is split into Streams 11 and 12. Purge Stream 12, used to maintain steady-state operation along with other exiting streams, is sent to the separation train, whereas Stream 11, depleted of ABE solvents, is recycled back to the fermenter.
4. Results and Discussion
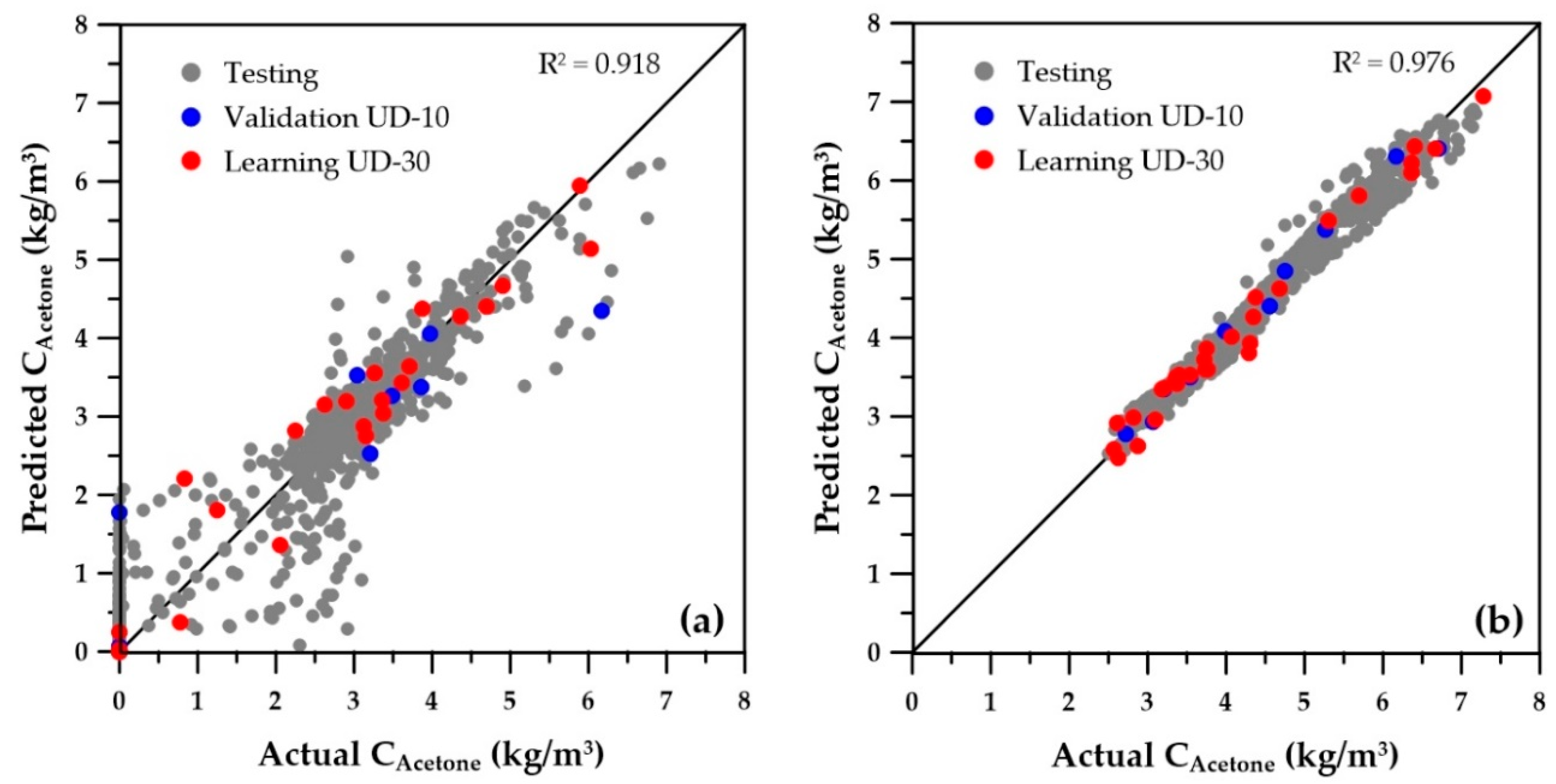
Results of the ANN predictions of the species concentrations are presented first. The parity plot giving the predicted versus actual values for the concentrations of butanol is presented in
Figure 5. Very similar results were obtained for the concentrations of the other seven species, so their graphs are not shown. In this graph, points represented by red, blue, and gray symbols correspond to the training (30 solutions), validation (10 solutions), and testing (1000 solutions) data, respectively. The testing data was generated by randomly choosing the five decision variables subjected to the same minimum and maximum bounds of the training and validation datasets. The graph on the left of
Figure 5 presents the predictions obtained by the ANNs when the decision variables for training and validation were selected using a wider range (
Table 1). Results show that the predicted concentrations have a high degree of scatter, especially at the lower concentrations. The residuals are heteroskedastic for the initial range, as the variance of the error is not constant, and two sections with distinct variability prevail in
Figure 5a. There are many solutions with zero concentrations in the actual fermenter, corresponding to operating conditions where the microorganisms were washed out, i.e., the culture was not able to sustain itself through the fermenter due to high dilution rates and high cell retention factor α
8/12.
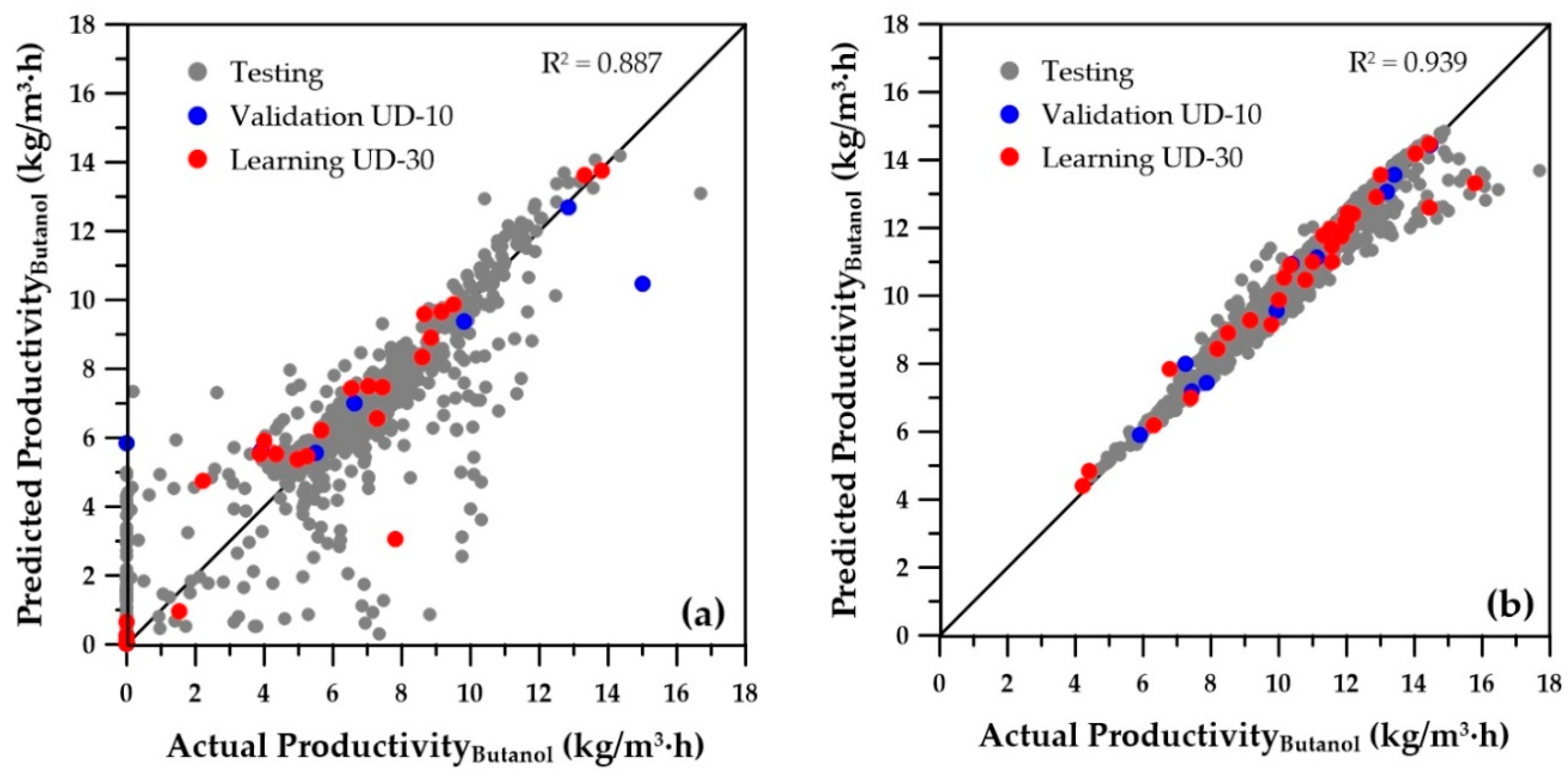
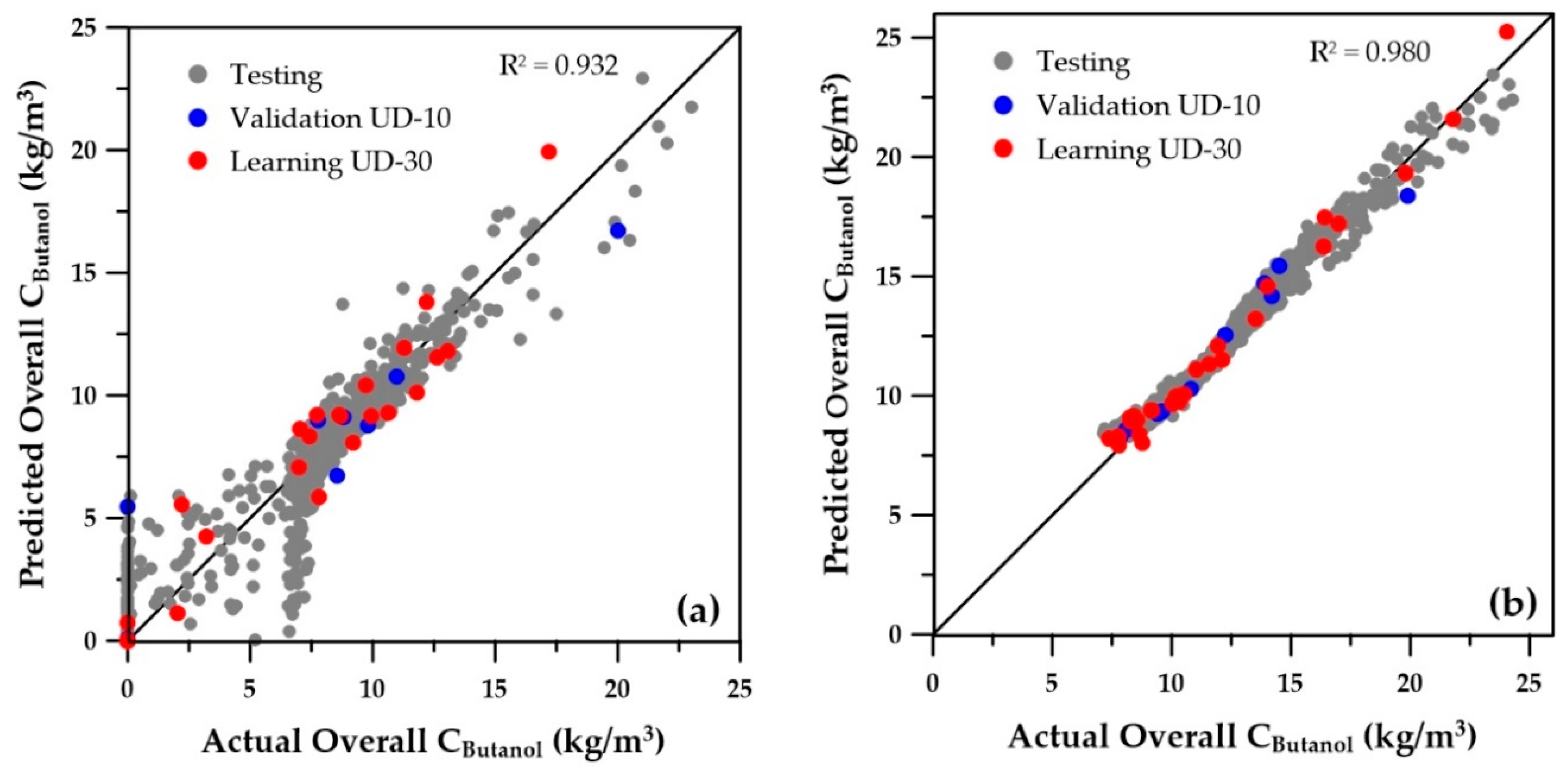
Figure 6 and
Figure 7 present the parity plots of the first two objectives obtained with the same set of decision variables. The predictions based on the ANNs for the wider range of decision variables are also relatively scattered, especially at very low values. A similar plot was obtained for the third objective (sugar conversion), whereas predictions of the number of membrane modules showed a perfect regression (data not shown). On the other hand, at higher values of butanol productivity, overall butanol concentration, and sugar conversion, the predictions seem to be acceptable. Nevertheless, they could certainly be improved, provided the ranges of the operating conditions are refined to eliminate solutions that were generated in the lower range of the first three objectives, which in reality would never be part of the final Pareto domain. Indeed, these solutions are clearly dominated when compared to the solutions with higher objective values. To refine the ranges of the decision variables, the genetic algorithm was used to generate the Pareto domain from the four ANN metamodels of the objectives. The obtained Pareto domain allowed for reducing the ranges of the decision variables to those of the second row of
Table 1. It was then possible to generate new sets of training and validation data, which were used to generate the 12 new ANNs. The parity plots of the butanol concentration for the first two objectives are presented on the right graphs of
Figure 5,
Figure 6 and
Figure 7. It is obvious that the new ANNs show much better predictions than those obtained with the wider ranges of decision variables. It is believed that these predictions should provide sufficient accuracy to use the ANNs with confidence for directly obtaining the Pareto domain or providing good initial species concentrations. The overall coefficients of determination (R
2) are included on each graph and clearly indicate a significant improvement of the metamodels when the reduced ranges are used. Moreover, for all variables, the numerous low values and zeros present with the wider ranges of decision variables disappeared for the ANN predictions obtained with the reduced decision variable ranges. The main change in the ranges was the cell retention factor, which now assumes a unique value of 0.1, allowing elimination of the fermenter washout and retention of a higher microorganism concentration within the fermenter.
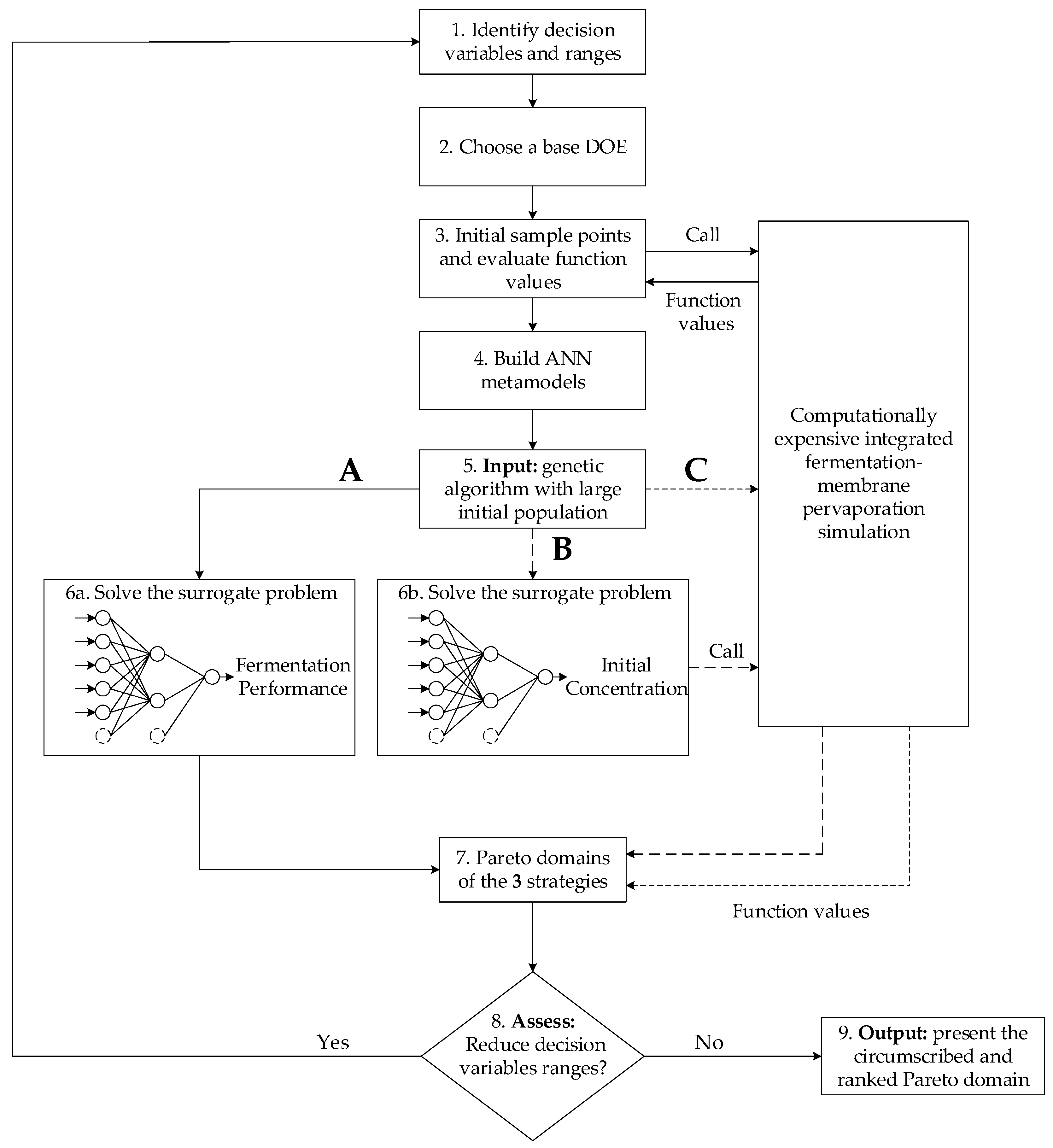
A Pareto domain was obtained for each of the three strategies described in
Figure 4 using the same generic algorithm. In strategy A, the Pareto domain was obtained from the ANN metamodels of the entire process where the four objectives are predicted from the five decision variables. In strategy B, the phenomenological simulator of continuous fermentation integrated with a pervaporation unit was used with the initial estimates of the concentrations of the eight species in the fermenter being predicted with the eight ANN metamodels. Each concentration estimate was predicted from the five decision variables. Finally, in strategy C, the Pareto domain was circumscribed akin to strategy B, except the initial estimates of the concentrations were set arbitrarily. It is obvious that strategies B and C led to similar Pareto domains, since the phenomenological simulator of the continuous integrated fermentation was used in both cases until convergence was achieved.
With the initial ranges of the decision variables, strategy A was used to determine the Pareto domain (not shown), which made reducing the ranges of the decision variables possible. With the 12 ANN metamodels developed with the decision variables of the reduced ranges, Pareto domains with a population of 5000 solutions were obtained with strategies A, B and C. All Pareto-optimal solutions were then ranked with the NetFlow method. The method’s relative weights and the three threshold values for each of the four objective functions are summarized in
Table 2. The plots of the four objective functions and two of the decision variables are presented in
Figure 8,
Figure 9,
Figure 10 and
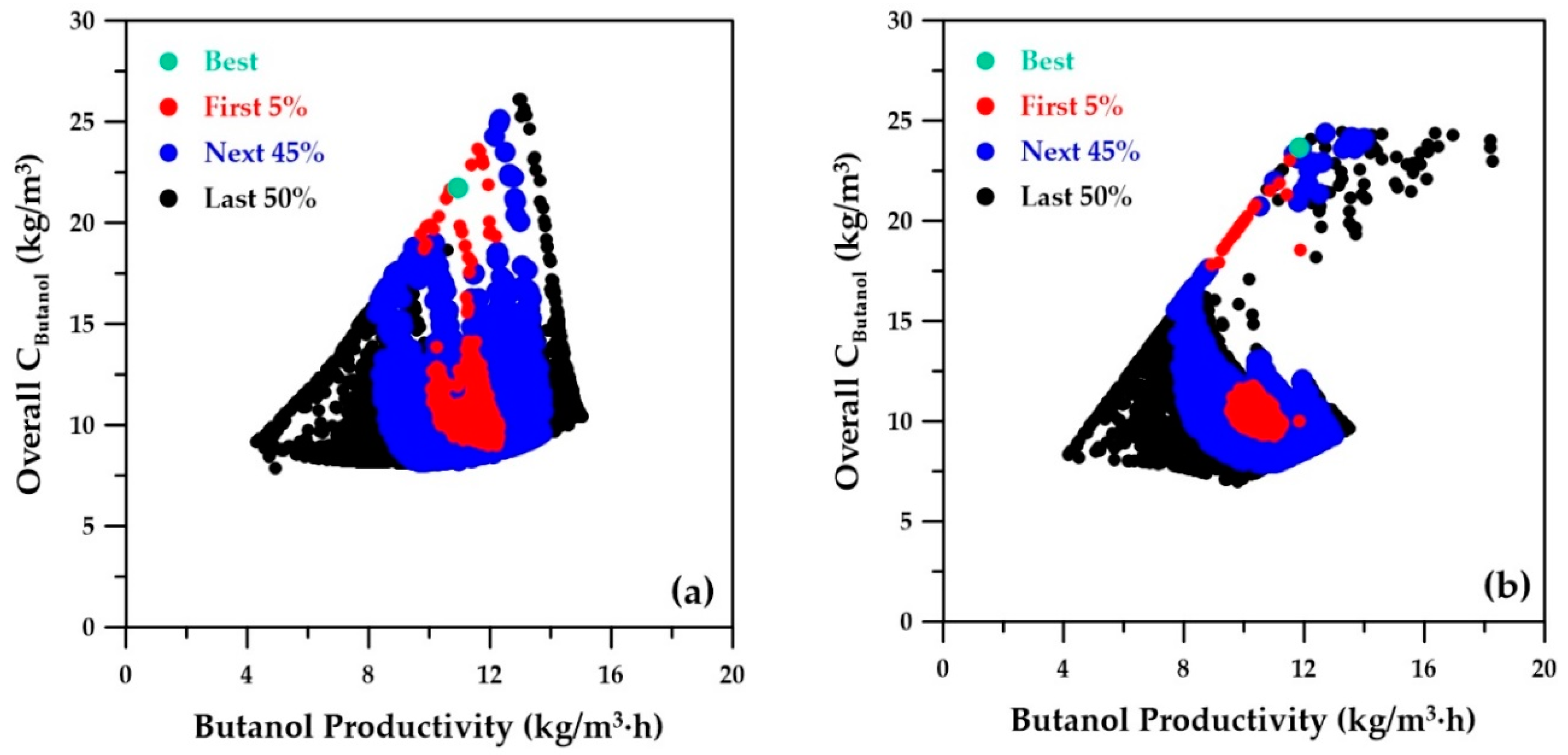
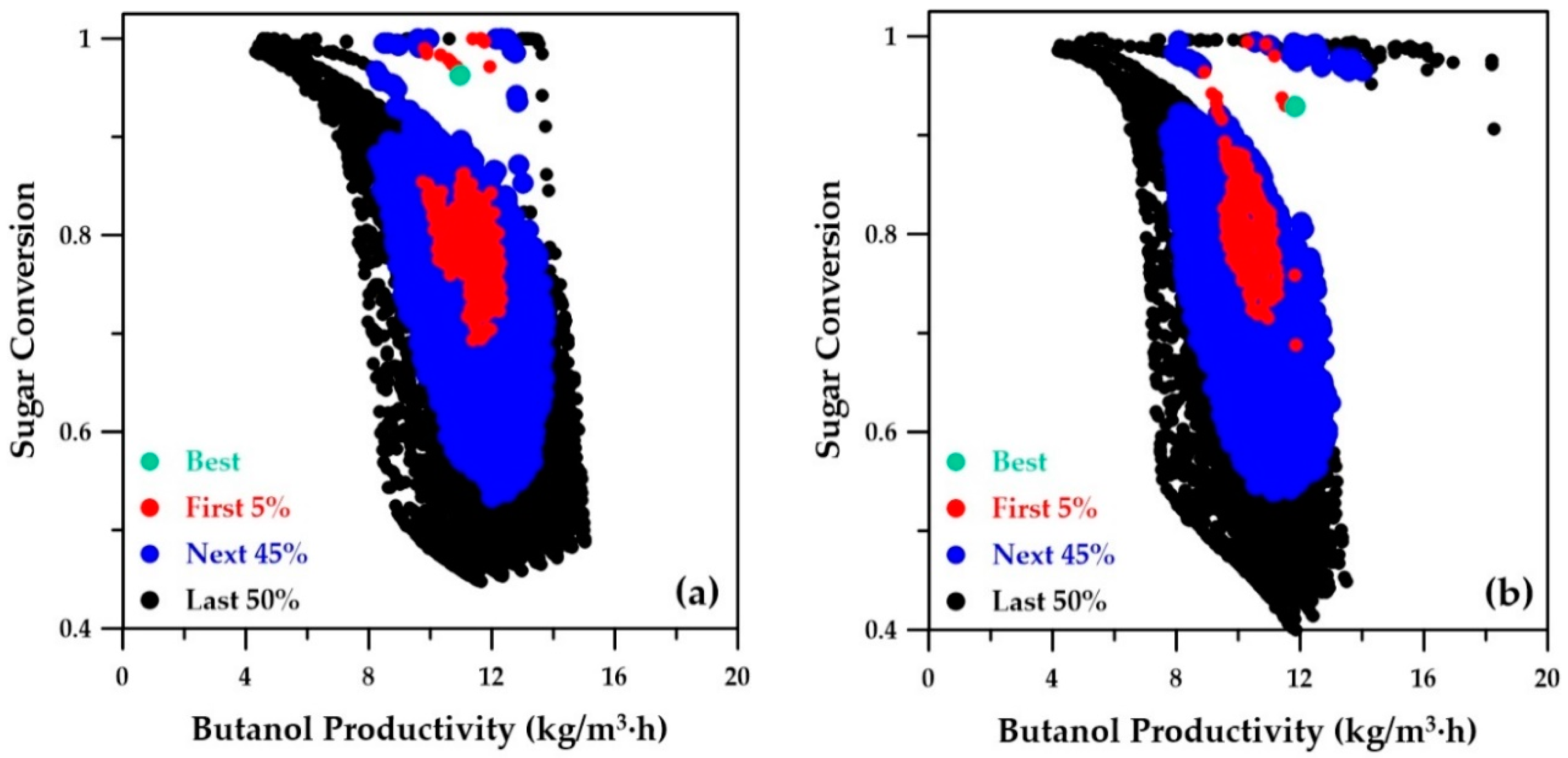
Figure 11. The Pareto domain is plotted with four distinct regions: (1) best-ranked solution (green point), (2) solutions ranked in the first 5% (red points), (3) solutions ranked in the next 45% (blue points), and (4) solutions of the remaining 50% (black points).
Figure 8a depicts the overall concentration of butanol as a function of butanol productivity, as determined by the genetic algorithm using the four ANN metamodels. The best-ranked solution is located at a butanol productivity of 10.95 kg/m
3∙h and an overall butanol concentration of 21.74 kg/m
3 (
Table 3, column A). When the decision variables associated with the optimal solution obtained with the ANN were used in the phenomenological simulator to validate this optimal point, values of 12.14 kg/m
3∙h and 24.04 kg/m
3 were obtained, respectively. This is comparable to the best-ranked solution obtained by the genetic algorithm using the phenomenological simulator, as depicted in
Figure 8b, where butanol productivity of 11.83 kg/m
3∙ was obtained (
Table 3, column C).
Figure 8 shows the positive correlation between butanol productivity and overall butanol concentration at a constant dilution rate. The dilution rate increases diagonally (left to right) from a lower bound of 0.5 h
−1 to an upper bound of 1.4 h
−1. The empty portion depicted in the Pareto domain of
Figure 8b corresponds to an inoperable range due to the constraints that exist between elevated dilution rate, butanol concentration, and flow rates to achieve steady state. The metamodel failed to recognize these limitations and instead filled the empty region accordingly by interpolating the data. This observation is expected, as a metamodel is based on input–output observations without accounting for the intrinsic constraints of the system. Nevertheless, the best-ranked solution and the solutions ranked in the first 5% were well identified with the metamodels.
Sugar conversion as a function of the butanol productivity of the Pareto domain is depicted in
Figure 9.
Figure 9a was obtained by the genetic algorithm using the ANN metamodels, while
Figure 9b presents the Pareto domain obtained using the phenomenological simulator. Both Pareto domains are nearly identical, which clearly indicates that the ANN metamodels were able to adequately model and well predict the relationship between conversion and butanol productivity. The sugar conversion corresponding to the best-ranked solution is 0.96 and 0.93 for the metamodel and phenomenological simulator, respectively. The same sugar conversion was obtained when the decision variables of the best-ranked solution identified with the ANN metamodels was used in the phenomenological simulator (
Table 3). The first three objective functions need to be maximized, whereas the fourth objective, the number of membrane modules in series, needs to be minimized. A trade-off between all four objectives needs to prevail in order to determine the optimal operating conditions for the decision variables via the NetFlow ranking algorithm.
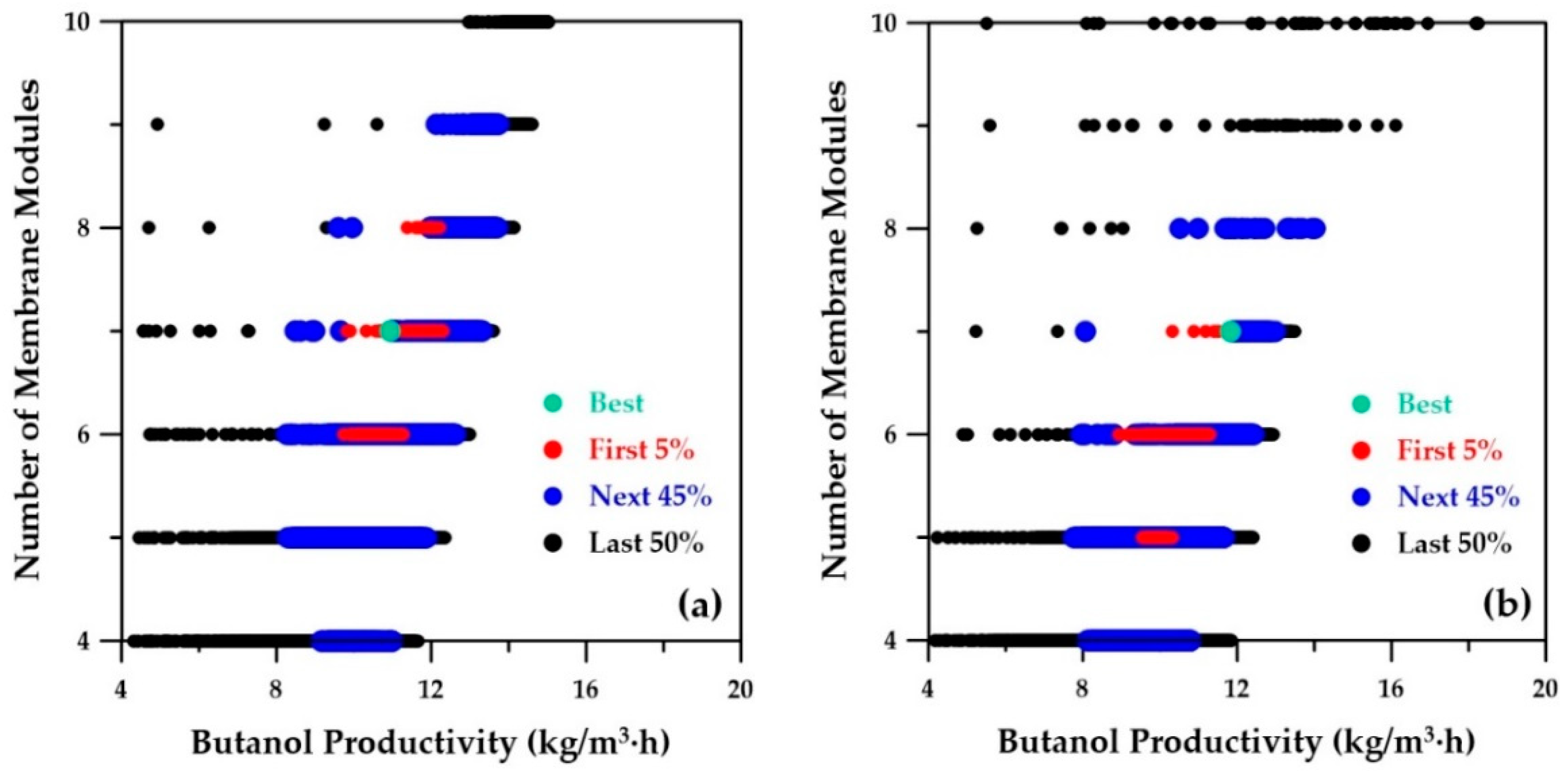
Figure 10a depicts the number of membrane modules, also a decision variable, as a function of butanol productivity as determined by the ANN metamodels. The best-ranked solution suggests seven membrane modules, which is the same value as the best-ranked solution obtained with the phenomenological simulator depicted in
Figure 10b. An increase in the number of membrane modules is accompanied by an increase in the overall membrane area, which in turn leads to higher solvent recovery, higher sugar conversion, and alleviation of product inhibition.
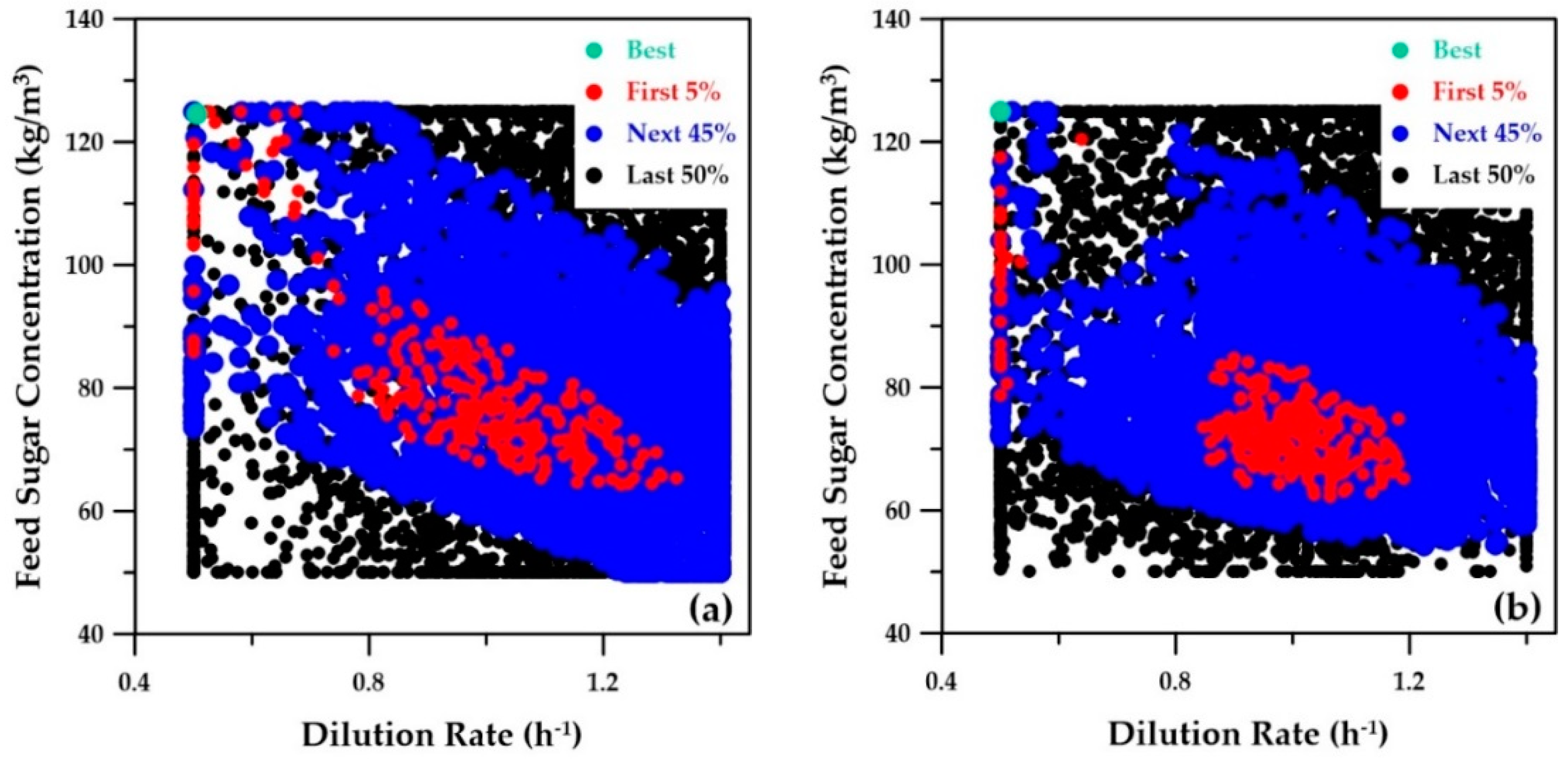
The first two decision variables, the dilution rate and the feed sugar concentration, are plotted in
Figure 11. Both strategies led to very similar graphs. The best-ranked solution shows that the optimal trade-off was obtained for a feed sugar concentration of 125 kg/m
3 and a dilution rate of 0.5 h
−1 for both strategies. The third decision variable, the cell retention factor, was kept constant at 0.1. A small value of the cell retention factor implies that a higher microorganism concentration prevails inside the fermenter. The optimal operating conditions as determined with the Pareto domains obtained with the three strategies described in
Figure 4 are summarized in
Table 3. The two sub-columns of
Table 3 for strategy A correspond to the first three objectives predicted with the five decision variables by the ANN metamodel and the phenomenological simulator, respectively. The latter is recorded for validation purposes.
Table 3 also provides the computation time needed to circumscribe the Pareto domain for each strategy. It only took 5.6 s to determine the complete Pareto domain with the ANN metamodels, whereas it took about 1500 and 2500 times more computation time with strategies B and C, respectively. It is clear that there is a net advantage to using the ANN metamodels for circumscribing the Pareto domain. This computational time advantage would be even more impressive if the time to perform a single simulation was longer. Previous research has also clearly illustrated the advantage of using neural networks as surrogate models for the optimization of processes [
21,
22]. In this investigation, the number of evaluations using the phenomenological model for circumscribing the Pareto domain is given in
Table 3. It took 81 simulations for the two iterations (initial and reduced ranges of decision variables) to derive the ANN metamodels, including the simulation for validating the optimum solution identified by strategy A. On the other hand, it took more than 250 times the number of evaluations for strategies B and C.
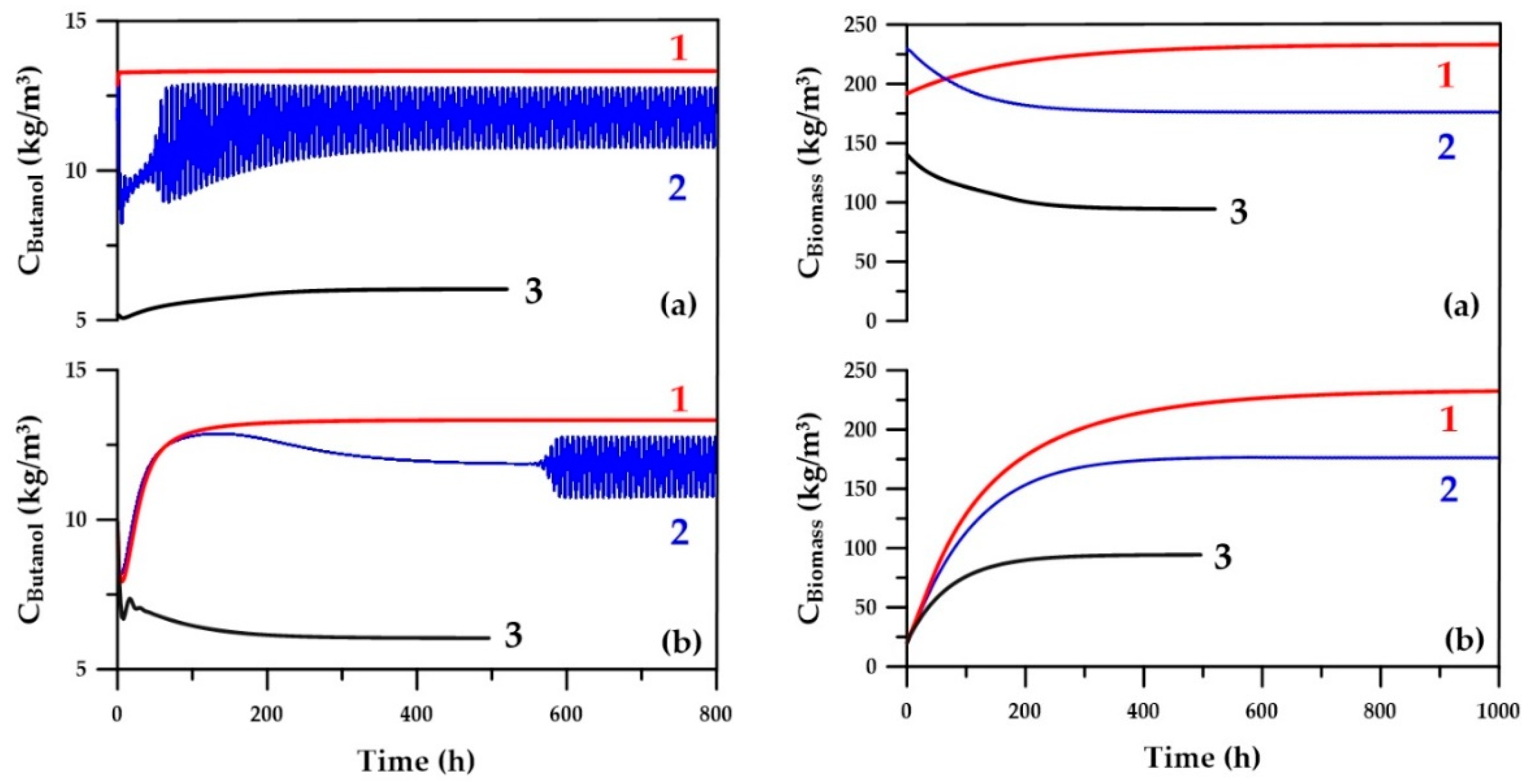
The use of ANN metamodels in strategy B for estimating the initial species concentrations is to accelerate the convergence to steady state. However, only mitigated results were obtained, the main reason being the stringent concentration tolerance for convergence, combined with the accuracy of ANNs.
Figure 12 presents variation of butanol and microorganism concentration as a function of time. These results show that for many operating conditions, the time to convergence is significantly improved. For some operating conditions, the concentrations within the fermenter oscillate in a quasi-steady state. This phenomenon, referred to as a chemical feedback loop, sometimes occurs for some chemical systems, such as the oxidation of malonic acid by bromate ions catalyzed by cerium [
23]. In the current fermentation system integrated with a pervaporation unit, the dynamics of production and consumption of intermediate metabolites, butyric and acetic acids, and the ABE solvents along with their partial recovery induces this oscillatory behavior under some particular decision variables. This oscillatory behavior prevents satisfaction of the convergence criterion, which was met when all concentrations within the fermenter did not change with time within a given tolerance. Under these conditions, the computation time was obviously longer; therefore, the average steady-state value of each concentration is determined by taking an average of the last segment of each respective curve in order to evaluate the objective functions. As shown in
Figure 12, it would be possible to use a shorter simulation time in the case where initial species concentrations are estimated with an ANN.