Variable Pitch Approach for Performance Improving of Straight-Bladed VAWT at Rated Tip Speed Ratio
Abstract
Featured Application
Abstract
1. Introduction
2. Explanation of Variable Pitch Concept
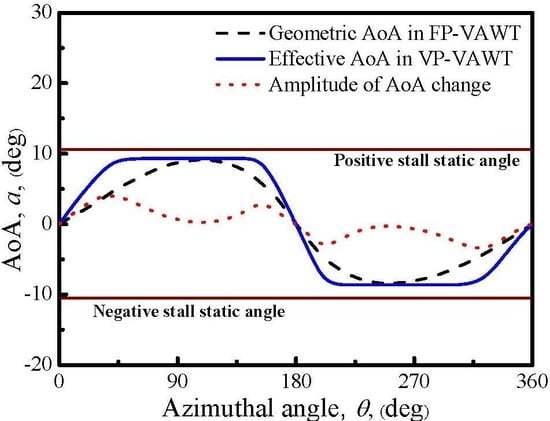
2.1. Oscillating AoA
2.2. Aerodynamics in Traditional VP-Technology
2.3. New VP-Approach
- (1)
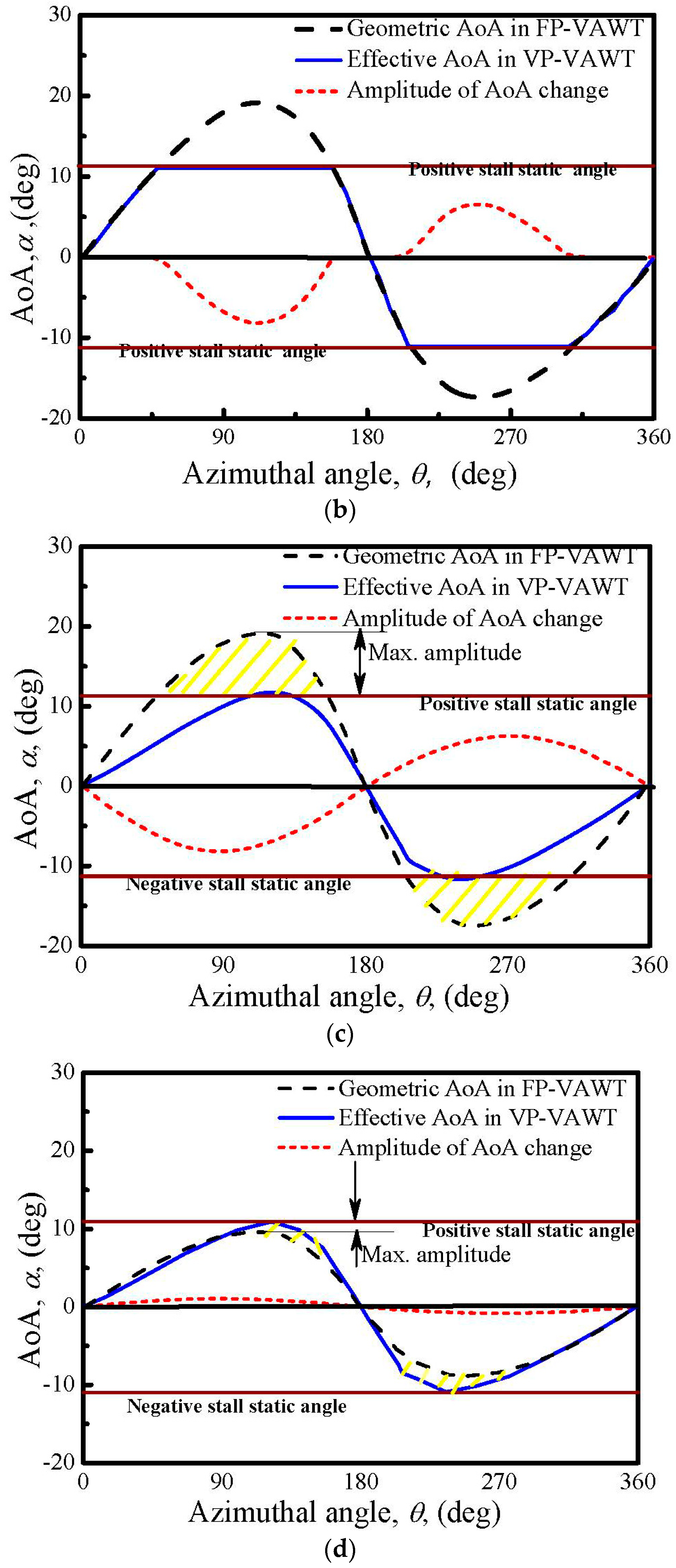
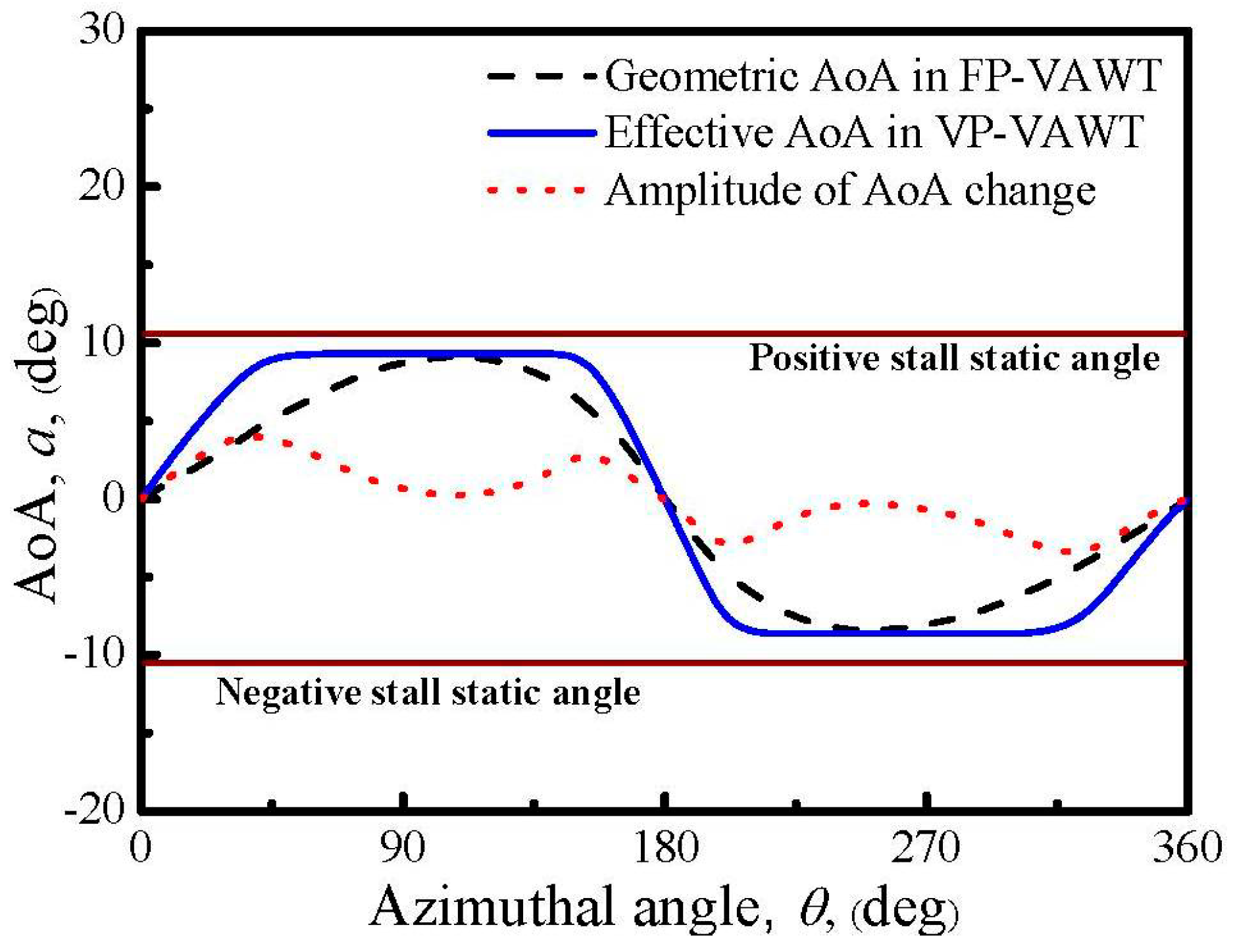
- How to deal with the zero AoA at the azimuthal angles of 0° and 180°: Since the positions of the 0° and 180° angles are the transformation points between the positive and negative AoAs, the design of the new VP-approach cannot avoid the zero value AoAs. The pitch angles in these two positions remain at the zero value.
- (2)
- How to set the value of the constant effective AoA in Figure 6: At the rated TSR, the largest local AoA in a cycle should be designed as the optimum AoA corresponding to the largest lift–drag ratio, rather than the static stall AoA. Thus, if the pitch curve of the new approach is designed for a blade operating at the rated TSR, the constant value in Figure 6 should be equal to the maximum geometric AoA in a FP-VAWT, since both a larger and a smaller value would contribute to a smaller torque. Consequently, the pitch angles are also kept at zero at the two inflection-point locations, namely the azimuthal angles of 90° and 270°.
- (3)
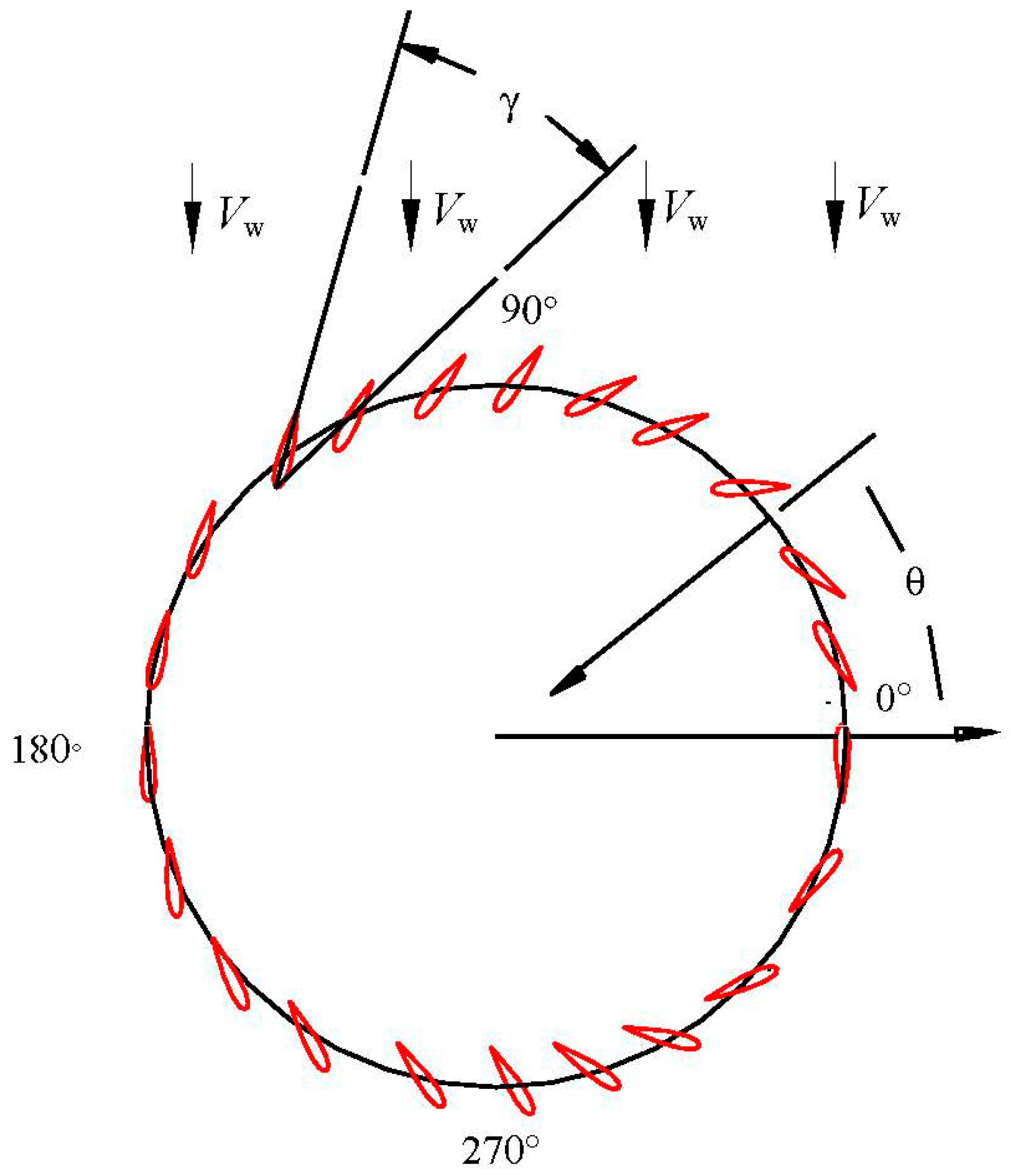
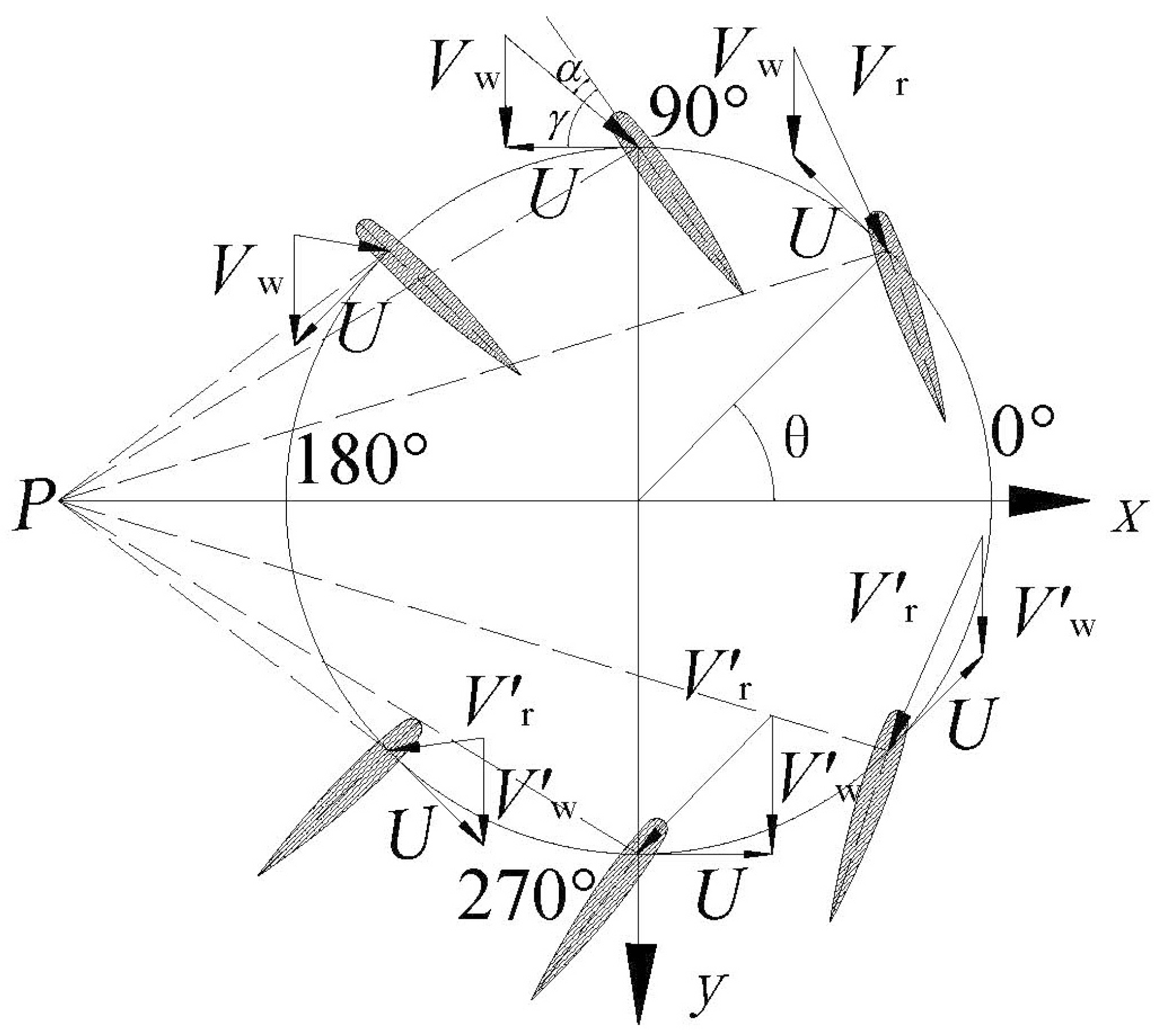
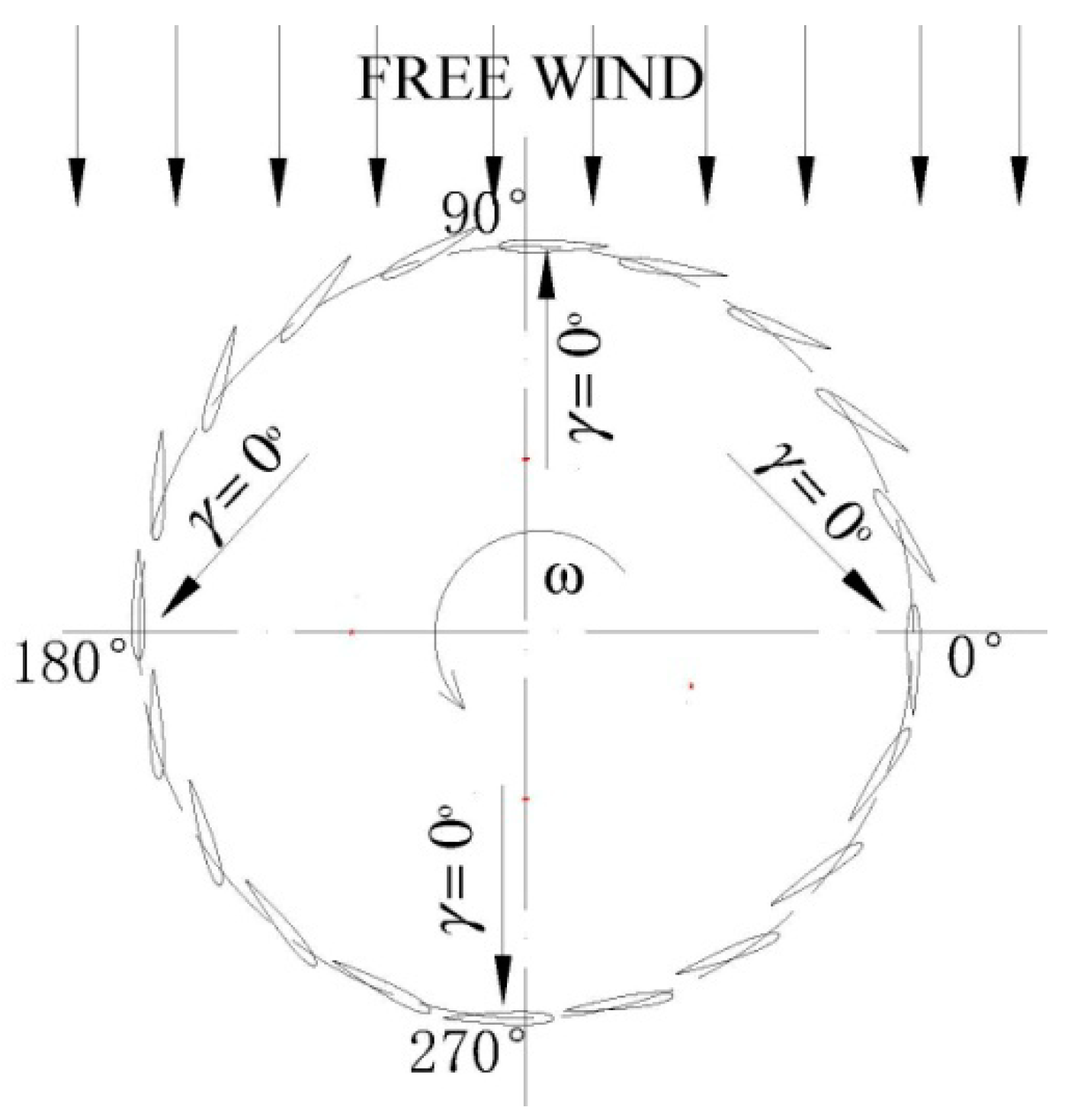
- Is the approach physically and mechanically feasible to implement? The amplitude of the change of the pitch angle is shown in Figure 6 as a dotted curve. In this curve, the pitch angle changes smoothly and continuously, and eliminates the drawback of the design in Figure 5b. The whole variation process of the pitch is illustrated in Figure 7, which is easily accomplished mechanically, such as a specially designed cam. As shown in Figure 7, the pitch angles varies in each ¼ circle (0°–90°, 90°–180°, 180°–270°, and 270°–360°), and returns to zero at four positions (0°, 90°, 180°, and 270°). Here, we defined the presence of a positive pitch angle when the blade rotates counterclockwise around its own axis, and the leading edge of the blade points toward the inner side of the circular path. In contrast, the angle is negative when the blade rotates and the leading edge points in the opposite direction.
- (4)
- What is the effect of the new VP-approach on the performance of the blade? After the mechanical feasibility of the approach is validated in theory, the following study focuses on the investigation of the effect of the new VP-approach using the DMST model.
3. Computational Model
3.1. Geometric Characteristics of VATW
3.2. Aerodynamic Model of Double Multi Stream Tube (DMST) Model
3.3. Tip Loss Consideration
3.4. Computational Procedure
4. Results Analysis
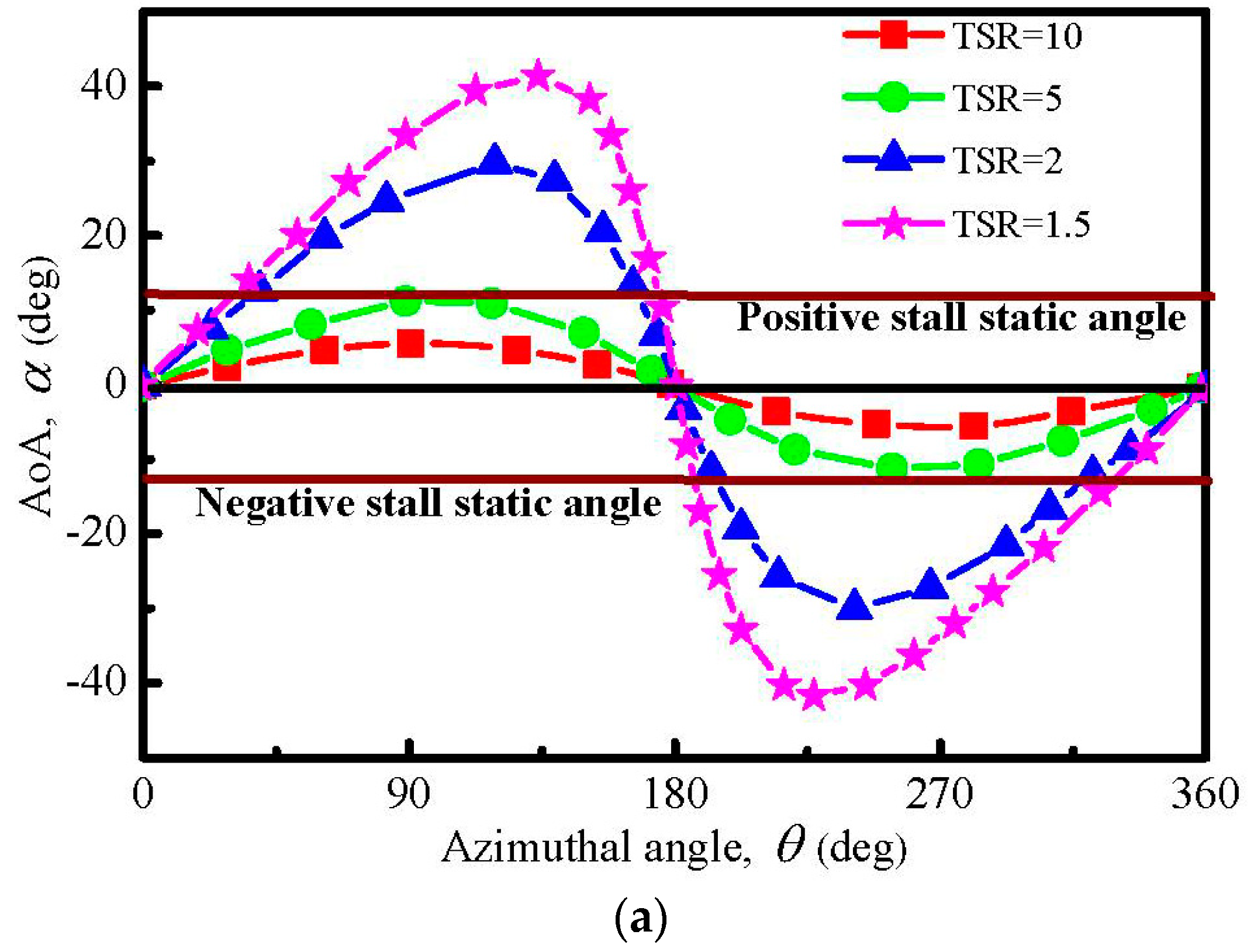
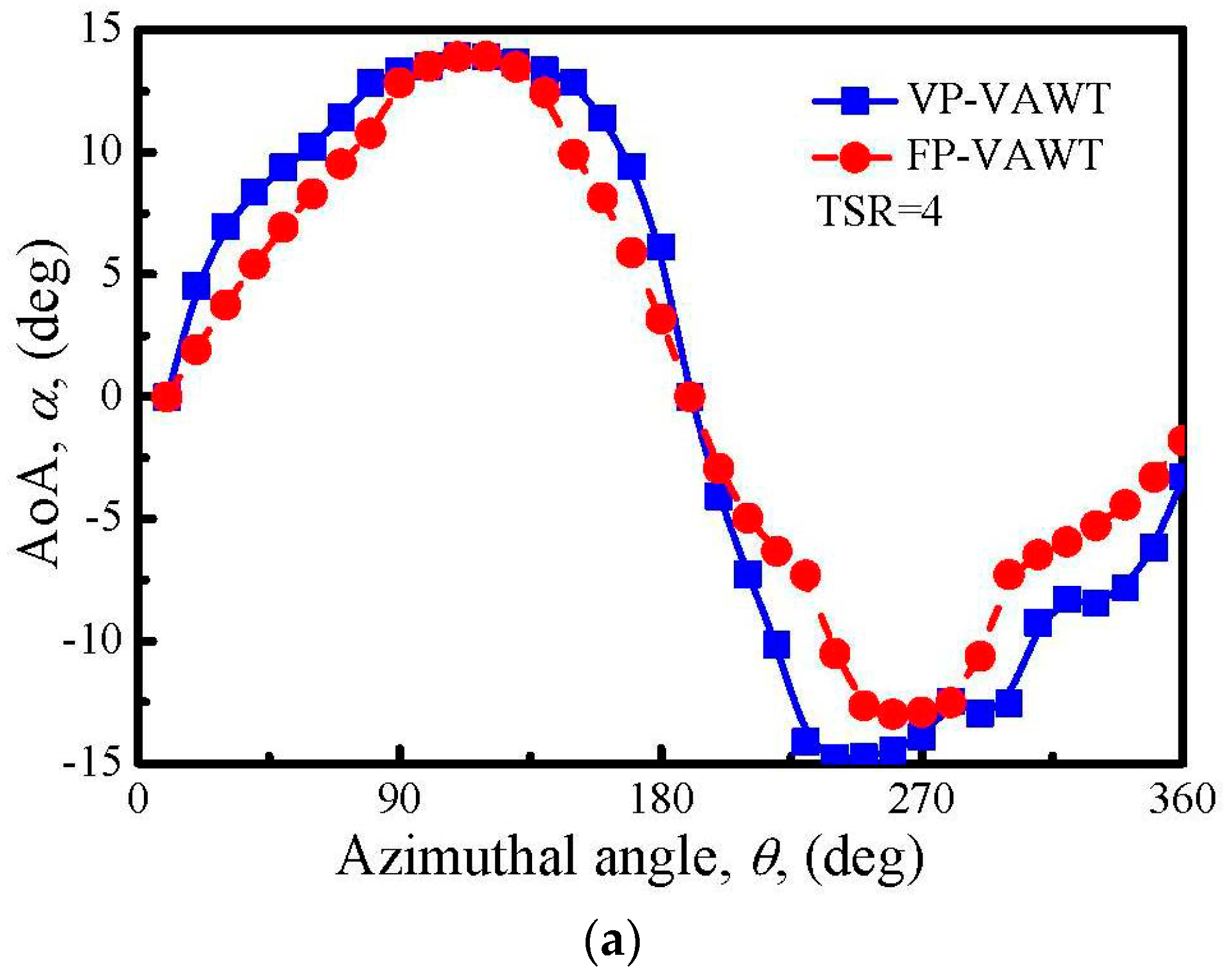
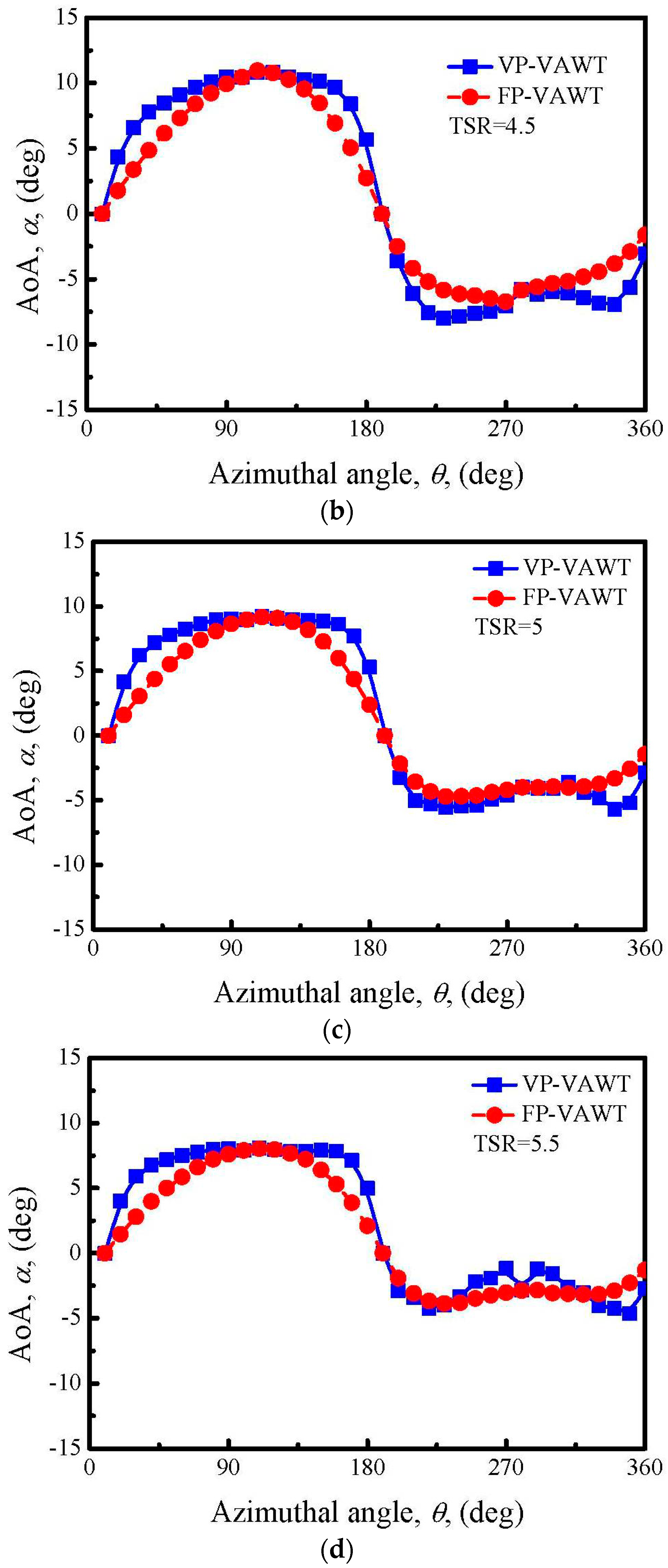
4.1. AoA Variation
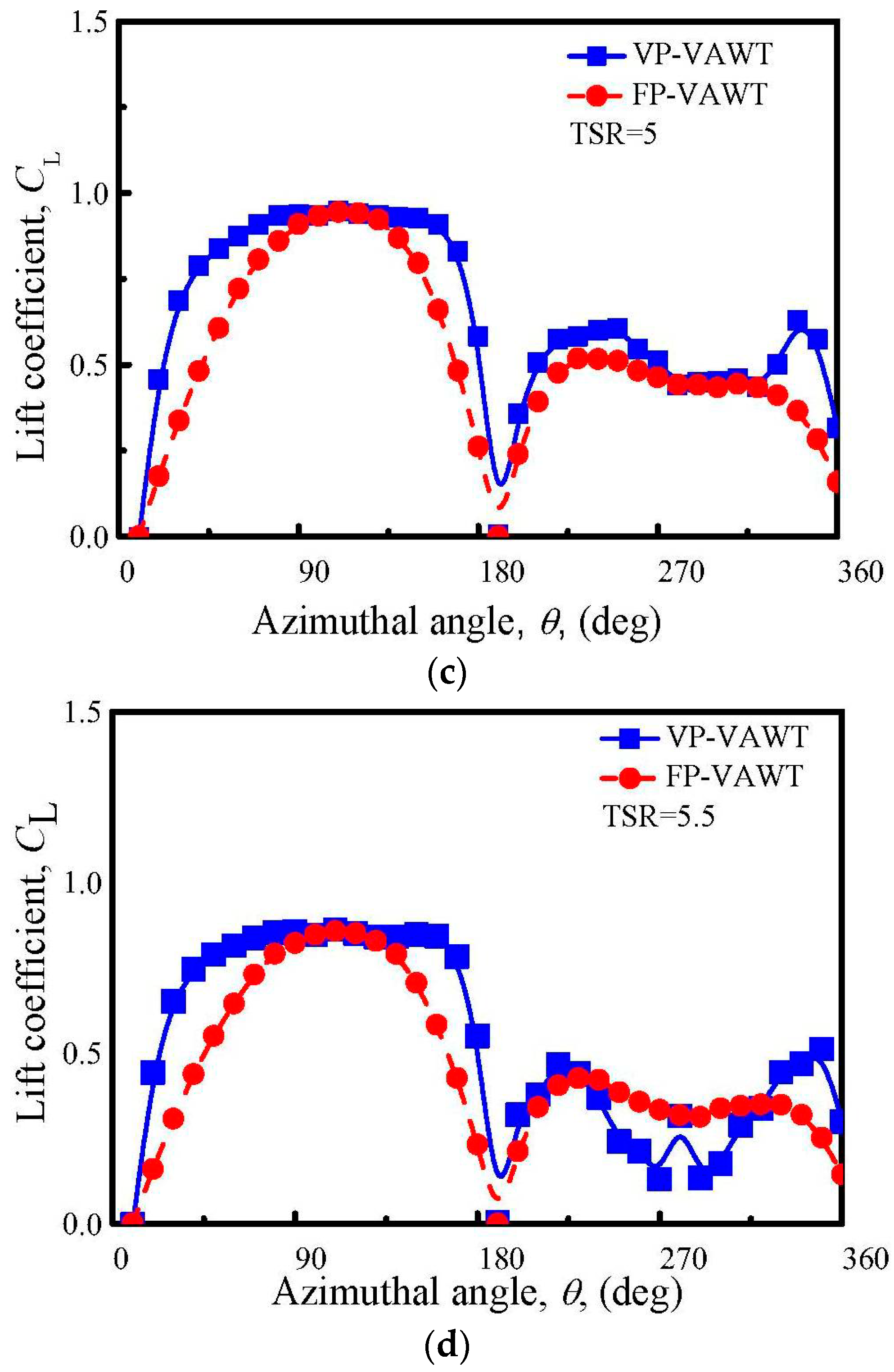
4.2. Lift Force Variation
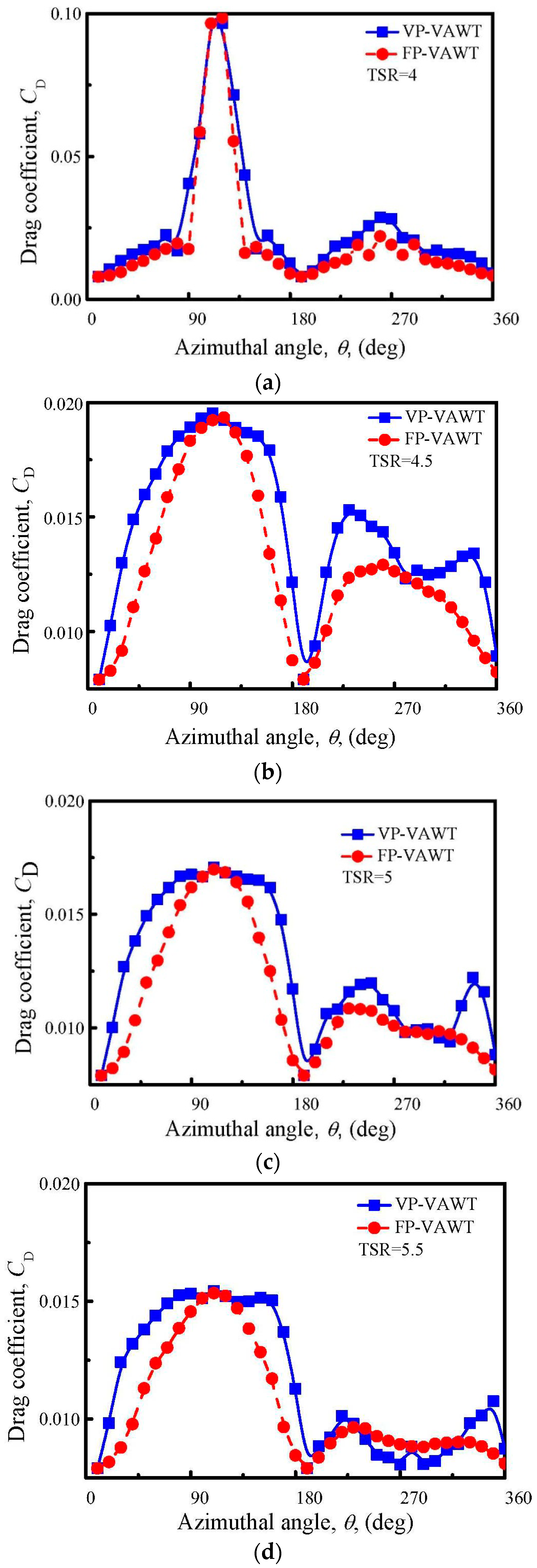
4.3. Drag Force Variation
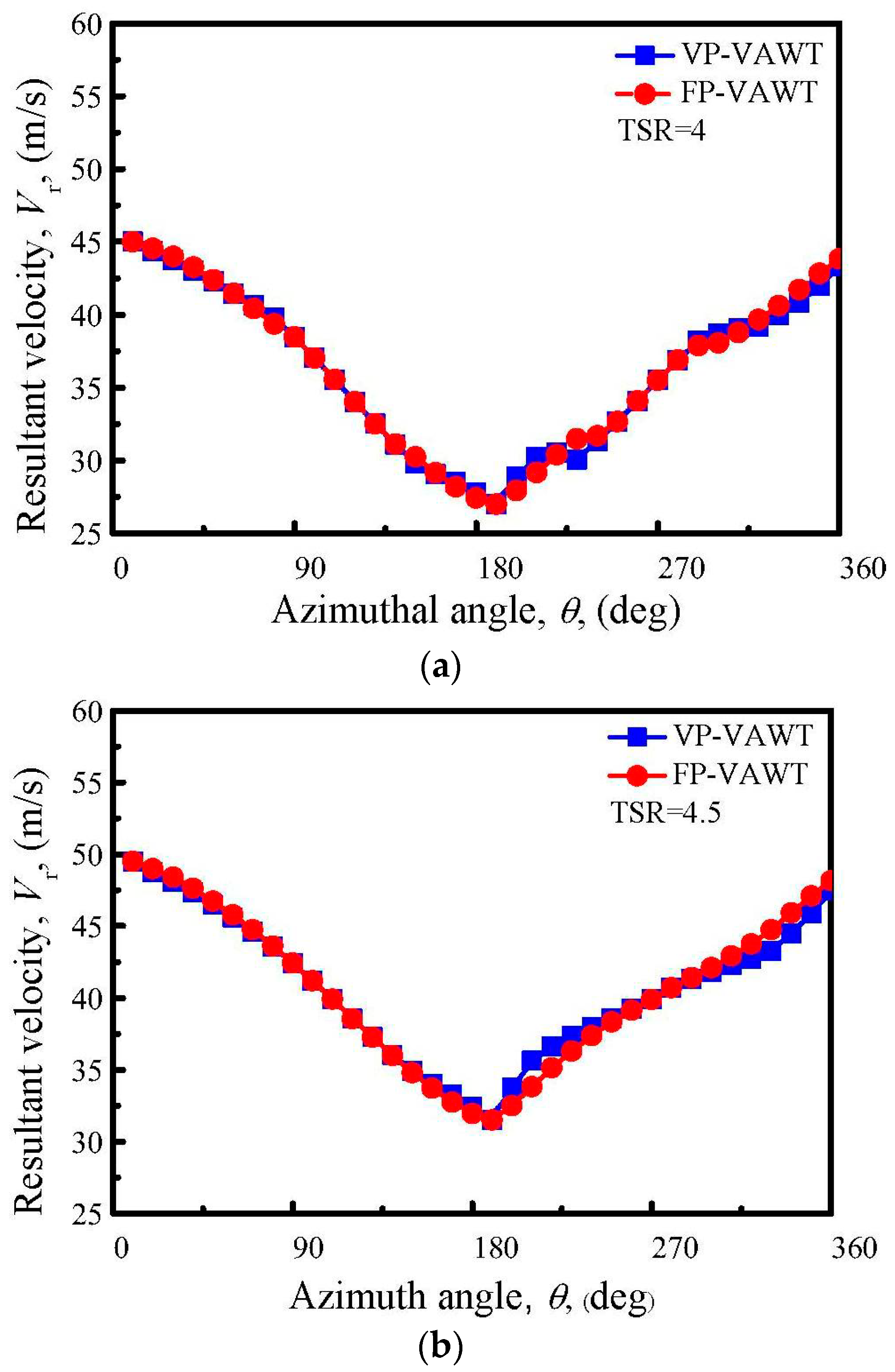
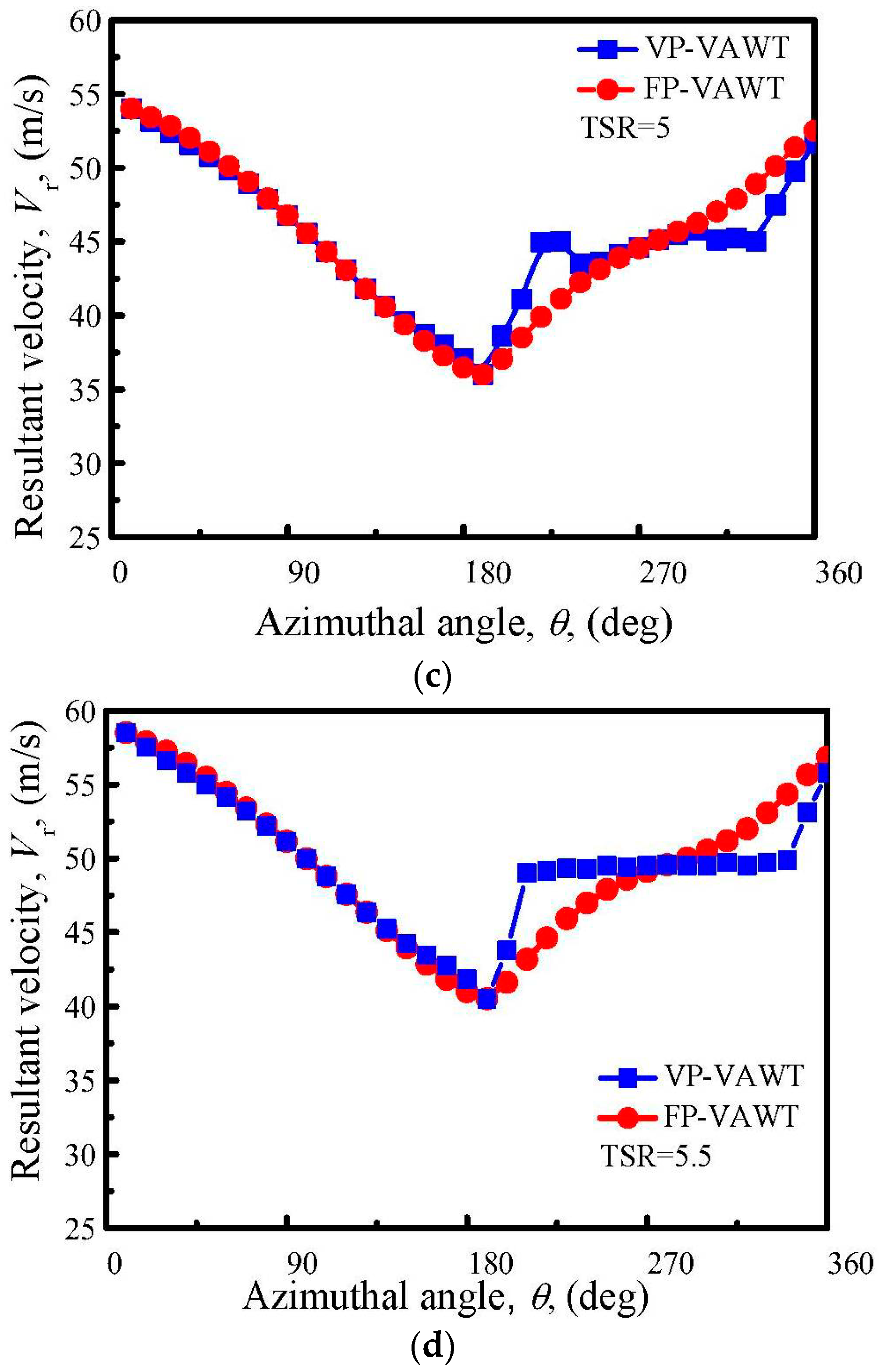
4.4. Resultant Velocity Variation
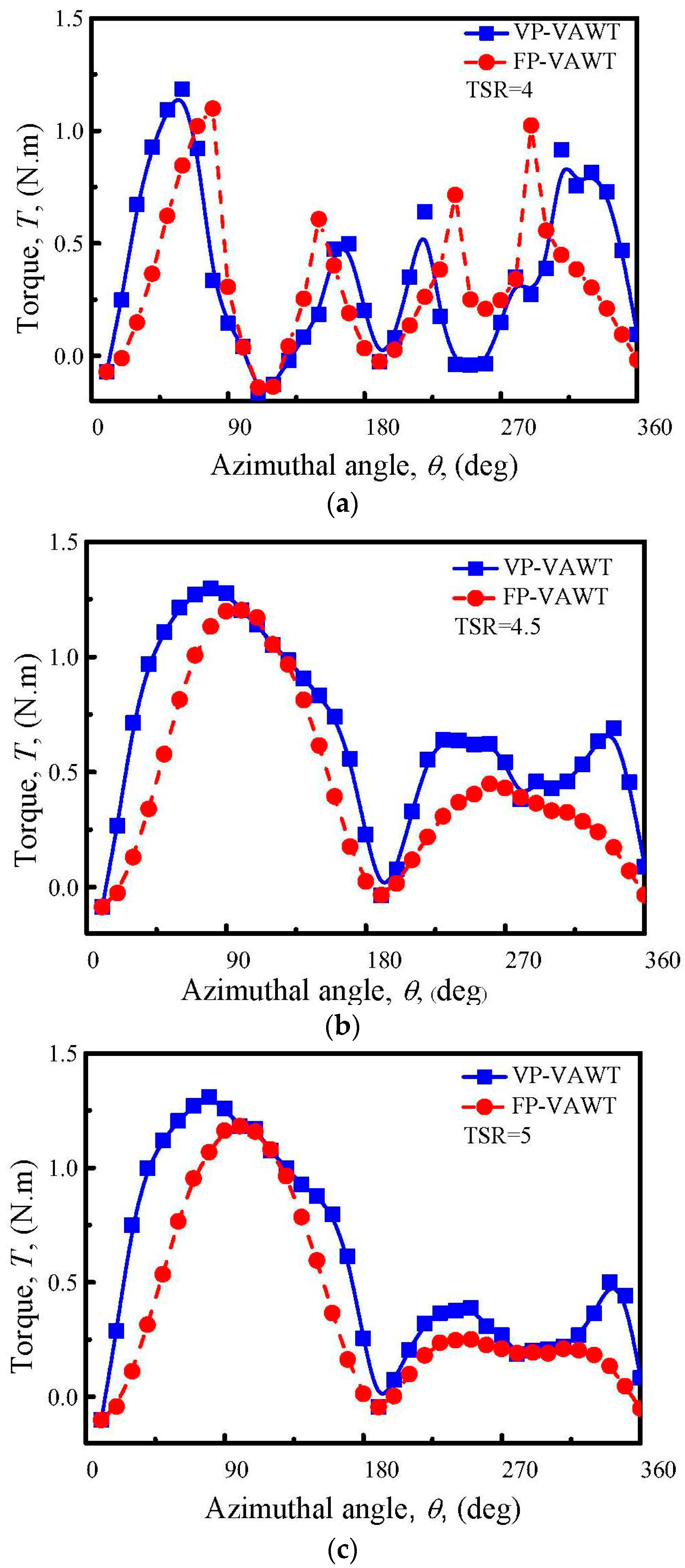
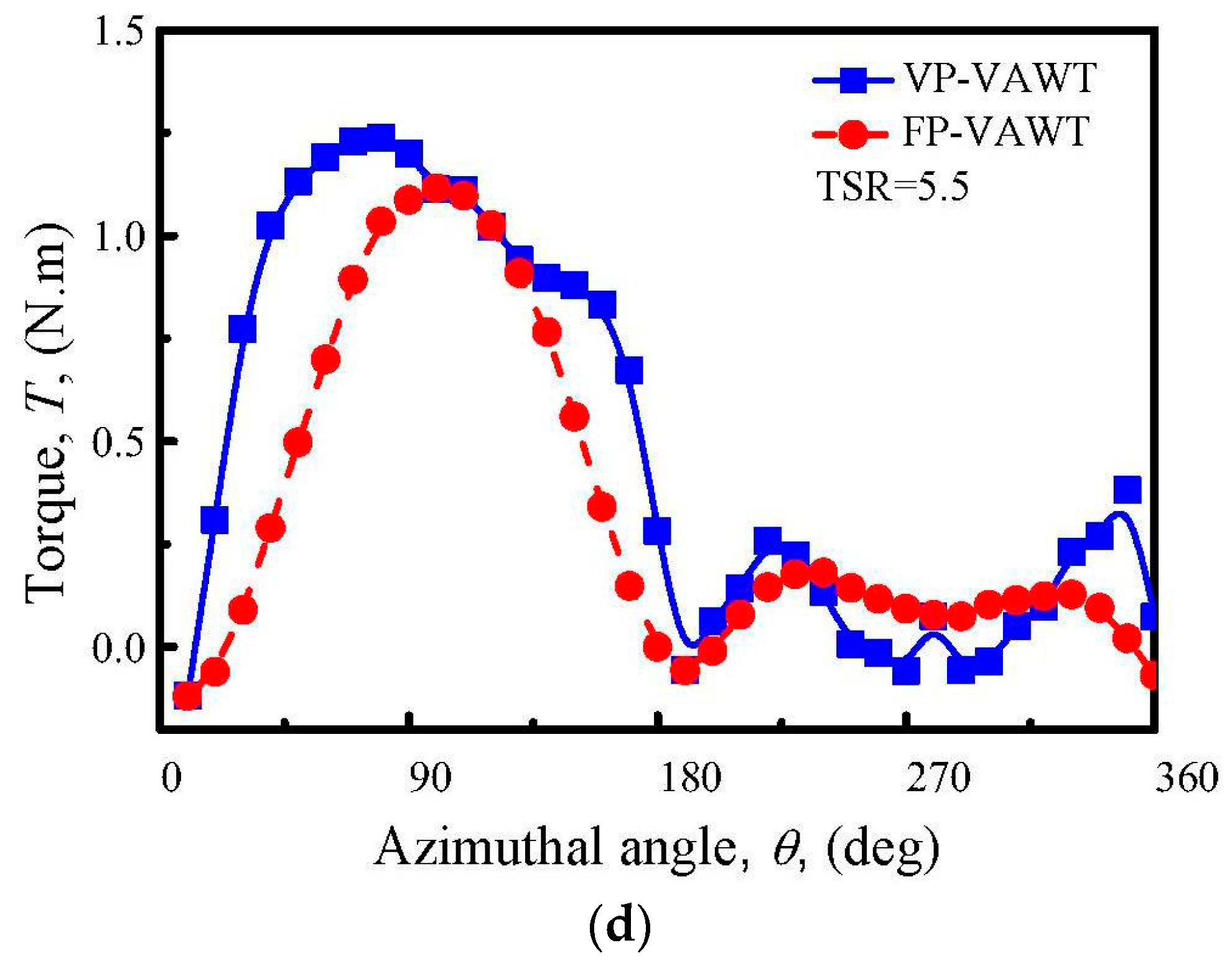
4.5. Torque of Blade Variation
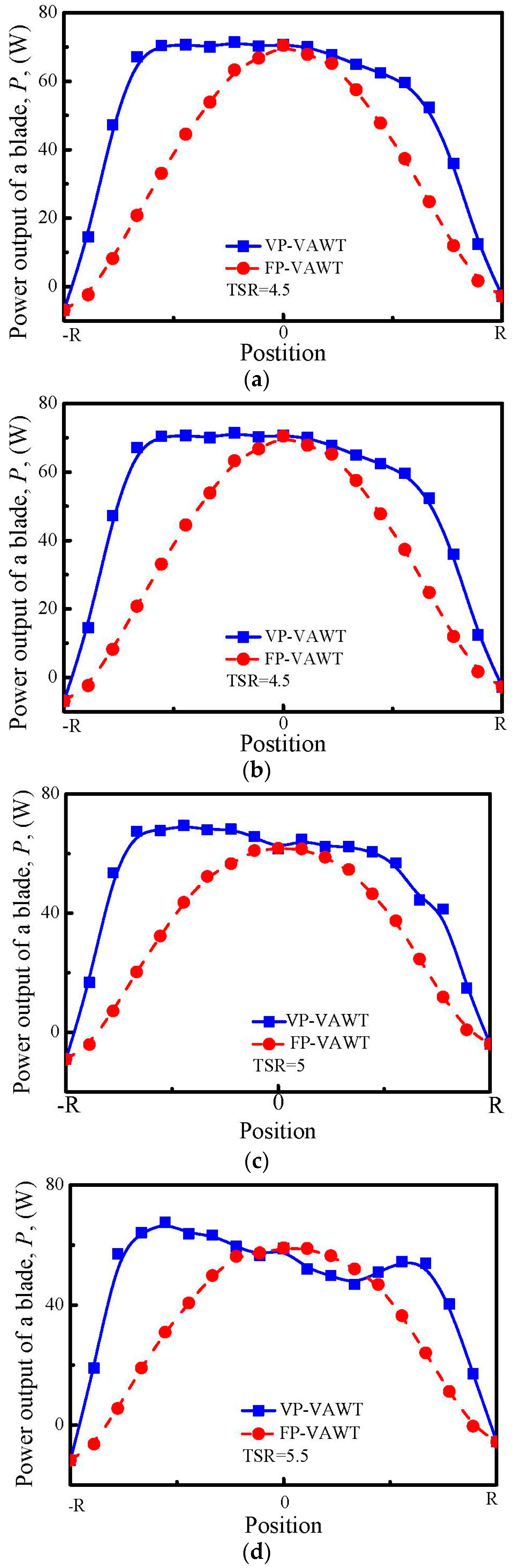
4.6. Power Output
5. Conclusions
- (1)
- Through the application of the new approach, a large increase in the AoA is produced in the upwind half-cycle of the VP-blade. A large increase in the AoA in the downwind half-cycle is also achieved when the TSR = 4, 4.5, and 5, but the increase becomes smaller as the TSR increases, so that a negative growth is shown when the TSR = 5.5.
- (2)
- The new approach greatly enhances the lift of the blade and distributes the maximum lift in a wider zone in the upwind region. In the downwind region, two new and larger maximum lifts are created when the TSR = 4.5 and 5, but a smaller lift is obtained when the TSR = 5.5.
- (3)
- The increased AoA leads to an increase of the drag of the blade in most of the positions. The trend of the distribution of the drag is similar to that of the lift.
- (4)
- The resultant velocity experiences little changes in the upwind region, while in the downwind region, the changes are obvious, and become more obvious as the TSR increases.
- (5)
- Influenced by the lift and drag, the ultimate effect of the torque shows that a large increase is obtained in the upwind region and downwind region at most of the TSRs. The distribution trend is also much like that of the lift.
- (6)
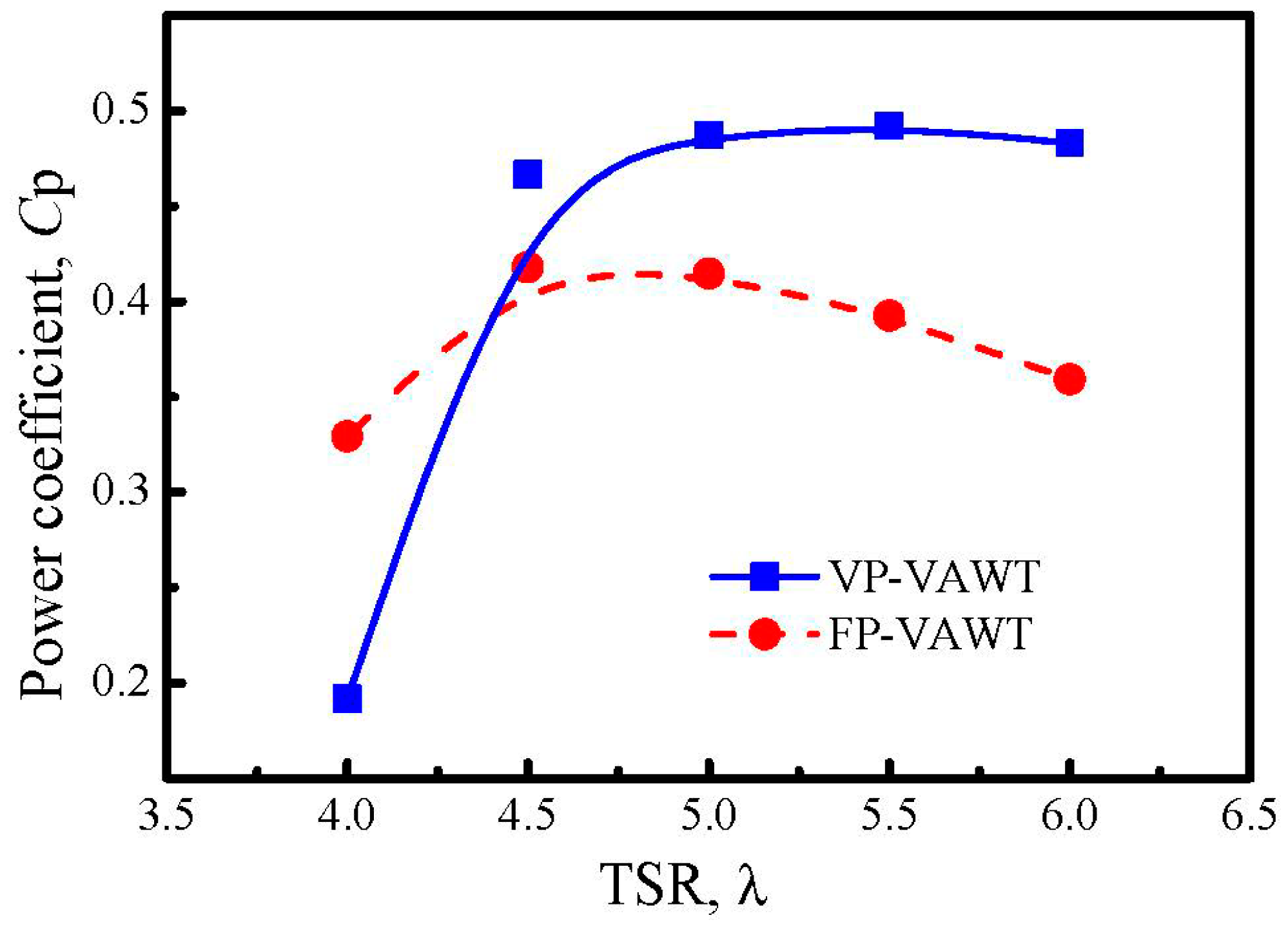
- The new VP-approach also enlarges the azimuthal zone of the blade with the highest power output. Consequently, an 18.9% increase of the peak power efficiency of the VAWT is achieved when the TSR = 4.5. Additionally, the turbines are capable of working with high efficiency in a wider TSR zone. The new VP-approach designed at the rated TSR is suitable to enhance the peak efficiency of VAWTs.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman Letters | |
| a | induction factor |
| Ac | amplitude of the pitch angle, [deg] |
| As | Max amplitude of the pitch angle, [deg] |
| c | length of chord line, [m] |
| CD | drag coefficient |
| CL | lift coefficient |
| CN | normal force coefficient |
| CT | tangential force coefficient |
| CP | power coefficient |
| N | number of blade |
| H | ½ height of rotor, [m] |
| R | equatorial radius of rotor, [m] |
| S | swept area of wind rotor, [m2] |
| U | Tangential velocity, [m/s] |
| Vr | resultant velocity, [m/s] |
| Vw | free wind velocity, [m/s] |
| X0 | TSR of max CP at zero Ac |
| AoA | angle of attack, [deg] |
| CFD | computational fluid dynamics |
| DMST | double multi stream tube (model) |
| FP | Fixed pitch |
| HAWT | horizontal axis wind turbine |
| VAWT | vertical axis wind turbine |
| TSR | tip speed ratio |
| VP | variable pitch |
| Greek Letters | |
| α | angle of attack, [deg] |
| ρ | density of air, [kg·m−3] |
| θ | azimuthal angle, [deg] |
| ω | rotor angular velocity, [rad·s−1] |
| λ | tip speed ratio (TSR) |
| γ | pitch angle changed with the azimuth, [deg] |
| ξ | dimensionless parameter of height |
References
- Kosaku, T.; Sano, M.; Nakatani, K. Optimum pitch control for variable-pitch vertical-axis wind turbines by a single stage model on the momentum theory. In Proceedings of the IEEE Conference on Systems, Man and Cybernetics, Yasmine Hammamet, Tunisia, 6–9 October 2002. [Google Scholar] [CrossRef]
- Bhutta, M.M.A.; Hayat, N.; Farooq, A.U.; Ali, Z.; Jamil, S.R.; Hussain, Z. Vertical axis wind turbine–A review of various configurations and design techniques. Renew. Sustain. Energy Rev. 2012, 16, 1926–1939. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.F.; Zhao, S.Y.; Feng, F.; Li, J.Y.; Wang, N.X.; Bai, R.B. A review on aerodynamic characteristics ofstragith-bladed vertical axis wind turbine. Acta Aerodyn. Sin. 2017, 35, 368–385. [Google Scholar]
- Kiwata, T.; Yamada, T.; Kita, T.; Takata, S.; Komatsu, N.; Kimura, S. Performance of a vertical axis wind turbine with variable-pitch straight blades utilizing a linkage mechanism. J. Environ. Eng. 2010, 5, 213–225. [Google Scholar] [CrossRef]
- Aggarwal, A.; Mishra, D.; Chandramaouli, V. Study on optimization of control mechanism in vertical axis wind turbine. Indian J. Sci. Technol. 2017, 10, 1–10. [Google Scholar] [CrossRef]
- Claessens, M.C. The Design and Testing of Airfoils in Small Vertical Axis Wind Turbines. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Staelens, Y.; Saeed, F.; Paraschivoiu, I. A straight-bladed variable-pitch VAWT concept for improved power generation. AIAA-2003-0524. In Proceedings of the ASME 2003 Wind Energy Symposium, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Kirke, B.K. Evaluation of Self-Starting Vertical Axis wind Turbines for Stand-Alone Applications. Ph.D. Thesis, Griffith University Gold Coast, Brisbane, Australia, 1998. [Google Scholar]
- Cooper, P.; Kennedy, O.C. Development and analysis of a new novel Vertical Axis Wind Turbine. In Proceedings of the 42nd Annual Conference of the Australian and New Zealand Solar Society, Perth, Australia, 30 November–3 December 2004. [Google Scholar]
- Beri, H.; Yao, Y. Effect of camber airfoil on self-starting of vertical axis wind turbine. J. Environ. Sci. Technol. 2011, 4, 302–312. [Google Scholar] [CrossRef]
- Zamani, M.; Maghrebi, M.J.; Moshizi, S.A. Numerical study of airfoil thickness effects on the performance of J-shaped straight blade vertical axis wind turbine. Wind Struct. 2016, 22, 595–616. [Google Scholar] [CrossRef]
- Zamani, M.; Maghrebi, M.J.; Varedi, S.R. Starting torque improvement using J-shaped straight-bladed Darrieus vertical axis wind turbine by means of numerical simulation. Renew. Energy 2016, 95, 109–126. [Google Scholar] [CrossRef]
- Sun, X.J.; Chen, Y.J.; Cao, Y.; Wu, G.Q.; Zheng, Z.Q.; Huang, D.G. Research on the aerodynamic characteristics of a lift drag hybrid vertical axis wind turbine. Adv. Mech. Eng. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Dwiyantoro, B.A.; Suphandani, V. The system design and performance test of hybrid vertical axis wind turbine. AIP Conf. Proc. 2017, 1831, 020030. [Google Scholar] [CrossRef]
- Bianchini, A.; Ferrara, G.; Ferrari, L. Pitch Optimization in small-size Darrieus wind turbines. Energy 2015, 81, 122–132. [Google Scholar] [CrossRef]
- Pawsey, N.C.K. Development and Evaluation of Passive Variable-Pitch Vertical Axis Wind Turbines. Ph.D. Thesis, The University of New South Wales, Sydney, NSW, Australia, 2002. [Google Scholar]
- Chougule, P.; Nielsen, S. Overview and Design of self-acting pitch control mechanism for vertical axis wind turbine using multi body simulation approach. J. Phys. 2014, 524, 012055. [Google Scholar] [CrossRef]
- Sagharichi, A.; Maghrebi, M.J.; ArabGolarcheh, A. Variable pitch blades: An approach for improving performance of Darrieuswind turbine. J. Renew. Sustain. Energy 2016, 8, 053305. [Google Scholar] [CrossRef]
- Xisto, C.M.; Páscoa, J.C.; Leger, J.A.; Trancossi, M. Wind energy production using an optimized variable pitch vertical axis rotor. In Proceedings of the Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Erickson, D.W.; Wallace, J.J.; Peraire, J. Performance Characterization of Cyclic Blade Pitch Variation on a Vertical Axis Wind Turbine. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Hwang, I.S.; Yun, H.L.; Kim, S.J. Optimization of cycloidal water turbine and the performance improvement by individual blade control. Appl. Energy 2009, 86, 1532–1540. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.S.K.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087–1109. [Google Scholar] [CrossRef]
- Schonborn, A.; Chantzidakis, M. Development of a hydraulic control mechanism for cyclic pitch marine current turbines. Renew. Energy 2007, 32, 662–679. [Google Scholar] [CrossRef]
- Camporealea, S.M.; Magi, V. Streamtube model for analysis of vertical axis variable pitch turbine for marine currents energy conversion. Energy Convers. Manag. 2000, 41, 1811–1827. [Google Scholar] [CrossRef]
- Zuo, W.; Kang, S. Numerical simulation of aerodynamic performance of H-type wind turbine with pitch angle changing. J. Eng. Thermophys. 2015, 36, 501–504. [Google Scholar]
- Paraschivoiu, I. Wind Turbine Desigh with Emphasis on Darrieus Concept; Polytechnic International Press: Montreal, QC, Canada, 2002. [Google Scholar]
- Templin, R.J. Aerodynamic Performance Theory for the NRC Vertical-Axis Wind Turbine; LTR-LA-160; National Research Council of Canada: Ottawa, ON, Canada, 1974. [Google Scholar]
- Strickland, J.H. Darrieus Turbine: A Performance Prediction Model Using Multiple Streamtubes; SAND75-0431; Sandia National Laboratories: Livermore, CA, USA, 1975. [Google Scholar]
- Paraschivoiu, I.; Delclaux, F. Double multiple streamtube model with recent improvements (for predicting aerodynamic loads and performance of Darrieus vertical axis wind turbines). J. Energy 1983, 7, 250–255. [Google Scholar] [CrossRef]
- Paraschivoiu, I.; Trifu, O.; Saeed, F. H-Darrieus Wind Turbine with Blade Pitch Control. Int. J. Rotat. Mach. 2009, 2009, 505343. [Google Scholar] [CrossRef]
- Soraghan, C.E.; Leithead, W.E.; Yue, H.; Feuchtwang, J. Double Multiple Streamtube Model for Variable Pitch Vertical Axis Wind Turbines; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar]
- Saeidi, D.; Sedaghat, A.; Alamdari, P.; Alemrajabi, A.A. Aerodynamic design and economical evaluation of site specific small vertical axis wind turbines. Appl. Energy 2013, 101, 765–775. [Google Scholar] [CrossRef]
- Zhao, Z.Z.; Yan, C.; Wang, T.G.; Xu, B.F.; Zheng, Y. Study on approach of performance improvement of VAWT employing double multiple stream tubes model. J. Sustain. Renew. Energy 2017, 9, 023305. [Google Scholar] [CrossRef]
- Ferrer, E.; Willden, R. Blade-wake interactions in cross-flow turbines. Int. J. Mar. Energy 2015, 11, 71–83. [Google Scholar] [CrossRef]
- Elkhoury, M.; Kiwata, T.; Aoun, E. Experimental and numerical investigation of a three-dimensional vertical-axis wind turbine with variable-pitch. J. Wind Eng. Ind. Aerodyn. 2015, 139, 111–123. [Google Scholar] [CrossRef]
- Firdaus, R.; Kiwata, T.; Kono, T.; Nagao, K. Numerical and experimental studies of a small vertical-axis wind turbine with variable-pitch straight blades. J. Fluid Sci. Technol. 2015, 10, 14–29. [Google Scholar] [CrossRef]
- Sengupta, A.; Biswas, A.; Gupta, R. Studies of some high solidity symmetrical and unsymmetrical blade H-Darrieus rotors with respect to starting characteristics, dynamic performances and flow physics in low wind streams. Renew. Energy 2016, 93, 536–547. [Google Scholar] [CrossRef]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; SAND80-2114; Sandia National Laboratories: Livermore, CA, USA, 1981. [Google Scholar]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Wang, R.; Shen, W.; Wang, T.; Xu, B.; Zheng, Y.; Qian, S. Variable Pitch Approach for Performance Improving of Straight-Bladed VAWT at Rated Tip Speed Ratio. Appl. Sci. 2018, 8, 957. https://doi.org/10.3390/app8060957
Zhao Z, Wang R, Shen W, Wang T, Xu B, Zheng Y, Qian S. Variable Pitch Approach for Performance Improving of Straight-Bladed VAWT at Rated Tip Speed Ratio. Applied Sciences. 2018; 8(6):957. https://doi.org/10.3390/app8060957
Chicago/Turabian StyleZhao, Zhenzhou, Ruixin Wang, Wenzhong Shen, Tongguang Wang, Bofeng Xu, Yuan Zheng, and Siyue Qian. 2018. "Variable Pitch Approach for Performance Improving of Straight-Bladed VAWT at Rated Tip Speed Ratio" Applied Sciences 8, no. 6: 957. https://doi.org/10.3390/app8060957
APA StyleZhao, Z., Wang, R., Shen, W., Wang, T., Xu, B., Zheng, Y., & Qian, S. (2018). Variable Pitch Approach for Performance Improving of Straight-Bladed VAWT at Rated Tip Speed Ratio. Applied Sciences, 8(6), 957. https://doi.org/10.3390/app8060957