In this research two test systems are used to evaluate the performance of the proposed algorithm which are the 33-bus radial distribution system and the 69-bus radial distribution systems along with different load levels were utilized.
5.1. Results of 33-Bus Radial Distribution System
The 33-bus radial distribution system consists of a feeder, 5 tie switches. The total nominal load of this system is 3715 kW and 2300 kVAr. On the other hand, the 69-bus radial distribution system consists of a feeder and involves 5 tie switches. The total nominal load system is 3802 kW and 2695 kVAr. Both systems MVA base has a base power constant, of 100 MVA and base voltage of 12.66 kV. The maximum active output of DG in this study is set at 50% of the connected load. The size of a population for test systems is assumed to be 20, while, the convergence value is taken as 0.0001.
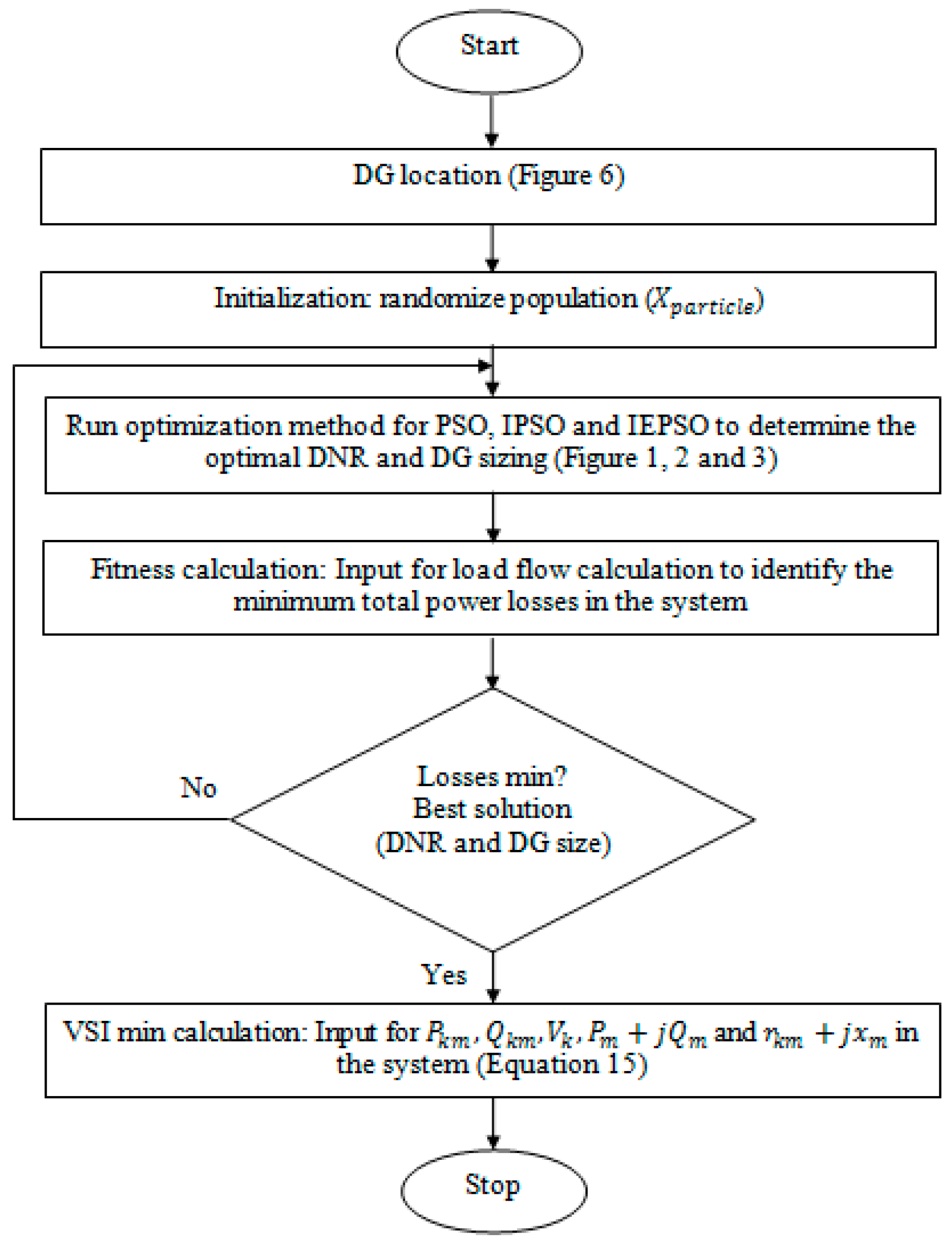
The analysis of the results has been divided into three main parts, which are: (i) determination of DG location; (ii) minimization of total power losses (TPL) and VSI improvement with DNR implementation; and (iii) minimization of TPL and VSI improvement with DNR and DG implementation. Three situations have been considered in this study, which are base case, DNR, and DNR with DG. Three load levels are classified into; light, nominal and heavy load in order to evaluate the performance of TPL and VSI respectively. Each situation except for base case has been analyzed among PSO, IPSO and IEPSO algorithms.
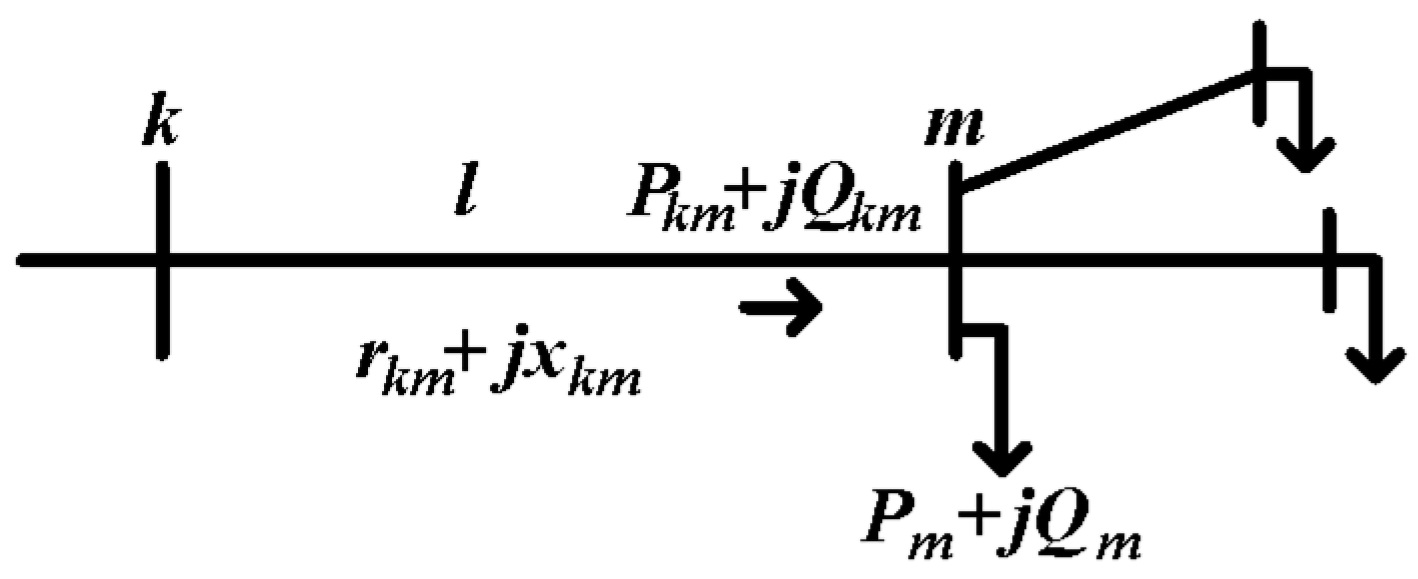
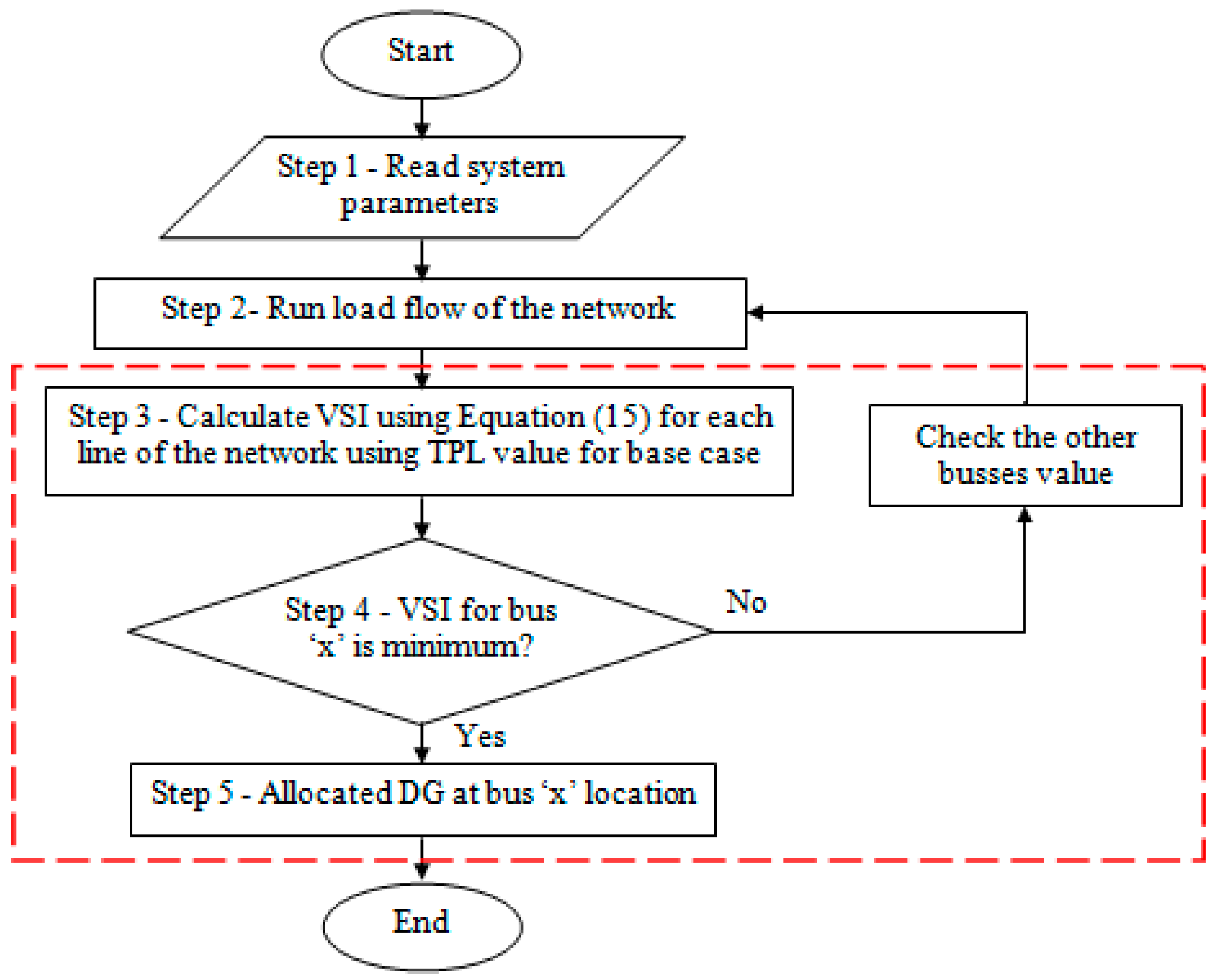
Initially, the DG location has been set up according to the bus with minimum VSI. The minimum VSI means the most sensitive probability to voltage collapse. The DG is assumed to operate in PQ mode, where the power output is constant. Then, the stability index,
is calculated to verify the results obtained as shown in
Table 1.
In this research, there are three categories to be analyzed namely base case, DNR and DNR with DG sizing. The analysis is discussed according to three identified load levels as light, nominal and heavy load. Thus, the performances are evaluated among case 1 (base case), case 2 (PSO), case 3 (IPSO) and case 4 (IEPSO).
Table 2 shows base case results without reconfiguration and DG placement (case 1). From the table, the VSI values are inversely proportional with TPL for each possibility load levels. In other words, by increasing the load levels, the total loss has significantly increased and the stability is decreased.
On the other hand,
Table 3 summarizes the performance of three optimization techniques for DNR switches, the TPL, VSI, the minimum bus voltage profile and computational time for these three different load levels. From the result obtained in
Table 3, the IEPSO technique provided the best optimal solution with the lowest power losses, improved VSI and less computational time as indicated in bold among all load conditions. From the results, IEPSO technique offered the most completion reduction with 4.16% for TPL, the fastest in computational time, 2.62% highest VSI in light load among others with identified methods.
In addition to that, tor nominal load, IEPSO technique also gave the most reduction with 23.26% in TPL, 5.21% highest VSI, but slightly defeated in computational time compared to IPSO by 0.7 s in nominal load. Finally, for heavy load, IEPSO technique gave the most reduction with 31.36% in TPL, 21.14% highest VSI, the fastest in computational time in heavy load compared to other techniques.
As for the DNR with DG placement case,
Table 4 summarizes the performances of three optimization techniques in DNR with DG sizing simultaneously for switches, TPL, VSI, voltage profile, DG sizing and computational time at three different load levels. As noted from
Table 4, the IEPSO technique gives the best optimal solution with the lowest power losses, improved VSI and computational time as indicated in bold for all load conditions. The increased in load levels, gave results in increasing power losses and decreasing VSI.
For light load, IEPSO technique gave the most reduction with 17.98% in TPL, 10.34% highest VSI, the fastest in computational time in light load compared to other techniques. Meanwhile, for nominal load IEPSO technique gave the most reduction with 36.33% in TPL, 18.16% highest VSI, but slightly defeated for the computational time compared to IPSO by 4.45 s in nominal load level. Finally, for heavy load IEPSO technique gave also the most reduction with 37.73% in TPL, 28.22% highest VSI, the fastest in computational time in heavy load compared to other techniques.
As for system’s stability,
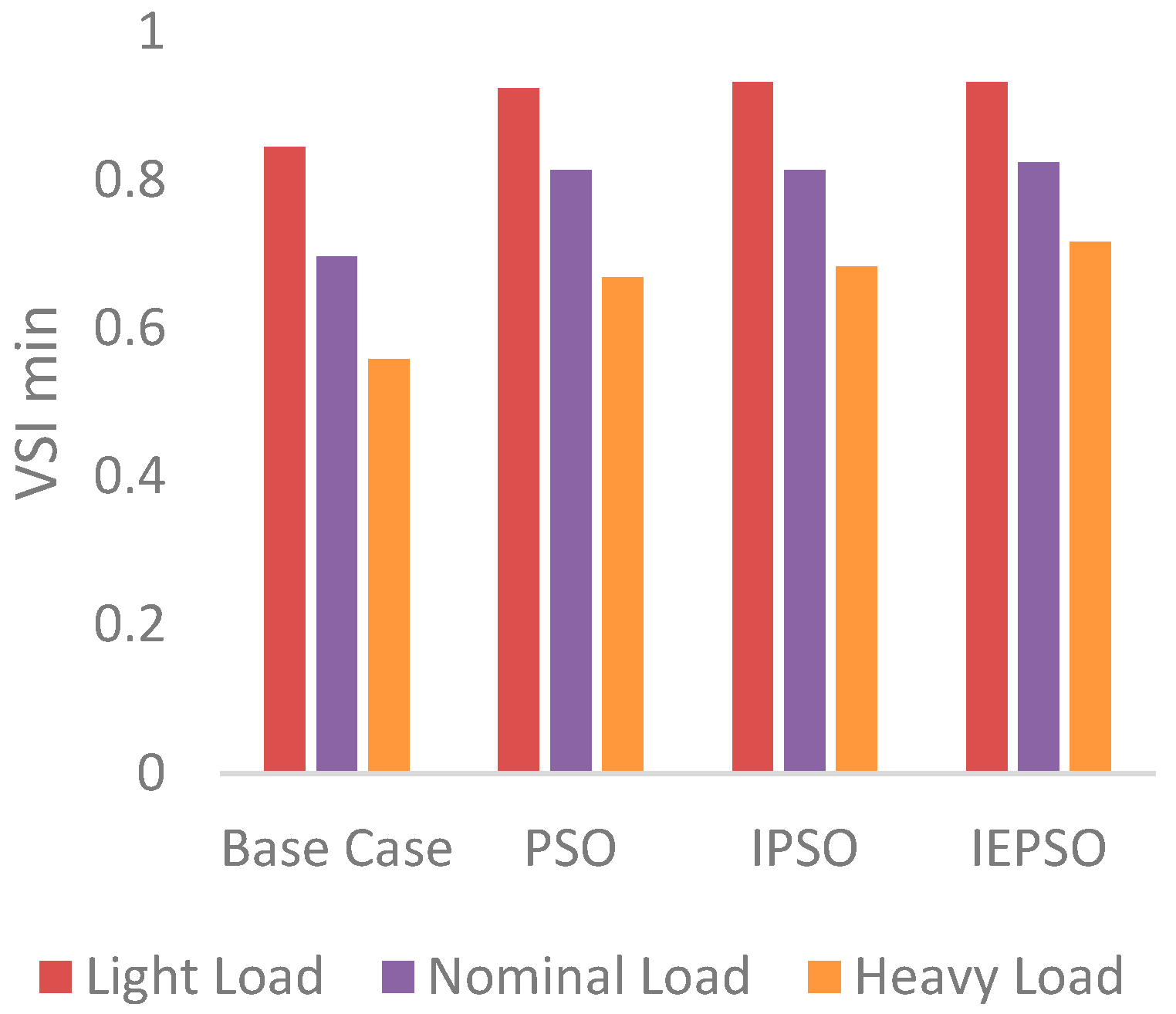
Figure 5 and
Figure 6 show some improvement in the stability for all cases, especially with proposed algorithm application on 33-bus test system. Generally, by increasing the load levels, the VSI will decreases. Thus, the stability of the system which leads to voltage collapse form the load demands increase.
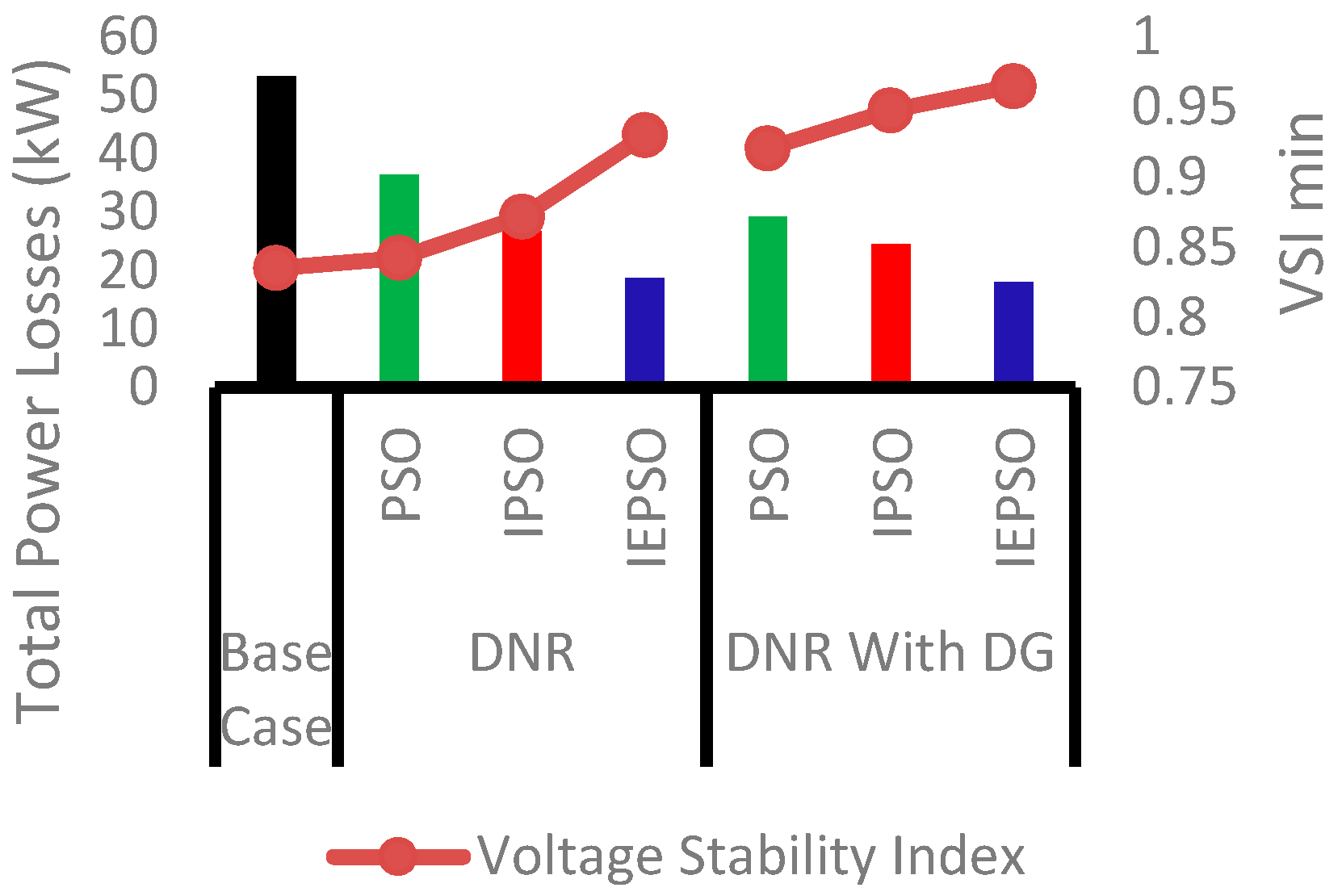
For comparison purposes,
Figure 7 shows a comparison of TPL and VSI for three cases which are base case, DNR without DG and DNR with DG for light, nominal and heavy load condition in 33-bus system. From the figures, it is shown that TPL is slightly reduced with DNR implementation. However, the TPL has a significant reduced when DNR and DG was applied to the system. Moreover, the VSI also improved when DNR and DG are implemented optimally in the system.
In addition, it is observed that during light load of 33-bus test system, the total power loss obtained from the PSO algorithm (case 2) with DG is 39.1 kW as compared to 45.9 kW without DG resulted to 14.45% TPL reduction. The VSI without DG is 0.8622 which is improved to be 0.9239 p.u. with DG integration. For IPSO algorithm (case 3), the total power loss is 38.9 kW with DG compared to 45.4 kW without DG with 6.5 kW differences, with 13.81% TPL reduction. The VSI without DG is 0.8657 which is improved to be 0.9316 with DG integration. Finally, For IEPSO algorithm (case 4), the total power loss is 38.6 kW with DG compared to 45.1 kW without DG with 6.5 kW differences, with 13.81% TPL reduction. The VSI without DG is only 0.8664 and enhanced to e 0.9316 with DG integration.
Similarly, it is observed that at nominal load in 33-bus test system, the total power loss obtained from the PSO algorithm (case 2) with DG is 145.1 kW compared to 167 kW without DG with 22 kW differences, resulted to 10.86% TPL reduction. The VSI without DG is 0.7181 which is improved to be 0.7861 with DG integration. For IPSO algorithm (case 3), the total power loss is 131.3 kW with DG compared to be 158.8 kW without DG with 27.5 kW differences, with 13.57% TPL reduction. The VSI without DG is 0.7216 which is improved to be 0.8133 with DG integration. Finally, For IEPSO algorithm (case 4), the total power loss is 129 kW with DG compared to 155.5 kW without DG with 26.5 kW differences, with 13.08% TPL reduction. The VSI without DG is 0.7333 which is improved to be 0.8236 with DG integration.
As for heavy load in 33-bus test system, the total power loss obtained from the PSO algorithm (case 2) with DG is 384.5 kW compared to 391 kW without DG with 6.5 kW differences, resulted in 1.31% TPL reduction. The VSI without DG is 0.6618 which is improved to be 0.6687 with DG integration. For IPSO algorithm (case 3), the total power loss is 309.8 kW with DG compared to 342.9 kW without DG with 33.1 kW differences, with 6.67% TPL reduction. The VSI without DG is 0.6718 which is improved to be 0.6828 with DG integration. For IEPSO algorithm (case 4), the total power loss is 309 kW with DG compared to 340.6 kW without DG with 31.6 kW differences, 6.37% TPL reduction. The VSI without DG is 0.6763 which is improved to be 0.7159 with DG integration.
5.2. Results of 69-Bus Radial Distribution System
Similarly, as before in 33-bus system, there are three parts to be analyzed; base case, DNR and DNR with DG sizing. At each part, the analysis is divided into three different load levels. Meanwhile, the comparison of the effectiveness of the proposed method is compared with the base case, PSO and IPSO.
Table 5 shows the base case without reconfiguration and DG placement. In light load level (50% of nominal load), the total power loss is 53.24 kW, while the minimum VSI is 0.8351.
For nominal load level, the total power loss is 229.73 kW, with the minimum VSI is 0.6799. Meanwhile, at heavy load level (150% of nominal load), the total power loss is 573.24 kW with minimum VSI is 0.5321. The VSI value is inversely proportional with total power loss. By increasing the load levels, the total power loss is increased significantly and the system becomes unstable.
On the other hand,
Table 6 summarizes the performances of three optimization technique in DNR for switches, TPL, VSI, voltage profile, and computational time for three different load levels (see
Table 6).
From
Table 6, IEPSO technique gives the best optimal solution with the lowest power losses, improved VSI and computational time as indicated in bold for all load conditions. The increased in load levels, gave results in increasing power losses and decreasing VSI.
For light load in case 2 IEPSO technique gave the most reduction in TPL by 64.69%, 11.34% highest VSI, but slightly defeated in computational time compared to IPSO by 0.7 s at light load. Meanwhile, for nominal load in case 2 IEPSO technique gave the most reduction for TPL by 73.06%, 26.14% highest VSI, but slightly defeated in computational time compared to IPSO by 0.98 s at nominal load. Finally, for heavy load in case 2 IEPSO technique gave the most reduction for TPL by 74.95%, 49.03% highest VSI, but slightly defeated in computational time compared to IPSO by 0.68 s at heavy load.
Table 7 summarizes the performances of three optimization techniques in DNR with DG sizing simultaneously for switches, TPL, VSI, voltage profile, DG sizing and computational time for three different load levels.
From
Table 7, the IEPSO technique gives the best optimal solution with the lowest power losses, improved VSI and computational time as indicated in bold for all load conditions. The increased in load levels, gave results in increasing power losses and decreasing VSI.
For light load in case 2 IEPSO technique gave the most reduction for TPL by 66.19%, 15.54% highest VSI, and the fastest in computational time compared to other techniques at light load. Meanwhile, for nominal load in case 2 IEPSO technique gave the most reduction for TPL by 76.28%, 34.39% highest VSI, but slightly defeated in computational time compared to IPSO by 1 s at nominal load. Finally, for heavy load in case 2 IEPSO technique gave the most reduction for TPL by 79.26%, 58.41% highest VSI, and the fastest in computational time compared to other techniques at heavy load.
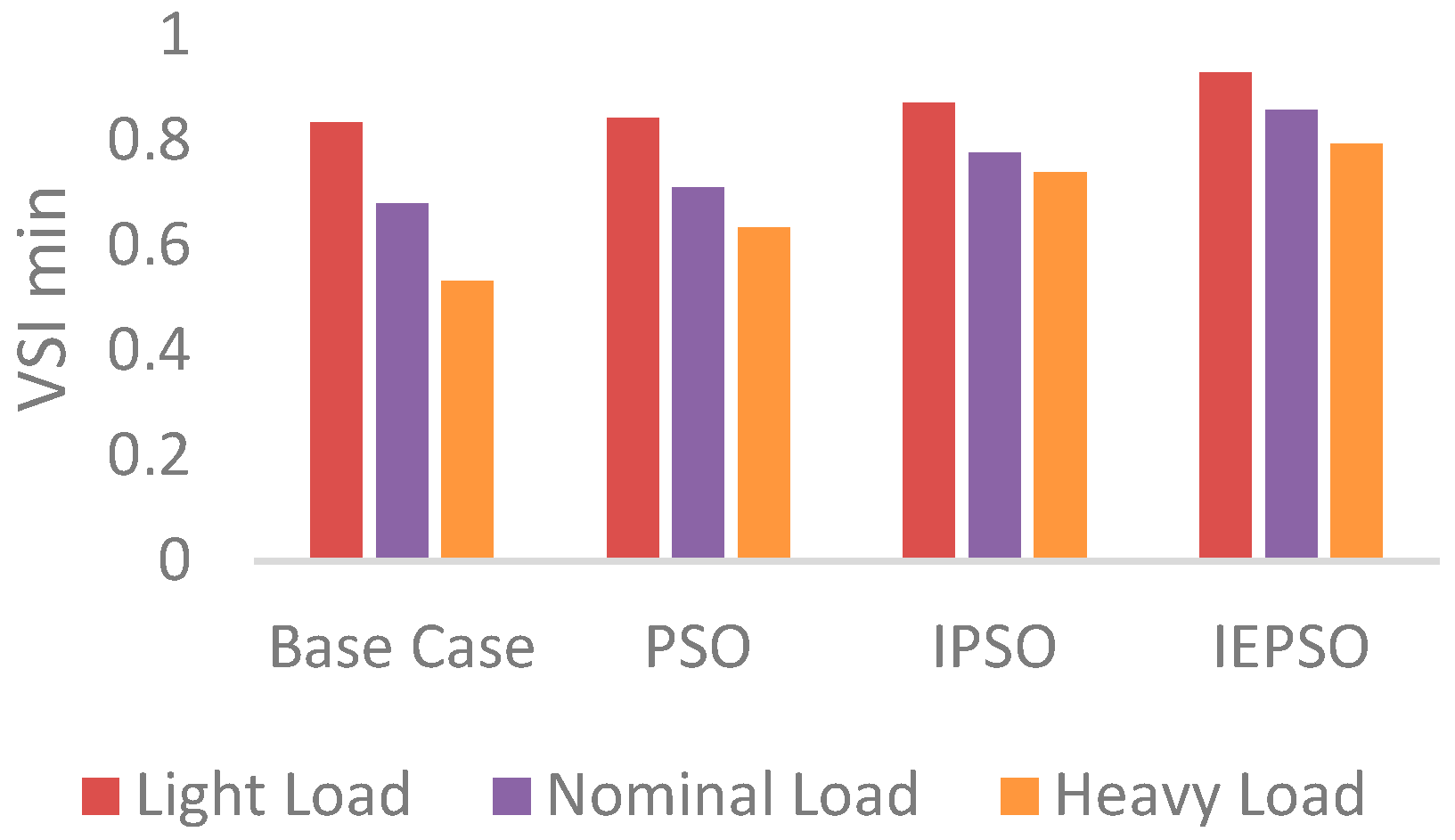
Figure 8 and
Figure 9 show the stability is improved for all cases, especially when the proposed algorithm is applied on 69-bus test system. Generally, by increasing the load levels, the VSI will decrease. Thus, the stability of the system is towards the voltage collapse with increasing load demand.
Figure 10 shows the comparison of TPL and VSI for three cases which are base case, DNR without DG and DNR with DG for light, nominal and heavy load condition in 69-bus system. From the figure, it is shown that TPL is slightly reduced with DNR implementation. However, the TPL has a significant reduced when DNR and DG was applied to the system.
At light load in 69-bus test system, the total power loss obtained from the PSO algorithm (case 2) with DG is 29.3 kW compared to 36.5 kW without DG with 7.2 kW differences, with 13.52% TPL reduction. The VSI without DG is 0.8423 which is improved to be 0.9205 with DG integration. For IPSO algorithm (case 3), the total power loss is 24.5 kW with DG compared to 26.7 kW without DG with 2.2 kW differences, with 4.13% TPL reduction. The VSI without DG is 0.8718 which is improved to be 0.9476 with DG integration. Finally, For IEPSO algorithm (case 4), the total power loss is 18 kW with DG compared to 18.8 kW without DG with 0.8 kW differences, with a 1.5% TPL reduction. The VSI without DG is 0.9298 which is improved to be 0.9649 with DG integration.
As for the last case, the total power loss obtained from the PSO algorithm (case 2) with DG is 108.1 kW compared to 145.5 kW without DG with 37.4 kW differences, with 16.28% TPL reduction, while, the VSI improved is by 3.74%. For IPSO algorithm (case 3), the total power loss is 62.7 kW with DG compared to 69 kW without DG with 6.3 kW differences, with 2.74% TPL reduction, while, The VSI is improved by 8.18%. Finally, For IEPSO algorithm (case 4), the total power loss is 54.5 kW with DG compared to 61.9 kW without DG with 7.4 kW differences, with 3.22% TPL reduction. The VSI is improved by 8.25%.
Similarly, at heavy load in 69-bus test system, the total power loss obtained from the PSO algorithm (case 2) with DG is 237.3 kW compared to 267.5 kW without DG with 30.2 kW differences, with 5.27% TPL reduction. The VSI is improved by 5.75%. For IPSO algorithm (case 3), the total power loss is 138.3 kW with DG compared to 160 kW without DG with 21.7 kW differences, with 3.79% TPL reduction. The VSI is improved by 13.64%. For IEPSO algorithm (case 4), the total power loss is 118.9 kW with DG compared to 143.6 kW without DG with 24.7 kW differences, with 4.31% TPL reduction. The VSI is improved by 9.38%.
From the results of both test systems, the following points can be summarized as below:
- (i)
the proposed IEPSO technique performed better results in terms of fitness function value and computational time as compared to PSO and IPSO techniques in terms of TPL reduction and VSI improvement as objective function as seen in
Table 8.
- (ii)
the proposed IEPSO technique is effective in finding the optimal sizing of DG in distribution power systems.
- (iii)
the TPL reduction and VSI enhancement can be obtained after DG placement and sizing.
- (iv)
by increasing the load condition of the test systems, from light to heavy load, the TPL is found to be increased and VSI decreased. This is to say that as far as the system is having a heavier the load, the system is getting more unstable with the increment in losses.
- (v)
the voltage profiles are improved when DGs are installed at the optimal size and bus locations.