Abstract
In this study, a dynamic response analysis procedure is proposed and applied to investigate the dynamic responses of a straddle-type concrete-filled steel tube tied arch bridge under train and truck loadings. A numerical model of the coupled monorail train–bridge system is established to investigate the dynamic behaviors of the bridge under moving trains. A refined three-dimensional finite element model is built for the bridge and a 15 degrees-of-freedom vehicle model is presented for the train. The numerical model is validated using in-situ test results and then used to analyze the dynamic displacement and acceleration of the bridge and the trains on the bridge. Based on the simulation results, the impact factor of the bridge is investigated and the riding comfort of the trains is evaluated. The investigation results show that the impact factor of vehicle loads reaches the maximum value when the resonance of the bridge is induced by the moving vehicles. The effect of train braking predominates the longitudinal vibration of the bridge but is negligible in the transverse and vertical directions. The vehicle speed is the dominating factor for the riding comfort of the train.
1. Introduction
In the last two decades, traffic problems in major cities worldwide presented demands of new transportation systems. The straddle-type monorail system has been identified as an alternative to the conventional railway systems [1]. Compared with the conventional urban subway transportation systems, the steering and stabilizing wheels in a monorail system firmly grasp the track beam of a monorail bridge, and thus, lead to better running stability. At the same time, the high integration of the monorail and the bridge led to the fact that the vibrations of the train and the bridge are coupled and interact with each other. The riding comfort of the train is also dependent on the dynamic responses of the train–bridge system under moving trains. Therefore, it is necessary to study the dynamic response of the monorail train–bridge system.
In the existing studies, the dynamic responses of the vehicle-structure system have been investigated. A track-bridge model was proposed by combining the direct stiffness method and the mode superposition method for analysis of the train-track-bridge interaction [2,3,4]. Zhang et al. [5] established a model of the vehicle, bridge, and wheel-rail interaction to analyze the dynamic response of a 24-m pre-stressed concrete high-speed railway bridge. Wang et al. [6] analyzed the dynamic behavior of the transition zones of subgrade and bridge with high moisture condition using the finite element method, and the coupling effect of the train was considered. As for the simulation of vehicle-pavement interaction, Shi and Darestani et al. [7,8] formulated a three-dimensional (3D) vehicle-pavement coupled model to simulate the pavement dynamic loads induced by the vehicle-pavement interaction where both the vehicle vibration and pavement deformation were considered. Some studies of the dynamic response of the coupled vehicle–bridge system of the high-speed railway bridge with impact load have been carried out [9,10]. Xu et al. [11] presented a framework for predicting the dynamic response of long suspension bridges to high winds and running trains. Malm et al. [12] carried out field testing and simulation to evaluate the dynamic effects on a tied arch railway bridge during train passages. Kwon et al. [13] presented a theoretical model for a guideway suspension bridge that is crossed by the urban maglev vehicle when subjected to gusty winds. A new bridge-vehicle model with consideration to the pre-stress effect was created through the principle of virtual works to address the pre-stressed continuous bridges and vehicle interaction [14]. Dynamic analyses of a bridge in Sweden and comparison with field tests were presented [15]. Madrazo-Aguirre et al. [16] investigated the dynamic response of under-deck cable-stayed bridges with steel-concrete composite decks with moving loads. Fu et al. [17] performed a numerical solution for the dynamic response of a simply supported bridge with a switching crack subjected to seismic excitation and moving trains. Model test and in situ test have been considered as effective approaches to investigate the dynamic and mechanical performance of bridge structures [18,19,20,21,22,23,24,25].
In recent years, there is an increasing interest in straddle-type monorail transportation systems, in particular, in the construction of urban transportation infrastructure. Wang et al. [26] proposed an analytical procedure of dynamic interaction analysis of the straddle monorail bridge-vehicle coupling system based on the finite element method and energy method. Goda [27] performed numerical simulations of curve negotiation performance of a monorail train. The tire models of walking wheel, steering wheel, and stabilizing wheel were established respectively. The kinetic equation was derived using the multi-body dynamics method. In the study of Lee et al. [1,28], the car body was reduced to a vehicle model with 15 degrees of freedom (DOFs), which described vertical settlement, nodding, head shaking, side-rolling, and yawing, respectively. The corresponding dynamic calculation program was developed to investigate the influence of train speed, passenger volume, and other parameters on the comfort of trains. However, there is a lack of studies on the dynamic responses of this kind of combined bridge subjected to a monorail vehicle load and the riding comfort of the monorail trains.
In this paper, a dynamic response analysis procedure is proposed and applied to investigate the dynamic responses of a straddle-type concrete-filled steel tube tied arch bridge under the train and truck loadings through numerical simulations. A three-dimensional model of the bridge was established with consideration to the coupled vehicle–bridge interaction and the track irregularity. The bridge model was optimized by reducing the bandwidth of the mass matrix, stiffness matrix, and damping matrix of the bridge. The motion equations of the vehicle model with 15 DOFs were derived using an energy method based on the Lagrange equation. The riding comfort of monorail trains is evaluated using the Sperling index based on GB5599-85 [29].
2. Bridge Description
The investigated bridge is the Caiyuanba Yangtze River Bridge, which is a composite bridge with a non-thrust rigid frame, a steel truss girder, and a steel box tied arch, as shown in Figure 1. The bridge has a total length of 800 m, which is composed of a 420-m main span, two 102-m side spans, and two 88-m flanking spans. The main span of the bridge is a basket handle tied arch, with a vector height of about 56.44 m, a span of 320 m, a rise-span ratio of 1/5.7, and a leaning angle of the main arch rib of 10.67°. The two ribs of the arch are connected as one through six steel boxes. The box section of the arch rib is 2.4 m by 4.0 m, and its thickness varies from 24 mm to 40 mm. The width of the carriageway is 2 × 3 × 3.75 m, the width of the central divider is 1.0 m, and the width of the two sides is 2 × 2 × 0.5 m. The longitudinal and transverse slopes of the main bridge are 0.59% and 2%, respectively.
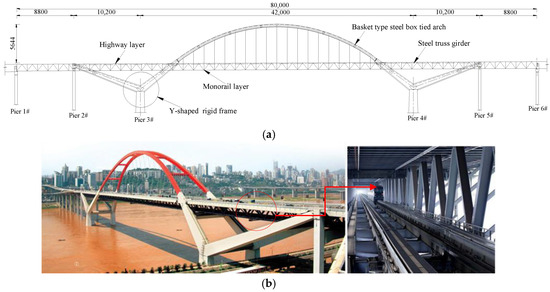
Figure 1.
The layout of the Caiyuanba Yangtze Bridge (unit: cm): (a) elevation view; (b) overview.
The main arch ribs produce the horizontal thrust both inside and outside the plane under the dead load and operating live load. The steel truss girder is a truss structure with an orthotropic bridge deck, bearing the vertical operating load as well as the large horizontal thrust. The horizontal thrust of the arch is supported by the steel beam of the ribs and the rigid frame concrete beam.
The highway layer is the two-way 6-lane car load plus 2 sides of the sidewalk load, the car load rating is the City-A, and the design speed is 60 km/h. The design crowd load is 2.4 kN/m2. The track layer is a two-lane monorail, the design load is composed of two head vehicles and six standard vehicles, with a design speed of 75 km/h.
3. Coupled Monorail Train–Bridge System
The coupling behaviors of the train and the bridge are considered in the analysis. First, the displacement equations are established for the bridge and vehicle subsystems, respectively. Then, the two subsystems are assembled into one couple system through the compatibility of contact condition, with the consideration of track irregularity. Finally, the Sperling index is used to evaluate the riding comfort level of monorail vehicles.
3.1. Bridge Subsystem
Figure 2 shows the finite element model of the bridge subsystem. The arch ribs are divided into 23 segments along the axis of the bridge. The transverse bracing of the arch rib and arch rib are modeled by three-dimensional beam elements. The suspenders and tied bars are modeled using three-dimensional truss elements. The effect of pre-tension on a bar member is simulated by specifying an initial tensile strain in the member. The steel truss girder, Y-shaped rigid frame, and piers are modeled using 3D beam elements. Each of the beam elements has two nodes, and each node has six DOFs. In total, the bridge model has 3257 nodes and 6515 elements, which include 136 truss elements and 6319 beam elements. In light of the boundary conditions, the steel truss girder is supported using eight basin type rubber bearings placed on the bridge piers, which are fixed at the bottom. A linking bar support is arranged at the pier top of the transition pier. In order to control the displacement of steel truss girder under the action of the braking force, wind force, and earthquake force, the bottom chord bar of the steel truss girder is connected with the beam of the abutment pier. The mechanical properties of the materials are listed in Table 1.

Figure 2.
The finite element model of the bridge.

Table 1.
The material properties.
Each node of the beam element has 6 displacement DOFs. The displacement vector and the force vector of the node in the local coordinate system are as follows:
The general form of the element stiffness matrix and the element mass matrix in the local coordinate system of the space beam element can be expressed by Equation (3).
where B and D are the strain matrix and the beam modulus matrix, which can be derived by the stress–strain relation of the element; ρ is the bulk density of materials; and N is the shape function of the element, which can be expressed as follows:
where N1 = 1 − x/l; N2 = x/l; N3 = 1 − 3x2/l2 + 2x3/l3; N4 = x − 2x2/l + x3/l2; N5 = 3x2/l2 − 2x3/l3; N6 = −x2/l + x3/l2; N7 = −6x/l2 + 6x2/l3; N8 = 1 − 4x/l + 3x2/l2; N9 = −2x/l + 3x2/l2. x is the coordinates of a point in the beam element and l is the length of the beam element.
The expression of the displacement of any point in the beam element:
The total mass, stiffness, and force matrices of the bridge can be obtained by converting the element matrix in the local coordinate system into the whole coordinate system and then integrating them [30]. The damping of the bridge structure is assumed to be Rayleigh damping:
where , and are the damping, mass, and stiffness matrices of the bridge, respectively; α and β are the Rayleigh damping coefficients, which can be calculated by the following formula:
where ωi and ωj are the ith and jth natural vibration frequencies; ξi and ξj are the corresponding damping ratio. According to Li’s research [31], for the vehicle–bridge coupled system, the fundamental frequency of the structure can be used as the reference frequency ωi and the maximum excitation frequency (ωf) produced by track irregularities can be used as the reference frequency ωj. In this study, the ω10 is close to the ωf. Therefore, the first and tenth order frequencies were used to calculate the Rayleigh damping coefficient and the damping ratio was selected as 0.5%. The calculated values of α and β are 0.0113 and 0.0019, respectively.
The displacement equations of the bridge subsystem can be expressed as follows:
where , and represent the nodal dynamic acceleration, velocity, and displacement vectors of the bridge; and is the external force vector due to the moving train.
3.2. Monorail Train
In general, a monorail train is composed of a train body, a suspension system, two bogies, traveling wheels, steering wheels, stabilizing wheels, and shock absorbers. The traveling wheels are under the bogie; the steering wheels and stabilizing wheels are at the two sides of the bogie. The following three assumptions are employed in the model development for the monorail train:
- (1)
- The train body and two bogies are considered rigid bodies without any deformation.
- (2)
- The effects of variation in the vertical loads on the stiffness of the traveling wheel are neglected.
- (3)
- The wheels are in direct contact with the bridge deck.
Figure 3 shows the idealized train model with 15 DOFs. In the coordinate system, X, Y, Z, and θ represent the longitudinal, transverse, vertical, and rotational displacements, respectively. Yawing, vertical settlement, side-rolling, head shaking, and nodding motions of the body and each bogie are incorporated in this model, as shown in Table 2. The detailed mechanical and geometric parameters of the Monorail train are listed in Table 3.
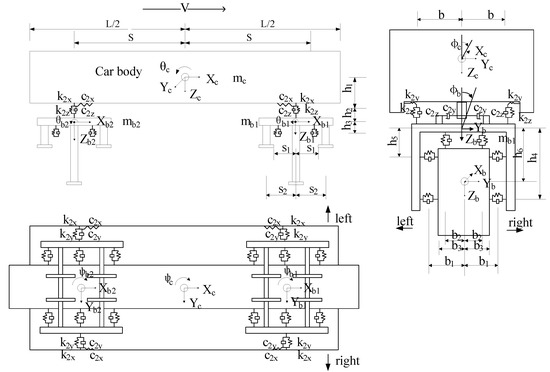
Figure 3.
The idealized monorail train with 15 DOFs.

Table 2.
The Degree of Freedom (DOF) of the vehicle model.

Table 3.
The major parameters of the monorail vehicle model.
The DOFs of the car body can be expressed as uc = {yc zc φc ψc θc}T, and the DOFs of the bogie can be expressed as ubj = {ybj zbj φbj ψbj θbj}T, where j = 1 and j = 2 represent the front and the rear bogies, respectively. The governing equations of the train are derived using an energy method based on the Lagrange equation, as shown in Equation (9) [28].
where T is the kinetic energy, U is the potential energy, Q is the dissipation energy of the system, and ai is a generalized coordinate.
The kinetic energy, potential energy, and dissipation energy of a train on a bridge are developed by modifying the energy equation for a vehicle on a highway bridge [32]. These energy equations are expressed in a set of generalized coordinates as follows:
where j = 1, when η = −1, or j = 2, when η = 1.
The displacement equation of the monorail train can be derived by substituting Equations (10)–(12) into Equation (9).
Yawing of the car body:
Vertical settlement of the car body:
Side-rolling of the car body:
Head shaking of the car body:
Nodding of the car body:
Yawing of the bogie:
Vertical settlement of the bogie:
Side-rolling of the bogie:
Head shaking of the bogie:
Nodding of the bogie:
where yB = the lateral displacement of bridge; zB = the vertical displacement of bridge; ry = the track lateral irregularity; and rz = the track vertical irregularity.
According to the dynamic-static method, the dynamic balance equation of the monorail train can be expressed as follows:
where v denotes the monorail vehicle; denotes the force vector of the gravity of the vehicle; denotes the external force applied to the vehicle through the bridge. The specific expressions of the components in Equation (23) are as follows.
The displacement vector of the vehicle:
The mass matrix of the vehicle:
in which .
The stiffness matrix of the vehicle:
The damping matrix of the vehicle is in the same form as the stiffness matrix and the damping matrix Cv can be obtained by replacing the k in Equations (26)–(30) with c.
The vehicle gravity vector:
The force vector of the bridge to the vehicle:
3.3. Track Irregularity
The track irregularity is a critical factor of the track, which may significantly affect the dynamic responses of the train–bridge system [33,34]. In this study, the track irregularity is taken into consideration based on a power spectral density function in Equation (38):
where S denotes the spectral density function of the track irregularity; Ω denotes the spatial frequency (cycle/m); α, β, and n are the parameters which reflect the shape of the spectral density function. The parameters α, β, and n of the track beam under the traveling wheel are 0.005, 0.35, and 3.0, respectively; under the steering wheel they are 0.0006, 0.5, and 2.8, respectively; and under stabilizing wheel they are 0.0006, 0.5, and 2.6, respectively.
The track irregularity spectrum can be generated by using the harmony superposition method:
where x, Ωi and ΔΩ indicate the coordinate of mileage, frequency point, and the spacing of the frequency points, respectively. represents a random phase angle which is uniformly distributed from 0 to 2π. The specific simulation sample of the track irregularity spectrum of the track beam under the traveling wheel, steering wheel, and stabilizing wheel is shown in Figure 4.
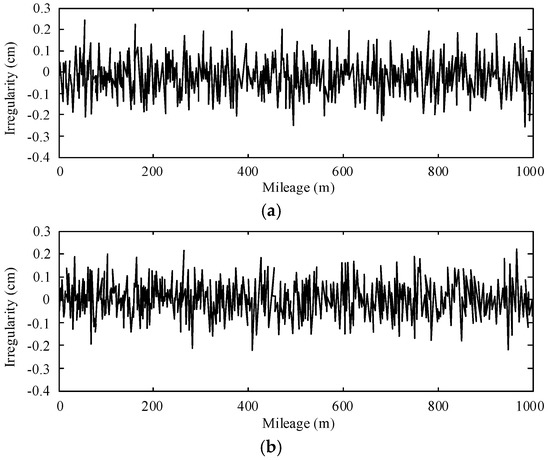
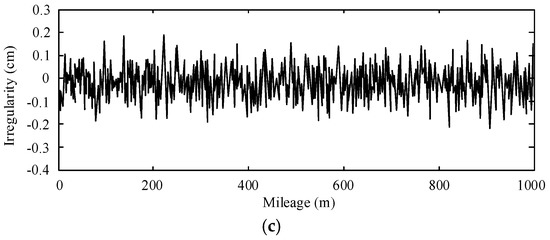
Figure 4.
The track irregularity spectrum of the track beam: (a) under the traveling wheel; (b) under the steering wheel; (c) under the stabilizing wheel.
3.4. Monorail Train–Bridge Interaction
The vehicle system and the bridge system are coupled through the wheel-rail contact relationship. The force vector of the vehicles acting on the bridge can be expressed as:
where δvmjin is the distribution vector of the vehicle wheel loads delivered to each node of the bridge element; fvmjin is the wheel load of the monorail trains acting on the bridge. nv denotes the number of carriages in a monorail train; v denotes the number of carriages on the bridge; m = 1, 2, 3 indicating the traveling wheel, steering wheel, and the stabilizing wheel, respectively; j = 1, 2 indicating the front and rear bogies, respectively; i = 1, 2 indicating the front and rear wheel, respectively; n = 1, 2 indicating the left and right wheel, respectively. The expression of the wheel load fvmjin is as follows:
According to the coordination condition of displacement, the surface of the bridge is always in contact with the wheels when the train passes the bridge. Meanwhile, the dynamic interaction between the bridge and the train is simulated based on the Darren Bell principle. In the process of the analysis for the train bridge coupled vibration, the force of a wheel acting on the bridge is equal to the force of the bridge acting on the wheel. Therefore, the governing equation of the train–bridge system can be determined as shown in Equation (42) by combining the motion equations of the monorail train and the bridge and the interaction force at the contact point [35].
where M, C, and K indicate the mass, damping, and stiffness matrices, respectively. P is the force vector. Subscripts b, v, and bv (or vb) denote the bridge, vehicle, and vehicle–bridge interaction system, respectively.
The mass matric of the bridge:
The mass matric of the train (a monorail train consists of 6 carriages):
3.5. Investigated Cases
The numerical model was used to analyze the vertical displacement (deflection), transverse displacement, vertical acceleration, and transverse acceleration of the mid-span section of the bridge, as well as the accelerations of the train in the two loading cases: (1) single line loading: one train running on the track, and (2) double line loading: two trains running on the track. In each of the two cases, the train moves at constant speeds of 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, and 75 km/h, respectively. The impact factor of deflection of the bridge was evaluated based on the deflection results. The riding comfort of the train was assessed with the accelerations of the train.
Besides the normal driving scenario, the effects of the train braking were investigated in a scenario where one train was braked at the mid-span of the bridge at the speeds of 20, 30, and 40 km/h, respectively. The maximum braking acceleration was −1.25 m/s2; the braking acceleration increased linearly from zero to the maximum; the braking time was fixed to 2 seconds.
4. Model Optimization and Validation
In the finite element analysis, the bandwidth of the overall mass, stiffness, and damping matrices is determined by the node number. In order to improve the computational efficiency, the node number is optimized to reduce the difference between the related node numbers in the same element, thus, reducing the bandwidth of the overall matrix. The AD algorithm [36] is selected to optimize the node number and the algorithm is as follows. (1) Calculate the sum (Mn) of the number of the adjacent nodes of each node; (2) Calculate the node quotient Qn = Mn/Me, where Me is the number of related elements of the node; (3) Calculate the sum (Mm) of the maximum node number and the minimum node number in the adjacent nodes of each node; (4) Renumber all nodes according to the size of the node quotient (Qn). If the Qn of the two nodes is equal, the number of the two nodes is determined according to the size of the Mm.
With the AD algorithm, the bandwidth of the mass, stiffness, and damping matrices of the bridge was reduced from 2820 to 167, as shown in Figure 5.
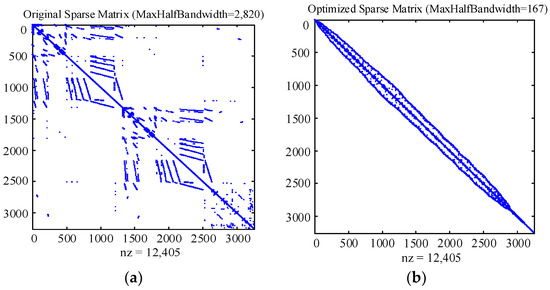
Figure 5.
The comparison of the bandwidth of the bridge characteristic matrix before and after optimization: (a) Before optimization; (b) After optimization.
The two methods, which are of the general finite element software ANSYS (ANSYS Inc., Pittsburgh, PA, USA)adopting the Lancoz method [37] and the self-compiling program (SCP) adopting the subspace iteration method [38], are used in the numerical model to analyze the vibrational frequency and mode shapes of the bridge. The analysis results of the first six vibrational frequencies and mode shapes of the bridge are listed in Table 4. The maximum discrepancy of the frequency resulting from the two methods is only 0.3%. The first six modes of the bridge vibration are longitudinal displacement and lateral bending, and the minimum lateral bending frequency is 0.32 Hz, revealing that the lateral stiffness is smaller than the vertical stiffness.

Table 4.
The free frequency and mode shapes.
An in-situ train loading test was carried out to validate the finite element model [39] and the test data were used for model updating. In the process, the modeling parameters such as Young’s modulus, mass density, and moments of inertia were modified using the sensitivity method [40] to make the correlation between the analytical and test results meet the practical requirements. The numerical and experimental results are compared in Figure 6. It can be seen that the numerical results are in reasonable agreement with the experimental results. The relative errors of the response values are less than 5% for the displacement and strain of the bridge. The good agreement between the measured and numerical results for the different bridge components and response types shows that the proposed FE model of the vehicle–bridge coupled system works very well and has a high calculation precision. Thus, the FE coupled model is considered to be valid.
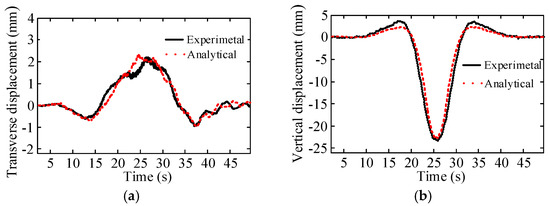
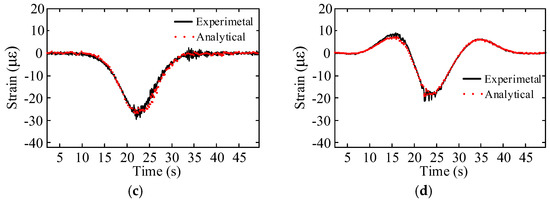
Figure 6.
The comparison of test and numerical results with one train running through the bridge at a speed of 60 km/h: (a) the track beam in middle span; (b) the track beam in middle span; (c) the vault; (d) the skewback.
5. Simulation Results and Discussions
5.1. Displacements
Figure 7a,b plot the simulation results of the time-displacement curves of the track beam, joint of the down chord, joint of the upper chord, and the arch rib in the vertical and transverse direction of the bridge, respectively, under one train running through the bridge at a speed of 60 km/h. The horizontal axis represents the distance along the bridge, which is measured from one end of the bridge. Both the vertical and transverse displacements reach their maximum values when the train arrives at a distance of 530 m on the bridge. Figure 7a shows that the vertical deflection of the track beam is the largest, followed by the deflection of the joint of the down and upper chords. Figure 7b shows that the transverse displacement of the arch rib is larger than that of the girder, which suggests that the transverse vibration of the arch rib is greater due to the smaller out-plane stiffness.
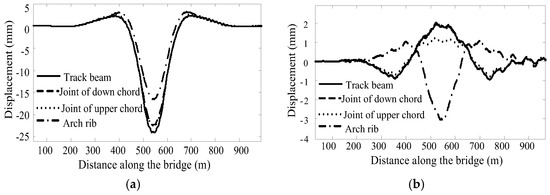
Figure 7.
The time–history curves of the displacements of the bridge at the mid-span with one train running through the bridge at a speed of 60 km/h: (a) the vertical direction; (b) the transverse direction.
The peak values of the displacements in Figure 7a,b represent the vibration amplitudes, which are plotted in Figure 8a,b. Both the vertical and transverse amplitudes do not change significantly with the train’s speed when the speed is no more than 30 km/h. When the speed is increased to 40 km/h, the amplitude of the vertical displacement is abruptly increased and a peak appears in Figure 8a. The peak is likely due to the resonance between the bridge and the train moving on it at the speed of 40 km/h. However, the transverse amplitude is insensitive to the change of the train speed. When the loading case is changed from a single line to a double line, the vertical amplitude of the bridge is increased while the transverse amplitude of the bridge is reduced. The transverse amplitude of the bridge approaches zero as the two trains run on the double line, while the transverse amplitude of the bridge increases obviously as one train runs on a single line. The transverse vibration of the bridge is mainly caused by the eccentric train loading.
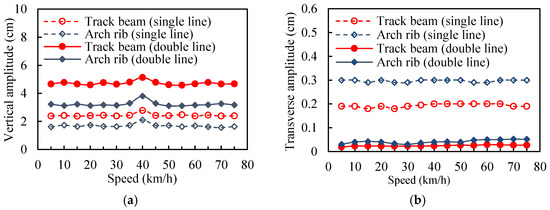
Figure 8.
The displacements of the bridge at the mid-span: (a) the vertical direction; (b) the transverse direction.
5.2. Impact Factors
The impact factor is defined as the ratio of the increased vertical deflection induced by moving trains to the static deflection of the bridge. Figure 9 shows the simulation results of the impact factor in the single line and double line loadings, respectively. The impact factor reaches the maximum values when the vehicle speed is 40 km/h in both the single line and double line loading cases due to resonance induced by the moving trains. Overall, a slightly greater impact factor is achieved in the double line loading case. The largest impact factor is 4.2% in the double line case and 2.7% in the single line case, both achieved by the arch rib. The reason could be that the stiffness of the arch is larger than that of the beam due to the “arch effect” [41,42] and that the structure with the bigger stiffness will bear the greater impact force. The results from the two loading cases follow a similar trend and resonance occurs at the same speed in the two loading cases, indicating that whether single line or double line, the loading applied does not significantly affect the impact factor of the bridge.
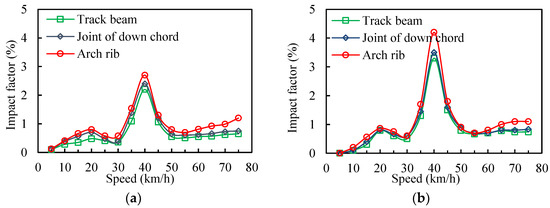
Figure 9.
The impact factors of the bridge at the mid-span: (a) single line; (b) double line.
5.3. Accelerations
Figure 10 shows the time-history curves of the mid-span acceleration of the bridge with a single line train loading at the speed of 60 km/h. The maximum lateral and vertical accelerations occur when the train travels to the mid-span. The peak value of the transverse acceleration of the bridge is slightly larger than the peak value of the vertical acceleration.
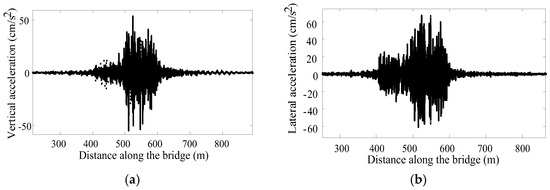
Figure 10.
The time–history curves of the mid-span acceleration of the bridge under a monorail train running on a single line at a speed of 60 km/h: (a) the vertical direction; (b) the transverse direction.
Figure 11 shows the simulation results of the amplitudes of the vertical and transverse accelerations of the track beam of the bridge under running trains. The results indicate that the dynamic accelerations of the bridge approximately linearly increase with the train’s speed. In the single line loading case, the discrepancies of the amplitudes of the vertical and transverse accelerations of different parts of the bridge are no more than 18%. In the double line loading case, the amplitudes of the vertical and transverse accelerations of the quarter of the main span and the middle of the Y-shape frame are still very close to each other, but the amplitudes of the vertical and transverse accelerations of the middle of the main span of the bridge are significantly greater than those of the quarter of the main span and the middle of the Y-shape frame. Their difference increases with the train’s speed and is up to 44% as the train’s speed is increased from 5 to 75 km/h.
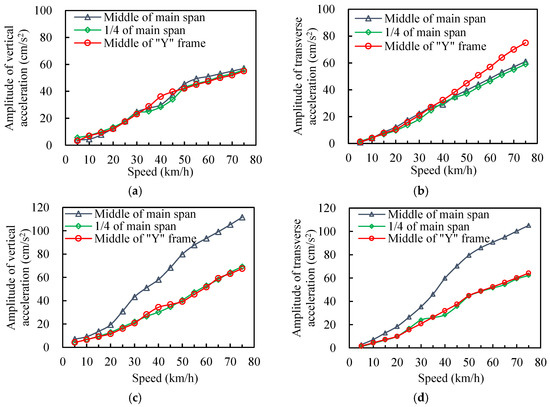
Figure 11.
The amplitude of the accelerations of the bridge: (a) and (b) single line; (c) and (d) double line.
Figure 12 shows the calculated results of the acceleration of the arch rib at the mid-span. It can be seen that the vertical acceleration is greater than the transverse acceleration and the acceleration of the arch rib with two trains running on the double line is greater than that with one train running on a single line. The maximum acceleration is 9.8 cm/s2, which is much less than 140 cm/s2, which is the limit of the transverse acceleration specified in the code for rating existing railway bridges [43]. The comparison of Figure 11 and Figure 12 shows that the acceleration of the track beam is much greater than that of the arch rib. The reason could be that the track beam is subjected to direct loading and the vehicle is coupled with the track beam, while the arch rib is subjected to indirect loading.
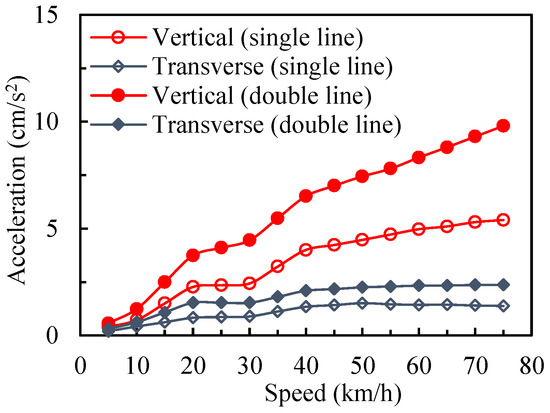
Figure 12.
The accelerations of the arch rib at the mid-span.
5.4. Effects of Train Braking
Figure 13 plot the time–history curves of the longitudinal displacement of the bridge with one train braked at the middle of the bridge at a speed of 40 km/h. There is little difference in the longitudinal displacements at the investigated locations of the truss girder.
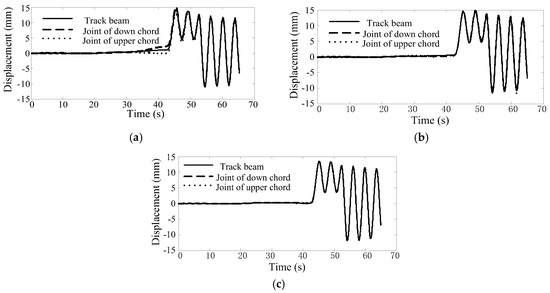
Figure 13.
The time–history curves of the longitudinal displacements with the train braking in the mid-span of the bridge at a speed of 40 km/h: (a) the middle of the main span; (b) the quarter position of the main span; (c) the middle of the Y-shaped rigid frame.
The time–history curves of the longitudinal accelerations shown in Figure 14 indicate that when the temporary impact occurs, the longitudinal accelerations of each calculated position varies greatly. As the distance from the braking position increases, the longitudinal acceleration of the steel truss girder becomes smaller. After the temporary impact, the amplitude and phase of the longitudinal acceleration of each position are consistent.
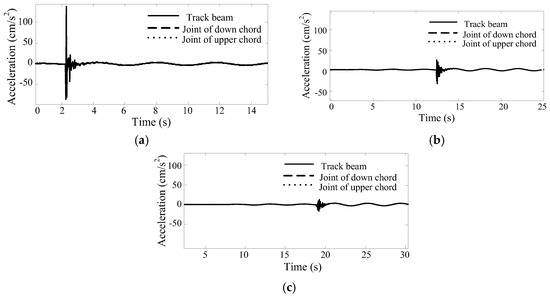
Figure 14.
The longitudinal acceleration with the train braking in the middle of the bridge at a speed of 40 km/h: (a) the middle of the main span; (b) the quarter position of the main span; (c) the middle of the Y-shaped rigid frame.
Figure 15 shows the accelerations of the track beam with one train braking in the middle of the bridge. It can be seen that the braking load leads to larger longitudinal vibrations of the bridge, but has limited effects on the transverse and vertical vibrations.
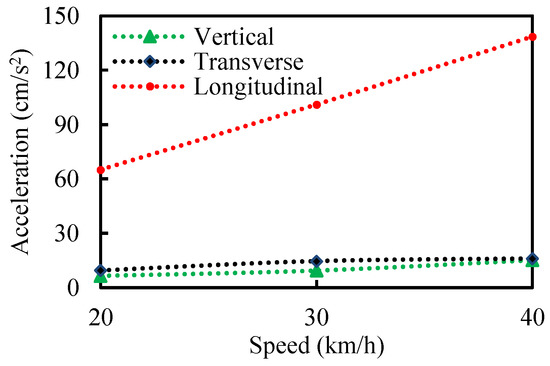
Figure 15.
The accelerations of the track beam with one train braking in the middle of the bridge.
6. Evaluation of Riding Comfort
There is no specific standard for the evaluation of riding comfort. Therefore, the Sperling index [44] is used to evaluate the ride stability of the monorail vehicles. The Sperling index, Wz, is expressed as follows:
where a is the acceleration (cm/s2); f is the vibration frequency (Hz); F(f) is the correction coefficient related to f. For vertical vibrations: (1) when 0.5 Hz < f < 5.9 Hz, F(f) = 0.325f2; (2) when 5.9 Hz < f < 20 Hz, F(f) = 400/f2; (3) when f > 20 Hz, F(f) = 1. For transverse vibrations: (1) when 0.5 Hz < f < 5.4 Hz, F(f) = 0.8f2; (2) when 5.4 Hz < f < 26 Hz, F(f) = 650/f2; (3) when f > 26 Hz, F(f) = 1.
The above formula is applicable to the condition where the vibration contains only one frequency component. However, actually, the vibration acceleration of a vehicle often includes multiple frequency components. Therefore, it is necessary to decompose the acceleration time history according to the frequency firstly. After that, the Sperling index Wzi (i = 1, 2, ..., n) is determined for each frequency component and the overall Sperling index can be expressed as follows:
The evaluation standard for the Sperling index is shown in Table 5. The running stability grade of the vehicle in China is shown in Table 6.

Table 5.
The evaluation criteria of the Sperling index.

Table 6.
The running stability grade of vehicles in China [29].
Figure 16 shows the simulation results of the acceleration and the Sperling index of monorail trains. It can be seen that there is almost no difference between the acceleration of one train running on a single line and the acceleration of two trains running on the double line. With the increase of the speed, the vibration acceleration and Sperling index of the train increase, but the riding comfort decreases. Furthermore, the transverse acceleration of the vehicle is significantly greater than the vertical one and the transverse comfort is worse than the vertical comfort. The data indicate that the running speed is the control index for the riding comfort evaluation, rather than the number of trains.
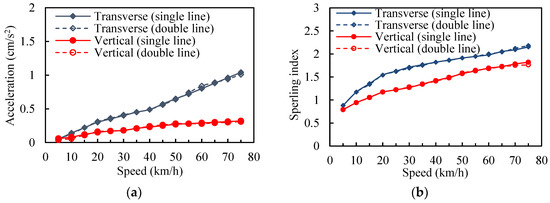
Figure 16.
The responses of the monorail trains: (a) acceleration; (b) comfort index.
The vehicle comfort level is mostly between “just feel” to “obvious feeling”. According to the standard of the vehicle running stability stipulated by the railway code GB5599-85 [29], the vehicle running stability grade is excellent.
7. Conclusions
Based on the above investigations, the following conclusions can be drawn:
- The impact factor reaches the maximum values when the vehicle speed is 40 km/h in both the single line and double line loading cases. The largest impact factor is 4.2% in the double line case and 2.7% in the single line case, both achieved by the arch rib. Whether single line or double line loading is applied does not significantly affect the impact factor of the bridge.
- Both the vertical and transverse amplitudes do not change significantly with the train’s speed when the speed is no more than 30 km/h. When the speed is increased to 40 km/h, the vertical amplitude is increased and a peak appeared, likely due to the resonance between the bridge and the train. The transverse amplitude is insensitive to the change of the train speed. When the loading case is changed from single line to double line, the vertical amplitude increases while the transverse amplitude of the bridge reduces. The transverse amplitude of the bridge approaches zero as two trains run on the double line, revealing that the transverse vibration of the bridge is mainly caused by eccentric train loadings.
- The dynamic accelerations of the bridge approximately linearly increase with the train’s speed. In the single line loading case, the discrepancies of the amplitudes of the vertical and transverse accelerations of different parts of the bridge are no more than 18%. In the double line loading case, the amplitudes of the vertical and transverse accelerations of the quarter of main span and the middle of the Y-shape frame are still very close to each other, but the amplitudes of the vertical and transverse accelerations of the middle of the main span of the bridge are significantly greater than those of the quarter of the main span and the middle of the Y-shape frame. Their difference increases with the train’s speed and is up to 44% as the train’s speed is increased from 5 to 75 km/h. The acceleration of the track beam is much greater than that of the arch rib. The reason can be that the track beam is subjected to direct loading and the vehicle is coupled with the track beam, while the arch rib is subjected to indirect loading.
- The braking load mainly leads to larger longitudinal vibration of the bridge but its influence on the transverse and vertical vibration is less. When the braking load acts on the bridge, the longitudinal displacement and the vibration phase at each calculated position of the steel truss girder is consistent, that is, the steel truss girder makes longitudinal integral translational vibration. When the temporary impact occurs, the longitudinal accelerations of each calculated position varies greatly. As the distance from the braking position increases, the longitudinal acceleration of the steel truss girder becomes smaller.
- The acceleration of the vehicles increases with the vehicle speed, not the number of vehicles. The transverse acceleration of the vehicle is significantly greater than the vertical one, and the transverse comfort is worse than the vertical comfort. The maximum transverse acceleration of the vehicle is 1.01cm/s2. The grade of the vehicle running stability is excellent.
Acknowledgments
The research described in this paper was financially supported by the National Natural Science Foundation of China (Grant No. 51508474 and 51108382), the Fundamental Research Funds for the Central Universities (Grant No. 2682015CX07), and the Science and Technology Research and Development Plan of China Railway Construction (Grant No. 2014-C34). The visiting scholarship for the first author to visit the Department of Civil, Architectural and Environmental Engineering at the Missouri University of Science and Technology (Rolla, MO) was made possible by the Chinese Scholarship Council (Grant No. P-1-02556).
Author Contributions
The authors have contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, C.H.; Kim, C.W.; Kawatani, M. Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains. Eng. Struct. 2005, 27, 1999–2013. [Google Scholar] [CrossRef]
- Yang, S.C.; Hwang, S.H. Train-track-bridge interaction by coupling direct stiffness method and mode superposition method. J. Bridge Eng. 2016, 21, 04016058. [Google Scholar] [CrossRef]
- Wang, S.J.; Xu, Z.D.; Li, S.; Dyke, S.J. Safety and stability of light-rail train running on multispan bridges with deformation. J. Bridge Eng. 2016, 21, 06016004. [Google Scholar] [CrossRef]
- Dinh, V.N.; Kim, K.D.; Warnitchai, P. Dynamic analysis of three-dimensional bridge-high-speed train interactions using a wheel-rail contact model. Eng. Struct. 2009, 31, 3090–3106. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, H.; Guo, W.W. Vehicle-bridge interaction analysis under high-speed trains. J. Sound Vib. 2008, 309, 407–425. [Google Scholar] [CrossRef]
- Wang, H.; Silvast, M.; Markinei, V.; Wiljanen, B. Analysis of the Dynamic Wheel Loads in Railway Transition Zones Considering the Moisture Condition of the Ballast and Subballast. Appl. Sci. 2017, 7, 1208. [Google Scholar] [CrossRef]
- Shi, X.M.; Cai, C.S. Simulation of dynamic effects of vehicles on pavement using a 3D interaction model. J. Transp. Eng. 2009, 135, 736–744. [Google Scholar] [CrossRef]
- Darestani, M.Y.; Thambiratnam, D.P.; Nataatmadja, A.; Baweja, D. Structural response of concrete pavements under moving truck loads. J. Transp. Eng. 2007, 133, 670–676. [Google Scholar] [CrossRef]
- Xia, C.Y.; Lei, J.Q.; Zhang, N.; Xia, H.; Roeck, G.D. Dynamic analysis of a coupled high-speed train and bridge system subjected to collision load. J. Sound Vib. 2012, 331, 2334–2347. [Google Scholar] [CrossRef]
- Olmos, J.M.; Astiz, M.A. Analysis of the lateral dynamic response of high pier viaducts under high-speed train travel. Eng. Struct. 2013, 56, 1384–1401. [Google Scholar] [CrossRef]
- Xu, Y.L.; Xia, H.; Yan, Q.S. Dynamic response of suspension bridge to high wind and running train. J. Bridge Eng. 2003, 8, 46–55. [Google Scholar] [CrossRef]
- Malm, R.; Andersson, A. Field testing and simulation of dynamic properties of a tied arch railway bridge. Eng. Struct. 2006, 28, 143–152. [Google Scholar] [CrossRef]
- Kwon, S.D.; Lee, J.S.; Moon, J.W.; Kim, M.Y. Dynamic interaction analysis of urban transit maglev vehicle and guideway suspension bridge subjected to gusty wind. Eng. Struct. 2008, 30, 3445–3456. [Google Scholar] [CrossRef]
- Zhong, H.; Yang, M.; Gao, Z. Dynamic responses of prestressed bridge and vehicle through bridge-vehicle interaction analysis. Eng. Struct. 2015, 87, 116–125. [Google Scholar] [CrossRef]
- Kaliyaperumal, G.; Imam, B.; Righiniotis, T. Advanced dynamic finite element analysis of a skew steel railway bridge. Eng. Struct. 2011, 33, 181–190. [Google Scholar] [CrossRef]
- Madrazo-Aguirre, F.; Ruiz-Teran, A.M.; Wadee, A. Dynamic behavior of steel-concrete composite under-deck cable-stayed bridges under the action of moving loads. Eng. Struct. 2015, 103, 260–274. [Google Scholar] [CrossRef]
- Fu, C. Dynamic behavior of a simply supported bridge with a switching crack subjected to seismic excitations and moving trains. Eng. Struct. 2016, 110, 59–69. [Google Scholar] [CrossRef]
- Gou, H.Y.; Shi, X.Y.; Zhou, W.; Cui, K.; Pu, Q.H. Dynamic performance of continuous railway bridges: Numerical analyses and field tests. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2018, 232, 936–955. [Google Scholar] [CrossRef]
- Gou, H.Y.; Long, H.; Bao, Y.; Chen, G.D.; Pu, Q.H.; Kang, R. Experimental and numerical studies on stress distributions in girder-arch-pier connections of long-span continuous rigid frame arch railway bridge. J. Bridge Eng. 2018, in press. [Google Scholar]
- Gou, H.Y.; He, Y.N.; Zhou, W.; Bao, Y.; Chen, G.D. Experimental and numerical investigations of the dynamic responses of an asymmetrical arch railway bridge. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2018, in press. [Google Scholar] [CrossRef]
- Gou, H.Y.; Long, H.; Bao, Y.; Chen, G.D.; Pu, Q.H. Dynamic behavior of hybrid framed arch railway bridge under moving trains. Steel Compos. Struct. 2018, in press. [Google Scholar]
- Gou, H.Y.; Wang, W.; Shi, X.Y.; Pu, Q.H.; Kang, R. Behavior of steel-concrete composite cable anchorage system. Steel Compos. Struct. 2018, 26, 115–123. [Google Scholar]
- Cui, K.; Qin, X. Virtual reality research of the dynamic characteristics of soft soil under metro vibration loads based on BP neural networks. Neural Comput. Appl. 2017, 1–10. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, Q.H.; Luo, Y.; Hao, H.; Li, J. Fatigue Reliability Evaluation of Deck-to-Rib Welded Joints in OSD Considering Stochastic Traffic Load and Welding Residual Stress. Int. J. Fatigue 2018, 111, 151–160. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Liu, Y.M.; Bao, Y.; Jia, D.L.; Bu, Y.Z.; Li, Q. Fatigue performance of orthotropic steel-concrete composite deck with large-size longitudinal trough. Eng. Struct. 2017, 150, 864–874. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, E.; Chen, Z. Dynamic Response Analysis of the Straddle-Type Monorail Bridge-Vehicle Coupling System. Urban Rail Transit 2017, 3, 172–181. [Google Scholar] [CrossRef]
- Goda, K.; Nishigaito, T.; Hiraishi, M.; Iwasaki, K. A curving simulation for a monorail car. In Proceedings of the 2000 ASME/IEEE Joint Railroad Conference, Newark, NJ, USA, 4–6 April 2000; pp. 171–177. [Google Scholar]
- Lee, C.H.; Kawatani, M.; Kim, C.W.; Nishimura, N.; Kobayashi, Y. Dynamic response of a monorail steel bridge under a moving train. J. Sound Vib. 2006, 294, 562–579. [Google Scholar] [CrossRef]
- Chinese National Bureau of Standards. Railway Vehicles-Specification for Evaluation the Dynamic Performance and Accreditation Test; Chinese Railway Ministry: Beijing, China, 1985. (In Chinese) [Google Scholar]
- Zeng, Q.Y.; Yang, P. The “set-in-right position” rule for forming structural matrices and truss segment finite element method for spatial analysis of truss girder. J. China Railw. Soc. 1986, 8, 48–58. [Google Scholar]
- Li, X.Z.; Lei, H.J.; Zhu, Y. Analysis of rayleigh damping parameters in a dynamic system of vehicle-track-bridge. J. Vib. Shock 2013, 32. [Google Scholar] [CrossRef]
- Mitsuo, K.; Chul-woo, K. Computer simulation for dynamic wheel loads of heavy vehicles. Struct. Eng. Mech. 2001, 12, 409–428. [Google Scholar]
- Liu, Z.; Luo, S.; Ma, W.; Song, R. Application research of track irregularity PSD in the high-speed train dynamic simulation. In Proceedings of the International Conference on Transportation Engineering, Chengdu, China, 25–27 July 2009; pp. 2845–2850. [Google Scholar]
- Liu, X.; Lian, S.; Yang, W. Influence analysis of irregularities on vehicle dynamic response on curved track of speed-up railway. In Proceedings of the Third International Conference on Transportation Engineering, Chengdu, China, 23–25 July 2011; pp. 2643–2648. [Google Scholar]
- Guo, W.H.; Xu, Y.L. Fully computerized approach to study cable-stayed bridge-vehicle interaction. J. Sound Vib. 2001, 248, 745–761. [Google Scholar] [CrossRef]
- Arkars, G.; Dhatt, G. An automatic node relabeling scheme for minimizing a matrix or network bandwidth. Int. J. Numer. Meth. Eng. 1976, 10, 787–797. [Google Scholar]
- He, R.; He, W.; Geng, G.H. Research on Dynamic Properties of Concrete Steel Tubular Arch Bridge Based on ANSYS. Appl. Mech. Mater. 2011, 71–78, 3233–3236. [Google Scholar] [CrossRef]
- Lee, I.W.; Kim, C.H.; Kim, B.W.; Cho, S.W. Determination of natural frequencies and mode shapes of structures using subspace iteration method with accelerated Starting vectors. J. Struct. Eng. 2005, 131, 1146–1149. [Google Scholar]
- Gou, H.Y.; Zhou, W.; Chen, G.D.; Bao, Y.; Pu, Q.H. In-situ test and dynamic analysis of a double-deck tied-arch bridge. Steel Compos. Struct. 2018, 27, in press. [Google Scholar]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Accornero, F. Evolution of fracturing process in masonry arches. J. Struct. Eng. 2015, 141, 1–10. [Google Scholar] [CrossRef]
- Block, P.; Dejong, M.J.; Ochsendorf, J. As hangs the flexible line: Equilibrium of masonry arches. Nexus Netw. J. 2006, 8, 9–19. [Google Scholar] [CrossRef]
- Chinese Railway Ministry. Code for Rating Existing Railway Bridges; Chinese Railway Ministry: Beijing, China, 2004. [Google Scholar]
- Graa, M.; Nejlaoui, M.; Houidi, A.; Affi, Z.; Romdhane, L. Modeling and control for lateral rail vehicle dynamic vibration with comfort evaluation. Adv. Acoust. Vib. 2017, 5, 89–100. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).