Solar Radiation Parameters for Assessing Temperature Distributions on Bridge Cross-Sections
Abstract
1. Introduction
2. State of Art of Estimation Models for Solar Radiation
2.1. Estimation Models for Global Solar Radiation
2.1.1. Estimation Models for Daily Global Solar Radiation
- Sunshine duration fraction models
- Non-sunshine duration models
- Artificial intelligence approach
2.1.2. Estimation Model for Hourly Global Solar Radiation
2.2. Estimation Model for Beam and Diffuse Solar Radiation
3. Monitoring of Solar Radiation
4. Estimation Model for Solar Radiation in Fujian
4.1. Estimation Model for Daily Global Solar Radiation
4.1.1. Influence of Time Scale on Empirical Coefficients
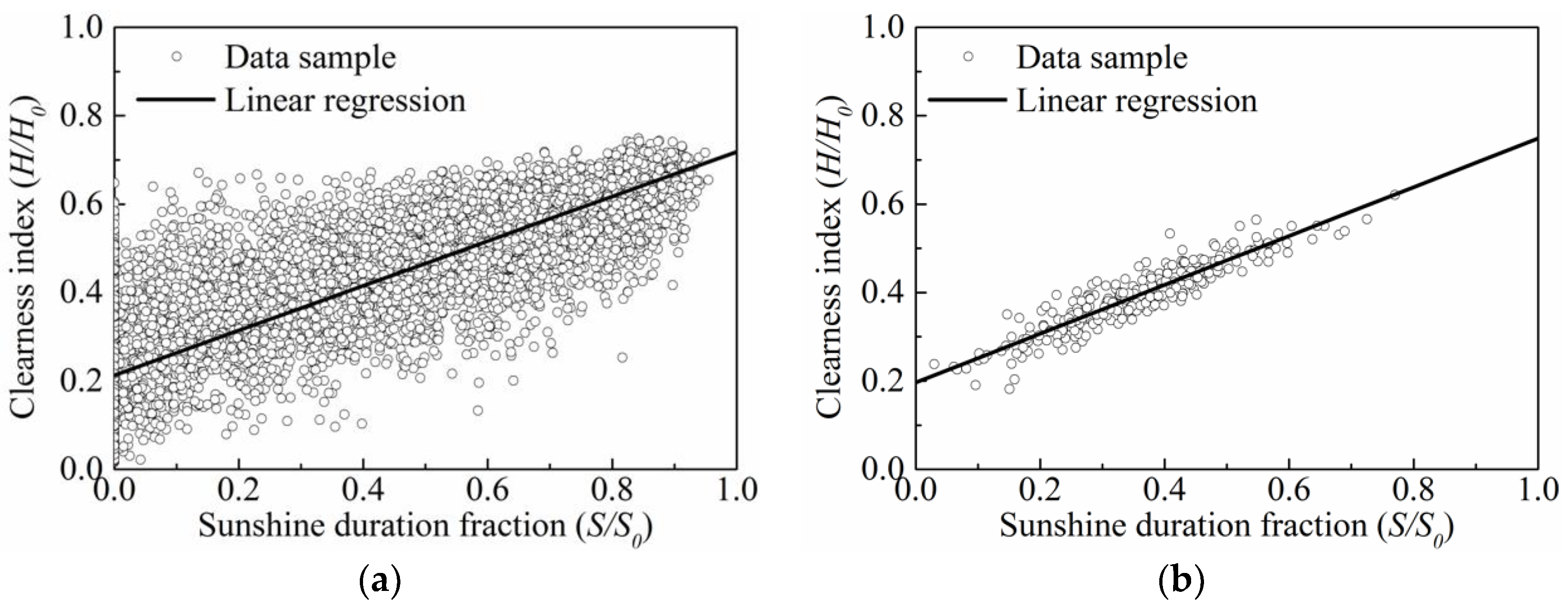
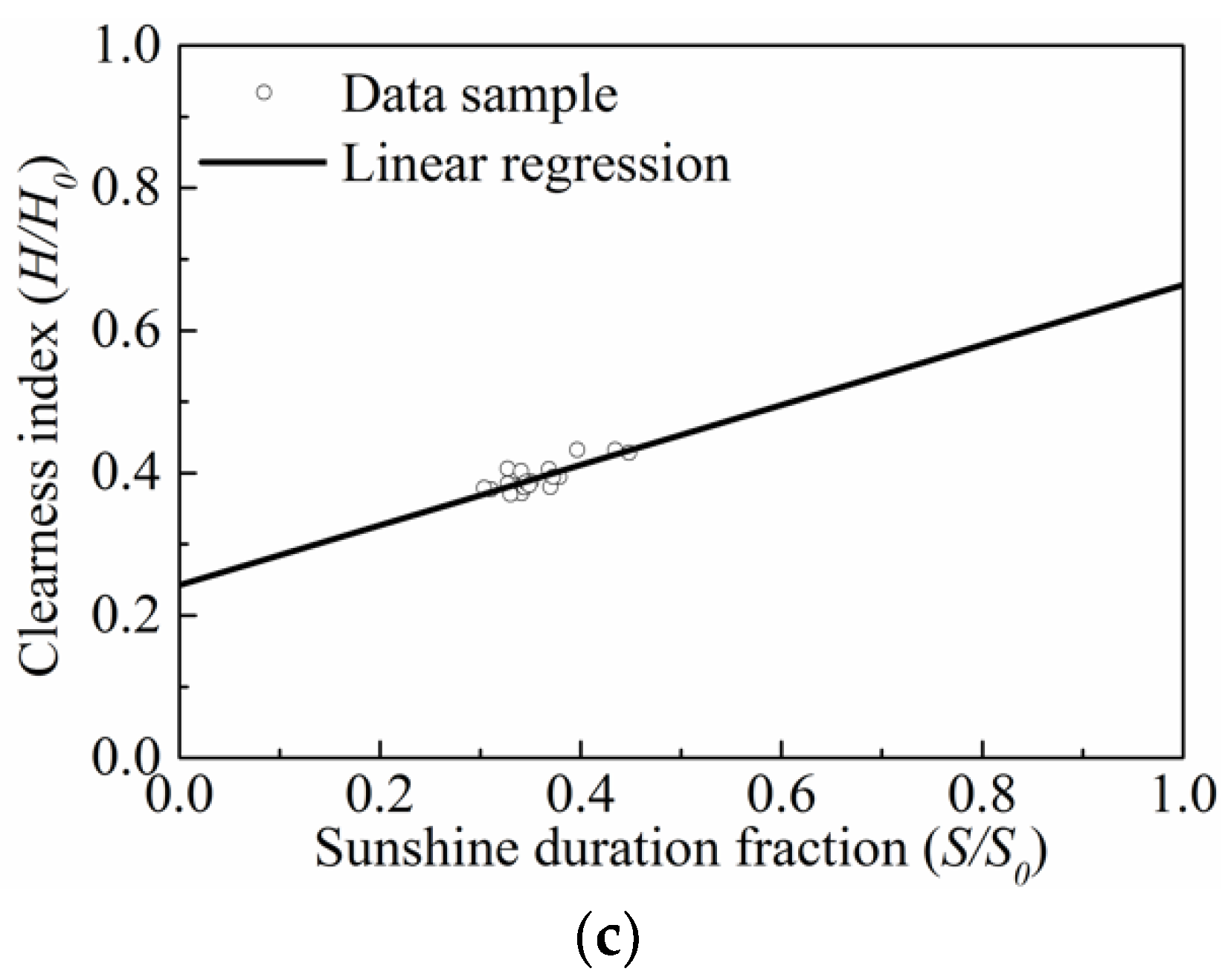
4.1.2. Influence of Sunshine Duration on the Empirical Coefficients
4.1.3. Verification of Ångström–Page Equation
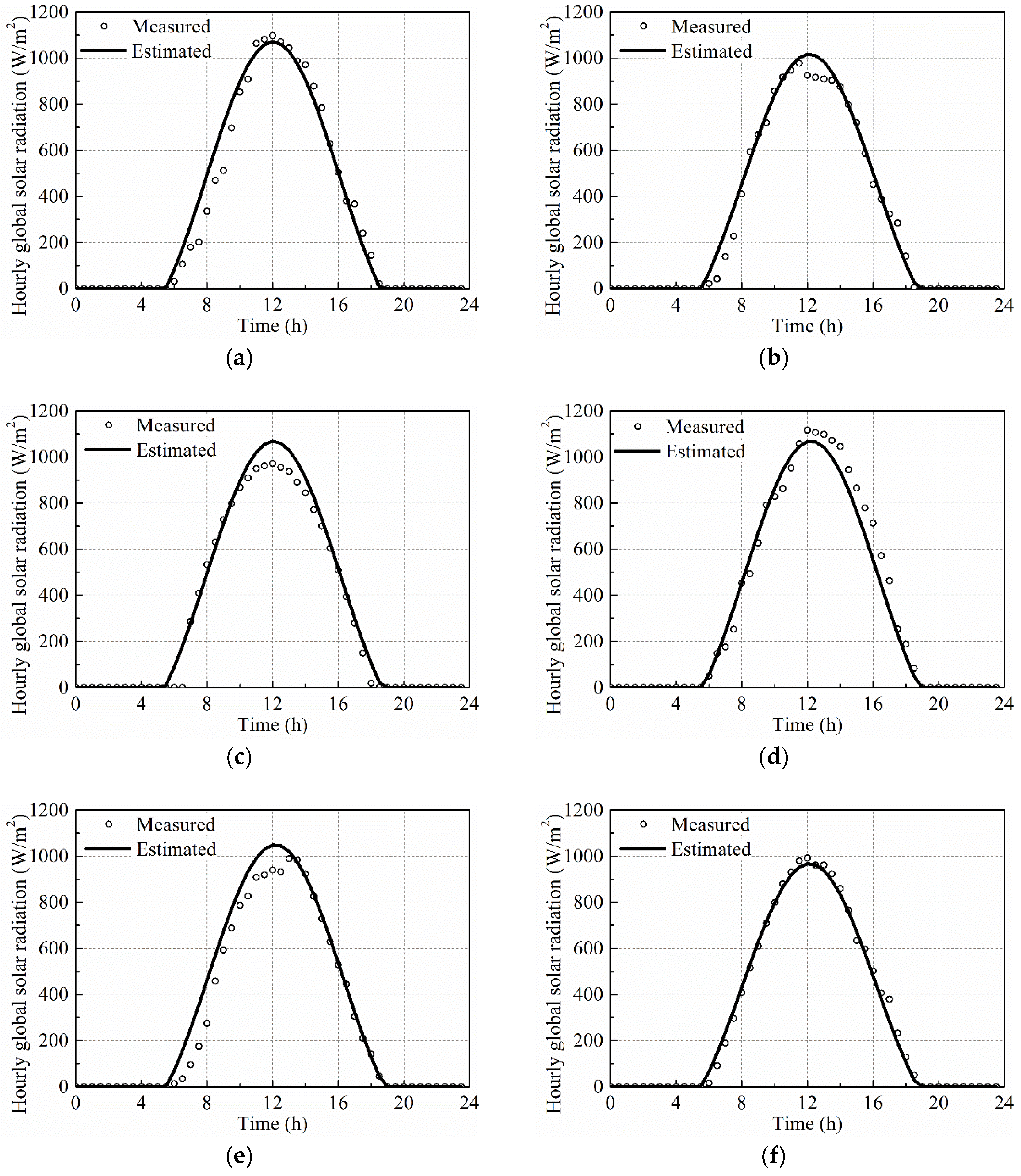
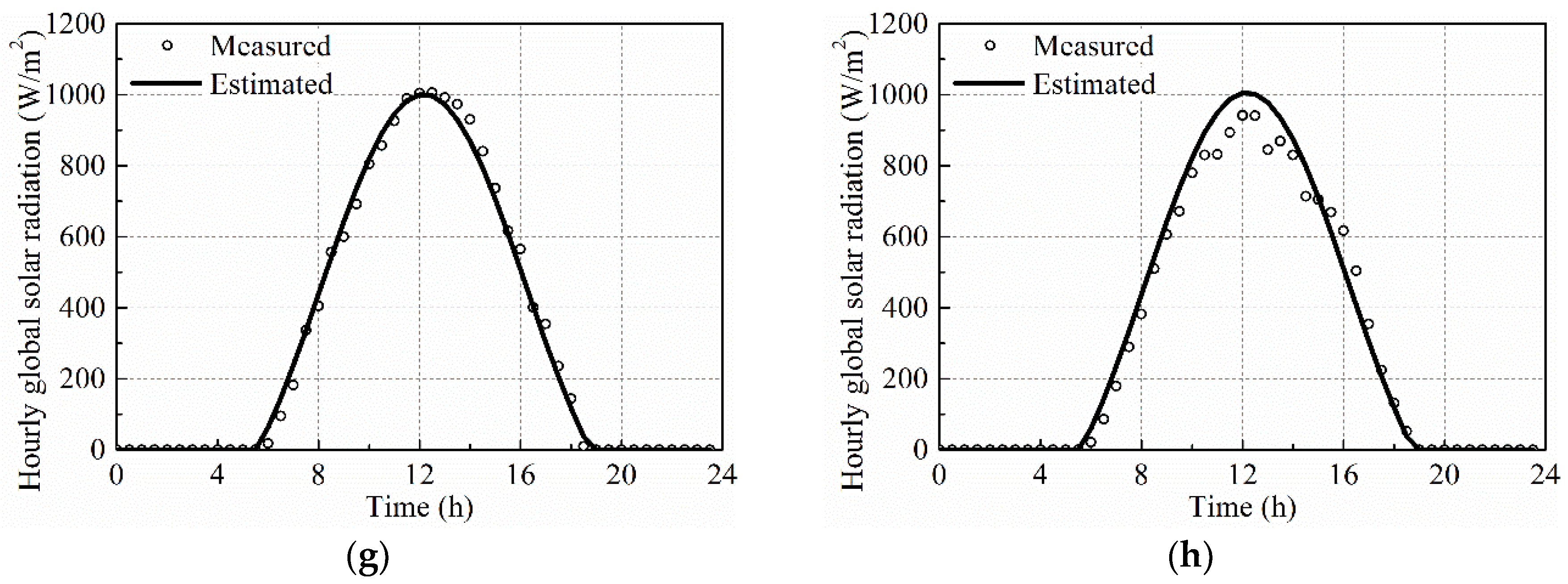
4.2. Estimation Model for Hourly Global Solar Radiation
4.3. Estimation Model for Hourly Beam and Diffuse Solar Radiation
4.3.1. Estimation Model for Hourly Beam Solar Radiation
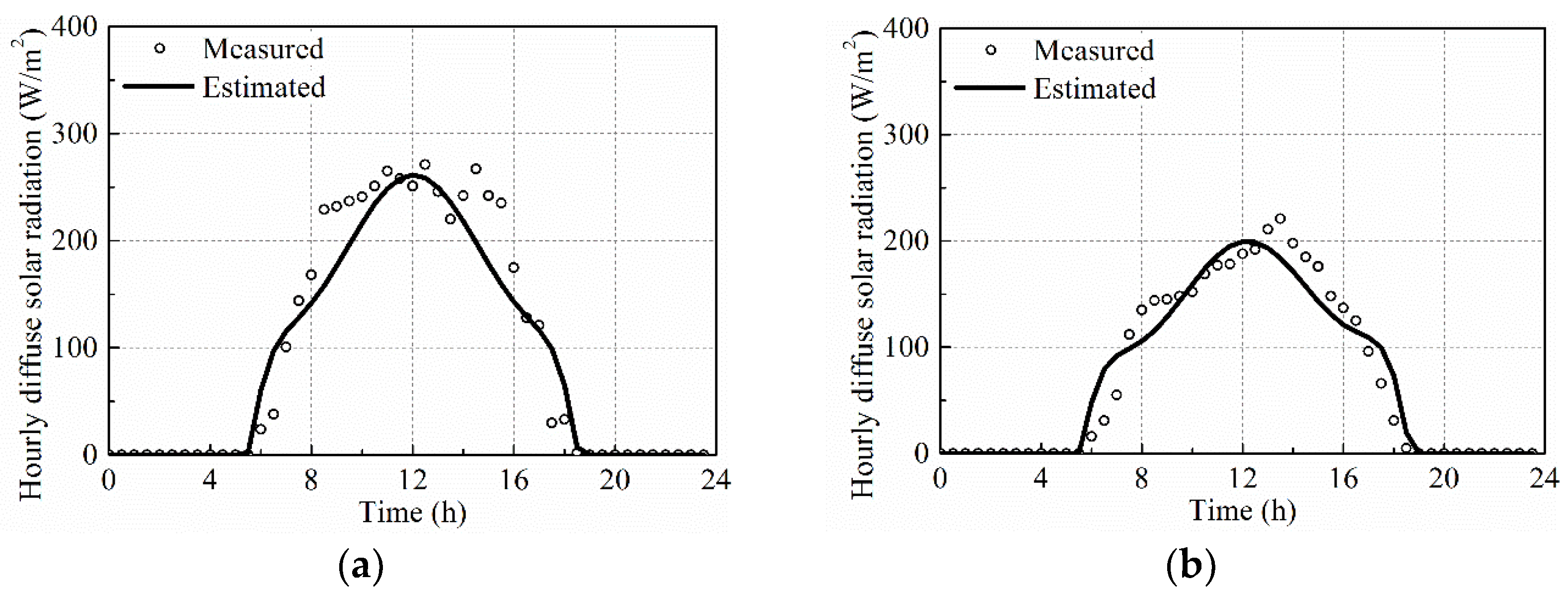
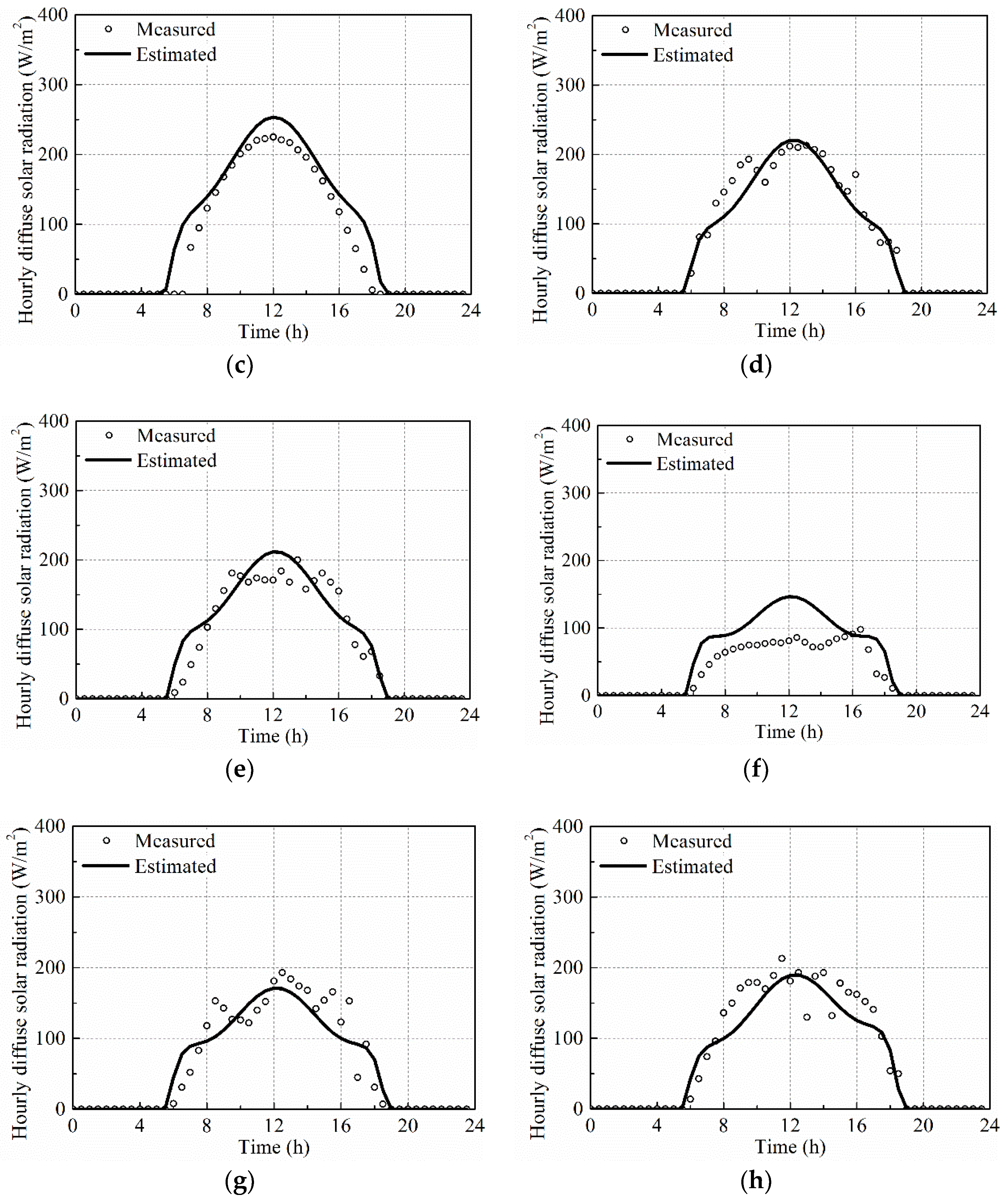
4.3.2. Estimation Model for Hourly Diffuse Solar Radiation
5. Solar Radiation in Fujian
6. Influence of Solar Radiation on Temperature Distribution on Bridge Girder Cross-Sections
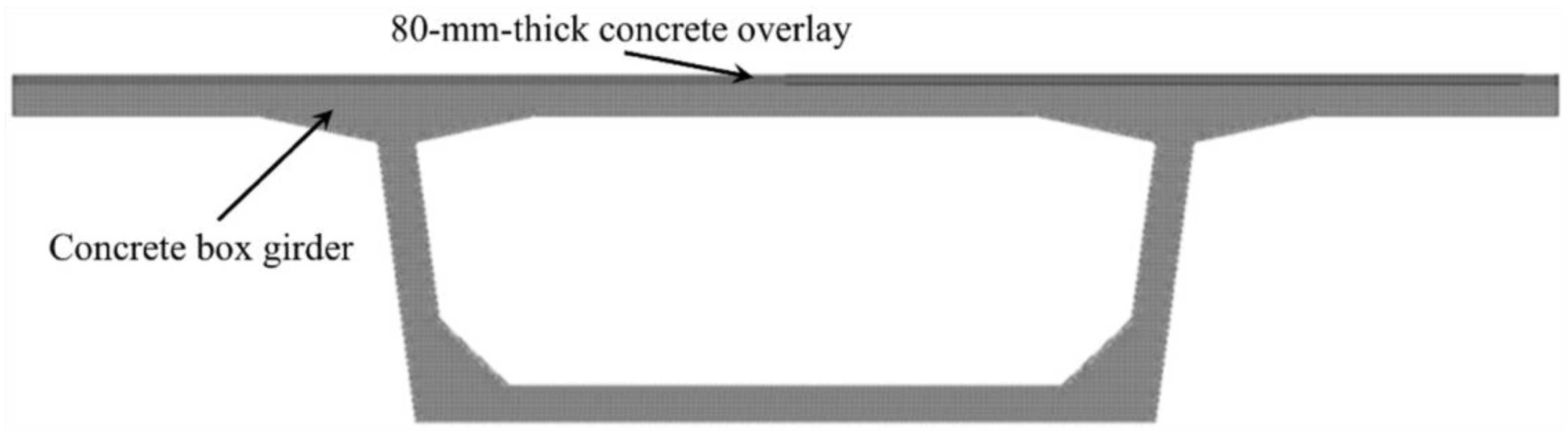
6.1. Box Girder Bridge
6.1.1. Finite Element Model
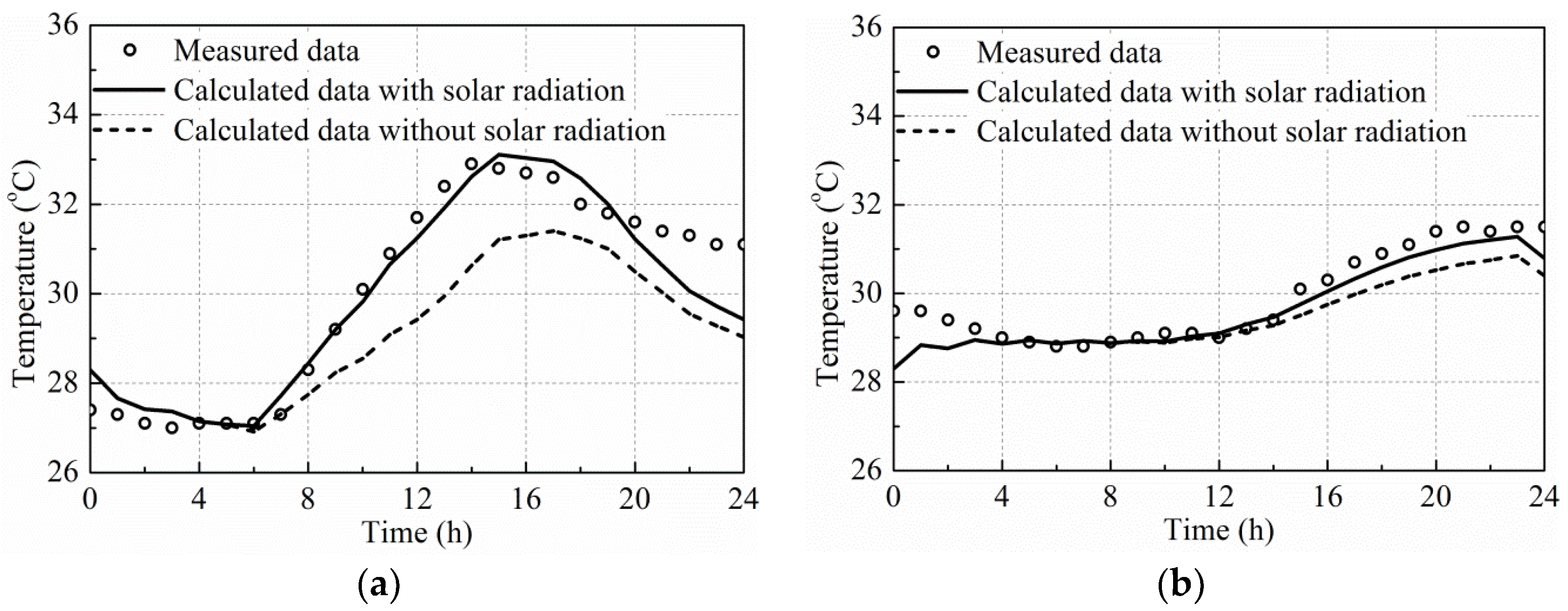
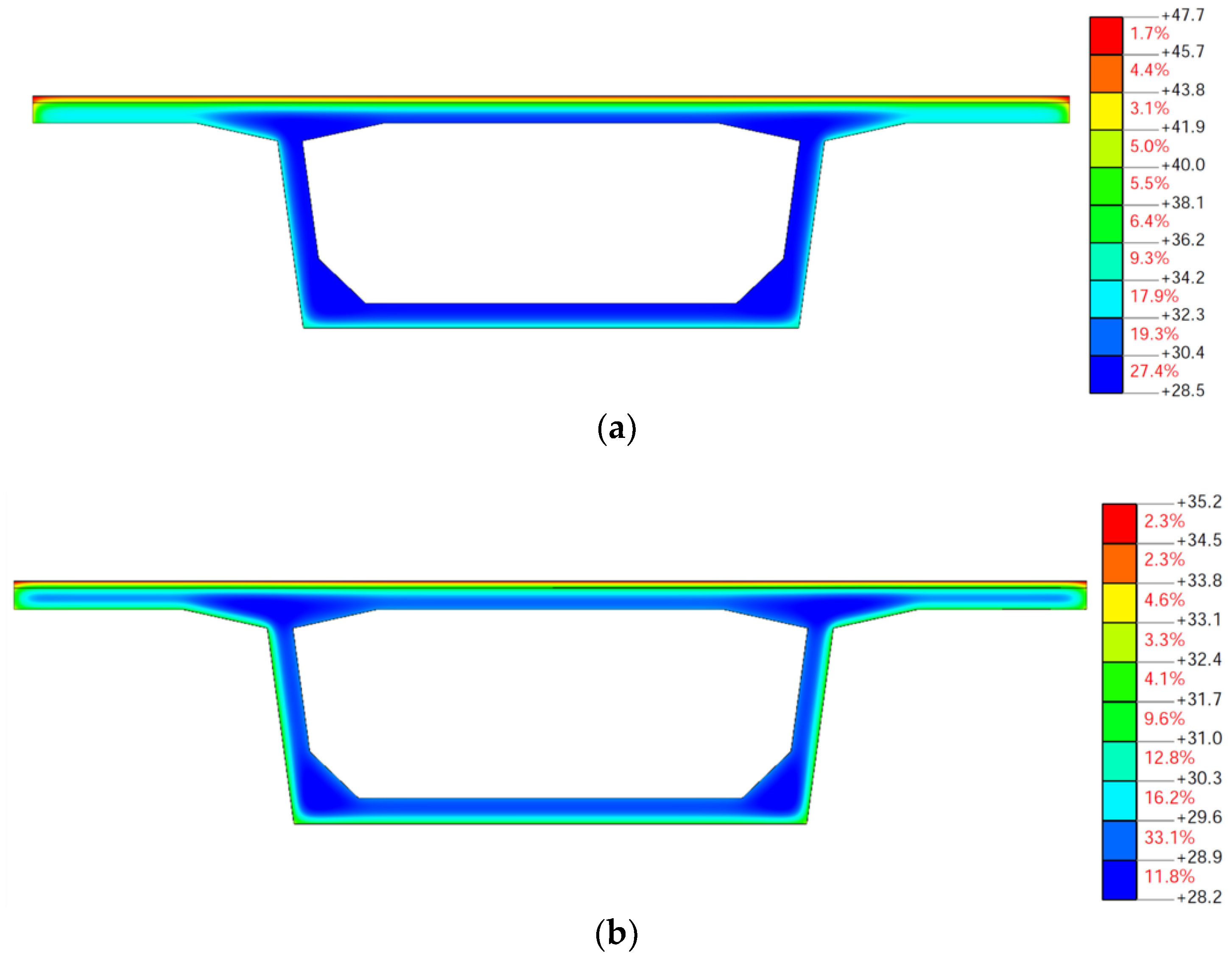
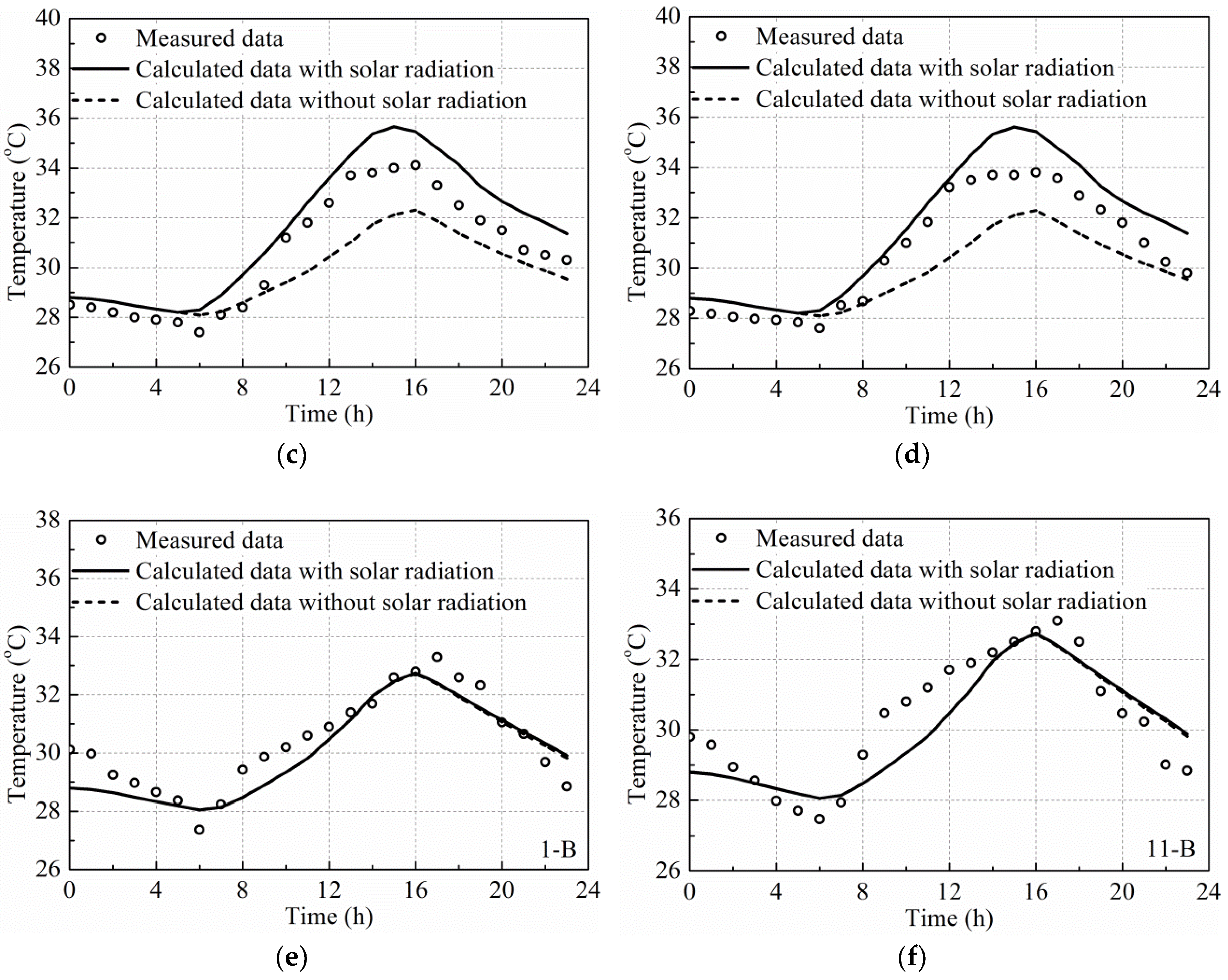
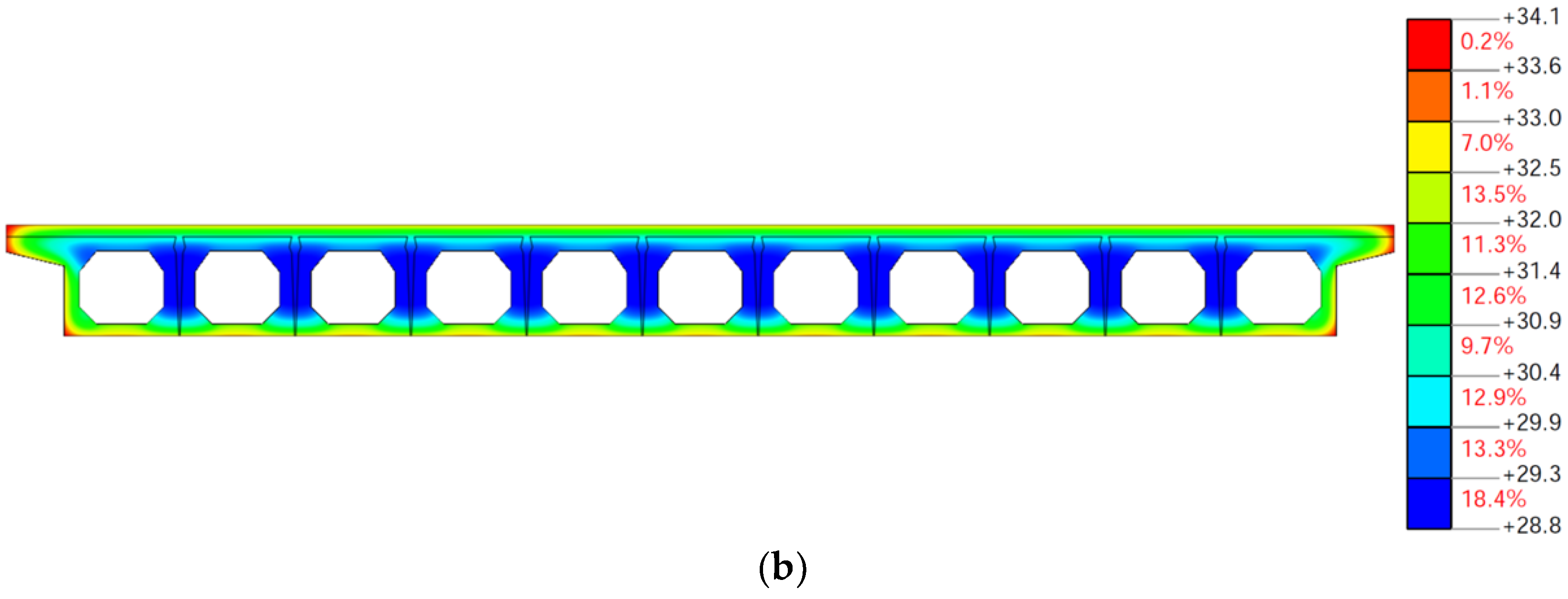
6.1.2. Influence of Solar Radiation on Temperature Distribution on Cross-Section of Box Girder
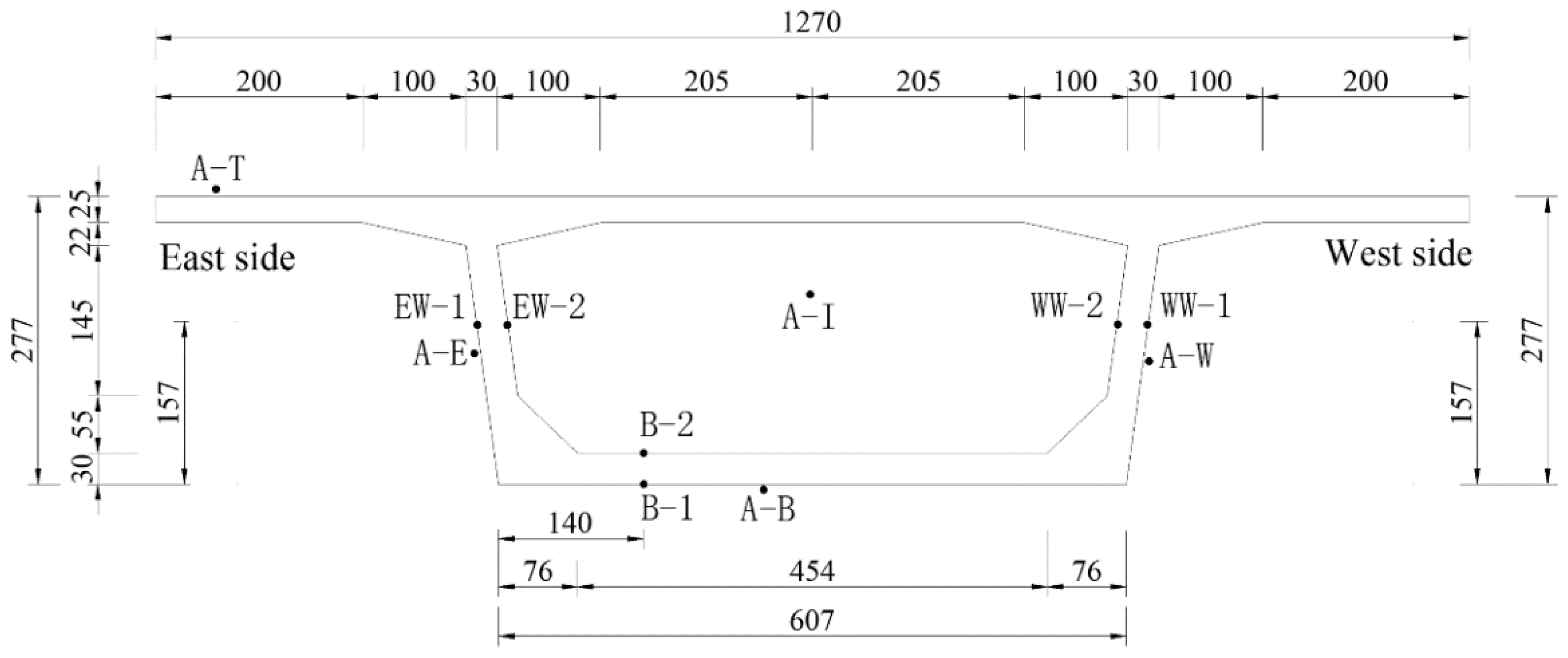
6.2. Side-by-Side Box Girder Bridge
6.2.1. Finite Element Model
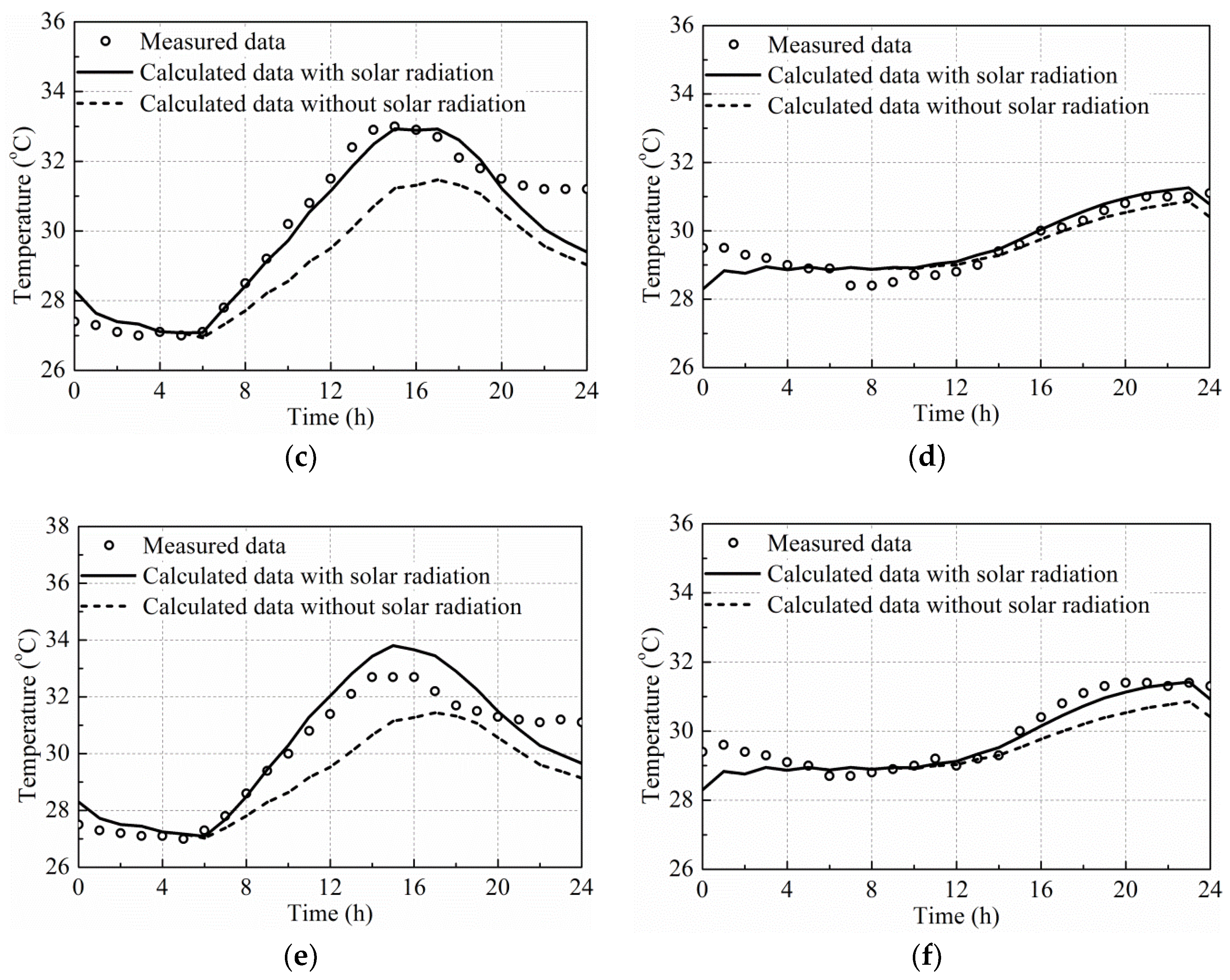
6.2.2. Influence of Solar Radiation on Temperature Distribution on Cross-Section of Side-by-Side Box Girder
6.3. T-Shaped Girder Bridge
6.3.1. Finite Element Model
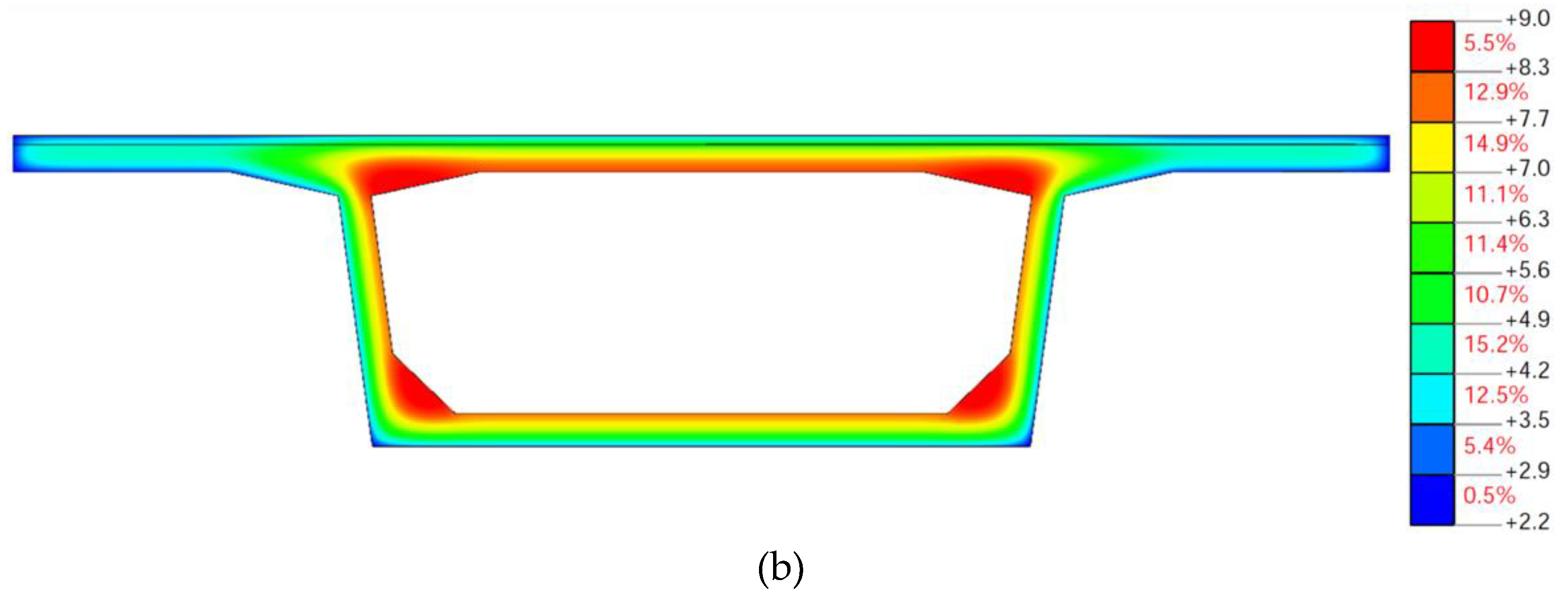
6.3.2. Influence of Solar Radiation on Temperature Distribution on Cross-Section of T-Shaped Girder
7. Discussion
- (1)
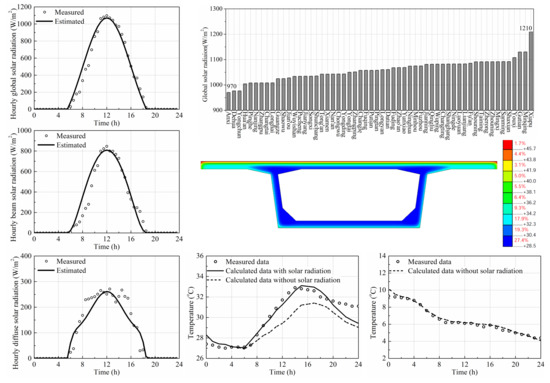
- The variation trends for all hourly solar radiation curves are similar, with the solar radiation appearing at about 6:00 a.m., reaching the maxima at about 12:00 p.m. and disappearing at about 6:00 p.m. The maximum measured global solar radiation for Ninghua (about 1100 W/m2) was the highest and the difference between maximum global solar radiation for different cities was about 100 W/m2. The maximum measured diffuse solar radiation for Fu’an (about 250 W/m2) and the calculated beam solar radiation for Ninghua (about 900 W/m2) was the highest. The difference between the maximum diffuse or beam solar radiation for different cities were both about 150 W/m2.
- (2)
- The linear regression of Ångström–Page equation using the monthly time scale of data sample can predict the global solar radiation for different cities in Fujian. For the cities in Fujian that did not have actual data on sunshine duration, the empirical coefficients can be estimated using the available sunshine duration for the nearest city.
- (3)
- The Collares-Pereira and Rabl equation can estimate the hourly global solar radiation for different cities in Fujian based on the daily global solar radiation. The hourly beam solar radiation for different cities in Fujian can be predicted well using the Hottel equation. The hourly diffuse solar radiation for different cities in Fujian can be calculated by subtracting the hourly beam solar radiation from the corresponding hourly global solar radiation.
- (4)
- The maximum global solar radiation, beam solar radiation and diffuse solar radiation (for 21 June, the summer solstice) for 56 cities in Fujian were calculated. The maximum global solar radiation for Xiapu (about 1210 W/m2) is the highest and the maximum global solar radiation for Anxi (about 970 W/m2) is the lowest. The biggest difference among the global solar radiation maxima in different cities is about 240 W/m2. The maximum beam solar radiation for Zhouning (about 909 W/m2) is the highest and the maximum beam solar radiation for Ningde (about 821 W/m2) is the lowest. The biggest difference among the beam solar radiation maxima in different cities is about 88 W/m2. The maximum diffuse solar radiation for Xiapu (about 388 W/m2) is the highest and the maximum diffuse solar radiation for Dehua (about 102 W/m2) is the lowest. The biggest difference among the diffuse solar radiation maxima in different cities is about 286 W/m2.
- (5)
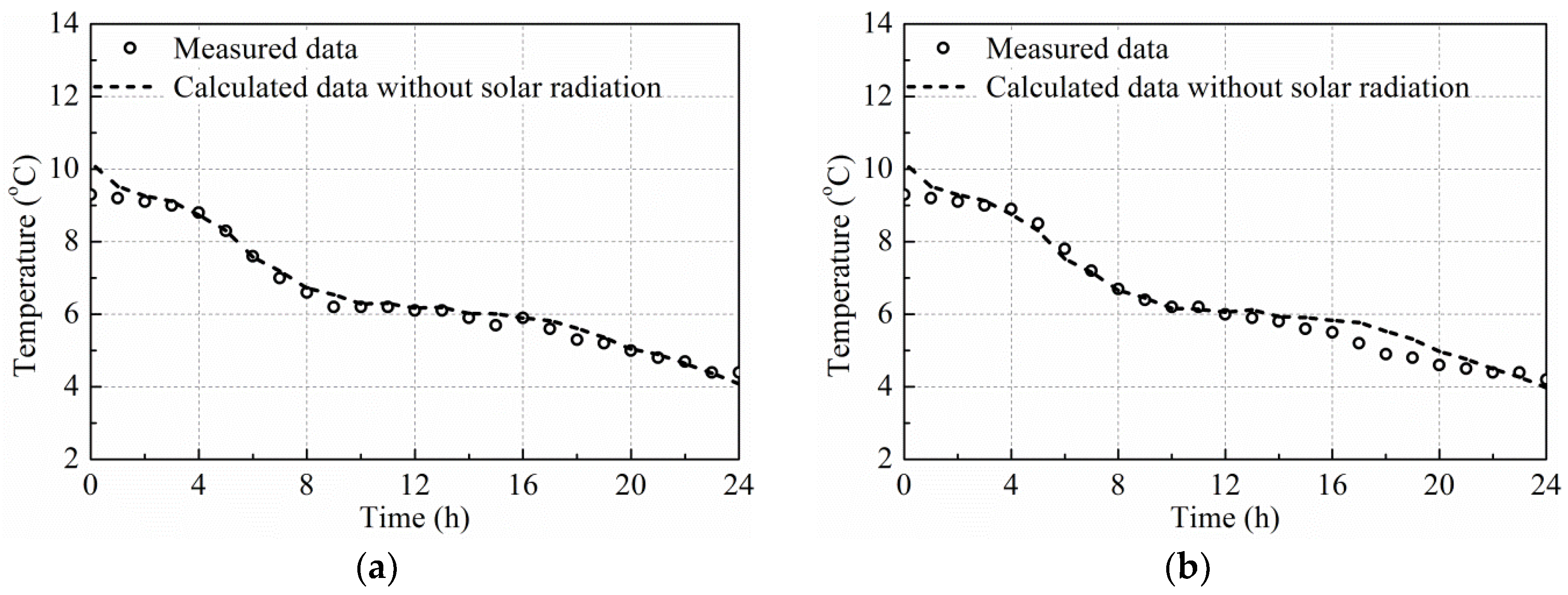
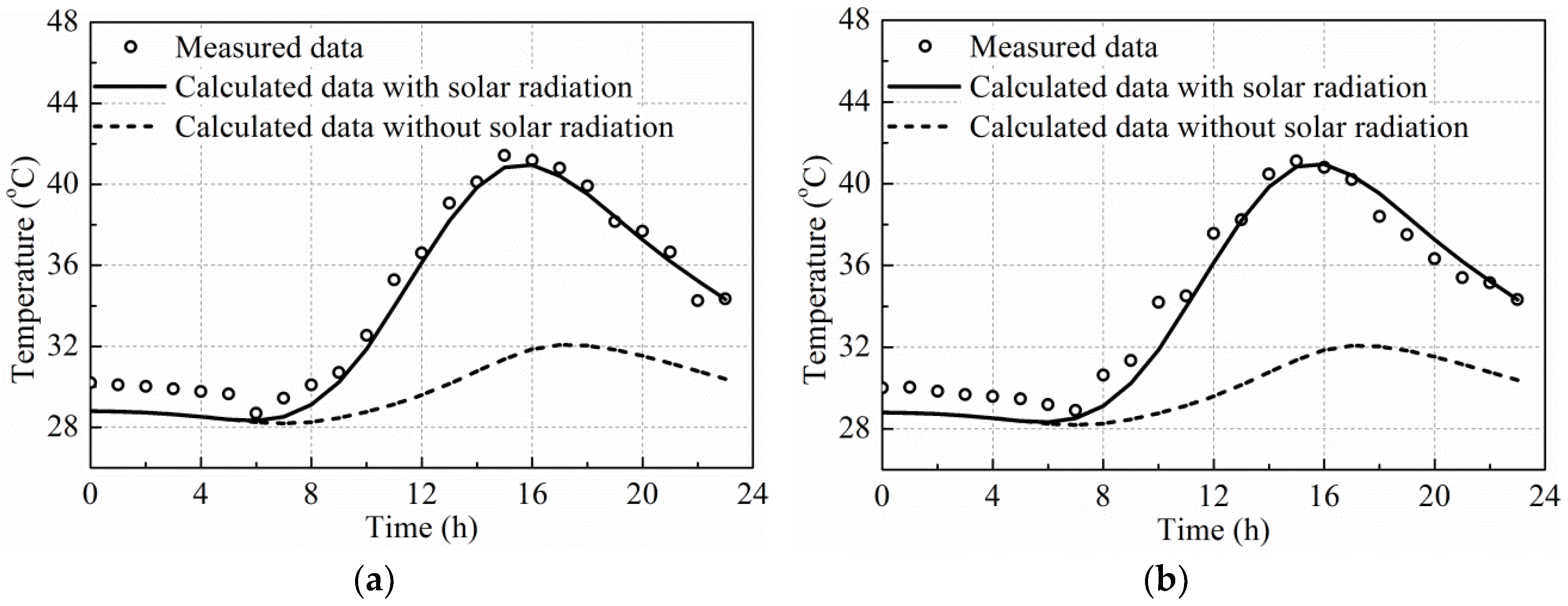
- Comparisons of the measured and calculated temperature–time responses for the concrete box girder, side-by-side box girder and T-shaped girder with or without the consideration of solar radiation indicates that the influence of solar radiation should be considered in the analyses of the temperature distribution on the bridge girder cross-sections in summer. The accuracy of the solar radiation calculated using the estimation models can meet the engineering requirements. The highest calculated temperatures without the consideration of solar radiation were lower and had a time delay, especially for top flanges in the summertime. The vertical temperature variation when considering the effect of solar radiation was significantly larger than that without the consideration of solar radiation. The influence of solar radiation on the temperature distribution decreases as the distance from external surfaces. The influence of solar radiation on the temperature distribution of the bridge girder cross-sections is negligible in winter.
- (6)
- The solar radiation parameters for other cities and regions in China and elsewhere, as well as different bridge superstructure types, can be similarly developed based on more case studies to establish the relevant estimation models. This can serve as a prelude for future development of specifications related to temperature effects in bridge engineering.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kehlbeck, F. Einfluss der Sonnenstrahlung bei Bruckenbauwerken; Werner: Dusseldorf, Germany, 1975. [Google Scholar]
- Peng, Y.S.; Qiang, S.Z. Analytical solution to temperature variations in highway concrete bridges due to solar radiation. In Proceedings of the First International Conference on Transportation Engineering, Chengdu, China, 22–24 July 2007; American Society of Civil Engineers: Reston, VA, USA, 2017; pp. 1536–1541. [Google Scholar]
- Emerson, M. Bridge Temperatures Estimated from the Shade Temperature; TRRL Laboratory Report 696; TRRL: Berkshire, UK, 1976. [Google Scholar]
- Imbsen, R.A.; Vandershaf, D.E.; Schamber, R.A.; Nutt, R.V. Thermal Effects in Concrete Bridge Superstructures; NCHRP Report 276; Transportation Research Board: Washington, DC, USA, 1985. [Google Scholar]
- Shiu, K.N.; Russell, H.G.; Tabatabai, H. Instrumentation of the Red River Bridge at Boyce; Report No. FHWA/LA-91/223; Louisiana Transportation Research Center: Baton Rouge, LA, USA, 1991. [Google Scholar]
- Shiu, K.N.; Tabatabai, H. Measured Thermal Response of Concrete Box-Girder Bridge; Transportation Research Record No. 1460; Transportation Research Board: Washington, DC, USA, 1994; pp. 94–105. [Google Scholar]
- Qin, Y.; Lin, L.; Tie, M.; Zhang, L. Observation and research on temperature distribution of concrete box girder in diurnal change of temperature. In Proceedings of the International Conference on Transportation, Mechanical, and Electrical Engineering, Changchun, China, 16–18 December 2011. [Google Scholar]
- Avossa, A.M.; Giacinto, D.D.; Malangone, P.; Rizzo, F. Seismic retrofit of a multispan prestressed concrete girder bridge with friction pendulum devices. Shock Vib. 2018, 2018, 1–22. [Google Scholar] [CrossRef]
- Zang, H.X.; Xu, Q.S.; Bian, H.H. Generation of typical solar radiation data for different climates of China. Energy 2012, 38, 236–248. [Google Scholar] [CrossRef]
- Angstrom, A. Solar and terrestrial radiation. Quart. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Page, J.K. The estimation of monthly mean values of daily total short wave radiation on-vertical and inclined surfaces from sun shine records for latitudes 40° N-40° S. In Proceedings of the United Nations Conference on New Sources of Energy, Rome, Italy, 21–31 August 1961; pp. 378–387. [Google Scholar]
- Ögelman, H.; Ecevit, A.; Tasdemiroǧlu, E. A new method for estimating solar radiation from bright sunshine data. Sol. Energy 1984, 33, 619–625. [Google Scholar] [CrossRef]
- Bahel, V.; Bakhsh, H.; Srinivasan, R. A correlation for estimation of global solar radiation. Energy 1987, 12, 131–135. [Google Scholar] [CrossRef]
- Bakirci, K. Correlations for estimation of daily global solar radiation with hours of bright sunshine in Turkey. Energy 2009, 34, 485–501. [Google Scholar] [CrossRef]
- Duzen, H.; Aydin, H. Sunshine-based estimation of global solar radiation on horizontal surface at Lake Van region (Turkey). Energy Convers. Manag. 2012, 58, 35–46. [Google Scholar] [CrossRef]
- Li, H.S.; Ma, W.B.; Lian, Y.W.; Wang, X.L.; Zhao, L. Global solar radiation estimation with sunshine duration in Tibet, China. Renew. Energy 2011, 36, 3141–3145. [Google Scholar] [CrossRef]
- Katiyar, A.K.; Pandey, C.K. Simple correlation for estimating the global solar radiation on horizontal surfaces in India. Fuel Energy Abstr. 2010, 35, 5043–5048. [Google Scholar] [CrossRef]
- Weng, D.M. Radiation Climate in China; China Meteorological Press: Beijing, China, 1997. [Google Scholar]
- Chen, R.S.; Kang, E.S.; Yang, J.P.; Lu, S.H.; Zhao, W.Z. Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Chen, R.S.; Lu, S.H.; Kang, E.S.; Yang, J.P.; Ji, X.B. Estimating daily global radiation using two types of revised models in China. Energy Convers. Manag. 2006, 47, 865–878. [Google Scholar]
- Zhao, N.; Zeng, X.F.; Han, S.M. Solar radiation estimation using sunshine hour and air pollution index in China. Energy Convers. Manag. 2013, 76, 846–851. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Zhao, L.; Deng, S.; Xu, W.C.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Annandale, J.; Jovanovic, N.; Benadé, N.; Allen, R. Software for missing data error analysis of Penman-Monteith reference evapotranspiration. Irrig. Sci. 2002, 21, 57–67. [Google Scholar]
- De, J.R.; Stewart, D.W. Estimating global solar radiation from common meteorological observations in western Canada. Can. J. Plant Sci. 1993, 73, 509–518. [Google Scholar]
- Hamby, A.L. Estimation of solar radiation for use in crop modeling. Agric. For. Meteorol. 1998, 91, 293–300. [Google Scholar]
- Wu, G.F.; Liu, Y.L.; Wang, T.J. Methods and strategy for modeling daily global solar radiation with measured meteorological data—A case study in Nanchang Station, China. Energy Convers. Manag. 2007, 48, 2447–2452. [Google Scholar] [CrossRef]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. For. Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Grillone, G.; Agnese, C.; D’asaro, F. Estimation of daily solar radiation from measured air temperature extremes in the Mid-Mediterranean area. J. Irrig. Drain. Eng. 2012, 138, 939–947. [Google Scholar] [CrossRef]
- Liu, X.Y.; Mei, X.R.; Li, Y.Z.; Wang, Q.S.; Jens, R.J.; Zhang, Y.Q.; Johnroy, P. Evaluation of temperature-based global solar radiation models in China. Agric. For. Meteorol. 2009, 149, 1433–1446. [Google Scholar] [CrossRef]
- Kimball, H.H. Solar and sky radiation measurements during June. Mon. Weather Rev. 1928, 56, 230. [Google Scholar] [CrossRef]
- Bennett, I. Monthly maps of mean daily insolation for the United States. Sol. Energy 1965, 9, 145–158. [Google Scholar] [CrossRef]
- Wang, B.Z.; Zhang, F.G.; Li, L.X. Solar energy resources in China. Acta Energ. Sol. Sin. 1980, 1, 229–241. [Google Scholar]
- Alsina, E.F.; Bortolini, M.; Gamberi, M.; Regattieri, A. Artificial neural network optimisation for monthly average daily global solar radiation prediction. Energy Convers. Manag. 2016, 120, 320–329. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.C.; Lin, A.W.; Zhu, H.J.; Peng, Y.L.; Zhao, Z.Z. Estimation of global solar radiation using an artificial neural network based on an interpolation technique in southeast China. J. Atmos. Sol. Terr. Phys. 2016, 146, 110–122. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Comparison of artificial intelligence methods and empirical equations to estimate daily solar radiation. J. Atmos. Sol. Terr. Phys. 2016, 146, 215–227. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Collares-Pereira, M.; Rabl, A. The average distribution of solar radiation-correlations between diffuse and hemispherical and between daily and hourly insolation values. Sol. Energy 1979, 22, 155–164. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Pashiardis, S.; Pashiardi, A. Statistical analysis and inter-comparison of the global solar radiation at two sites in Cyprus. Renew. Energy 2017, 101, 1102–1123. [Google Scholar] [CrossRef]
- Yao, W.X.; Li, Z.G.; Xiu, T.B.; Lu, Y.; Li, X.B. New decomposition models to estimate hourly global solar radiation from the daily value. Sol. Energy 2015, 120, 87–99. [Google Scholar] [CrossRef]
- Newell, T.A. Simple models for hourly to daily radiation ratio correlations. Sol. Energy 1983, 31, 339–342. [Google Scholar] [CrossRef]
- Zhang, S.N.; Tian, S.Y. The institution of the hourly solar radiation model. Acta Energy Sol. Sin. 1997, 18, 273–277. [Google Scholar]
- Jain, P.C. Comparison of techniques for the estimation of daily global irradiation and a new technique for the estimation of hourly global irradiation. Sol. Wind Technol. 1984, 1, 123–134. [Google Scholar] [CrossRef]
- Baig, A.; Akhter, P.; Mufti, A. A novel approach to estimate the clear day global radiation. Renew. Energy 1991, 1, 119–123. [Google Scholar] [CrossRef]
- American Society of Heating. Refrigerating, and Air Conditioning Engineers. In ASHRAE Handbook of Fundamentals; ASHRAE: New York, NY, USA, 1972. [Google Scholar]
- Nijegorodov, N. Improved ASHRAE model to predict hourly and daily solar radiation components in Botswana, Namibia, and Zimbabwe. Renew. Energy 1996, 9, 1270–1273. [Google Scholar] [CrossRef]
- Song, A.G.; Wang, F.R. Preliminary study on clear-day solar radiation model of Beijing region. Acta Energ. Sol. Sin. 1993, 14, 251–255. [Google Scholar]
- Al-Sanea, S.A.; Zedan, M.F.; Al-Ajlan, S.A. Adjustment factors for the ASHRAE clear-sky model based on solar-radiation measurements in Riyadh. Appl. Energy 2004, 79, 215–237. [Google Scholar] [CrossRef]
- Hottel, H.C. A simple model for estimating the transmittance of direct solar radiation through clear atmospheres. Sol. Energy 1976, 18, 129–134. [Google Scholar] [CrossRef]
- Jiang, Y.N. Correlation for diffuse radiation from global solar radiation and sunshine data at Beijing, China. J. Energy Eng. 2009, 135, 363–372. [Google Scholar] [CrossRef]
- Janjai, S.; Praditwong, P.; Moonin, C. A new model for computing monthly average daily diffuse radiation for Bangkok. Renew. Energy 1996, 9, 1283–1286. [Google Scholar] [CrossRef]
- Bai, J.S.; Chen, X.P.; Dobermann, A.; Yang, H.S.; Kennethg, C.; Zhang, F.S. Evaluation of NASA Satellite- and Model-Derived weather data for simulation of Maize yield potential in China. Agron. J. 2010, 102, 9–16. [Google Scholar] [CrossRef]
- Kaplanis, S.; Kumar, J.; Kaplani, E. On a universal model for the prediction of the daily global solar radiation. Renew. Energy 2016, 91, 178–188. [Google Scholar] [CrossRef]
- Bakirci, K. Prediction of global solar radiation and comparison with satellite data. J. Atmos. Sol. Terr. Phys. 2017, 152, 41–49. [Google Scholar] [CrossRef]
- Ma, X.Q. Estimation of Solar Radiation Using Nasa/Power Data. Master’s Thesis, Southwest University, Chongqing, China, 2015. [Google Scholar]
- National Meteorological Information Center, China Meteorological Administration. Available online: http://data.cma.cn/site/index.html (accessed on 15 March 2018).
- Zhang, J.F. Estimation Models of Solar Radiation at Different Time Scales. Master’s Thesis, Southwest University, Chongqing, China, 2013. [Google Scholar]
- Elbadry, M.M.; Ghali, A. Temperature Variations in Concrete Bridges. J. Struct. Eng. 1983, 109, 2355–2374. [Google Scholar] [CrossRef]
- Zhang, X.Y. Practical Handbook of Chemistry; National Defense Industry Press: Beijing, China, 2011. [Google Scholar]
- Chen, X.Y. Research on Sunlight Thermal Effect of Integral Abutment Bridge. Master’s Thesis, Fuzhou University, Fuzhou, China, 2012. [Google Scholar]













| Time Scale Types | Data Points | a’ | b’ | γxy | RMSE |
|---|---|---|---|---|---|
| Daily | 8030 | 0.213 | 0.505 | 0.86 | 0.10 |
| Monthly | 264 | 0.196 | 0.553 | 0.92 | 0.03 |
| Yearly | 22 | 0.242 | 0.422 | 0.79 | 0.01 |
| Solar Radiation Data Source | Sunshine Duration Data Source | a’ | b’ | γxy | RMSE |
|---|---|---|---|---|---|
| Hua’an | Nanping | 0.216 | 0.467 | 0.81 | 0.05 |
| Hua’an | Fuzhou | 0.217 | 0.519 | 0.82 | 0.06 |
| Hua’an | Yong’an | 0.212 | 0.519 | 0.85 | 0.06 |
| Hua’an | Xiamen | 0.178 | 0.522 | 0.90 | 0.04 |
| City | Solar Radiation Data Source | Sunshine Duration Data Source | a’ | b’ | γxy | RMSE |
|---|---|---|---|---|---|---|
| Fu’an | Fu’an | Fuzhou | 0.211 | 0.546 | 0.84 | 0.05 |
| Jian’ou | Jian’ou | Nanping | 0.180 | 0.537 | 0.84 | 0.05 |
| Fuzhou | Fuzhou | Fuzhou | 0.196 | 0.553 | 0.92 | 0.03 |
| Ninghua | Ninghua | Yong’an | 0.179 | 0.571 | 0.85 | 0.05 |
| Zhangping | Zhangping | Yong’an | 0.213 | 0.520 | 0.84 | 0.05 |
| Anxi | Anxi | Xiamen | 0.197 | 0.479 | 0.88 | 0.04 |
| Hua’an | Hua’an | Xiamen | 0.178 | 0.522 | 0.90 | 0.04 |
| Zhangzhou | Zhangzhou | Xiamen | 0.196 | 0.506 | 0.89 | 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Lin, J.; Briseghella, B.; Tabatabai, H.; Chen, B. Solar Radiation Parameters for Assessing Temperature Distributions on Bridge Cross-Sections. Appl. Sci. 2018, 8, 627. https://doi.org/10.3390/app8040627
Xue J, Lin J, Briseghella B, Tabatabai H, Chen B. Solar Radiation Parameters for Assessing Temperature Distributions on Bridge Cross-Sections. Applied Sciences. 2018; 8(4):627. https://doi.org/10.3390/app8040627
Chicago/Turabian StyleXue, Junqing, Jianhui Lin, Bruno Briseghella, Habib Tabatabai, and Baochun Chen. 2018. "Solar Radiation Parameters for Assessing Temperature Distributions on Bridge Cross-Sections" Applied Sciences 8, no. 4: 627. https://doi.org/10.3390/app8040627
APA StyleXue, J., Lin, J., Briseghella, B., Tabatabai, H., & Chen, B. (2018). Solar Radiation Parameters for Assessing Temperature Distributions on Bridge Cross-Sections. Applied Sciences, 8(4), 627. https://doi.org/10.3390/app8040627