Abstract
In this study, we propose to define a connectivity factor as the inverse of the diffusional tortuosity to measure quantitatively the connectivity of whatever type of structure. The concept of connectivity used here is related to the diffusional accessibility of the structure voids. This definition of connectivity factor arises from the consideration that, if we ideally imagine to decrease progressively the porosity of a regular structure, the porosity itself reaches a limit value below which the inner pores are not interconnected anymore. This leads to an evident situation of zero connectivity and infinite tortuosity, where there is no continuous diffusion path able to connect the structure voids. According to the proposed definition, the connectivity factor is comprised within [0, 1], with zero corresponding to a completely disconnected structure and unity to a completely connected one. To show the efficacy of the presented approach, a case study on the regular structure of mono-sized (mono-disperse) spherical particles (Simple Cubic (SC), Face-Centred Cubic (FCC), Body-Centred Cubic (BCC) and Tetragonal structures) is provided. In particular, the tortuosity of such structures is evaluated by Computational Fluid Dynamics simulations, calculating the connectivity factor consequently. The morphological modification with porosity is induced by changing the surface–surface interparticle distance, allowing us to take both positive (detached particles) and negative values (overlapping particles). For each structure, a comparison between the calculated trends and some correlations of literature is made, and a novel “hidden” morphological parameter has been identified, that is, the here-called Limit Porosity Value, below which the connectivity is zero. The presented approach represents a systematic methodology to quantify the connectivity of any structure and to compare the morphology of membranes, catalysts, and porous media in general.
1. Introduction
It may be redundant to say that a correct characterization of mass transport phenomena occurring in particle assemblies, membranes, and porous media is crucial in a number of applications in engineering, chemistry, and physics. The fluid path through a catalyst and/or adsorbent particle beds can severely affect the performance of a mass transfer-based process, and a number of works of literature are aimed at optimising the catalyst distribution [1,2,3,4,5].
However, for this purpose, it is required to understand not only the dependence of the transport properties on the operating conditions (temperature, pressure, etc.) but also the morphology of the structure, which are characteristics involving several important geometrical parameters, like specific area, porosity, tortuosity, etc.
Among such parameters, relatively minor attention is paid to the so-called connectivity of a structure, representing a property measuring a sort of degree of connection of the inner voids. However, if the meaning of connectivity is relatively intuitive, its formal definition and quantification are not obvious at all. For example, Leichtner et al. (2015) provide a sort of quantification of connectivity by reconstructing the considered structures through image analysis techniques, classifying all the inner void channels into connected, disconnected, and unknown voids, and simply evaluating the percentage of the connected void volume to the total volume [6]. Slightly differently, Promentilla et al. (2009) defined a connectivity factor in terms of percentage of voxels connected in all directions [7]. However, the drawback of these approaches is that they cannot be applied to all the cases in which there are experimental evaluations of tortuosity [8,9,10,11,12,13], where there are no voxels that it is possible to analyse directly.
In informatics, connectivity of a communication network is generally related to the ease for nodes of exchanging information pieces, which are transported along available branches (i.e., connection paths). By analogy, the connectivity of a physical structure can be defined as the ease for a particular phenomenon of propagating within a particular mean.
From this point of view, the key-concept to understand in defining a proper connectivity factor for a material is that, in principle, connectivity depends on the particular transport phenomenon involved in the transfer. This can be understood if considering that, for example, two generic internal points inside a porous structure belonging to solid and void volume, respectively, are disconnected with respect to diffusion but connected with respect to heat transfer.
In this work, we are interested in quantifying the connectivity that measures the degree of physically connected voids, where at least one path exists along which a hypothetical molecule can reach any two points of the void space by diffusion without interpenetrating into the solid space (allowed path, Figure 1a). We can refer to this type of connectivity as diffusional connectivity, whose mathematical definition must depend on geometry only to be effective for a morphological characterization. For this purpose, we choose and propose here to define a Connectivity Factor (φ) as the inverse of the diffusional tortuosity τ (Equation (1)):
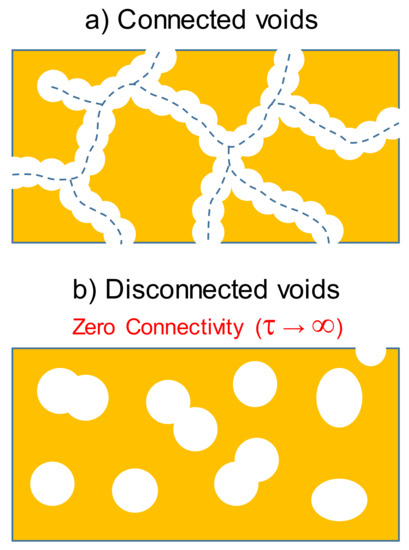
Figure 1.
Sketch of two different structure morphologies: (a) Interconnected voids (with a certain value of tortuosity) and (b) Completely disconnected voids (zero connectivity and infinite tortuosity).
It is highlighted that, according to Equation (1), the connectivity factor φ is comprised within [0, 1], this giving an immediate idea of the connectivity degree of the considered structure. Moreover, it is pointed out that the diffusional tortuosity considered in the present paper coincides with the tortuosity used to evaluate the effective diffusivity (Equation (2)) [14,15,16,17,18]:
where ε, Di and Di,Eff are porosity, free diffusivity, and effective diffusivity of the ith species, respectively. Some scholars prefer writing Equation (2) by distinguishing a more proper tortuosity factor as follows (Equation (3)):
However, such a distinction is not important for our purpose, as both parameters depend on geometry only. Therefore, we will use Equation (2) as the reference effective diffusivity definition, following the same approach as that of the pioneers of the volume average method [19,20,21,22].
The choice to define a connectivity factor as the inverse of tortuosity has been driven by several reasons. First, tortuosity can be viewed as a measure of the difficulty for a molecule to go from one point of a structure to another one within the available void space. Hence, the more the structure is tortuous, the less the connection between two voids is, whilst, on the contrary, a lower tortuosity implies a “more favourable” connection. In fact, as we will show in the following sections, tortuosity tends to infinity when a structure reaches a specific limit value of porosity (non-necessarily zero), below which all the internal voids are completely isolated from each other, as briefly sketched in Figure 1b. This situation can occur, for example, in real catalytic devices subjected to a high degree of sintering, resulting in a loss of specific area [23].
Second, as Kim et al. (1987) clearly state, the diffusional tortuosity is a parameter depending on geometry only [19], and, consequently, the same holds also for the here-defined connectivity factor (Equation (1)), whose value is comprised within the range [0, 1] because of the tortuosity ranges within [1, ∞].
Based on the previous considerations, we consider it straightforward to write the effective diffusivity in terms of connectivity factor φ (Equation (4)):
This is in line with the physical concept that the effective diffusivity increases with increasing connectivity, as one may expect from the dynamics of the mass transfer phenomenon. This allows us to further state that connectivity, and, dually, tortuosity, is not much related to the value of porosity, but rather to the porosity distribution within a structure.
We mention this fact because in a number of studies several scholars try to relate tortuosity and porosity to each other, as if this were generally possible [24]. However, this can be done only for the structures with a single geometrical degree of freedom, like regular structures of mono-sized spherical particles [25], structures with porosity tending to unity (Maxwell, 1881) [26], and infinitely-disperse random structures of particles (Neale and Nader, 1973) [27]. For other types of structures, the two parameters are completely independent of each other and, thus, should be evaluated independently.
After defining the connectivity factor, the next step for its quantitative measure consists in using a systematic way to evaluate tortuosity. In the past, tortuosity was generally considered a factor whose value was to be estimated by data regression. However, with the exponentially increased availability of computational resources and 3D image reconstruction tools based, for example, on computer tomography, a number of research groups have started to precisely evaluate tortuosity values of plenty of different structures by computational fluid dynamics and lattice-Boltzmann-based techniques (see e.g., [7,23,25,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]).
In the present investigation, this is done similarly to several literature papers considering the solution of the pure-diffusive problem [7,25,33,34,35,36,37,38,39,40,41,42]. The tortuosity values of the considered structures were calculated by Caravella et al. (2012) for non-overlapping particles [25], whereas Kim and Chen (2006) calculated the tortuosity of the SC, FCC, and BCC structures considering also the overlapping cases [37].
The general objective of this work is to provide a deeper insight into the structure morphology, linking the various geometrical parameters of the structure investigated, for which the concept of Limit Porosity Value is also introduced. Such a limit value represents the porosity value below which no diffusion is possible in the considered structure (i.e., a condition of completely disconnected voids).
2. Description of the System
The structures investigated—Simple Cubic (SC), Face-Centred Cubic (FCC), Body-Centred Cubic (BCC) and CaF2-type (Tetragonal)—are described in Figure 2, where the overlapping case is shown for convenience of the reader. Such an overlapping/interpenetrating geometry can occur in some high-temperature thermal treating processes, such as particle sintering, and result in strength increase because of the reinforced ties given by interpenetration, but also porosity losses, due to the appropriation of void space made by growing grains.
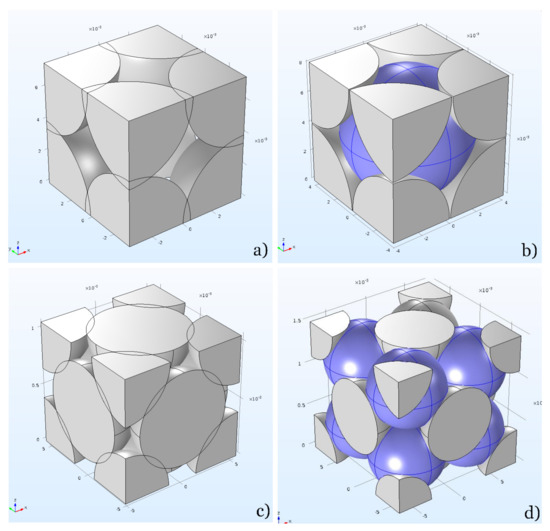
Figure 2.
Structures investigated in the present work (overlapping case): (a) SC (Simple Cubic), (b) BCC (Body-Centred Cubic), (c) FCC (Face-Centred Cubic), (d) Tetragonal (mono-sized CaF2). For BCC and Tetragonal structures, the overlapping occurs first between internal (blue-coloured) and external particles.
Specifically, their unit cells are composed of mono-sized (mono-disperse) spherical particles, whose porosity is allowed to change by changing the interparticle distance δ (i.e., the distance between the closest particles), which can assume also negative values to allow particles to overlap.
As the considered structures are regular and mono-disperse, they have one degree of freedom, which means that, keeping the particles size fixed (e.g., the diameter dp), morphology and topology are completely determined by a single dimensionless geometrical parameter, which in this study is chosen to be the following ratio:
3. Simulation Settings
3.1. Stacks of Unit Cells
For simulation, the unit cells are stacked to form assemblies of three cells, in order to minimize numerical errors due to possible perturbations in the diffusive streamlines. As the morphology of the overlapping cases can be complex to visualise, we show the qualitative evolution of the structures from a lower overlapping degree (i.e., a lower negative value of δ*) to a higher degree (i.e., a higher negative value of δ*), as depicted in Figure 3, Figure 4, Figure 5 and Figure 6, where the solid volume represents the void interparticle volume.
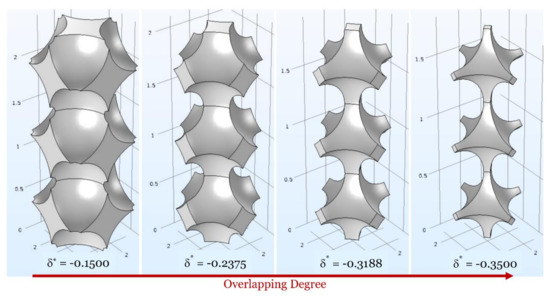
Figure 3.
Morphology evolution of the SC structure with increasing overlapping degree. The particular values of δ* are chosen just to better visualise the evolution of the structure.
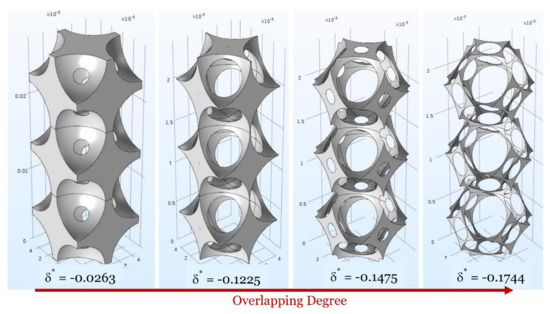
Figure 4.
Morphology evolution of the BCC structure with increasing overlapping degree. The particular values of δ* are chosen just to better visualise the evolution of the structure.
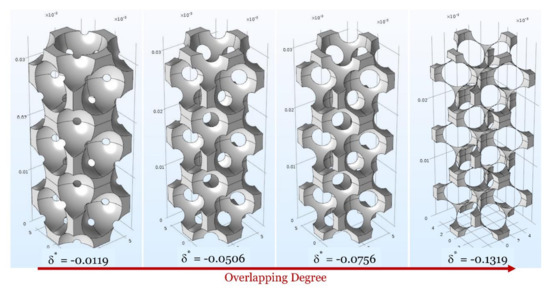
Figure 5.
Morphology evolution of the FCC structure with increasing overlapping degree. The particular values of δ* are chosen just to better visualise the evolution of the structure.
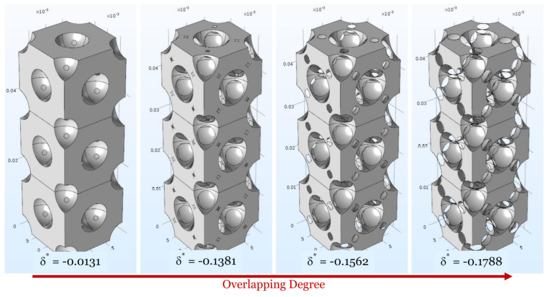
Figure 6.
Morphology evolution of the Tetragonal structure with increasing overlapping degree.
As can be observed, for higher overlapping degree, the void channels become progressively narrower and the structure morphology changes severely. In particular, the most peculiar change can be observed for BCC and Tetragonal structures, for which secondary holes are generated in the unit cell as the overlapping degree increases. From this point of view, there is almost no apparent relationship between starting and ending structure.
3.2. Computational Fluid Dynamic Approach
As mentioned above, tortuosity is here evaluated by solving the pure diffusion problem in a porous structure, using Fick’s law (Equation (6)) as constitutive equation for the molar flux of a homogeneous binary gas mixture in the structure voids:
where DAB is the free diffusivity in a fluid without obstacles, while is the concentration gradient.
Simulations are performed using the CFD software Comsol Multiphysics®, which provide as results the average diffusive flux between the two faces where the concentration has been set. From such information, the effective diffusivity is calculated as follows (Equation (7)):
where , , and indicate concentration difference, distance between faces, cross-sectional area available for diffusion (i.e., void area), and the total area (i.e., the nominal cell square area). Then, tortuosity is calculated as follows:
Figure 7 is a sketch of the boundary conditions set for simulation, for which the impenetrability of the particle walls (i.e., zero normal flux) is set along with symmetry (i.e., zero flux) on the flat lateral boundaries of the cell stacks, and concentration values on the respective bases.
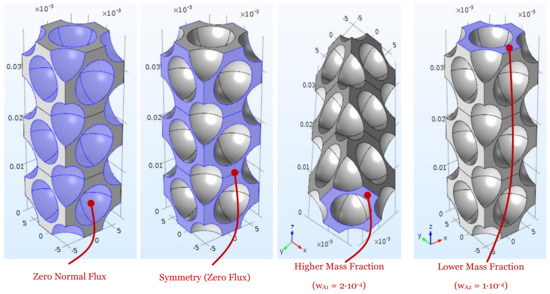
Figure 7.
Boundary conditions used for simulation. Visualisation example for the FCC structure.
3.3. Mesh Setup
Once the appropriate boundary conditions have been set, the computational mesh has to be constructed in order to carry out simulation. For this purpose, it is necessary to demonstrate the mesh-independency of the obtained results, this implies applying a systematic way to construct an effective and efficient mesh not requiring a too-heavy consumption of computational resources.
To do that, a preliminary test is performed by constructing two different meshes—referred to as coarser and finer—for the same non-overlapping FCC structure for a certain value of porosity sufficiently close to the condition of tangent particles (ε = 0.38319), which is the most severe condition for a mesh to be generated.
The results relative to the two meshes are reported in Table 1 in terms of tortuosity. As we can observe, the two values are equal up to the third decimal, which indicate that even the coarse mesh is effective for our calculation. However, to be conservative, in all simulations we used the finer-mesh type, that is, a mesh characterized by a minimum number of four elements between the closest boundaries (e.g., Figure 8a).

Table 1.
Example of tortuosity sensitivity to mesh for the FCC.
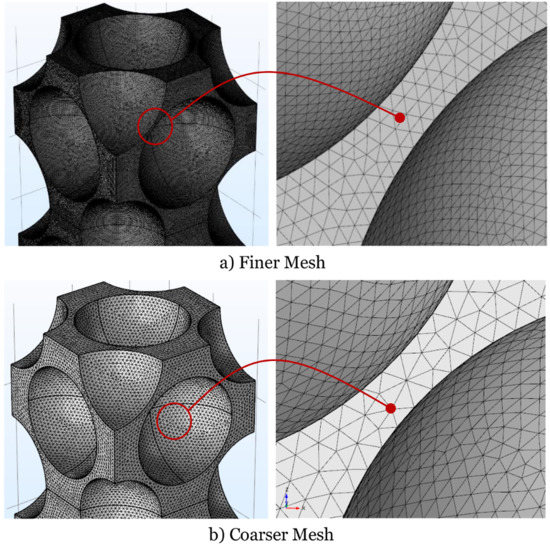
Figure 8.
Mesh details: (a) Finer mesh and (b) Coarser mesh.
4. Results and Discussion
The primary simulation results are provided by the software in terms of concentration profiles within the cells stack. An example of results is shown in Figure 9 for an overlapping FCC unit cell stack, where the concentration profile mainly develops from the bottom (higher concentration) towards the top (lower concentration). From these data, the total diffusive flux normal to the surface at the top and the bottom of the stack is calculated in post-processing, thus giving all the information required to evaluate the effective diffusivity and, from that, the tortuosity (Equation (7)).
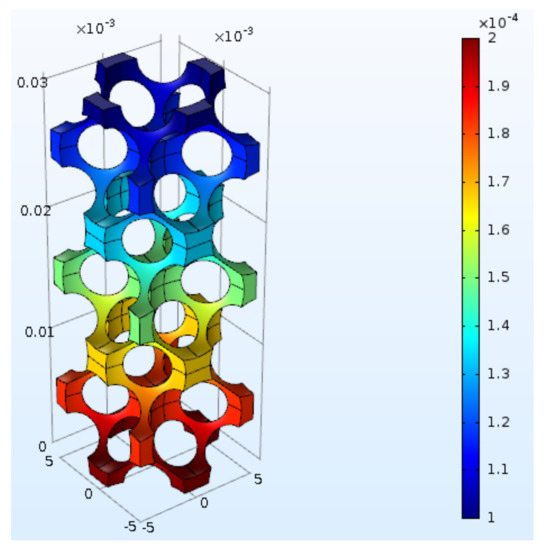
Figure 9.
Example of concentration gradient obtained as a solution of the simulation performed for the overlapping FCC structure.
Besides the meaning of the 3D profiles, an important aspect to notice is that the concentration gradient is steeper in the voids where boundaries are closer. This indicates that the diffusion resistance is mainly due to such zones of the stack, it implies that tortuosity, as well as connectivity, is determined by the shape of these narrow regions.
As voids become gradually narrower with decreasing porosity, the diffusion resistance increases; this causes a higher tortuosity and, thus, a lower connectivity. Therefore, in the limit case in which the volume of a narrow region becomes null, the diffusional path encounters a dead-end channel. If all channels become dead ends, the inner voids become completely disconnected islands (Figure 1b) and, thus, diffusional resistance and tortuosity become infinite (no diffusive flux possible).
Since the considered structures are regular, the condition of infinite diffusional resistance is reached at a specific porosity value—here referred to as Limit Porosity Value εLim—corresponding to the limit void volume that is not available for diffusion (VLim, Equation (10)). Such a parameter can be considered a sort of “hidden” morphological property, as it is not apparent when voids are interconnected. The numerically calculated εLim for all structures are reported in Table 2, from where we can observe as a mere coincident the very similar values of SC and FCC.

Table 2.
Limit Porosity Value εLim calculated numerically for each structure.
To clearly show the geometry corresponding to the limit porosity, Figure 10 shows the completely disconnected island-shaped morphology of the structures.
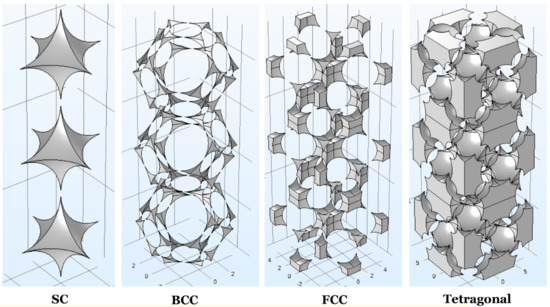
Figure 10.
Example of morphology of structures below the limit porosity value (εLim). The disconnected islands represent the remaining inner voids not available for diffusion.
The results obtained in terms of tortuosity vs. porosity are shown in Figure 11 and Figure 12. The lower bound for the structure is represented by the model developed by Neale and Nader (1973) [27] for a homogeneous non-overlapping swarm of spheres, which is actually an ideal structure composed of an infinitely dispersed particles (Equation (9)).
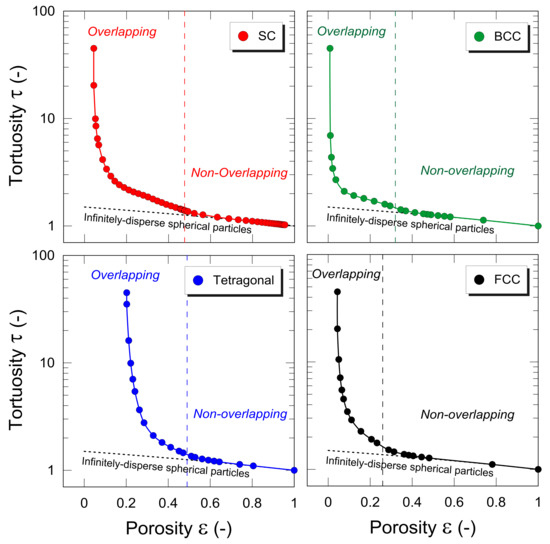
Figure 11.
Tortuosity τ as a function of porosity ε for the considered structures. The dashed line in each plot refers to the model developed by Neale and Nader (1973). Overlapping and Non-overlapping domains are distinguished in each plot.
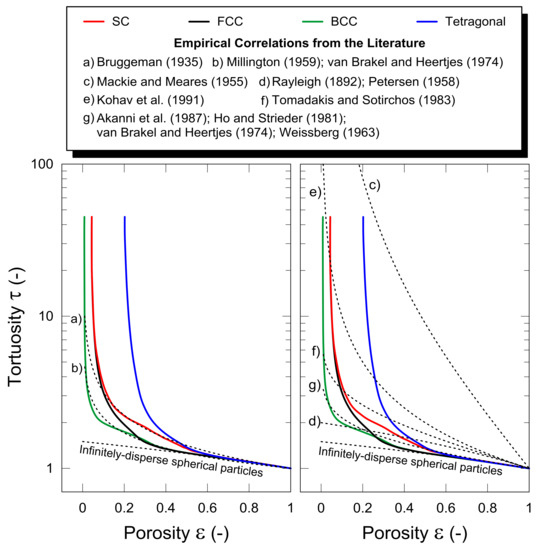
Figure 12.
Overall comparison among the considered structures and several empirical expressions from the literature (see Table 3) [44,45,46,47,48,49,50,51,52,53,54]. The trends are shown in two plots for a better readability.
It is curious as well as interesting that this expression is the same as that obtained by Maxwell (1881), which is valid in the limit of porosity approaching unity. In the plot, we prefer indicating the dashed line as Neale and Nader’s model instead of Maxwell’s one since the former is virtually valid in the whole porosity range. Another fact to observe is that all the curves, which are reported on log-scale on the y-axis (here represented by the actual calculated values) show a more or less large convex portion (i.e., negative second derivative), which means that the tortuosity trend increases with decreasing porosity with a functionality less than exponential.
A possible reason for such a behaviour is that, just after particles start overlapping because of decreasing inter-particle distance, the narrow channels present just before overlapping disappear because of the surface–surface merging, resulting in a certain limitation for tortuosity to increase. However, as porosity goes on decreasing, such a tendency is over-compensated by the size decrease of the larger void channels. As such voids become smaller and smaller, the tortuosity value increases, tending to infinity for channel section tending to zero (higher overlapping degree, Figure 3, Figure 4, Figure 5 and Figure 6d).
Figure 12 shows an overall comparison among the trend of all the considered structures along with several empirical expressions mostly used in literature to estimate the tortuosity of certain types of porous structures [44,45,46,47,48,49,50,51,52,53,54]. In particular, we can observe that some correlations among (a), (b), (d), and (g) describe partially well some of the trends calculated in the present work, with the goodness of the matching depending on the porosity range. Specifically, the expression of Bruggeman [47] describes well the SC trend for a porosity down to ca. 0.1. On the other hand, the Millington correlation [49], which is the same as that of Akanni et al. (1987) [53], Ho and Strieder (1981) [54], van Brakel and Heertjes (1974) [51] and Weissberg (1963) [52], represents satisfactorily the BCC trend in almost the whole porosity range and the FCC one within [0.25, 1]. All trends are well described by the Neale and Nader [27] theoretical expression within [0.55, 1]. Differently, the correlations (c), (e), and (f) do not represent satisfactorily any of the tortuosity trends calculated in the present work.
In order to check the existence of possible similarities among the different structures, from the concept of limit porosity, we can define what is called here “Effective Porosity” (εEff) as the difference between the nominal porosity and the limit porosity (Equation (10)), the tortuosity trend of all the considered structures will tend to infinity for εEff tending to zero.
However, the so-defined Effective Porosity has the drawback that it is not comprised between zero and unity. Therefore, analogously to what done by Pisani (2011) [24] and Caravella et al. (2012) [25] for non-overlapping particles, we can define here a Normalized Effective Porosity ranging within [0,1] by subtracting the limit volume from both total and void volume (Equation (11)):
It can be noticed that, for εMin equal to zero, the nominal porosity ε and the normalized effective porosity are coincident.
The functionality of tortuosity τ with is shown in Figure 13 for all the structures considered. The normalized data representation allows recognition of similarities and differences among structures. In particular, we notice that all structures show the same trend for a values higher than around 0.55, whereas the behaviour of the FCC, BCC, and Tetragonal structures is very similar in a wider range (higher than around 0.2). Therefore, the morphological difference is more relevant in the range of lower , in which tortuosity is very sensitive to the particular shape of the void channels.
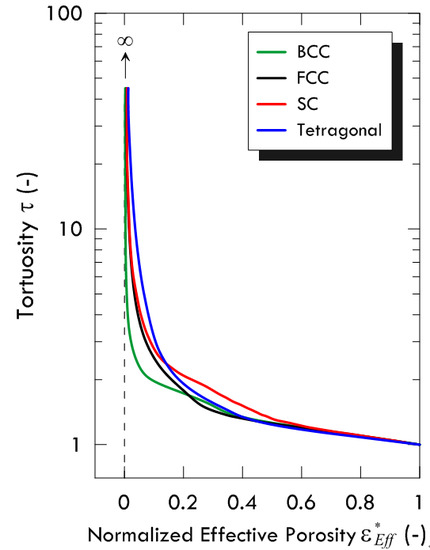
Figure 13.
Tortuosity τ as a function of the Normalized Effective Porosity for all the considered structures.
From tortuosity, we can finally plot the trend of connectivity factor φ (Figure 14). It is also noticeable that the equation developed by Neale and Nader represents an upper bound for connectivity of all structures, this being expected from Figure 11. However, it is interesting to find out the morphological reasons for that.
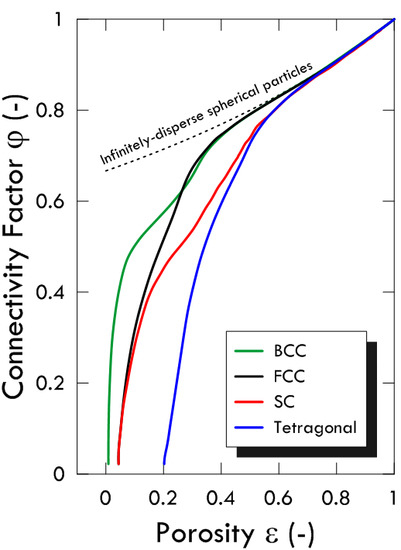
Figure 14.
Connectivity Factor φ as a function of porosity for all the considered structures.
Specifically, the virtual structure considered by Neale and Nader is peculiar, as it is ideally composed of non-overlapping spherical particles with an infinitely-disperse size, which means that porosity can progressively decrease by adding smaller and smaller particles that progressively fill the voids. In such an ideal morphology, the structure shows voids being completely interconnected even closely to the zero-porosity condition and, thus, connectivity should be the maximum possible, representing an upper bound in a {φ vs. ε} plot for all structures.
Concerning the particular trends of the structures, FCC and BCC show almost the same connectivity factor from a porosity value higher than ca. 0.25, whilst the same occurs for the SC and Tetragonal structures for porosity higher than ca. 0.55. All curves tend to zero for porosity tending to the respective limit values. In particular, the structure with the highest connectivity among the considered ones, at least in the low-porosity range, is the BCC structure, whereas the tetragonal structure shows the lowest connectivity degree at the same porosity.
5. Conclusions
In this work, a novel general definition of connectivity factor was proposed to measure the connection degree of the inner voids of a porous structure. Specifically, the connectivity factor was defined as the inverse of tortuosity, which was evaluated as a function of porosity for several regular isotropic structures of spherical particles in both non-overlapping and overlapping cases by computational fluid dynamics techniques. The considered structures are as follows: Simple Cubic (SC), Body-Centred Cubic (BCC), Face-Centred Cubic (FCC), and Tetragonal structure (i.e., mono-disperse CaF2-type), whose morphology was deeply analysed.
A novel morphological parameter, the here-called Limit Porosity Value (εLim), was identified and evaluated numerically for each structure considered. Such a parameter represents the porosity value below which all the inner voids are completely disconnected from each other, which corresponds to a condition of infinite tortuosity and, thus, zero connectivity.
After providing a comparison between the tortuosity trends calculated in the present work and some correlations of literature, the connectivity of all of the considered structures was calculated as a function of porosity. Such a trend has revealed that the connectivity of the BCC structure is the highest among the analysed structures, followed by FCC and SC, which show similar trends in the extreme limit values of porosity close to unity and close to zero. Within these limits, the connectivity of the FCC structure is found to be higher than SC. We highlight that, interestingly, they show a very similar value of εLim. As for the tetragonal structure, it was found to show the lowest connectivity with respect to the others.
The proposed approach, which is applicable also to studies where tortuosity is evaluated experimentally, represents a systematic and general methodology to easily define and measure the connectivity degree of whatever structure, providing a powerful tool for morphological investigation on porous media membranes.
Acknowledgments
A. Caravella has received funding for this research through the “Programma Per Giovani Ricercatori “Rita Levi Montalcini” granted by the “Ministero dell’Istruzione, dell’Università e della Ricerca, MIUR” (Grant no. PGR12BV33A), which is gratefully acknowledged.
Author Contributions
S.B. performed the simulations on the BCC, FCC and Tetragonal structures and wrote the paper with input from all Authors. G.A., Y.S. and A.C. carried out the data analysis. M.G. performed the simulations on the SC structures. V.S. contributed to structure construction and data analysis. G.D. contributed to the computational settings for the solution of the diffusion problem. A.C. devised the study, supervised the manuscript progress and introduced the presented novel morphological parameters (connectivity factor and limit porosity value).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chiappetta, G.; Clarizia, G.; Drioli, E. Theoretical analysis of the effect of catalyst mass distribution and operation parameters on the performance of a Pd-based membrane reactor for water-gas shift reaction. Chem. Eng. J. 2008, 136, 373–382. [Google Scholar] [CrossRef]
- Li, A.; Lim, C.J.; Grace, J.R. Staged-separation membrane reactor for steam methane reforming. Chem. Eng. J. 2008, 138, 452–459. [Google Scholar] [CrossRef]
- Caravella, A.; Di Maio, F.P.; Di Renzo, A. Computational Study of Staged Membrane Reactor Configurations for Methane Steam Reforming: I. Optimization of Stage Lengths. AIChE J. 2010, 56, 248–258. [Google Scholar] [CrossRef]
- Caravella, A.; Di Maio, F.P.; Di Renzo, A. Computational Study of Staged Membrane Reactor Configurations for Methane Steam Reforming: II. Effect of Number of Stages and Catalyst Amount. AIChE J. 2010, 56, 259–267. [Google Scholar] [CrossRef]
- Caravella, A.; Di Maio, F.P.; Di Renzo, A. Optimization of membrane area and catalyst distribution in a permeative-stage membrane reactor for methane steam reforming. J. Membr. Sci. 2008, 321, 209–221. [Google Scholar] [CrossRef]
- Lichtner, A.Z.; Jauffrès, D.; Roussel, D.; Charlot, F.; Martin, C.L.; Bordia, R.K. Dispersion, connectivity and tortuosity of hierarchical porosity composite SOFC cathodes prepared by freeze-casting. J. Eur. Ceram. Soc. 2015, 35, 585–595. [Google Scholar] [CrossRef]
- Promentilla, M.A.B.; Sugiyama, T.; Hitomi, T.; Takeda, N. Quantification of tortuosity in hardened cement pastes using synchrotron- based X-ray computed microtomography. Cement Concrete Res. 2009, 39, 548–557. [Google Scholar] [CrossRef]
- Guo, P. Dependency of Tortuosity and Permeability of Porous Media on Directional Distribution of Pore Voids. Transp. Porous Media 2012, 95, 285–303. [Google Scholar] [CrossRef]
- Kong, W.; Zhang, Q.; Gao, X.; Zhang, J.; Chen, D.; Su, S. A Method for Predicting the Tortuosity of Pore Phase in Solid Oxide Fuel Cells Electrode. Int. J. Electrochem. Sci. 2015, 10, 5800–5811. [Google Scholar]
- Popova, L.; van Dusschoten, D.; Nagel, K.A.; Fiorani, F.; Mazzola, B. Plant root tortuosity: An indicator of root path formation in soil with different composition and density. Ann. Bot. 2016, 118, 685–698. [Google Scholar] [CrossRef] [PubMed]
- Manickam, S.S.; Gelb, J.; McCutcheon, J.R. Characterization of Thin Film Composite Membranes Using Porosimetry and X-ray Microscopy. Microsc. Microanal. 2013, 19, 634–635. [Google Scholar] [CrossRef]
- Wiedenmann, D.; Keller, L.; Holzer, L.; Stojadinovic, J.; Munch, B.; Suarez, L.; Fumey, B.; Hagendorfer, H.; Bronnimann, R.; Modregger, P.; et al. Three-Dimensional Pore Structure and Ion Conductivity of Porous Ceramic Diaphragms. AIChE J. 2013, 59, 1446–1457. [Google Scholar] [CrossRef]
- Landesfeind, J.; Hattendorff, J.; Ehrl, A.; Wall, W.A.; Gasteiger, H.A. Tortuosity Determination of Battery Electrodes and Separators by Impedance Spectroscopy. J. Electrochem. Soc. 2016, 163, A1373–A1387. [Google Scholar] [CrossRef]
- Epstein, N. On Tortuosity and the Tortuosity Factor in Flow and Diffusion through Porous Media. Chem. Eng. Sci. 1989, 44, 777–779. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in porous media—A critical review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through a granular bed. Trans. Inst. Chem. Eng. 1937, 15, 150–167. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases through Porous Media; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Scheidegger, A.E. The Physics of Flow through Porous Media; University of Toronto Press: Toronto, ON, Canada, 1974. [Google Scholar]
- Kim, J.H.; Ochoa, J.A.; Whitaker, S. Diffusion in anisotropic media. Transp. Porous Media 1987, 2, 327–356. [Google Scholar] [CrossRef]
- Whitaker, S. Simultaneous heat, mass and momentum transfer in porous media: A theory of drying. Adv. Heat Transf. 1977, 13, 119–203. [Google Scholar]
- Quintard, M. Diffusion in isotropic and anisotropic porous systems: Three- dimensional calculations. Transp. Porous Media 1993, 11, 187–199. [Google Scholar] [CrossRef]
- Quintard, M.; Whitaker, S. Transport in ordered and disordered porous media: Volume-averaged equations, closure problems and comparison with experiments. Chem. Eng. Sci. 1993, 48, 2537–2564. [Google Scholar] [CrossRef]
- Gao, H.Y.; He, Y.H.; Zou, J.; Xu, N.P.; Liu, C.T. Tortuosity factor for porous FeAl intermetallics fabricated by reactive synthesis. Trans. Nonferr. Met. Soc. China 2012, 22, 2179–2183. [Google Scholar] [CrossRef]
- Pisani, L. Simple Expression for the Tortuosity of Porous Media. Transp. Porous Media 2011, 88, 193–203. [Google Scholar] [CrossRef]
- Caravella, A.; Hara, S.; Obuchi, A.; Uchisawa, J. Role of the bi-dispersion of particle size on tortuosity in isotropic structures of spherical particles by three-dimensional computer simulation. Chem. Eng. Sci. 2012, 84, 351–371. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism, 2nd ed.; Clarendon Press: Oxford, UK, 1881; Volume I. [Google Scholar]
- Neale, G.H.; Nader, W.K. Prediction of transport processes within porous media, Diffusive flow processes within a homogeneous swarm of spherical particles. AlChE J. 1973, 19, 112–119. [Google Scholar] [CrossRef]
- Solorzano, E.; Pardo-Alonso, S.; Brabant, L.; Vicente, J.; Van Hoorebeke, L.; Rodríguez-Pérez, M.A. Computational Approaches for Tortuosity Determination in 3D Structures. In Proceedings of the 1st International Conference on Tomography of Materials and Structures (ICTMS 2013), Ghent, Belgium, 1–5 July 2013; pp. 71–74. Available online: https://biblio.ugent.be/publication/4178455/file/4178457.pdf (accessed on 17 February 2018).
- Wang, P. Lattice Boltzmann Simulation of Permeability and Tortuosity for Flow through Dense Porous Media. Math. Prob. Eng. 2014. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Cole, D.R. Characterization and Analysis of Porosity and Pore Structures. Rev. Mineral. Geochem. 2015, 80, 61–164. [Google Scholar] [CrossRef]
- Berg, C.F. Permeability Description by Characteristic Length, Tortuosity, Constriction and Porosity. Transp. Porous Media 2015, 103, 381–400. [Google Scholar] [CrossRef]
- Annunziata, R.; Kheirkhah, A.; Aggarwal, S.; Hamrah, P.; Trucco, E. A Fully Automated Tortuosity Quantification System with Application to Corneal Nerve Fibres in Confocal Microscopy Images. Med. Image Anal. 2016, 32, 216–232. [Google Scholar] [CrossRef] [PubMed]
- Deepagoda, T.K.K.C.; Moldrup, P.; Yoshikawa, S.; Kawamoto, K.; Komatsu, T.; Rolston, D.E. The gas-diffusivity-based Buckingham tortuosity factor from pF 1 to 6.91 as a soil structure fingerprint. In Proceedings of the 19th World Congress of Soil Science, Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010; pp. 2008–2011. [Google Scholar]
- Vallavh, R. Modeling Tortuosity in Fibrous Porous Media using Computational Fluid Dynamics. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2009. [Google Scholar]
- Chen-Wiegart, Y.C.K.; Demike, R.; Erdonmez, C.; Thornton, K.; Barnett, S.A.; Wang, J. Tortuosity characterization of 3D microstructure at nano-scale for energy storage and conversion materials. J. Power Sources 2014, 249, 349–356. [Google Scholar] [CrossRef]
- Moldrup, P.; Olesen, T.; Komatsu, T.; Schjonning, P.; Rolston, D.E. Tortuosity, Diffusivity, and Permeability in the Soil Liquid and Gaseous Phases. Soil Sci. Soc. Am. J. 2001, 65, 613–623. [Google Scholar] [CrossRef]
- Kim, A.S.; Chen, H. Diffusive tortuosity factor of solid and soft cake layers: A random walk simulation approach. J. Membr. Sci. 2006, 279, 129–139. [Google Scholar] [CrossRef]
- Rezanezhad, F.; Quinton, W.L.; Price, J.S.; Elrick, D.; Elliot, T.R.; Heck, R.J. Examining the effect of pore size distribution and shape on flow through unsaturated peat using 3-D computed tomography. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 3835–3862. [Google Scholar] [CrossRef]
- Matyka, M.; Khalili, A.; Koza, Z. Tortuosity-porosity relation in porous media flow. Phys. Rev. E 2008, 78, 026306. [Google Scholar] [CrossRef] [PubMed]
- Luquot, L.; Rodriguez, O.; Gouze, P. Experimental Characterization of Porosity Structure and Transport Property Changes in Limestone Undergoing Different Dissolution Regimes. Transp. Porous Media 2014, 101, 507–532. [Google Scholar] [CrossRef]
- Shen, L.; Chen, Z. Critical review of the impact of tortuosity on diffusion. Chem. Eng. Sci. 2007, 62, 3748–3755. [Google Scholar] [CrossRef]
- Melo, L.F. Biofilm physical structure, internal diffusivity and tortuosity. Water Sci. Technol. 2005, 52, 77–84. [Google Scholar]
- Promentilla, M.A.B.; Sugiyama, T. Studies on 3D Micro-Geometry and Diffusion Tortuosity of Cement-Based Materials Using X-ray Microtomography. In Proceedings of the 32nd Conference on Our World in Concrete & Structures, Singapore, 28–29 August 2007. [Google Scholar]
- Mackie, J.S.; Meares, P. The diffusion of electrolytes in a cation exchange resin membrane. Proc. R. Soc. A 1955, 232, 498–509. [Google Scholar] [CrossRef]
- Elias-Kohav, T.; Moshe, S.; Avnir, D. Steady-state diffusion and reactions in catalytic fractal porous media. Chem. Eng. Sci. 1991, 46, 2787–2798. [Google Scholar] [CrossRef]
- Rayleigh, L. On the influence of obstacles arranged in rectangular order upon the properties of a medium. Philos. Mag. 1892, 34, 481–489. [Google Scholar] [CrossRef]
- Bruggeman, D.A. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 24, 636–664. [Google Scholar] [CrossRef]
- Petersen, E.E. Diffusion in a pore of varying cross section. AIChE J. 1958, 4, 343–345. [Google Scholar] [CrossRef]
- Millington, R.J. Gas diffusion in porous media. Science 1959, 130, 100–102. [Google Scholar] [CrossRef] [PubMed]
- Tomadakis, M.M.; Sotirchos, S.V. Transport properties of random arrays of freely overlapping cylinders with various orientation distributions. J. Chem. Phys. 1983, 98, 616–626. [Google Scholar] [CrossRef]
- van Brakel, J.; Heertjes, P.M. Analysis of diffusion in macroporous media in terms of a porosity, a tortuosity and a constrictivity factor. Int. J. Heat Mass Transf. 1974, 17, 1093–1103. [Google Scholar] [CrossRef]
- Weissberg, H. Effective diffusion coefficients in porous media. J. Appl. Phys. 1963, 34, 2636–2639. [Google Scholar] [CrossRef]
- Akanni, K.A.; Evans, J.W.; Abramson, I.S. Effective transport coefficients in heterogeneous media. Chem. Eng. Sci. 1987, 42, 1945–1954. [Google Scholar] [CrossRef]
- Ho, F.G.; Strieder, W. A variational calculation of the effective surface diffusion coefficient and tortuosity. Chem. Eng. Sci. 1981, 36, 253–258. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).