Predicting Output Power for Nearshore Wave Energy Harvesting
Abstract
:1. Introduction
1.1. A Summary of Wave Energy Conversion
1.2. Methods for Predicting Power Generation
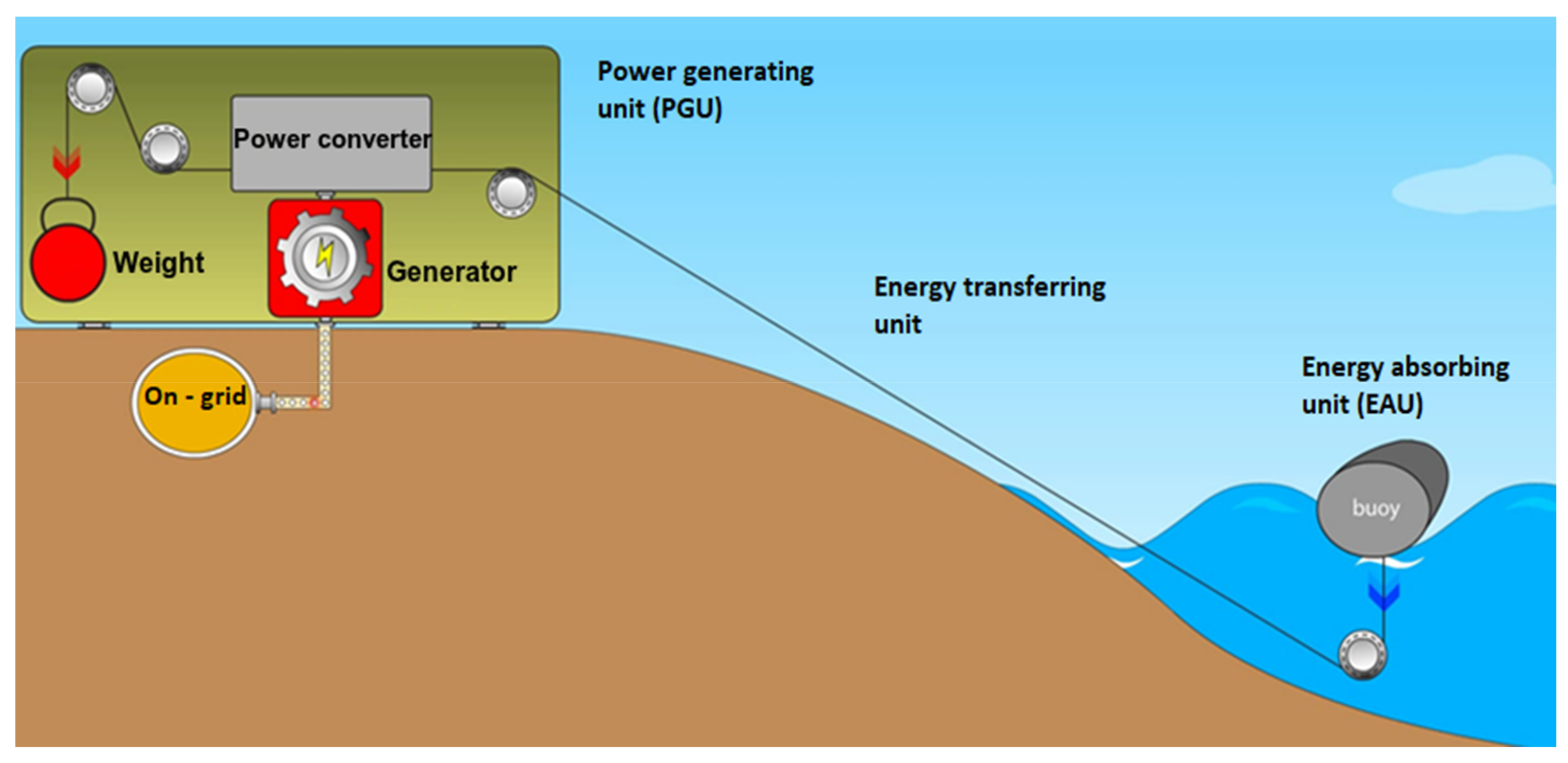
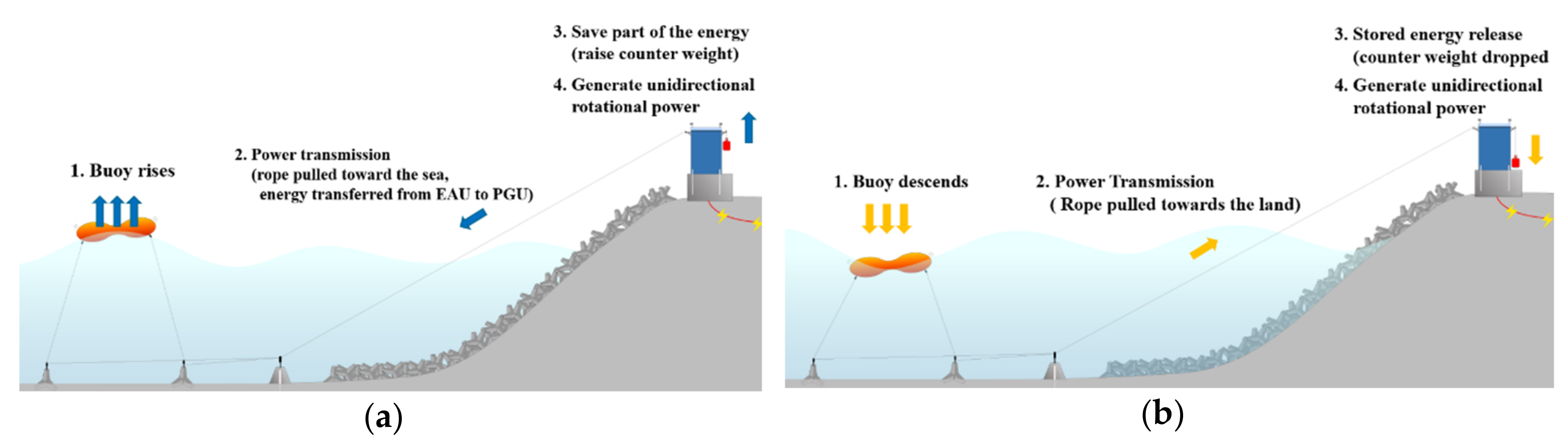
2. Wave Energy Generation
3. Methods
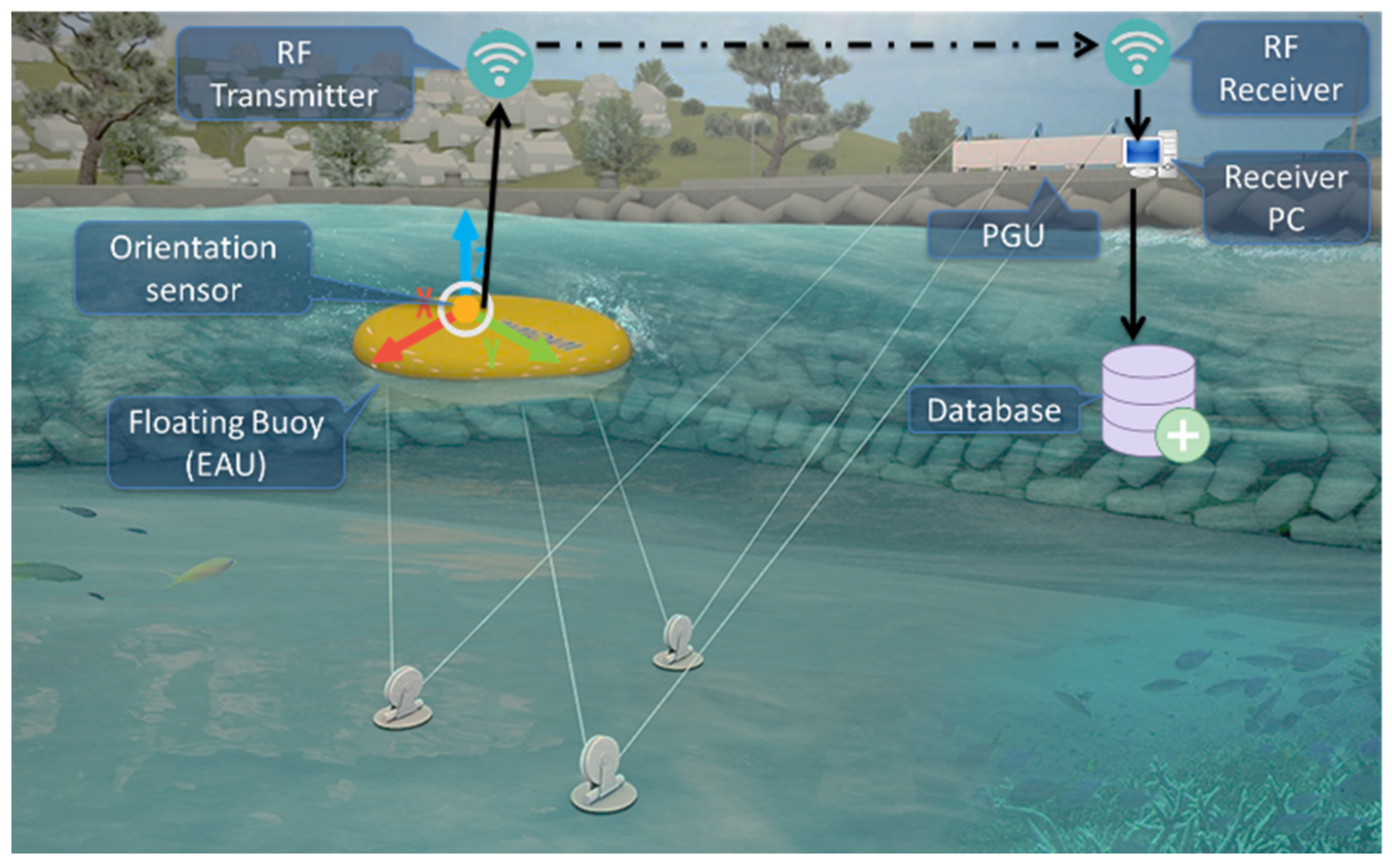
3.1. Data Collection
3.2. Data Segmentation and Feature Selection
3.3. Principal Component Analysis
3.4. Machine Learning Algorithms
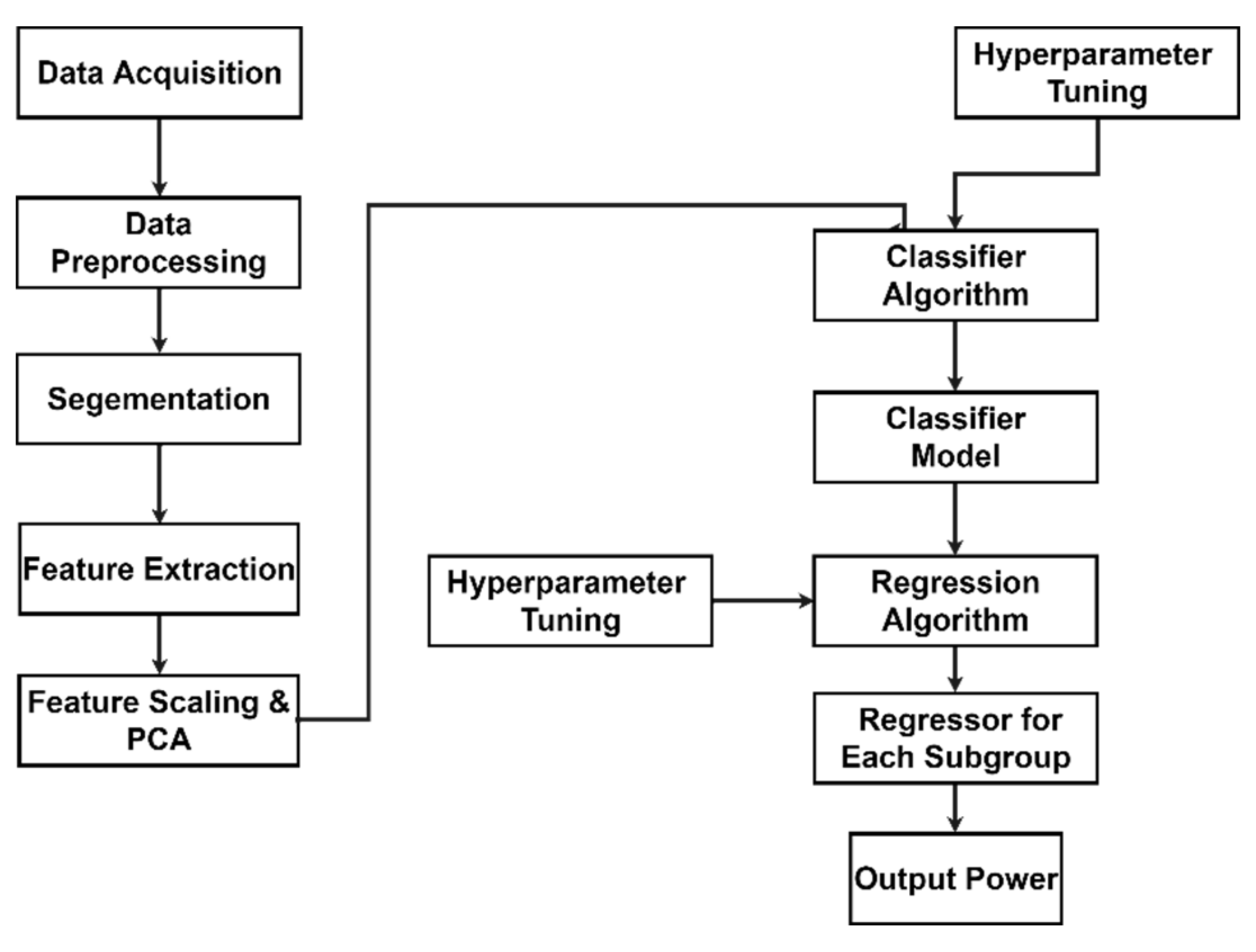
3.5. Architecture of the Proposed Approach
4. Experiments
5. Results and Discussion
5.1. Evaluation Metrics
5.2. Wave Tank Experiment
5.2.1. Data Segmentation
5.2.2. Output Power Estimation
5.3. Actual Wave Energy Harvesting Plant Experiment
5.3.1. Data Segmentation
5.3.2. Output Power Estimation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. IMechE Part A 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Cruz, J. Ocean Wave Energy: Current Status and Future Prespectives; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Brekken, T.K.; Von Jouanne, A.; Han, H.Y. Ocean wave energy overview and research at oregon state university. In Proceedings of the Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009; Volume 24, pp. 1–7. [Google Scholar]
- Kim, G.; Jeong, W.M.; Lee, K.S.; Jun, K.; Lee, M.E. Offshore and nearshore wave energy assessment around the korean peninsula. Energy 2011, 36, 1460–1469. [Google Scholar] [CrossRef]
- Korea Energy Agency. Available online: http://www.energy.or.kr/renew_eng/new/standards.aspx (accessed on 2 February 2018).
- Sung, Y.; Kim, J.; Lee, D. Power Converting Apparatus. U.S. Patent 20150275847A1, 1 October 2015. [Google Scholar]
- Margheritini, L.; Vicinanza, D.; Frigaard, P. Ssg wave energy converter: Design, reliability and hydraulic performance of an innovative overtopping device. Renew. Energy 2009, 34, 1371–1380. [Google Scholar] [CrossRef]
- Czech, B.; Bauer, P. Wave energy converter concepts: Design challenges and classification. IEEE Ind. Electron. Mag. 2012, 6, 4–16. [Google Scholar] [CrossRef]
- Jang, H.S.; Bae, K.Y.; Park, H.-S.; Sung, D.K. Solar power prediction based on satellite images and support vector machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Phaiboon, S.; Tanukitwattana, K. Fuzzy model for predicting electric generation from sea wave energy in Thailand. In Proceedings of the Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 2646–2649. [Google Scholar]
- Shi, J.; Lee, W.-J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Perera, K.S.; Aung, Z.; Woon, W.L. Machine learning techniques for supporting renewable energy generation and integration: A survey. In Proceedings of the International Workshop on Data Analytics for Renewable Energy Integration, Nancy, France, 19 September 2014; Springer: Cham, Switzerland, 2014; pp. 81–96. [Google Scholar]
- Ingine, Inc. Available online: http://www.ingine.co.kr/en/ (accessed on 2 February 2018).
- Deberneh, H.M.; Kim, I. Wave Power Prediction Based on Regression Models. In Proceedings of the 18th International Symposium on Advanced Intelligent Systems, Daegu, Korea, 11–14 October 2017. [Google Scholar]
- Banos, O.; Galvez, J.-M.; Damas, M.; Pomares, H.; Rojas, I. Window size impact in human activity recognition. Sensors 2014, 14, 6474–6499. [Google Scholar] [CrossRef] [PubMed]
- Hira, Z.M.; Gillies, D.F. A review of feature selection and feature extraction methods applied on microarray data. Adv. Bioinform. 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Juszczak, P.; Tax, D.; Duin, R.P. Feature scaling in support vector data description. In Proceedings of the ASCI; Citeseer: State College, PA, USA, 2002; pp. 95–102. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Chapelle, O.; Vapnik, V.; Bousquet, O.; Mukherjee, S. Choosing multiple parameters for support vector machines. Mach. Learn. 2002, 46, 131–159. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Peres, D.; Iuppa, C.; Cavallaro, L.; Cancelliere, A.; Foti, E. Significant wave height record extension by neural networks and reanalysis wind data. Ocean Model. 2015, 94, 128–140. [Google Scholar] [CrossRef]
- Raschka, S. Python Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2015. [Google Scholar]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; National Taiwan University: Taipei City, Taiwan, 2003. [Google Scholar]
- Scikit Learn. Available online: http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html (accessed on 2 February 2018).
- Trivedi, S.; Pardos, Z.A.; Heffernan, N.T. Clustering students to generate an ensemble to improve standard test score predictions. In Proceedings of the International Conference on Artificial Intelligence in Education, Auckland, New Zealand, 28 June–1 July 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 377–384. [Google Scholar]



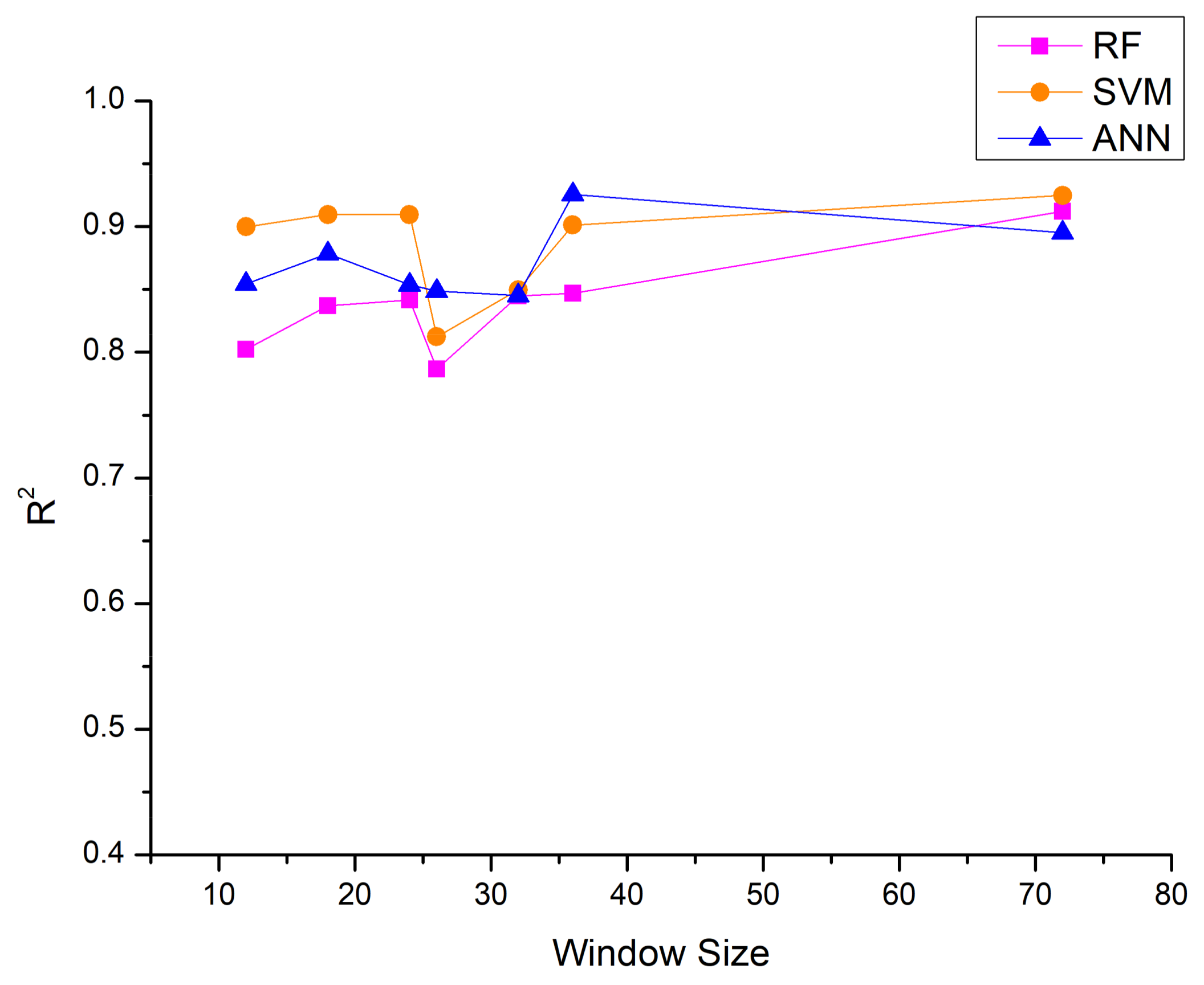
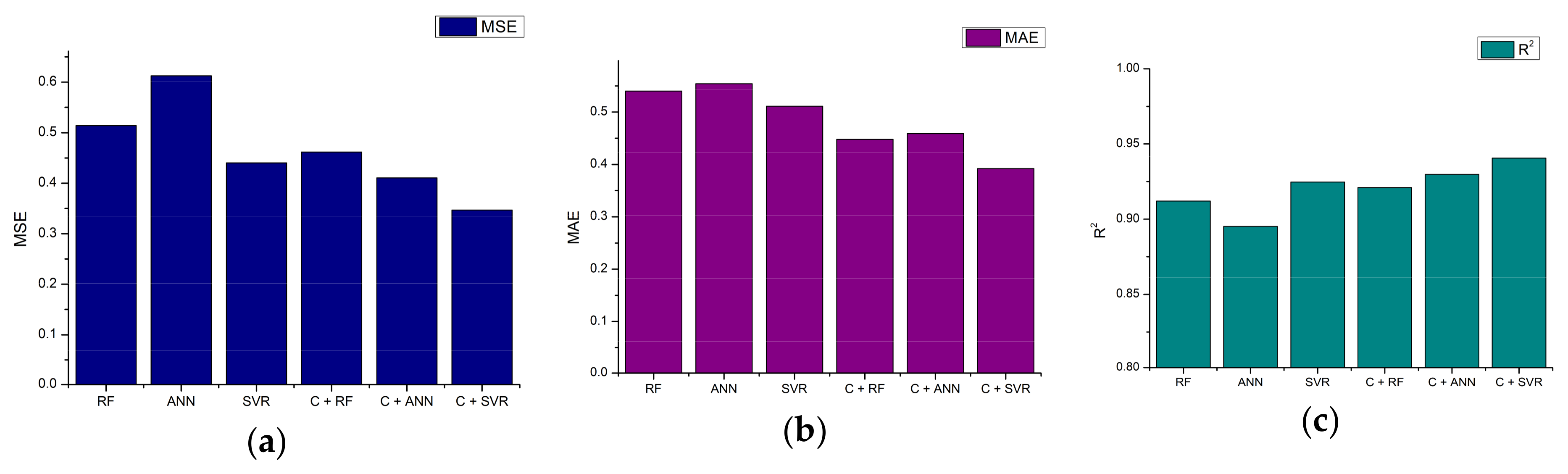
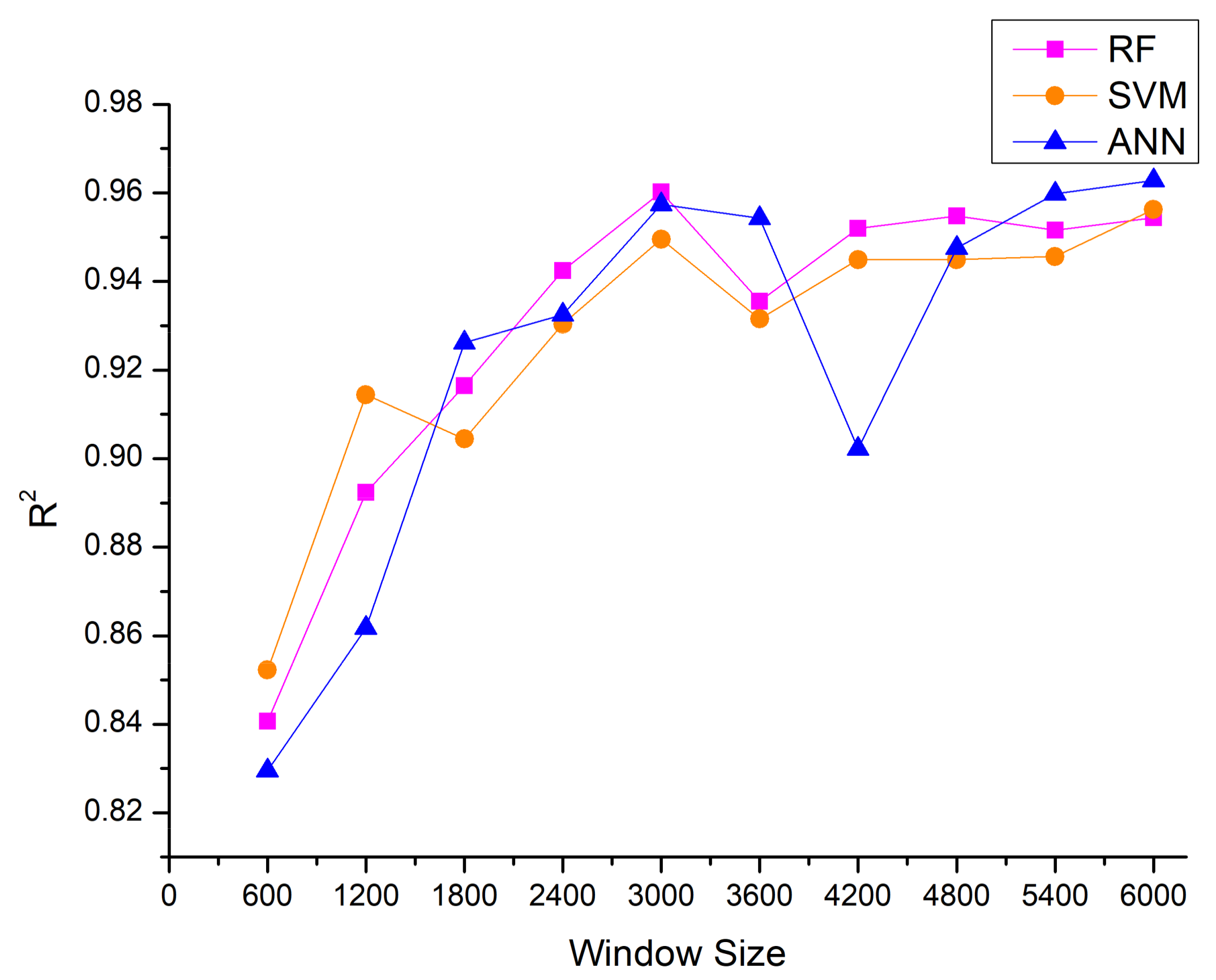
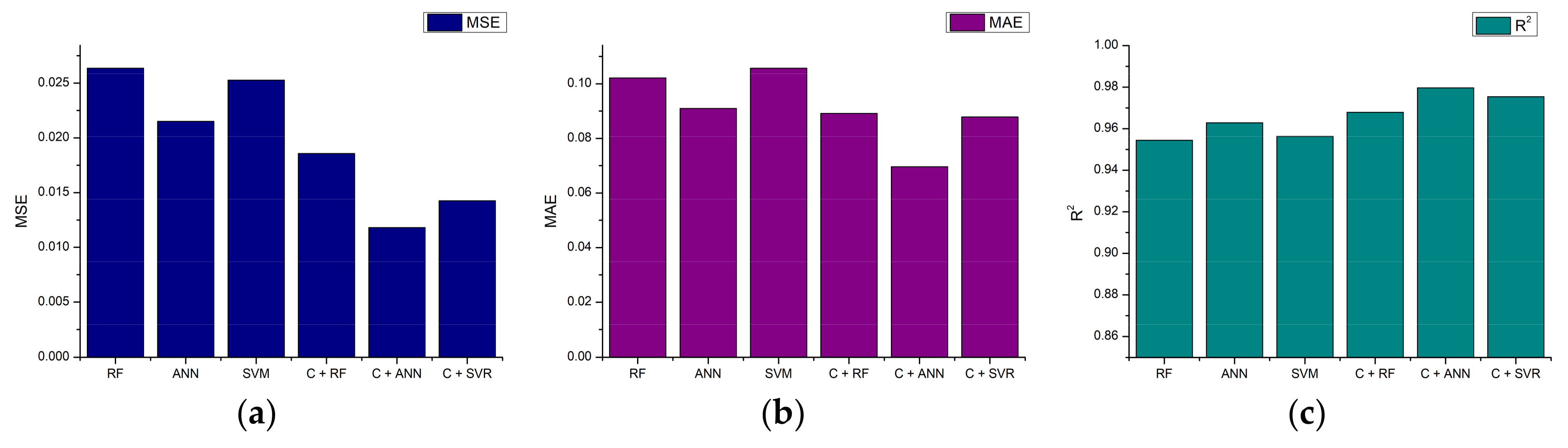
| Experimental Cases | Actual Values | Scaled Values | Scaled Average Power (W) | ||
|---|---|---|---|---|---|
| Height | Period | Height | Period | ||
| Case 1 | 4 m | 12 s | 20 cm | 2.68 s | 9.36 |
| Case 2 | 3 m | 10 s | 15 cm | 2.24 s | 5.82 |
| Case 3 | 2.5 m | 10 s | 12.5 cm | 2.24 s | 3.22 |
| Metric | Definition |
|---|---|
| Window Size | 12 | 18 | 24 | 26 | 32 | 36 | 72 |
|---|---|---|---|---|---|---|---|
| Number of training | 657 | 438 | 329 | 303 | 246 | 220 | 111 |
| Number of testing | 282 | 189 | 142 | 131 | 106 | 95 | 48 |
| Window Size | 600 | 1200 | 1800 | 2400 | 3000 | 3600 | 4200 | 4800 | 5400 | 6000 |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of training | 3625 | 1813 | 1208 | 906 | 725 | 604 | 518 | 453 | 403 | 362 |
| Number of testing | 1554 | 777 | 519 | 389 | 311 | 260 | 222 | 195 | 173 | 156 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deberneh, H.M.; Kim, I. Predicting Output Power for Nearshore Wave Energy Harvesting. Appl. Sci. 2018, 8, 566. https://doi.org/10.3390/app8040566
Deberneh HM, Kim I. Predicting Output Power for Nearshore Wave Energy Harvesting. Applied Sciences. 2018; 8(4):566. https://doi.org/10.3390/app8040566
Chicago/Turabian StyleDeberneh, Henock Mamo, and Intaek Kim. 2018. "Predicting Output Power for Nearshore Wave Energy Harvesting" Applied Sciences 8, no. 4: 566. https://doi.org/10.3390/app8040566
APA StyleDeberneh, H. M., & Kim, I. (2018). Predicting Output Power for Nearshore Wave Energy Harvesting. Applied Sciences, 8(4), 566. https://doi.org/10.3390/app8040566




