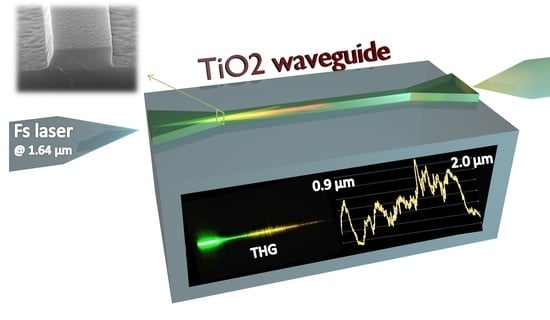
Octave Spanning Supercontinuum in Titanium Dioxide Waveguides
Abstract
1. Introduction
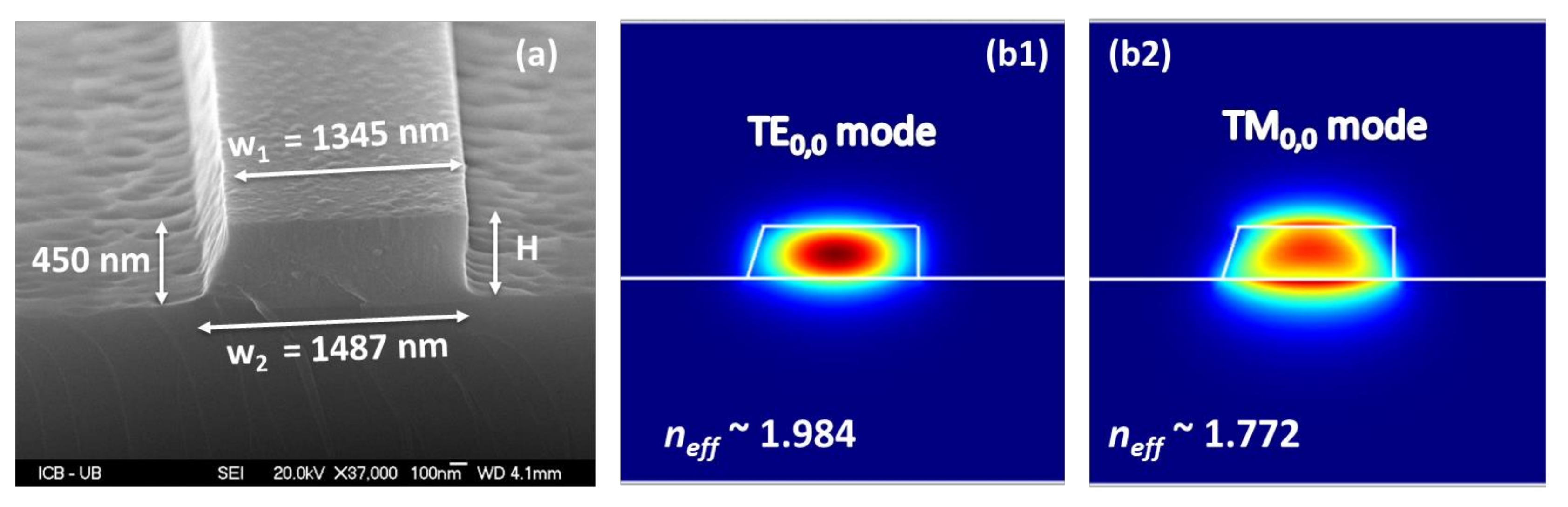
2. TiO2 Waveguide Design and Fabrication
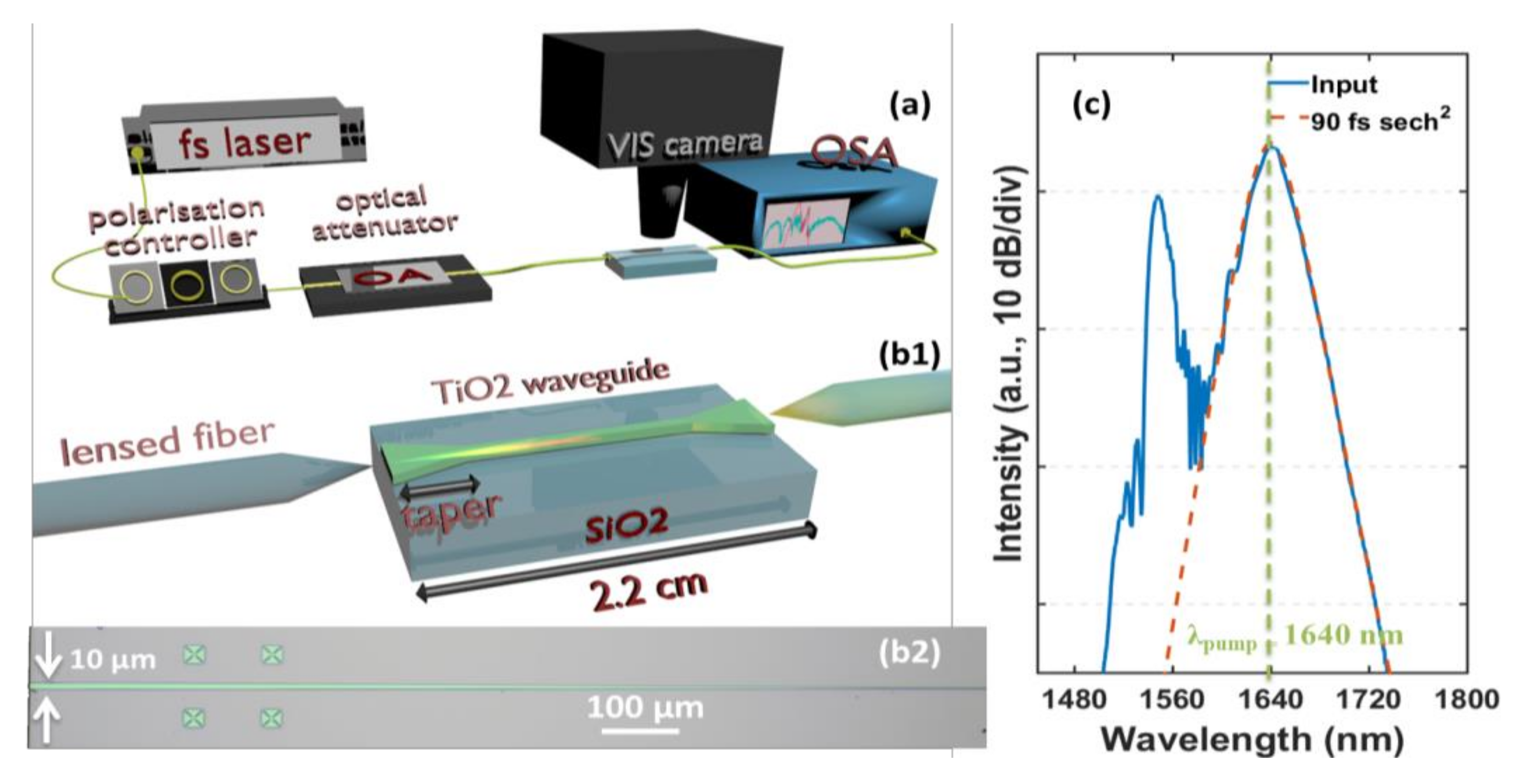
3. Experimental Setup
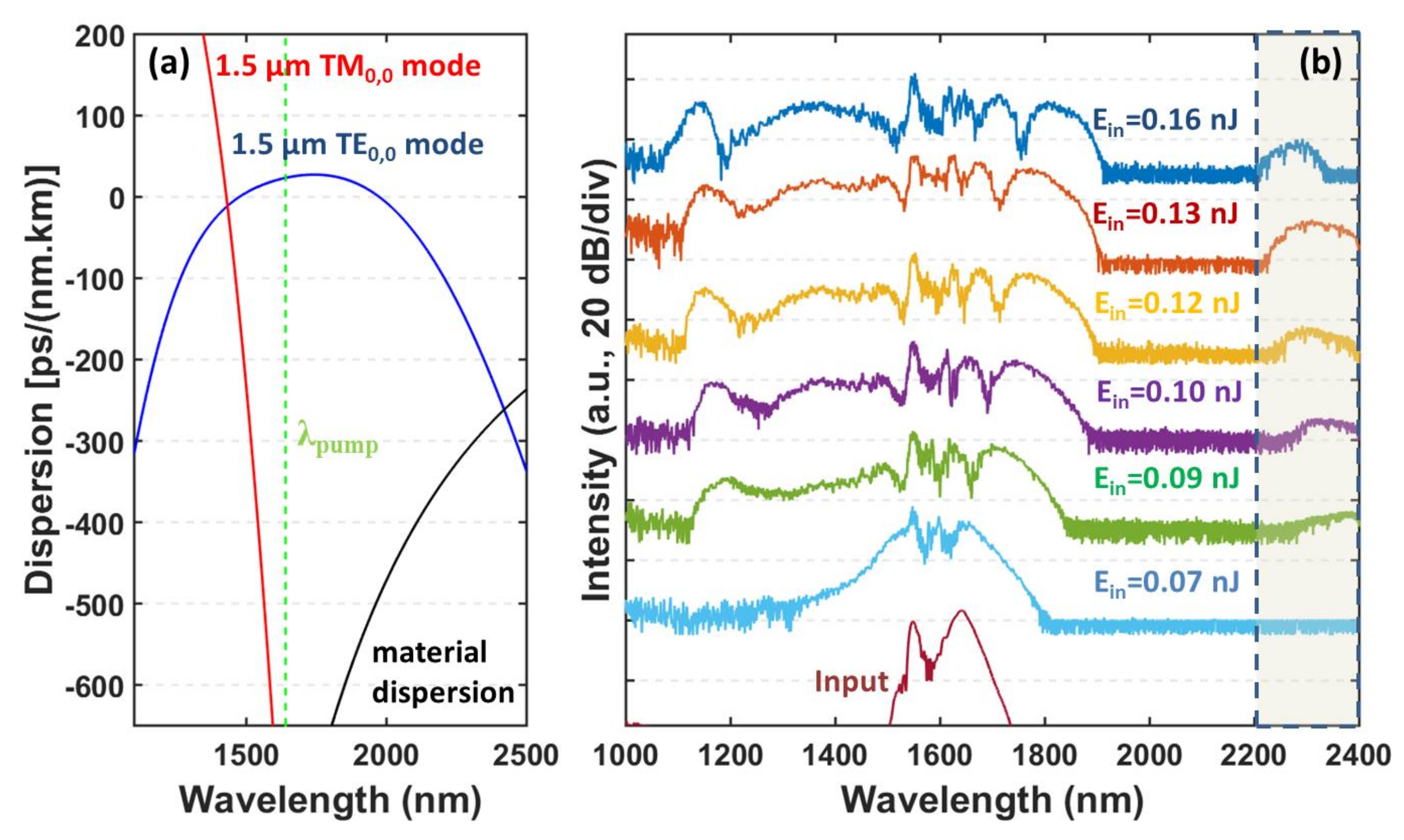
4. Supercontinuum Generation
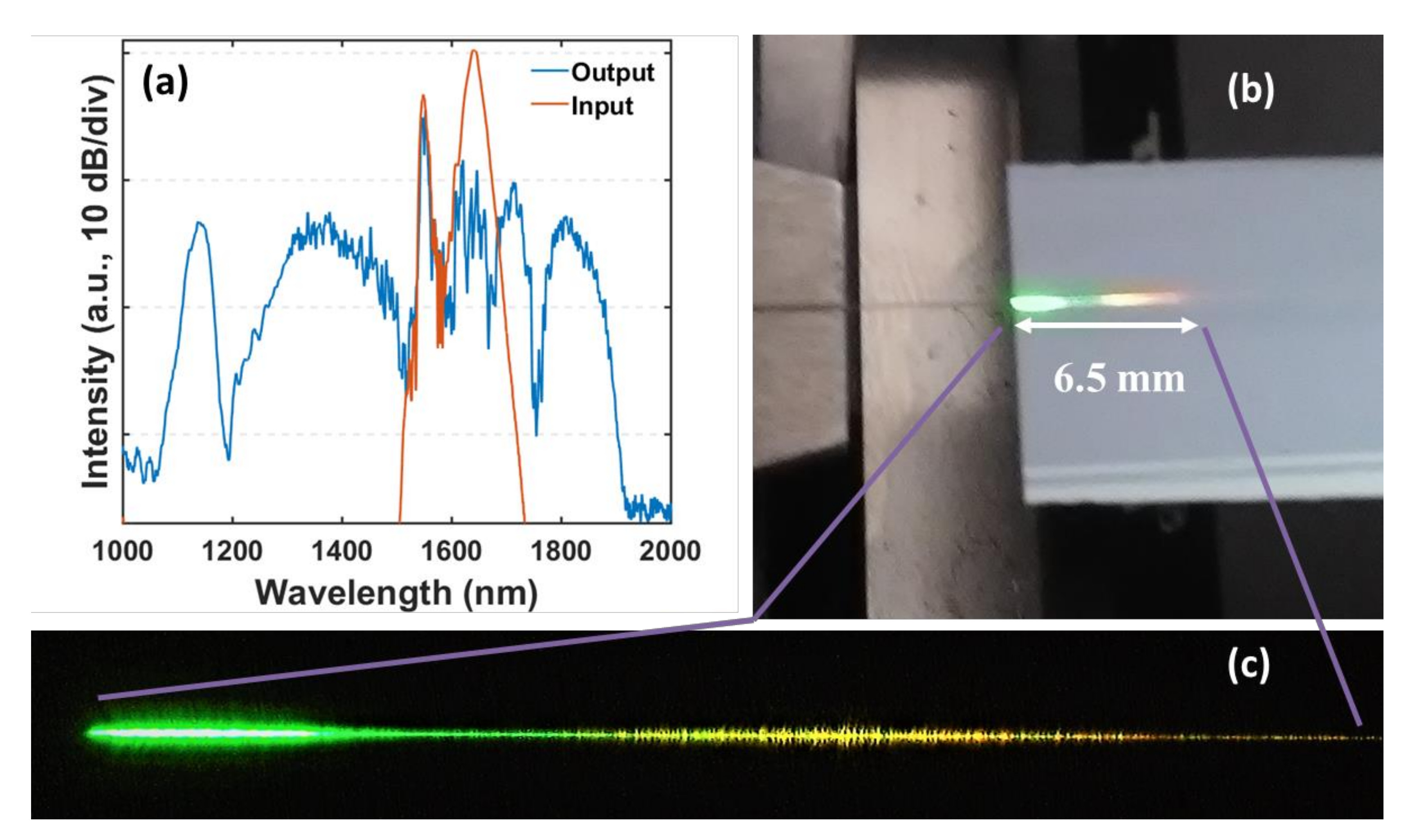
4.1. Experimental Results
4.2. Numerical Simulations
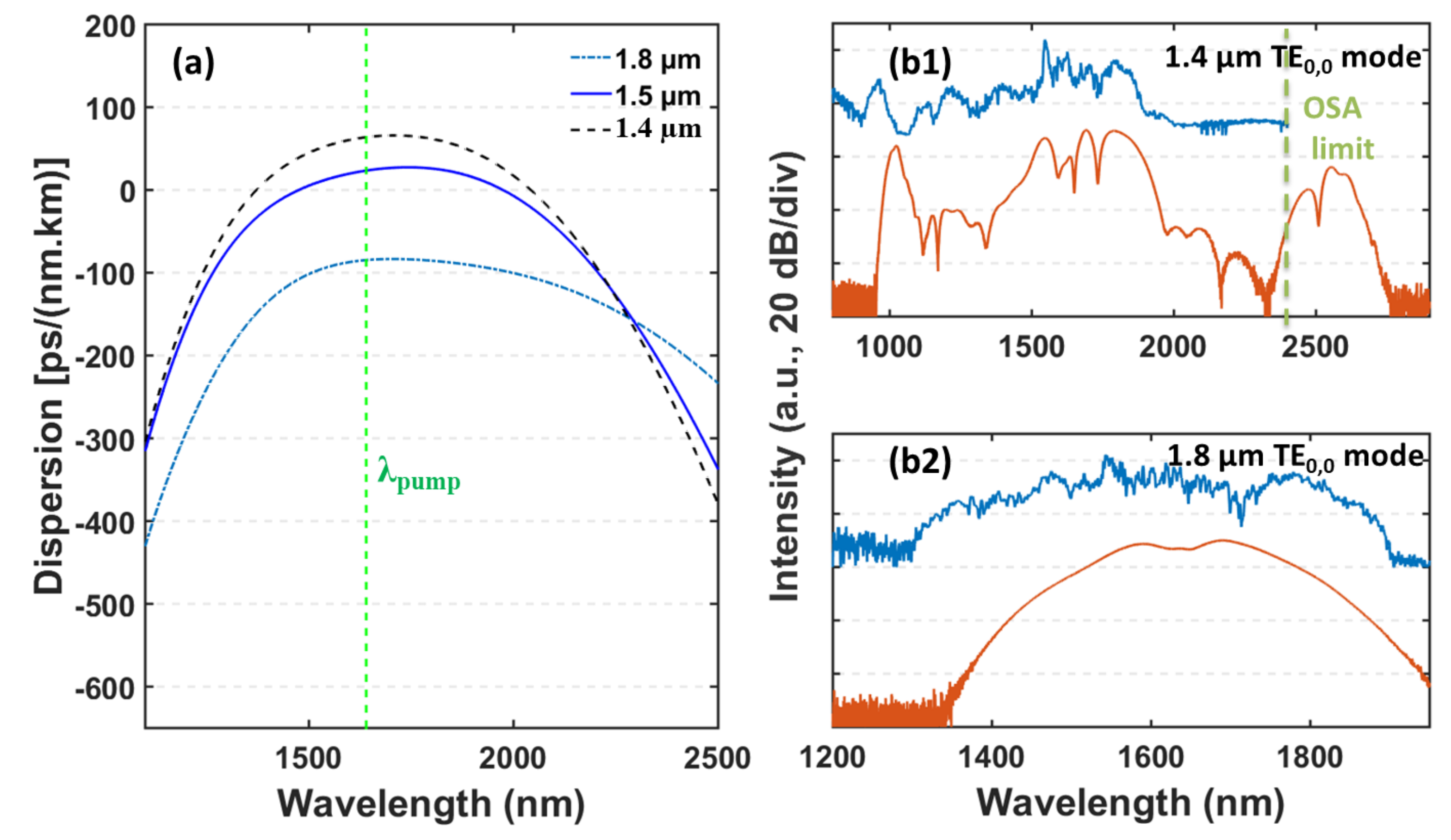
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alfano, R.R. The Supercontinuum Laser Source: The Ultimate White Light; Springer: New York, NY, USA, 2016. [Google Scholar]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fibre. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Dudley, J.M.; Taylor, J.R. Supercontinuum Generation in Optical Fibers; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Jiang, X.; Joly, N.Y.; Finger, M.A.; Babic, F.; Wong, G.K.L.; Travers, J.C.; Russell, P.S.J. Deep-ultraviolet to mid-infrared supercontinuum generated in solid-core ZBLAN photonic crystal fibre. Nat. Photonics 2015, 9, 133–139. [Google Scholar] [CrossRef]
- Savelli, I.; Mouawad, O.; Fatome, J.; Kibler, B.; Désévédavy, F.; Gadret, G.; Jules, J.-C.; Bony, P.-Y.; Kawashima, H.; Gao, W.; et al. Mid-infrared 2000-nm bandwidth supercontinuum generation in suspended-core microstructured Sulfide and Tellurite optical fibres. Opt. Express 2012, 20, 27083–27093. [Google Scholar] [CrossRef] [PubMed]
- Møller, U.; Yu, Y.; Kubat, I.; Petersen, C.R.; Gai, X.; Brilland, L.; Méchin, D.; Caillaud, C.; Troles, J.; Luther-Davies, B.; et al. Multi-milliwatt mid-infrared supercontinuum generation in a suspended core chalcogenide fibre. Opt. Express 2015, 23, 3282–3291. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Nagasaka, K.; Tuan, T.H.; Xue, X.; Matsumoto, M.; Tezuka, H.; Suzuki, T.; Ohishi, Y. Mid-infrared supercontinuum generation spanning 20 to 151 μm in a chalcogenide step-index fibre. Opt. Lett. 2016, 41, 2117–2120. [Google Scholar] [CrossRef] [PubMed]
- Domachuk, P.; Wolchover, N.A.; Cronin-Golomb, M.; Wang, A.; George, A.K.; Cordeiro, C.M.B.; Knight, J.C.; Omenetto, F.G. Over 4000 nm bandwidth of mid-IR supercontinuum generation in sub-centimeter segments of highly nonlinear tellurite PCFs. Opt. Express 2008, 16, 7161–7168. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, I.-W.; Chen, X.; Liu, X.; Dadap, J.I.; Panoiu, N.C.; Chou, C.-Y.; Xia, F.; Green, W.M.; Vlasov, Y.A.; Osgood, R.M. Supercontinuum generation in silicon photonic wires. Opt. Express 2007, 15, 15242–15249. [Google Scholar] [CrossRef] [PubMed]
- Kuyken, B.; Liu, X.; Osgood, R.M., Jr.; Baets, R.; Roelkens, G.; Green, W.M.J. Mid-infrared to telecom-band supercontinuum generation in highly nonlinear silicon-on-insulator wire waveguides. Opt. Express 2011, 19, 20172–20181. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Xin, M.; Vermeulen, D.; Shtyrkova, K.; Li, N.; Callahan, P.T.; Magden, E.S.; Ruocco, A.; Fahrenkopf, N.; Baiocco, C.; et al. Octave-spanning coherent supercontinuum generation in silicon on insulator from 1.06 μm to beyond 2.4 μm. Light Sci. Appl. 2018, 7, 17131. [Google Scholar] [CrossRef]
- Ettabib, M.A.; Xu, L.; Bogris, A.; Kapsalis, A.; Belal, M.; Lorent, E.; Labeye, P.; Nicoletti, S.; Hammani, K.; Syvridis, D.; et al. Broadband telecom to mid-infrared supercontinuum generation in a dispersionengineered silicon germanium waveguide. Opt. Lett. 2015, 40, 4118–4121. [Google Scholar] [CrossRef] [PubMed]
- Lacava, C.; Ettabib, M.; Petropoulos, P. Nonlinear Silicon Photonic Signal Processing Devices for Future Optical Networks. Appl. Sci. 2017, 7, 103. [Google Scholar] [CrossRef]
- Hammani, K.; Ettabib, M.A.; Bogris, A.; Kapsalis, A.; Syvridis, D.; Brun, M.; Labeye, P.; Nicoletti, S.; Petropoulos, P. Towards nonlinear conversion from mid- to near-infrared wavelengths using Silicon Germanium waveguides. Opt. Express 2014, 22, 9667–9674. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Pu, M.; Zhou, B.; Krückel, C.J.; Fülöp, A.; Torres-Company, V.; Bache, M. Octave-spanning supercontinuum generation in a silicon-rich nitride waveguide. Opt. Lett. 2016, 41, 1–4. [Google Scholar]
- Halir, R.; Okawachi, Y.; Levy, J.S.; Foster, M.A.; Lipson, M.; Gaeta, A.L. Ultrabroadband supercontinuum generation in a CMOS-compatible platform. Opt. Lett. 2012, 37, 1685–1687. [Google Scholar] [CrossRef] [PubMed]
- Okawachi, Y.; Saha, K.; Levy, J.S.; Wen, Y.H.; Lipson, M.; Gaeta, A.L. Octave-spanning frequency comb generation in a silicon nitride chip. Opt. Lett. 2011, 36, 3398–3400. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.R.; Mayer, A.S.; Klenner, A.; Luke, K.; Lamb, E.S.; Lamont, M.R.E.; Joshi, C.; Okawachi, Y.; Wise, F.W.; Lipson, M.; et al. Octave-spanning coherent supercontinuum generation in a silicon nitride waveguide. Opt. Lett. 2015, 40, 5117–5120. [Google Scholar] [CrossRef] [PubMed]
- Feigel, B.; Castelló-Lurbe, D.; Thienpont, H.; Vermeulen, N. Opportunities for visible supercontinuum light generation in integrated diamond waveguides. Opt. Lett. 2017, 42, 3804–3807. [Google Scholar] [CrossRef] [PubMed]
- Lamont, M.R.; Luther-Davies, B.; Choi, D.-Y.; Madden, S.; Eggleton, B.J. Supercontinuum generation in dispersion engineered highly nonlinear (γ = 10 /W/m) As2S3 chalcogenide planar waveguide. Opt. Express 2008, 16, 14938–14944. [Google Scholar] [CrossRef] [PubMed]
- Dave, U.D.; Ciret, C.; Gorza, S.-P.; Combrie, S.; de Rossi, A.; Raineri, F.; Roelkens, G.; Kuyken, B. Dispersive-wave-based octave-spanning supercontinuum generation in InGaP membrane waveguides on a silicon substrate. Opt. Lett. 2015, 40, 3584–3587. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.; Ottaviano, L.; Semenova, E.; Yvind, K. Efficient frequency comb generation in AlGaAs-on-insulator. Optica 2016, 3, 823–826. [Google Scholar] [CrossRef]
- Kischkat, J.; Peters, S.; Gruska, B.; Semtsiv, M.; Chashnikova, M.; Klinkmüller, M.; Fedosenko, O.; Machulik, S.; Aleksandrova, A.; Monastyrskyi, G.; et al. Mid-infrared optical properties of thin films of aluminum oxide, titanium dioxide, silicon dioxide, aluminum nitride, and silicon nitride. Appl. Opt. 2012, 51, 6789–6798. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.C.; Shtyrkova, K.; Bradley, J.D.B.; Reshef, O.; Ippen, E.; Mazur, E. Spectral broadening in anatase titanium dioxide waveguides at telecommunication and near-visible wavelengths. Opt. Express 2013, 21, 18582–18591. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Hu, H.; Oxenløwe, L.K.; Frandsen, L.H. Compact titanium dioxide waveguides with high nonlinearity at telecommunication wavelengths. Opt. Express 2018, 26, 1055–1063. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.; Spring, A.M.; Yokoyama, S. Athermal and high-Q hybrid TiO2-Si3N4 ring resonator via an etching-free fabrication technique. ACS Photonics 2015, 2, 405–409. [Google Scholar] [CrossRef]
- Reshef, O.; Shtyrkova, K.; Moebius, M.G.; Griesse-Nascimento, S.; Spector, S.; Evans, C.C.; Ippen, E.; Mazur, E. Polycrystalline anatase titanium dioxide microring resonators with negative thermo-optic coefficient. J. Opt. Soc. Am. B 2015, 32, 2288–2293. [Google Scholar] [CrossRef]
- Guha, B.; Cardenas, J.; Lipson, M. Athermal silicon microring resonators with titanium oxide cladding. Opt. Express 2013, 21, 26557–26563. [Google Scholar] [CrossRef] [PubMed]
- Hadjoub, I.; Touam, T.; Chelouche, A.; Atoui, M.; Solard, J.; Chakaroun, M.; Fischer, A.; Boudrioua, A.; Peng, L.H. Post-deposition annealing effect on RF-sputtered TiO2 thin-film properties for photonic applications. Appl. Phys. A Mater. Sci. Process. 2016, 122, 1–8. [Google Scholar] [CrossRef]
- Quidant, R.; Weeber, J.-C.; Dereux, A.; Peyrade, D.; Chen, Y.; Girard, C. Near-field observation of evanescent light wave coupling in subwavelength optical waveguides. Europhys. Lett. 2002, 57, 191–197. [Google Scholar] [CrossRef][Green Version]
- Choy, J.T.; Bradley, J.D.B.; Deotare, P.B.; Burgess, I.B.; Evans, C.C.; Mazur, E.; Lon, M. Integrated TiO2 resonators for visible photonics. Opt. Lett. 2012, 37, 539–541. [Google Scholar] [CrossRef] [PubMed]
- Giudicatti, S.; Marz, S.M.; Soler, L.; Madani, A.; Jorgensen, M.R.; Sanchez, S.; Schmidt, O.G. Photoactive rolled-up TiO2 microtubes: fabrication, characterization and applications. J. Mater. Chem. C 2014, 2, 5892–5901. [Google Scholar] [CrossRef] [PubMed]
- Lamy, M.; Finot, C.; Fatome, J.; Arocas, J.; Weeber, J.-C.; Hammani, K. Demonstration of High-Speed Optical Transmission at 2 µm in Titanium Dioxide Waveguides. Appl. Sci. 2017, 7, 631. [Google Scholar] [CrossRef]
- Madani, A.; Harazim, S.M.; Quiñones, V.A.B.; Kleinert, M.; Finn, A.; Naz, E.S.G.; Ma, L.; Schmidt, O.G. Optical microtube cavities monolithically integrated on photonic chips for optofluidic sensing. Opt. Lett. 2017, 42, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.C.; Liu, C.; Suntivich, J. TiO2 Nanophotonic Sensors for Efficient Integrated Evanescent Raman Spectroscopy. ACS Photonics 2016, 3, 1662–1669. [Google Scholar] [CrossRef]
- Moebius, M.G.; Herrera, F.; Griesse-Nascimento, S.; Reshef, O.; Evans, C.C.; Guerreschi, G.G.; Aspuru-Guzik, A.; Mazur, E. Efficient photon triplet generation in integrated nanophotonic waveguides. Opt. Express 2016, 24, 9932–9954. [Google Scholar] [CrossRef] [PubMed]
- Abe, K.; Teraoka, E.Y.M.; Kita, T.; Yamada, H. Nonlinear optical waveguides with rutile TiO2. Proc. SPIE 2011, 79401. [Google Scholar] [CrossRef]
- Ma, Y.-J.; Lu, F.; Xiang, B.-X.; Zhao, J.-L.; Ruan, S.-C. Fabrication of TiO2 thin films with both anatase and rutile structures together using the ion-implantation method. Opt. Mater. Express 2018, 8, 532–540. [Google Scholar] [CrossRef]
- Jiang, L.; Evans, C.C.; Reshef, O.; Mazur, E. Optimizing anatase-TiO2 deposition for low-loss planar waveguides. Proc. SPIE 2013, 8626. [Google Scholar] [CrossRef]
- Bradley, J.D.B.; Evans, C.C.; Choy, J.T.; Reshef, O.; Parag, B.; Parsy, F.; Phillips, K.C.; Lon, M.; Mazur, E. Submicrometer-wide amorphous and polycrystalline anatase TiO2 waveguides for microphotonic devices. Opt. Express 2012, 20, 8336–8346. [Google Scholar] [CrossRef] [PubMed]
- Foster, M.A.; Moll, K.D.; Gaeta, A.L. Optimal waveguide dimensions for nonlinear interactions. Opt. Express 2004, 12, 2880–2887. [Google Scholar] [CrossRef] [PubMed]
- Lamy, M.; Hammani, K.; Arocas, J.; Finot, C.; Weeber, J.-C. Broadband etching-free metal grating couplers embedded in titanium dioxide waveguides. Opt. Lett. 2017, 42, 2778–2781. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Evans, C.C.; Liu, C.; Suntivich, J. Low-loss titanium dioxide waveguides and resonators using a dielectric lift-off fabrication process. Opt. Express 2015, 23, 11160–11169. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.C.; Shtyrkova, K.; Reshef, O.; Moebius, M.; Bradley, J.D.B.; Griesse-Nascimento, S.; Ippen, E.; Mazur, E. Multimode phase-matched third-harmonic generation in sub-micrometer-wide anatase TiO2 waveguides. Opt. Express 2015, 23, 7832–7841. [Google Scholar] [CrossRef] [PubMed]
- Skryabin, D.V.; Gorbach, A.V. Colloquium: Looking at a soliton through the prism of optical supercontinuum. Rev. Mod. Phys. 2010, 82, 1287–1299. [Google Scholar] [CrossRef]
- Mussot, A.; Beaugeois, M.; Bouazaoui, M.; Sylvestre, T. Tailoring CW supercontinuum generation in microstructured fibers with two-zero dispersion wavelengths. Opt. Express 2007, 15, 11553–11563. [Google Scholar] [CrossRef] [PubMed]
- Porcel, M.A.G.; Schepers, F.; Epping, J.P.; Hellwig, T.; Hoekman, M.; Heideman, R.G.; van der Slot, P.J.M.; Lee, C.J.; Schmidt, R.; Bratschitsch, R.; et al. Two-octave spanning supercontinuum generation in stoichiometric silicon nitride waveguides pumped at telecom wavelengths. Opt. Express 2017, 25, 1542–1554. [Google Scholar] [CrossRef] [PubMed]
- Kibler, B.; Fischer, R.; Genty, G.; Neshev, D.N.; Dudley, J.M. Simultaneous fs pulse spectral broadening and third harmonic generation in highly nonlinear fibre: Experiments and simulations. Appl. Phys. B 2008, 91, 349–352. [Google Scholar] [CrossRef]
- Genty, G.; Kinsler, P.; Kibler, B.; Dudley, J.M. Nonlinear envelope equation modeling of sub-cycle dynamics and harmonic generation in nonlinear waveguides. Opt. Express 2007, 15, 5382–5387. [Google Scholar] [CrossRef] [PubMed]
- Finot, C.; Kibler, B.; Provost, L.; Wabnitz, S. Beneficial impact of wave-breaking for coherent continuum formation in normally dispersive nonlinear fibers. J. Opt. Soc. Am. B 2008, 25, 1938–1948. [Google Scholar] [CrossRef]
- Heidt, A.M. Pulse preserving flat-top supercontinuum generation in all-normal dispersion photonic crystal fibers. J. Opt. Soc. Am. B 2010, 27, 550–559. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammani, K.; Markey, L.; Lamy, M.; Kibler, B.; Arocas, J.; Fatome, J.; Dereux, A.; Weeber, J.-C.; Finot, C. Octave Spanning Supercontinuum in Titanium Dioxide Waveguides. Appl. Sci. 2018, 8, 543. https://doi.org/10.3390/app8040543
Hammani K, Markey L, Lamy M, Kibler B, Arocas J, Fatome J, Dereux A, Weeber J-C, Finot C. Octave Spanning Supercontinuum in Titanium Dioxide Waveguides. Applied Sciences. 2018; 8(4):543. https://doi.org/10.3390/app8040543
Chicago/Turabian StyleHammani, Kamal, Laurent Markey, Manon Lamy, Bertrand Kibler, Juan Arocas, Julien Fatome, Alain Dereux, Jean-Claude Weeber, and Christophe Finot. 2018. "Octave Spanning Supercontinuum in Titanium Dioxide Waveguides" Applied Sciences 8, no. 4: 543. https://doi.org/10.3390/app8040543
APA StyleHammani, K., Markey, L., Lamy, M., Kibler, B., Arocas, J., Fatome, J., Dereux, A., Weeber, J.-C., & Finot, C. (2018). Octave Spanning Supercontinuum in Titanium Dioxide Waveguides. Applied Sciences, 8(4), 543. https://doi.org/10.3390/app8040543