1. Introduction
The seakeeping performance of floating bodies such as ships in harsh sea conditions is one of most important hydrodynamic characteristics that need to be carefully investigated by engineers. Generally, ship motions can be acceptably predicted using inviscid linear potential theories except for roll response. The difficulty of predicting roll response originates from the nonlinearity of roll motion and viscous effects of water. As compared to other motions, the roll motion is inherently highly nonlinear when the roll amplitude is medium to large. The viscous effects always accompany with the roll motion, and they become increasingly significant when ships are fitted with bilge keels. To accurately predict the roll motion, both nonlinear and viscous effects should be considered in the analysis.
As far back as a century ago, William Froude discovered that the roll motion of ships in regular beam waves is nonlinear in certain conditions and should be described using nonlinear equations [
1]. Systematic studies on the nonlinearity of ship roll motion only started from 1950s, when nonlinear dynamics theories began to be applied to investigate the nonlinear roll characteristics. Typically, the roll response of ships in regular beam waves can be modeled using a single degree of freedom differential equation, which includes linear terms and nonlinear damping and stiffness terms. The nonlinear stiffness terms mainly characterize the shape of the static stability diagram, while the nonlinear damping terms reflect the viscous effects as well as the nonlinearity. The effect of these nonlinear terms is enhanced as the wave amplitude increases. However, it is hard to obtain the exact analytical solution for the nonlinear differential equation with respect to roll response. Therefore, various approximate analytical methods have been developed for solving the nonlinear roll equation to this day, such as the multi-scale method [
2], perturbation-based method [
3], Krylov-Bogoliubov asymptotic method [
4], and so on.
To model and solve the nonlinear differential equation for roll response, the nonlinear damping and stiffness terms must be determined beforehand. There are two approaches to achieve this: one is the parametric identification approach [
5], and the other is the non-parametric identification approach [
6]. In the parametric identification approach, one needs to presuppose the expressions of damping and stiffness, which are generally assumed to be odd-ordered polynomials, e.g., linear plus cubic damping (
), and linear plus cubic, quintic stiffness (
) [
7], where
are roll angle and roll angular velocity, respectively, and
are damping and stiffness coefficients, respectively. However, as in some works, the even-ordered terms might also be adopted, such as linear plus quadric damping [
1] or linear plus quadric, cubic, quintic stiffness [
8]. The nonlinear stiffness could be evaluated using hydrostatic restoring curve fitting method, while nonlinear damping coefficients are difficult to obtain using the classical potential theories. Thereby, most studies that made parametric identification for nonlinear roll models concentrated on investigating the nonlinear damping coefficients. Generally, roll damping can be identified using either the extinction curve method [
5] or the energy method [
9] from the free roll decay curves. To enhance the numerical stability, some ingenious data processing tools such as support vector regression [
10], kalman filter [
11], and wavelets [
12] are employed in the damping identification. In contrast to the parametric identification approach, which depends on the given nonlinear damping and stiffness models, the non-parametric identification approach does not make any priori assumption of the damping form. A pioneer work using this approach was made by Jang et al. [
6], which identified the nonlinear damping by solving the nonlinear Volterra integral equation of the first kind.
All abovementioned studies and methods were based on the differential equation of roll with nonlinear damping models. In fact, in the ship engineering field, sometimes the nonlinear damping is approximated to an equivalent linear one for simplicity. Normally, the equivalent linear roll damping coefficient depends upon not only the roll frequency and forward speed, but also on the roll amplitude. Therefore, it is vital to correctly determine the equivalent linear roll damping coefficient for the large-amplitude roll analysis.
Currently, there are two main ways to obtain the equivalent roll damping coefficient. One is from carrying out ship model tank tests, which can provide reliable resulting data. The other is computational fluid dynamics (CFD) methods, which are preferred due to their lower cost and shorter time consumption. Yeung et al. [
13] experimentally and numerically investigated hydrodynamic coefficients of various forced rolling sections and observed that viscous effects were significantly present for sharply edged sections. Korpus and Falzarano [
14] compared the roll moment from the potential theory with that from using Reynolds-averaged Navier-Stokes equations (RANS) and found that the shear roll moment was negligible, while the vortex effect was identified to have significant influence on the phase and magnitude. Yıldız et al. [
15] demonstrated that the unsteady RANS (URANS) calculations are in a good agreement with experimental results under large amplitudes and shallow draft conditions. Lavrov et al. [
16] clearly captured the vortex shedding around a forced rolling hull section with sharp keel by using the RANS solver in OpenFOAM, which suggests that the viscous effects mainly originate from the vortex shedding. Similar results were achieved by using the mesh-free numerical model [
17]. Actually, the vortex shedding around sharp edges is the major source of viscous effects in the roll damping.
However, CFD methods still require significant computational resources, which might not meet the engineering demand. An alternative approach is to exploit semi-empirical methods. One of the most common semi-empirical methods is Ikeda’s estimation method [
18], which divides the total equivalent linear roll damping coefficient into skin friction damping, eddy damping, wave damping, lift damping, and bilge keel damping. Amongst these, only wave damping and lift damping can be calculated using potential theories, while the rest are associated with fluid viscous effects and can be obtained using empirical approaches. Beyond Ikeda’s estimation method, Brown and Patel [
19] incorporated the Direct Vortex Method (DVM) into a potential theory to model viscous effects within an inviscid model, in which the roll center of bilge keels needs to be estimated. Based on the work of Brown and Patel [
19], Downie et al. [
20] developed a method using DVM to assess the roll damping of ships.
More recently, Guo et al. [
21] first proposed a linear time-domain Green’s function method (
) for assessing the interaction between floating bodies and water waves with viscous dissipation effects, which can accurately evaluate the hydrodynamic coefficients of sharply edged floating bodies with small roll amplitude. The
[
21] can consider the full viscous dissipation effects of water, while other similar Green’s functions [
22,
23,
24] can only take the partial viscous dissipation effects into account. However, the linear
or other Green’s functions cannot be employed to evaluate the equivalent damping coefficient of large-amplitude roll motion, which is known to be highly nonlinear.
In this paper, a body-nonlinear time-domain Green’s function method (
) is first developed for evaluating the equivalent damping of large-amplitude roll motion for two-dimensional floating bodies with consideration of viscous dissipation effects of water. The
is a significant development of the
[
25] with both nonlinear and viscous dissipation effects of the large-amplitude roll motion into account.
The paper is organized as follows. The mathematical model of the
is developed in
Section 2. Then, in
Section 3, the
is employed to calculate the equivalent roll damping of hull sections with bilge keels under different roll amplitudes, and the numerical results are compared with experimental ones and those using
. Finally, the conclusions are drawn in
Section 4.
3. Application of the for Solving Roll Damping of Hull Sections with Bilge Keels
A novel body-nonlinear Green’s function method with viscous dissipation effects (
) was developed in
Section 2. In this section,
is employed to solve the roll damping of hull sections with bilge keels under small and large roll amplitude. For comparison purpose, numerical results from linear inviscid time-domain Green’s function method (
) [
25], body-nonlinear inviscid time-domain Green’s function method (
) [
25], and experimental fluid dynamic (EFD) results [
13] are also provided in the cases.
3.1. Hull Section Under Small Amplitude Roll
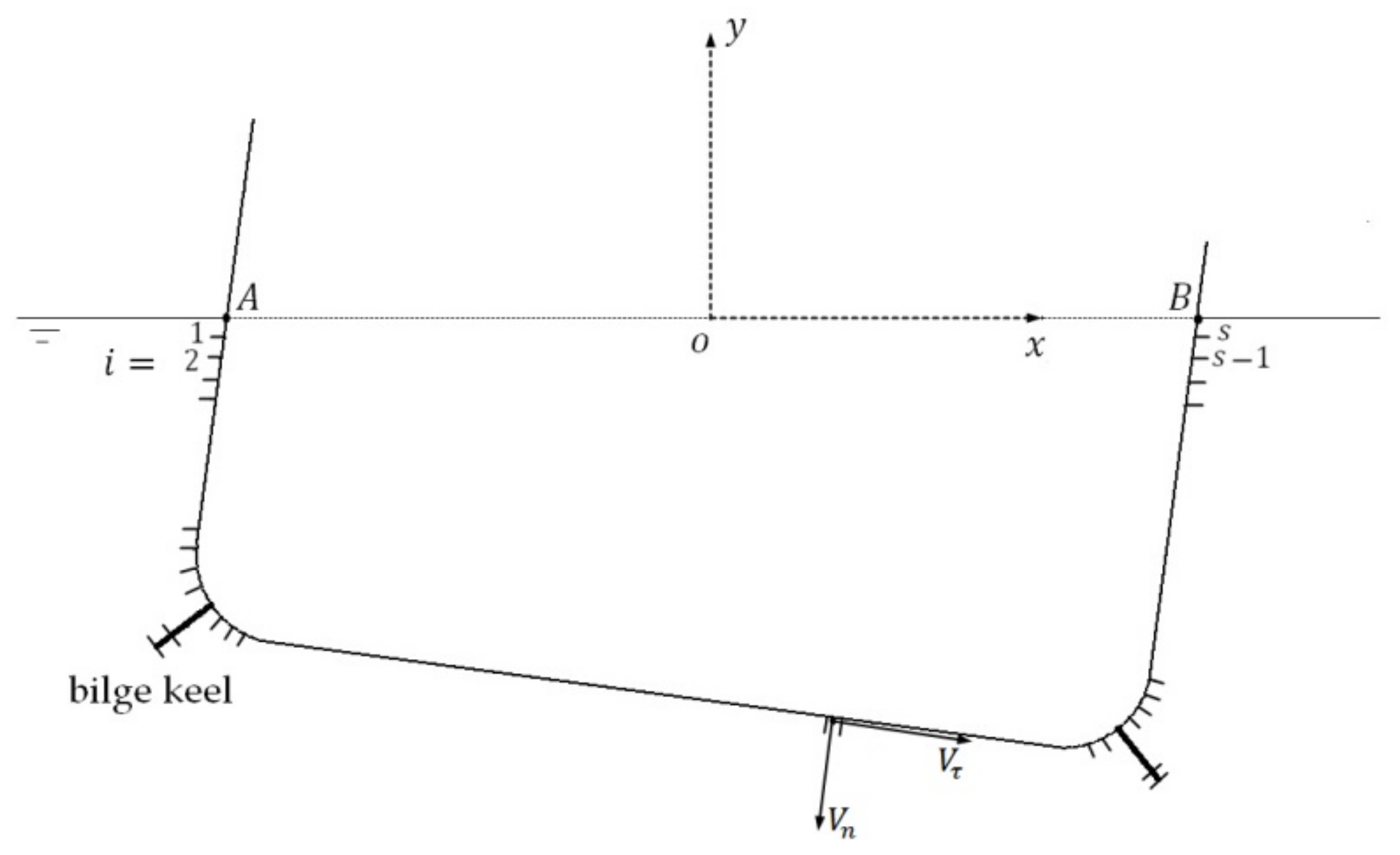
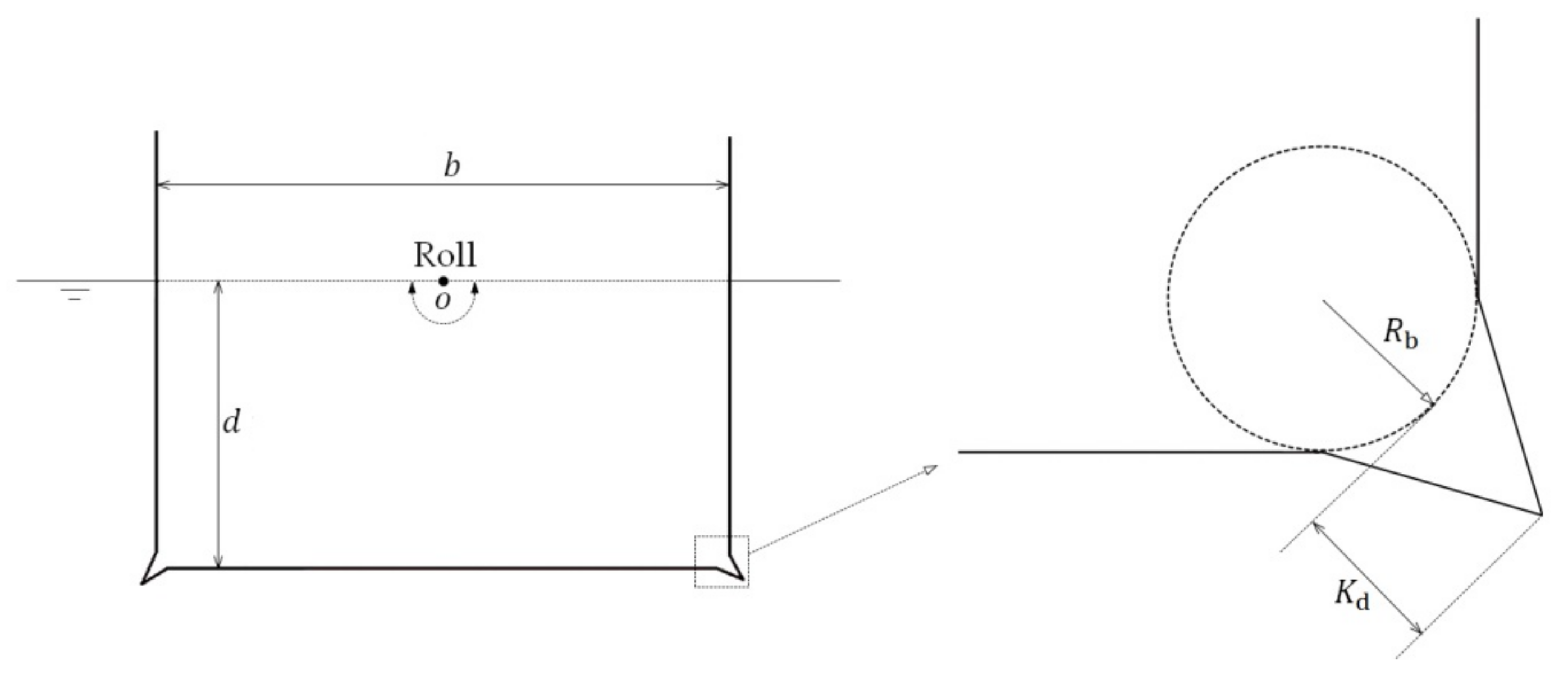
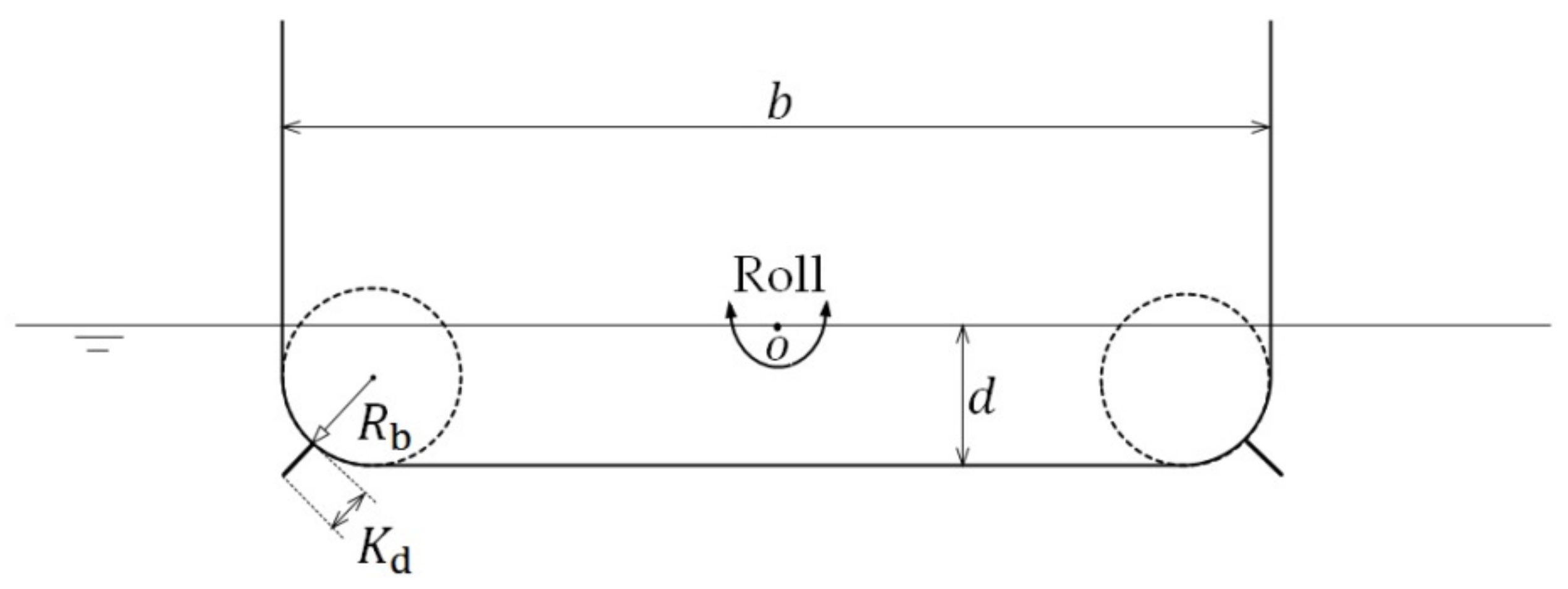
A rectangular hull section with bilge keels is shown in
Figure 2. The beam and mean draught of the hull section are
and
, respectively. Two bilge keels are set at the corners that connect the wall and bottom of the hull section, and the bilge radius and bilge keel depth are
and
, respectively. The hull section harmonically rolls on the water surface with small amplitude
. The axis of rotation is located at the center of waterplane of the hull section. The detailed description of the experiments can be found in Yeung et al. [
13].
As abovementioned, the novel Green’s function method
and two contrast methods (
and
[
25]) are employed for the roll damping calculation. In each Green’s function method, the hull section is discretized into 160 segments (30 for each wall, 20 for each bilge keel, 60 for the flat bottom). In the linear method
, all segments are located on the mean wetted surface of the hull section and kept constant. On the other hand, in the nonlinear methods
and
, all segments move with roll motion, and the segments on two sidewalls need to be remeshed due to the change of draught.
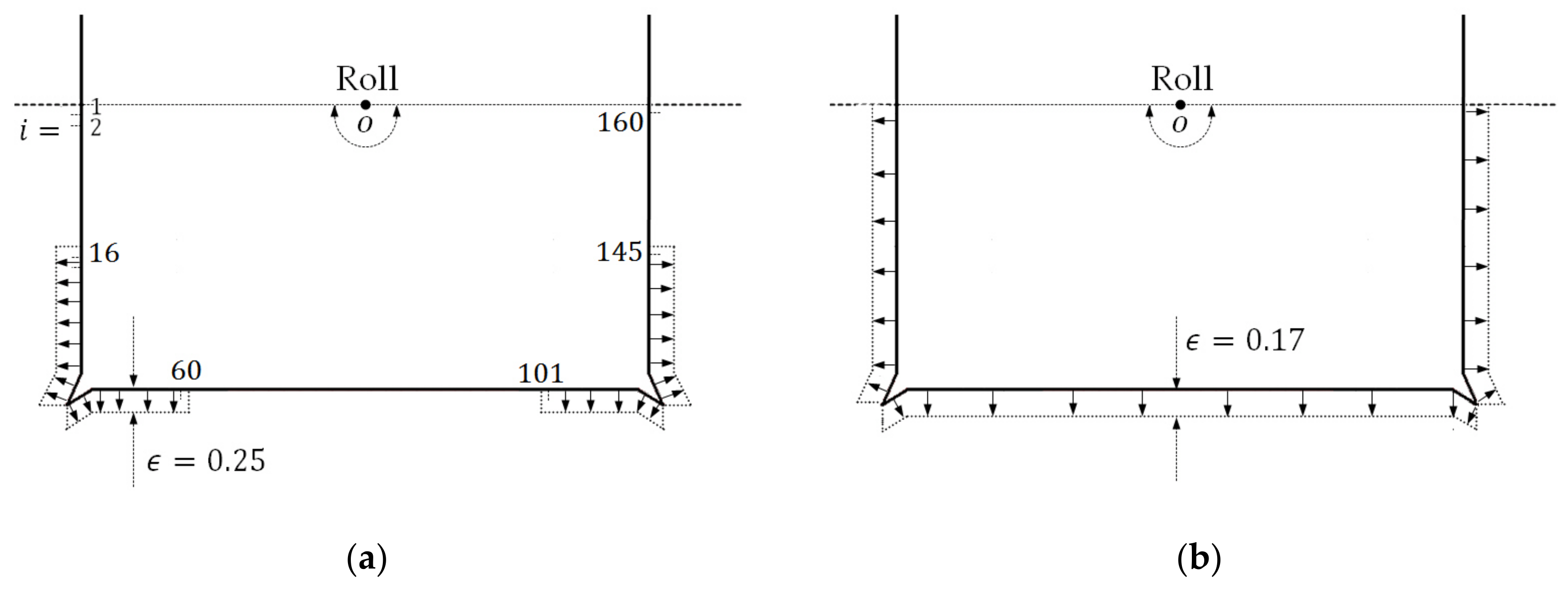
Two viscosity distribution approaches are adopted for
in this case. As shown in
Figure 3a, in the first approach a non-zero viscosity is set only on the segments in the vicinity of bilge keels (
), while on the rest segments the viscosity is set to zero. In the second approach (see
Figure 3b) a non-zero viscosity is set on all segments (
). The non-dimensional viscosity coefficient
should be empirically selected or obtained through the CFD or EFD methods. It is found that desirable results can be achieved if taking the non-dimensional viscosity coefficient as
for the first approach and
for the second approach. The roll frequency
is taken as the reference frequency
in
(see Equation (27)).
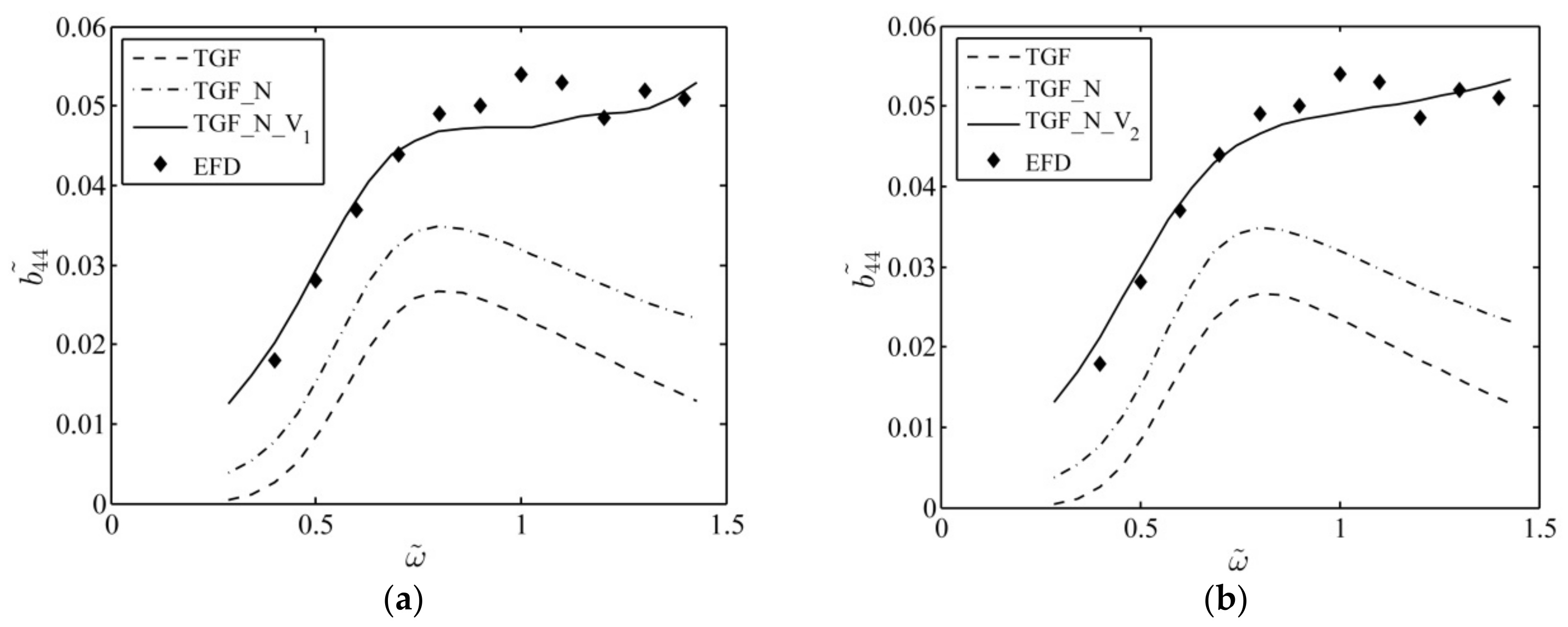
Figure 4 portrays the equivalent roll damping using
,
, and
as compared with EFD. The lines labeled with “
” and “
” denote results from
by using the first and second viscosity distribution approach, respectively. Comparing the
result with the
one, one can find that both of two viscosity distribution approaches are effective for evaluating the roll damping of a hull section with bilge keels. Nonetheless, it can be observed that the second approach can yield smoother results. Thereby, in the next case, only the second viscosity distribution approach will be employed for study.
From
Figure 4, one can observe that, as compared with EFD data, the linear inviscid method
and body-nonlinear inviscid method
significantly underestimate the roll damping, though the discrepancy between
result and EFD data is smaller than that between the
result and EFD data, which suggests that the numerical results could be improved when the nonlinear effects are taken into account. Moreover, the
and
results decrease when
, which are in the opposite trend as compared to EFD data. On the other hand, the
results agree well with EFD data under the given non-dimensional viscosity coefficients, even when
.
The numerical results in this case suggest that, for the hull section with bilge keels under roll motion of small amplitude, the viscous effects in the roll damping are more important than the nonlinear effects. The study also confirms the possibility of employing to estimate the viscous effects as well as nonlinear effects of a hull section with bilge keels rolling on the free surface. In contrast, the inviscid methods and are not appropriate for evaluating the roll damping of the hull section with bilge keels.
3.2. Hull Section Under Large Amplitude Roll
Figure 5 depicts an S60 midship section with bilge keels. The beam and mean draught of the hull section are
and
, respectively. The bilge radius and bilge keel depth are
and
, respectively. The single degree of freedom model experiment was carried out by Yıldız et al. [
15], in which the S60 midship section model is fixed by a forced rolling device, and the roll moment is measured through the torque transducer. The S60 midship section model harmonically rolls on the water surface with large amplitudes
. The axis of rotation is located at the center of waterplane of the hull section. More detailed description on the model experiments can be found in Yıldız et al. [
15].
As in the previous case, the S60 midship section is discretized into 160 segments (30 for each wall, 20 for each bilge keel, 60 for the flat bottom). It is worth mention that the bilge keels in this case are simplified to lines without thickness, and each side of the bilge keel is discretized into 10 segments. The numerical error may occur when the source point and field point located on the two sides of the bilge keel are overlapped. To avoid this, the value of the Green’s function is set as zero once the source point and field point are overlapped. Note that for the body-nonlinear methods, the segments on walls could be stretched or compressed with the roll motion of the S60 midship section. The second viscosity distribution approach, i.e., a non-zero viscosity for all segments on the wetted surface, is employed for in this case. It is found that for the non-dimensional viscosity coefficient for the roll motion with amplitude respectively, could lead to desirable results. It can be noted that for larger roll amplitudes, it requires larger non-dimensional viscosity coefficient for . The roll frequency is taken as the reference frequency in .
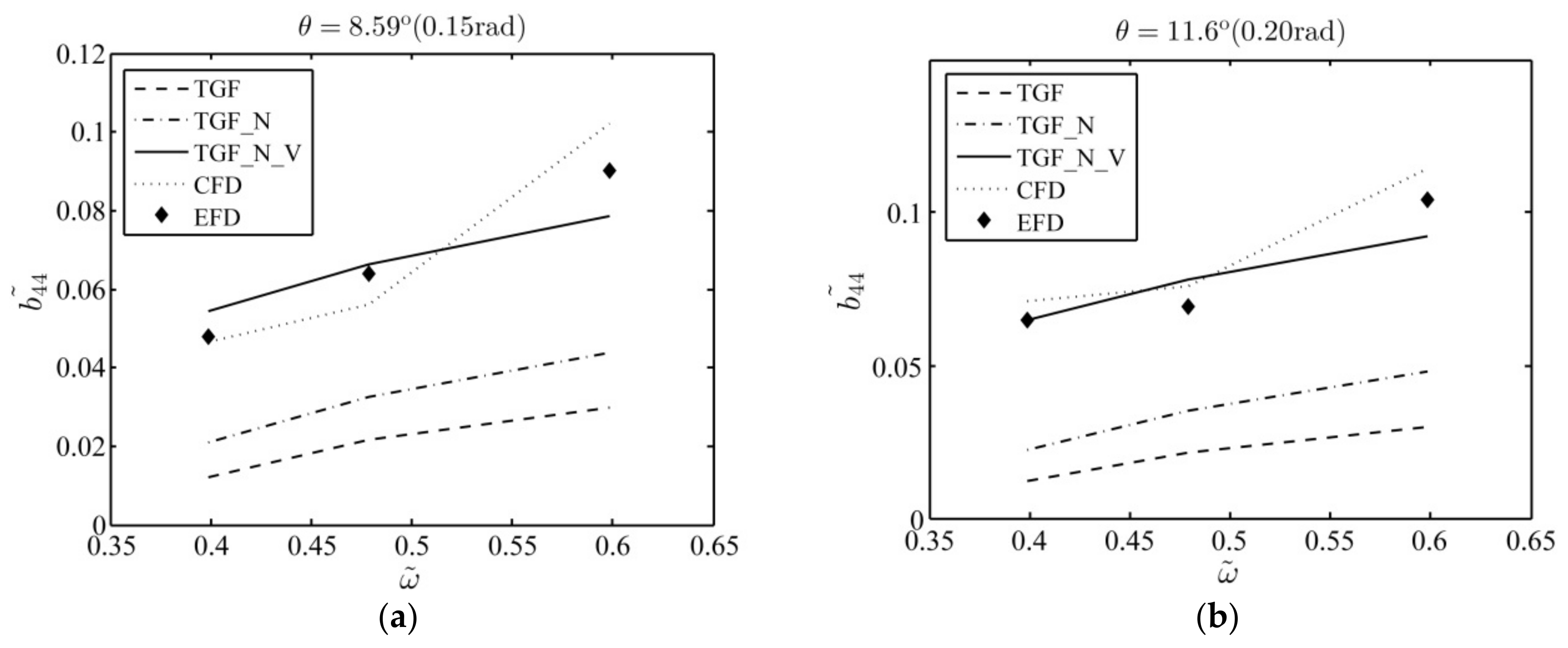
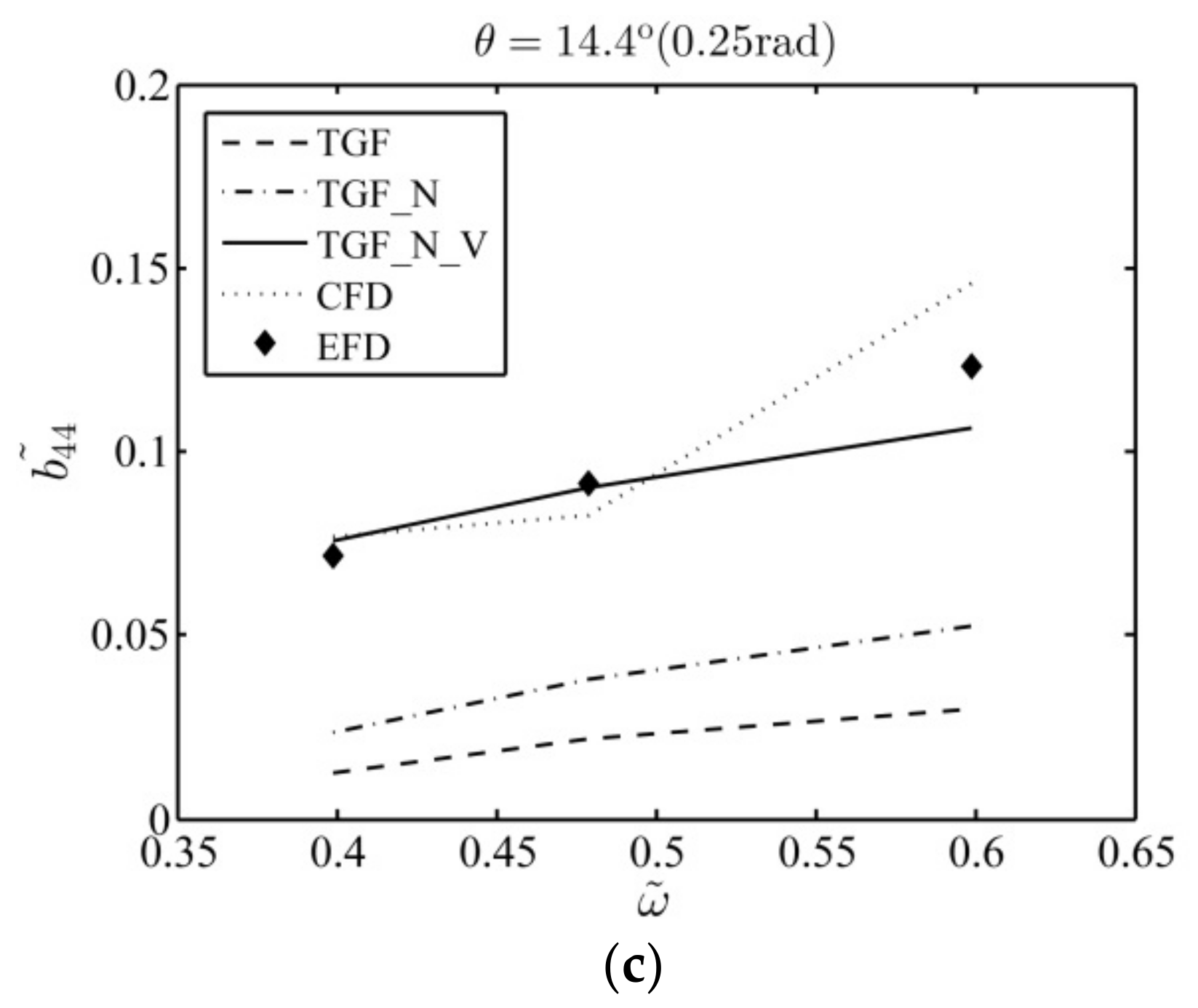
Figure 6 portrays the equivalent roll damping using
,
and
as compared with CFD [
15] and EFD [
15]. One can find that, under all roll amplitudes, the linear inviscid method
and body-nonlinear inviscid method
dramatically underestimate the roll damping as compared with EFD data. Nonetheless, as compared to
, the
results are closer to EFD, which suggests that there exist nonlinear effects in the roll damping. On the other hand, the
results agree well with EFD data, though at high roll frequency
slightly underestimates the equivalent roll damping. In contrast, the CFD results also agree well with EFD data, though it overestimates the damping at high roll frequency.
The numerical results in this case suggest that for the hull section with bilge keels under large amplitude roll, the viscous effects in the roll damping are much more important than the nonlinear effects, and one could obtain desirable numerical results only when both of nonlinear and viscous effects are considered. The study also confirms the effectiveness of in evaluating the equivalent roll damping of a hull section with bilge keels rolling on the free surface with large amplitude.