An Ensemble Based Evolutionary Approach to the Class Imbalance Problem with Applications in CBIR
Abstract
:1. Introduction
2. Related Work
3. Class Imbalance Problem
3.1. Dealing with Class Imbalance
- Algorithm level approaches: These approaches adapt the existing classifier to bias their learning towards the minority class. The knowledge about the application domain and the corresponding classifier is required by these methods to comprehend the reasons for classifier failure in the presence of uneven class distribution.
- Data level approaches: These approaches proceed by re-balancing the class distribution by re-sampling the data space. Due to their versatility, these methods can be applied with any classifier. The class imbalance effect is decreased with a data preprocessing step.
- Cost-sensitive learning: These frameworks add the misclassification cost to the instances and bias the classifier towards the class having the higher misclassification costs that is usually the minority class. The overall goal is to minimize the total cost errors of both classes. However, as the misclassification costs are not explicitly available in the datasets, these techniques cannot be tuned in a practical manner.
- Ensemble Approaches: The ensemble based techniques that combine multiple classifiers for classification are appearing as another category to address the class imbalance problem [29]. The ensemble based methods are usually applied in combination with any of the approaches mentioned earlier.
3.2. Classifier Ensembles
- Combine different classifiers or learning algorithms instead of keeping only one classifier which is giving the lowest estimation value of the expected risk.
- For a given learning algorithm, apply various initialization procedures or model selection strategies to obtain different candidate solutions. After obtaining candidate solutions, combine them.
- Generate subsets of training set or feature sets and train several classifiers on these subsets. Some classifiers can be more efficient on local subspaces and they will act like experts on their local domain.
3.3. Motivations of Genetic Algorithm for Class Imbalance
Proof of Effectiveness
3.4. Genetic Algorithm Architecture for Class Imbalance Problem
3.4.1. Feature Extraction and Chromosome Generation
- Curvelet Transform: The Curvelet transform was originally proposed to overcome the missing directional selectivity of conventional 2D discrete wavelet transforms (DWTs). The 2D Curvelet transform allows an almost optimal sparse representation of objects with singularities along smooth curves [35].As a first step of feature extraction, we represent images in the Curvelet transform via wrapping and obtain multiple bands and sub-bands. For every sub-band, we compute the variance of image transformation, and for every band, we take the mean of the variances of the associated sub-bands. These mean values are placed in a vector, which serves as the Curvelet representation.
- Wavelet Packets: As a second step of feature extraction, the complete wavelet packets tree [36] of image is computed with 64 nodes. From this tree we select more predictable nodes on the basis of Shanon entropy and compute the standard deviation as the feature of the corresponding node. These standard deviation values are placed in a vector that serves as the feature representation of the wavelet packets tree.
- Gabor Filters: We take the smallest approximation image of wavelet packets tree for Gabor analysis. The convolution kernels are defined as:whereis the standard deviation of the Gaussian function, is the wavelength of the harmonic function, is the orientation, and is the spatial aspect ratio, which is left constant at 0.5. For obtaining the Gabor responses, images are convolved by the kernels of size 9 × 9. In our implementation 12 kernels are used, which are tuned to four orientations () and three frequencies (). Orientation, varies from 0 to (stepping by ) and frequency varies from 0.3 to 0.5. After generating the response images following scheme is used for feature extraction:Twelve Gabor based response images are obtained by applying the above mentioned parameters. Corresponding to every response image, we obtain the eigenvalues in the form of vectors. Each vector is represented by a single value that is obtained by taking the mean. Therefore, finally there will be twelve mean values as the final representation by the Gabor transform.
3.4.2. Genetic Operators
| Algorithm 1 Genetic Algorithm. |
| Input: Positive set , number of generated populations , population size ‘P’, GA method ‘m’. |
|
3.4.3. Fitness Function and Termination Conditions
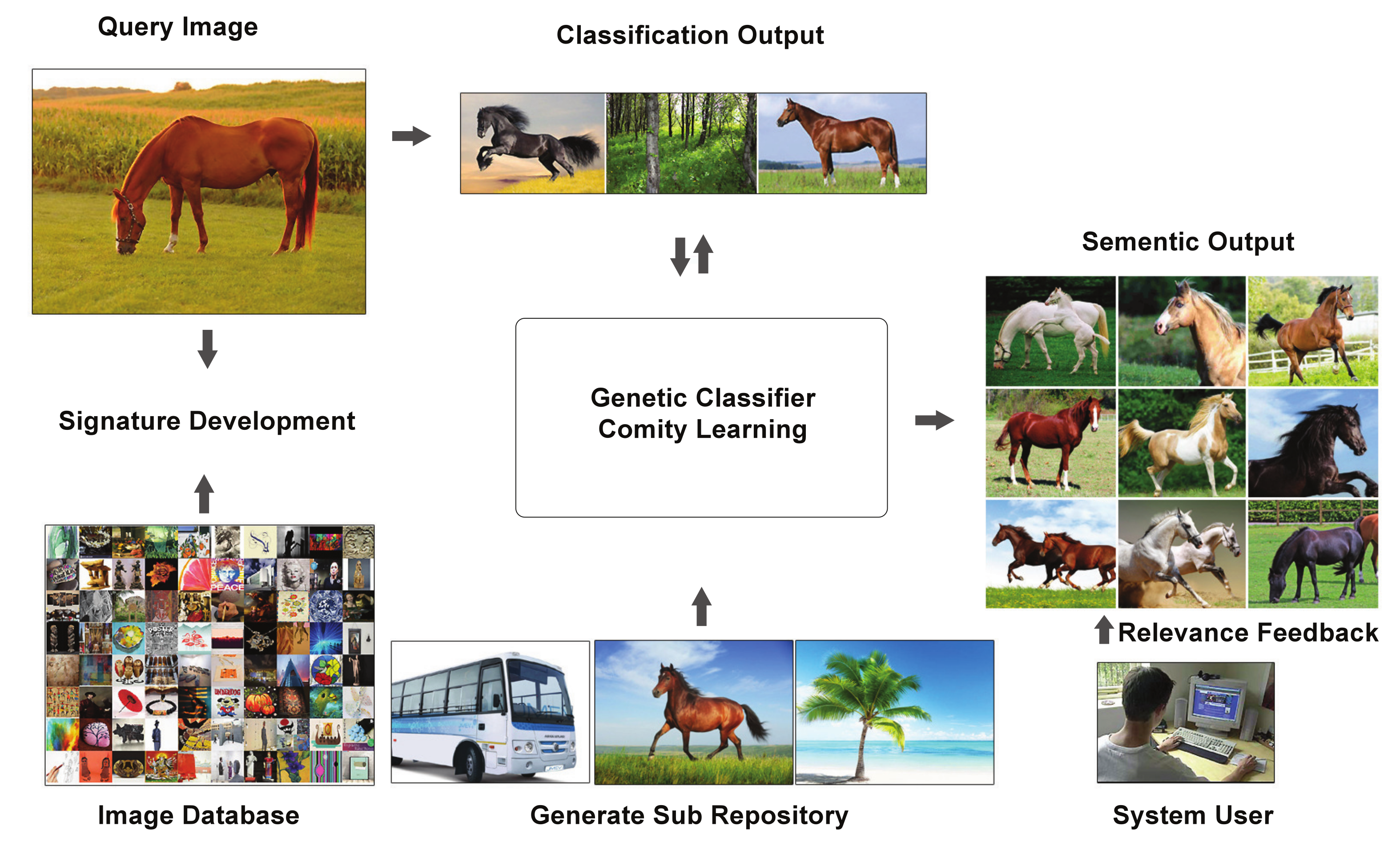
4. Genetic Classifier Comity Learning for Image Classification
4.1. Image Classification through Support Vector Machines
4.1.1. Asymmetric Bagging Based on Elitism for Support Vector Machines
| Algorithm 2 Asymmetric bagging based on elite parents through GA for SVM . |
| Input: Positive set , negative set , weak classifier I (SVM), integer (number of generated classifiers) and the test sample x Output: Classifier |
|
4.1.2. Bagging Based on Tournament Selection for Support Vector Machines
| Algorithm 3 Bagging based on tournament selection through GA for SVM. |
| Input: Positive set , negative set , weak classifier I (SVM), integer (number of generated classifiers) and the test sample x Output: Classifier |
|
4.1.3. Semantic Association Using Support Vector Machines
4.2. Image Classification through Artificial Neural Networks
Asymmetric Bagging for Neural Networks
| Algorithm 4 Asymmetric bagging using neural networks. |
| Input: Positive set , negative set , weak classifier I (ANN), integer (number of generated classifiers) and the test sample x Output: Classifier |
|
4.3. Class Finalization through Genetic Classifier Comity Learning
4.4. Content Based Image Retrieval
5. Experiment and Results
5.1. Database Description
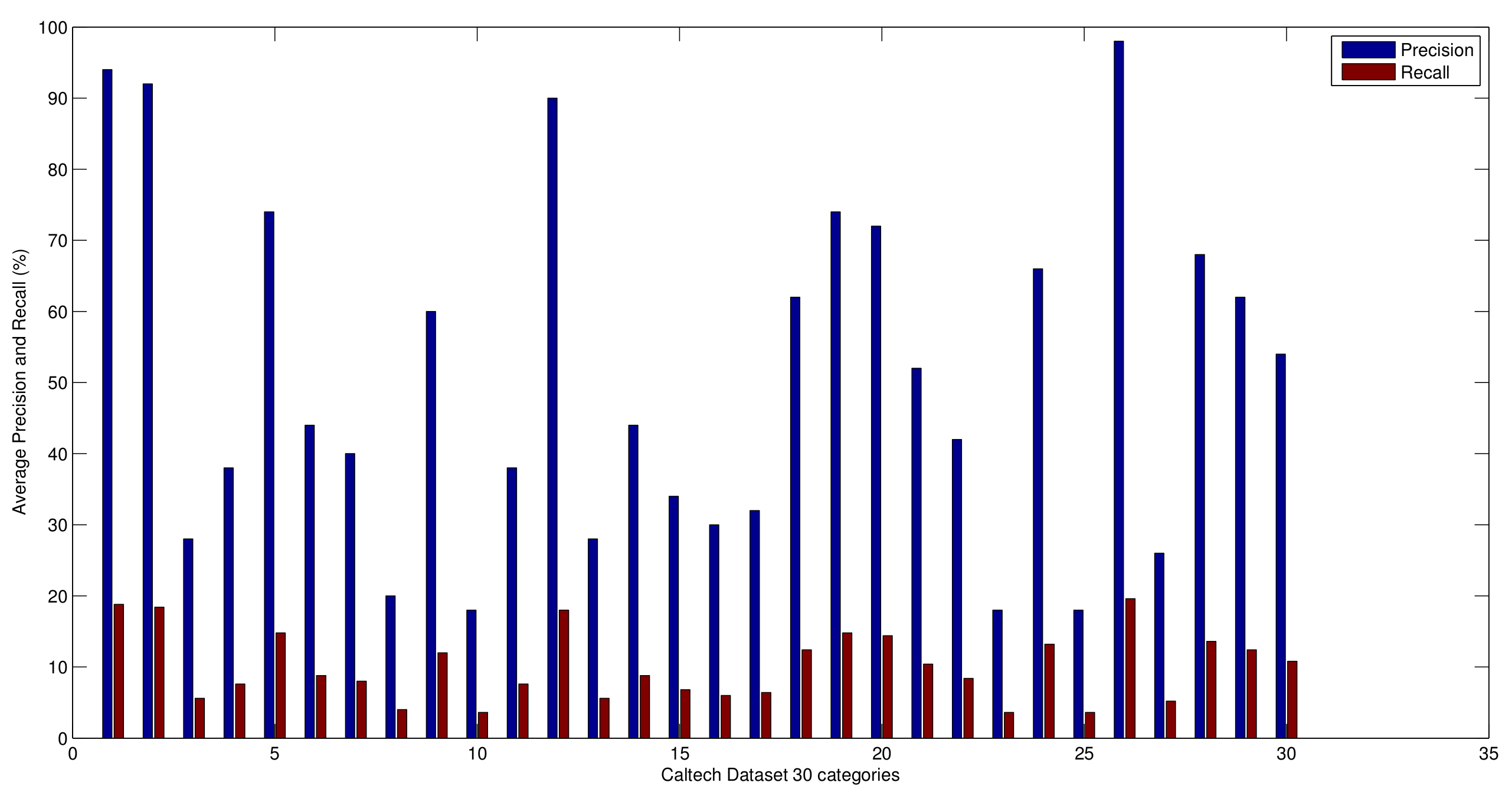
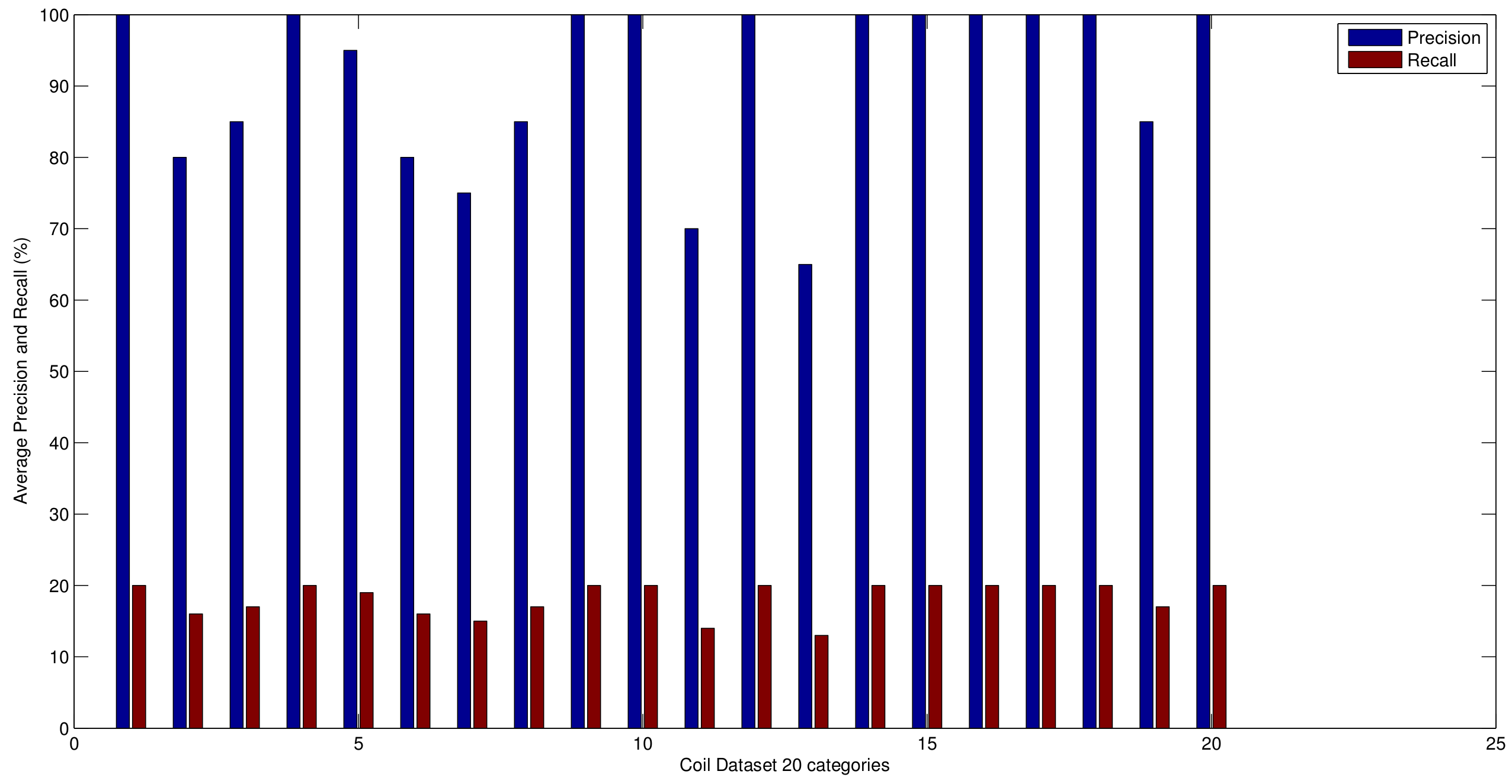
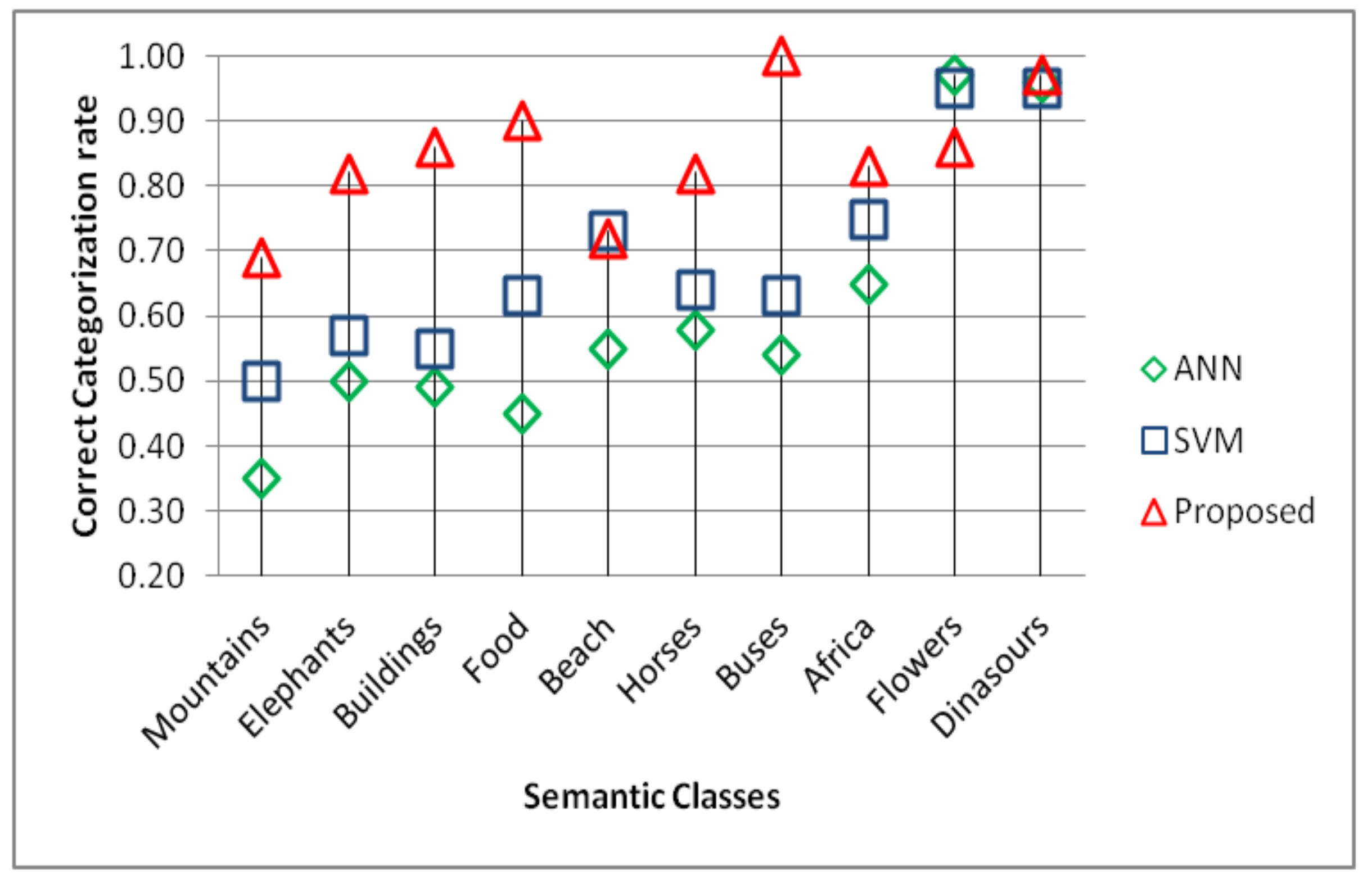
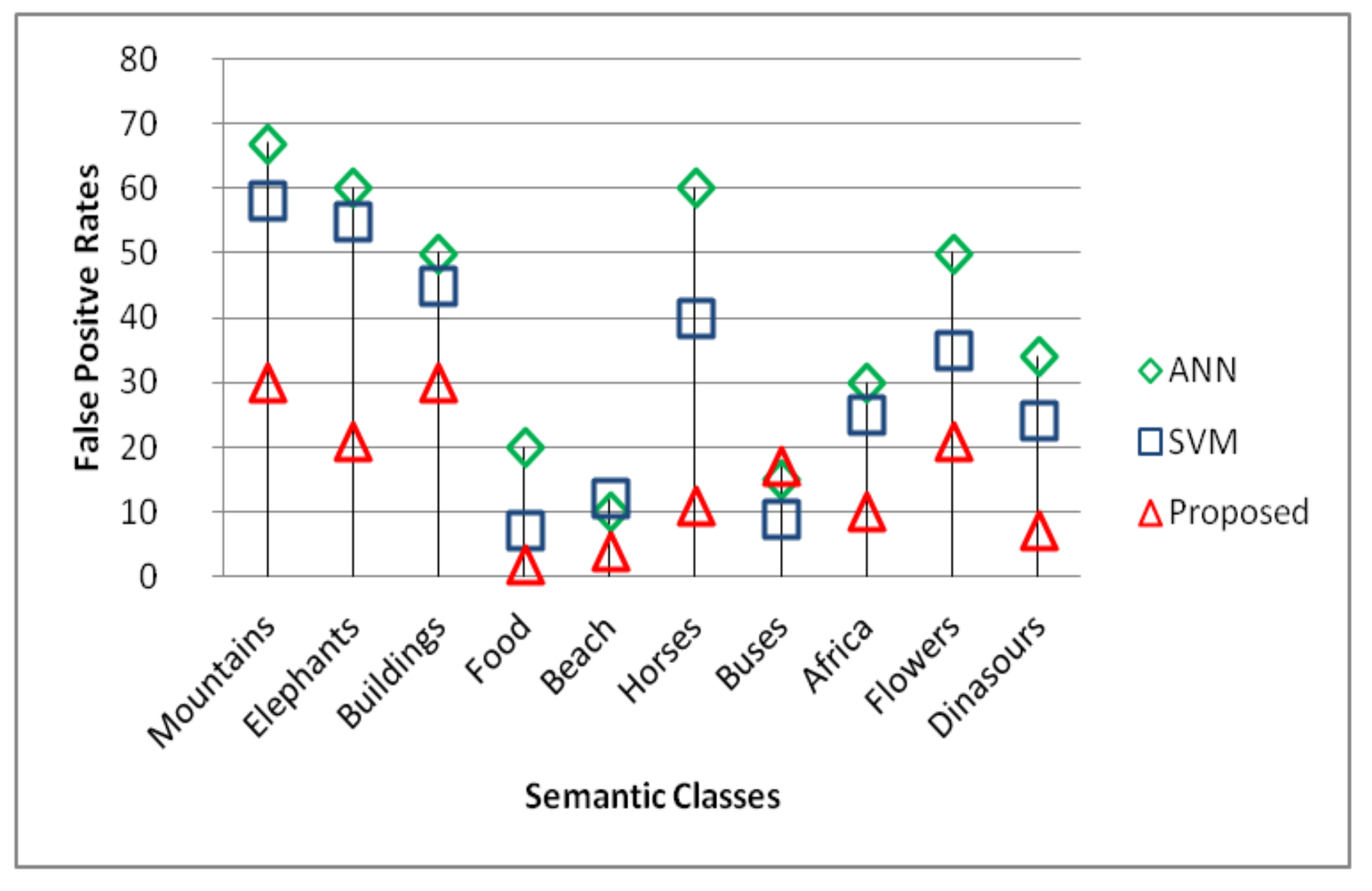
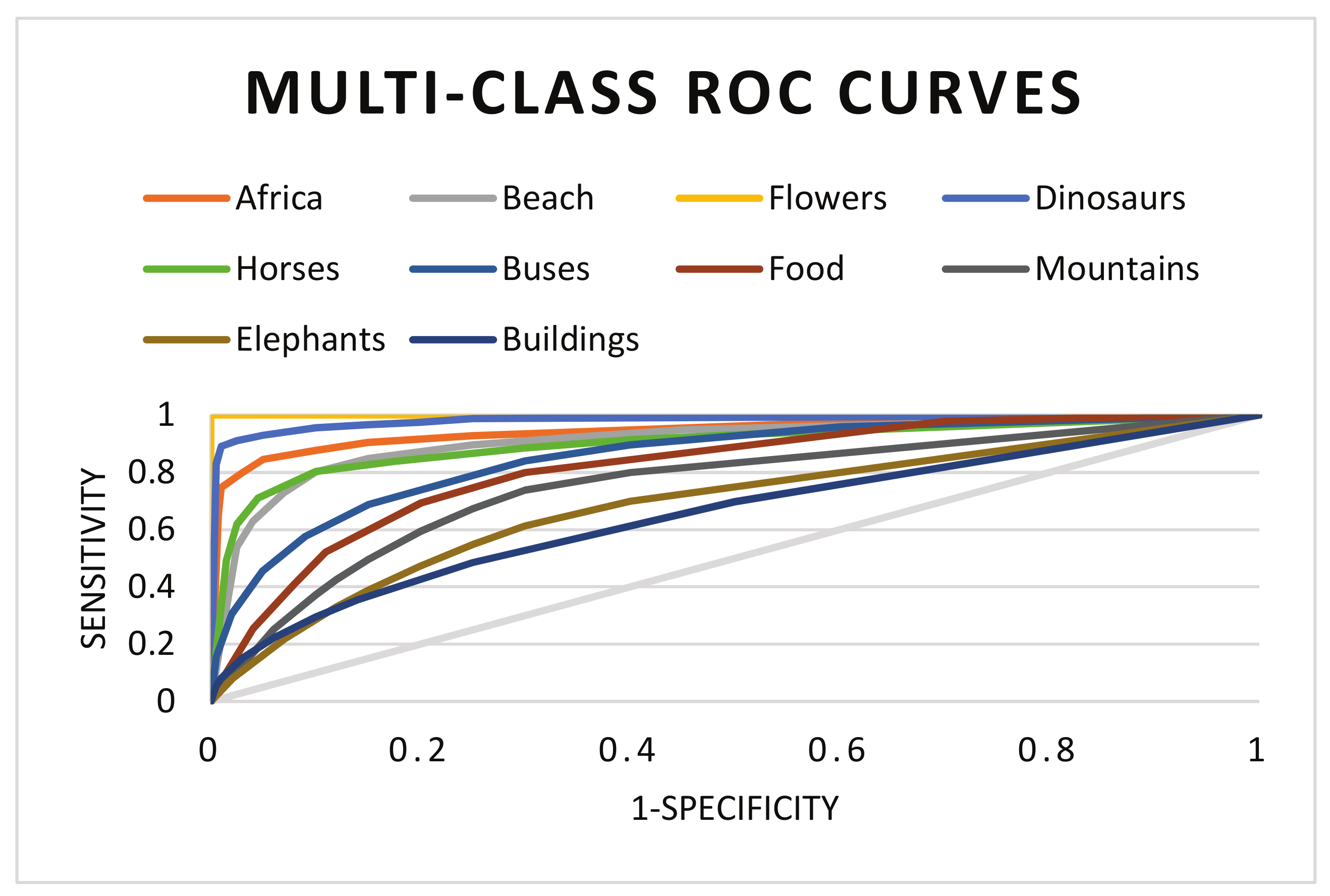
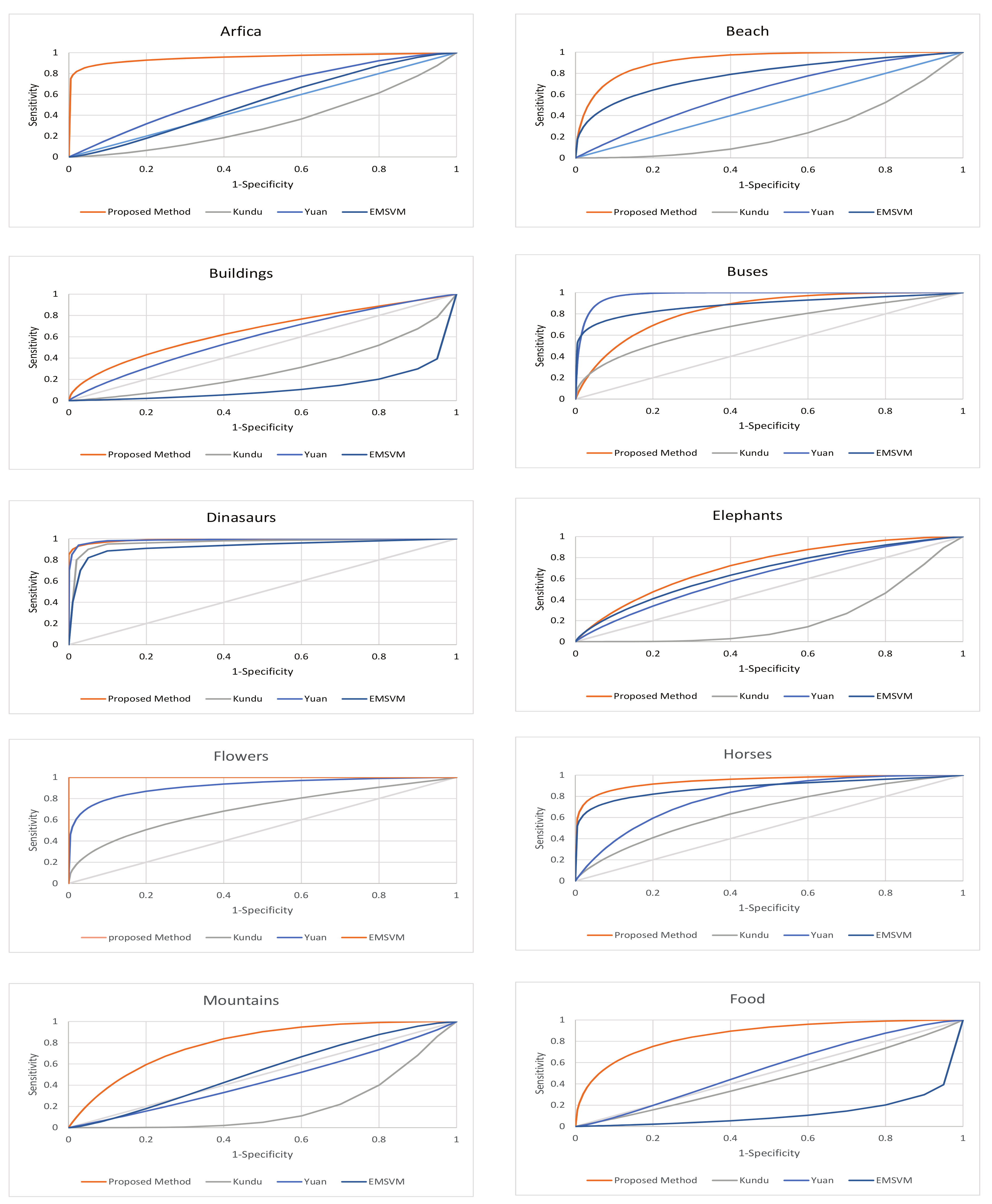
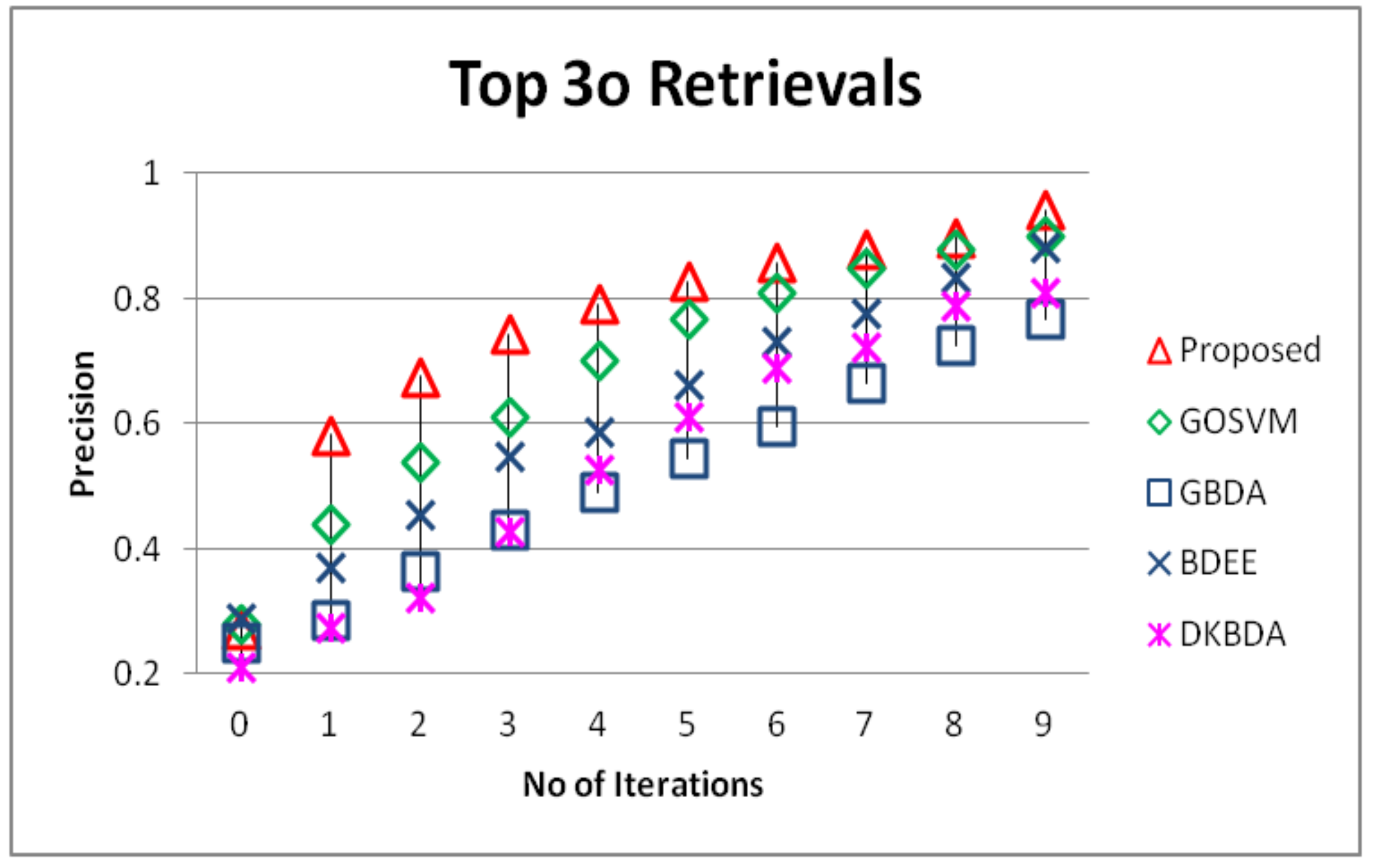
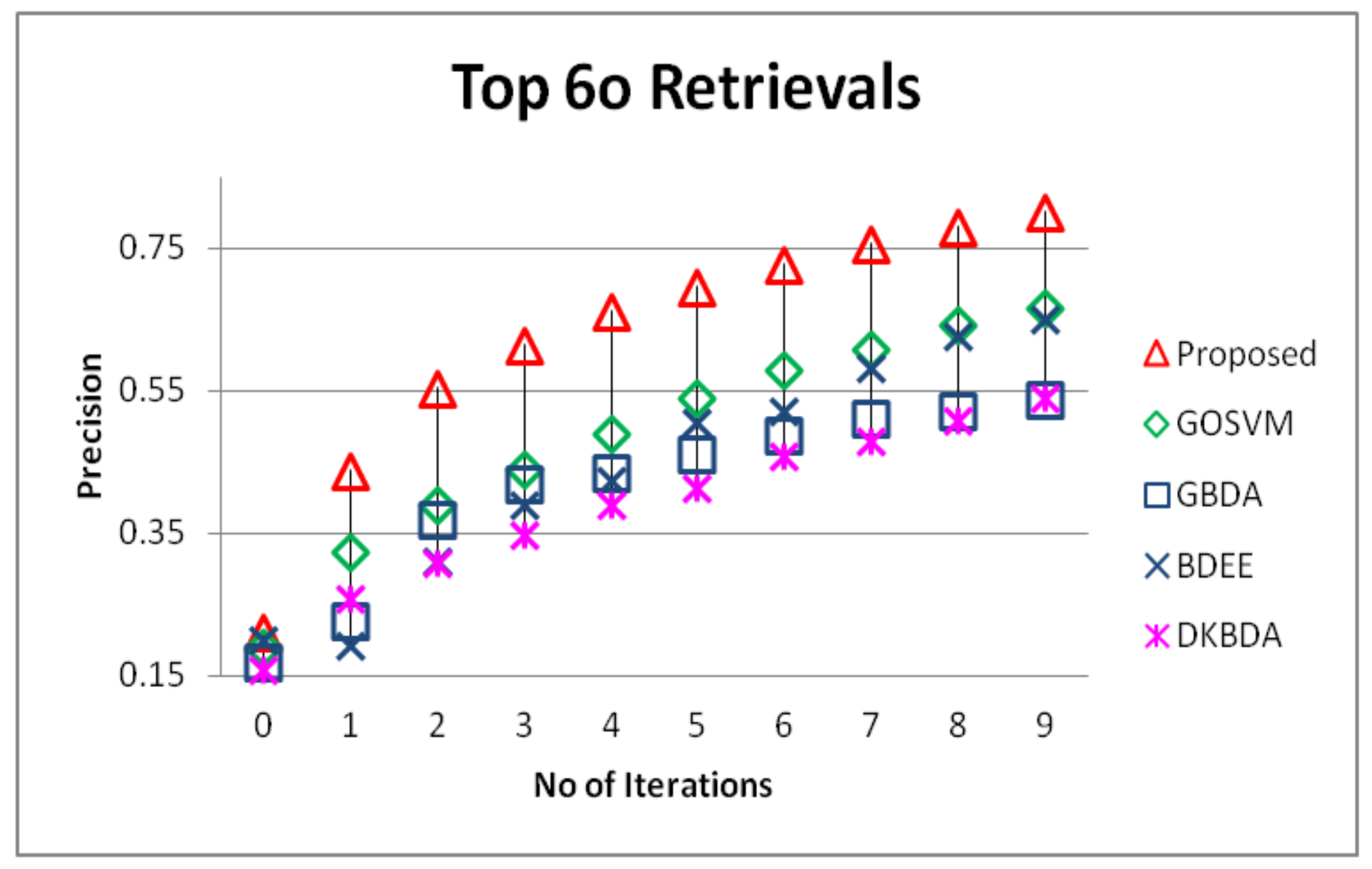
5.2. Precision and Recall Evaluation
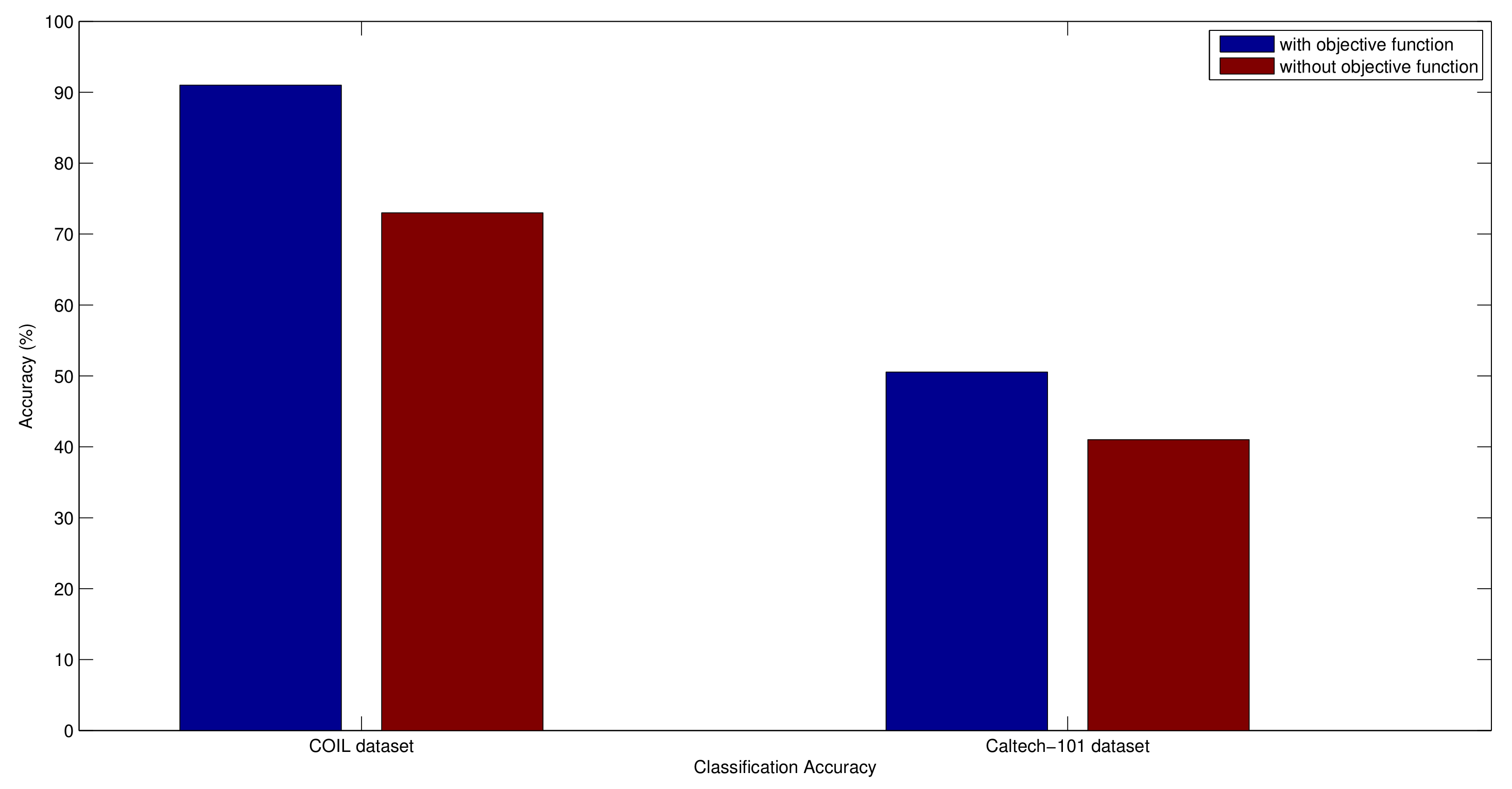
5.3. Bagging Impact
5.4. Performance Evaluation in Imbalanced Domains
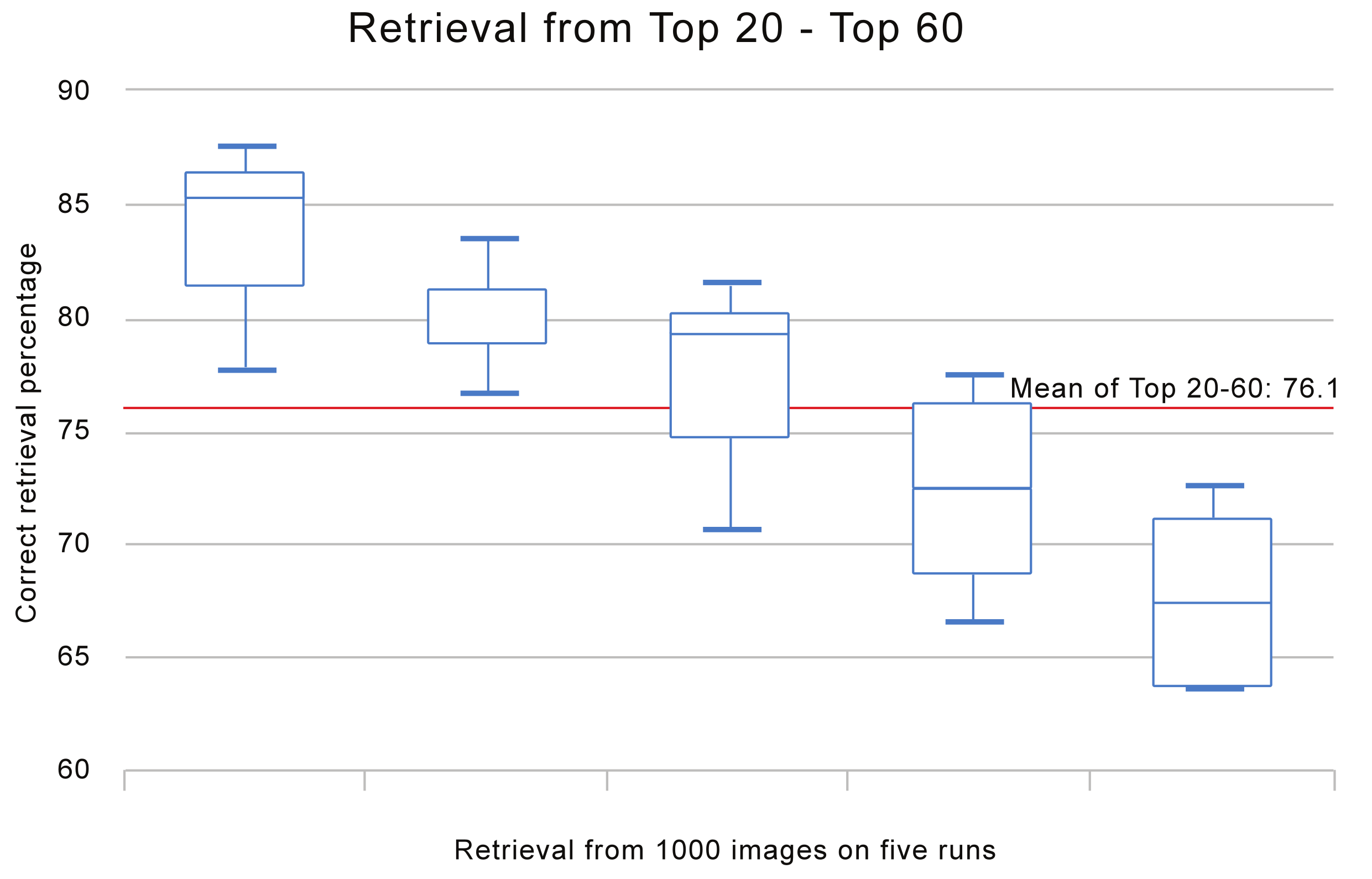
5.5. Relevance Feedback
| Algorithm 5 The relevance feedback algorithm. |
| Input: Positive set , negative set , weak classifier (SVM), (neural networks), integer = 1 (number of generated classifiers) and the test sample x Output: Classifier |
|
Experimental Details
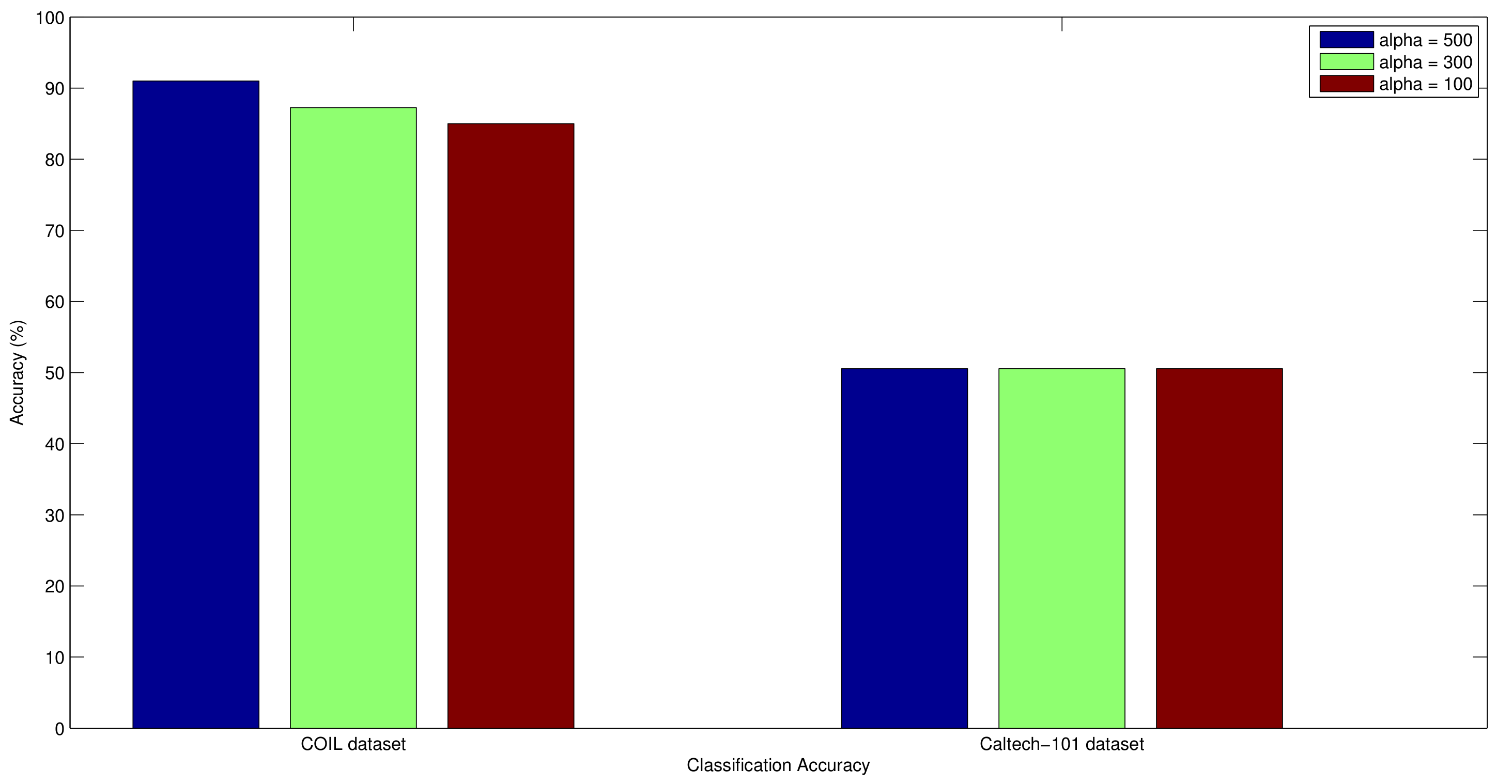
5.6. Genetic Algorithm Evaluation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smeulders, A.W.; Worring, M.; Santini, S.; Gupta, A.; Jain, R. Content-based image retrieval at the end of the early years. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1349–1380. [Google Scholar] [CrossRef]
- Hafiane, A.; Chaudhuri, S.; Seetharaman, G.; Zavidovique, B. Region-based CBIR in GIS with local space filling curves to spatial representation. Pattern Recognit. Lett. 2006, 27, 259–267. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C. An interactive semantic video mining and retrieval platform—Application in transportation surveillance video for incident detection. In Proceedings of the ICDM’06, IEEE Sixth International Conference on Data Mining, Hong Kong, China, 18–22 December 2006; pp. 129–138. [Google Scholar]
- Bian, W.; Tao, D. Biased discriminant Euclidean embedding for content-based image retrieval. IEEE Trans. Image Process. 2010, 19, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Saadatmand-Tarzjan, M.; Moghaddam, H.A. A novel evolutionary approach for optimizing content-based image indexing algorithms. IEEE Trans. Syst. Man, Cybern. B Cybern. 2007, 37, 139–153. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Medasani, S.; Jung, S.H.; Choi, Y.S.; Balasubramaniam, R. Content-based image retrieval based on a fuzzy approach. IEEE Trans. Knowl. Data Eng. 2004, 16, 1185–1199. [Google Scholar] [CrossRef]
- Demir, B.; Bruzzone, L. A novel active learning method in relevance feedback for content-based remote sensing image retrieval. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2323–2334. [Google Scholar] [CrossRef]
- Ashraf, R.; Bashir, K.; Mahmood, T. Content-based Image Retrieval by Exploring Bandletized Regions through Support Vector Machines. J. Inf. Sci. Eng. 2016, 32, 245–269. [Google Scholar]
- Le, T.M. Clustering Binary Signature Applied in Content-Based Image Retrieval. In New Advances in Information Systems and Technologies; Springer: Cham, Switzerland, 2016; pp. 233–242. [Google Scholar]
- Zhuang, Y.T.; Yang, Y.; Wu, F. Mining semantic correlation of heterogeneous multimedia data for cross-media retrieval. IEEE Trans. Multimedia 2008, 10, 221–229. [Google Scholar] [CrossRef]
- Xue, H.; Chen, S.; Yang, Q. Structural regularized support vector machine: A framework for structural large margin classifier. IEEE Trans. Neural Netw. 2011, 22, 573–587. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Liu, G.; Wang, S.; Zhang, J.; Zheng, K. Graph-based clustering and ranking for diversified image search. Multimed. Syst. 2014, 23, 41–52. [Google Scholar] [CrossRef]
- Wang, S.; Chang, X.; Li, X.; Sheng, Q.Z.; Chen, W. Multi-task Support Vector Machines for Feature Selection with Shared Knowledge Discovery. Signal Process. 2014, 120, 746–753. [Google Scholar] [CrossRef]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A review on ensembles for the class imbalance problem: Bagging-, boosting-, and hybrid-based approaches. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Irtaza, A.; Jaffar, M.A. Categorical image retrieval through genetically optimized support vector machines (GOSVM) and hybrid texture features. Signal Image Video Process. 2015, 9, 1503–1519. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, X. 10 challenging problems in data mining research. Int. J. Inf. Technol. Decis. Mak. 2006, 5, 597–604. [Google Scholar] [CrossRef]
- Qi, G.J.; Aggarwal, C.; Rui, Y.; Tian, Q.; Chang, S.; Huang, T. Towards cross-category knowledge propagation for learning visual concepts. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 897–904. [Google Scholar]
- Yang, L.; Gong, W.; Gu, X.; Li, W.; Liu, Y. Bagging null space locality preserving discriminant classifiers for face recognition. Pattern Recognit. 2009, 42, 1853–1858. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, P.; Liu, W.; Zou, L. SVM classification for imbalanced data using conformal kernel transformation. In Proceedings of the 2014 IEEE International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2894–2900. [Google Scholar]
- Maratea, A.; Petrosino, A.; Manzo, M. Adjusted F-measure and kernel scaling for imbalanced data learning. Inf. Sci. 2014, 257, 331–341. [Google Scholar] [CrossRef]
- Tao, D.; Tang, X.; Li, X.; Wu, X. Asymmetric bagging and random subspace for support vector machines-based relevance feedback in image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1088–1099. [Google Scholar] [PubMed]
- Wang, X.Y.; Chen, J.W.; Yang, H.Y. A new integrated SVM classifiers for relevance feedback content-based image retrieval using EM parameter estimation. Appl. Soft Comput. 2011, 11, 2787–2804. [Google Scholar] [CrossRef]
- Chang, E.Y. Imbalanced Data Learning. In Foundations of Large-Scale Multimedia Information Management and Retrieval; Springer: New York, NY, USA, 2011; pp. 191–211. [Google Scholar]
- Yuan, B.; Ma, X. Sampling+ reweighting: Boosting the performance of AdaBoost on imbalanced datasets. In Proceedings of the 2012 IEEE International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–6. [Google Scholar]
- Belattar, K.; Mostefai, S.; Draa, A. A Hybrid GA-LDA Scheme for Feature Selection in Content-Based Image Retrieval. Int. J. Appl. Metaheuristic Comput. 2018, 9, 48–71. [Google Scholar] [CrossRef]
- Luong, A.V.; Nguyen, T.T.; Pham, X.C.; Nguyen, T.T.T.; Liew, A.W.C.; Stantic, B. Automatic Image Region Annotation by Genetic Algorithm-Based Joint Classifier and Feature Selection in Ensemble System. In Intelligent Information and Database Systems, Proceedings of the 10th Asian Conference on Intelligent Information and Database Systems, Dong Hoi City, Vietnam, 19–21 March 2018; Springer: Cham, Switzerland, 2018; pp. 599–609. [Google Scholar]
- Irtaza, A.; Jaffar, M.A.; Muhammad, M.S. Content based image retrieval in a web 3.0 environment. Multimed. Tools Appl. 2015, 74, 5055–5072. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Multiclass imbalance problems: Analysis and potential solutions. IEEE Trans. Syst. Man, Cybern B, Cybern. 2012, 42, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Galar, M.; Fernández, A.; Barrenechea, E.; Herrera, F. Eusboost: Enhancing ensembles for highly imbalanced data-sets by evolutionary undersampling. Pattern Recognit. 2013, 46, 3460–3471. [Google Scholar] [CrossRef]
- Lam, L.; Suen, C.Y. Optimal combinations of pattern classifiers. Pattern Recognit. Lett. 1995, 16, 945–954. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems. MCS 2000. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1857, pp. 1–15. [Google Scholar]
- Meynet, J. Information Theoretic Combination of Classifiers with Application to Face Detection. Ph.D. Thesis, Pennsylvania State University, Pennsylvania, PA, USA, 2007. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Oza, N.C.; Tumer, K. Classifier ensembles: Select real-world applications. Inf. Fusion 2008, 9, 4–20. [Google Scholar] [CrossRef]
- Ma, J.; Plonka, G. The curvelet transform. IEEE Signal Process. Mag. 2010, 27, 118–133. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y. A comparative study of wavelet and curvelet transform for face recognition. In Proceedings of the 3rd International Congress on Image and Signal Processing (CISP), Yantai, China, 16–18 October 2010; Volume 4, pp. 1718–1722. [Google Scholar]
- Herrera, F.; Lozano, M.; Sánchez, A.M. Hybrid crossover operators for real-coded genetic algorithms: An experimental study. Soft Comput. 2005, 9, 280–298. [Google Scholar] [CrossRef]
- Arevalillo-Herráez, M.; Ferri, F.J.; Moreno-Picot, S. Distance-based relevance feedback using a hybrid interactive genetic algorithm for image retrieval. Appl. Soft Comput. 2011, 11, 1782–1791. [Google Scholar] [CrossRef]
- Stejić, Z.; Takama, Y.; Hirota, K. Genetic algorithm-based relevance feedback for image retrieval using local similarity patterns. Inf. Process. Manag. 2003, 39, 1–23. [Google Scholar] [CrossRef]
- Weber, M.; Crilly, P.; Blass, W.E. Adaptive noise filtering using an error-backpropagation neural network. IEEE Trans. Instrum. Meas. 1991, 40, 820–825. [Google Scholar] [CrossRef]
- Lai, C.C.; Chen, Y.C. A user-oriented image retrieval system based on interactive genetic algorithm. IEEE Trans. Instrum. Meas. 2011, 60, 3318–3325. [Google Scholar] [CrossRef]
- Yildizer, E.; Balci, A.M.; Hassan, M.; Alhajj, R. Efficient content-based image retrieval using multiple support vector machines ensemble. Expert Syst. Appl. 2012, 39, 2385–2396. [Google Scholar] [CrossRef]
- Youssef, S.M. ICTEDCT-CBIR: Integrating curvelet transform with enhanced dominant colors extraction and texture analysis for efficient content-based image retrieval. Comput. Electr. Eng. 2012, 38, 1358–1376. [Google Scholar] [CrossRef]
- Han, K.; Rezende, R.S.; Ham, B.; Wong, K.Y.K.; Cho, M.; Schmid, C.; Ponce, J. SCNet: Learning Semantic Correspondence. arXiv, 2017; arXiv:1705.04043. [Google Scholar]
- Dubey, S.R.; Singh, S.K.; Singh, R.K. Multichannel decoded local binary patterns for content-based image retrieval. IEEE Trans. Image Process. 2016, 25, 4018–4032. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Wu, J.; Yuan, J. mCENTRIST: A multi-channel feature generation mechanism for scene categorization. IEEE Trans. Image Process. 2014, 23, 823–836. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zeng, F.Z.; Zhao, H.M.; Murray, P.; Ren, J. Hierarchical visual perception and two-dimensional compressive sensing for effective content-based color image retrieval. Cogn. Comput. 2016, 5, 877–889. [Google Scholar] [CrossRef]
- Shrivastava, N.; Tyagi, V. An efficient technique for retrieval of color images in large databases. Comput. Electr. Eng. 2015, 46, 314–327. [Google Scholar] [CrossRef]
- Kundu, M.K.; Chowdhury, M.; Bulò, S.R. A graph-based relevance feedback mechanism in content-based image retrieval. Knowl. Based Syst. 2015, 73, 254–264. [Google Scholar] [CrossRef]
- Zeng, S.; Huang, R.; Wang, H.; Kang, Z. Image retrieval using spatiograms of colors quantized by Gaussian Mixture Models. Neurocomputing 2016, 171, 673–684. [Google Scholar] [CrossRef]
- Walia, E.; Pal, A. Fusion framework for effective color image retrieval. J. Vis. Commun. Image Represent. 2014, 25, 1335–1348. [Google Scholar] [CrossRef]
- Ashraf, R.; Bashir, K.; Irtaza, A.; Mahmood, M.T. Content based image retrieval using embedded neural networks with bandletized regions. Entropy 2015, 17, 3552–3580. [Google Scholar] [CrossRef]
- ElAlami, M.E. A new matching strategy for content based image retrieval system. Appl. Soft Comput. 2014, 14, 407–418. [Google Scholar] [CrossRef]
- Yuan, X.; Yu, J.; Qin, Z.; Wan, T. A SIFT-LBP image retrieval model based on bag of features. In Proceedings of the IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011. [Google Scholar]
- Zhang, L.; Wang, L.; Lin, W. Generalized biased discriminant analysis for content-based image retrieval. IEEE Trans. Syst. Man, Cybern B, Cybern. 2012, 42, 282–290. [Google Scholar] [CrossRef] [PubMed]
- Tao, D.; Tang, X.; Li, X.; Rui, Y. Direct kernel biased discriminant analysis: A new content-based image retrieval relevance feedback algorithm. IEEE Trans. Multimed. 2006, 8, 716–727. [Google Scholar]


| INPUT | |||
|---|---|---|---|
| Input: | dim() = N | (I.1) | |
| MIDDLE (HIDDEN) LAYER | |||
| Input: | = M | (I.2) | |
| Output: | = M | (I.3) | |
| U: | weight matrix | ||
| f: | hidden layer activation function | ||
| : | thresholds | ||
| OUTPUT LAYER | |||
| Input: | (I.4) | ||
| Output: | = 1 | (I.5) | |
| W: | weight matrix | ||
| g: | output layer activation function | ||
| : | thresholds | ||
| ERROR CORRECTION | |||
| MSE: | E = 1/2() | (I.6) | |
| = − | (I.6) | ||
| = | (I.7) | ||
| = − | (I.8) |
| Class | Proposed | Dubey | Xiao | Zhou | Shriv | Kundu | Zeng | Walia | Ash | ElAl |
|---|---|---|---|---|---|---|---|---|---|---|
| [45] | [46] | [47] | [48] | [49] | [50] | [51] | [52] | [53] | ||
| Africa | 0.83 | 0.75 | 0.67 | 0.85 | 0.74 | 0.44 | 0.72 | 0.51 | 0.55 | 0.72 |
| Beach | 0.72 | 0.55 | 0.60 | 0.53 | 0.58 | 0.32 | 0.65 | 0.90 | 0.63 | 0.59 |
| Buildings | 0.86 | 0.67 | 0.56 | 0.72 | 0.62 | 0.52 | 0.70 | 0.58 | 0.67 | 0.58 |
| Buses | 1.00 | 0.95 | 0.96 | 0.85 | 0.80 | 0.60 | 0.89 | 0.78 | 0.84 | 0.89 |
| Dinosaurs | 0.97 | 0.97 | 0.98 | 1.00 | 1.00 | 0.40 | 1.00 | 1.00 | 0.89 | 0.99 |
| Elephants | 0.82 | 0.63 | 0.53 | 0.68 | 0.75 | 0.80 | 0.70 | 0.84 | 0.77 | 0.70 |
| Flowers | 0.86 | 0.93 | 0.93 | 0.94 | 0.92 | 0.57 | 0.94 | 1.00 | 0.90 | 0.92 |
| Horses | 0.82 | 0.89 | 0.82 | 0.99 | 0.89 | 0.75 | 0.91 | 1.00 | 0.81 | 0.85 |
| Mountains | 0.69 | 0.45 | 0.46 | 0.55 | 0.56 | 0.57 | 0.72 | 0.84 | 0.71 | 0.56 |
| Food | 0.90 | 0.70 | 0.58 | 0.86 | 0.80 | 0.56 | 0.78 | 0.38 | 0.71 | 0.77 |
| Mean | 0.847 | 0.749 | 0.709 | 0.797 | 0.766 | 0.553 | 0.801 | 0.783 | 0.748 | 0.757 |
| Class | Proposed | Dubey | Xiao | Zhou | Shriv | Kundu | Zeng | Walia | Ash | ElAl |
|---|---|---|---|---|---|---|---|---|---|---|
| [45] | [46] | [47] | [48] | [49] | [50] | [51] | [52] | [53] | ||
| Africa | 0.17 | 0.15 | 0.13 | 0.17 | 0.15 | 0.09 | 0.14 | 0.10 | 0.11 | 0.14 |
| Beach | 0.14 | 0.11 | 0.12 | 0.11 | 0.12 | 0.06 | 0.13 | 0.18 | 0.13 | 0.12 |
| Buildings | 0.17 | 0.13 | 0.11 | 0.14 | 0.12 | 0.10 | 0.14 | 0.12 | 0.13 | 0.12 |
| Buses | 0.20 | 0.19 | 0.19 | 0.17 | 0.16 | 0.12 | 0.18 | 0.16 | 0.17 | 0.18 |
| Dinosaurs | 0.19 | 0.19 | 0.20 | 0.20 | 0.20 | 0.08 | 0.20 | 0.20 | 0.18 | 0.20 |
| Elephants | 0.16 | 0.13 | 0.11 | 0.14 | 0.15 | 0.16 | 0.14 | 0.17 | 0.15 | 0.14 |
| Flowers | 0.17 | 0.19 | 0.19 | 0.19 | 0.18 | 0.11 | 0.19 | 0.20 | 0.18 | 0.18 |
| Horses | 0.16 | 0.18 | 0.16 | 0.20 | 0.18 | 0.15 | 0.18 | 0.20 | 0.16 | 0.17 |
| Mountains | 0.14 | 0.09 | 0.05 | 0.11 | 0.11 | 0.11 | 0.14 | 0.17 | 0.14 | 0.11 |
| Food | 0.18 | 0.07 | 0.12 | 0.17 | 0.16 | 0.11 | 0.16 | 0.08 | 0.15 | 0.14 |
| Mean | 0.169 | 0.149 | 0.141 | 0.159 | 0.153 | 0.111 | 0.160 | 0.157 | 0.149 | 0.151 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irtaza, A.; Adnan, S.M.; Ahmed, K.T.; Jaffar, A.; Khan, A.; Javed, A.; Mahmood, M.T. An Ensemble Based Evolutionary Approach to the Class Imbalance Problem with Applications in CBIR. Appl. Sci. 2018, 8, 495. https://doi.org/10.3390/app8040495
Irtaza A, Adnan SM, Ahmed KT, Jaffar A, Khan A, Javed A, Mahmood MT. An Ensemble Based Evolutionary Approach to the Class Imbalance Problem with Applications in CBIR. Applied Sciences. 2018; 8(4):495. https://doi.org/10.3390/app8040495
Chicago/Turabian StyleIrtaza, Aun, Syed M. Adnan, Khawaja Tehseen Ahmed, Arfan Jaffar, Ahmad Khan, Ali Javed, and Muhammad Tariq Mahmood. 2018. "An Ensemble Based Evolutionary Approach to the Class Imbalance Problem with Applications in CBIR" Applied Sciences 8, no. 4: 495. https://doi.org/10.3390/app8040495
APA StyleIrtaza, A., Adnan, S. M., Ahmed, K. T., Jaffar, A., Khan, A., Javed, A., & Mahmood, M. T. (2018). An Ensemble Based Evolutionary Approach to the Class Imbalance Problem with Applications in CBIR. Applied Sciences, 8(4), 495. https://doi.org/10.3390/app8040495







