A Pseudo-3D Model for Electromagnetic Acoustic Transducers (EMATs)
Abstract
:1. Introduction
2. Vertical Plane Modelling
2.1. EMAT-EM Model
2.1.1. Adapted Analytical Solutions to the Vector Potential for a Straight Wire
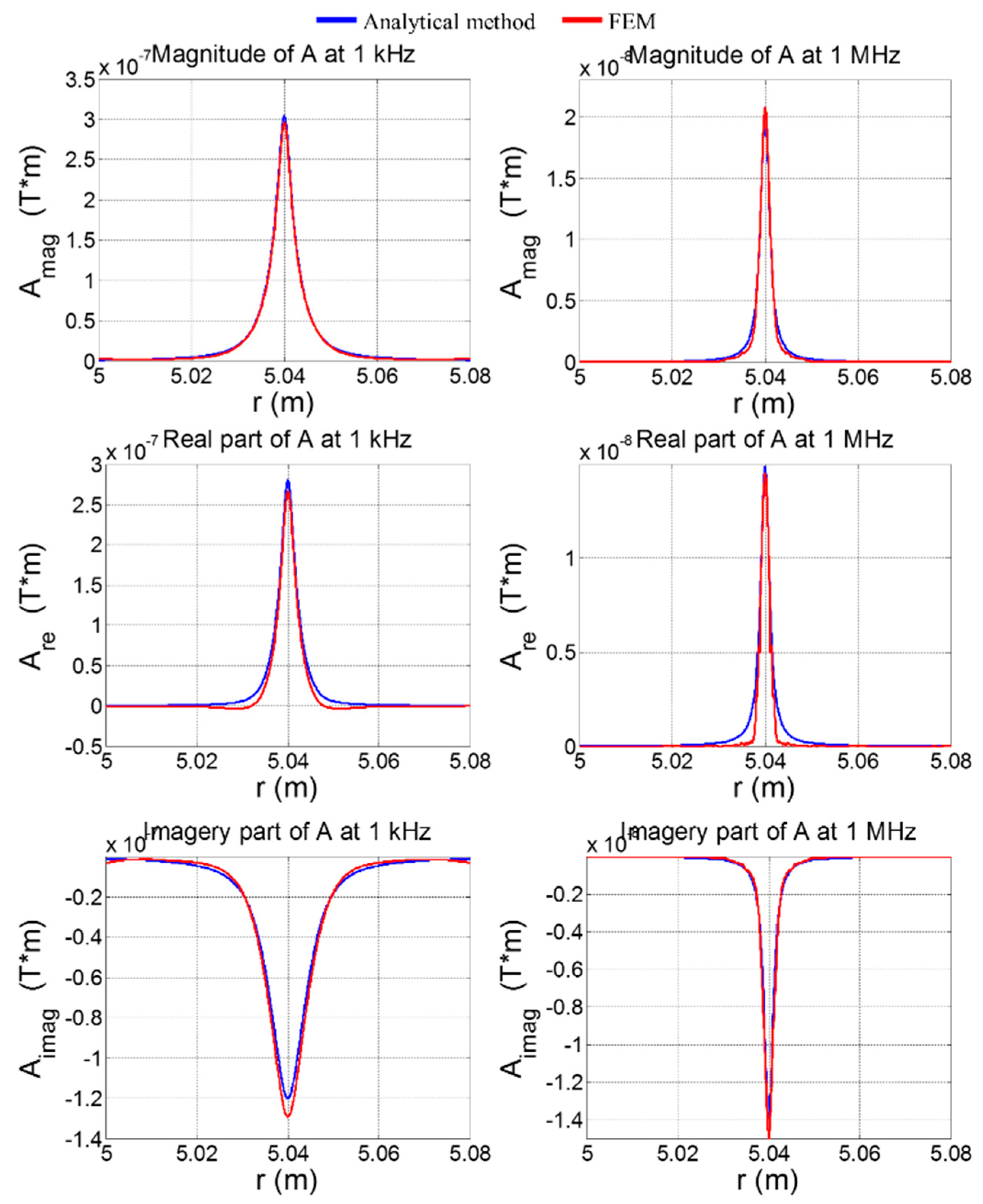
2.1.2. Comparison between the Adapted Solution and FEM
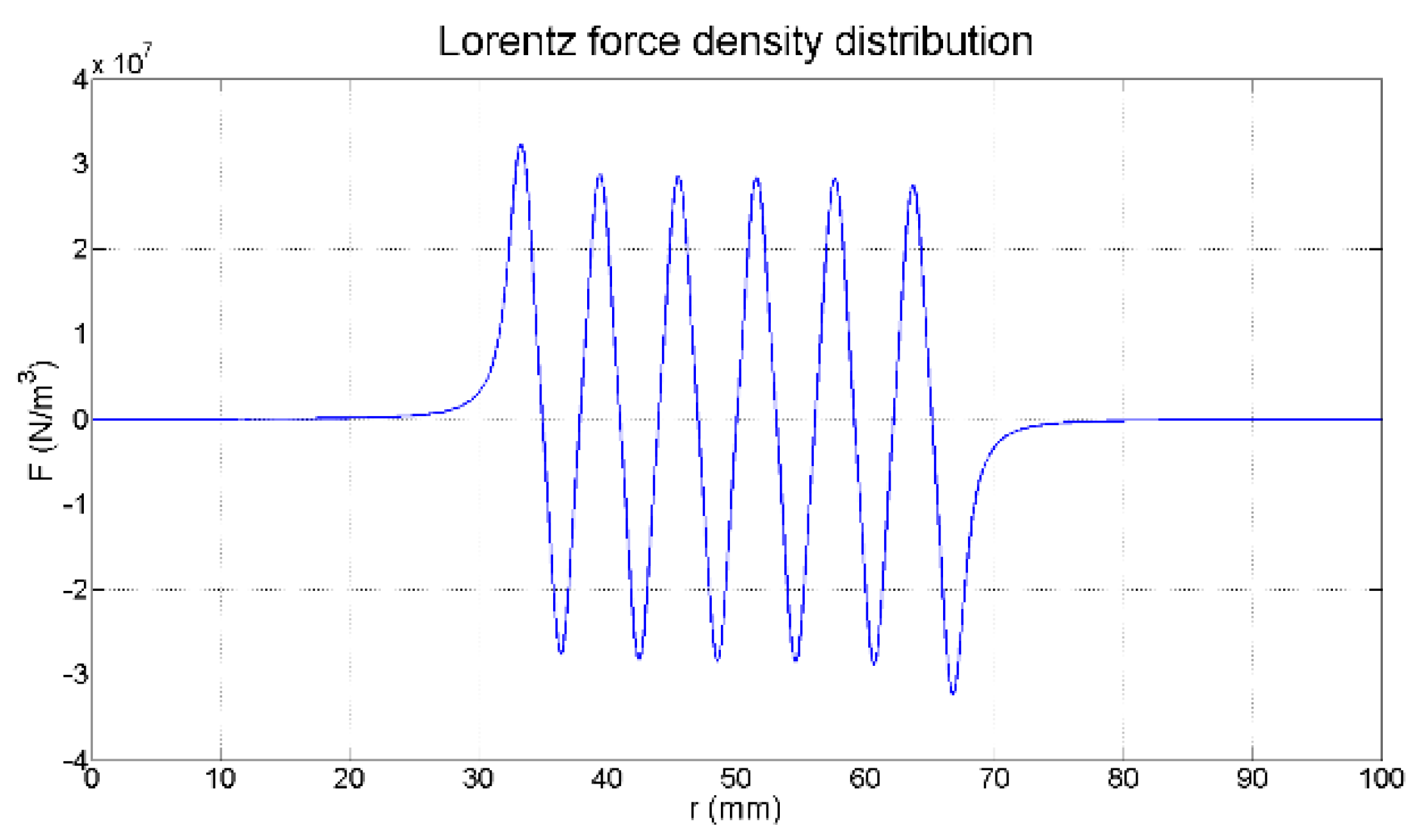
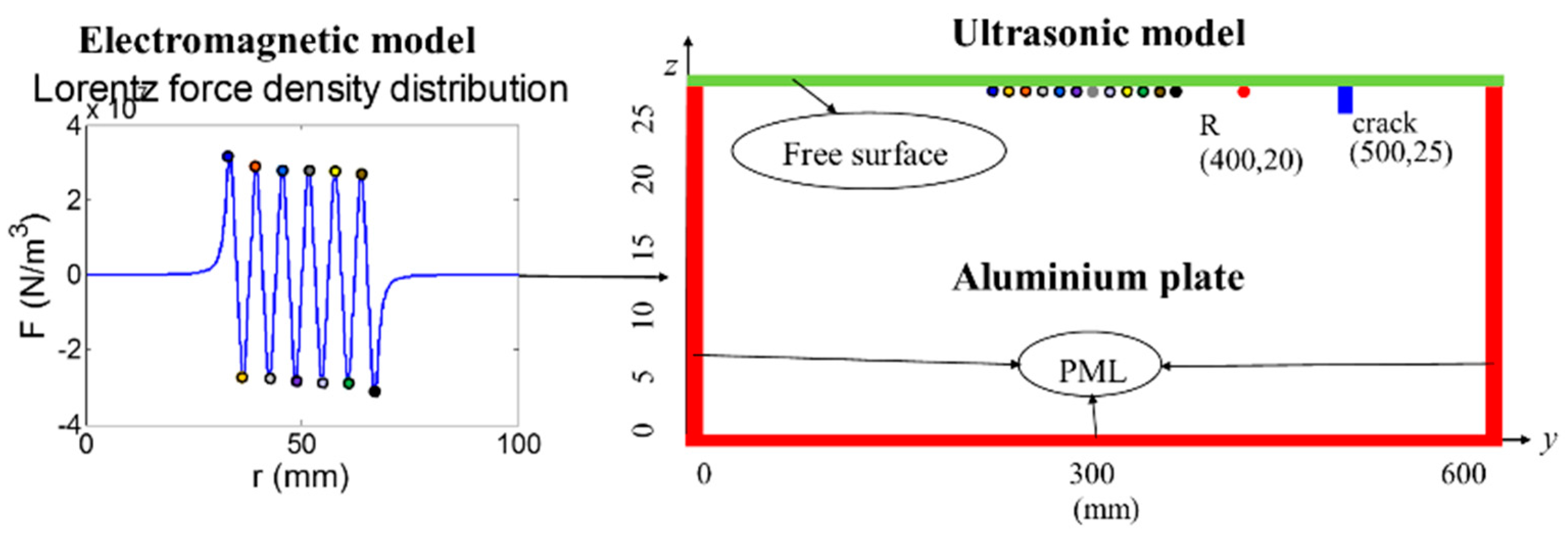
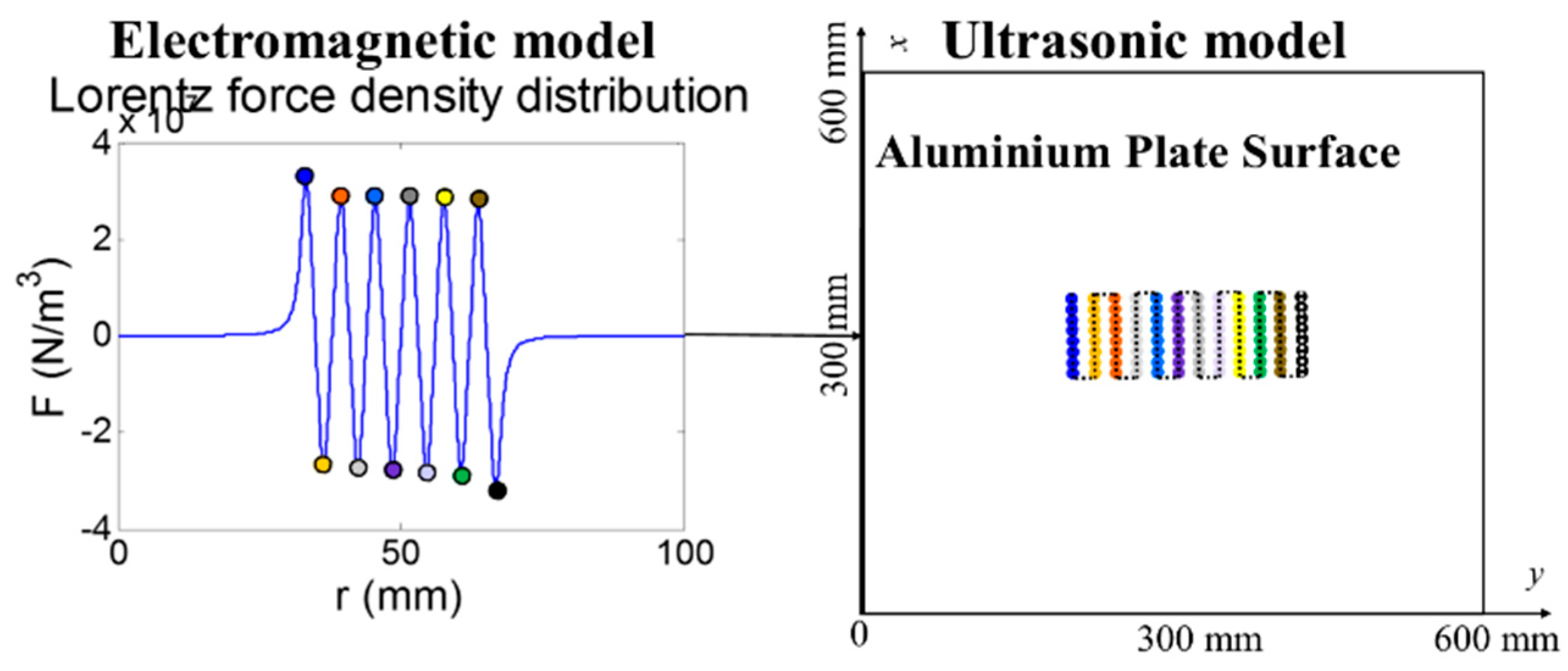
2.1.3. EMAT-Lorentz Force Calculation
2.2. EMAT-US Simulation
2.2.1. Elastodynamic Equations
2.2.2. Combination of EMAT-EM and EMAT-US Models
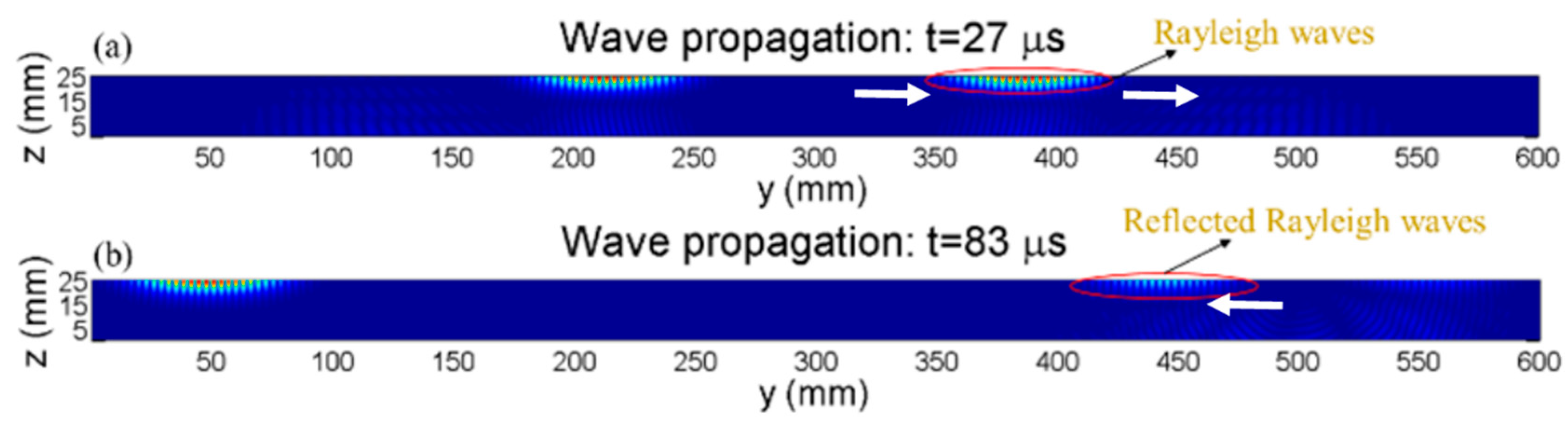
2.2.3. Wave Propagations
2.3. EMAT-Reception Simulation
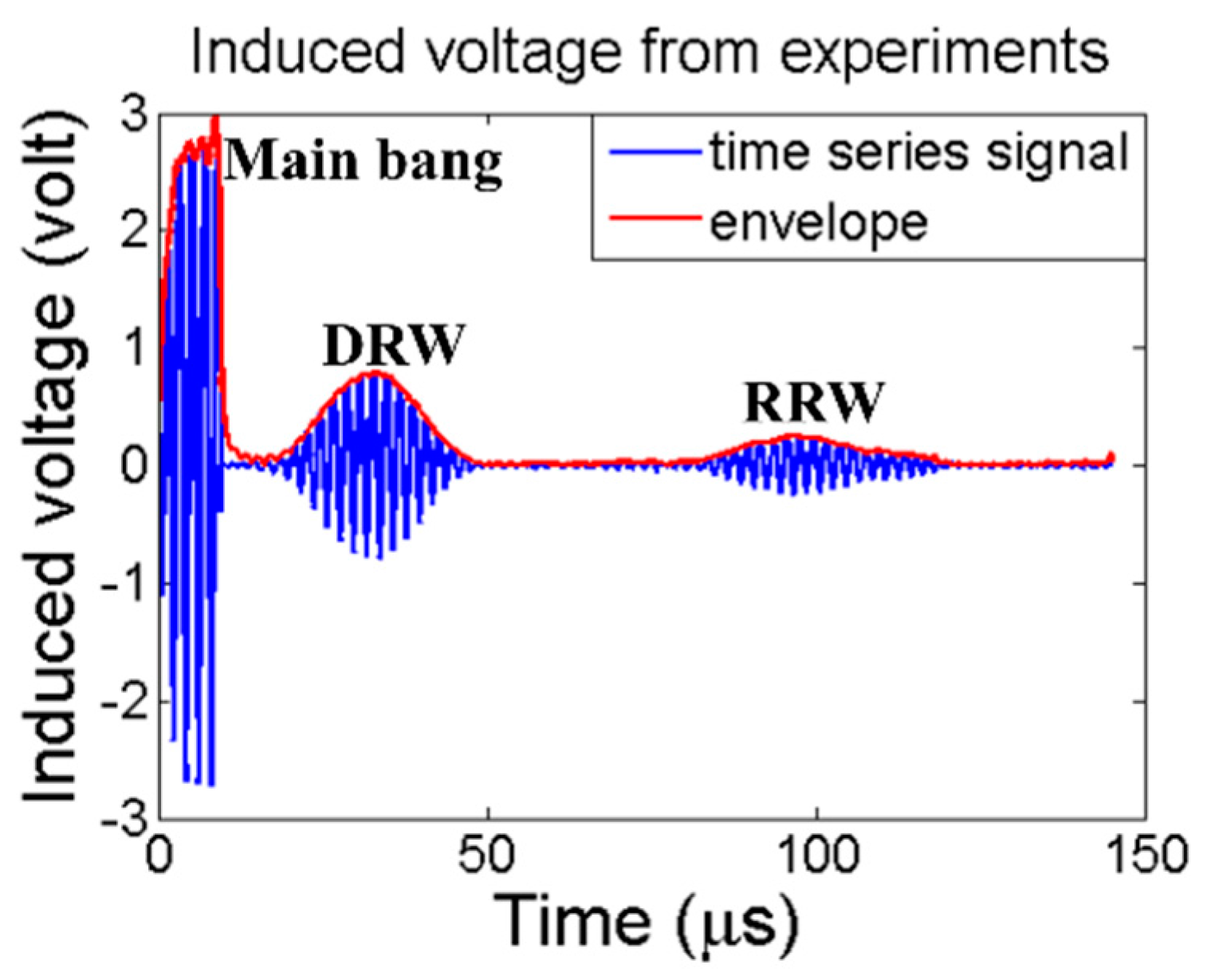
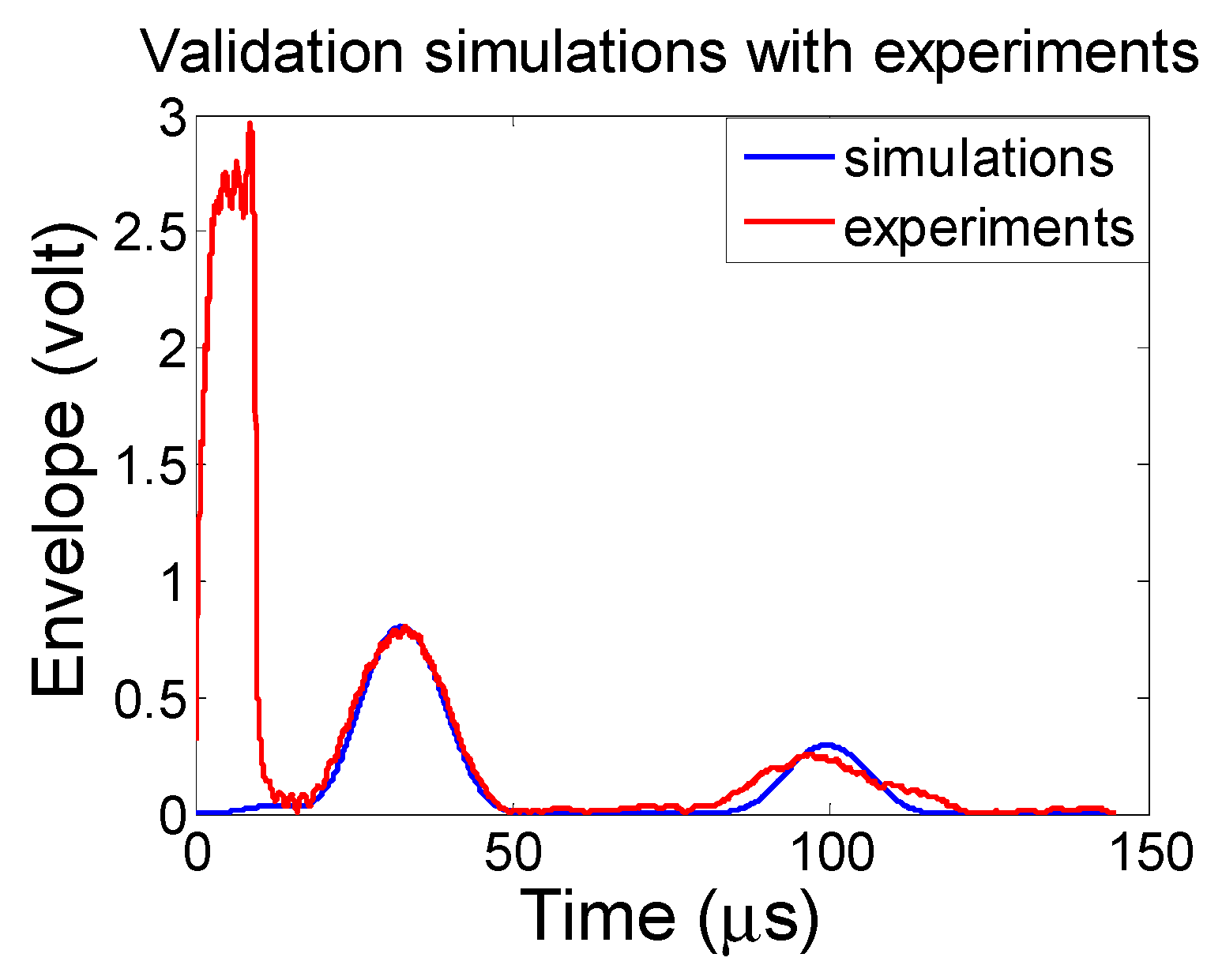
2.4. Experimental Validations
3. Horizontal Surface Plane Modelling—Directivity Analysis of Rayleigh Waves
3.1. The Analytical Solution to the Displacement of Rayleigh Waves
3.2. Linking EMAT-EM and EMAT-US Models
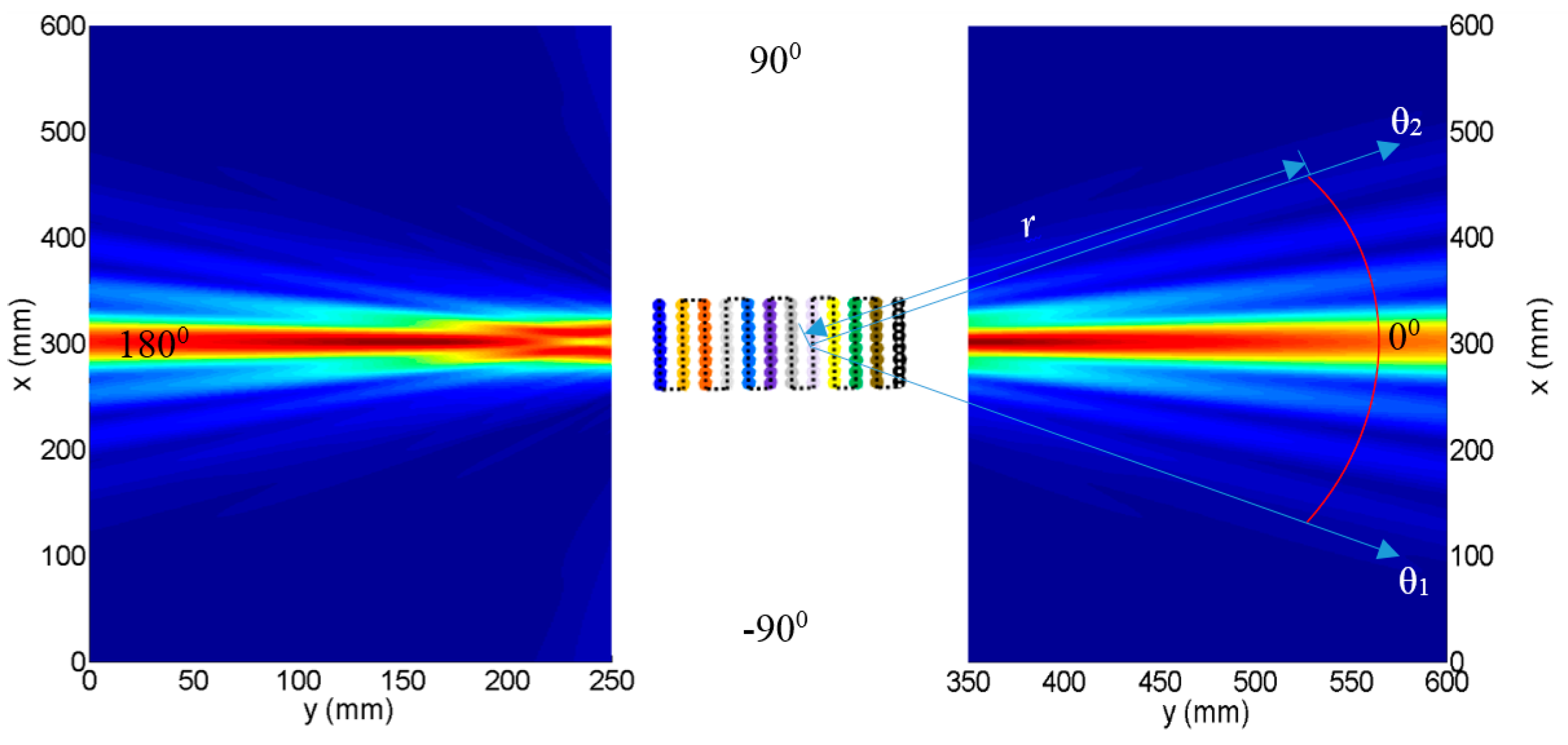
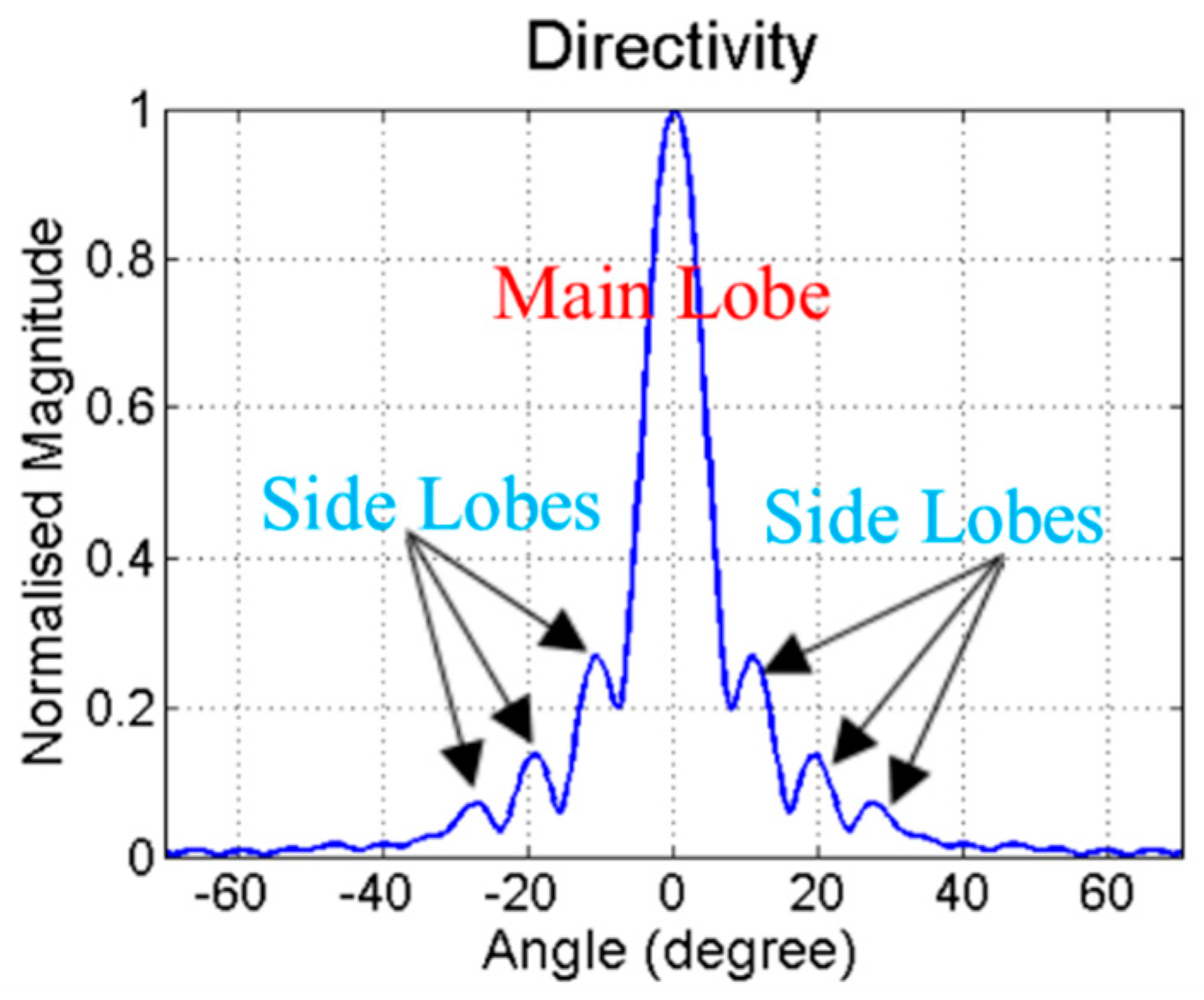
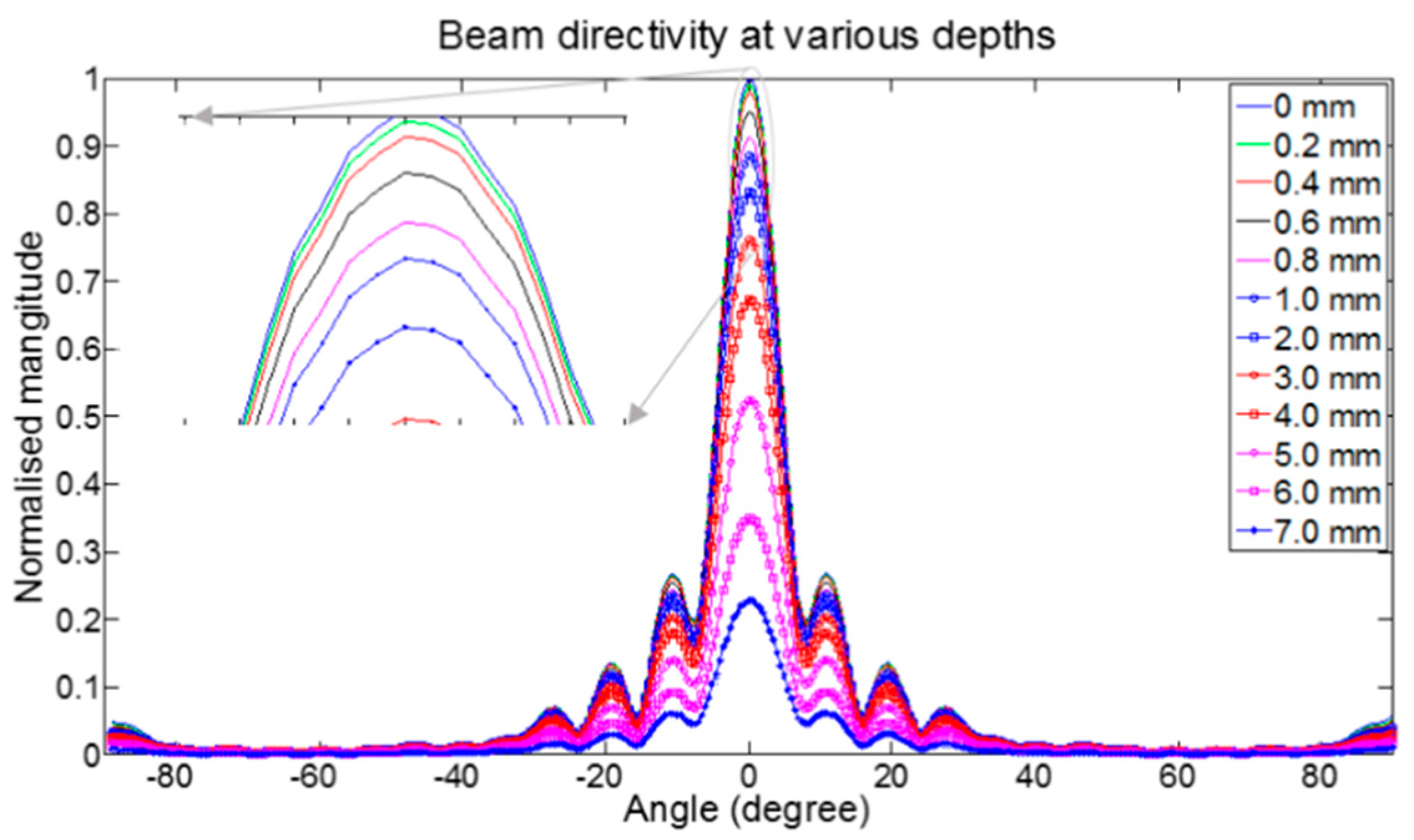
3.3. Analysis of the Beam Directivity of Rayleigh Waves
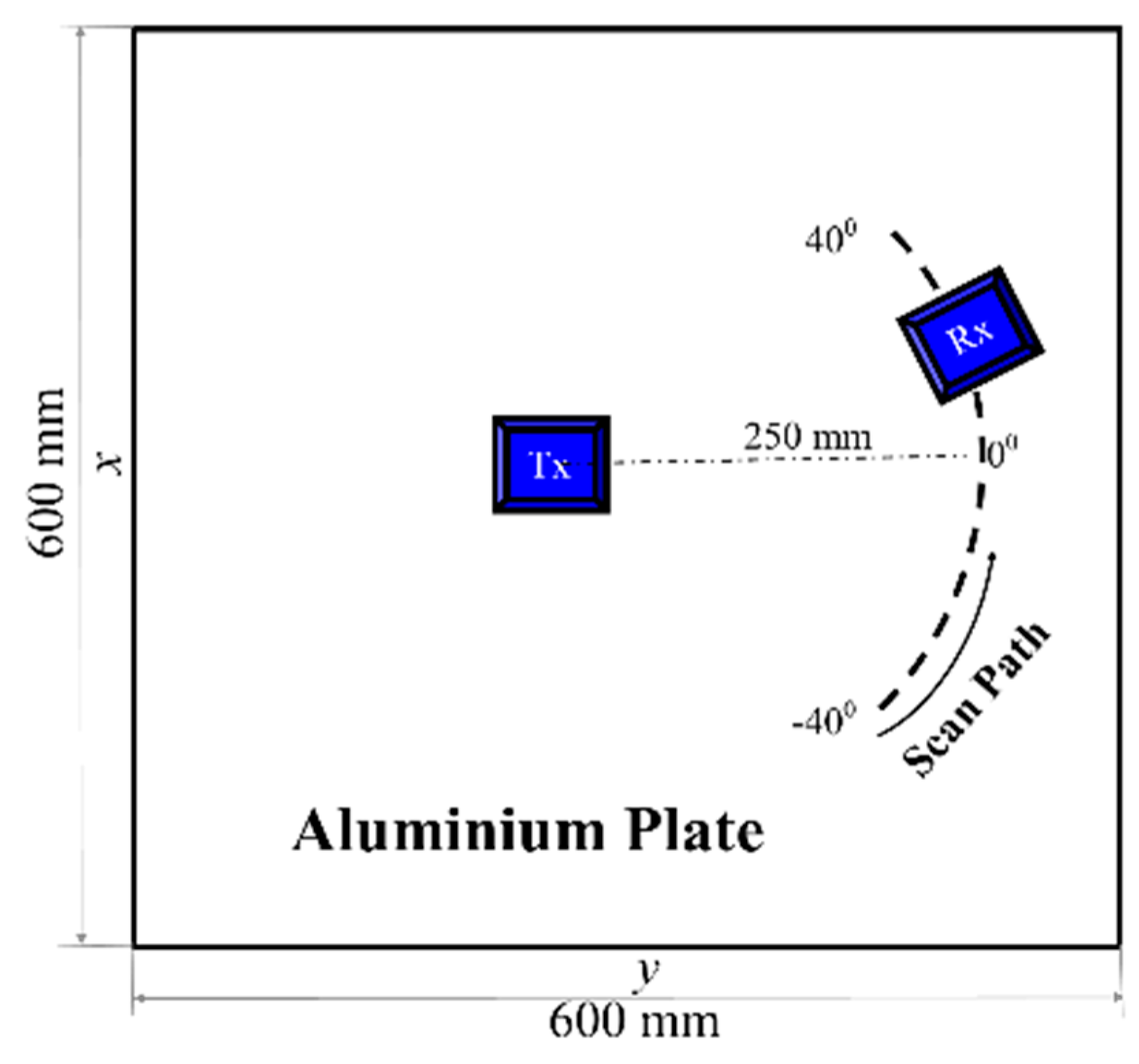
3.4. Experimental Validations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Buchner, S.P.; Miller, F.; Pouget, V.; McMorrow, D.P. Pulsed-laser testing for single-event effects investigations. IEEE Trans. Nucl. Sci. 2013, 60, 1852–1875. [Google Scholar] [CrossRef]
- Taheri, H.; Delfanian, F.; Du, J. Ultrasonic phased array techniques for composite material evaluation. J. Acoust. Soc. Am. 2013, 134, 4013. [Google Scholar] [CrossRef]
- Yin, W.; Dickinson, S.; Peyton, A. A multi-frequency impedance analysing instrument for eddy current testing. Meas. Sci. Technol. 2006, 17, 393. [Google Scholar] [CrossRef]
- Yin, W.; Peyton, A.J.; Dickinson, S.J. Simultaneous measurement of distance and thickness of a thin metal plate with an electromagnetic sensor using a simplified model. IEEE Trans. Instrum. Meas. 2004, 53, 1335–1338. [Google Scholar] [CrossRef]
- Dixon, S.; Edwards, C.; Palmer, S. High accuracy non-contact ultrasonic thickness gauging of aluminium sheet using electromagnetic acoustic transducers. Ultrasonics 2001, 39, 445–453. [Google Scholar] [CrossRef]
- Edwards, R.S.; Dixon, S.; Jian, X. Non-contact ultrasonic characterization of defects using EMATs. AIP Conf. Proc. 2005, 760, 1568. [Google Scholar]
- Edwards, R.S.; Sophian, A.; Dixon, S.; Tian, G.-Y.; Jian, X. Dual EMAT and PEC non-contact probe: Applications to defect testing. NDT E Int. 2006, 39, 45–52. [Google Scholar] [CrossRef]
- Hutchins, D.; Schindel, D. Advances in non-contact and air-coupled transducers (US materials inspection). In Proceedings of the Ultrasonics Symposium, Cannes, France, 31 October–3 November 1994; IEEE: Piscataway, NJ, USA, 1994. [Google Scholar]
- Hirao, M.; Ogi, H. EMATs for Science and Industry: Noncontacting Ultrasonic Measurements, 1st ed.; Springer Science & Business Media: New York, NY, USA, 2003; 372p. [Google Scholar]
- Jian, X.; Dixon, S.; Grattan, K.T.V.; Edwards, R.S. A model for pulsed Rayleigh wave and optimal EMAT design. Sens. Actuators A Phys. 2006, 128, 296–304. [Google Scholar] [CrossRef]
- Wang, S.; Kang, L.; Li, Z.; Zhai, G.; Zhang, L. A novel method for modeling and analysis of meander-line-coil surface wave EMATs. In Life System Modeling and Intelligent Computing; Kang, L., Fei, M., Jia, L., Irwin, G.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 467–474. [Google Scholar]
- Kang, L.; Dixon, S.; Wang, K.; Dai, J. Enhancement of signal amplitude of surface wave EMATs based on 3-D simulation analysis and orthogonal test method. NDT E Int. 2013, 59, 11–17. [Google Scholar] [CrossRef]
- Dhayalan, R.; Balasubramaniam, K. A hybrid finite element model for simulation of electromagnetic acoustic transducer (EMAT) based plate waves. NDT E Int. 2010, 43, 519–526. [Google Scholar] [CrossRef]
- Dhayalan, R.; Balasubramaniam, K. A two-stage finite element model of a meander coil electromagnetic acoustic transducer transmitter. Nondestruct. Test. Eval. 2011, 26, 101–118. [Google Scholar] [CrossRef]
- Xie, Y.; Rodriguez, D.S.; Yin, W.; Peyton, A.; Liu, Z.; Hao, J.; Zhao, Q.; Wang, B. Simulation and experimental verification of a meander-line-coil electromagnetic acoustic transducers (EMATs). In Proceedings of the Instrumentation and Measurement Technology Conference (I2MTC), Taipei, Taiwan, 23–26 May 2016; IEEE International: Piscataway, NJ, USA, 2016. [Google Scholar]
- Xie, Y.; Yin, L.; Rodriguez, S.G.; Yang, T.; Liu, Z.; Yin, W. A wholly analytical method for the simulation of an electromagnetic acoustic transducer array. Int. J. Appl. Electromagn. Mech. 2016, 51, 1–15, (Preprint). [Google Scholar] [CrossRef]
- Xie, Y.; Yin, W.; Liu, Z.; Peyton, A. Simulation of ultrasonic and EMAT arrays using FEM and FDTD. Ultrasonics 2016, 66, 154–165. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Liu, Z.; Yin, L.; Wu, J.; Deng, P.; Yin, W. Directivity analysis of Meander-Line-Coil EMATs with a wholly analytical method. Ultrasonics 2017, 73, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Kang, L.; Li, Z.; Zhai, G.; Zhang, L. 3-D modeling and analysis of meander-line-coil surface wave EMATs. Mechatronics 2012, 22, 653–660. [Google Scholar] [CrossRef]
- Dodd, C.; Deeds, W. Analytical Solutions to Eddy-Current Probe-Coil Problems. J. Appl. Phys. 1968, 39, 2829–2838. [Google Scholar] [CrossRef]
- Jian, X.; Dixon, S.; Quirk, K.; Grattan, K.T.V. Electromagnetic acoustic transducers for in-and out-of plane ultrasonic wave detection. Sens. Actuators A Phys. 2008, 148, 51–56. [Google Scholar] [CrossRef]
- Haskell, N. Radiation pattern of Rayleigh waves from a fault of arbitrary dip and direction of motion in a homogeneous medium. Bull. Seismol. Soc. Am. 1963, 53, 619–642. [Google Scholar]
- Haskell, N. Radiation pattern of surface waves from point sources in a multi-layered medium. Bull. Seismol. Soc. Am. 1964, 54, 377–393. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Dover Publication: New York, NY, USA, 1944; 643p. [Google Scholar]






| Description | Symbol | Value |
|---|---|---|
| Length of the aluminium plate | Y | 600 mm |
| Width of the aluminium plate | X | 600 mm |
| Field spatial step | ∆xf | 1 mm |
| Length of the meander-line-coil | L | 50 mm |
| Source spatial step for each wire | ∆xs | 0.2 mm |
| Density of the aluminium plate | ρ | 2700 kg/m3 |
| Frequency | f | 483 kHz |
| Longitudinal waves’ velocity | Cl | 6.375 mm/ |
| Shear waves’ velocity | Cs | 3.14 mm/ |
| Rayleigh waves’ velocity | Cr | 2.93 mm/ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, W.; Xie, Y.; Qu, Z.; Liu, Z. A Pseudo-3D Model for Electromagnetic Acoustic Transducers (EMATs). Appl. Sci. 2018, 8, 450. https://doi.org/10.3390/app8030450
Yin W, Xie Y, Qu Z, Liu Z. A Pseudo-3D Model for Electromagnetic Acoustic Transducers (EMATs). Applied Sciences. 2018; 8(3):450. https://doi.org/10.3390/app8030450
Chicago/Turabian StyleYin, Wuliang, Yuedong Xie, Zhigang Qu, and Zenghua Liu. 2018. "A Pseudo-3D Model for Electromagnetic Acoustic Transducers (EMATs)" Applied Sciences 8, no. 3: 450. https://doi.org/10.3390/app8030450
APA StyleYin, W., Xie, Y., Qu, Z., & Liu, Z. (2018). A Pseudo-3D Model for Electromagnetic Acoustic Transducers (EMATs). Applied Sciences, 8(3), 450. https://doi.org/10.3390/app8030450






