Gauge-Invariant Formulation of Time-Dependent Configuration Interaction Singles Method
Abstract
1. Introduction
2. Theory
2.1. System Hamiltonian and Gauge Transformation
2.2. Review of CI Coefficient-Based TDCIS with Fixed Orbitals
2.3. Review of Channel Orbital-Based TDCIS with Fixed Orbitals
2.4. Channel Orbital-Based TDCIS in the Velocity Gauge with Rotated Orbitals
2.5. Evaluation of the Time Derivative of an Observable
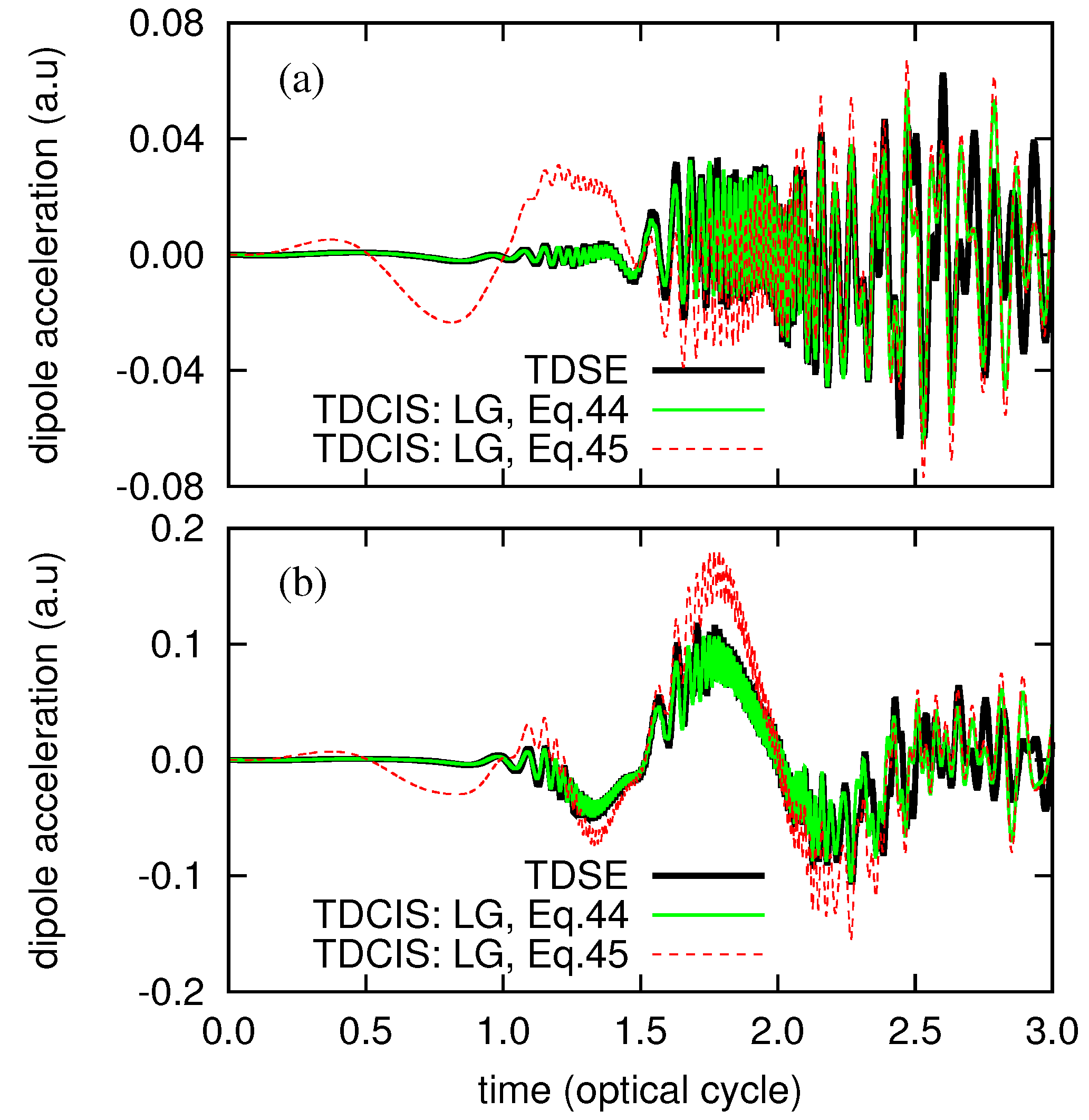
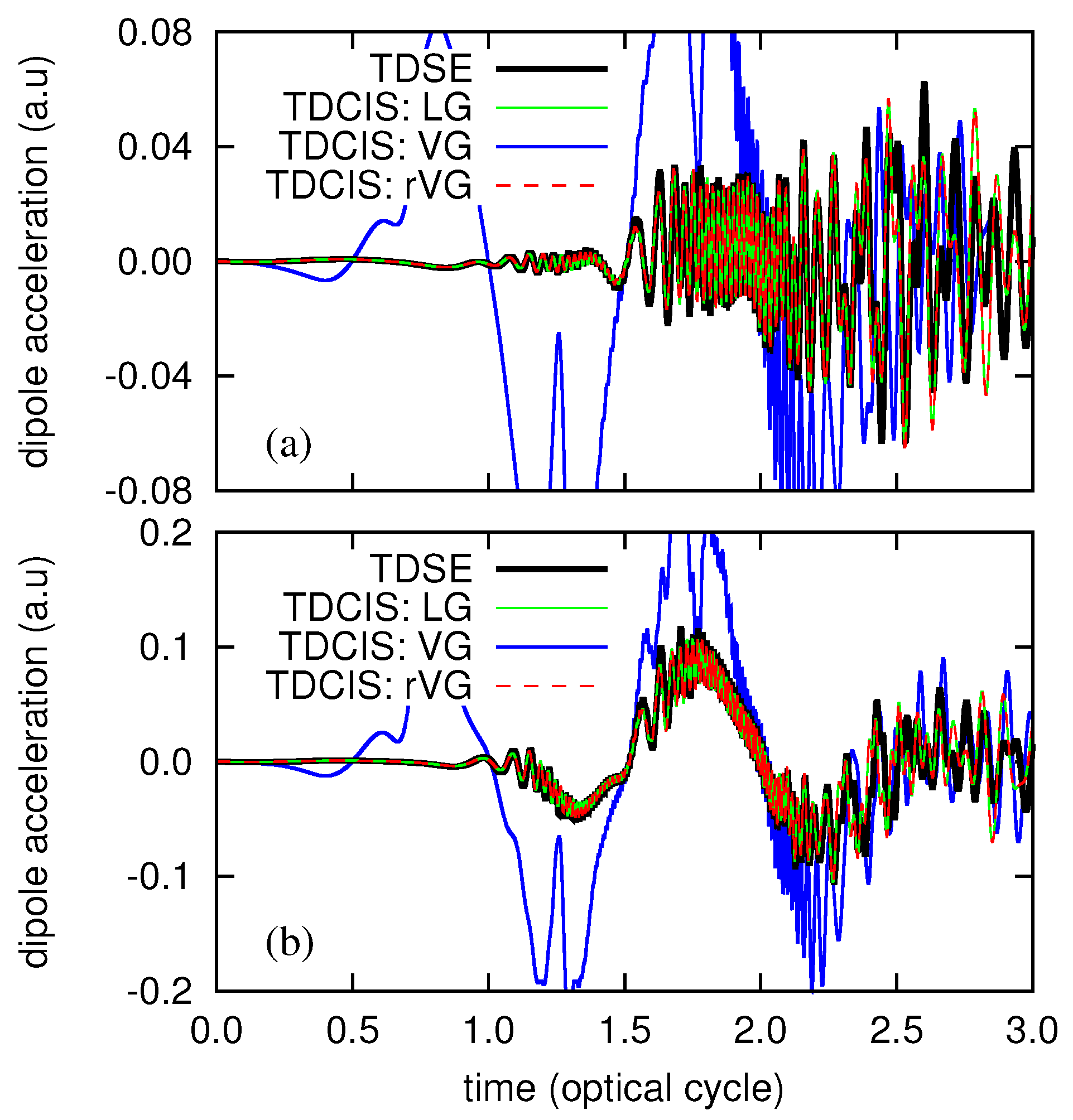
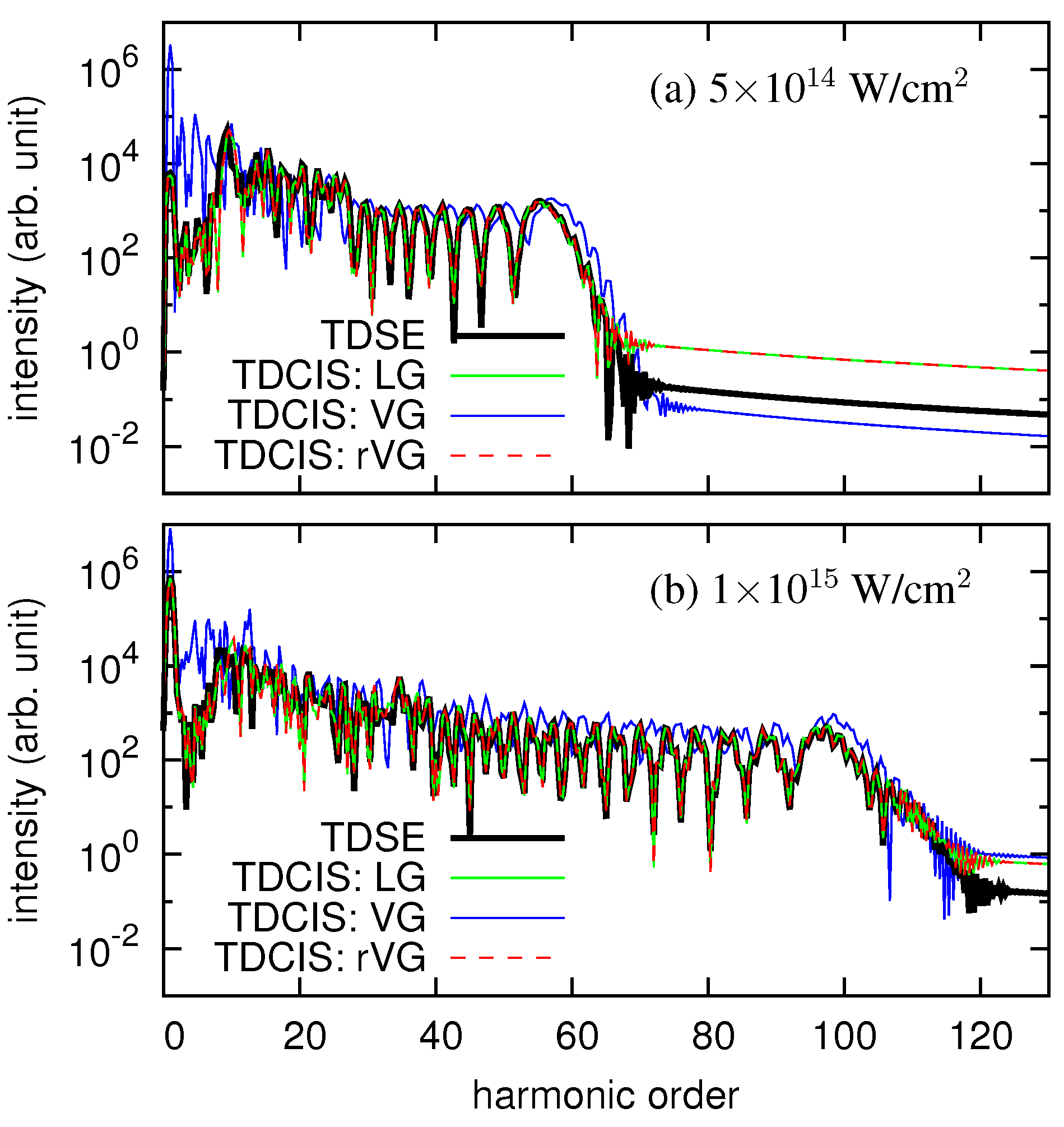
3. Numerical Examples
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gordon, A.; Kärtner, F.X.; Rohringer, N.; Santra, R. Role of Many-Electron Dynamics in High Harmonic Generation. Phys. Rev. Lett. 2006, 96, 223902. [Google Scholar] [CrossRef] [PubMed]
- Rohringer, N.; Gordon, A.; Santra, R. Configuration-interaction-based time-dependent orbital approach for ab initio treatment of electronic dynamics in a strong optical laser field. Phys. Rev. A 2006, 74, 043420. [Google Scholar] [CrossRef]
- Rohringer, N.; Santra, R. Multichannel coherence in strong-field ionization. Phys. Rev. A 2009, 79, 053402. [Google Scholar] [CrossRef]
- Greenman, L.; Ho, P.J.; Pabst, S.; Kamarchik, E.; Mazziotti, D.A.; Santra, R. Implementation of the time-dependent configuration-interaction singles method for atomic strong-field processes. Phys. Rev. A 2010, 82, 023406. [Google Scholar]
- Pabst, S.; Greenman, L.; Ho, P.J.; Mazziotti, D.A.; Santra, R. Decoherence in Attosecond Photoionization. Phys. Rev. Lett. 2011, 106, 053003. [Google Scholar] [CrossRef] [PubMed]
- Pabst, S.; Greenman, L.; Mazziotti, D.A.; Santra, R. Impact of multichannel and multipole effects on the Cooper minimum in the high-order-harmonic spectrum of argon. Phys. Rev. A 2012, 85, 023411. [Google Scholar] [CrossRef]
- Sytcheva, A.; Pabst, S.; Son, S.K.; Santra, R. Enhanced nonlinear response of Ne8+ to intense ultrafast X rays. Phys. Rev. A 2012, 85, 023414. [Google Scholar] [CrossRef]
- Pabst, S.; Sytcheva, A.; Moulet, A.; Wirth, A.; Goulielmakis, E.; Santra, R. Theory of attosecond transient-absorption spectroscopy of krypton for overlapping pump and probe pulses. Phys. Rev. A 2012, 86, 063411. [Google Scholar]
- Pabst, S.; Santra, R. Strong-Field Many-Body Physics and the Giant Enhancement in the High-Harmonic Spectrum of Xenon. Phys. Rev. Lett. 2013, 111, 233005. [Google Scholar] [CrossRef] [PubMed]
- Pabst, S. Atomic and molecular dynamics triggered by ultrashort light pulses on the atto- to picosecond time scale. Eur. Phys. J. Spec. Top. 2013, 221, 1–71. [Google Scholar] [CrossRef]
- Heinrich-Josties, E.; Pabst, S.; Santra, R. Controlling the 2p hole alignment in neon via the 2s–3p Fano resonance. Phys. Rev. A 2014, 89, 043415. [Google Scholar] [CrossRef]
- Pabst, S.; Santra, R. Spin-orbit effects in atomic high-harmonic generation. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 124026. [Google Scholar] [CrossRef][Green Version]
- Hollstein, M.; Pfannkuche, D. Multielectron dynamics in the tunneling ionization of correlated quantum systems. Phys. Rev. A 2015, 92, 053421. [Google Scholar] [CrossRef]
- You, J.A.; Rohringer, N.; Dahlströ, J.M. Attosecond photoionization dynamics with stimulated core-valence transitions. Phys. Rev. A 2016, 93, 033413. [Google Scholar] [CrossRef]
- You, J.A.; Dahlströ, J.M.; Rohringer, N. Attosecond dynamics of light-induced resonant hole transfer in high-order-harmonic generation. Phys. Rev. A 2017, 95, 023409. [Google Scholar] [CrossRef]
- Grosser, M.; Slowik, J.M.; Santra, R. Attosecond X-ray scattering from a particle-hole wave packet. Phys. Rev. A 2017, 95, 062107. [Google Scholar] [CrossRef]
- Krebs, D.; Pabst, S.; Santra, R. Introducing many-body physics using atomic spectroscopy. Am. J. Phys. 2014, 82, 113. [Google Scholar] [CrossRef]
- Karamatskou, A.; Pabst, S.; Chen, Y.J.; Santra, R. Calculation of photoelectron spectra within the time-dependent configuration-interaction singles scheme. Phys. Rev. A 2014, 89, 033415. [Google Scholar] [CrossRef]
- Chen, Y.J.; Pabst, S.; Karamatskou, A.; Santra, R. Theoretical characterization of the collective resonance states underlying the xenon giant dipole resonance. Phys. Rev. A 2015, 91, 032503. [Google Scholar] [CrossRef]
- Tilley, M.; Karamatskou, A.; Santra, R. Wave-packet propagation based calculation of above-threshold ionization in the X-ray regime. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 124001. [Google Scholar] [CrossRef][Green Version]
- Karamatskou, A.; Pabst, S.; Chen, Y.J.; Santra, R. Erratum: Calculation of photoelectron spectra within the time-dependent configuration-interaction singles scheme [Phys. Rev. A 89, 033415 (2014)]. Phys. Rev. A 2015, 91, 069907(E). [Google Scholar] [CrossRef]
- Goetz, R.E.; Karamatskou, A.; Santra, R.; Koch, C.P. Quantum optimal control of photoelectron spectra and angular distributions. Phys. Rev. A 2016, 93, 013413. [Google Scholar] [CrossRef]
- Karamatskou, A.; Santra, R. Time-dependent configuration-interaction-singles calculation of the 5p-subshell two-photon ionization cross section in xenon. Phys. Rev. A 2017, 95, 013415. [Google Scholar] [CrossRef]
- Karamatskou, A. Nonlinear effects in photoionization over a broad photon-energy range within the TDCIS scheme. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 013002. [Google Scholar] [CrossRef]
- Ishikawa, K.L.; Sato, T. A Review on Ab Initio Approaches for Multielectron Dynamics. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 8700916. [Google Scholar] [CrossRef]
- Zanghellini, J.; Kitzler, M.; Fabian, C.; Brabec, T.; Scrinzi, A. An MCTDHF Approach to Multielectron Dynamics in Laser Fields. Laser Phys. 2003, 13, 1064. [Google Scholar]
- Kato, T.; Kono, H. Time-dependent multiconfiguration theory for electronic dynamics of molecules in an intense laser field. Chem. Phys. Lett. 2004, 392, 533. [Google Scholar] [CrossRef]
- Caillat, J.; Zanghellini, J.; Kitzler, M.; Koch, O.; Kreuzer, W.; Scrinzi, A. Correlated multielectron systems in strong laser fields: A multiconfiguration time-dependent Hartree-Fock approach. Phys. Rev. A 2005, 71, 012712. [Google Scholar] [CrossRef]
- Miyagi, H.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for laser-driven many-electron dynamics. Phys. Rev. A 2013, 87, 062511. [Google Scholar] [CrossRef]
- Sato, T.; Ishikawa, K.L. Time-dependent complete-active-space self-consistent-field method for multielectron dynamics in intense laser fields. Phys. Rev. A 2013, 88, 023402. [Google Scholar] [CrossRef]
- Miyagi, H.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for laser-driven many-electron dynamics. II. Extended formulation and numerical analysis. Phys. Rev. A 2014, 89, 063416. [Google Scholar] [CrossRef]
- Haxton, D.J.; McCurdy, C.W. Two methods for restricted configuration spaces within the multiconfiguration time-dependent Hartree-Fock method. Phys. Rev. A 2015, 91, 012509. [Google Scholar] [CrossRef]
- Sato, T.; Ishikawa, K.L. Time-dependent multiconfiguration self-consistent-field method based on occupation restricted multiple active space model for multielectron dynamics in intense laser fields. Phys. Rev. A 2015, 91, 023417. [Google Scholar] [CrossRef]
- Burke, P.G.; Burke, V.M. Time-dependent R-matrix theory of multiphoton processes. J. Phys. B 1997, 30, L383–L391. [Google Scholar] [CrossRef]
- Lysaght, M.A.; Burke, P.G.; van der Hart, H.W. Ultrafast Laser-Driven Excitation Dynamics in Ne: An Ab Initio Time-Dependent R-Matrix Approach. Phys. Rev. Lett. 2008, 101, 253001. [Google Scholar] [CrossRef] [PubMed]
- Lysaght, M.A.; van der Hart, H.W.; Burke, P.G. Time-dependent R-matrix theory for ultrafast atomic processes. Phys. Rev. A 2009, 79, 053411. [Google Scholar] [CrossRef]
- Lackner, F.; Břesinová, I.; Sato, T.; Ishikawa, K.L.; Burgdörfer, J. Propagating two-particle reduced density matrices without wave functions. Phys. Rev. A 2015, 91, 023412. [Google Scholar] [CrossRef]
- Lackner, F.; Břesinová, I.; Sato, T.; Ishikawa, K.L.; Burgdörfer, J. High-harmonic spectra from time-dependent two-particle reduced-density-matrix theory. Phys. Rev. A 2017, 95, 033414. [Google Scholar] [CrossRef]
- Nurhuda, M.; Faisal, F.H.M. Numerical solution of time-dependent Schrödinger equation for multiphoton processes: A matrix iterative method. Phys. Rev. A 1999, 60, 3125. [Google Scholar] [CrossRef]
- Grum-Grzhimailo, A.N.; Abeln, B.; Bartschat, K.; Weflen, D. Ionization of atomic hydrogen in strong infrared laser fields. Phys. Rev. A 2010, 81, 043408. [Google Scholar] [CrossRef]
- Sato, T.; Ishikawa, K.L.; Břesinová, I.; Lackner, F.; Burgdörfer, J. Time-dependent complete-active-space self-consistent-field method for atoms: Application to high-harmonic generation. Phys. Rev. A 2016, 94, 023405. [Google Scholar] [CrossRef]
- Dahlstrom, J.M.; Pabst, S.; Lindroth, E. Attosecond transient absorption of a bound wave packet coupled to a smooth continuum. J. Opt. 2017, 19, 114004. [Google Scholar] [CrossRef]
- Scrinzi, A. Infinite-range exterior complex scaling as a perfect absorber in time-dependent problems. Phys. Rev. A 2010, 81, 053845. [Google Scholar] [CrossRef]
- Orimo, Y.; Sato, T.; Scrinzi, A.; Ishikawa, K.L. Implementation of infinite-range exterior complex scaling to the time-dependent complete-active-space self-consistent-field method. Phys. Rev. A 2018, 97, 023423. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Chelkowski, S.; Diestler, D.J.; Manz, J.; Yuan, K.J. Quantum simulation of high-order harmonic spectra of the hydrogen atom. Phys. Rev. A 2009, 79, 023403. [Google Scholar] [CrossRef]
- Han, Y.C.; Madsen, L.B. Comparison between length and velocity gauges in quantum simulations of high-order harmonic generation. Phys. Rev. A 2010, 81, 063430. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Fillion-Gourdeau, F.; Lorin, E. Atoms and molecules in intense laser fields: Gauge invariance of theory and models. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 153001. [Google Scholar] [CrossRef]
- Sato, T.; Ishikawa, K.L. The structure of approximate two electron wavefunctions in intense laser driven ionization dynamics. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 204031. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sato, T.; Teramura, T.; Ishikawa, K.L. Gauge-Invariant Formulation of Time-Dependent Configuration Interaction Singles Method. Appl. Sci. 2018, 8, 433. https://doi.org/10.3390/app8030433
Sato T, Teramura T, Ishikawa KL. Gauge-Invariant Formulation of Time-Dependent Configuration Interaction Singles Method. Applied Sciences. 2018; 8(3):433. https://doi.org/10.3390/app8030433
Chicago/Turabian StyleSato, Takeshi, Takuma Teramura, and Kenichi L. Ishikawa. 2018. "Gauge-Invariant Formulation of Time-Dependent Configuration Interaction Singles Method" Applied Sciences 8, no. 3: 433. https://doi.org/10.3390/app8030433
APA StyleSato, T., Teramura, T., & Ishikawa, K. L. (2018). Gauge-Invariant Formulation of Time-Dependent Configuration Interaction Singles Method. Applied Sciences, 8(3), 433. https://doi.org/10.3390/app8030433




