Full Characterization of a Molecular Cooper Minimum Using High-Harmonic Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Details
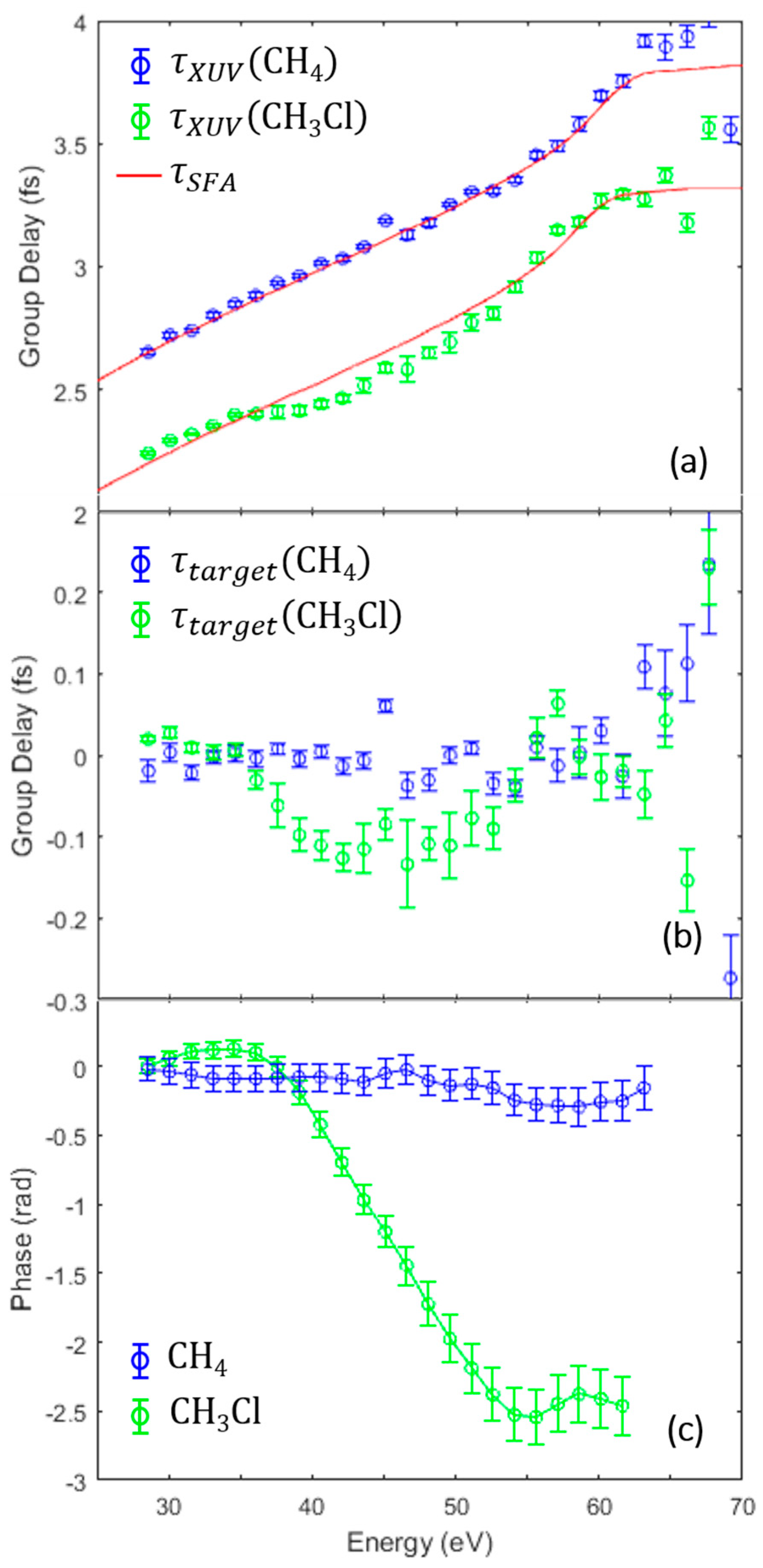
2.2. High-Harmonic Spectral Analysis
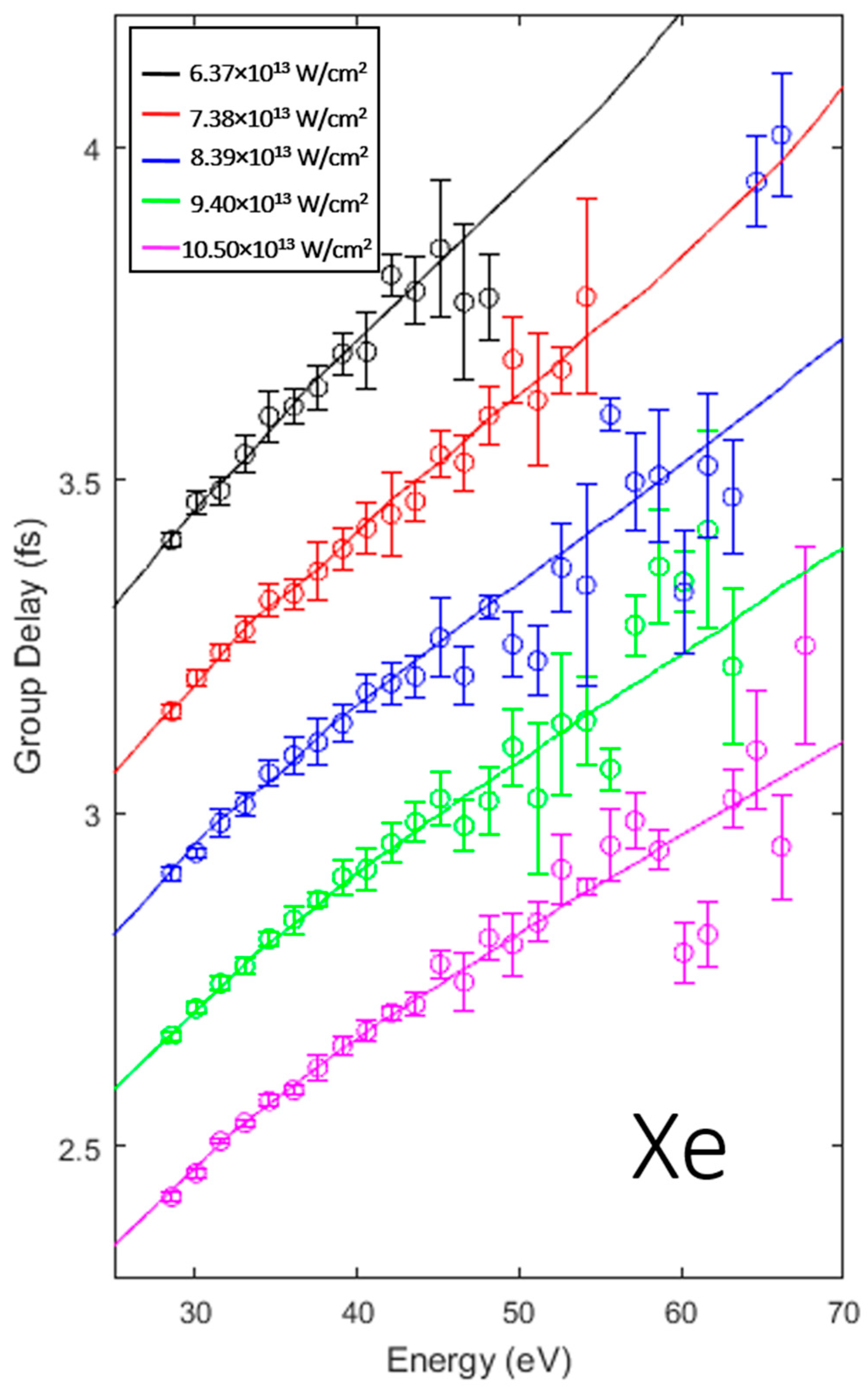
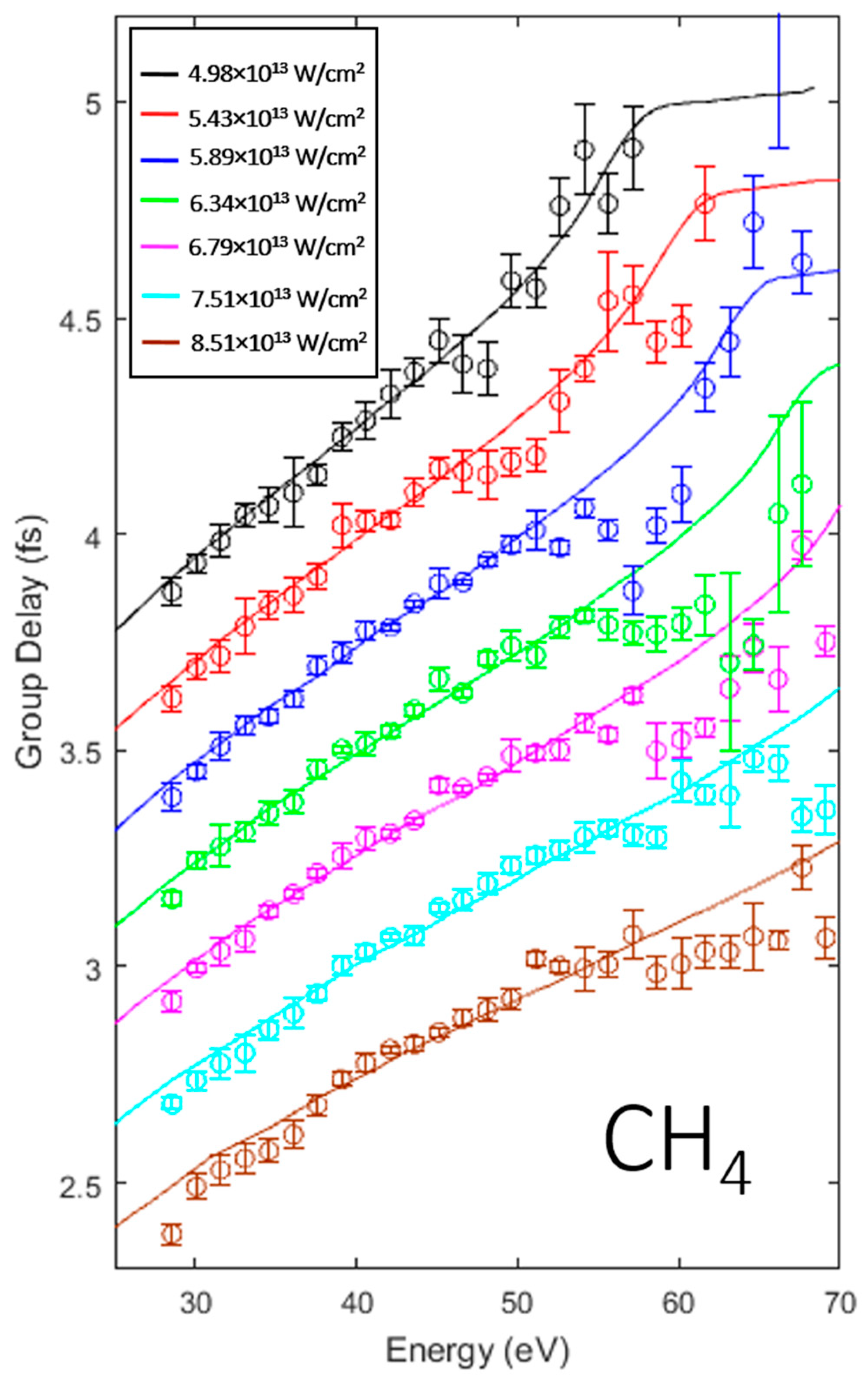
3. Results and Discussion
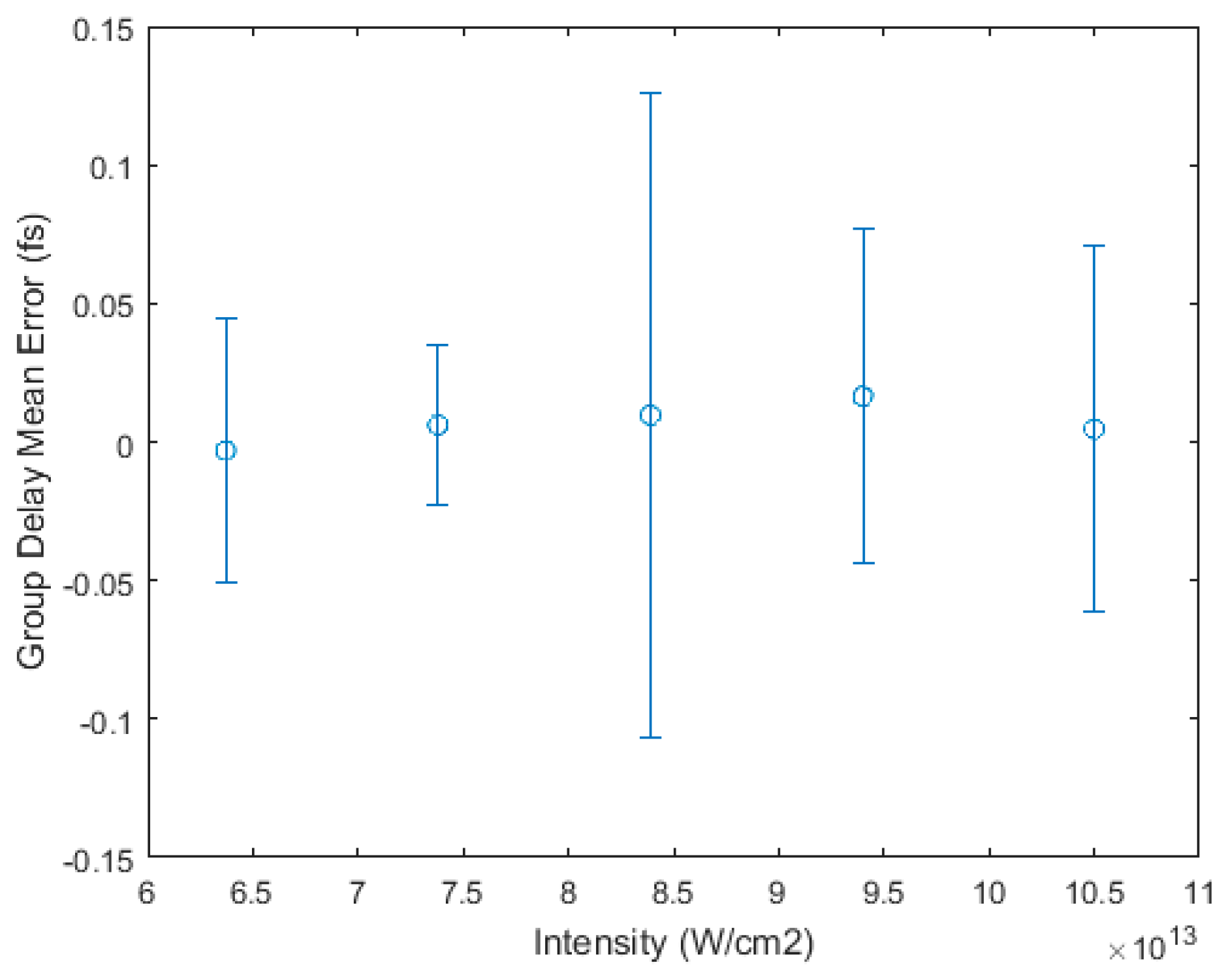
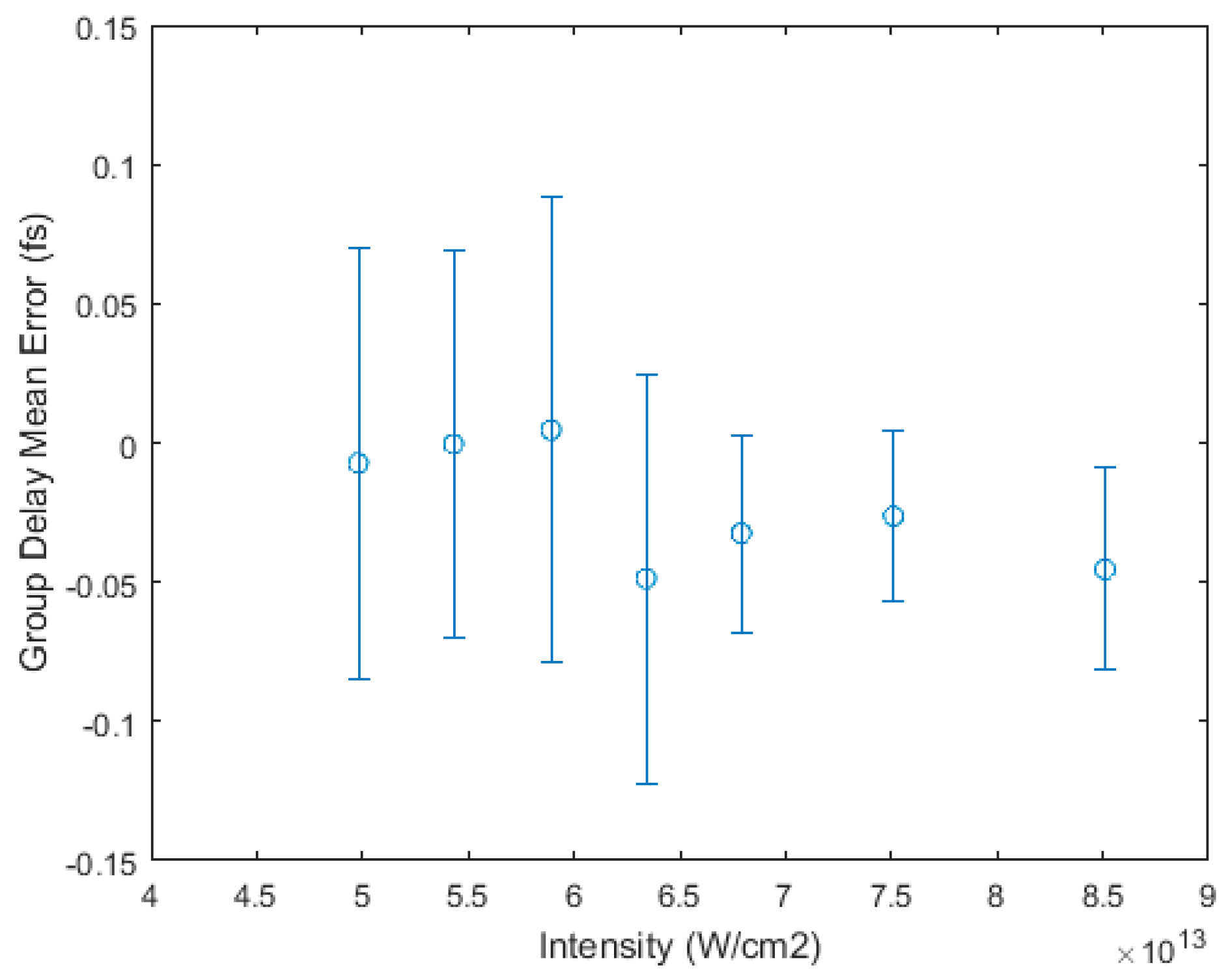
3.1. Intensity Scaling and Calibration
3.2. Identifying the Cooper Minimum in Methyl Chloride
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Marangos, J.P. Development of high harmonic generation spectroscopy of organic molecules and biomolecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 132001. [Google Scholar] [CrossRef]
- Haessler, S.; Fabre, B.; Higuet, J.; Caillat, J.; Ruchon, T.; Breger, P.; Carré, B.; Constant, E.; Maquet, A.; Mével, E.; et al. Phase-resolved attosecond near-threshold photoionization of molecular nitrogen. Phys. Rev. A 2009, 80, 011404(R). [Google Scholar] [CrossRef]
- Huppert, M.; Jordan, I.; Baykusheva, D.; von Conta, A.; Wörner, H.J. Attosecond Delays in Molecular Photoionization. Phys. Rev. Lett. 2016, 117, 093001. [Google Scholar] [CrossRef] [PubMed]
- Wörner, H.J.; Arrell, C.A.; Banerji, N.; Cannizzo, A.; Chergui, M.; Das, A.K.; Hamm, P.; Keller, U.; Kraus, P.M.; Liberatore, E.; et al. Charge migration and charge transfer in molecular systems. Struct. Dyn. 2017, 4, 061508. [Google Scholar] [CrossRef] [PubMed]
- Kraus, P.M.; Mignolet, B.; Baykusheva, D.; Rupenyan, A.; Horný, L.; Penka, E.F.; Grassi, G.; Tolstikhin, O.I.; Schneider, J.; Jensen, F.; et al. Measurement and laser control of attosecond charge migration in ionized iodoacetylene. Science 2015, 350, 790–795. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.W. Photoionization from Outer Atomic Subshells. A Model Study. Phys. Rev. 1962, 128, 681. [Google Scholar] [CrossRef]
- Higuet, J.; Ruf, H.; Thiré, N.; Cireasa, R.; Constant, E.; Cormier, E.; Descamps, D.; Mével, E.; Petit, S.; Pons, B.; et al. High-order harmonic spectroscopy of the Cooper minimum in argon: Experimental and theoretical study. Phys. Rev. A 2011, 83, 053401. [Google Scholar] [CrossRef]
- Carlson, T.A.; Krause, M.O.; Svensson, W.A.; Gerard, P.; Grimm, F.A.; Whitley, T.A.; Pullen, B.P. Photoelectron Dynamics of the Cooper Minimum in Free Molecules. Z. Phys. D At. Mol. Clust. 1986, 2, 309–318. [Google Scholar] [CrossRef]
- Novak, I.; Benson, J.M.; Potts, A.W. UV Angle Resolved Photoelectron-Spectra of Fluoro and Chloromethane using Synchrotron Radiation. J. Electron. Spectrosc. Relat. Phenom. 1986, 41, 225–233. [Google Scholar] [CrossRef]
- Holland, D.M.P.; Powis, I.; Ohrwall, G.; Karlsson, L.; von Niessen, W. A study of the photoionisation dynamics of chloromethane and iodomethane. Chem. Phys. 2006, 326, 535–550. [Google Scholar] [CrossRef]
- Schoun, S.B.; Chirla, R.; Wheeler, J.; Roedig, C.; Agostini, P.; DiMauro, L.F.; Schafer, K.J.; Gaarde, M.B. Attosecond Pulse Shaping around a Cooper Minimum. Phys. Rev. Lett. 2014, 112, 153001. [Google Scholar] [CrossRef] [PubMed]
- Wörner, H.J.; Niikura, H.; Bertrand, J.B.; Corkum, P.B.; Villeneuve, D.M. Observation of Electronic Structure Minima in High-Harmonic Generation. Phys. Rev. Lett. 2009, 102, 103901. [Google Scholar] [CrossRef] [PubMed]
- Wong, M.C.H.; Le, A.T.; Alharbi, A.F.; Boguslavskiy, A.E.; Lucchese, R.R.; Brichta, J.P.; Lin, C.D.; Bhardwaj, V.R. High Harmonic Spectroscopy of the Cooper Minimum in Molecules. Phys. Rev. Lett. 2013, 110, 033006. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of High-Harmonic Generation by Low-Frequency Laser Fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Mairesse, Y.; De Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovačev, M.; Taïeb, R.; Carré, B.; et al. Attosecond synchronization of high-harmonic soft x-rays. Science 2003, 302, 1540–1543. [Google Scholar] [CrossRef] [PubMed]
- Kazamias, S.; Balcou, P. Intrinsic chirp of attosecond pulses: Single-atom model versus experiment. Phys. Rev. A 2004, 69, 063416. [Google Scholar] [CrossRef]
- Mairesse, Y.; De Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovačev, M.; Auguste, T.; Carré, B.; et al. Optimization of attosecond pulse generation. Phys. Rev. Lett. 2004, 93, 163901. [Google Scholar] [CrossRef] [PubMed]
- Varjú, K.; Mairesse, Y.; Carré, B.; Gaarde, M.B.; Johnsson, P.; Kazamias, S.; López-Martens, R.; Mauritsson, J.; Schafer, K.J.; Balcou, P.H.; et al. Frequency chirp of harmonic and attosecond pulses. J. Mod. Opt. 2005, 52, 379–394. [Google Scholar] [CrossRef]
- Doumy, G.; Wheeler, J.; Roedig, C.; Chirla, R.; Agostini, P.; DiMauro, L.F. Attosecond Synchronization of High-Order Harmonics from Midinfrared Drivers. Phys. Rev. Lett. 2009, 102, 093002. [Google Scholar] [CrossRef] [PubMed]
- Lias, S.G. Ionization Energy Evaluation. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005. Available online: https://webbook.nist.gov/cgi/cbook.cgi?Contrib=L (accessed on 10 June 2018).
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Muller, H.G. Reconstruction of attosecond harmonic beating by interference of two-photon transitions. Appl. Phys. B 2002, 74, S17–S21. [Google Scholar] [CrossRef]
- Etches, A.; Madsen, L.B. Extending the strong-field approximation of high-order harmonic generation to polar molecules: Gating mechanisms and extension of the harmonic cutoff. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 155602. [Google Scholar] [CrossRef]
- Mauritsson, J.; Gaarde, M.B.; Schafer, K.J. Accessing properties of electron wave packets generated by attosecond pulse trains through time-dependent calculations. Phys. Rev. A 2005, 72, 013401. [Google Scholar] [CrossRef]
- Rakić, A.D. Algorithm for the determination of intrinsic optical constants of metal films: Application to aluminum. Appl. Opt. 1995, 34, 4755–4767. [Google Scholar] [CrossRef] [PubMed]
- Dahlström, J.M.; Guénot, D.; Klünder, K.; Gisselbrecht, M.; Mauritsson, J.; L’Huillier, A.; Maquet, A.; Taïeb, R. Theory of attosecond delays in laser-assisted photoionization. Chem. Phys. 2013, 414, 53–64. [Google Scholar] [CrossRef]
- Lin, C.D.; Le, A.-T.; Chen, Z.; Morishita, T.; Lucchese, R. Strong-field rescattering physics-self-imaging of a molecule by its own electrons. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 122001. [Google Scholar] [CrossRef]
- Frolov, M.V.; Manakov, N.L.; Sarantseva, T.S.; Starace, A.F. Analytic formulae for high harmonic generation. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 035601. [Google Scholar] [CrossRef]
- Boutu, W.; Haessler, S.; Merdji, H.; Breger, P.; Waters, G.; Stankiewicz, M.; Frasinski, L.J.; Taieb, R.; Caillat, J.; Maquet, A.; et al. Coherent control of attosecond emission from aligned molecules. Nat. Phys. 2008, 4, 545–549. [Google Scholar] [CrossRef]
- Diveki, Z.; Camper, A.; Haessler, S.; Auguste, T.; Ruchon, T.; Carré, B.; Salières, P.; Guichard, R.; Caillat, J.; Maquet, A. Spectrally resolved multi-channel contributions to the harmonic emission in N2. New J. Phys. 2012, 14, 023062. [Google Scholar] [CrossRef]
- McFarland, B.K.; Farrell, J.P.; Bucksbaum, P.H.; Gühr, M. High Harmonic Generation from Multiple Orbitals in N2. Science 2008, 322, 1232–1235. [Google Scholar] [CrossRef] [PubMed]
- Le, A.-T.; Morishita, T.; Lin, C.D. Extraction of the species-dependent dipole amplitude and phase from high-order harmonic spectra in rare-gas atoms. Phys. Rev. A 2008, 78, 023814. [Google Scholar] [CrossRef]
- Jin, C.; Le, A.-T.; Lin, C.D. Medium propagation effects in high-order harmonic generation of Ar and N2. Phys. Rev. A 2011, 83, 023411. [Google Scholar] [CrossRef]
- Farrell, J.P.; Spector, L.S.; McFarland, B.K.; Bucksbaum, P.H.; Gühr, M.; Gaarde, M.B.; Schafer, K.J. Influence of phase matching on the Cooper minimum in Ar high-order harmonic spectra. Phys. Rev. A 2011, 83, 023420. [Google Scholar] [CrossRef]
- Gaarde, M.B.; Buth, C.; Tate, J.L.; Schafer, K.J. Transient absorption and reshaping of ultrafast XUV light by laser-dressed helium. Phys. Rev. A 2011, 83, 013419. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarborough, T.D.; Gorman, T.T.; Mauger, F.; Sándor, P.; Khatri, S.; Gaarde, M.B.; Schafer, K.J.; Agostini, P.; DiMauro, L.F. Full Characterization of a Molecular Cooper Minimum Using High-Harmonic Spectroscopy. Appl. Sci. 2018, 8, 1129. https://doi.org/10.3390/app8071129
Scarborough TD, Gorman TT, Mauger F, Sándor P, Khatri S, Gaarde MB, Schafer KJ, Agostini P, DiMauro LF. Full Characterization of a Molecular Cooper Minimum Using High-Harmonic Spectroscopy. Applied Sciences. 2018; 8(7):1129. https://doi.org/10.3390/app8071129
Chicago/Turabian StyleScarborough, Timothy D., Timothy T. Gorman, François Mauger, Péter Sándor, Sanjay Khatri, Mette B. Gaarde, Kenneth J. Schafer, Pierre Agostini, and Louis F. DiMauro. 2018. "Full Characterization of a Molecular Cooper Minimum Using High-Harmonic Spectroscopy" Applied Sciences 8, no. 7: 1129. https://doi.org/10.3390/app8071129
APA StyleScarborough, T. D., Gorman, T. T., Mauger, F., Sándor, P., Khatri, S., Gaarde, M. B., Schafer, K. J., Agostini, P., & DiMauro, L. F. (2018). Full Characterization of a Molecular Cooper Minimum Using High-Harmonic Spectroscopy. Applied Sciences, 8(7), 1129. https://doi.org/10.3390/app8071129




