Implications of Rigid Gripping Constraints on Clubhead Dynamics in Steel Golf Shafts
Abstract
Featured Application
abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Propagation Speeds
2.1.1. Longitudinal Strain
2.1.2. Torsional Strain
2.1.3. Bending Strain
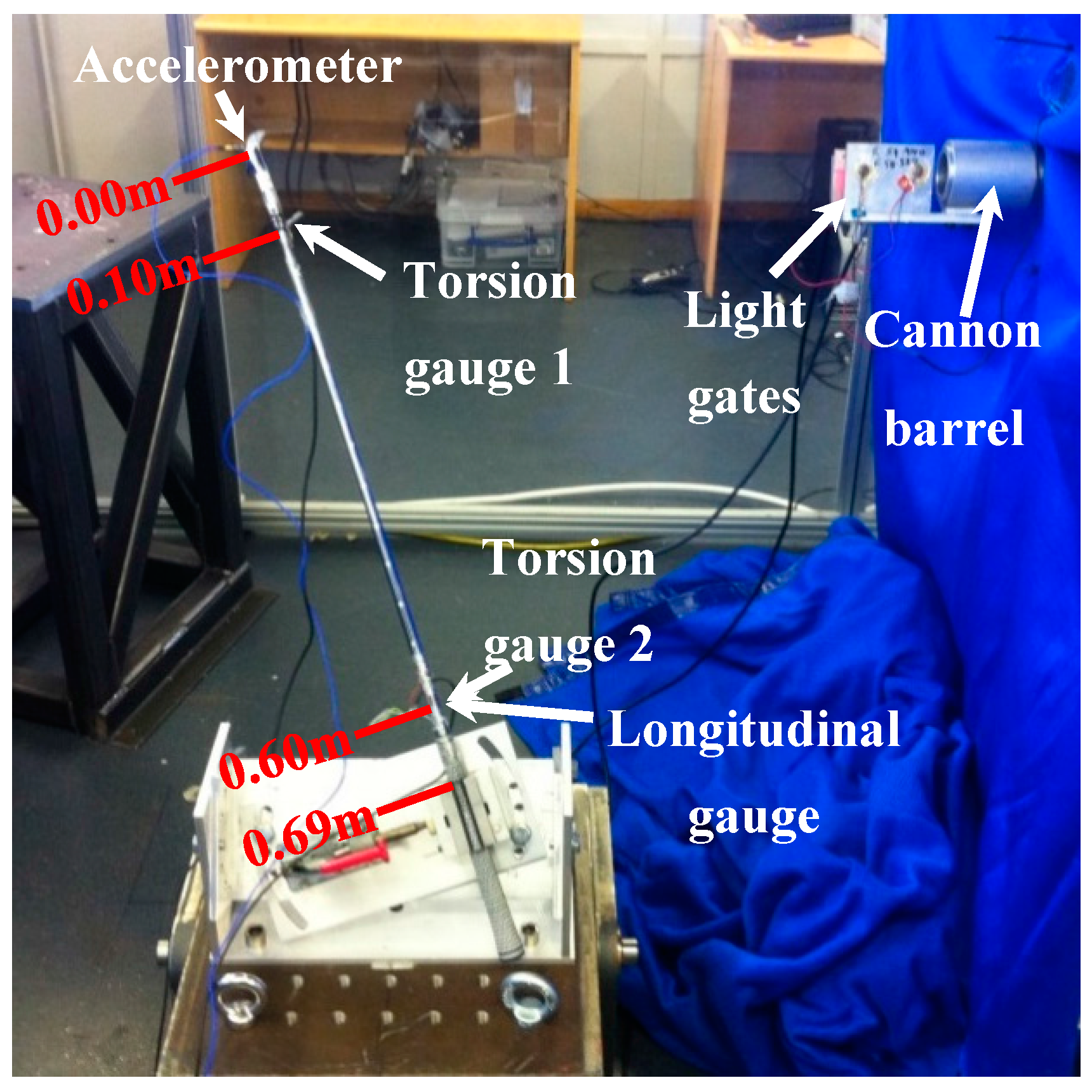
2.2. Experimental Setup
2.3. Assumptions
3. Results
3.1. Inbound Ball Speed and Contact Time
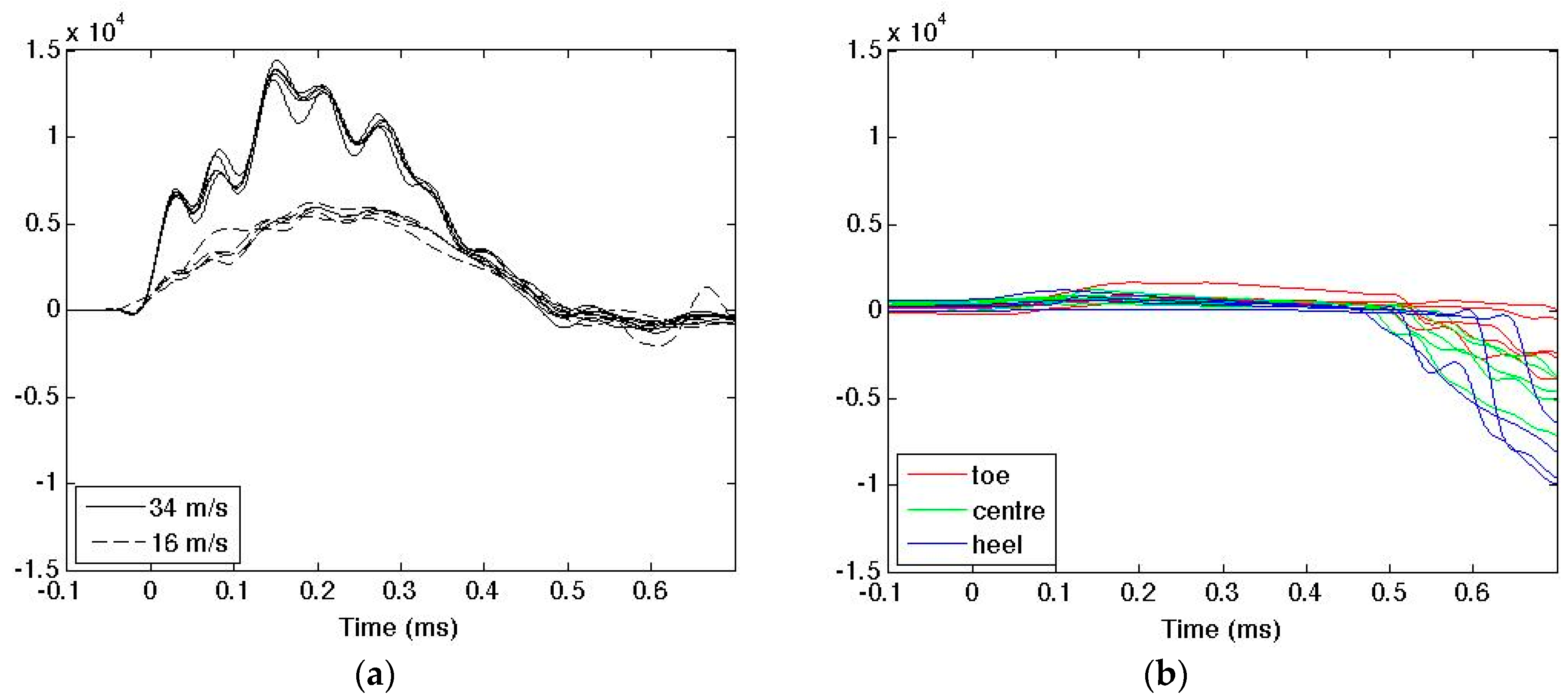
3.2. Longitudinal Strain Measurement
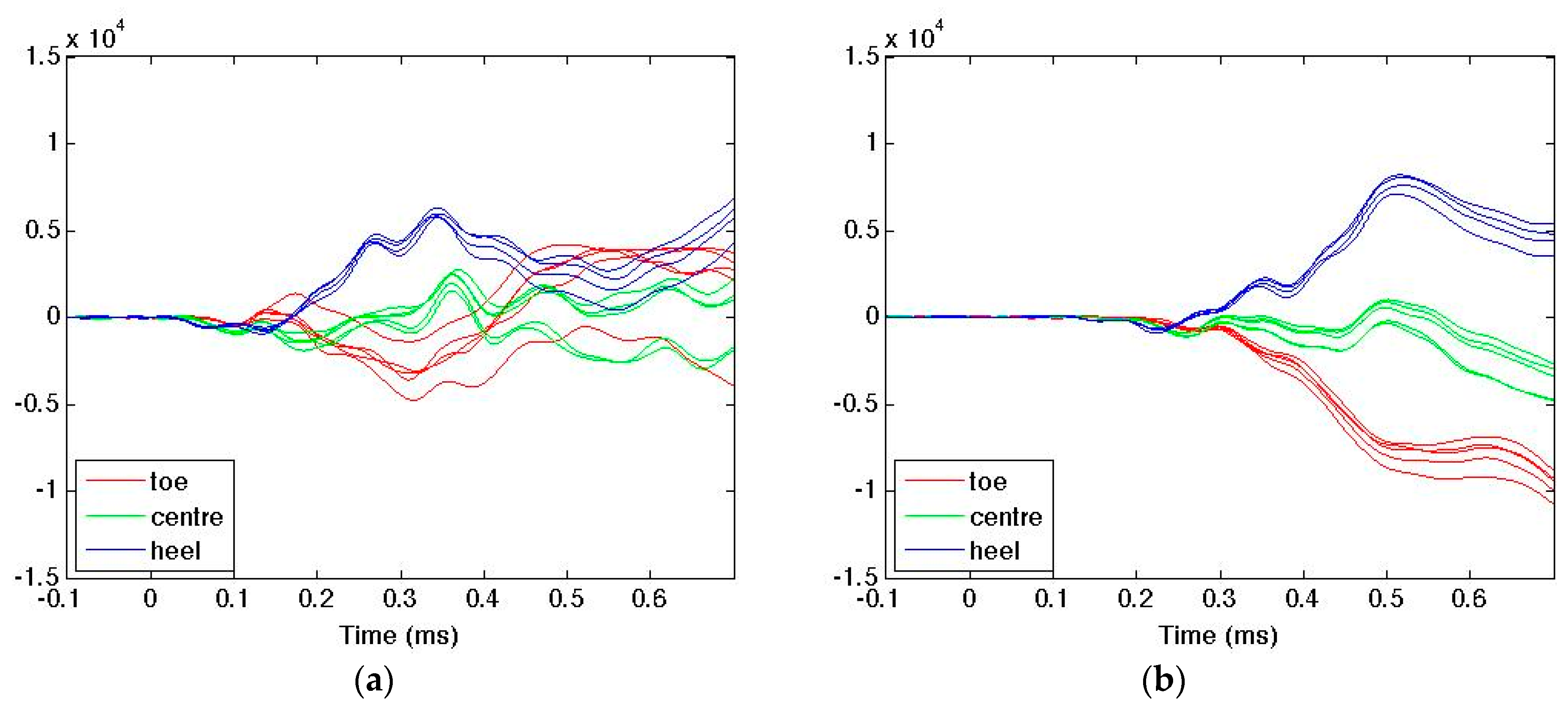
3.3. Torsional Strain Measurement
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Whittaker, A.; Thomson, R.; McKeown, D.; McCafferty, J. The application of computer-aided engineering techniques in advanced clubhead design. In Proceedings of the World Scientific Congress of Golf, St. Andrews, Scotland, 22–26 July 2002; Cochran, A.J., Ed.; E. & F. N. Spon: London, UK, 1990; pp. 286–291. [Google Scholar]
- Milne, R.D.; Davis, J.P. The role of the shaft in the golf swing. J. Biomech. 1992, 25, 975–983. [Google Scholar] [CrossRef]
- Harper, T. The Efficacy of a Golf Robot for Simulating Indvidual Golfer’s Swings. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2007. [Google Scholar]
- Wicks, A.L.; Knight, C.E.; Braunwart, P.; Neighbors, J. Dynamics of a golf club. In Proceedings of the 17th International Modal Analysis Conference, Kissimmee, FL, USA, 8–11 February 1999; pp. 503–508. [Google Scholar]
- Cochran, A.J.; Stobbs, J. Search for the Perfect Swing; Triumph Books: Chicago, IL, USA, 1968. [Google Scholar]
- Daish, C.B. The Physics of Ball Games; English Universities Press: London, UK, 1979. [Google Scholar]
- Iwatsubo, T.; Kawamura, S.; Miyamoto, K.; Yamaguchi, T. Numerical analysis of golf club head and ball at various impact points. Sports Eng. 2000, 3, 195–204. [Google Scholar] [CrossRef][Green Version]
- Harper, T.; Roberts, J.R.; Jones, R.; Carrott, A.J. Development and evaluation of new control algorithms for a mechanical golf swing device. Proc. Inst. Mech. Eng. Part 1 J. Syst. Control Eng. 2008, 222, 595–604. [Google Scholar] [CrossRef]
- Roberts, J.R.; Harper, T.; Jones, R. Development of a golf robot for simulating individual golfer’s swings. Procedia Eng. 2010, 2, 2643–2648. [Google Scholar] [CrossRef][Green Version]
- Johnson, S.H.; Lieberman, B.B. Experimental determination of apparent contact time in normal impact. In Science and Golf IV; Thain, E., Ed.; Routledge: London, UK, 2002; pp. 524–530. [Google Scholar]
- Arakawa, K.; Mada, T.; Komatsu, H.; Shimizu, T.; Satou, M.; Takehara, K.; Etoh, G. Dynamic Contact Behavior of a Golf Ball During an Oblique Impact. Exp. Mech. 2006, 46, 691–697. [Google Scholar] [CrossRef]
- Roberts, J.R.; Jones, R.; Rothberg, S. Measurement of contact time in short duration sports ball impacts: An experimental method and correlation with the perceptions of elite golfers. Sports Eng. 2001, 4, 191–203. [Google Scholar] [CrossRef]
- Horwood, G.P. Golf shafts—A technical perspective. In Science and Golf II; Cochran, A.J., Farrally, M.R., Eds.; E. & F. N. Spon: London, UK, 1994; pp. 247–258. [Google Scholar]
- Masuda, M.; Kojima, S. Kick back effect of club-head at impact. In Science and Golf II; Cochran, A.J., Farrally, M.R., Eds.; E. & F. N. Spon: London, UK, 1994; pp. 284–289. [Google Scholar]
- Nesbit, S.M.; Hartzell, T.A.; Nalevanko, J.C.; Starr, R.M.; White, M.G.; Anderson, J.R.; Gerlacki, J.N. A Discussion of Iron Golf Club Head Inertia Tensors and Their Effects on the Golfer. J. Appl. Biomech. 1996, 12, 449–469. [Google Scholar] [CrossRef]
- Whittaker, A. A study of the dynamics of the golf club. Sports Eng. 1998, 1, 115–124. [Google Scholar] [CrossRef]
- Rossing, T.D.; Russell, D.A. Laboratory observation of elastic waves in solids. Am. J. Phys. 1990, 58, 1153–1162. [Google Scholar] [CrossRef]
- Hall, D.E. Musical Acoustics, 2nd ed.; Brooks/Cole Pub. Co.: Pacific Grove, CA, USA, 1991. [Google Scholar]
- Corke, T.W.; Betzler, N.F.; Wallace, E.S.; Otto, S.R. Clubhead presentation and spin control capability of elite golfers. Procedia Eng. 2013, 60, 136–142. [Google Scholar] [CrossRef][Green Version]
- Wishon, T.W. The New Search for the Perfect Golf Club; Fireship Press: Tuscon, AZ, USA, 2011. [Google Scholar]
| Location | Distance (m) | Longitudinal | Torsional | ||
|---|---|---|---|---|---|
| Predicted | Measured | Predicted | Measured | ||
| Tip | 0.10 | 0.020 | - | 0.032 | 0.03–0.06 |
| Grip | 0.60 | 0.119 | ≈0.1 | 0.190 | 0.19–0.22 |
| Clamp | 0.69 | 0.137 | - | 0.218 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corke, T.W.; Betzler, N.F.; Wallace, E.S.; Strangwood, M.; Otto, S.R. Implications of Rigid Gripping Constraints on Clubhead Dynamics in Steel Golf Shafts. Appl. Sci. 2018, 8, 422. https://doi.org/10.3390/app8030422
Corke TW, Betzler NF, Wallace ES, Strangwood M, Otto SR. Implications of Rigid Gripping Constraints on Clubhead Dynamics in Steel Golf Shafts. Applied Sciences. 2018; 8(3):422. https://doi.org/10.3390/app8030422
Chicago/Turabian StyleCorke, Tom W., Nils F. Betzler, Eric S. Wallace, Martin Strangwood, and Steve R. Otto. 2018. "Implications of Rigid Gripping Constraints on Clubhead Dynamics in Steel Golf Shafts" Applied Sciences 8, no. 3: 422. https://doi.org/10.3390/app8030422
APA StyleCorke, T. W., Betzler, N. F., Wallace, E. S., Strangwood, M., & Otto, S. R. (2018). Implications of Rigid Gripping Constraints on Clubhead Dynamics in Steel Golf Shafts. Applied Sciences, 8(3), 422. https://doi.org/10.3390/app8030422




