Robust Image Watermarking Algorithm Based on ASIFT against Geometric Attacks

Featured Application

This work embeds the watermark images into host images, realizing the robustness to common attacks and geometric attacks, which can be applied for copyright protection in the field of image transmission, medical, and military research.

Abstract

Image processing technology has been developed rapidly in recent years, and altering the content of an image is easy for everyone, but may be illegal for an attacker. Thus, it is urgent and necessary to overcome this problem to protect the integrity and authenticity of images. Watermarking is a powerful technique proposed to solve this problem. This paper introduces a robust image watermarking algorithm working in the wavelet domain, embedding the watermark information into the third level low frequency coefficients after the three-level discrete wavelet transform (DWT) and singular value decomposition (SVD). Additionally, to improve the robustness to geometric attacks, the affine-scale-invariant feature transform (ASIFT) is applied to obtain feature points which are invariant to geometric attacks. Then, features of acquired points between the watermarked image and the received image are used to realize the resynchronization to improve the robustness. Experimental results show that the proposed algorithm achieves great balance between robustness and imperceptibility, and is robust against geometric attacks, JPEG compression, noise addition, cropping, median filters, and so on.

1. Introduction

With the fast development of information technology, multimedia data has become the most important carrier for information transmission. Digital images, as one of the most important ways for transmitting the information in one or more images, can be easily altered and destroyed by the developed techniques. Thus, to protect the authenticity and integrity of images, schemes applied for copyright protection of images can be essential and meaningful. Based on this purpose, there are mainly two methods proposed to overcome the above problems, which are digital signature [1,2] and digital image watermarking [3,4,5]. Digital signature is a kind of number string produced by the sender, which can be used as the secret key for both senders and receivers. But it can only detect that images have been tampered or not, and it cannot identify the tampered region location. Thus, watermarking technique is proposed as an effective method to solve the copyright issue of image contents. The categories of digital watermarking algorithms can be divided on the basis of their different robustness and functions: robust watermarking, semi-fragile watermarking, and fragile watermarking. Robust watermarking, as its name implies, should have robustness to all kinds of attacks, which is used for copyright protection. On the converse, fragile watermarking is sensitive to image modification, which includes malicious tampering and un-malicious processing. The last one is semi-fragile watermarking, which can be utilized to make the judgement between malicious tampering and non-malicious modification. Actually, semi-fragile watermarking integrates advantages in robust and fragile watermarking with each other. In addition, semi-fragile watermarking is superior to fragile watermarking when considering the ability of resisting common image operations. In perspective of the domain where the watermark works, watermarking technique can be categorized as spatial or frequency domain [6]. The embedding method of watermark information in spatial domain methods is to directly alter the pixel value of the digital image, and advantages of spatial domain watermarking are easy implementation and low computational complexity. But it has shortcoming that spatial watermarking is not robust to some image processing operations in some degree. Accordingly, the frequency domain methods embed the watermark information by use of modifying frequency coefficients of the original image after transforms. Compared with spatial methods, with the help of mathematical transform, frequency domain watermarking has the better imperceptibility and robustness. There are common mathematical transforms applied in the frequency domain watermarking: discrete wavelet transform (DWT), discrete cosine transform (DCT), singular value decomposition (SVD), and discrete Fourier transform (DFT) [7]. Many typical watermarking schemes are proposed as well as applied in the field of the medical research. Based on Lagrangian support vector regression (LSVR) and lifting wavelet transform (LWT), Mehta et al. [8] proposed an efficient image watermarking scheme, where the Arnold scrambled watermark is embedded into the selected blocks from low frequency sub-band by one level DWT. Makbol et al. [9] presented an innovative image watermarking scheme based on SVD and integer wavelet transform (IWT) to overcome the false positive problem (FPP). In [9], the singular matrix of the watermark is embedded into the singular values of the host image. To obtain the optimized scaling factor, multi-objective ant colony optimization (MOACO) is utilized. Rasti et al. [10] proposed a colour image watermarking algorithm to divide the host image into three channels and calculate the entropy of the patches obtained in the blocks. Certain patches are selected according to the comparison with a predefined threshold for further transforms to embed the watermark. In the aspect of functional magnetic resonance imaging (FMRI) protection, Castiglione et al. [11] introduced a fragile reversible watermarking scheme for achieving authenticity and integrity. In the field of microscopy images protection, Pizzolante et al. [12] introduced a novel watermarking scheme to embed the watermark information into the confocal microscopy image.

Traditional watermarking algorithms have robustness to the common attacks, such as noise addition, filter operation, cropping, and so on. However, owing to the unique features of geometric attacks, the watermark synchronization can be destroyed, bringing about the failure in watermark extraction [13]. Thus, it is urgent to propose watermarking algorithms which have resistance to geometric attacks. In recent years, there have been many schemes proposed to solve these problems, which are based on Zernike moments [14], harmonic transform [15], feature points [16], and so on. Due to the fact that SIFT is efficient for the application obtaining the image feature and matching the two images, which makes it more suitable for watermark embedding. However, the scale-invariance feature transform (SIFT) has some advantages: firstly, the significant amount of feature points can be extracted with appropriate parameter settings; secondly, the image feature extracted by SIFT has great uniqueness, which is suitable for accurate matching; finally, SIFT features are invariant to the rotation, scaling, and translations [17], which can be applied as an efficient tool for robust watermarking to acquire the robustness to the geometric attacks. Lee et al. [18] introduced to use local invariant feature for embedding the watermark into the patches of circle shapes generated by SIFT, and proposed an innovative image watermarking scheme. To deal with the watermark synchronization errors, Luo et al. [19] proposed an innovative watermarking scheme based on DFT and SIFT. Based on two techniques, SIFT and DWT, Lyu et al. [20] presented an image watermarking scheme, performing the DWT on the SIFT areas which are selected for watermark embedding. Thorat and Jadhav [21] proposed a watermarking scheme resistant to the geometric attacks based on IWT and SIFT, where SIFT is utilized on the red channels, and the feature points are extracted. Then, blue and green components are performed by IWT, and low-frequency coefficients can be extracted for watermark embedding. In [22], Pham et al. introduced a robust watermarking algorithm on the basis of SIFT and DCT, where the watermark information is embedded into the specific feature region performed by DCT. In [23], based on SVD and SIFT, Zhang and Tang proposed a robust watermarking scheme for solving the watermark synchronization problem, and SIFT is applied for watermarking resynchronization. To deal with the issue of copyright protection for depth image based rendering (DIBR) 3D images, Nam et al. [24] proposed a SIFT features-based blind watermarking algorithm, where feature points are extracted from different view images. Besides, a watermark pattern selection algorithm based on feature points orientation and spread spectrum technique for watermark embedding are applied in this algorithm. In [25], Kwawamura and Uchida presented a SIFT-based watermarking method, which is evaluated by the information hiding criteria (IHC). The local feature regions around SIFT features are applied for scaling and rotation robustness, and two error correction algorithms are used, which are weighted majority voting (WMV) and low density parity check (LDPC) code to correct the errors of extracted watermarks. As the fast algorithm compared with SIFT, speed up robust feature (SURF) algorithm is applied into watermarking algorithm. Fazli and Moeini [26] presented a geometric-distortion resilient watermarking algorithm, using the fuzzy C-means clustering to process the feature points extracted by SURF, and extracted feature point sets are used to divide the image into triangular patches for watermark embedding.

However, the traditional SIFT algorithm can match feature points under the condition of rotation and scaling. As for the tilted image, the feature extracted from the image can be of a small quantity. Concretely, the SIFT algorithm has the feature of scale invariance instead of affine invariance, which can result in the limitation that extraction for an image whose shooting angle changes with a large angle is difficult. In this paper, a novel robust watermarking based on affine-scale-invariance feature transform (ASIFT) [27] in the wavelet domain is presented. Firstly, DWT is performed on the host image for three times, and SVD is operated on the selected low frequency component in horizontal and vertical directions (LL) sub-band. Secondly, the watermark information is embedded into the obtained three-level LL sub-band. The ASIFT points are saved as feature keys for the correction of attacks. Thus, anti-attacks capability can be attained with the help of matching ASIFT feature points in the extraction phase. Finally, experimental results demonstrate that the proposed scheme is imperceptible and resilient to common image processing such as Gaussian noise, salt and pepper noise, speckle noise, median filters, cropping, and so on. Especially for geometric attacks, it has better performance than SIFT-based watermarking.

The remainder of this paper is arranged as follows: in Section 2, the related work is reviewed, including the theories of DWT, SVD, and ASIFT; Section 3 introduces the distortion correction by the ASIFT points; Section 4 gives concrete watermark embedding and extraction procedure; comparison with previous schemes in evaluation of robustness and imperceptibility and demonstration of the advantages in the proposed scheme are given in Section 5; conclusions and future work are illustrated finally in Section 6.

2. Related Work

2.1. DWT Theory

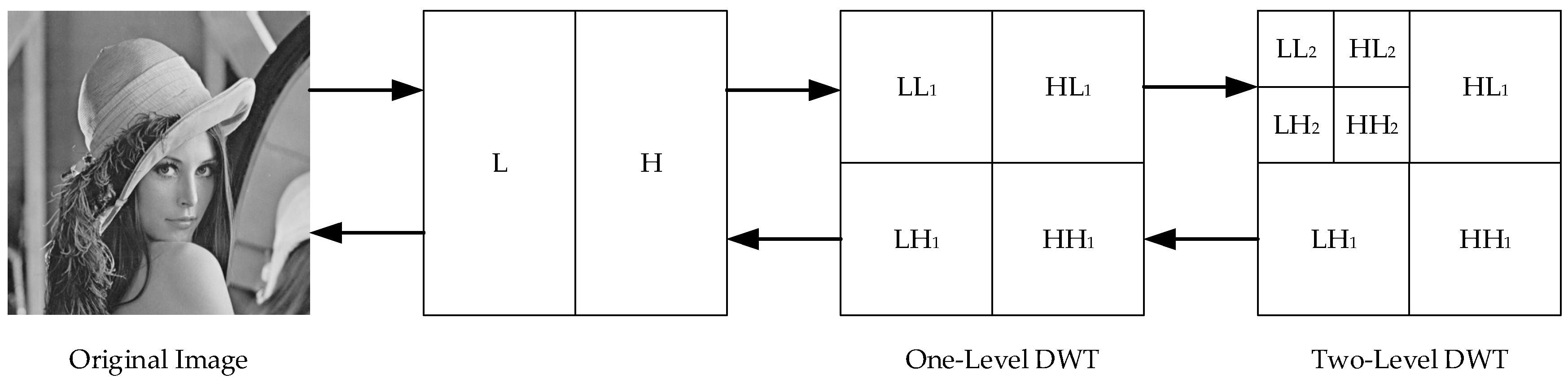
DWT is the discretization of scaling and translation in basic wavelet theory, which has become a widespread transform in many fields such as signal analysis, image processing, computer recognition, etc. The procedure of DWT decomposition and reconstruction on an image can be illustrated in Figure 1.

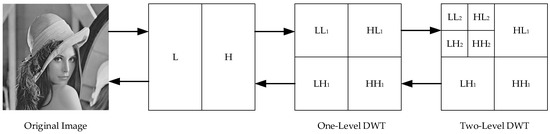
Figure 1. Two-level discrete wavelet transform (DWT) decomposition and reconstruction of an image.

As can be seen in Figure 1, the original image is firstly performed by one-dimensional DWT in the direction of every row, obtaining the low frequency component (L) and high frequency component (H) horizontally. Then, obtained components are performed by one-dimensional DWT again in the direction of every column. Finally, low frequency component in horizontal and vertical directions (LL), low frequency in horizontal direction and high frequency in vertical direction (LH), the high frequency in horizontal direction and low frequency in vertical direction (HL), and high frequency in horizontal and vertical directions (HH) can be obtained. Additionally, the first level DWT can be noted as LL₁, LH₁, HL₁, and HH₁. Similarly, taking the LL₁ sub-band as an example for the transform, the second level DWT can be performed with same procedure to get the LL₂, LH₂, HL₂, and HH₂. In the converse, the reconstruction of inverse DWT (IDWT) can be concluded: IDWT is performed on transformed components in every column and in every row next. After two-level IDWT, the reconstructed image can be obtained.

2.2. SVD Theory

SVD is a common transform applied in image processing, especially in digital image watermarking, which is an orthogonal transform to get the diagonal form of the matrix. To be more concrete, suppose that $\mathit{I}$ is an $m\times n$ image matrix with rank $r$, and Equation (1) can be acquired.

$${\mathit{U}}^{\mathrm{T}}\mathit{I}\mathit{V}=\left[\begin{array}{cc}\mathit{\Sigma }& 0\\ 0& 0\end{array}\right],$$

(1)

where $\mathit{U}$ and $\mathit{V}$ are two orthogonal matrices, $\mathit{\Sigma }=\mathrm{diag}\{{\sigma }_1,\cdots ,{\sigma }_r\}$, and ${\sigma }_1\ge \cdots \ge {\sigma }_r>0$. ${{\sigma }_1}^2,\cdots ,{{\sigma }_r}^2$ are positive singular values in the matrix ${\mathit{I}}^{\mathrm{T}}\mathit{I}$, and SVD of matrix $\mathit{I}$ is represented by

$$\mathit{I}=\mathit{U}\left[\begin{array}{cc}\sum & 0\\ 0& 0\end{array}\right]{\mathit{V}}^{\mathrm{T}},$$

(2)

where $\left[\begin{array}{cc}\sum & 0\\ 0& 0\end{array}\right]$ is the singular value matrix of the image, which can be noted as $\mathit{S}$. Thus, the typical SVD of the image can be expressed as

$$\mathit{I}=\mathit{U}\mathit{S}{\mathit{V}}^{\mathrm{T}}.$$

(3)

In practice, SVD becomes the research hotspot because of its three advantages: (i) matrices obtained by SVD are unfixed; (ii) singular values can still remain intact when an image is perturbed; and (iii) singular values can represent intrinsic algebraic properties of an image.

2.3. ASIFT

In 1999, Lowe [28] introduced a novel algorithm for extracting the local scale-invariant feature points of descriptors, and these descriptors are utilized for matching two related images, which can be used for many fields such as image recognition, image registration, image retrieval, 3D reconstruction, and so on. SIFT can deal with the similarity invariance like rotation, scaling, and translation, while some invariance exploration related to different axis orientation are not concerned. Yu and Morel [29] presented to consider changing the two camera with axis orientation parameters, as known as latitude and longitude angles, for obtaining a set of sample views of the initial images.

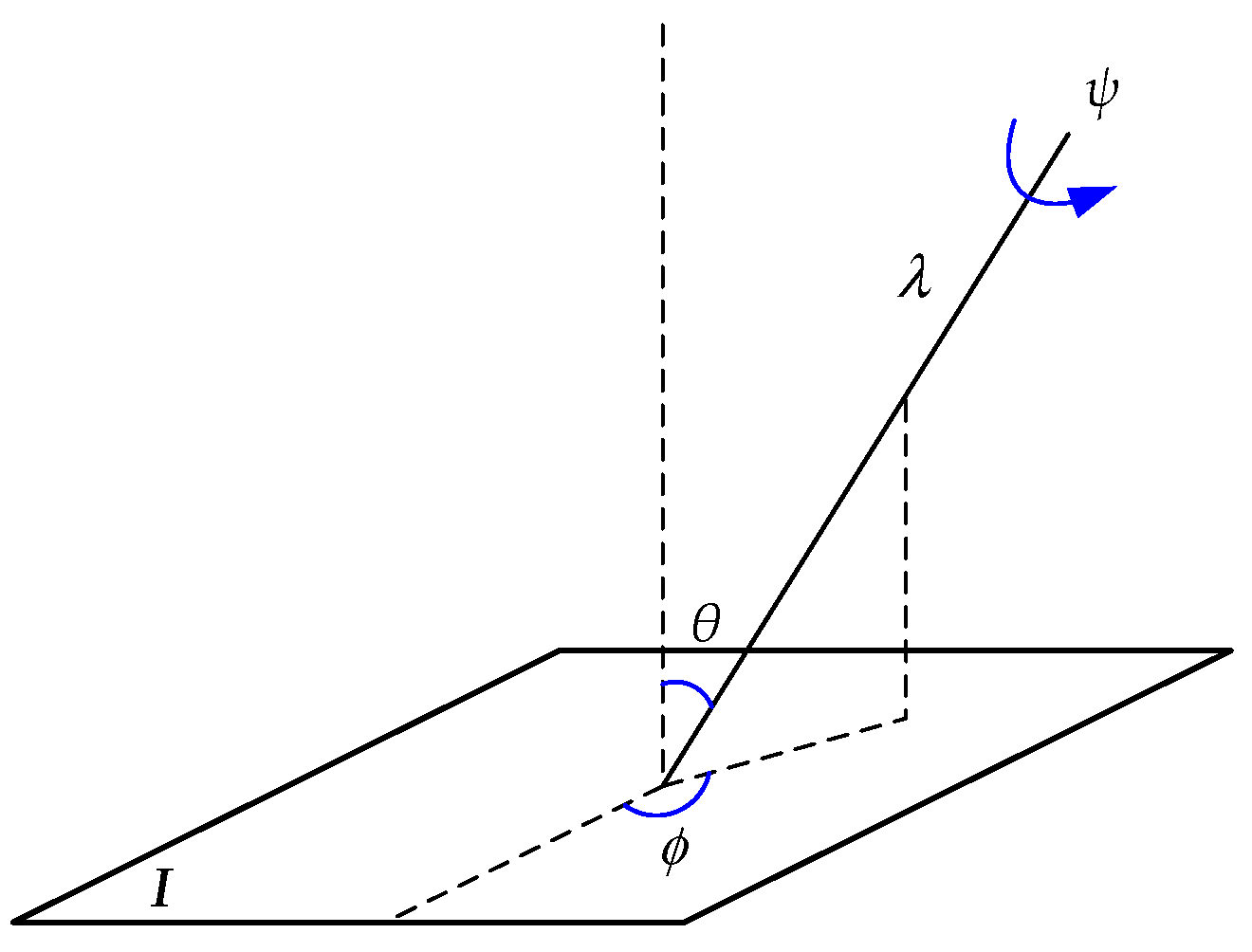
The core idea of the ASIFT is changing the spatial position of camera optical axis to simulate different viewpoints of images, and then the procedure which is similar to the SIFT algorithm is applied to extract feature points from simulated images. The affine map $\mathit{A}$ can be decomposed uniquely as Equation (4):

$$\mathit{A}={\mathit{H}}_{\lambda }{\mathit{R}}_1(\psi ){\mathit{T}}_t{\mathit{R}}_2(\mathit{\varphi })=\lambda \left[\begin{array}{cc}\cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{array}\right]\left[\begin{array}{cc}t& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}\cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \end{array}\right],$$

(4)

where $\lambda >0$, and $\lambda t$ is the determinant of $\mathit{A}$. ${\mathit{R}}_1$ and ${\mathit{R}}_2$ are rotation matrices. $\varphi$ is a rotation angle around image normal by the camera, and $\psi$ is the roll angle around the camera axis. Additionally, ${\mathit{T}}_t$ is a tilt parameter, which is a diagonal matrix whose first eigenvalue $t>1$ and the second one is equal to 1.

The description of affine decomposition in the geometric aspect is shown in Figure 2, which demonstrates the viewpoints angles $\varphi$ and $\theta$, the camera spin $\psi$, the zoom parameter $\lambda$, and the image $\mathit{I}$. When the camera starts to move around the image, latitude and longitude angles will be obtained. The plane including the normal and the optical axis forms an angle $\varphi$ with a fixed vertical plane, which is named as longitude. Its optical axis then forms an angle $\theta$ with the normal to the image plane $\mathit{I}$, which is named as latitude. Compared with SIFT, there are three parameters in ASIFT, which are the scale, the camera longitude angle, and the camera latitude angle. Besides, rotation and scaling parameters are normalized.

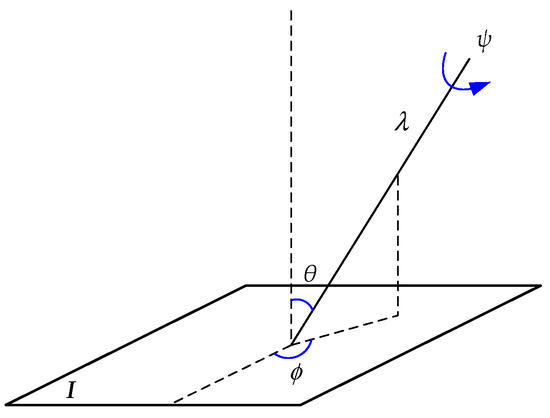
Figure 2. Geometric interpolation of affine decomposition.

The procedures of ASIFT can be concluded generally as following steps.

Step 1

The original image is performed by simulating all affine distortions resulted from camera optical axis change a frontal position. As is introduced above, these distortions are achieved by changing the longitude $\varphi$ and latitude $\theta$ gradually. Concretely, the experimental image is performed by rotations $\varphi$ and tilts with the parameter of $t=1/\left|\cos \theta \right|$, respectively.

Step 2

The image stimulated in Step 1 is compared with a similarity invariant matching algorithm, where the SIFT is applied.

Step 3

As we all know, SIFT algorithm has its own elimination methods for the wrong points matching, which can still result in a certain number of false matches. Owing to the fact that ASIFT compares many pairs of points, many false matches can be accumulated. To consider the most reliable method, optimized random sampling algorithm (ORSA) [30] is applied to filter out false matches, which is more robust than the classic random sample consensus (RANSAC) algorithm.

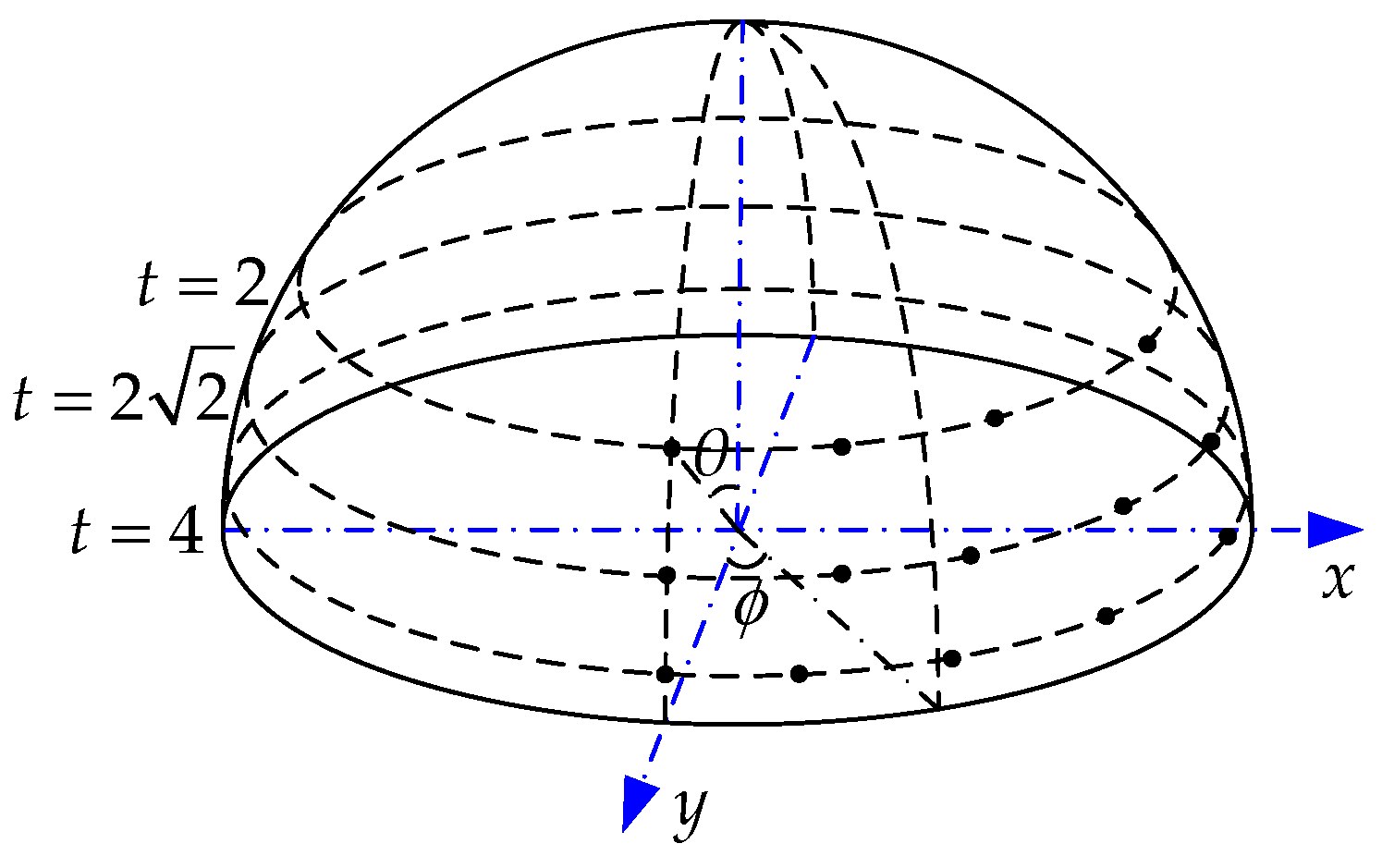
So far, by only changing the combination of the tilt and rotation parameters, ASIFT can be achieved for full affine invariance simulation. As is shown in Figure 3, examples of the camera position according to different pairs of $\varphi$ and $\theta$ are denoted. After locating the camera position, simulated affine images can be obtained from each position.

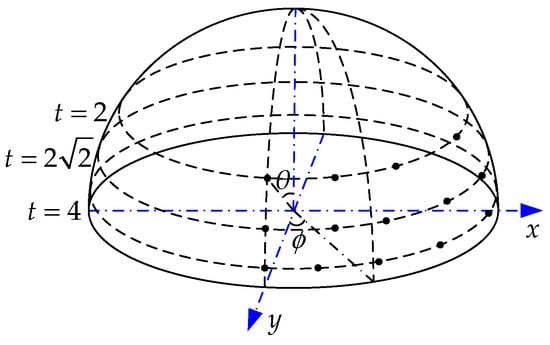
Figure 3. Observation hemisphere for different camera position.

3. Resynchronization Algorithm Based on ASIFT

In general, the image can be attacked by different kinds of factors, such as common image processing and geometric attacks. Most robust image watermarking can resist the common processing, but geometric attacks can change the properties of an image, which can result in the destruction of watermark synchronization. To overcome this problem, an ASIFT-based resynchronization algorithm is used to extract the feature points as reference points for matching establishment between watermarked and received images. Then, the distortion parameter will be calculated and inverse processing can be done before watermark extraction to get the corrected image.

3.1. Resynchronization of Rotation

The definition of rotation operation is to rotate the image by a certain angle, which may result in the information loss of the original image. After obtaining the feature points of the watermarked image and attacked image, the resynchronization process of rotation can be expressed as

$${\alpha }_{\mathrm{r}}=\frac{1}{q}{\displaystyle \sum _{k=1}^q{\beta }_k}, {\beta }_k=\arccos (\frac{\overrightarrow{i_{\mathrm{w}}{j}_{\mathrm{w}}}\times \overrightarrow{i_{\mathrm{a}}{j}_{\mathrm{a}}}}{\left|\overrightarrow{i_{\mathrm{w}}{j}_{\mathrm{w}}}\right|\times \left|\overrightarrow{i_{\mathrm{a}}{j}_{\mathrm{a}}}\right|}),$$

(5)

where ${\alpha }_{\mathrm{r}}$ is the correction factor of the rotation, $q$ is the quantity of the matching points between two images, $k$ is the rank of matchings, and ${\beta }_k$ is the angle between two images in one matching of the rank $k$. Moreover, according to the basic mathematic theory of the angle between two vectors, which is that $\overrightarrow{a}\times \overrightarrow{b}=\left|a\right|\left|b\right|\cos {\theta }_{a,b}$, the ${\beta }_k$ can be calculated. Based on the coordinates of the matching points, the vectors between two matching points can be obtained, which are $\overrightarrow{i_{\mathrm{w}}{j}_{\mathrm{w}}}$, vectors in the watermarked image and $\overrightarrow{i_{\mathrm{a}}{j}_{\mathrm{a}}}$, vectors in the received image. Finally, the ${\beta }_k$ can be obtained according to trigonometric function transform.

Figure 4 shows the matchings between watermarked image and rotated image ($45°$).

Figure 4. Matching points between image and rotated image ($45°$).

3.2. Resynchronization of Translation

The definition of a translation operation is to move the pixel points in an image from one coordinate to the other one vertically or horizontally, which can lead to the error position of the pixel points. After obtaining the feature points of the watermarked image and received image, the resynchronization process of translation can be expressed as

$$(x_{\mathrm{t}},y_{\mathrm{t}})=\{\begin{array}{cc}(x_{\mathrm{a}}-x_{\mathrm{w}}+M,y_{\mathrm{a}}-y_{\mathrm{w}}+N),\hfill & \hfill x_{\mathrm{a}}<x_{\mathrm{w}},y_{\mathrm{a}}<y_{\mathrm{w}},\hfill \\ (x_{\mathrm{a}}-x_{\mathrm{w}},y_{\mathrm{a}}-y_{\mathrm{w}}),\hfill & \hfill \mathrm{otherwise},\hfill \end{array}$$

(6)

where $(x_{\mathrm{t}},y_{\mathrm{t}})$ is the corrected coordinate of the received image, $(x_{\mathrm{a}},y_{\mathrm{a}})$ is the coordinate of the points in the attacked image, and $(x_{\mathrm{w}},y_{\mathrm{w}})$ is the coordinate in the watermarked image. Besides, sizes of both watermarked image and attacked image are $M\times N$. Apparently, the resynchronization of the translation is to move the pixel points with the same number of pixels in the converse direction for the translation compensation.

Figure 5 shows the matchings between watermarked image and translated image vertically (256 pixels).

Figure 5. Matching points between watermarked image and translated image vertically (256 pixels).

3.3. Resynchronization of Scaling

The definition of scaling operation is to zoom in and out of the image with a certain ratio, which can result in the ratio distortion of the original image. Similarly, after obtaining the feature points of the watermarked image and attacked image, the resynchronization process of scaling can be expressed as

$${\alpha }_s=\frac{1}{q}{\displaystyle \sum _{k=1}^q\frac{s_{{\mathrm{w}}_k}}{s_{{\mathrm{a}}_k}}},$$

(7)

where the scaling correction factor ${\alpha }_s$ can be calculated by the sum of the ratio between watermarked image $s_{{\mathrm{w}}_k}$ and attacked image $s_{{\mathrm{a}}_k}$. $q$ is the quantity of the matching points between two images, and $k$ is the rank of matchings. After ${\alpha }_s$ is obtained, the attacked image can be scaled with the inverse ratio, and the resynchronized image can be reconstructed.

Figure 6 shows the matchings between watermarked image and image after scaling (0.5).

Figure 6. Matching feature points between watermarked image and scaled image (0.5).

4. The Proposed Algorithm

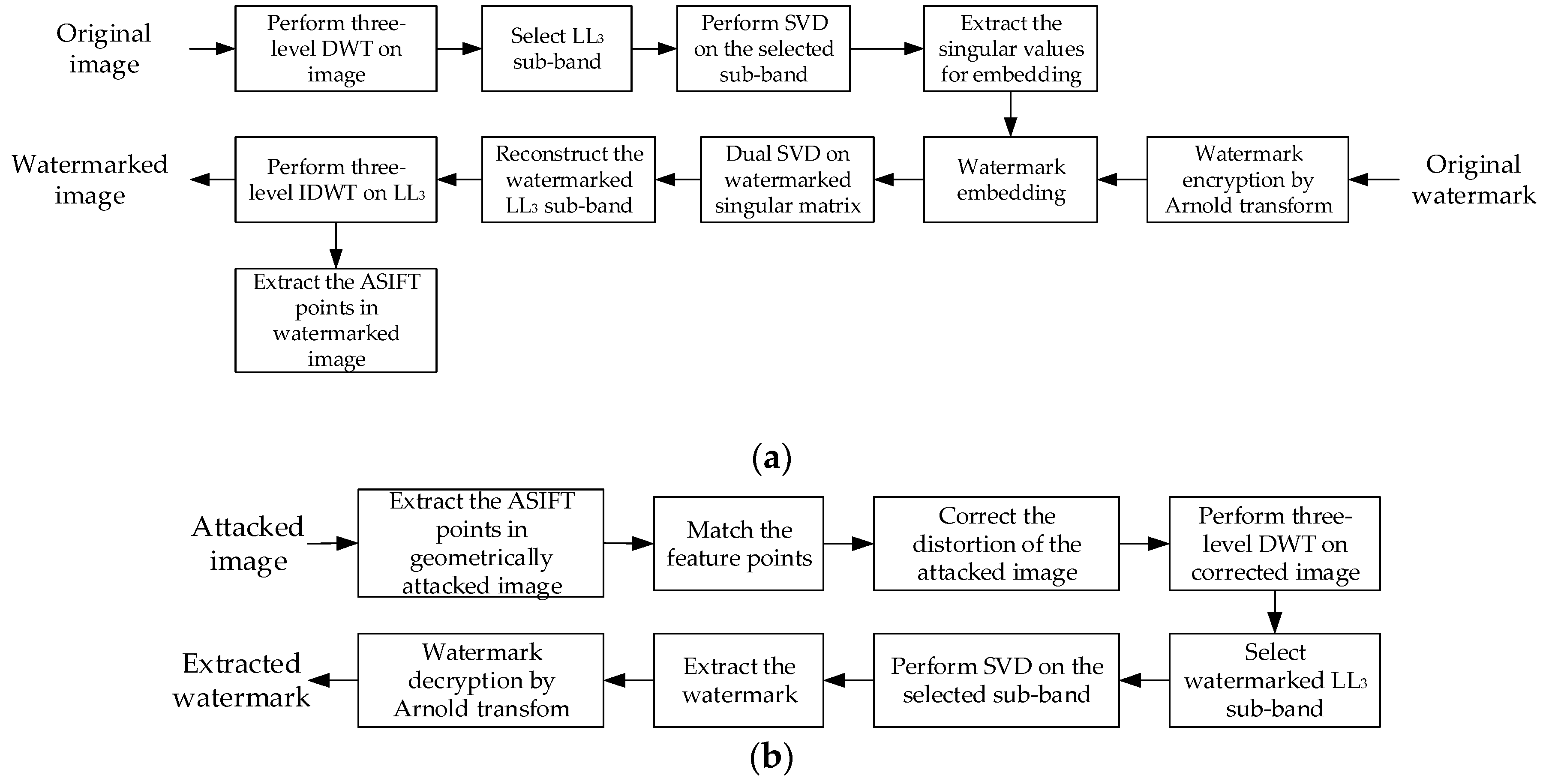
The basic procedure of the proposed algorithm can be concluded as three stages: the watermark embedding stage, resynchronization, and watermark extraction. For easy demonstration, the resynchronization process is categorized as a part of watermark extraction. Moreover, in order to improve the security of the watermarking scheme, Arnold transform is applied to scramble the watermark for encryption. With the help of a certain key, the watermark can be scrambled, and the extracted watermark can be decrypted similarly with the certain key in the extraction phase. The watermark embedding and extraction methods are shown in Figure 7a and Figure 7b, respectively. Watermark embedding and extraction algorithms are given below.

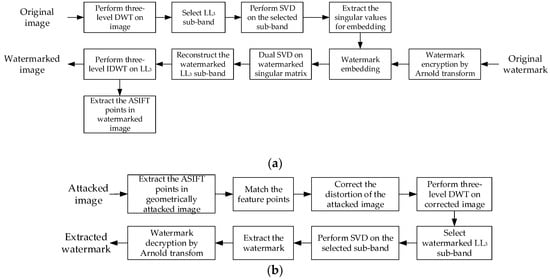
Figure 7. Flowchart of watermark embedding and extraction: (a) watermark embedding; (b) watermark extraction.

Algorithm 1 Watermark Embedding Algorithm

Variable Declaration: Elaine: host image SDU: watermark image I: read the host image W: read the watermark image $\alpha$: scaling factor for controlling the embedding intensity DWT, SVD and ASIFT: transform applied in the algorithm Wavelet filters: Haar Arnold: the scrambling algorithm K: the period for scrambling LL1, LH1, HL1, and HH1: first level DWT coefficients for host image LL2, LH2, HL2, and HH2: second level DWT coefficients for LL1 LL3, LH3, HL3, and HH3: third level DWT coefficients for LL2 $\mathit{W}$: watermark image $\mathit{S}$: diagonal matrix for LL3 $\mathit{U}$ and $\mathit{V}$: orthogonal matrices for LL3 ${\mathit{S}}_{\mathrm{w}}$: the watermarked diagonal matrix ${\mathit{S}}_{\mathrm{ww}}$: diagonal matrix for ${\mathit{S}}_{\mathrm{w}}$ ${\mathit{U}}_{\mathrm{w}}$ and ${\mathit{V}}_{\mathrm{w}}$: orthogonal matrices for ${\mathit{S}}_{\mathrm{w}}$ ${\mathit{I}}_{\mathrm{w}}$: watermarked image T: transpose of the matrix LL3w: the watermarked LL3 LL2w: the watermarked LL2 LL1w: the watermarked LL1 $P$: feature points key by ASIFT Embedding Procedure: 1 Read the images. I$\leftarrow$Elaine.bmp (host image with size of 512 × 512); W$\leftarrow$SDU.bmp (watermark image with size of 64 × 64); 2 Apply three-level DWT on the host image. [LL1, LH1, HL1, HH1]$\leftarrow$DWT (I, ‘Haar’); [LL2, LH2, HL2, HH2]$\leftarrow$DWT (LL1, ‘Haar’); [LL3, LH3, HL3, HH3]$\leftarrow$DWT (LL2, ‘Haar’); 3 Choose the LL3 sub-band in Step 4 $\mathit{U}\mathit{S}{\mathit{V}}^{\mathrm{T}}$$\leftarrow$SVD (LL3); 4 Select the optimized scaling factor from 0.1 to 1 manually. $\mathit{W}$ = Arnold (W, K); for $\alpha$$\leftarrow$0.01:1 ${\mathit{S}}_{\mathrm{w}}=\mathit{S}+\alpha \times \mathit{W}$; endfor; 5 Perform the dual SVD ${\mathit{U}}_{\mathrm{w}}{\mathit{S}}_{\mathrm{ww}}{\mathit{V}}_{\mathrm{w}}{}^{\mathrm{T}}$$\leftarrow$SVD (${\mathit{S}}_{\mathrm{w}}$); 6 Reconstruct the watermarked three-level LL sub-band. LL3w$\leftarrow$$\mathit{U}{\mathit{S}}_{\mathrm{ww}}{\mathit{V}}^{\mathrm{T}}$; 7 Apply inverse DWT for three times on the sub-band to reconstruct the watermarked image. LL2w$\leftarrow$inverse DWT (LL3w, LH3, HL3, HH3); LL1w$\leftarrow$inverse DWT (LL2w, LH2, HL2, HH2); ${\mathit{I}}_{\mathrm{w}}$$\leftarrow$inverse DWT (LL1w, LH1, HL1, HH1); 8 Acquire the ASIFT feature points. $P$$\leftarrow$ASIFT (${\mathit{I}}_{\mathrm{w}}$);

Algorithm 2 Watermark Extraction Algorithm

Variable Declaration: Ia: read the attacked image ${\mathit{I}}_{\mathrm{a}}$: attacked image at the receiving end $P$: feature points key by ASIFT in watermarked image $P_{\mathrm{a}}$: feature points key by ASIFT in attacked image ${\mathit{I}}_{\mathrm{c}}$: corrected image after the resynchronization process $\alpha$: scaling factor $M$: matchings $d_{\mathrm{r}}$: rotation distortion parameter $d_{\mathrm{s}}$: scaling distortion parameter $c_{\mathrm{r}}$: corrected parameter of rotation $c_{\mathrm{s}}$: corrected parameter of scaling $x_{\mathrm{c}}$: corrected x-coordinate of translation $y_{\mathrm{c}}$: corrected y-coordinate of translation $x_{\mathrm{w}}$: x-coordinate of feature points in watermarked image $y_{\mathrm{w}}$: y-coordinate of feature points in watermarked image $x_{\mathrm{a}}$: x-coordinate of feature points in attacked image $y_{\mathrm{a}}$: y-coordinate of feature points in attacked image $M$: length of image $N$: width of image Arnold: the scrambling algorithm K: the period of scrambling DWT, SVD and ASIFT: transform applied in the algorithm Wavelet filters: Haar LL1w*, LH1*, HL1*, and HH1*: first level DWT coefficients for ${\mathit{I}}_{\mathrm{c}}$ LL2w*, LH2*, HL2*, and HH2*: second level DWT coefficients for LL1w* LL3w*, LH3*, HL3*, and HH3*: third level DWT coefficients for LL2w* ${\mathit{W}}_{\mathrm{e}}^{*}$: extracted watermark image ${\mathit{U}}^{*}$ and ${\mathit{V}}^{*}$: orthogonal matrices for LL3* ${\mathit{S}}_{\mathrm{w}}^{*}$: watermarked diagonal matrix in corrected image ${\mathit{S}}_{\mathrm{ww}}^{*}$: watermarked diagonal matrix for ${\mathit{S}}_{\mathrm{w}}^{*}$ ${\mathit{U}}_{\mathrm{w}}$ and ${\mathit{V}}_{\mathrm{w}}$: orthogonal matrices for ${\mathit{S}}_{\mathrm{w}}$ T: transpose of the matrix Extraction Procedure: 1 Read the attacked image. Ia$\leftarrow$Attacked image.bmp; 2 Perform ASIFT on attacked image to extract the feature points for resynchronization $P_{\mathrm{a}}$$\leftarrow$ASIFT (${\mathit{I}}_{\mathrm{a}}$); 3 Feature matching and watermark resynchronization. Find the matchings between $P_{\mathrm{a}}$ and $P$. $M$$\leftarrow$matching ($P_{\mathrm{a}}$, $P$); Judge the type of attacks. if ($d_{\mathrm{r}}\ne 0$) then ${\mathit{I}}_{\mathrm{c}}$$\leftarrow$imrotate (${\mathit{I}}_{\mathrm{a}}$,$c_{\mathrm{r}}$); endif; if ($d_{\mathrm{s}}\ne 0$) then ${\mathit{I}}_{\mathrm{c}}$$\leftarrow$imresize (${\mathit{I}}_{\mathrm{a}}$,$c_{\mathrm{r}}$); endif; if ($d_{\mathrm{t}}\ne 0$) then //x-coordinate correction if ($x_{\mathrm{w}}>x_{\mathrm{a}}$) then $x_{\mathrm{c}}=x_{\mathrm{a}}-x_{\mathrm{w}}+M$ else $x_{\mathrm{c}}=x_{\mathrm{a}}-x_{\mathrm{w}}$; endif; //y-coordinate correction if ($y_{\mathrm{w}}>y_{\mathrm{a}}$) then $y_{\mathrm{c}}=y_{\mathrm{a}}-y_{\mathrm{w}}+N$; else $y_{\mathrm{c}}=y_{\mathrm{a}}-y_{\mathrm{w}}$; endif; endif; 4 Perform DWT on corrected Image to get the LL3 with watermark information [LL1w*, LH1, HL1, HH1]$\leftarrow$DWT (${\mathit{I}}_{\mathrm{c}}$, ‘Haar’); [LL2w*, LH2, HL2, HH2]$\leftarrow$DWT (LL1w*, ‘Haar’); [LL3w*, LH3, HL3, HH3]$\leftarrow$DWT (LL2w*, ‘Haar’); 5 Perform SVD on the selected sub-band. ${\mathit{U}}_{\mathrm{w}}{\mathit{S}}_{\mathrm{ww}}{\mathit{V}}_{\mathrm{w}}{}^{\mathrm{T}}$$\leftarrow$SVD (${\mathit{S}}_{\mathrm{w}}$); 6 Matrix ${\mathit{S}}_{\mathrm{w}}^{*}$ retrieval. ${\mathit{S}}_{\mathrm{w}}^{*}={\mathit{U}}_{\mathrm{w}}{\mathit{S}}_{\mathrm{ww}}^{*}{\mathit{V}}_{\mathrm{w}}^{\mathrm{T}}$; 7 Watermark extraction and decryption. ${\mathit{W}}_{\mathrm{e}}^{*}=({\mathit{S}}_{\mathrm{w}}^{*}-\mathit{S})/\alpha$; ${\mathit{W}}_{\mathrm{e}}^{*}$ = Arnold (${\mathit{W}}_{\mathrm{e}}^{*}$, K);

5. Experimental Results and Discussion

In this section, performances of the ASIFT-based watermarking method are shown and discussed, which is executed on the 512 × 512 host image and 64 × 64 binary watermark. Additionally, the scheme is tested on MATLAB R2015a with an Intel (R) Core (TM), i7-6500U 2.50 GHz CPU, 6 GB memory computer. To testify the effectiveness of the proposed algorithm, the watermarking scheme is performed on several images, which are shown in Figure 8.

Figure 8. Test images: (a) Airplane; (b) Elaine; (c) Lena; (d) Mountain; (e) Bank; (f) Peppers; (g) Milk drop; (h) Gold hill.

5.1. Performance Evaluation

The performance of the watermarking algorithm can be evaluated in aspects of imperceptibility and robustness mainly by two indexes: peak signal-to-noise ratio (PSNR) and normalized correlation (NC) coefficients. Generally, a larger PSNR value represents a better visual quality and imperceptibility, and watermarked image whose PSNR is greater than 35 dB can be acceptable. The definition of PSNR for the image with size of $M\times N$ can be

$$\mathrm{PSNR}=10\lg \frac{{255}^2}{\mathrm{MSE}}=10\lg \left[\frac{{255}^{2}MN}{{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}{\left[\mathit{I}(i,j)-{\mathit{I}}_{\mathrm{w}}(i,j)\right]}^2}}}\right](\mathrm{dB}),$$

(8)

where $\mathit{I}(i,j)$ is the pixel coordinate in the original image, and ${\mathit{I}}_{\mathrm{w}}(i,j)$ is that in the watermarked image. MSE is the short form for mean square error.

The robustness of the algorithm can be determined by NC with the value range from 0 to 1, which evaluates the similarity between original watermark and extracted watermark. Similarly, the NC should be 1, but the value greater than 0.7 is acceptable.

$$\mathrm{NC}=\frac{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n\mathit{W}(i,j)\times {\mathit{W}}_{\mathrm{e}}(i,j)}}}{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n\mathit{W}(i,j)\times \mathit{W}(i,j)}}},$$

(9)

where $\mathit{W}(i,j)$ and ${\mathit{W}}_{\mathrm{e}}(i,j)$ are original watermark and the extracted watermark, respectively. The size of the watermark is $m\times n$.

5.2. Results and Discussion

5.2.1. Performance of Imperceptibility

To test the watermark transparency of the watermarked image, the image labelled ‘Elaine’ is used, which contains abundant information, and watermark image of the letter ‘SDU’ (the abbreviation for Shandong University) is used to finish the experiments. As is shown in Figure 9, the watermarked image can achieve good quality of transparency compared with the original image.

Figure 9. Transparency of the watermarked image: (a) original image; (b) original watermark; (c) watermarked image; (d) extracted watermark.

Additionally, the number of ASIFT feature points in test images are shown in Table 1.

Table 1. Number of affine-scale-invariant feature transform (ASIFT) feature points.

Watermarked Images	Number of Points
Airplane	14,184
Elaine	9864
Lena	10,068
Mountain	25,833
Bank	11,728
Peppers	8651
Milk drop	6674
Gold hill	17,073

As can be seen in Table 1, the number of points obtained by ASIFT are significant, which has advantages for points matching and distortion correction.

5.2.2. Performance of Robustness

To test the robustness of the proposed watermarking scheme thoroughly, common attacks and geometric attacks are performed on the watermarked images. Here, the image labelled ‘Elaine’ is selected as the specific illustration. Figure 10 gives the attacked images and extracted watermarks under different kinds of processes and attacks, which contains JPEG (50 and 70), salt and pepper noise with densities of 0.01 and 0.05, speckle noise with density of 0.01 and 0.1, Gaussian noise with the mean of 0 and the variances of 0.05 and 0.1, median filter with the window sizes of 3 × 3, 4 × 4, and 5 × 5, and center cropping (25%).

Figure 10. Attacked images and extracted watermarks under different kinds of attacks: (a) JPEG (70); (b) extracted watermark from (a); (c) JPEG (50); (d) extracted watermark from (c); (e) salt and pepper noise (0.01); (f) watermark extracted from (e); (g) salt and pepper noise (0.05); (h) extracted watermark from (g); (i) speckle noise (0.01); (j) extracted watermark from (i); (k) speckle noise (0.1); (l) extracted watermark from (k); (m) Gaussian noise (0, 0.01); (n) extracted watermark from (m); (o) Gaussian noise (0, 0.05); (p) extracted watermark from (o); (q) median filter (3 × 3); (r) extracted watermark from (q); (s) median filter (4 × 4); (t) extracted watermark from (s); (u) median filter (5 × 5); (v) extracted watermark from (u); (w) center cropping (25%); (x) extracted watermark from (w).

In Figure 11, attacked images and extracted watermarks under different kinds of geometric attacks are given, including scaling with parameters of 0.25, 0.5, 0.9, and 1.2, rotation with parameters of $5°$, $10°$, $30°$, and $45°$, and translation with parameters of 128 pixels and 256 pixels in horizontal and vertical directions.

Figure 11. Attacked images and extracted watermarks under geometric attacks: (a) $5°$ rotation; (b) extracted watermark from (a); (c) $10°$ rotation; (d) extracted watermark from (c); (e) $30°$ rotation; (f) extracted watermark from (e); (g) $45°$ rotation; (h) extracted watermark from (g); (i) scaling (0.25); (j) extracted watermark from (i); (k) scaling (0.5); (l) extracted watermark from (k); (m) scaling (0.9); (n) extracted watermark from (m); (o) scaling (1.2); (p) extracted watermark from (o); (q) vertical translation (256 pixels); (r) extracted watermark from (q); (s) horizontal translation (256 pixels); (t) extracted watermark from (s).

Table 2 and Table 3 give the robustness performance of the proposed scheme on different images, and the image labelled ‘Elaine’ with less points as well as the image labelled ‘Gold hill’ with more points are selected as the representatives.

Table 2. Robustness of the proposed algorithm on image Elaine.

Common Attacks	NC	Geometric Attacks	NC
No attacks	0.9980	Scaling 0.25	0.9904
JPEG (50)	0.9966	Scaling 0.5	0.9969
JPEG (70)	0.9971	Scaling 0.9	0.9961
Median filter (3 × 3)	0.9939	Scaling 1.2	0.9911
Median filter (4 × 4)	0.9868	Rotation $2°$	0.9704
Median filter (5 × 5)	0.9858	Rotation $5°$	0.9542
Gaussian noise (0, 0.05)	0.9293	Rotation $10°$	0.9784
Gaussian noise (0, 0.1)	0.8315	Rotation $30°$	0.9685
Speckle noise (0.01)	0.9873	Rotation $45°$	0.9608
Speckle noise (0.1)	0.9254	Horizontally translation (256 pixels)	0.9974
Salt and pepper noise (0.01)	0.9856	Vertically translation (256 pixels)	0.9974
Salt and pepper noise (0.05)	0.9452	Horizontally translation (128 pixels)	0.9978
Center cropping (25%)	0.8461	Vertically translation (128 pixels)	0.9978

Table 3. Robustness of the proposed algorithm on image Gold hill.

Common Attacks	NC	Geometric Attacks	NC
No attacks	0.9978	Scaling 0.25	0.9910
JPEG (50)	0.9964	Scaling 0.5	0.9972
JPEG (70)	0.9973	Scaling 0.9	0.9968
Median filter (3 × 3)	0.9955	Scaling 1.2	0.9943
Median filter (4 × 4)	0.9885	Rotation $2°$	0.9802
Median filter (5 × 5)	0.9896	Rotation $5°$	0.9867
Gaussian noise (0, 0.05)	0.9253	Rotation $10°$	0.9909
Gaussian noise (0, 0.1)	0.8492	Rotation $30°$	0.9893
Speckle noise (0.01)	0.9921	Rotation $45°$	0.9909
Speckle noise (0.1)	0.9670	Horizontally translation (256 pixels)	0.9973
Salt and pepper noise (0.01)	0.9835	Vertically translation (256 pixels)	0.9973
Salt and pepper noise (0.05)	0.9507	Horizontally translation (128 pixels)	0.9976
Center cropping (25%)	0.8597	Vertically translation (128 pixels)	0.9976

As can be seen in Table 2, the robustness performance of the proposed algorithm is given on the host image ‘Elaine’ and the watermark image ‘SDU’. The PSNR value of the proposed method is 52.57 dB, which illustrates the good transparency of the watermarked image.

In Table 3, the robustness performance of the proposed algorithm is given on the host image ‘Gold hill’ and the watermark image ‘SDU’. The PSNR value is 51.01 dB. In general, the image labelled ‘Gold hill’ has more points than the image labelled ‘Elaine’. Thus, the robustness to geometric attacks on ‘Gold hill’ is a little better than that on ‘Elaine’.

5.3. Performance Comparison

To further prove the performance of the proposed algorithm, the experiments were executed on comparing the proposed method with previous scheme [31], which applied the SIFT algorithm for distortion correction. The NC results are shown in Table 4. It can be concluded that, the ASIFT-based watermarking scheme has better robustness in scaling, translation, and rotation in small angles than the watermarking algorithm based on SIFT.

Table 4. Performance comparisons with previous algorithms.

Attacks	SIFT [31]	ASIFT
Scaling 0.25	0.9832	0.9904
Scaling 0.5	0.9889	0.9969
Scaling 0.9	0.9901	0.9961
Scaling 1.2	0.9871	0.9911
Rotation $2°$	0.9887	0.9704
Rotation $5°$	0.9918	0.9542
Rotation $10°$	0.9954	0.9784
Rotation $30°$	0.9954	0.9685
Rotation $45°$	0.9941	0.9608
Horizontally translation (256 pixels)	0.9847	0.9974
Vertically translation (256 pixels)	0.9847	0.9974
Horizontally translation (128 pixels)	0.9853	0.9978
Vertically translation (128 pixels)	0.9853	0.9978

6. Conclusions

With the rapid development of image processing technology, altering the content of an image is easy for everyone, but may be illegal for an attacker. It is urgent and necessary to overcome this problem, to protect the integrity and authenticity of images. Watermarking is a powerful technique proposed to solve this problem. In this paper, an ASIFT-based robust watermarking algorithm is proposed to solve the geometric attacks in copyright protection issues. In the proposed algorithm, the watermark information is inserted into the low frequency sub-band after DWT three times, where the SVD is performed again for watermark embedding. While in the extraction process, to improve the robustness to geometric attacks, ASIFT is applied to obtain feature points which are invariant to geometric attacks. Then, features of acquired points between the watermarked image and received image are used to realize the resynchronization to improve the robustness. Experimental results show that the proposed algorithm achieves great balance between robustness and imperceptibility, and is robust against geometric attacks, JPEG compression, noise addition, copping, filter operation, and so on. In the future work, SIFT correction can be applied to video watermarking for rotation resistance.