A Biomimetic Approach for Designing a Full External Breast Prosthesis: Post-Mastectomy
Abstract
1. Introduction
- Symmetry and balance.
- Realism and sensitivity, analogous to a real breast.
- Lightness, which helps avoid and alleviate lymphedemas.
- Suitable for maintaining a comfortable environment in the scar region.
- Safe and reliable when carrying out a range of activities.
- Suitable for providing smooth adherence without pressure.
- Reusable and accessible for any person.
2. Materials and Methods
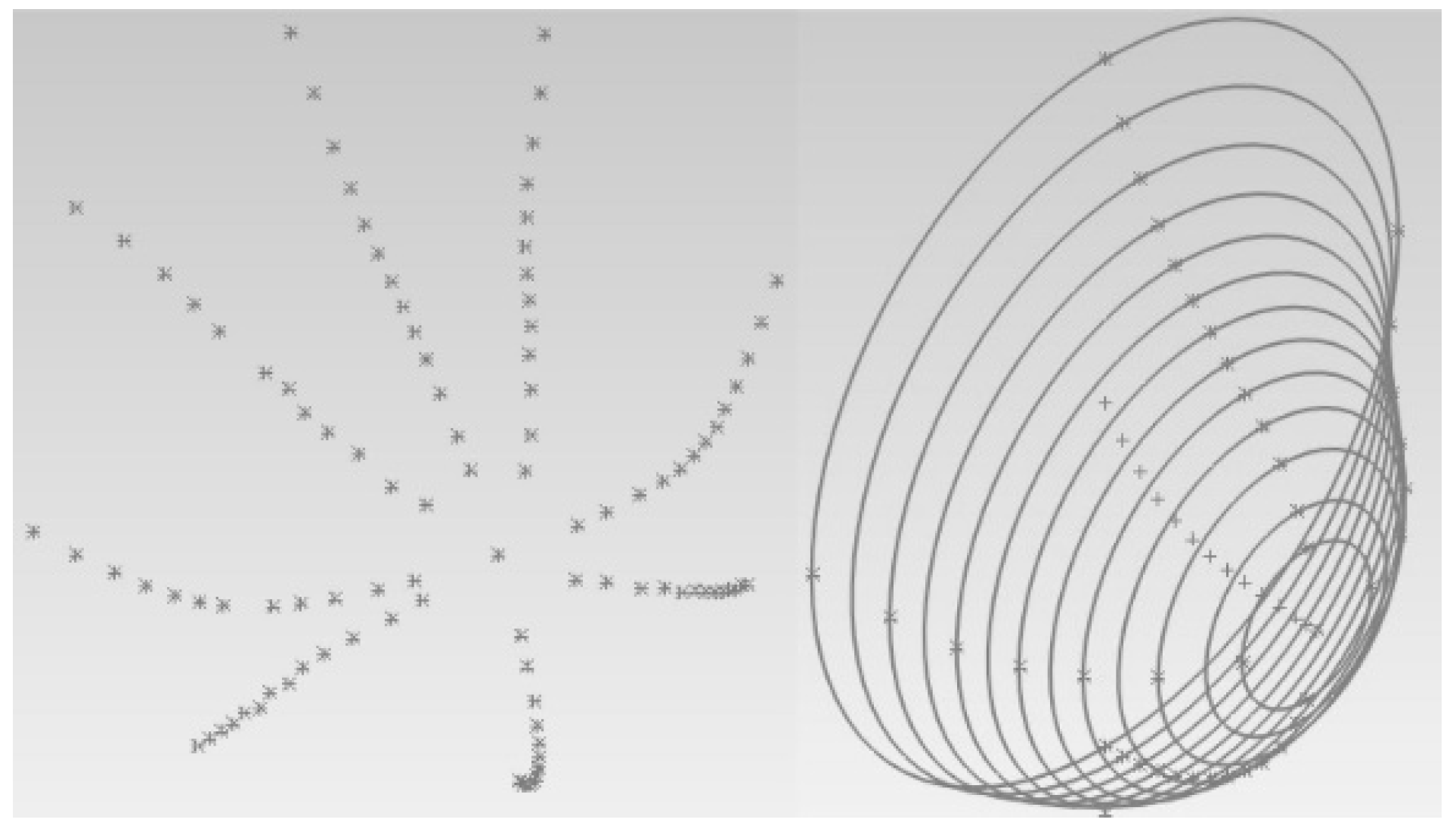
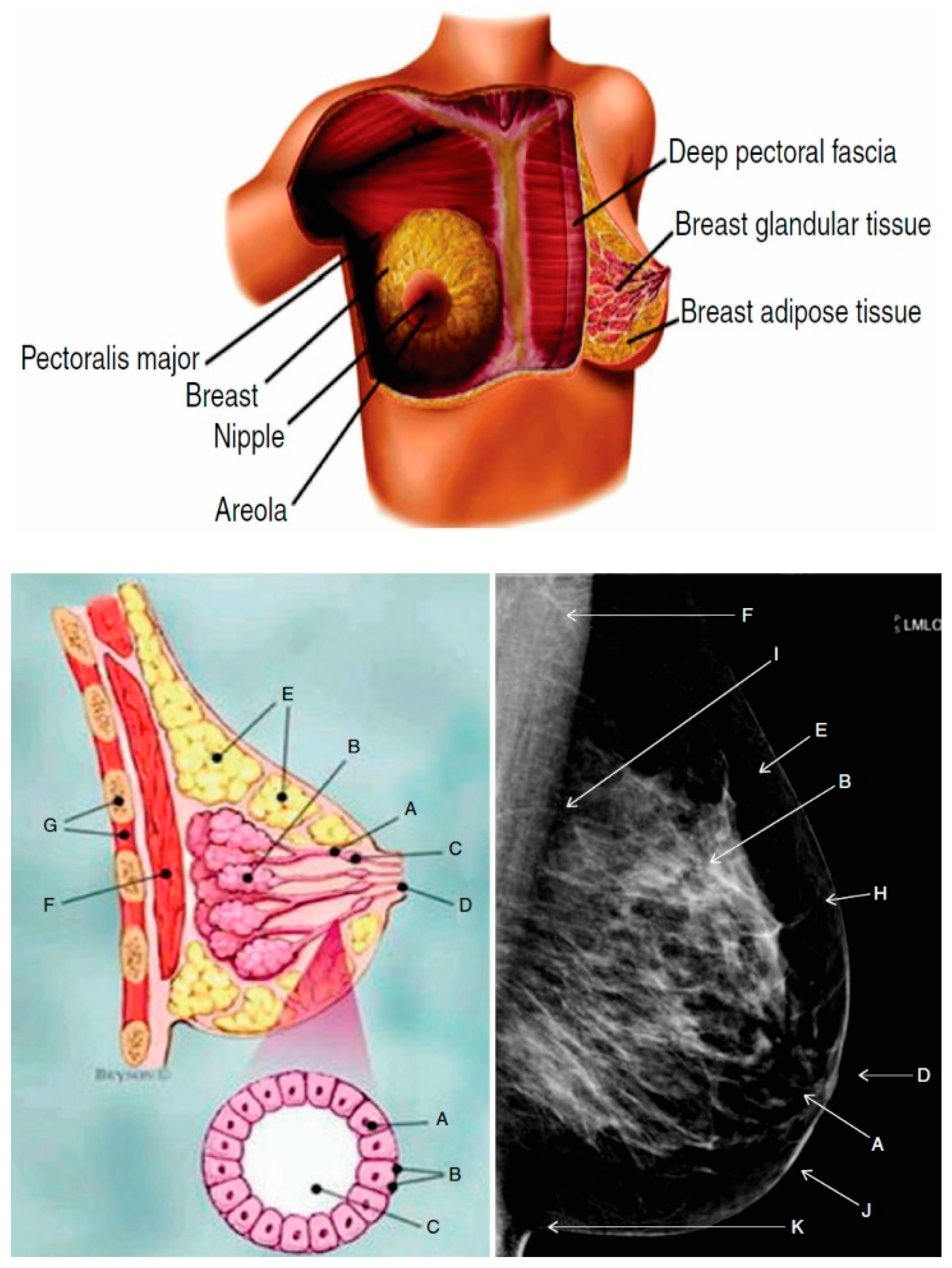
Morphology and Histology of the Female Mammary Gland
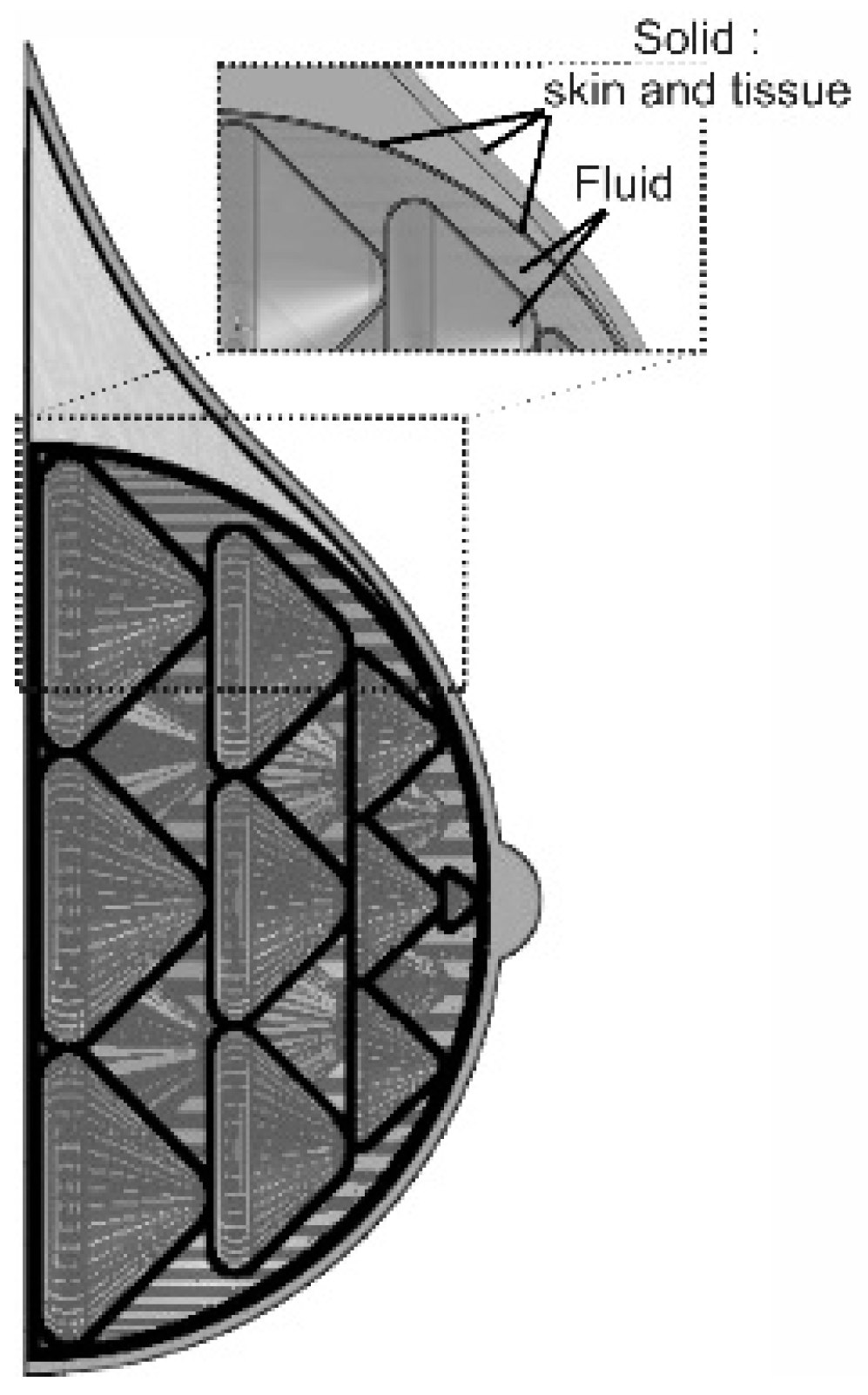
3. Model FEM: Modeling and Analysis in Finite Element
4. Results and Discussion
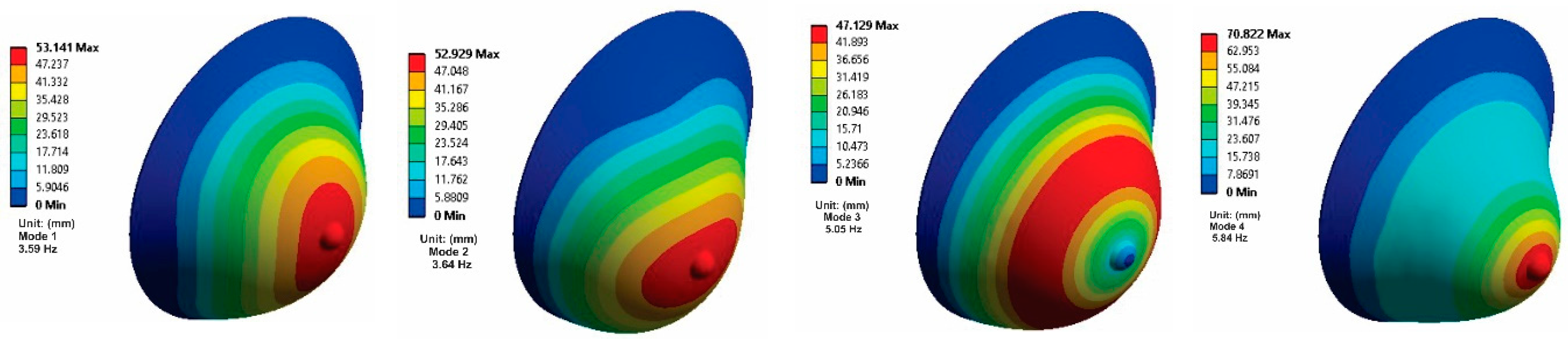
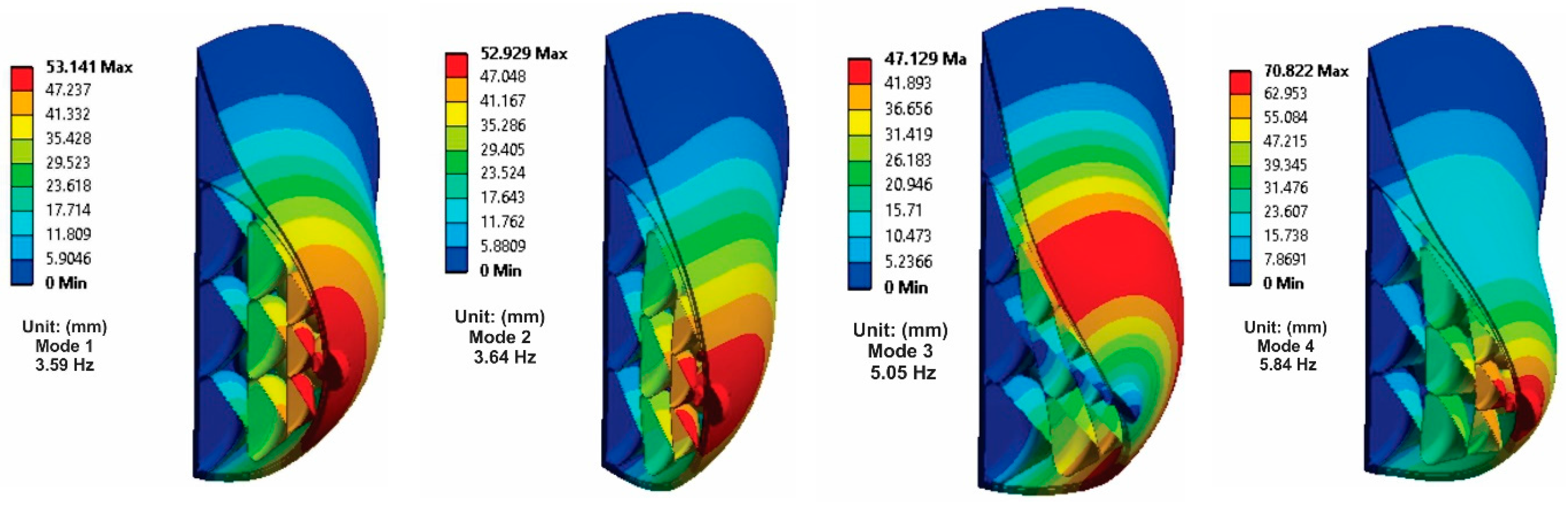
Modal Analysis
5. Discussion
6. Conclusions
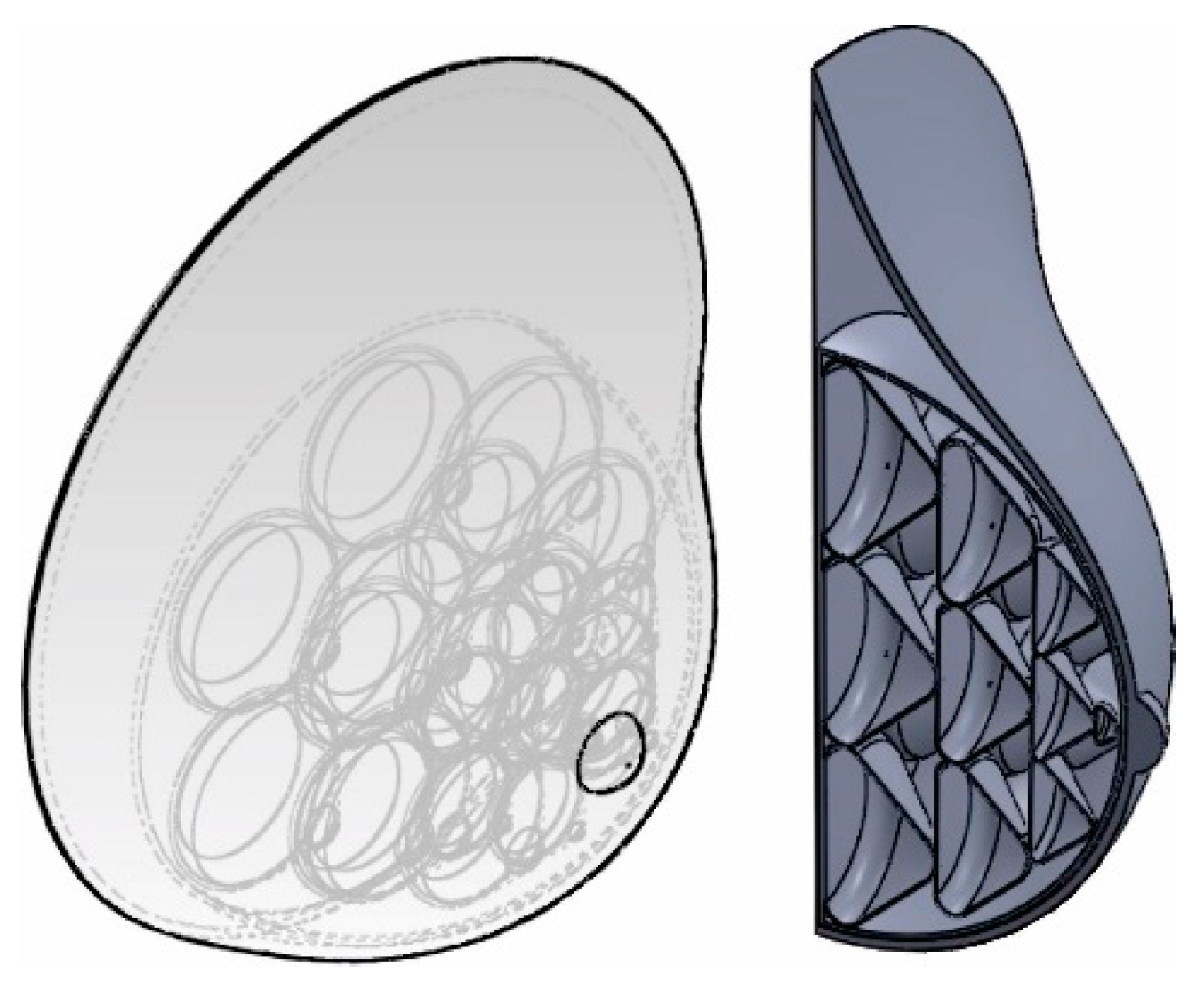
- We successfully biomimetize the internal structures of a real breast to design and analyze a breast prosthesis for cases of complete mastectomy. With the biomimetic technique, a realistic model of the prosthesis can be easily obtained.
- The lobular (biomimetic) geometry used for the design and the spherical adjustment that was adapted to define the internal structure of the prosthesis proposed in this work properly distributes the stress generated by the loads it was subject to. In addition, it can be concluded that the qualities and functioning of the prosthesis designed in this work will allow it to be adapted to different body types, by scaling the model, without affecting its functionality.
- The load cases considered for the prosthesis study do not show irregularities in contour or shape on their surface nor in the internal structure. The displacements and stress found in the prosthesis analysis are within the ranges reported in works related to diagnosis, detection, and evaluation of brassieres.
- Regarding final dimensions, finish, and manufacturability, the model was printed using ABS material. With this, it is possible that the prosthesis can be printed in 3D in an easy and uncomplicated way with the appropriate technology.
- With the dynamic analysis performed in the prosthesis model the fundamental frequencies were obtained. This will prevent reaching conditions of resonance (critical deformations) during use that can affect the natural behavior of the prosthesis or damage its structure. The above ensures that the proposed prosthesis design will not fail and can be used for a variety of activities.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Health Organization (OMS). Cáncer. 2017. Available online: http://www.who.int/topics/cancer/es/ (accessed on 26 June 2017).
- Jorge, L.M.T. Breast Cancer. 2007. Available online: https://www.insp.mx/images/stories/Centros/nucleo/docs/pme_19.pdf (accessed on 26 February 2016).
- National Institute of Statistics and Geography. Statistics for the Purpose of the World Day of the Fight against Breast Cancer. 19 October 2007. Available online: http://www.inegi.org.mx/saladeprensa/aproposito/2016/mama2016_0.pdf (accessed on 12 March 2016).
- American Cancer Society. Treatment of Breast Cancer According to Its Stage; American Cancer Society: Atlanta, GA, USA, 2016. [Google Scholar]
- Ciesla, S.; Polom, K. The effect of immediate breast reconstruction with Becker-25 prosthesis on the preservation of proper body posture in patients after mastectomy. Eur. J. Surg. Oncol. 2010, 36, 625–631. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H.-I.; Han, J.-S. Prosthetic rehabilitation with an implant-supported fixed prosthesis using computer-aided design and computer-aided manufacturing dental technology for a patient with a mandibulectomy: A clinical report. J. Prosthet. Dent. 2016, 115, 133–136. [Google Scholar] [CrossRef] [PubMed]
- Patel, G.; Harcourt, D.; Naqvi, H.; Rumsey, N. Black and South Asian women’s experiences of breast cancer: A qualitative study. Divers. Equal. Health Care J. 2014, 11, 135–149. [Google Scholar]
- Cieśla, S.; Bąk, M. The Effect of Breast Reconstruction on Maintaining a Proper Body Posture in Patients after Mastectomy. In Breast Reconstruction—Current Techniques; InTech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef][Green Version]
- Hojan, K.; Manikowska, F.; Chen, B.P.; Lin, C.C. The influence of an external breast prosthesis on the posture of women after mastectomy. J. Back Musculoskelet. Rehabil. 2016, 29, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Rincón Fernández, M.E.; Pérez San Gregorio, M.A.; Borda Más, M.; Martín Rodríguez, A. Psychological differences of breast cancer patients according to the type of breast surgery. Cir. Plást. 2010, 36, 359–368. [Google Scholar]
- American Cancer Society. Breast Reconstruction after Mastectomy. 2014. Available online: https://www.mwbreast.com/wp-content/uploads/2015/04/002992-pdf.pdf (accessed on 1 April 2016).
- Gallagher, P.; Buckmaster, A.; O’Carroll, S.; Kiernan, G.; Geraghty, J. External breast prostheses in post-mastectomy care: Women’s qualitative accounts. Eur. J. Cancer Care 2010, 19, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Fradinho, N.; Varanda, A.; Martins, J.B.; Martins, P.A. Heterotopic Ossification in Breast Prosthesis. Eplasty 2015, 15, ic7. [Google Scholar] [PubMed]
- Ramião, N.; Martins, P.; Fernandes, A.A.; da Luz Barroso, M.; Santos, D. Mechanical tests in all regions of the PIP breast implants. In Proceedings of the 2015 IEEE 4th Portuguese Meeting on Bioengineering (ENBENG), Porto, Portugal, 26–28 February 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Rynkevic, R.; Martins, P.; Parente, M.; Natal, R.; Barroso, M.; Santos, D. Implant shape influence on the mechanical behavior of breast implants. In Proceedings of the 2013 IEEE 3rd Portuguese Meeting in Bioengineering (ENBENG), Braga, Portugal, 20–23 February 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Mendonça, A.; Di Pompeo, F.S.; De Mezerville, R. Nanotechnology, nanosurfaces and silicone gel breast implants: current aspects. Case Rep. Plast. Surg. Hand Surg. 2017, 4, 99. [Google Scholar] [CrossRef] [PubMed]
- Mansoori, G.A.; Mohazzabi, P.; McCormack, P.; Jabbari, S. Nanotechnology in cancer prevention, detection and treatment: Bright future lies ahead. World Rev. Sci. 2007, 4, 226–257. [Google Scholar] [CrossRef]
- Borghesan, D.H.; Gravena, A.A.; Lopes, T.C.; Brischiliari, S.C.; de Oliveira Demitto, M.; Dell Agnolo, C.M.; de Barros Carvalho, M.D.; Pelloso, S.M. Variables that Affect the Satisfaction of Brazilian Women with External Breast Prostheses after Mastectomy. Asian Pac. J. Cancer Prev. 2014, 15, 9631–9634. [Google Scholar] [CrossRef] [PubMed]
- Moinina, D.; Herr, H. A Variable-Impedance Prosthetic Socket for a Transtibial Amputee Designed from Magnetic Resonance Imaging Data. J. Prosthet. Orthot. 2013, 25, 129–137. [Google Scholar]
- Eggbeer, D.; Evans, P. Computer-aided methods in bespoke breast prosthesis design and fabrication. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2011, 225, 94–99. [Google Scholar] [CrossRef] [PubMed]
- Azar, F.S.; Metaxas, D.N.; Schnall, M.D. A Deformable Finite Element Model of the Breast for Predicting Mechanical Deformations under External Perturbations. Acad. Radiol. 2001, 8, 965–975. [Google Scholar] [CrossRef]
- Raith, S.; Eder, M.; Von Waldenfels, F.; Jalali, J.; Volf, A.; Kovacs, L. Finite Element Simulation of the Deformation of the Female Breast Based on MRI Data and 3-D Surface Scanning: An In-Vivo Method to Assess Biomechanical Material Parameter Sets. In Proceedings of the 3rd International Conference on 3D Body Scanning Technologies, Lugano, Switzerland, 16–17 October 2012; pp. 196–203. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, P.Y.; Huang, M.L.; Hsu, J.T.; Han, R.P.; Wu, J. Simulation of breast compression in mammography using finite element analysis: A preliminary study. Radiat. Phys. Chem. 2017, 140, 295–299. [Google Scholar] [CrossRef]
- Mohammadyari, P.; Faghihi, R.; Mosleh-Shirazi, M.A.; Lotfi, M.; Hematiyan, M.R.; Koontz, C.; Meigooni, A.S. Calculation of dose distribution in compressible breast tissues using finite element modeling, Monte Carlo simulation and thermoluminescence dosimeters. Phys. Med. Biol. 2015, 60, 9185. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.H.; Ng, S.P.; Yu, W.; Zhou, J.; Wan, K.W. A study of breast motion using non-linear dynamic FE analysis. Ergonomics 2013, 56, 868–878. [Google Scholar] [CrossRef] [PubMed]
- Weis, J.A.; Miga, M.I.; Arlinghaus, L.R.; Li, X.; Chakravarthy, A.B.; Abramson, V.; Farley, J.; Yankeelov, T.E. A mechanically coupled reaction–diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy. Phys. Med. Biol. 2013, 58, 5851. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Hipwell, J.H.; Tanner, C.; Taylor, Z.; Mertzanidou, T.; Cardoso, J.; Ourselin, S.; Hawkes, D.J. Development of patient-specific biomechanical models for predicting large breast deformation. Phys. Med. Biol. 2012, 57, 455. [Google Scholar] [CrossRef] [PubMed]
- Unnikrishnan, V.U.; Unnikrishnan, G.U.; Reddy, J.N. Biomechanics of breast tumor: Effect of collagen and tissue density. Int. J. Mech. Mater. Des. 2012, 8, 257. [Google Scholar] [CrossRef]
- Smith, L.M.; Hall, N. A Numerical Investigation of Breast Compression: Lesion Modeling. Int. J. Contempor. Adv. Math. 2011, 2, 8–21. [Google Scholar]
- Carter, F.J. Biomechanical Modeling of the Breast for Image Guided Surgery. Ph.D. Thesis, University College, London, UK, 2009. Available online: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=3544B0E10859AD38D10BFFB1E68EF358?doi=10.1.1.452.5397&rep=rep1&type=pdf (accessed on 20 August 2016).
- Thanoon, D.; Garbey, M.; Kim, N.H.; Bass, B. A Computational Framework for Breast Surgery: Application to Breast Conserving Therapy. In Computational Surgery and Dual Training; Garbey, M., Bass, B., Collet, C., Mathelin, M., Tran-Son-Tay, R., Eds.; Springer: Boston, MA, USA, 2010. [Google Scholar]
- Conci, A.; Borchartt, T.B.; Resmini, R.; Motta, L.S.; Viana, M.J.; Santos, L.C.; Lima, R.; Diniz, E.M.; Santos, A.M.; Paiva, A.C.; et al. Biomedical use of infrared images. In Proceedings of the 2011 18th International Conference on Systems, Signals and Image Processing, Sarajevo, Bosnia-Herzegovina, 16–18 June 2011; pp. 1–4. [Google Scholar]
- Bakic, P.R.; Zhang, C.; Andrew, D.A. Maidment. Development and characterization of an anthropomorphic breast software phantom based upon region-growing algorithm. Med. Phys. 2011, 38, 3165–3176. [Google Scholar] [CrossRef] [PubMed]
- Hipwell, J.H.; Vavourakis, V.; Han, L.; Mertzanidou, T.; Eiben, B.; Hawkes, D.J. A review of biomechanically informed breast image registration. Phys. Med. Biol. 2016, 61, R1–R31. [Google Scholar] [CrossRef] [PubMed]
- Viana, M.J.; Santos, F.G.; Rolim, T.L.; Lima, R.C.; Silva, S.V.; Conci, A. Simulating breast temperature profiles through substitute geometries from breast prostheses. In Proceedings of the 17th International Conference on Systems, Signals and Image Processing (IWSSIP 2010), Rio de Janeiro, Brazil, 17–19 June 2010. [Google Scholar]
- Chu, C.-L.; Chiu, C.-Y. Development of a low-cost nanoscale touch trigger probe based on two commercial DVD pick-up heads. Meas. Sci. Technol. 2007, 18, 1831. [Google Scholar] [CrossRef]
- Küng, A.; Meli, F.; Thalmann, R. Ultraprecision micro-CMM using a low force 3D touch probe. Meas. Sci. Technol. 2007, 18, 319. [Google Scholar] [CrossRef]
- Weckenmann, A.; Knauer, M.; Killmaier, T. Uncertainty of coordinate measurements on sheet-metal parts in the automotive industry. J. Mater. Process. Technol. 2001, 115, 9–13. [Google Scholar] [CrossRef]
- Kita, Y.; Tohno, E.; Highnam, R.P.; Brady, M. A CAD system for the 3D location of lesions in mammograms. Med. Image Anal. 2002, 6, 267–273. [Google Scholar] [CrossRef]
- Fernandez, M.; Akogwu, S.; McNamara, L.; Zeugolis, D.; Pandit, A.; Biggs, M. Biomimetic approaches in bone tissue engineering: Integrating biological and physicomechanical strategies. Adv. Drug Deliv. Rev. 2015, 84, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Saal, H.; Bensmaia, S. Biomimetic approaches to bionic touch through a peripheral nerve interface. Neuropsychologia 2015, 79, 344–353. [Google Scholar] [CrossRef] [PubMed]
- Bogatyrev, N.; Bogatyreva, O. TRIZ-based Algorithm for Biomimetic Design. Procedia Eng. 2015, 131, 377–387. [Google Scholar] [CrossRef]
- Yang, M.; Yuan, J.; Guo, F.; Wang, K.; Zhang, Z.; Men, X.; Liu, W. A biomimetic approach to improving tribological properties of hybrid PTFE/Nomex fabric/phenolic composites. Eur. Polym. J. 2016, 78, 163–172. [Google Scholar] [CrossRef]
- Darlington, A. Anatomy of the Breast. In Digital Mammography: A Holistic Approach; Springer: Cham, Switzerland, 2015; Chapter 1; pp. 3–10. [Google Scholar]
- Prendergast, P. Anatomy of the Breast in Cosmetic Surgery: Art and Techniques; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 3; pp. 47–55. [Google Scholar]
- Kalimuthu, R.; Yegiyants, S.; Brenzek, C. Anatomy of the Breast, Axilla, and Chest Wall. In Breast Disease: Comprehensive Management; Springer Science Business Media: New York, NY, USA, 2015; Chapter 1; pp. 1–22. [Google Scholar]
- Tanner, C.; Schnabel, J.; Smith, A.C.; Sonoda, L.; Hill, D.; Hawkes, D.; Degenhard, A.; Hayes, C.; Leach, M.; Hose, D. The comparison of biomechanical breast models: Initial results. In Proceedings of the ANSYS Convergence, Pittsburgh, PA, USA, 22–24 April 2002. [Google Scholar]
- Tanner, C.; Schnabel, J.A.; Hill, D.; Hawkes, D.J.; Leach, M.O.; Hose, D.R. Factors influencing the accuracy of biomechanical breast models. Med. Phys. 2006, 33, 1758–1769. [Google Scholar] [CrossRef] [PubMed]
- Gefen, A.; Dilmoney, B. Mechanics of the Normal Woman Breast. Technol. Health Care Eur. Soc. Eng. Med. 2007, 15, 259–272. [Google Scholar]
- Rajagopal, V. Modelling Breast Tissue Mechanics under Gravity Loading. Ph.D. Thesis, The University of Auckland New Zealand, Auckland, New Zealand, 2007. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.136.391&rep=rep1&type=pdf (accessed on 20 May 2015).
- Mills, C.; Sanchez, A.; Scurr, J. Estimating the gravity induced three dimensional deformation of the breast. J. Biomech. 2016, 49, 4134–4137. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Stewart, M.L.; Smith, L.M.; Hall, N. A Numerical Investigation of Breast Compression: A Computer-Aided Design Approach for Prescribing Boundary Conditions. IEEE Trans. Biomed. Eng. 2011, 58, 2876–2884. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.H.; Rajagopal, V.; Nielsen, P.M.F.; Nash, M.P. Modelling Mammographic Compression of the Breast. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2008; Metaxas, D., Axel, L., Fichtinger, G., Székely, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5242. [Google Scholar]
- Jamkrajang, P.; Limroongreungrat, W. Comparison of vertical breast displacement between two different sports bra. Turk. J. Sport Exerc. 2014, 16, 97–99. [Google Scholar] [CrossRef]
- Scurr, J.; White, J.; Hedger, W. Breast displacement in three dimensions during the walking and running gait cycles. J. Appl. Biomech. 2009, 25, 322–329. [Google Scholar] [CrossRef] [PubMed]
- Haake, S.; Scurr, J. A dynamic model of the breast during exercise. Sports Eng. 2010, 12, 189–197. [Google Scholar] [CrossRef]
- Hsu, C.M.L.; Palmeri, M.L.; Segars, W.P.; Veress, A.I.; Dobbins, J.T. An analysis of the mechanical parameters used for finite element compression of a high-resolution 3D breast phantom. Med. Phys. 2011, 38, 5756–5770. [Google Scholar] [CrossRef] [PubMed]
- Calleja, A.; Gonzalez-Barrio, H.; Polvorosa-Teijeiro, R.; Lopez-De La Calle Marcaide, L. Multitasking machines: Evolution, resources, processes and scheduling. DYNA 2017, 92, 637–642. [Google Scholar] [CrossRef]
- Urbikain, G.; López De Lacalle, L.N.; Alonso, M.A.; Arsuaga, M.; Alvarez, A. A Reliable Turning Process by the Early Use of a Deep Simulation Model at Several Manufacturing Stages. Preprints 2016. [Google Scholar] [CrossRef]




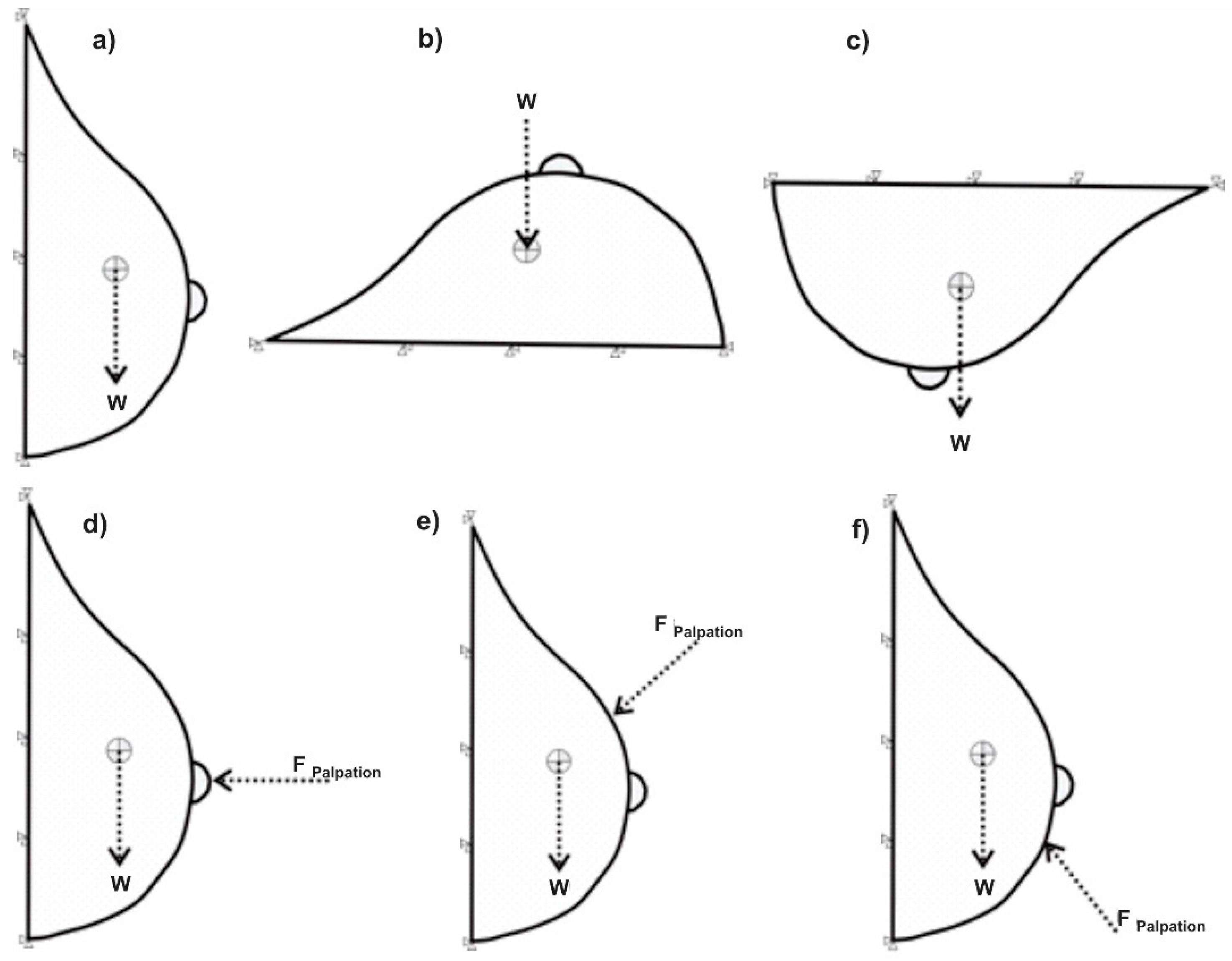
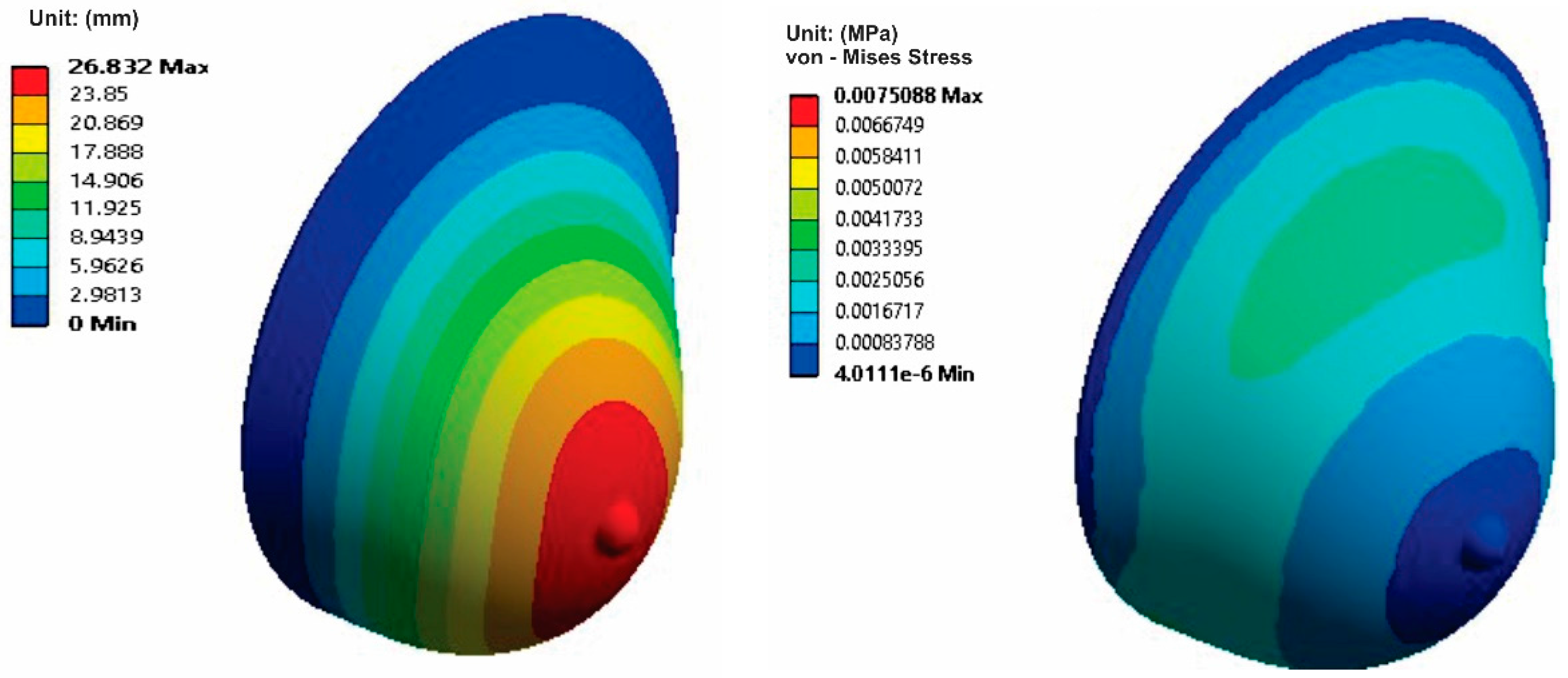
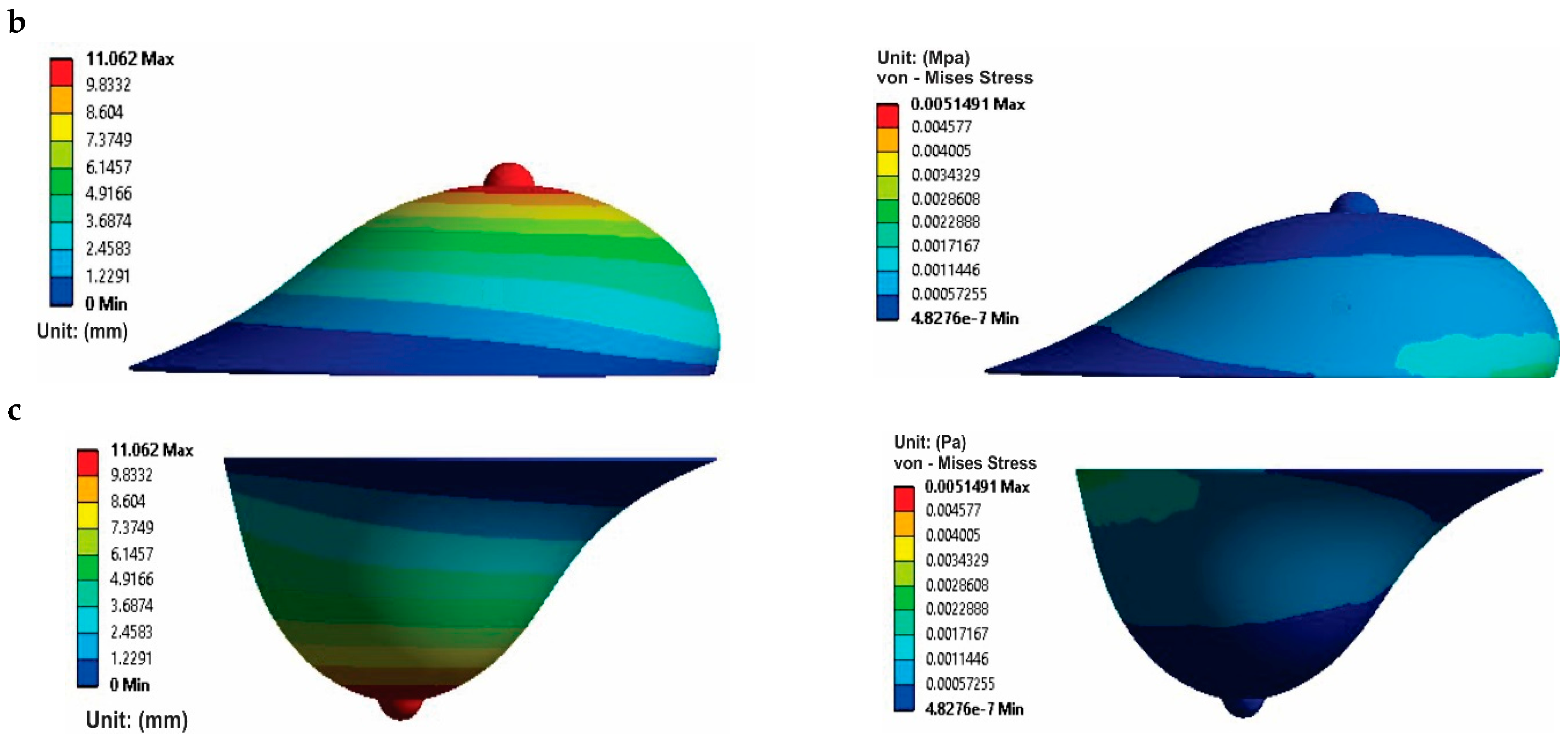


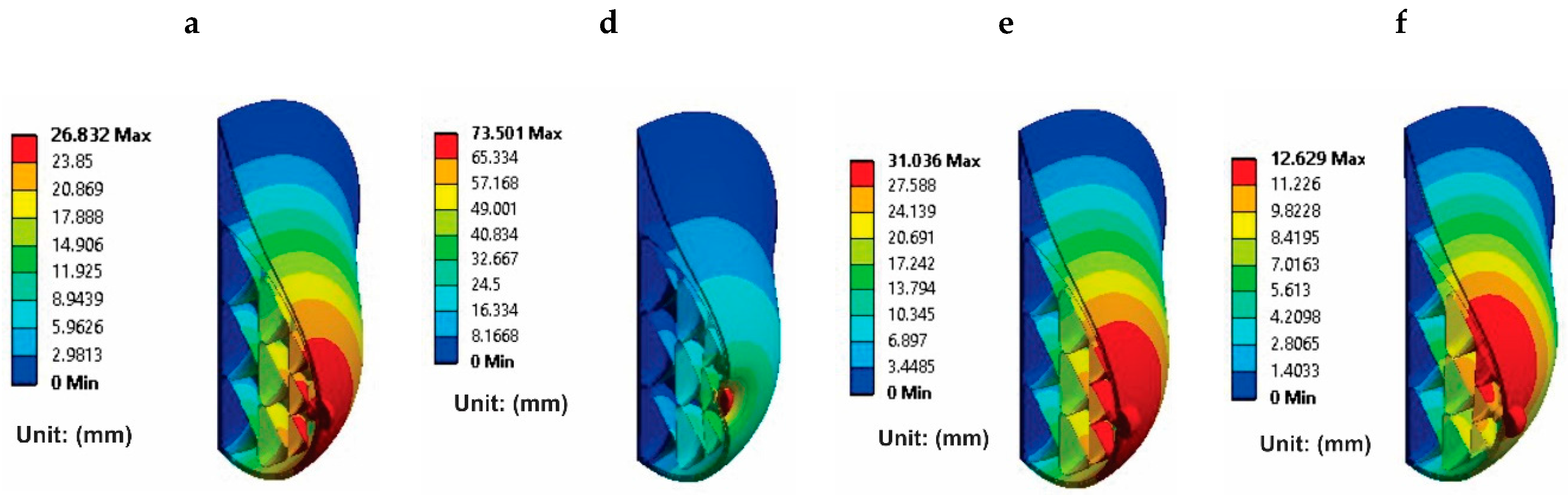
| Breast Position | Maximum Displacement Obtained (mm) | Maximum Displacement Reported (mm) |
|---|---|---|
| Standing | 26 | 27.5 [22], 30 [50], 20 [31] |
| Prone | 11.06 | 15.6 [53], 24 [27]] |
| Supine | 11.06 | 11 [44], 14 [24] |
| Mode | Frequency Obtained (Hz) | Frequency (Hz) [25] |
|---|---|---|
| 1 | 3.59 | 4.87 |
| 2 | 3.64 | 4.91 |
| 3 | 5.05 | 4.99 |
| 4 | 5.84 | 5.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz, P.; Hernandez, F.J.; Zuñiga, M.L.; Rodríguez, J.M.; Figueroa, R.; Vertiz, A.; Pineda, Z. A Biomimetic Approach for Designing a Full External Breast Prosthesis: Post-Mastectomy. Appl. Sci. 2018, 8, 357. https://doi.org/10.3390/app8030357
Cruz P, Hernandez FJ, Zuñiga ML, Rodríguez JM, Figueroa R, Vertiz A, Pineda Z. A Biomimetic Approach for Designing a Full External Breast Prosthesis: Post-Mastectomy. Applied Sciences. 2018; 8(3):357. https://doi.org/10.3390/app8030357
Chicago/Turabian StyleCruz, Pedro, F. Josue Hernandez, Ma. Lourdes Zuñiga, Jose Maria Rodríguez, Rafael Figueroa, Antonio Vertiz, and Zaira Pineda. 2018. "A Biomimetic Approach for Designing a Full External Breast Prosthesis: Post-Mastectomy" Applied Sciences 8, no. 3: 357. https://doi.org/10.3390/app8030357
APA StyleCruz, P., Hernandez, F. J., Zuñiga, M. L., Rodríguez, J. M., Figueroa, R., Vertiz, A., & Pineda, Z. (2018). A Biomimetic Approach for Designing a Full External Breast Prosthesis: Post-Mastectomy. Applied Sciences, 8(3), 357. https://doi.org/10.3390/app8030357






