Interpolating Spline Curve-Based Perceptual Encryption for 3D Printing Models

Abstract

With the development of 3D printing technology, 3D printing has recently been applied to many areas of life including healthcare and the automotive industry. Due to the benefit of 3D printing, 3D printing models are often attacked by hackers and distributed without agreement from the original providers. Furthermore, certain special models and anti-weapon models in 3D printing must be protected against unauthorized users. Therefore, in order to prevent attacks and illegal copying and to ensure that all access is authorized, 3D printing models should be encrypted before being transmitted and stored. A novel perceptual encryption algorithm for 3D printing models for secure storage and transmission is presented in this paper. A facet of 3D printing model is extracted to interpolate a spline curve of degree 2 in three-dimensional space that is determined by three control points, the curvature coefficients of degree 2, and an interpolating vector. Three control points, the curvature coefficients, and interpolating vector of the spline curve of degree 2 are encrypted by a secret key. The encrypted features of the spline curve are then used to obtain the encrypted 3D printing model by inverse interpolation and geometric distortion. The results of experiments and evaluations prove that the entire 3D triangle model is altered and deformed after the perceptual encryption process. The proposed algorithm is responsive to the various formats of 3D printing models. The results of the perceptual encryption process is superior to those of previous methods. The proposed algorithm also provides a better method and more security than previous methods.

1. Introduction

Three-dimensional (3D) printing is widely used in many areas of life [1,2]. Due to the fact that the benefits of 3D printing are enormous in many domains, 3D printing models are often attacked by pirates and distributed in commercial transactions without agreement from the original providers. The price of a 3D printer is cheap enough now that any individual user can buy a 3D printer, download 3D weapon models from the Internet, and print out real weapons such as knives and gun without any restriction. Moreover, certain special 3D printing models must be protected against unauthorized users. Consequently, security in the 3D printing industry is necessary.

Looking at 3D printing security techniques, watermarking methods have recently been proposed [3,4,5]. However, watermarking techniques do not alter the shape of 3D printing models. They only embed watermark data into 3D printing models, and anybody can view the shape of 3D printing models and design them again for printing. Therefore, watermarking is not suitable for secured storage and transmission; 3D printing models need to be encrypted. In addition, encrypting techniques must change the entire content of 3D printing models after the encryption process and be responsive to various model formats.

We propose an algorithm for perceptually encrypting 3D printing models. Facet data, the main component of 3D printing models, is used to interpolate a spline curve of degree 2 in three-dimensional space (3D space) that is determined by three control points, curvature coefficients, and an interpolating vector. The algorithm encrypts and distorts these features of the interpolating spline curve of degree 2 to obtain an encrypted 3D printing model. This paper is arranged as follows. We look into previous encryption techniques for 3D models and discuss 3D printing models related to the proposed method in Section 2. Section 3 presents the proposed algorithm in detail. In Section 4, we report visualization experiments, evaluations, and analysis of the proposed algorithm. Section 5 concludes.

2. Related Works

2.1. 3D Model Security

Watermarking techniques for 3D models have been researched. 3D model watermarking methods focus on the frequency domain and geospatial domain [6,7]. The key point of watermarking methods in the frequency domain is to embed watermark data into the spectrum coefficients of DFT, DWT, and DCT of a sequence of vertices or topologies, while the main concept of watermarking methods in the geospatial domain is based on modifying the value of vertices or geometric features such as length, area, or topology. Consequently, 3D model watermarking is not suitable for secured storage and transmission, as it fails to prevent attacks and illegal copying.

Some techniques that secretly share the content of 3D models and encrypt 3D CAD models have been proposed. Esam et al. [8] presented two methods that secretly transmit 3D models using Blakely, Thien, and Lin schemes. 3D models are separated into parts before they are shared, and users then reconstruct the 3D model from the shared parts of that model. However, this method is only for secured transmission. It is not an encryption method, and none of the 3D model is encrypted. Marc et al. [9] proposed a method by which 3D objects are encrypted based on geometry-preserving. This algorithm encrypts 3D objects by permuting the vertices of a given 3D object and distorting their shape while preserving its intrinsic geometrical properties. However, it does not alter the entire content of a 3D object and is not sensitive to the various formats of 3D objects. Moreover, the reconstruction cannot fully restore the original 3D object from the encrypted 3D object. Furthermore, the security of this method is very low. Cai et al. [10,11,12] proposed an encryption approach for 3D CAD models based on the geometric transformation of features of 3D CAD models. Here, a 3D CAD model is encrypted by randomization of the features of the 3D CAD model with an enhanced encryption transformation matrix. This method slightly changes the shape of 3D CAD models. Consequently, these methods do not achieve secured storage and transmission needed for 3D printing.

2.2. 3D Triangle Mesh-Based Encryption

A 3D triangle mesh has been used as an input for 3D printing [13,14]. A 3D triangle mesh is a set of facets. Each facet contains three vertices (a triangle) and a normal vector (see Figure 1). Each vertex is presented by three coordinates, x, y, and z. Thus, to encrypt a 3D triangle mesh, we only extract facets and encrypt all facets by the secret key. However, the normal vector of a facet only describes the direction of a facet and does not determine the shape of a 3D triangle mesh. Therefore, we only need to encrypt the triangles of 3D triangle mesh to generate the encrypted 3D triangle mesh.

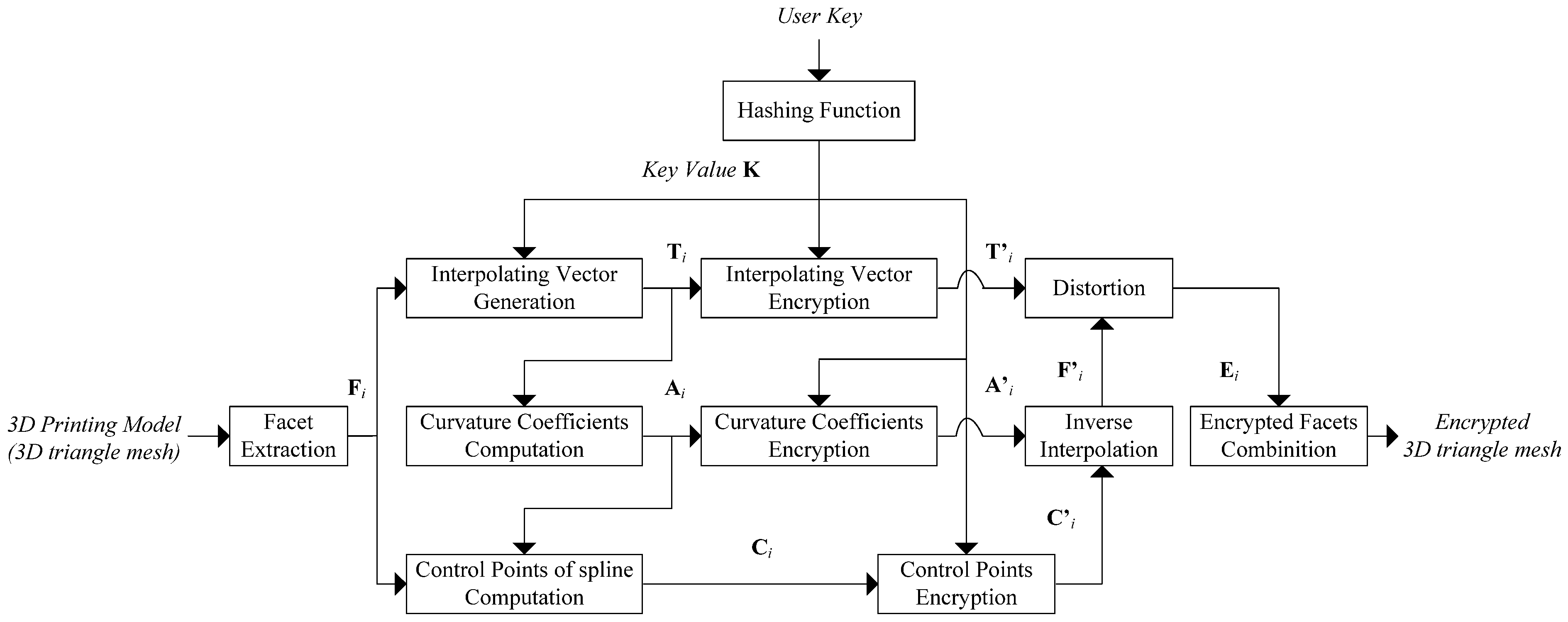
3. The Proposed Algorithm

3.1. Overview

Figure 2 describes the proposed algorithm. Each facet is extracted from a 3D triangle mesh. The index of each facet is then used with the key value K to generate an interpolating vector corresponding to that facet. The key value K is created from a user’s key input by a key hashing function. The interpolating vector is then used to calculate the curvature coefficients of a spline curve of degree 2 in 3D space. These curvature coefficients of degree 2 are then used together with three vertices of facet to calculate three control points of the interpolated spline curve of degree 2 in 3D space. Next, the interpolating vector, curvature coefficients, and three control points of the spline curve are encrypted by the key value K. The encrypted curvature coefficients and the encrypted control points are used in an inverse interpolation process to compute three new vertices. These vertices will be distorted by the encrypted interpolating vector via the geometric distortion process in order to generate the encrypted facet. The encrypted facets are combined to obtain the encrypted 3D triangle mesh.

As mentioned above, a 3D triangle mesh contains a set of facets. Each facet includes three vertices. Each vertex is presented by x, y, and z coordinates. We assume that a 3D triangle mesh $M=\{F_i|i\in [1,|M|\}$ with |M| the number of facets; $F_i=\{v_{i,1},v_{i,2},v_{i,3} \mathrm{and} n_i\}$ is the $i^{th}$ facet with three vertices $\{v_{i,1},v_{i,2},v_{i,3}\}$ and the normal vector $n_i(n{x}_i,n{y}_i,n{z}_i)$. Due to the fact that the normal vector of a facet does not determine the shape of 3D triangle mesh, we briefly consider the facet $F_i$ includes three vertices as Equation (1):

$$\begin{array}{cc}\hfill F_i& =\left\{v_{i,1},v_{i,2},v_{i,3}|i\in [1,|M|]\right\}\hfill \\ & =\left\{v_{i,j}|i\in [1,|M|],j\in [1,3]\right\} \mathrm{with} v_{i,j}=\left(x_{i,j},y_{i,j},z_{i,j}\right).\hfill \end{array}$$

(1)

For brevity, main notations are defined as follows: $T_i=\{t_{i,j}|j\in [1,3]\}$ is the interpolating vector corresponding to $F_i$; $C_i=\{c_{i,k}|k\in [1, 3]\}$ is three control points of the facet $F_i$; $A_i$ is the constructed matrix from the curvature coefficients of the interpolated spline curve corresponding to $F_i$; $E_i=\{e_{i,j}|i\in [1,|M|],j\in [1,3]\}$ is the encrypted facet. Finally, $G_D(.)$ and $E_F(.)$ are the distortion function and the encryption function, respectively.

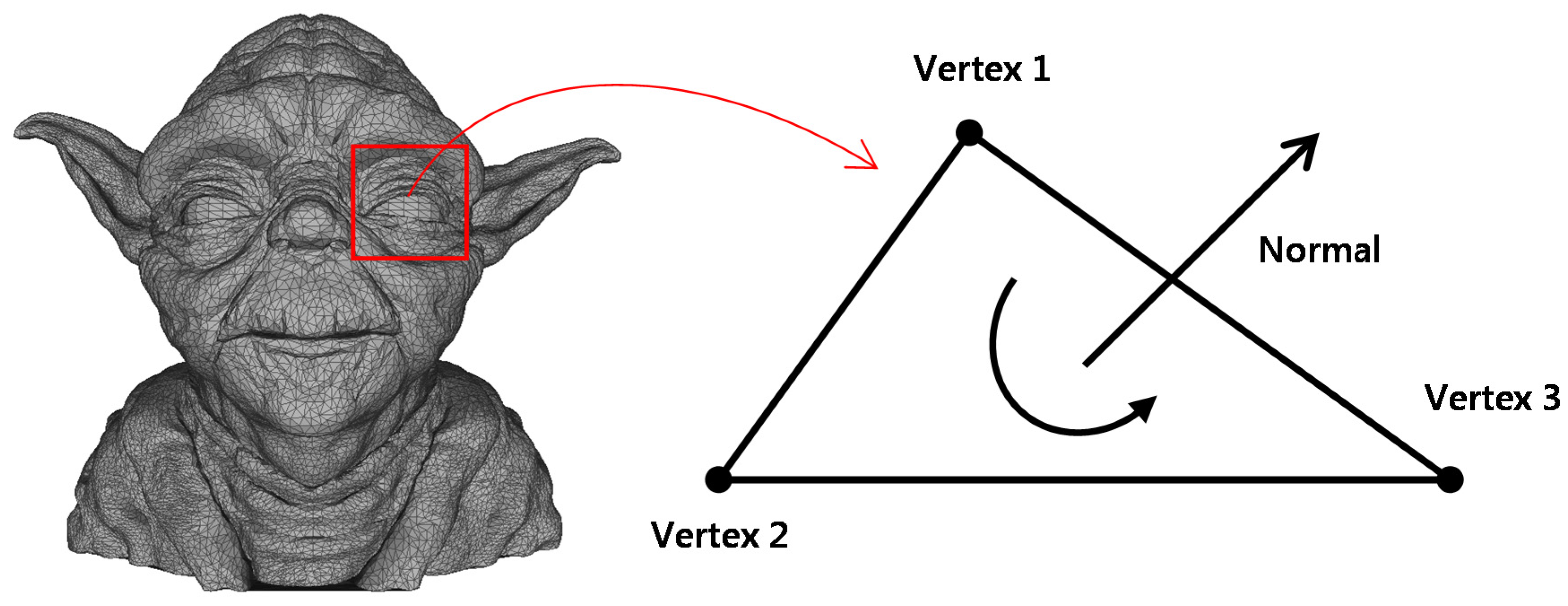
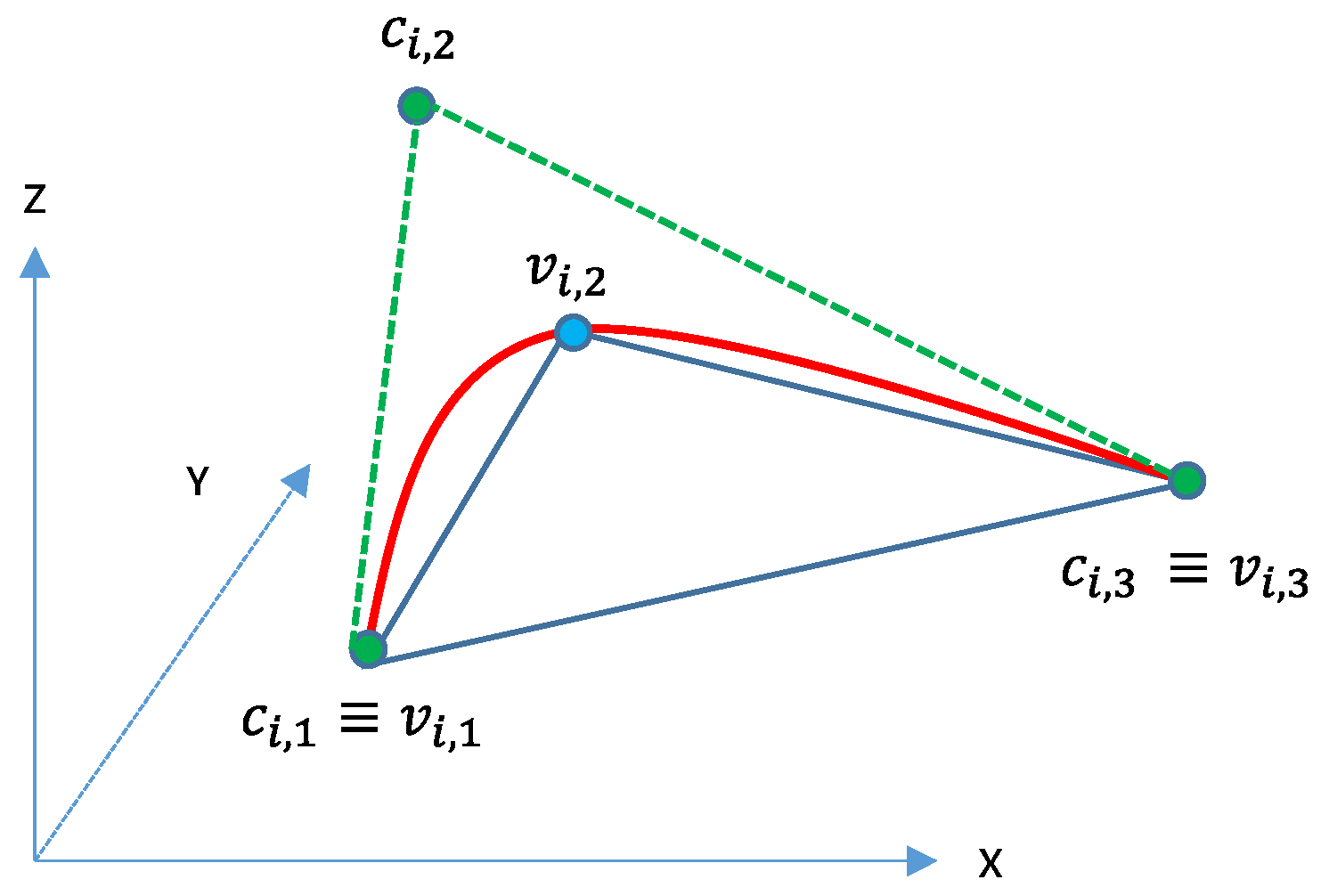
3.2. Features of the Interpolating Spline Curve in 3D Space

With each $F_i$ we have three vertices $\{v_{i,j}|j\in [1,3]\}$. Each facet $F_i$ is used to interpolate a spline curve of degree 2 in 3D space. This spline curve passes three vertices of the facet and is controlled by three control points (see Figure 3) [15,16]. However, these control points are determined by an interpolating vector and curvature coefficients. Thus, we could conclude that an interpolating spline curve of degree 2 in 3D space is determined by three control points, curvature coefficients, and an interpolating vector.

The interpolating vector $T_i=\{t_{i,j}|j\in [1,3]\}$ is a set of numbers therein $t_{i,j}<t_{i,j+1}$. The interpolating vector $T_i$ is then used to calculate the curvature coefficients. In order to respond to the condition $t_{i,j}<t_{i,j+1}$, we calculate $t_{i,j}$ by using indexes $i,j$, the value of |M| and K as described in Equation (2). The SHA-512 hashing function [17] is used to generate the key value K with a user’s key input. Each key value has a length of 512 bits.

$$t_{i,j}=\frac{i·(j+1)}{|M|}\times K.$$

(2)

With the three vertices of the facet and $T_i$, we can compute the curvature coefficients and three control points of spline curve of degree 2. The relationship between three control points $C_i=\{c_{i,k}|k\in [1, 3]\}$, $v_{i,j}$ and $t_{i,j}$ is defined as follows:

$$v_{i,j}={\displaystyle \sum }_{k=1}^3{B}_{k,d}(t_{i,j})·c_{i,k}$$

(3)

where $B_{k,d}(t_{i,j})$ is considered the curvature coefficient of degree $d=2$, corresponding to $t_{i,j}$ and the $k^{th}$ control point, computed via the recursive function in Equations (4) and (5).

$$B_{k,d}(t_{i,j})=\frac{t_{i,j}-t_{i,k}}{t_{i,k+d}-t_{i,k}}{B}_{k,d-1}(t_{i,j})+\frac{t_{i,k+d+1}-t_{i,j}}{t_{i,k+d+1}-t_{i,k+1}}{B}_{k+1,d-1}(t_{i,j})$$

(4)

$$B_{k,0}\left(t_{i,j}\right)=\{\begin{array}{cc}1\hfill & \hfill if t_{i,k}\le t_{i,j}<t_{i,k+1}\\ 0\hfill & \hfill otherwise\end{array}.$$

(5)

From Equation (3), we can see that there are three curvature coefficients $\{B_{1,2}(t_{i,j}), B_{2,2}(t_{i,j}), B_{3,2}(t_{i,j})\}$ with each $t_{i,j}$. Therefore, we have 3 × 3 coefficients with the interpolating vector $T_i$. These coefficients can be organized into a 3 × 3 matrix $A_i$ in which the $j^{th}$ row contains $B_{1,2}(t_{i,j}), B_{2,2}(t_{i,j}), B_{3,d}(t_{i,j})$:

$$\begin{array}{cc}{A}_i& =\left[\begin{array}{ccc}{B}_{1,2}\left(t_{i,1}\right)& B_{2,2}\left(t_{i,1}\right)& B_{3,2}\left(t_{i,1}\right)\\ B_{1,2}\left(t_{i,2}\right)& B_{2,2}\left(t_{i,2}\right)& B_{3,2}\left(t_{i,2}\right)\\ B_{1,2}\left(t_{i,3}\right)& B_{2,2}\left(t_{i,3}\right)& B_{3,2}\left(t_{i,3}\right)\end{array}\right]\hfill \\ & =\left[\begin{array}{ccc}{a}_{1,1}& a_{1,2}& a_{1,3}\\ a_{2,1}& a_{2,2}& a_{2,3}\\ a_{3,1}& a_{3,2}& a_{3,3}\end{array}\right]\hfill \\ & =\{a_{j,k}|j,k\in [1, 3]\} \mathrm{with} a_{j,k}=B_{k,2}\left(t_{i,j}\right).\hfill \end{array}$$

(6)

Now, we apply three vertices of $F_i$ and $t_{ij}|j\in [1,3]$ to Equation (3), the relationship between $F_i, T_i,$ and $C_i$ is described as follows:

$$\begin{array}{cc}\left[\begin{array}{c}{v}_{i,1}\\ v_{i,2}\\ v_{i,3}\end{array}\right]& =\left[\begin{array}{ccc}{B}_{1,2}\left(t_{i,1}\right)& B_{2,2}\left(t_{i,1}\right)& B_{3,2}\left(t_{i,1}\right)\\ B_{1,2}\left(t_{i,2}\right)& B_{2,2}\left(t_{i,2}\right)& B_{3,2}\left(t_{i,2}\right)\\ B_{1,2}\left(t_{i,3}\right)& B_{2,2}\left(t_{i,3}\right)& B_{3,2}\left(t_{i,3}\right)\end{array}\right]·\left[\begin{array}{c}{c}_{i,1}\\ c_{i,2}\\ c_{i,3}\end{array}\right]\hfill \\ & =\left[\begin{array}{ccc}{a}_{1,1}& a_{1,2}& a_{1,3}\\ a_{2,1}& a_{2,2}& a_{2,3}\\ a_{3,1}& a_{3,2}& a_{3,3}\end{array}\right]·\left[\begin{array}{c}{c}_{i,1}\\ c_{i,2}\\ c_{i,3}\end{array}\right]\hfill \\ \hfill \iff F_i& =A_i·C_i\hfill \end{array}$$

(7)

$$\begin{array}{l}{C}_i={(A_i)}^{-1}·F_i\\ \iff \left[\begin{array}{c}{c}_{i,1}\\ c_{i,2}\\ c_{i,3}\end{array}\right]={\left(\left[\begin{array}{ccc}{a}_{1,1}& a_{1,2}& a_{1,3}\\ a_{2,1}& a_{2,2}& a_{2,3}\\ a_{3,1}& a_{3,2}& a_{3,3}\end{array}\right]\right)}^{-1}·\left[\begin{array}{c}{v}_{i,1}\\ v_{i,2}\\ v_{i,3}\end{array}\right].\end{array}$$

(8)

Finally, we can calculate three control points $C_i$ from the curvature coefficients and three vertices of facet $F_i$ as shown in Equation (8).

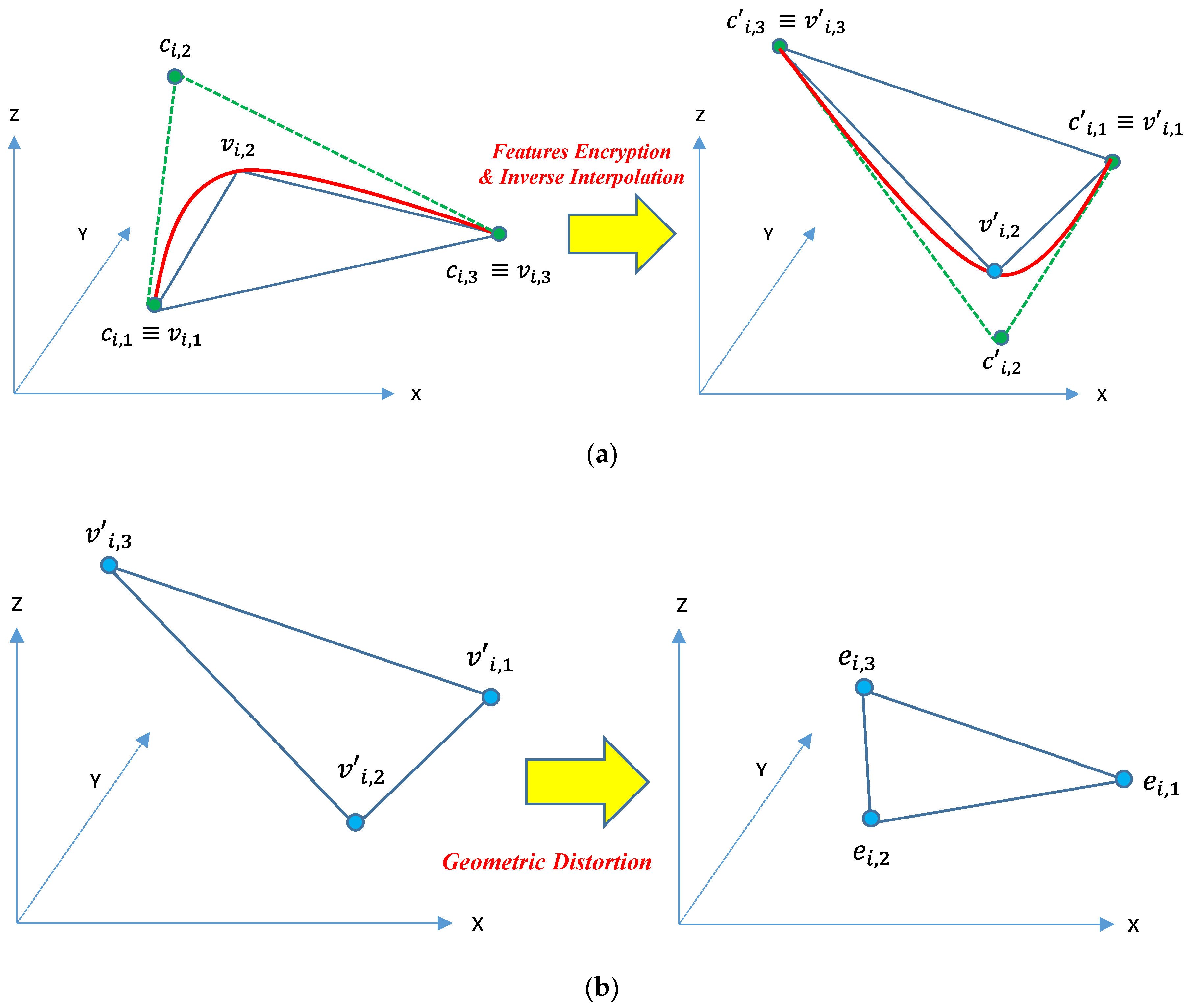
3.3. Features of Interpolating Spline Curve Encryption

After we compute the features of the interpolating spline curve in 3D space, we can encrypt them by the encryption function $E_F(.)$, which is the key value K. We can use conventional encryption functions such as AES, DES, or XOR for the encryption function $E_F(.)$. Here, for simplicity, we encrypted features by the secret key value K as described in Equations (9)–(11), where $T_i^{\prime }$, $A_i^{\prime }$, and $C_i^{\prime }$ are the encrypted interpolating vector, the encrypted curvature coefficients, and the encrypted control points, respectively.

$$\begin{array}{cc}\hfill T_i^{\prime }& =E_F(K,T_i)\hfill \\ & =\{(\frac{K}{\left|M\right|}+j)\times t_{i,j}|j\in [1, 3]\}\hfill \\ & =\{t_{i,j}^{\prime }|j\in [1, 3]\}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill A_i^{\prime }& =E_F(K,A_i)\hfill \\ & =\left\{\frac{K}{\left|M\right|}\times a_{j,k}|j,k\in [1, 3]\right\}\hfill \\ & =\{a_{j,k}^{\prime }|j,k\in [1, 3]\}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill C_i^{\prime }& =E_F(K,C_i)\hfill \\ & =\left\{\left(\frac{K}{\left|M\right|}+j\right)\times c_{i,j}|j\in [1, 3]\right\}\hfill \\ & =\{c_{i,j}^{\prime }|j\in [1, 3]\}.\hfill \end{array}$$

(11)

After the feature encryption process, the encrypted curvature coefficients $A_i^{\prime }$ and the encrypted control points $C_i^{\prime }$ are used in the inverse interpolation process in order to compute three new vertices as shown in Equation (12). Three new vertices are finally altered by the geometric distortion process in order to generate the encrypted facets $E_i$. The geometric distortion process uses the encrypted interpolating vector $T_i^{\prime }$ as shown in Equation (13).

$$\begin{array}{l}{F}_i^{\prime }=A_i^{\prime }·C_i^{\prime }\\ \iff \left[\begin{array}{c}{v}_{i,1}^{\prime }\\ v_{i,2}^{\prime }\\ v_{i,3}^{\prime }\end{array}\right]=\left[\begin{array}{ccc}{a}_{11}^{\prime }& a_{12}^{\prime }& a_{13}^{\prime }\\ a_{21}^{\prime }& a_{22}^{\prime }& a_{23}^{\prime }\\ a_{31}^{\prime }& a_{32}^{\prime }& a_{33}^{\prime }\end{array}\right]·\left[\begin{array}{c}{c}_{i,1}^{\prime }\\ c_{i,2}^{\prime }\\ c_{i,3}^{\prime }\end{array}\right]\end{array}$$

(12)

$$\begin{array}{cc}\hfill E_i& =G_D(T_i^{\prime },F_i^{\prime })\hfill \\ & =\{(t_{i,j}^{\prime }+1)\times v_{i,j}^{\prime }|j\in [1, 3]\}\hfill \\ & =\{e_{i,j}|j\in [1, 3]\} \mathrm{with} e_{i,j}=(e{x}_{i,j},e{y}_{i,j},e{z}_{i,j})\hfill \end{array}$$

(13)

$$E_M=\left\{E_i|i\in \left[1,\left|M\right|\right]\right\}.$$

(14)

The encrypted 3D triangle mesh $E_M$ is a set of the encrypted facets as shown in Equation (14). Figure 4 show the encryption process of a facet. Three control points are encrypted by the key value K and are then used to compute three new vertices $v_{i,1}^{\prime },v_{i,2}^{\prime }$ and $v_{i,3}^{\prime }$ by inverse interpolation (see Figure 4a). Three new vertices are formed into a new facet. Finally, this new facet is distorted by the geometric distortion to obtain the encrypted facets shown in Figure 4b.

3.4. Decryption Process

The decryption process is an inverse process of the encryption process. Each encrypted facet is also extracted from the encrypted 3D triangle mesh. The key value K and the index of each facet is used to generate the interpolating vector and the curvature coefficients as shown in Equation (2) and Equation (6) in Section 3.2. These features are then encrypted by the key value K that is used in Section 3.3. The encrypted interpolating vector and three vertices of the encrypted facet are used in the re-distortion process to compute three new vertices. These vertices are then used with the encrypted curvature coefficients to re-compute three encrypted control points. Three encrypted control points are then decrypted by the key value K in order to get three control points. Finally, three control points and the curvature coefficients are used to decrypt three vertices of the facet. The decrypted 3D triangle mesh is a set of decrypted facets.

The purpose of the proposed algorithm is to prevent illegal copying or illegal access from unauthorized users and attacks from hackers. Thus, if an authorized user or receiver would like to use the encrypted 3D printing models for 3D printing, they only need the secret key to decrypt and use them as 3D printing inputs. The decryption does not affect the printing process. To print a real object from a 3D triangle mesh, the 3D triangle mesh must be cut into a set of 2D slices and stored in G-code format. The content of the G-code format consists in paths that contain 2D coordinates for the CNC machine in a 3D printer. Consequently, the decryption process does not affect other aspects of the 3D printing process.

4. Experimental Results, Analysis, and Evaluation

We tested the proposed algorithm with 3D triangle meshes in

Table 1. Experimental results.

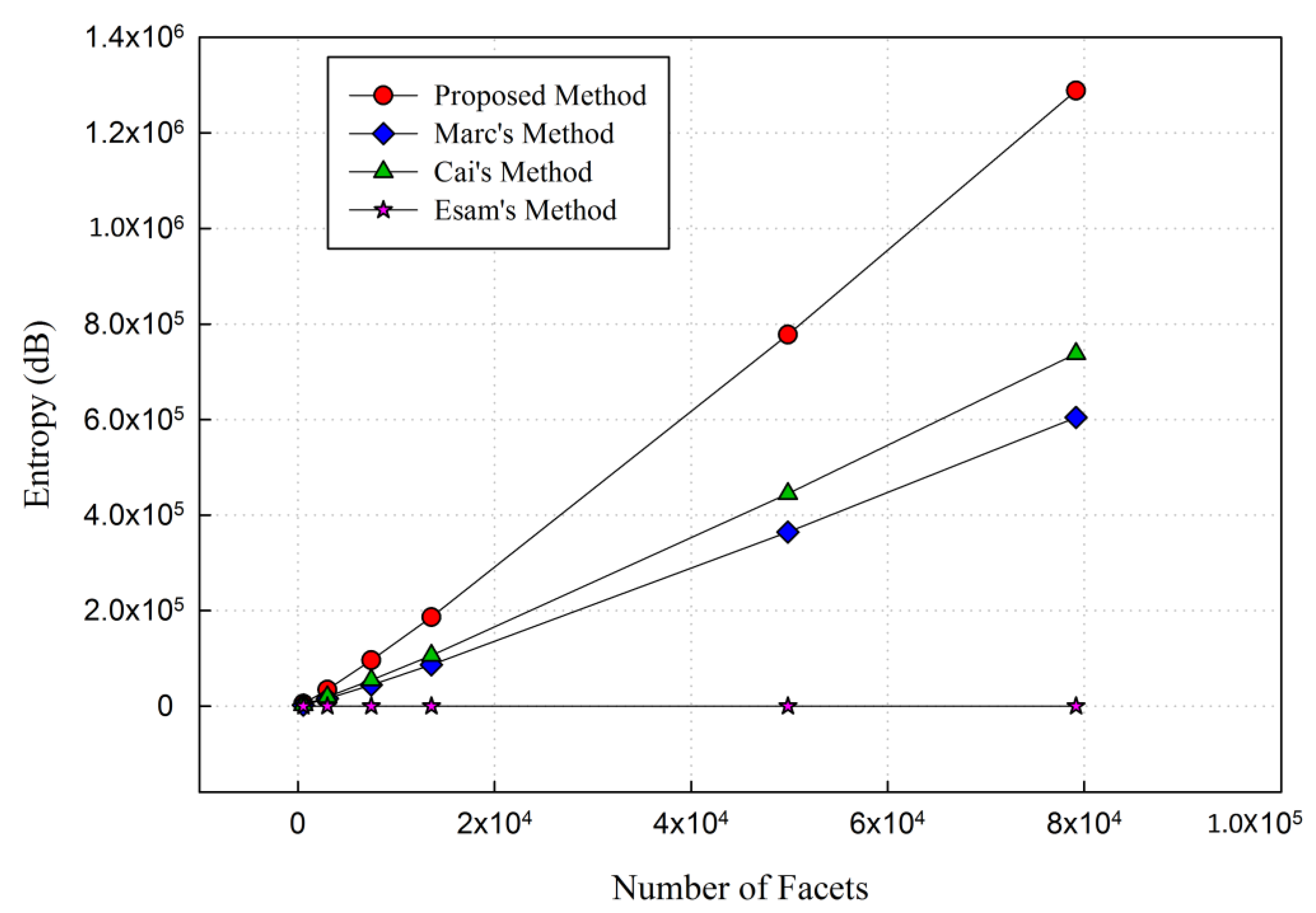
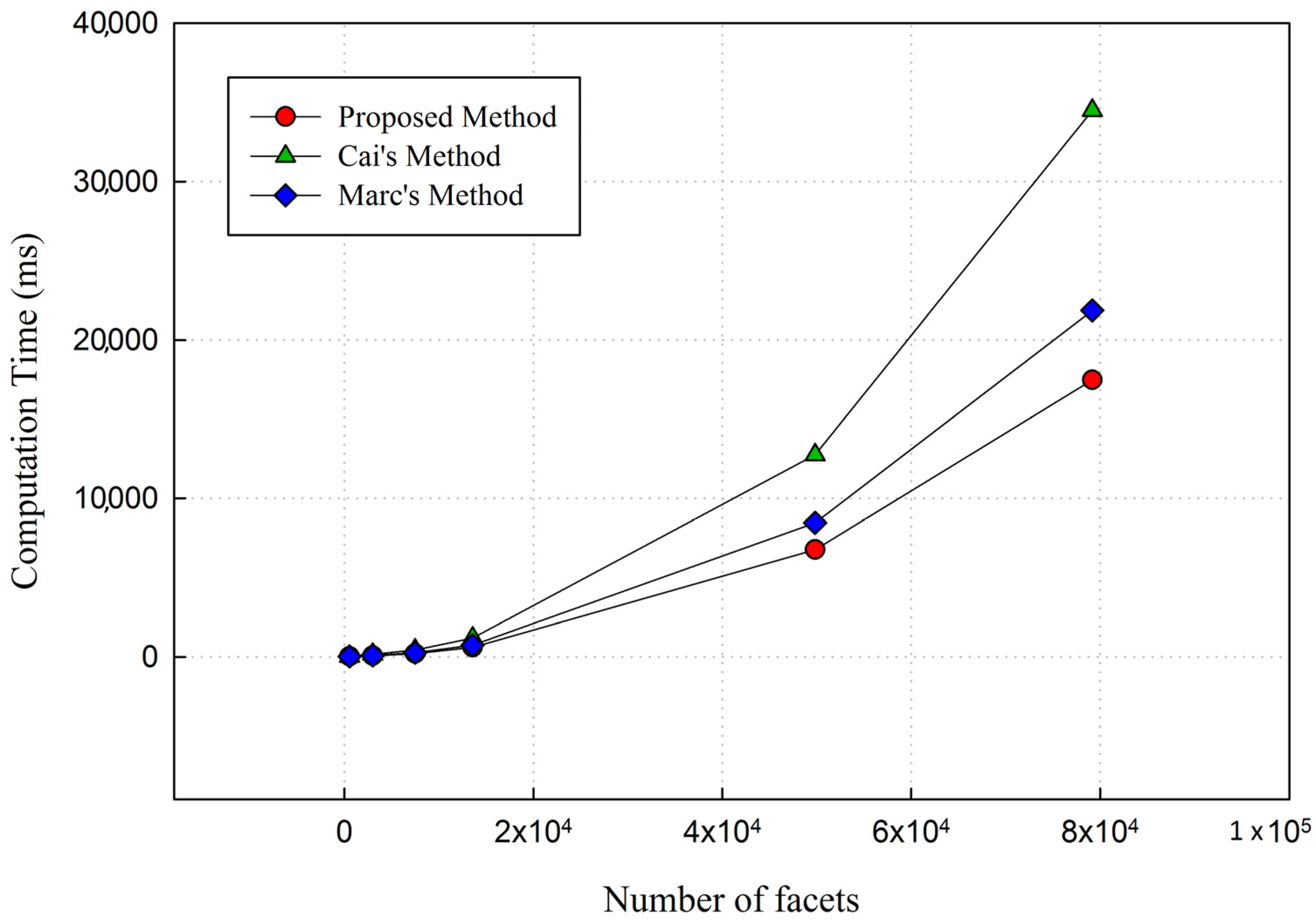
Name	# Facets	Entropy (dB)				Computation Time (ms)
		Proposed Method	Cai’s Method	Marc’s Method	Esam’s Method
Wheel Camping	544	4981	2754	2218	8.0	17.5
Knife	1176	12,032	6705	5430	8.0	29
Aperture Face	2026	22,292	12,485	10,137	8.0	46
Flower	2986	34,508	19,390	15,766	8.0	72
Gun	3961	47,378	26,681	21,714	8.0	90
Castle	7466	96,096	54,362	44,322	8.0	209
Batman	13,566	186,268	105,767	86,360	8.0	591
Rabbit	21,056	302,443	172,161	140,704	8.0	1312
Moto-bike	22,034	317,932	181,022	147,959	8.0	1421
Car	32,426	485,937	277,229	226,767	8.0	2951
Yoda	49,844	777,860	44,4681	364,021	8.0	6763
Lion	79,162	1,288,203	737,923	604,535	8.0	17,486

. The format of the 3D triangle meshes was an STL file or a VRML file [13,14]. The information of the 3D triangle meshes is given in Table 1. In order to evaluate the proposed algorithm, we evaluated the perceptual encryption results of the 3D triangle meshes, the security of the encrypted 3D triangle meshes, and the computation time of the algorithm. Section 4.1 shows the perceptual encryption result of the 3D triangle meshes (visualization experiments). The security of the 3D triangle meshes and the computation time of the proposed algorithm are explained in Section 4.2 and Section 4.3, respectively.

4.1. Visualization Experiments

To evaluate the visualization experiments, we evaluated the perceptual encryption results of the 3D printing models. The aim of the proposed algorithm is to alter and distort the shape of 3D printing models. Experimental results are shown in Figure 5. The number of facets in each 3D triangle mesh is different. The encryption process changes the values of the vertices of facets. Thus, the shape of the facets is also altered. After the encryption process, facets are distorted into big facets (see “Encrypted Wheel Camping”) or small facets (see “Encrypted Car” and “Encrypted Knife”) or changed location, positioned disorderly (see “Encrypted Yoda, Encrypted Lion”). Thus, the shape of the 3D triangle meshes is altered. The content of the 3D triangle meshes is completely altered after the perceptual encryption process. Pirates or unauthorized users cannot extract or view the content of 3D triangle meshes.

In Marc’s method [9], he permuted the vertices of 3D meshes. According to his permutation, the shape of the 3D mesh changed, but he did not show the experimental results of his method. Moreover, the decryption of this method cannot fully restore the original 3D meshes from the encrypted 3D objects. In Cai’s method [12], the encrypted CAD model was slightly changed (see Figure 6a,c). Anybody can view the content of the encrypted CAD model. We compared Cai’s model with our proposed algorithm. Results are shown in Figure 6b,d. No unauthorized user could view or steal it, but the entire model was altered. Thus, the perceptual results of our proposed method are superior to those of Cai’s method.

4.2. Security Evaluation

We analyzed the length of the secret key and the entropy of the encrypted 3D triangle mesh to evaluate the security of the proposed algorithm. If the secret key length is long, it is difficult to attack the encrypted 3D triangle mesh. If the entropy of the encrypted 3D triangle mesh is high, the security of the encrypted 3D triangle mesh will be high. In order to decrypt the encrypted 3D triangle mesh, a pirate must decrypt all of the encrypted facets of the 3D triangle mesh without the secret keys. In the proposed algorithm, the SHA-512 hashing function with a 512 bit salt is used to obtain random keys. Thus, if a user inputs a word with length $L_k$ as his/her password, an attacker has to compute $L_k\times 2^{512}$ keys to access the encrypted 3D triangle mesh.

The entropy $H\left(x\right)$ of a discrete random variable $x$ with a possible value $\{x_1,x_2,\dots ,x_n\}$ is defined as

$$H\left(x\right)=-{\displaystyle \sum }_{\tau =1}^{n}p(x_{\tau })·lo{g}_{2}p(x_{\tau })$$

(15)

where $p(x_{\tau })$ is the probability density function of $x$ on range $\{x_1,x_2,\dots ,x_n\}.$ Based on the equations in Section 3, the entropy of the encrypted 3D triangle mesh is dependent on both the secret key K, the interpolating vector $T_i$, the matrix of curvature coefficients $A_i$, three control points $C_i$, and the number of facets |M|. However, K, $T_i$, $A_i$, $C_i$, and |M| are random independent variables. Therefore, the entropy of the encrypted 3D triangle mesh $H_M$ is the sum of the entropies of variables K, $T_i$, $A_i$, $C_i$, and |M| and is determined by Equation (16):

$$\begin{array}{cc}\hfill H_M& =H\left(K\right)+H\left(T_i\right)+H\left(A_i\right)+H\left(C_i\right)+H\left(\left|M\right|\right)\hfill \\ & =\left|K\right|·{\log }_2\left|K\right|)+\left|T_i\right|·{\log }_2\left|T_i\right|+\left|A_i\right|·{\log }_2\left|A_i\right|+\left|C_i\right|·{\log }_2\left|C_i\right|+\left|M\right|·{\log }_2\left|M\right|).\hfill \end{array}$$

(16)

$\left|T_i\right|=\left|C_i\right|=3$ and $\left|A_i\right|=9$. In summary, the total entropy $H_M$ is dependent on K and the number of facets |M| in the 3D triangle mesh. If the secret key K is fixed, we can calculate the entropy of the encrypted 3D triangle mesh according to the number of facets |M| as shown in Table 1. The entropy of the encrypted 3D triangle mesh is formed from 4981 to 1.3 × 10⁶ dB with $\left|M\right|\in [544, 79162]$. From Equation (16) and Table 1, we can see that, if |M| is high, the entropy will be high.

Esam [8] divided the faces of a 3D model in N share hyper-planes before sharing. This mean a 3D model is divided into N parts before sharing. Thus, N is the secret key, and the entropy of Esam’s method is always fixed. In Esam’s method, N = 4, so the entropy of Esam’s method is always 8 dB. Moreover, in the 3D space of the 3D model, the maximum number of hyper-planes is 360. Therefore, the maximum entropy of Esam’s method is 3057 dB. Marc used the secret key K to encrypt and change the location of the vertices of the 3D mesh in OXYZ space. Clearly, Marc’s method encrypted the vertices of the 3D mesh with a secret key K. However, the number of vertices in a 3D mesh is always smaller than the number of facets. Thus, the entropy of this method is always lower than the proposed method. The entropy of Marc’s method is formed from 2218 to 6.04 × 10⁵ dB (see Table 1). Cai encrypted the features of the 3D CAD model with a random 3 × 3 matrix generated by a secret key. Thus, we can consider that Cai’s method is encrypted 3D CAD models based on features and a random matrix by a secret key K. Therefore, the entropy of this method is dependent on both the number of features and the 3 × 3 matrix. In the experimental results, around 50% of the facets are selected as the features of the 3D CAD model. Based on the test models in Table 1, the entropy of Cai’s method is formed from 2754 to 7.38 × 10⁵ dB. Figure 7 shows the entropy of the proposed method and the entropy of the previous methods according to the number of facets. The entropy of our method is always greater than the entropy of previous methods. Consequently, our method is superior, providing more security compared with previous methods.

4.3. Computation Time and Analysis

We tested the proposed algorithm with a computer Intel Core i7-CPU 3.5 GHz; RAM-8 GigaBytes; Operating System: Windows 7 Microsoft–64 bits; Visual Studio 2013–C++. The computation time of the proposed algorithm was dependent on the number of facets in each model. With the test models in Table 1, computation time ranged from 17.5 to 17,486 ms with $\left|M\right|\in [544,79162]$. Based on Table 1, we conclude that, if the number of facets is small, the computation time will be short.

Marc did not provide computation time. He only explained that his method will loop through all of the indices of the set of elements and will permute and swap at each iteration. As a result, the encryption time is expected to scale linearly with the complexity of the object. In addition, the decryption process requires swap operations to be performed in the reverse order than the one used for encryption. As a result, the decryption process is more “expensive” than encryption. We found that the encryption process of Marc’s method was twice as long as our method and that the decryption process of Marc’s method was three times as long. In our method, the encryption time and decryption time are similar. Moreover, the average computation time (including encryption and decryption times) of Marc’s method is 1.25 times greater than the average computation time of the proposed method. In Cai’s method, he only explained and analyzed factors affecting computation time. The computation time of Cai’s method depends on how long it takes for the valid CAD model to check the time of feature encryption and the time of edge and facet encryption. He concluded that his method will meet users’ requirements. We estimate that, with a computer has the same parameters, Cai’s method must compute three parameters: valid model checking, feature encryption, and edges & facet encryption. We were able to estimate that the computation time of Cai’s method is at least twice as long as our method. Therefore, we concluded that our method is faster than Cai’s method as well. Figure 8 shows the computation time of the proposed algorithm and Cai’s method with the test model in Table 1, according to the number of facets.

5. Conclusions

We present an algorithm for perceptually encrypting 3D printing models in this paper. The algorithm encrypts control points and curvature coefficients of the interpolating spline curve and geometric distortion. In light of the results of visualization experiments and evaluations, the proposed algorithm is shown to be effective and responsive to the various formats of 3D printing models. The perceptual encryption results show that the proposed algorithm is more effective than previous methods; security is higher and computation takes less time. Therefore, the proposed algorithm provides more security than previously proposed methods. Our algorithm can be used for secured storage and transmission. However, the proposed algorithm does have limitations: computation is complex, and the algorithm is only useful for directly encrypting original 3D printing models. Some applications may require a combination between encryption and compression, and some may require real-time operation. We seek to improve our algorithm so that it can secure transmission systems and can be used in real-time applications and applied in compression domains. We hope to find other applications for our method as well.