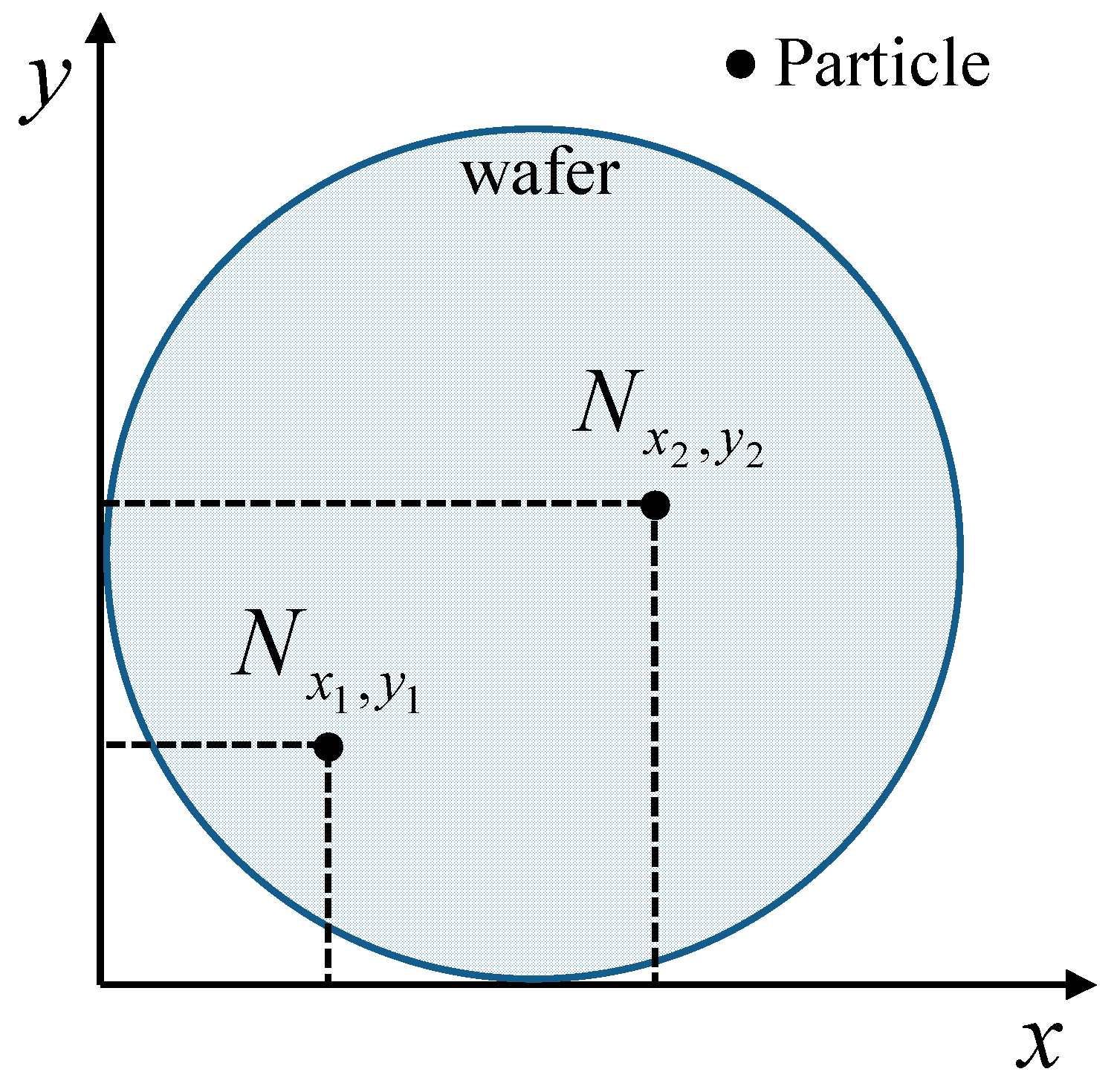1. Introduction
The worldwide semiconductor market is valued at 333 billion dollars [
1]. As the semiconductor industry accounts for 10–15% of the total exports of the Republic of Korea, it has a significant influence on the market economy. Owing to the recent proliferation of electronic devices such as mobile phones and tablet PCs (Personal Computers), market competition is becoming increasingly fierce [
2]. In the future, as the demand for the internet of things (IoT) products is expected to increase, most manufacturers endeavor to increase the production through maintenance of facilities [
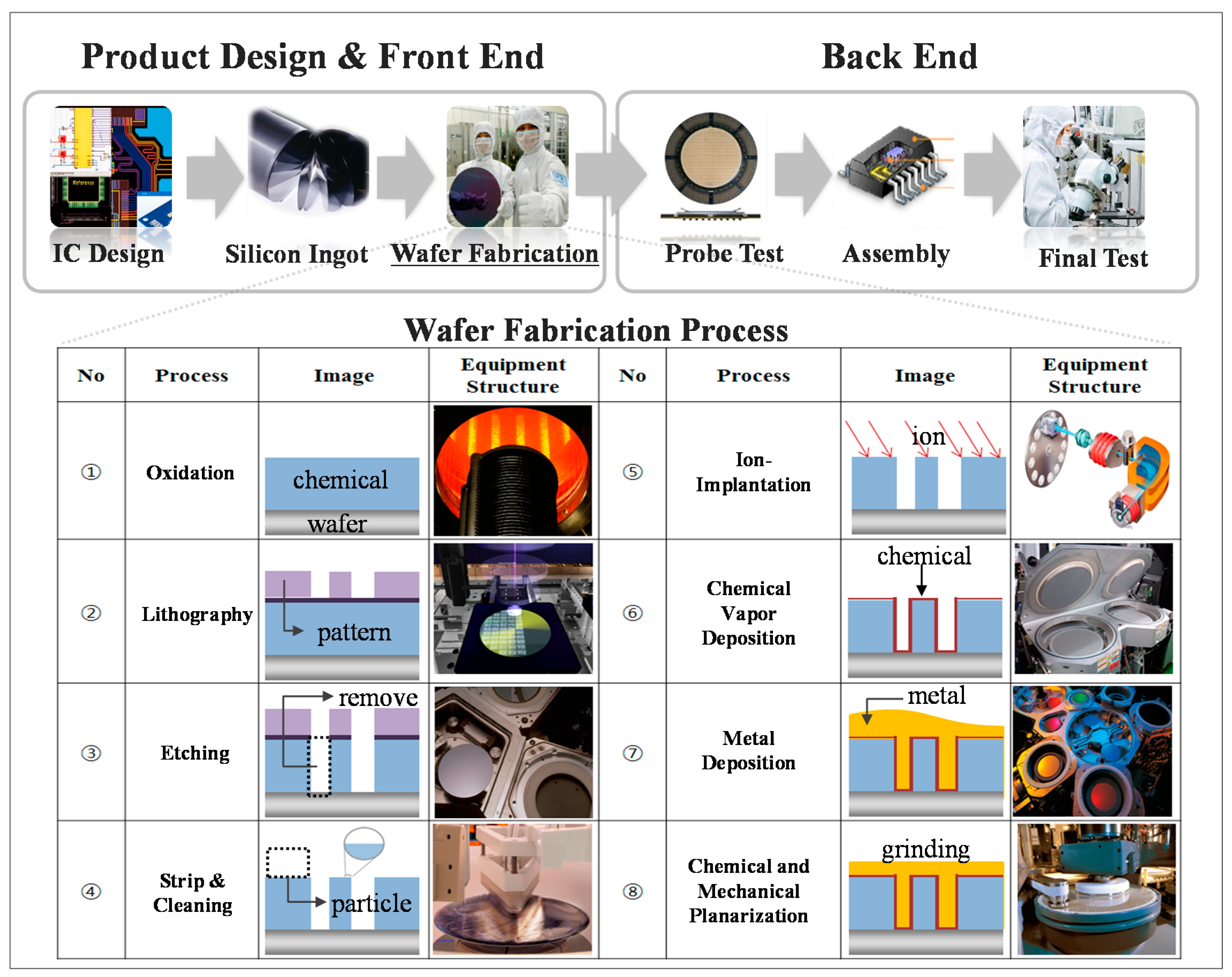
3]. The semiconductor manufacturing process consists of numerous steps. As shown in
Figure 1, in the front-end process, the ingot is cut to produce wafers and the circuit is designed. The wafers are subsequently undergone fabrication (FAB), which consists of the following eight processes: oxidation, lithography, etching, strip & clean, ion-implantation, chemical vapor deposition, metal deposition, and chemical mechanical planarization. Oxidation refers to a process whereby a thin and uniform silicon oxide film is formed by the chemical reaction of oxygen or water vapor and the surface of the wafer at a high temperature. Lithography is a process whereby patterns on the wafer is formed by photoresist coating, exposure, and development processes. Etching refers to the process whereby unnecessary portions are selectively removed by using the reactive gas to form a circuit pattern. Strip & clean refers to the process of removing particle contamination generated on the wafer amid other ongoing processes. Ion-implantation is the process whereby characteristics of the electronic device are generated by the implantation of impurities converted to a gas form in the circuit pattern. Chemical vapor deposition is the process whereby the water vapor formed in the particles are formed by the chemical reaction of gases to form an insulating film. Metal deposition interconnects each circuit formed on the surface of a wafer with aluminum and copper wire. Chemical mechanical planarization is a process whereby the oxide film and the metal thin film coated on the wafer are ground and flattened using chemical and physical processes. The subsequent step is the back-end process, in which the probe test, the assembly, and the package tests are conducted sequentially. Thereby, the final product is manufactured. These processes each have their own facilities, and each facility includes several chambers where a wafer must be placed for fabricating. The above-mentioned processes occur within those chambers.
Wafer fabrication for semiconductor devices such as microprocessors, memories, digital signal processors, and consumer electronics applications involves a complex and lengthy process with 30–40 reentrant loops, and the above-mentioned processes (①–⑧), as shown in
Figure 1 [
4]. This study focuses on these eight processes and the inter-process metrology.
Semiconductor FAB includes various physical and chemical treatments and takes six to eight weeks. Therefore, there is a considerable difficulty in identifying causes of failure in the fabrication process, which involves numerous facilities.
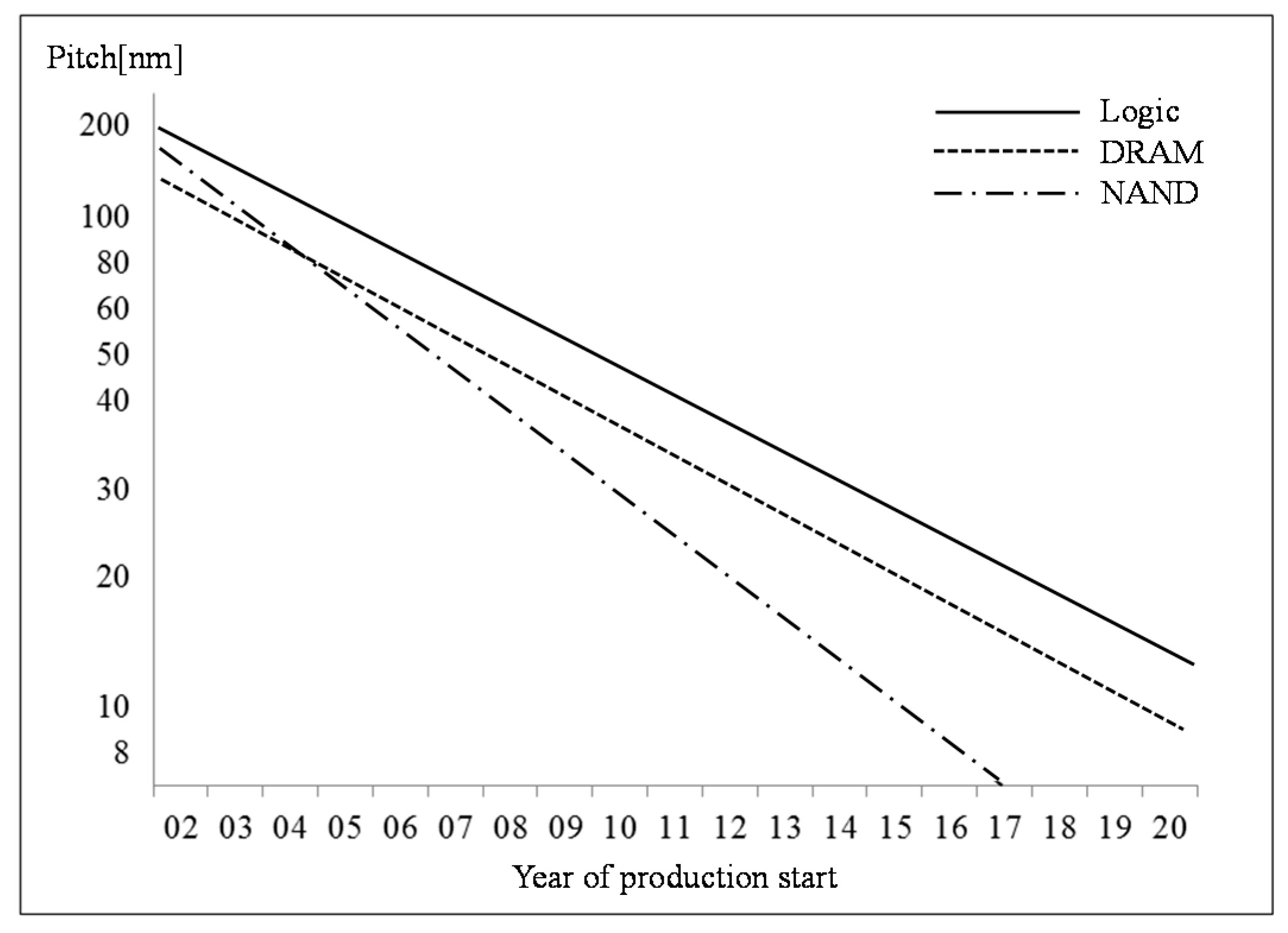
Figure 2 chronologically shows a pitch change in the lithography process used for fabricating DRAM (Dynamic Random-Access Memory), NAND (Negative-AND gate flash memory), and logic products that have been actively manufactured in recent years. The pitch on the
Y-axis illustrates the integration capacity of the semiconductor products and significantly affects product yield, hence the increasing significance of defect management as current FAB processes design and fabricate sophisticated patterns [
5].
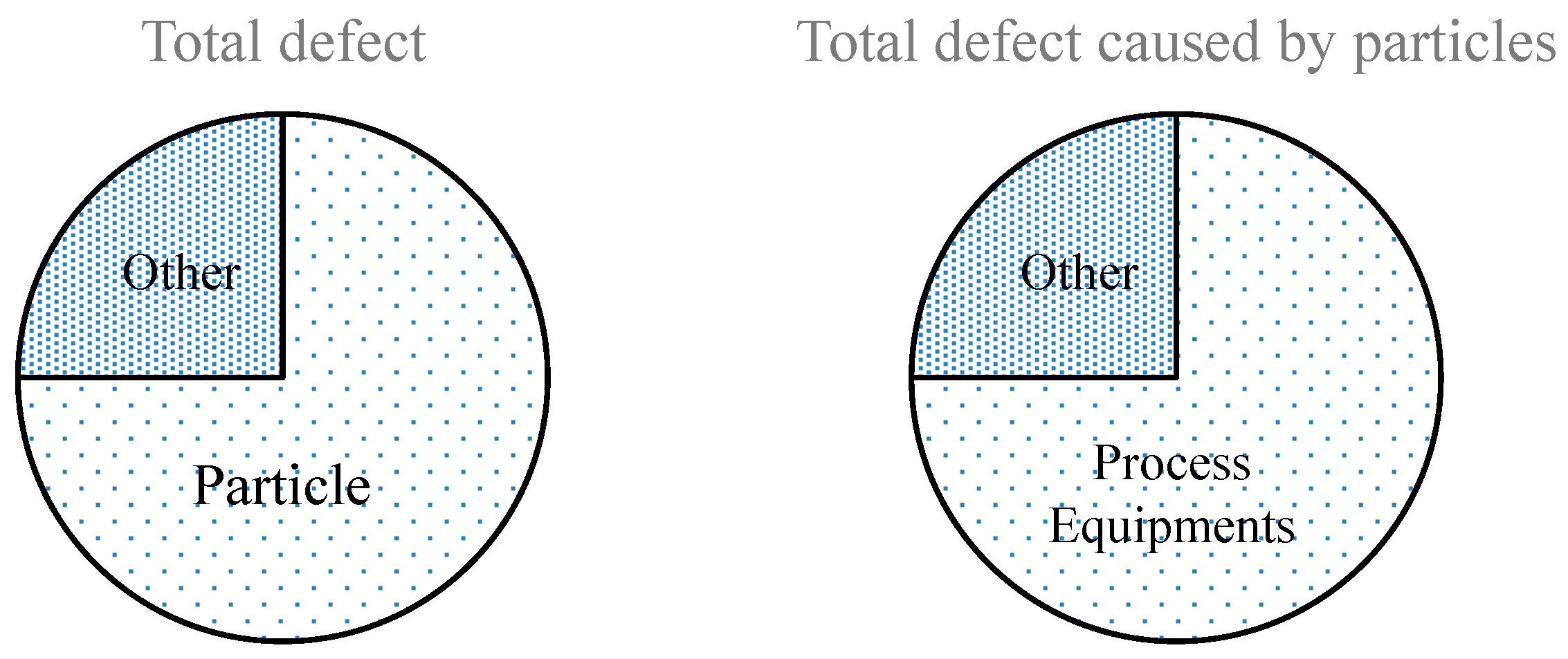
The defects in a semiconductor manufacturing process are generally distributed as shown in
Figure 3. The pie chart on the left shows that the particle defects account for 75% of the total defects. As shown in the pie chart on the right, 75% of the particle defects are caused by process equipment [
6].
In the field of semiconductor manufacturing, a particle defect indicates a failure resulting from fine particles, such as dust, that are present on the wafers during FAB. The size of the particle defect owing to the manufacturing environment has remained unchanged, but the FAB process has been improved to develop capabilities for the fabrication of fine patterns. During one inspection, as shown in
Figure 4, there was no defect when the pitch was 130 nm, but a pitch of 45 nm resulted in a defect because the size of the particle was greater than the pitch size. Therefore, the structure and stability of the deposited chemical must be carefully controlled, and reduction in contamination in particular becomes increasingly crucial as device sizes shrink [
7].
The particles in the chamber of a facility need to be monitored to maintain the chamber’s stability. Current manufacturing processes manage particle defects through a simple control chart (c-chart) that monitors the number of particles. As these monitoring charts do not consider the distribution or density of the particles on the wafers, engineers do not know whether the particles are assignable or what the common causes are. Therefore, this study proposes a particle defect management method to overcome the limitation of this monitoring chart.
This paper is organized as follows.
Section 2 reviews the conventional particle management method.
Section 3 provides the details of the proposed method, and
Section 4 presents the experimental results and evaluation. Finally,
Section 5 concludes this study.
2. The Conventional Industrial Method
In an actual semiconductor manufacturing process, conventional particle defect management involves manual action by engineers if, based on the monitoring chart, there is a cause for alarm. The procedure consists of three phases for the detection of the cause of the defect. In the first phase, when an alarm occurs, the insides of the manufacturing equipment are repeatedly cleaned. In the second phase, if the problem persists, the field engineers replace suspicious parts. In the final phase, if the previous replacement does not solve the prevailing problem, predictive maintenance (PM) of the equipment is performed. The second phase, in particular, consumes a substantial amount of time in terms of both decision-making and detection of the root cause, owing to an experience-based decision of the replacement. Therefore, reducing false alarms in the first phase is critical.
Among the aforementioned particle defect management phases, we focus on the first phase, wherein the particle defects are monitored. Particle defects in process equipment are primarily due to equipment aging. Other defects occur due to environmental factors. The counts control chart (c-chart) is commonly used to monitor particle defects. The c-chart is based on the assumption that the distribution of the number of nonconformities is sufficiently well fitted by a Poisson distribution [
8]. However, in the actual semiconductor manufacturing process, the particle count does not follow a Poisson distribution [
9]. Especially, in our case, random variables are not independent since the particles are cumulated with a time-varying property.
Figure 5 shows the metrology equipment gauging the number of particles on the wafer. The number of particles,
, at each coordinate on the wafer is stored.
Moreover, these particles indicate the status of the equipment, not of the wafer. Therefore, in conventional monitoring statistics, the particle defect (
) that indicates the number of particles on a test wafer can be denoted as follows:
where
and
are the
-th particle coordinates, and
indicates the number of particles at the designated coordinate.
The particle coordinates can be used to generate a wafer map to obtain the distribution and number of particles.
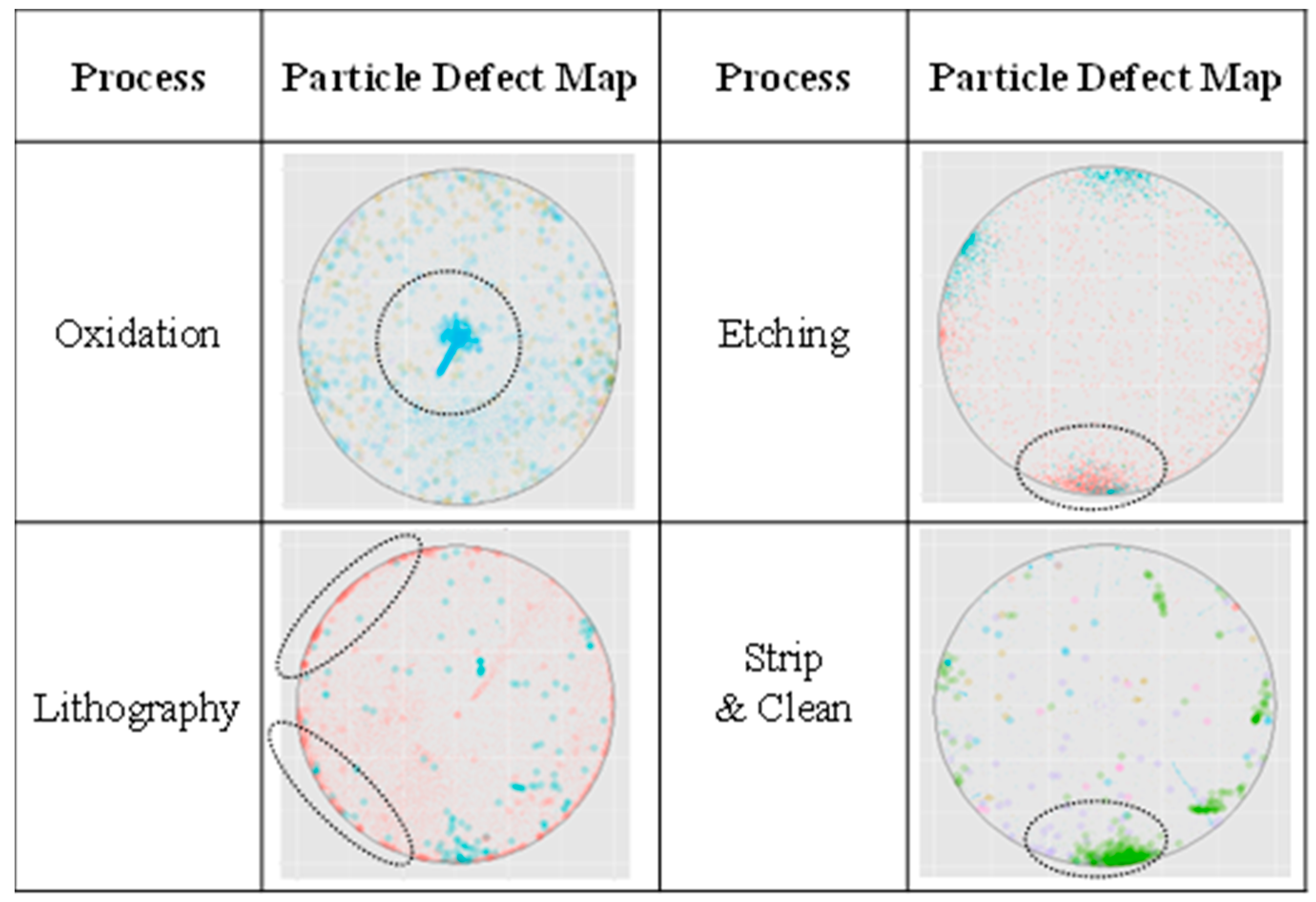
Figure 6 depicts four illustrative particle defect maps for four processes. The particle defect maps indicate high-density particles at a particular location on the wafer and the location is correlated with the structure of the process equipment. As indicated by the dotted ellipse in each particle defect map, a high-density area indicates that an ongoing wafer has a potential defect. The particle defect map of the oxidation is also affected by the structure of the equipment. Field engineers have discovered a problem at the center position, where the gas is injected into the furnace, using the particle map. The lithography process shows a higher density at the edges of the wafer. The lithography process includes a photo resist (PR) coating using a high-speed rotation of the spinner equipment in the wafer process. Therefore, the remnants of the chamber affect the density of the wafer edges owing to the characteristics of the high-speed spinning process. Both the etching and strip & clean processes exhibit the highest densities where the dotted ellipse is drawn. Engineers have checked the equipment that analyzes the causes of this phenomenon and discovered a particle resulting from the improper fastening of the O-ring in the chamber. Further, as the strip & clean process includes multiple baths that form bias chemicals at the bottom wafer, the particle defect map indicates high densities of the particles in the bottom area.
A real domain conducts monitoring based on the control chart in Equations (2)–(4) to monitor the particle counts [
9].
However,
(critical value) is decided through the experience of engineers because the particle defect cannot assume a specific distribution. Moreover, since the particle count is always positive,
is zero. Therefore, the actual process determines the abnormalities in the facility using the threshold of the particle count, as shown in
Figure 7.
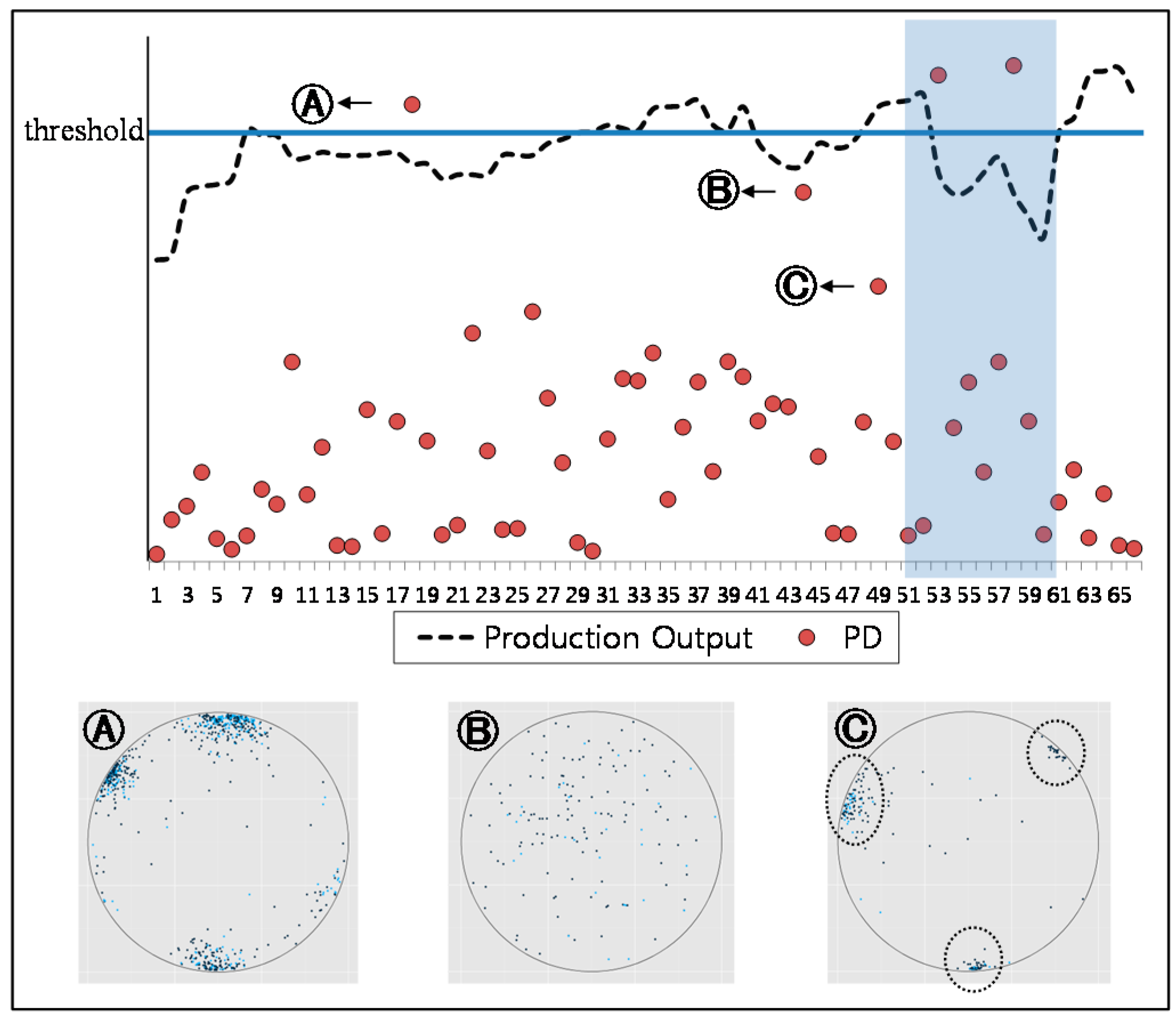
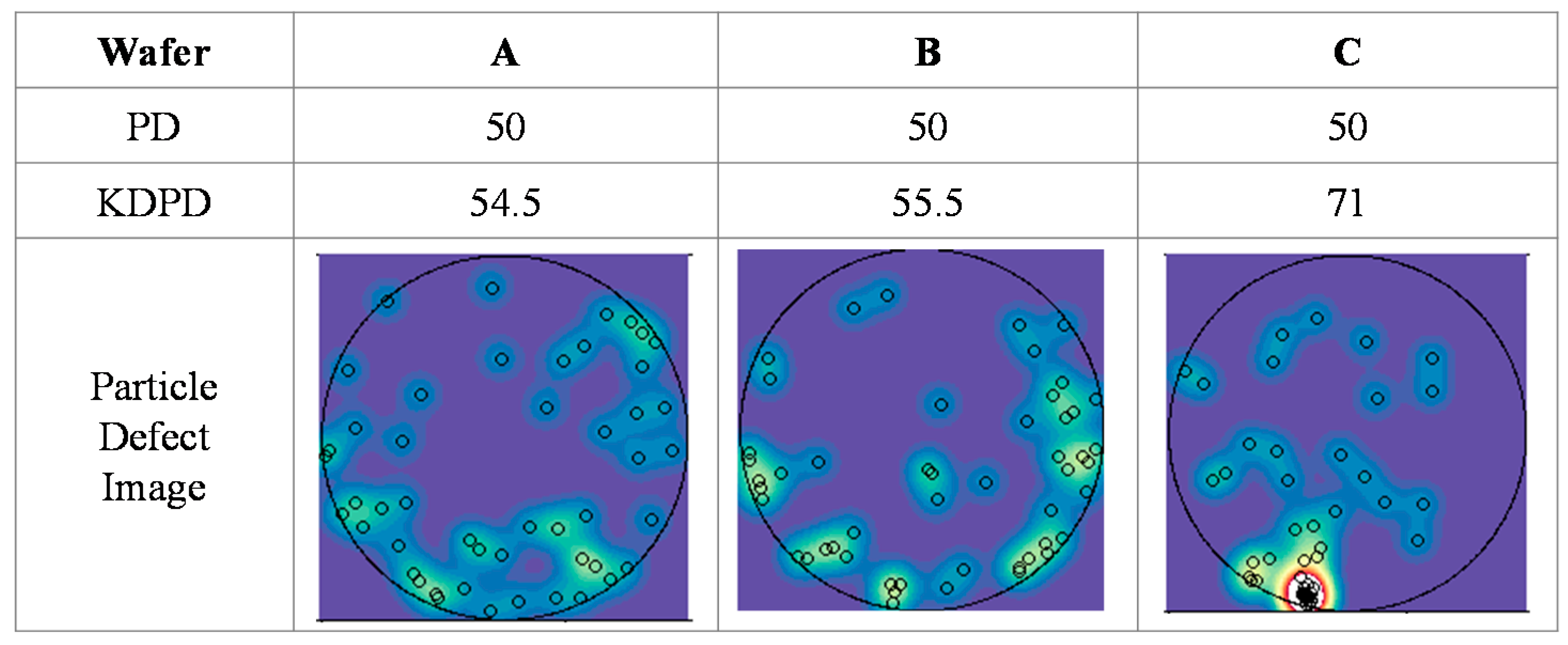
Figure 7 describes both the monitoring chart and the particle maps of the wafers required for observing the particles with specific equipment. In the monitoring chart, the horizontal axis is the wafer index and the vertical axis is the monitoring statistic,
. The dashed-polygonal line indicates production yield and the solid straight line indicates the criterion that distinguishes between a non-defect and a defect. As shown in the chart, Wafer A is beyond the threshold, whereas Wafers B and C are within the threshold. Although both Wafers B and C are within the threshold, they have different distributions, as shown by their respective maps. The three wafer maps depict their respective particle distributions. Wafer A shows high-density particles because
is beyond the threshold. The particles in Wafers B and C are differently distributed, whereas the monitoring chart indicates that
is within the threshold for both wafers. The particles on Wafer B are uniformly distributed, and the particles on Wafer C are concentrated around the edges of the wafer. Consequently, despite a smaller
, the particles concentrated on Wafer C can induce fatal risks, including out-of-threshold wafers or yield reductions, as shown by the shaded rectangular area of the plot. Therefore, since it is important to identify particle distributions, as in Wafer C, this study proposes a new monitoring method considering dense particles.
4. Experimental Results
This section describes an experiment for verifying the proposed method and its results. The particle maps used for this experiment were retrieved from the etching process. As several “killer-particles” originate from the deposition of a layer of by-product on the inside of the plasma-etching chamber, the etching process is sensitive to particles [
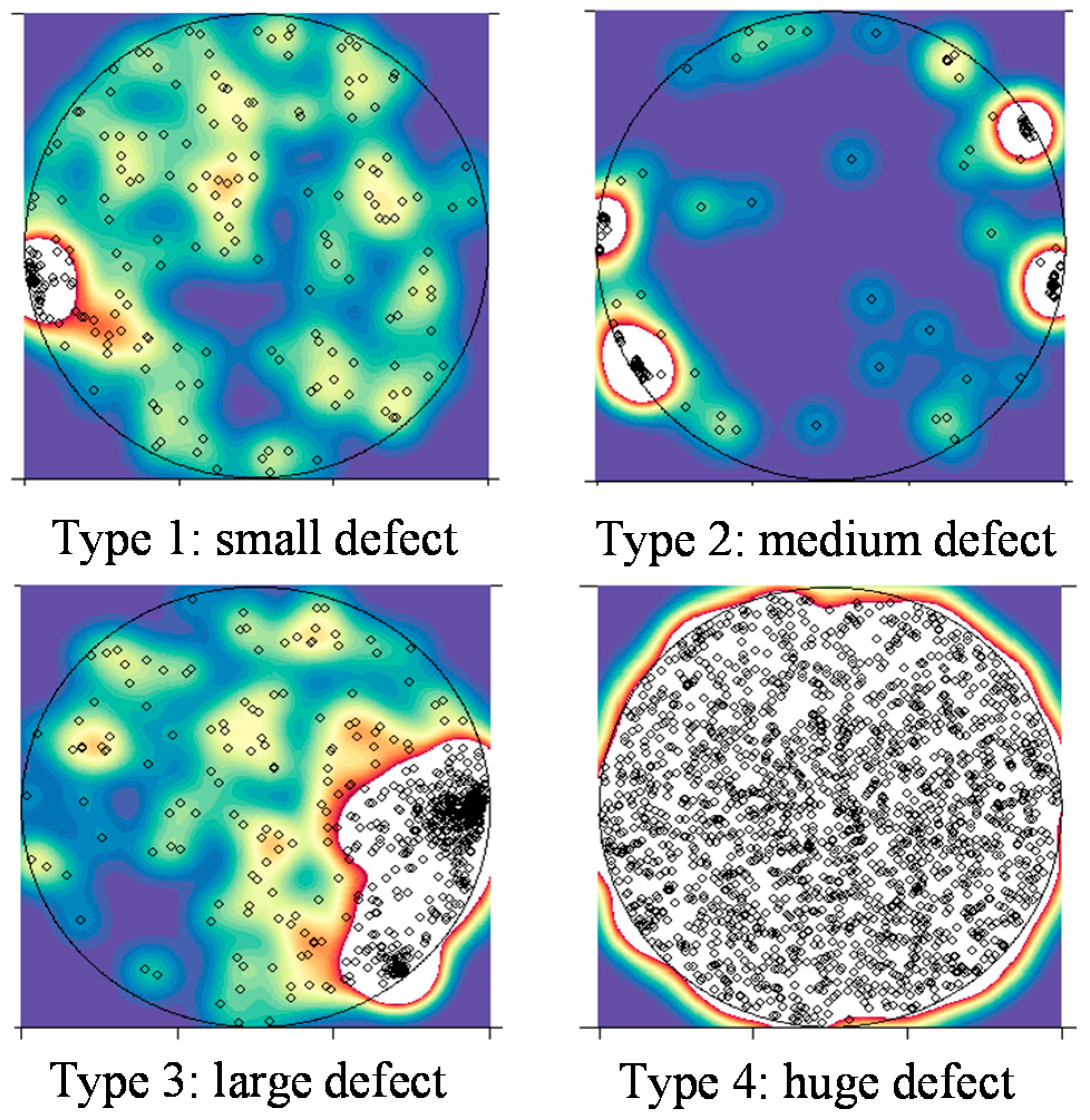
12]. Therefore, we used particle data from a real etching process in a Korean semiconductor manufacturing company, obtained over a period of five months. The entire dataset consists of 600 wafers, generating 600 particle maps. Among these particle maps, we defined the particle defect types using field knowledge. A dense particle indicates that the facility is abnormal. Therefore, the dataset with dense and even particles was selected. The four defect types are shown in
Figure 10. Our dataset consists of 300 normal wafers, 100 wafers of Type 1, 100 wafers of Type 2, 50 wafers of Type 3, and 50 wafers of Type 4. These types were determined by experienced engineers.
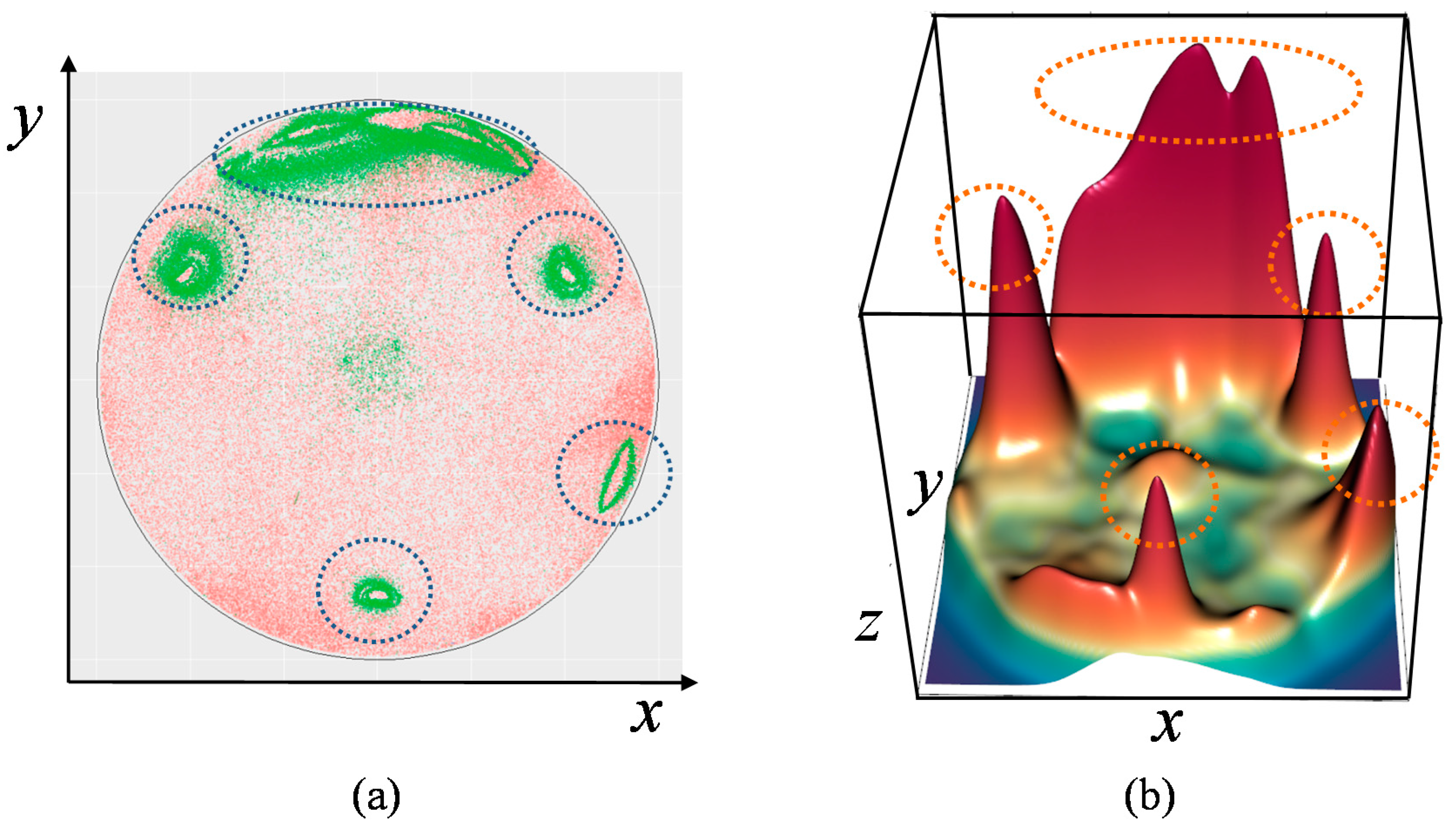
As shown in
Figure 10, Type 1 shows an illustrative particle map of a small defect. This map includes only one particle cluster, shown on the left side of the map. Type 2 map has two or more small defects. The Type 3 map has only one large-sized defect and the Type 4 map shows the particle distribution on the entire surface of the wafer.
According to the specified defect types, we generated four datasets for the experiment, as shown in
Table 1.
Dataset 1 includes non-defect wafer images and wafer images with Defect Types 1, 2, 3 and 4. On the other hand, Dataset 4 consists of non-defect wafers and Type 4 defect wafers only. In order to validate the monitoring performance for these datasets, we evaluated the use of , compared to the use of the conventional monitoring statistics, to identify a defect.
We used the monitoring method illustrated in
Figure 7 to classify non-defect and defect particle maps. The threshold in the monitoring chart corresponds to the upper control limit (UCL) in the statistical process control chart. Therefore, we compared the classification performance of the particle defect map by adjusting the decision threshold of the defect/non-defect. Further, we used the receiver operating characteristic (ROC) curve, a graphical plot that illustrates the performance of a binary classification. Moreover, in order to compare these curves, the area under the ROC (AUROC) curve was considered [
13]. A broader AUROC can detect a particle defect more accurately. As defect classification is more important than non-defect classification, the ROC curve uses a false negative rate for the
X-axis and a true negative rate for the
Y-axis.
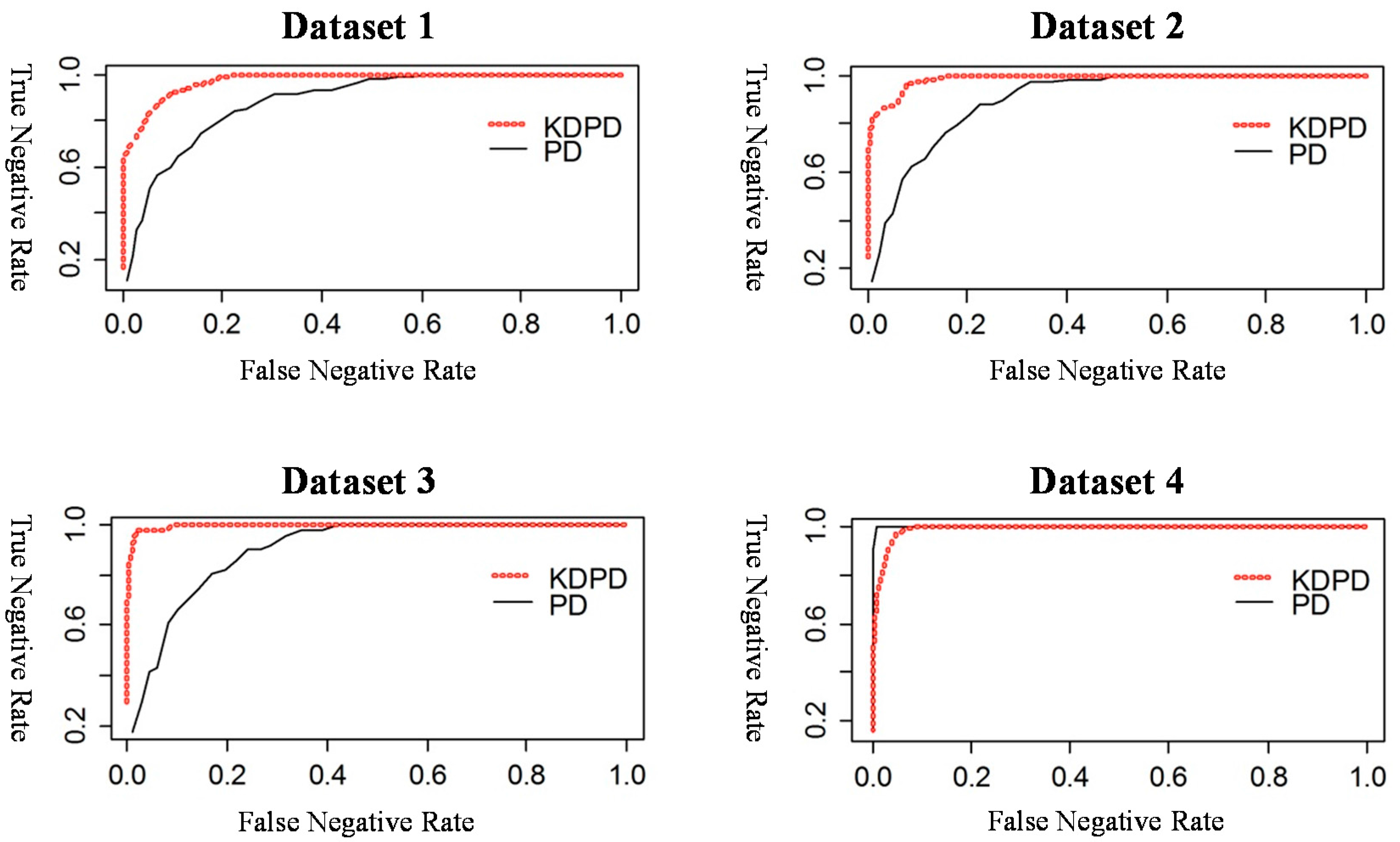
Figure 11 depicts the ROC curves for both
and
of the four datasets defined in
Table 1, and the AUROC examines the monitoring performances.
The ROC curves of Datasets 1, 2 and 3 show that the AUROCs of
are broader than those of
. Therefore,
outperforms
. Moreover, the results indicate an increase in the performance gap between
and
in proportion to the degree of the defects. On the other hand, Dataset 4 demonstrates that the conventional statistics
outperforms
. This dataset includes the Type 4 defect as specified in
Table 1 and is referred to as a fatal defect. This can be monitored using either
or
. Therefore, the proposed
is appropriate for detecting Type 1, 2, and 3 defects. Since the Type 1, 2 and 3 defects indicate potential factors that can result in fatal defectives of Type 4, field engineers can detect critical defects in early stages.
Table 2 represents the area under the ROC curves depicted in
Figure 11. In Datasets 1, 2 and 3, the area of
is much larger than
. However, in the case of Dataset 4, the area of
is slightly smaller than
.
5. Conclusions
This study is significant because the proposed method utilizes the real data of the particles in the chamber of a semiconductor process. Novel monitoring statistics that efficiently identify the particles on the wafers in a chamber are proposed in this study. These new statistics are based on multivariate kernel density estimation and indicate the densities of the particles. Thorough management is essential for reducing the failures caused by particles in a semiconductor manufacturing process. This study presents a particle defect management method using a kernel-density-based particle map for improving the conventional method of monitoring the number of particles. In particular, the main contribution of this study is the development of new monitoring statistics. The new statistics that consider the distribution of particles, when applied to an actual process, produce the following three effects. Firstly, the proposed method can reduce the number of unnecessary replacements. Secondly, according to a field internal review, when this study is applied to an actual process, a reduction of approximately 30% in the meantime to repair (MTTR), i.e., the time to find the cause of a failure, is expected. Third, regardless of the number of particles, dense particles increase the possibility of further failures. Therefore, using the proposed particle maps, it is possible to detect defects and predict future failures.
Since the semiconductor manufacturing processes are becoming finer, particle defect management becomes increasingly important. If the proposed kernel-density-based particle map can be applied to an actual process, it is expected to improve both the yield and the quality of the semiconductor product. The size of particle defect has a large influence on yield. The current wafer size is 300 mm, but the wafer size will grow and the defect rate will increase as the process is refined. Therefore, in the future, it is necessary to identify the relationship between the particle map and both the yield and quality of the wafer.