Soliton Molecules and Multisoliton States in Ultrafast Fibre Lasers: Intrinsic Complexes in Dissipative Systems
Abstract
Featured Application
Abstract
1. Introduction
2. Analytical Expression of Soliton Molecules for Optical Characterization in Frequency and Time Domain
2.1. Frequency Domain
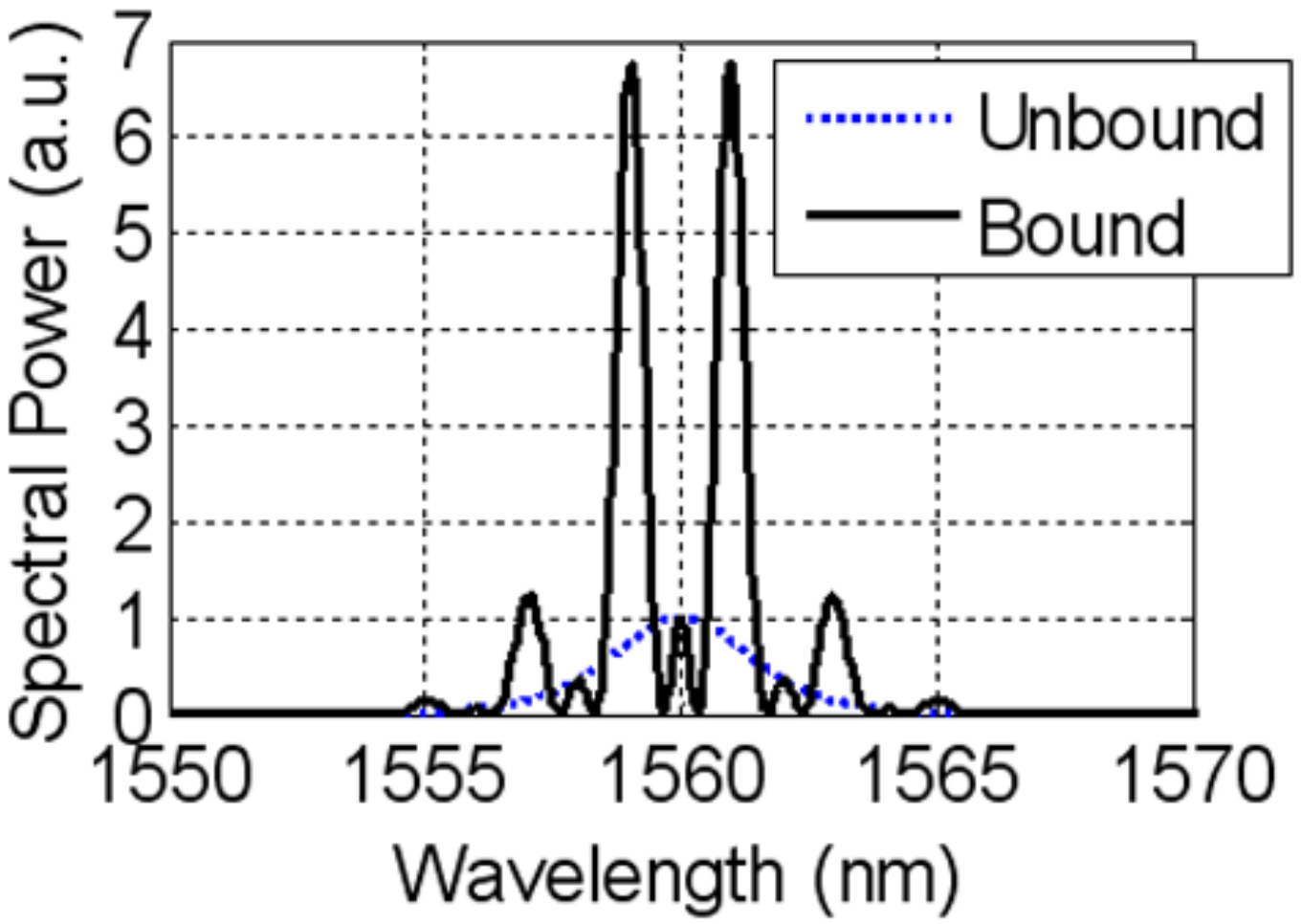
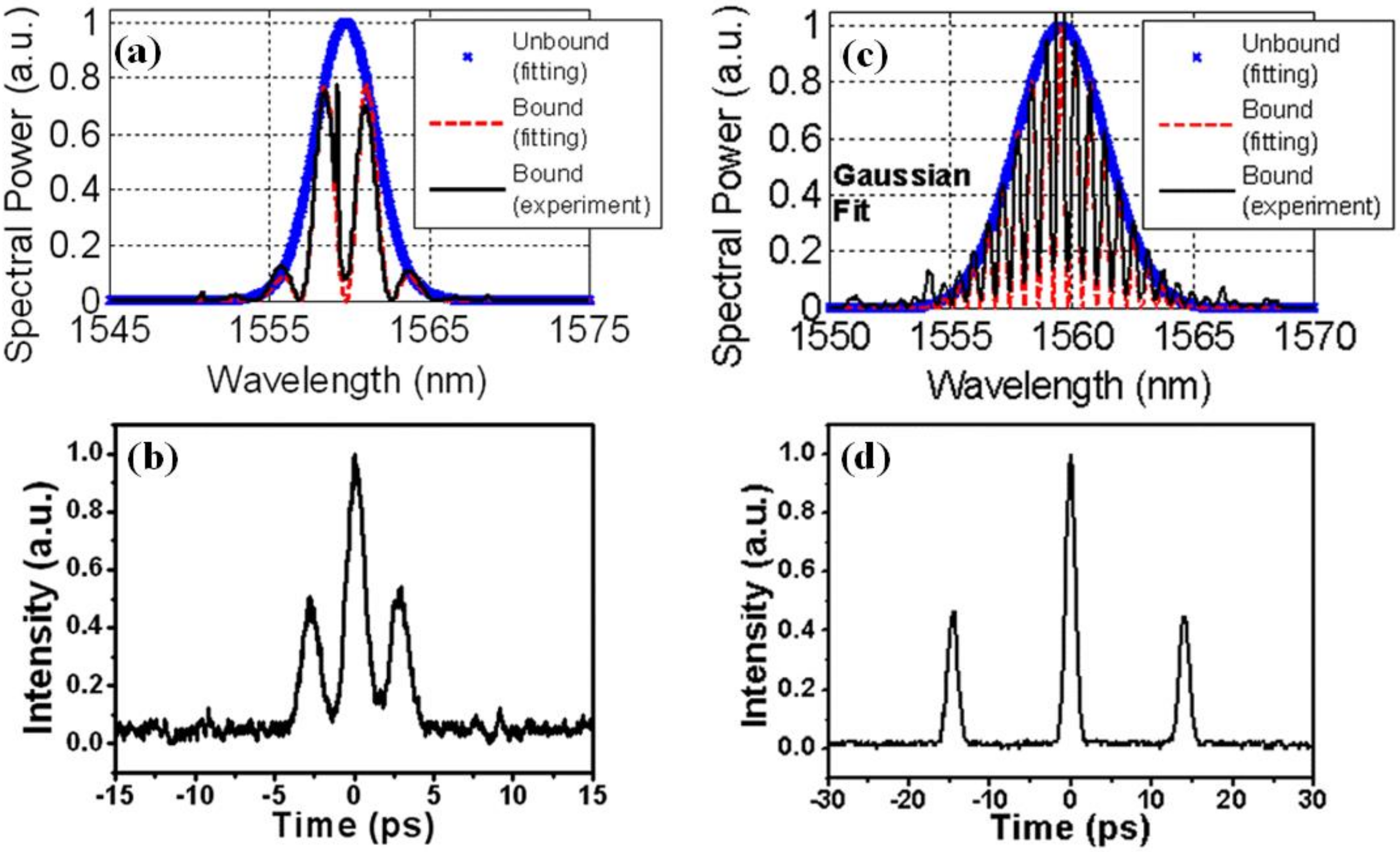
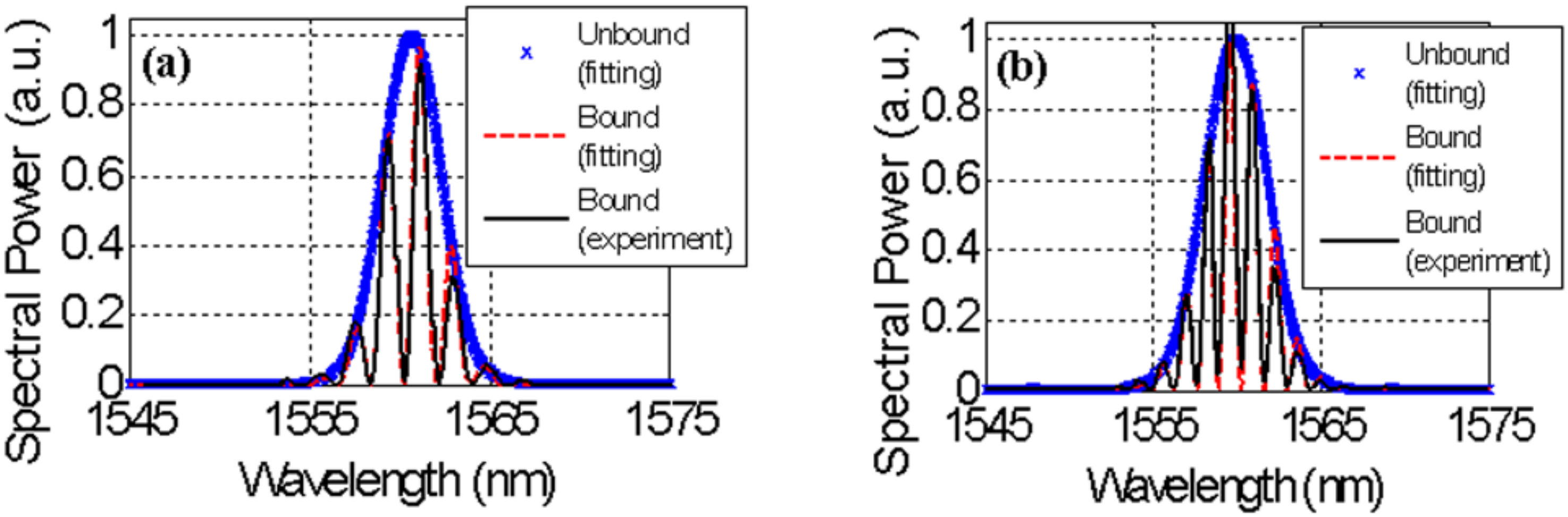
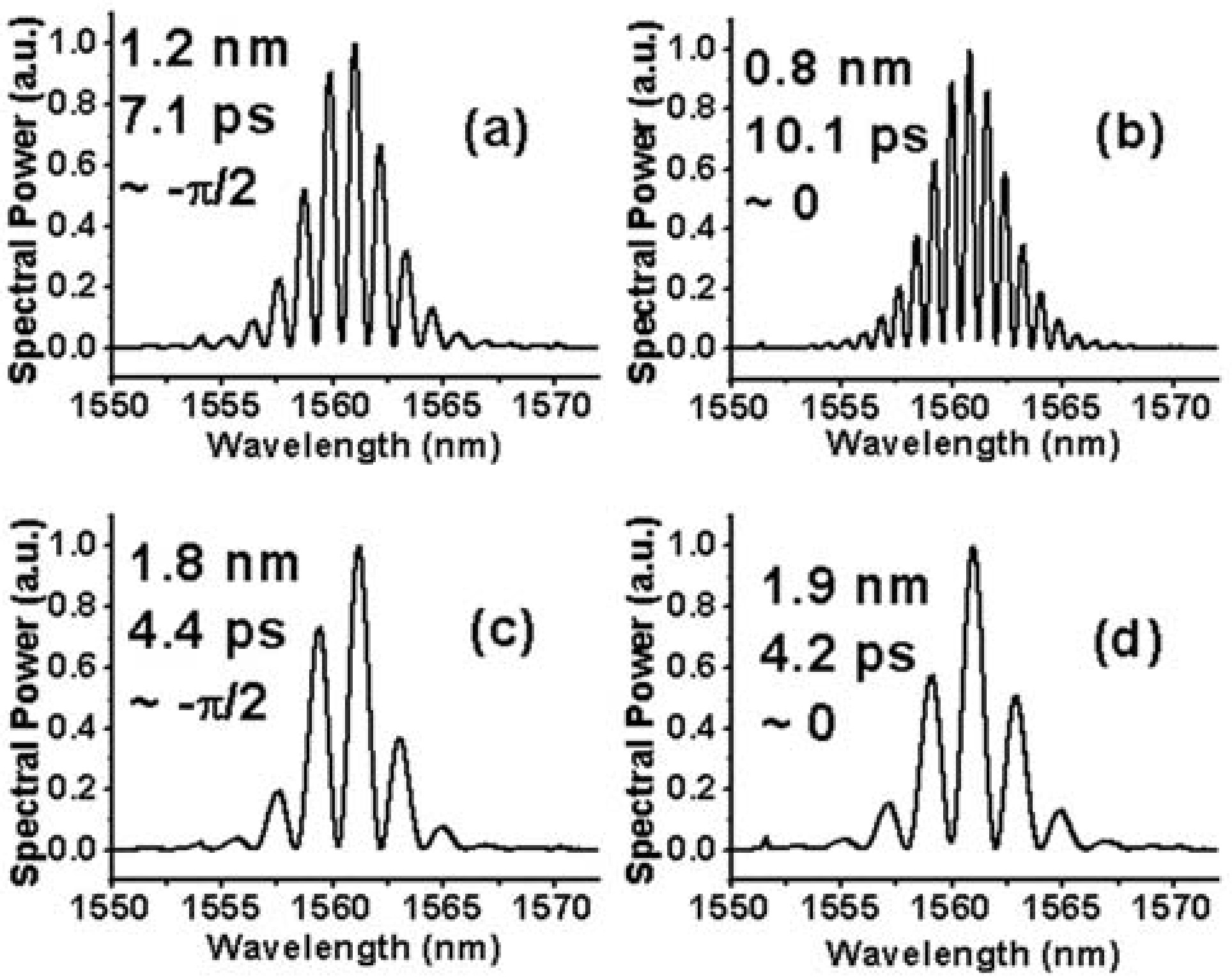
2.1.1. Two-Soliton Bound States
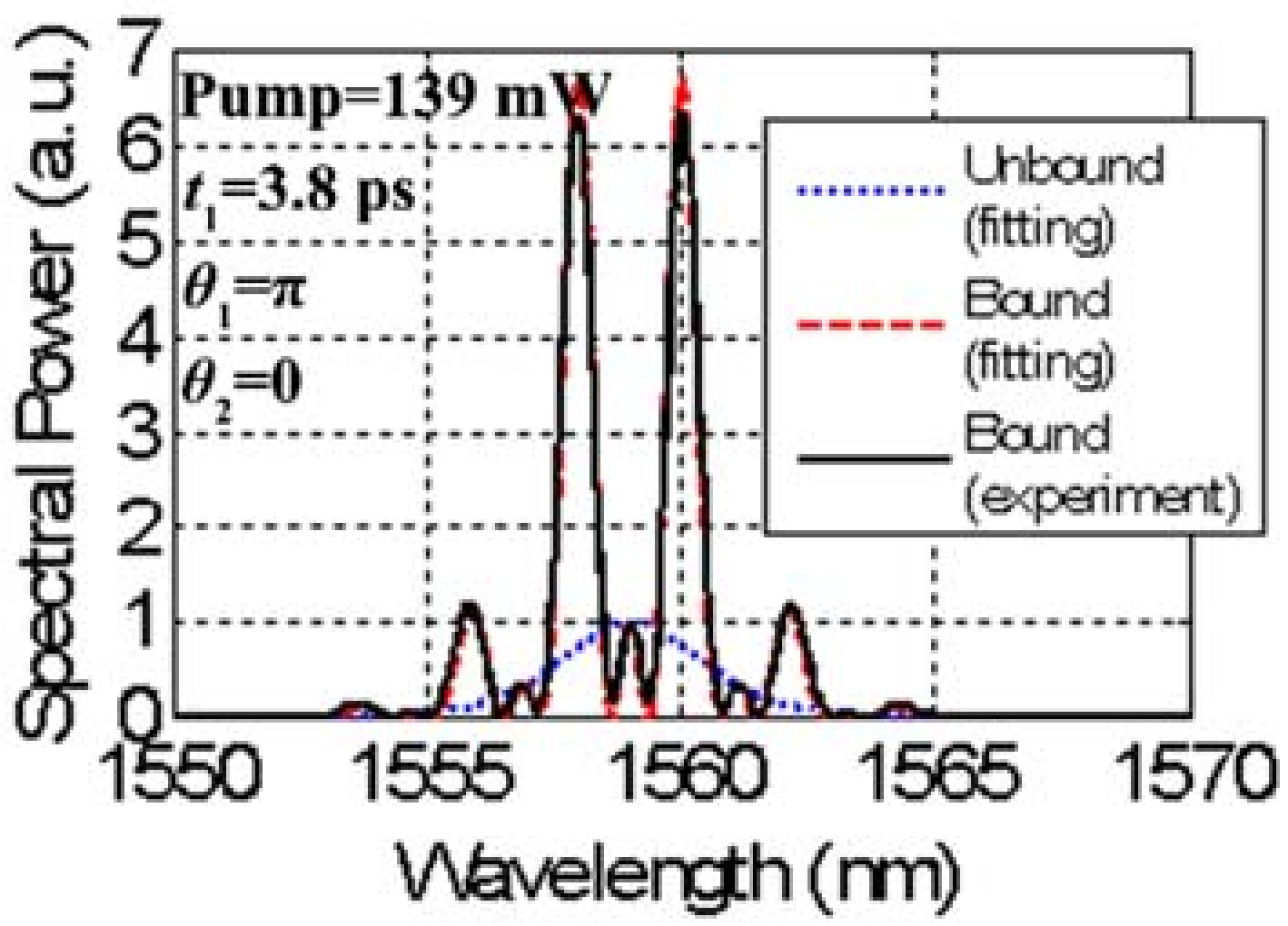
2.1.2. Triple-Soliton Bound States
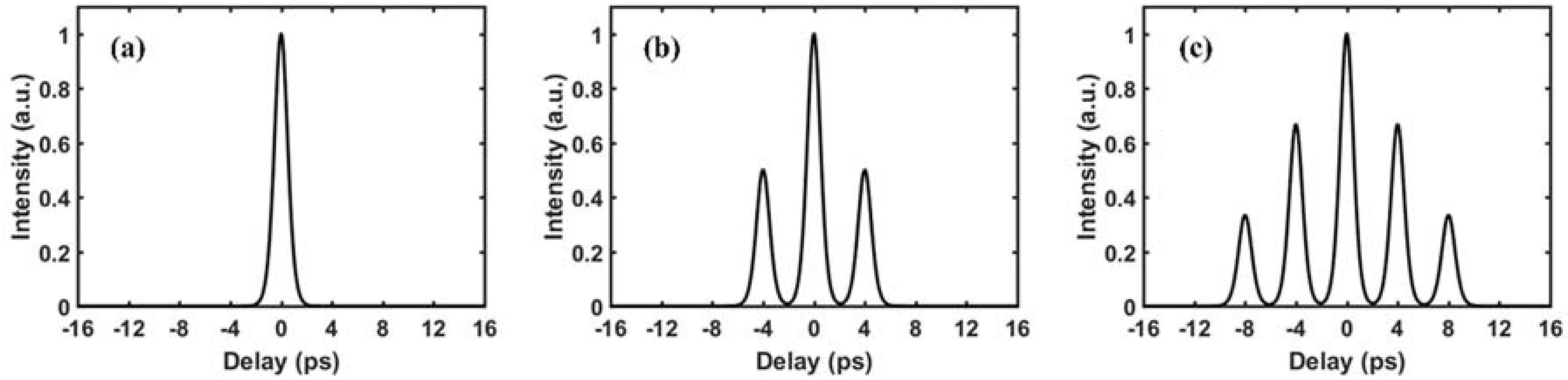
2.2. Time Domain
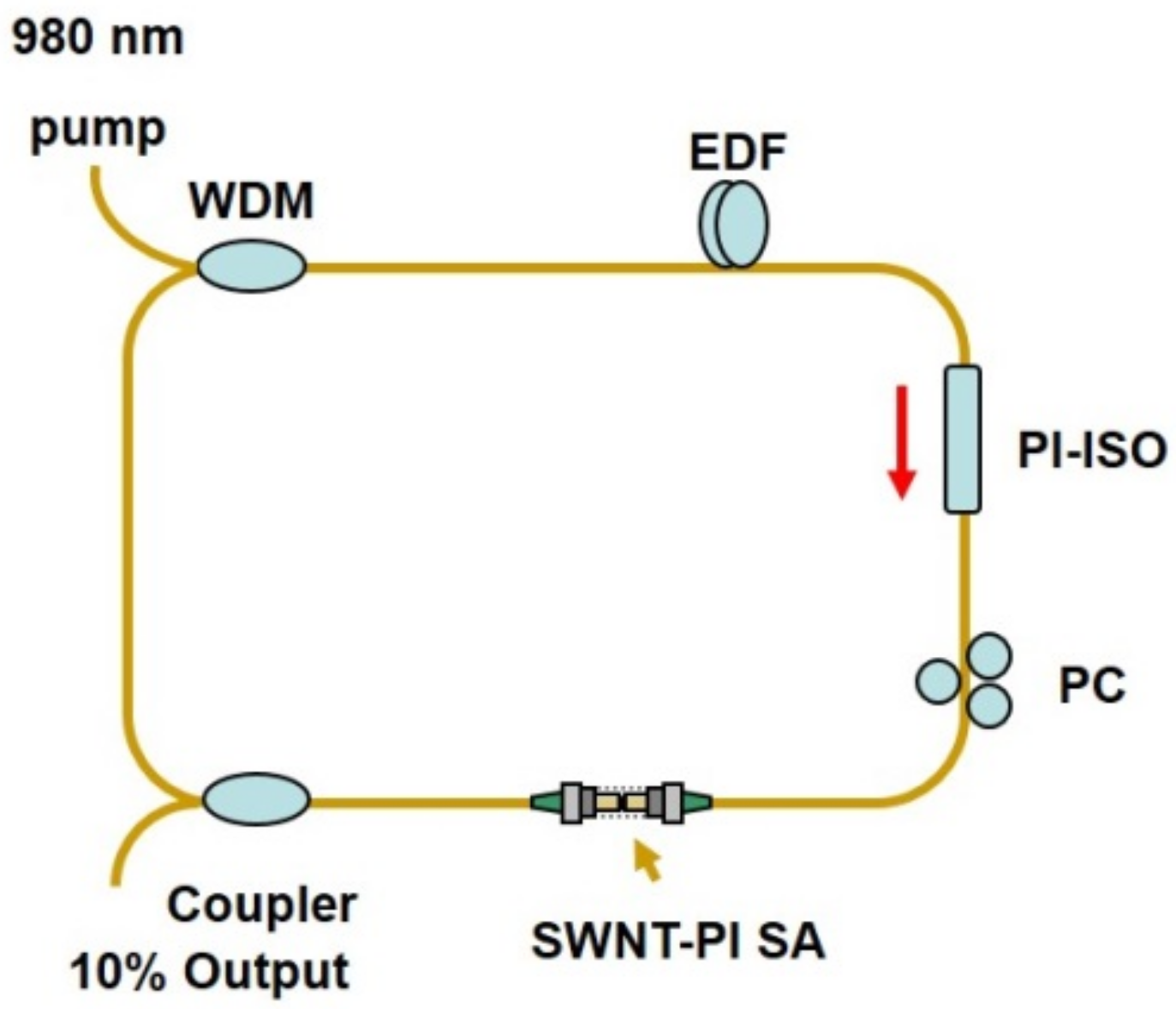
3. Experimental Observation of Various Soliton Molecules in Different Fibre Lasers
3.1. Anomalous Dispersion Regime
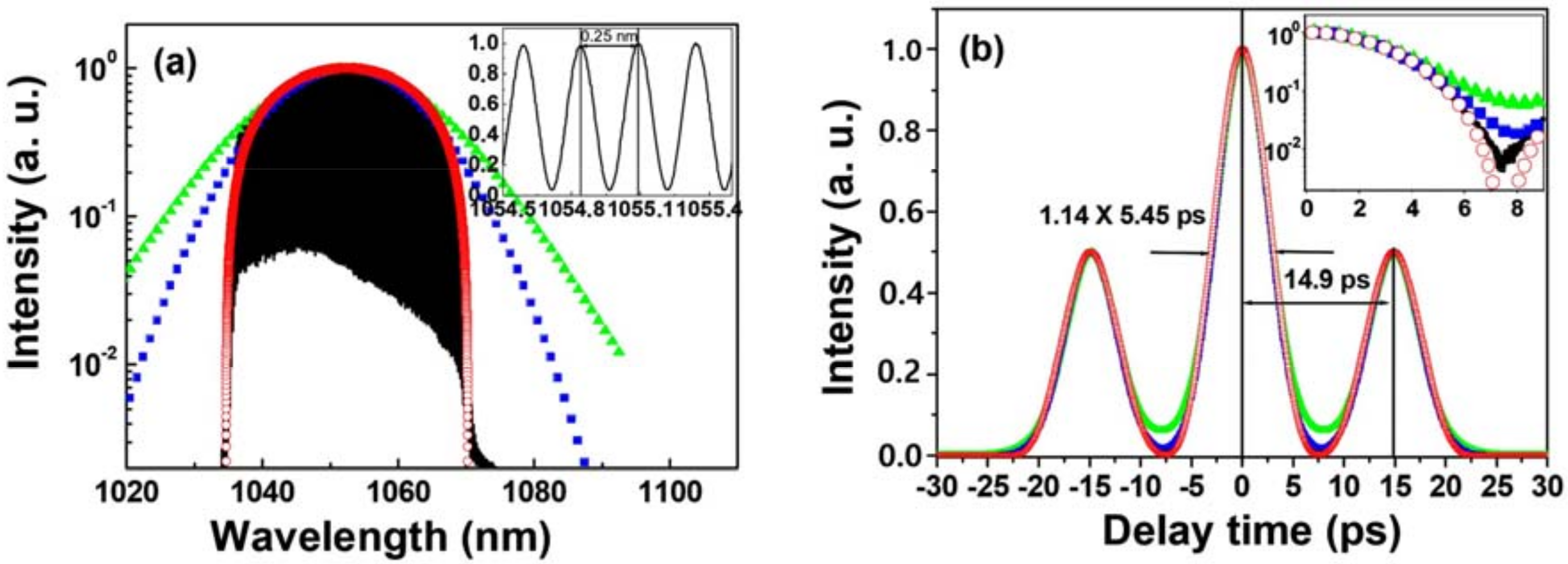
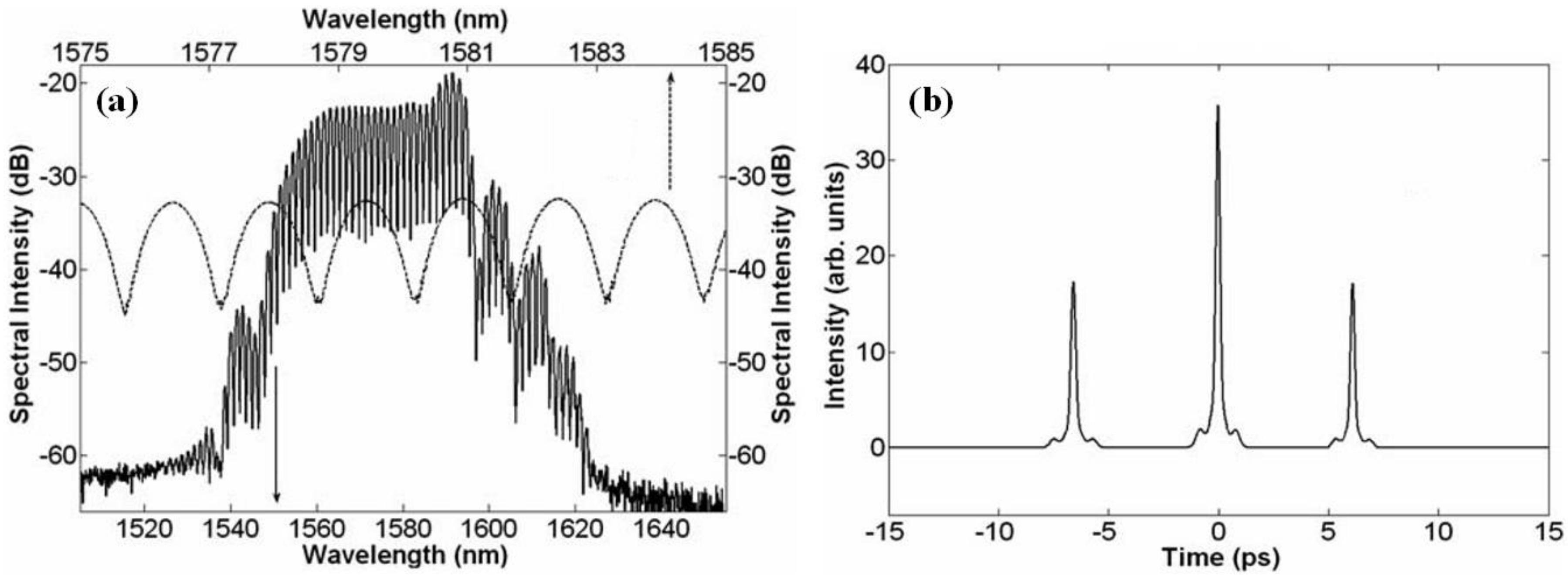
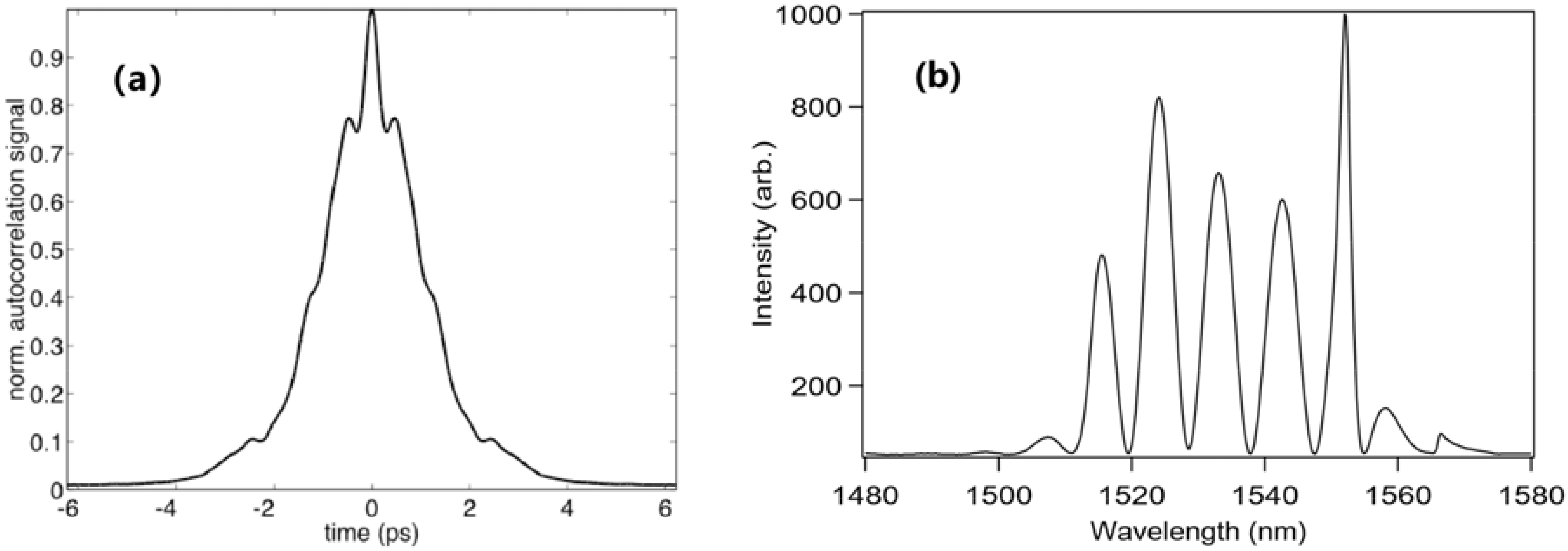
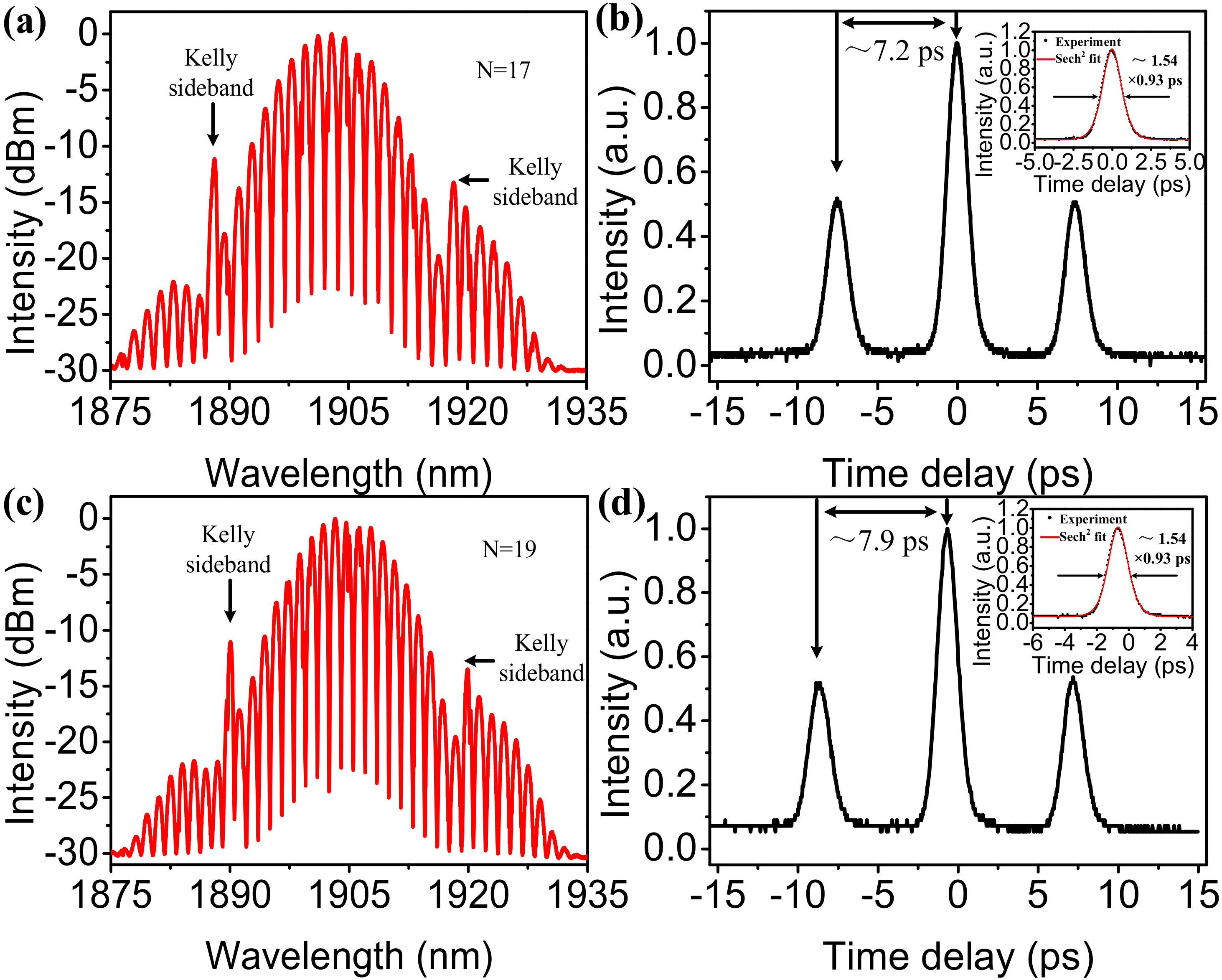
3.1.1. 1.5-Micron Wavelength Regime
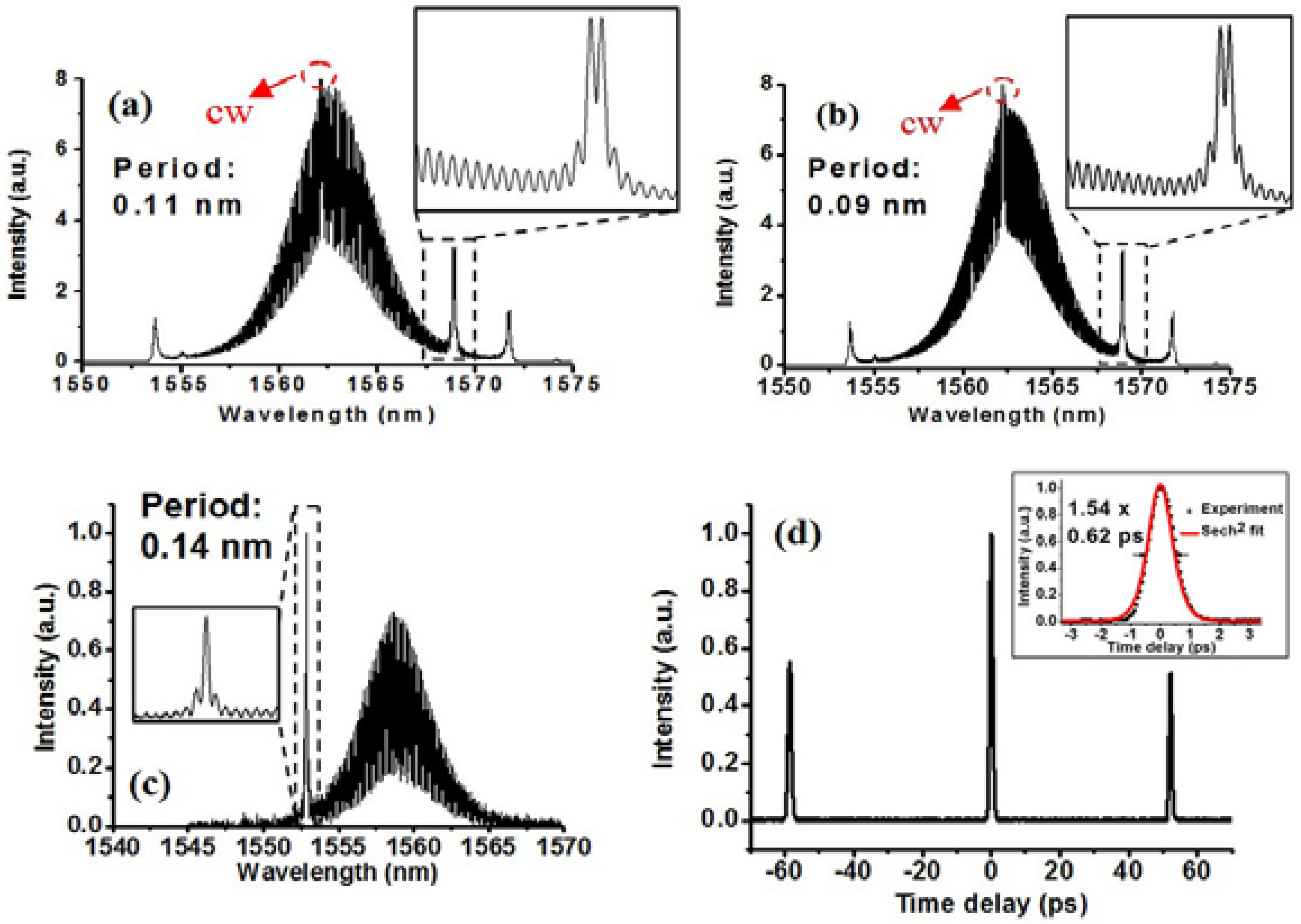
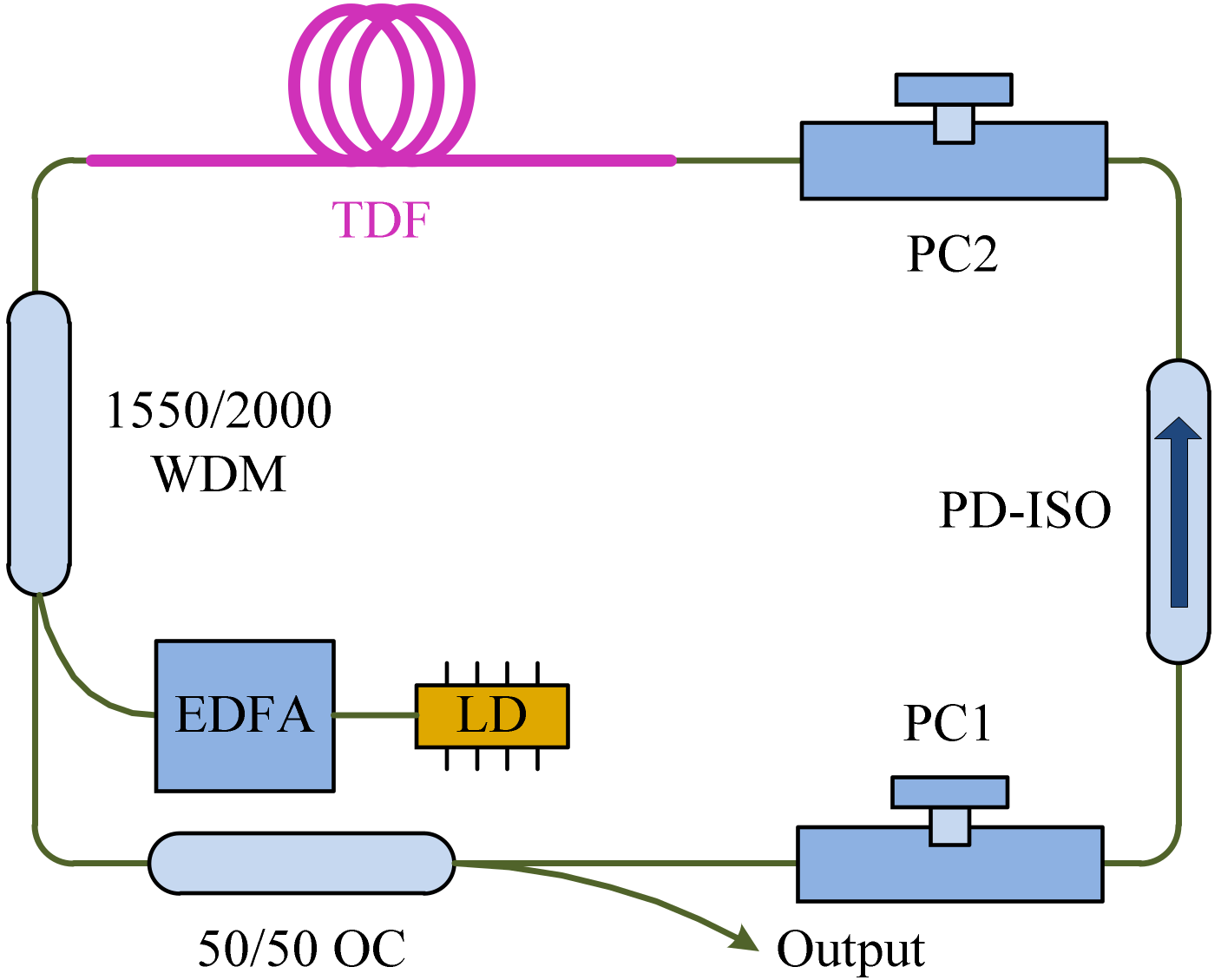
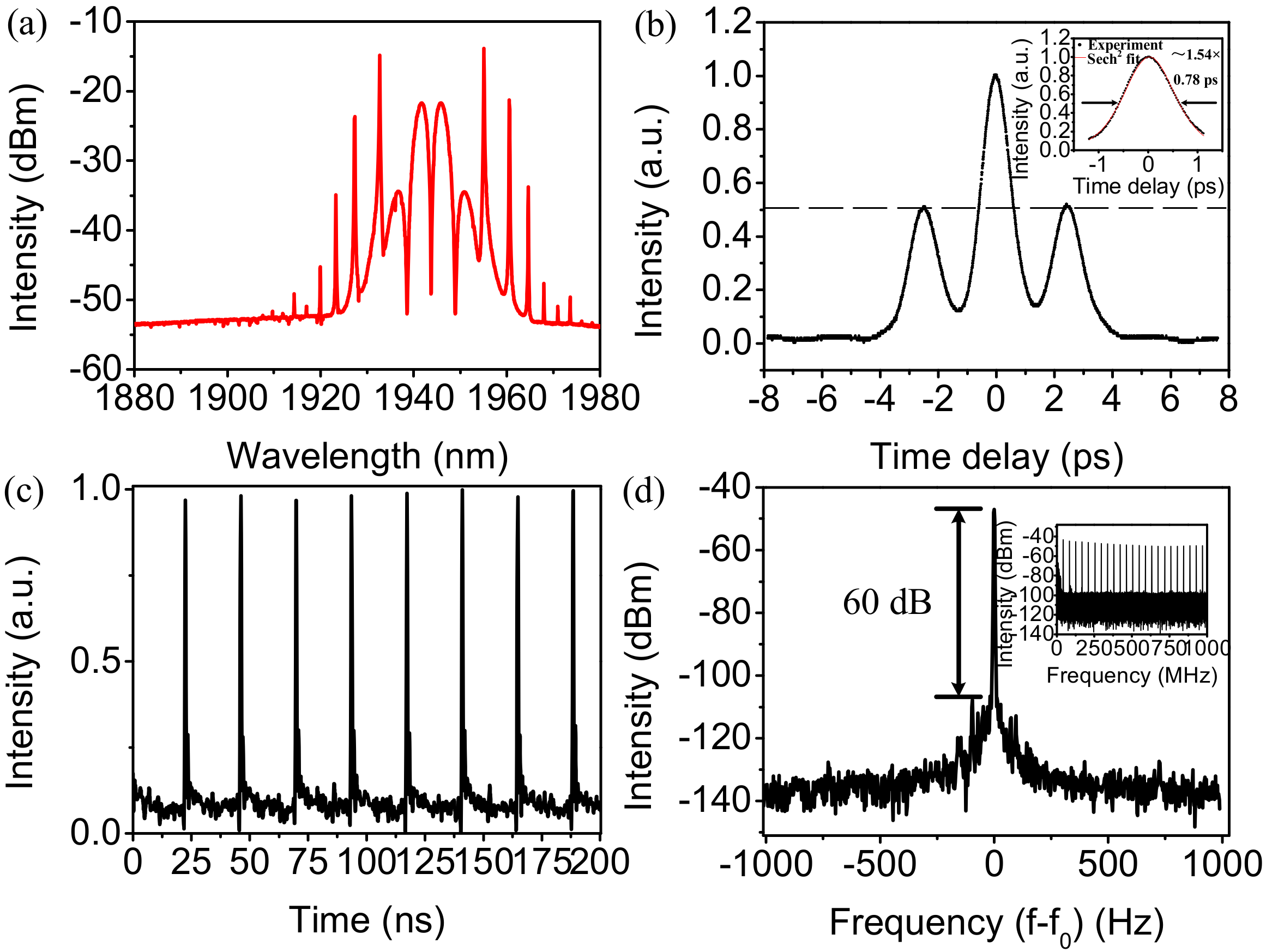
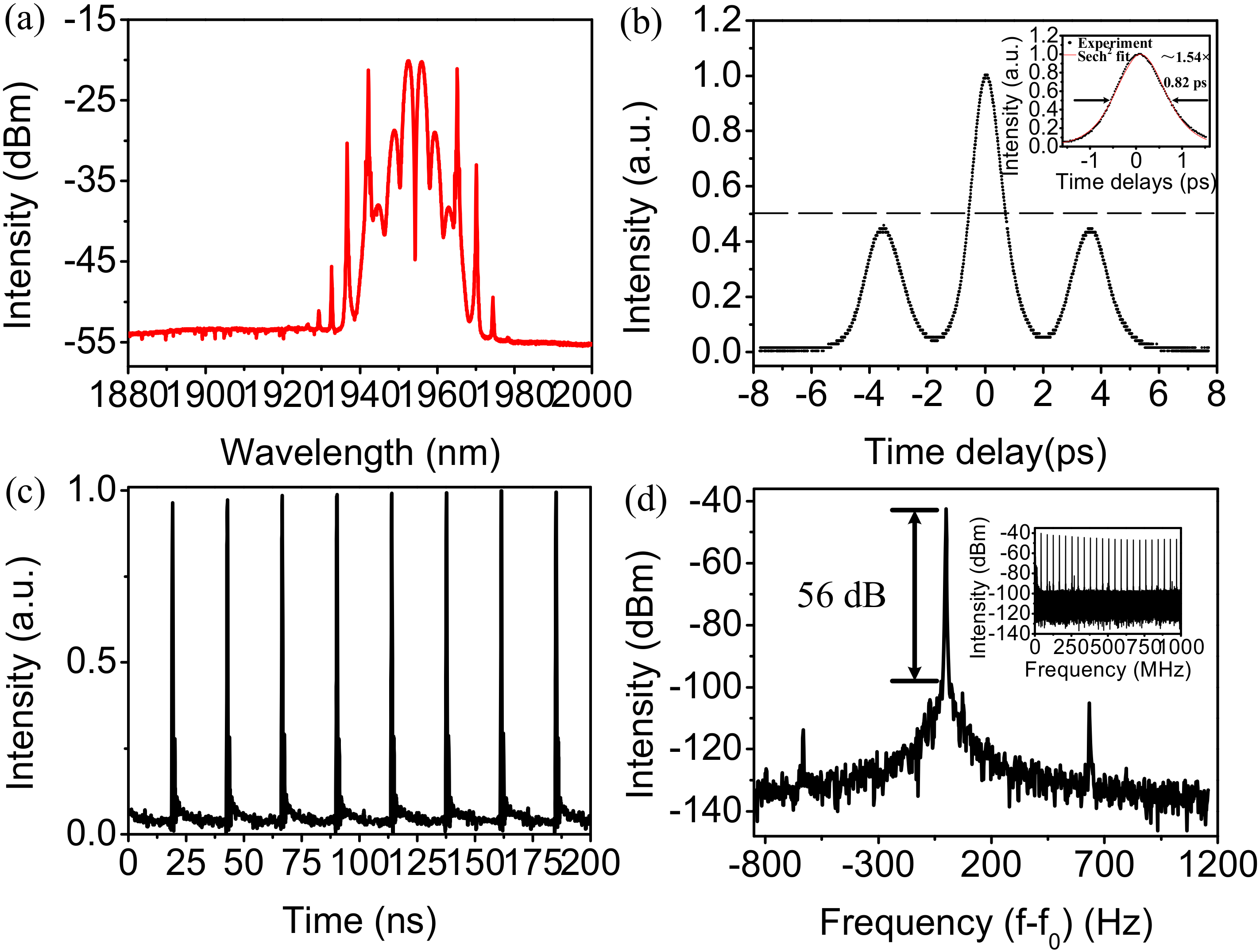
3.1.2. 2-Micron Wavelength Regime
3.2. Net Normal Dispersion Regime
3.3. Nearly Zero Net-Cavity Dispersion Regime
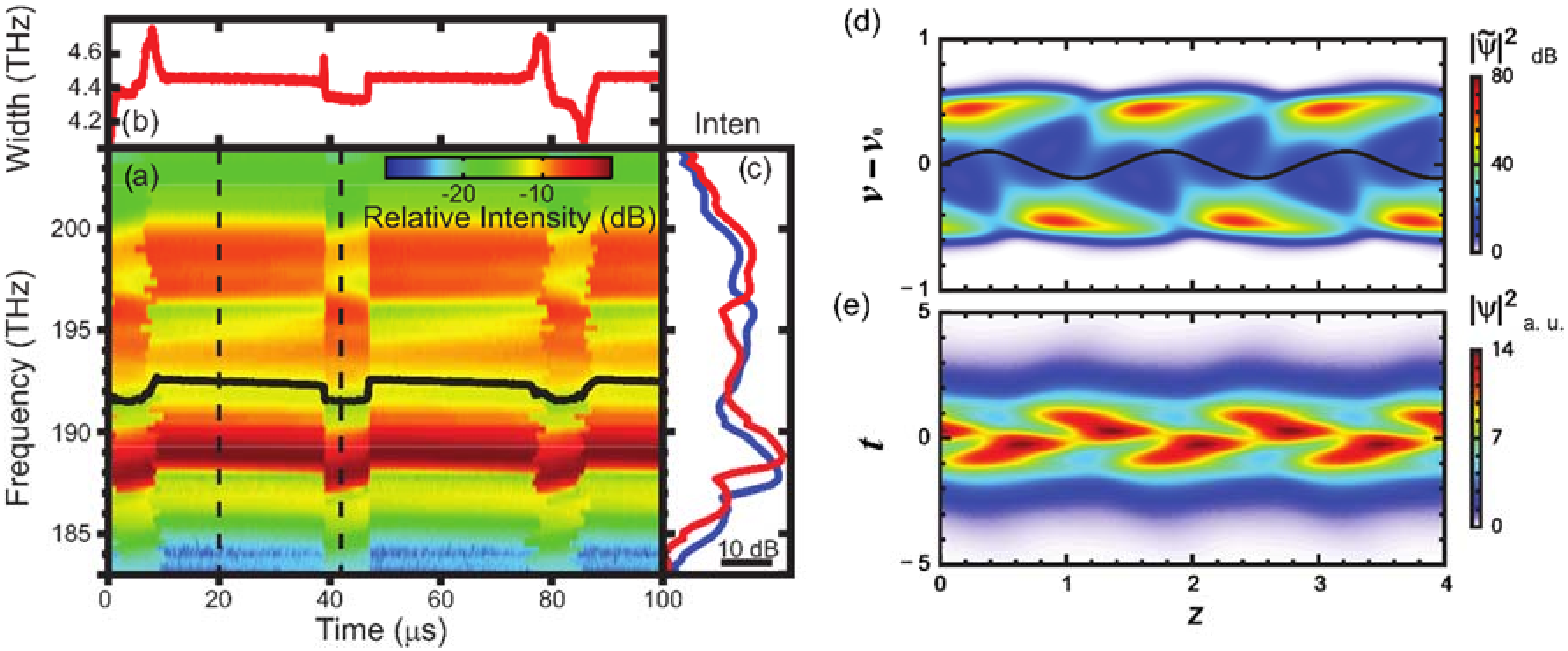
4. Numerical Simulation of Soliton Molecules
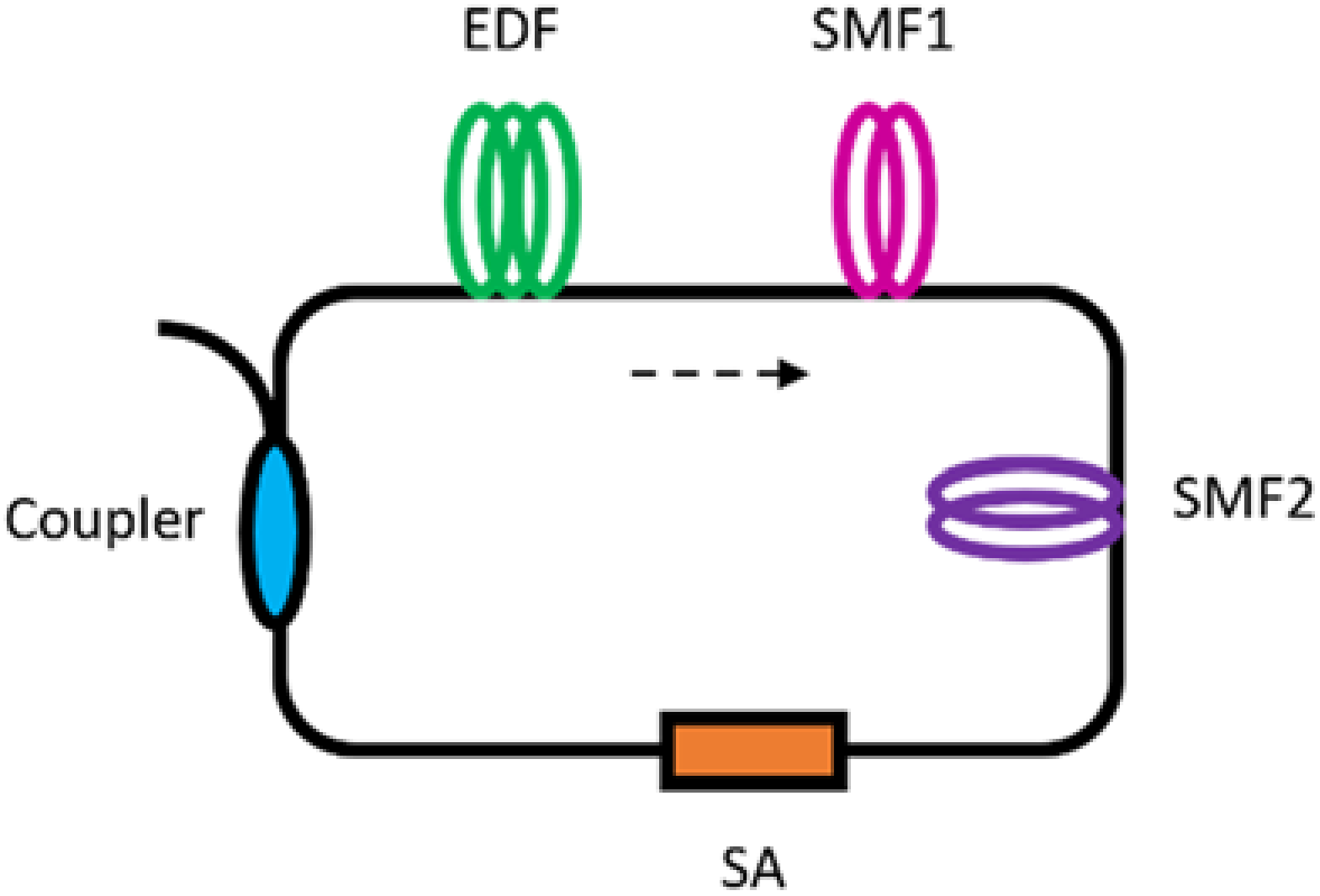
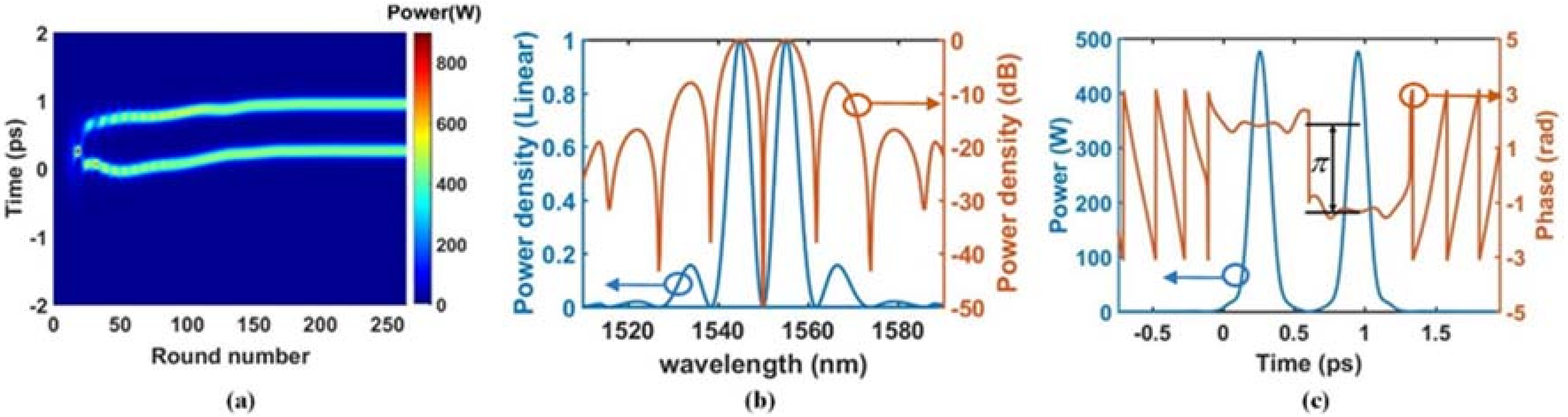
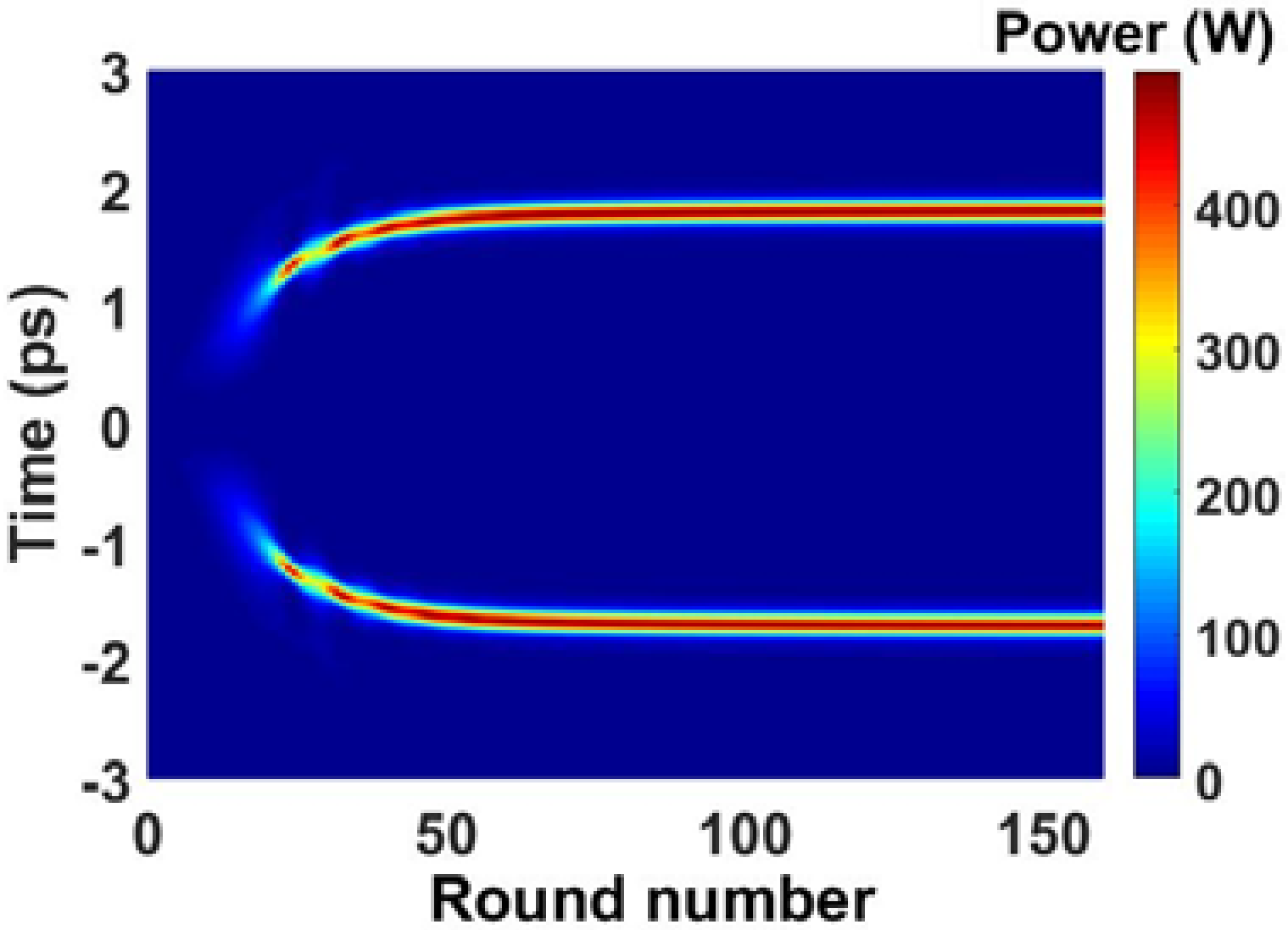
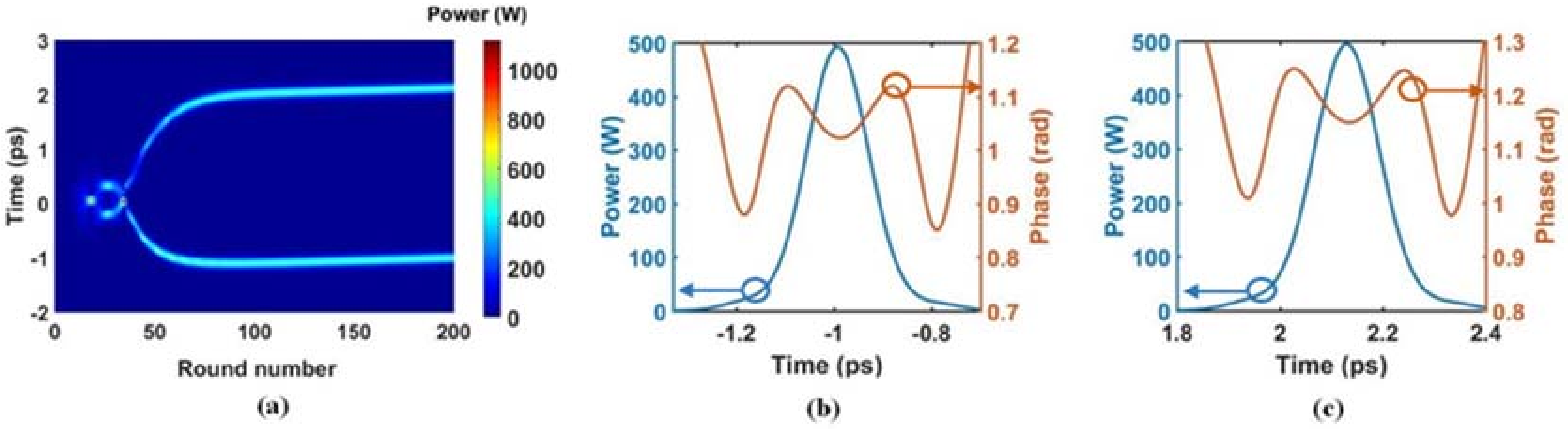
4.1. Out-of-Phase Two-Soliton Bound States
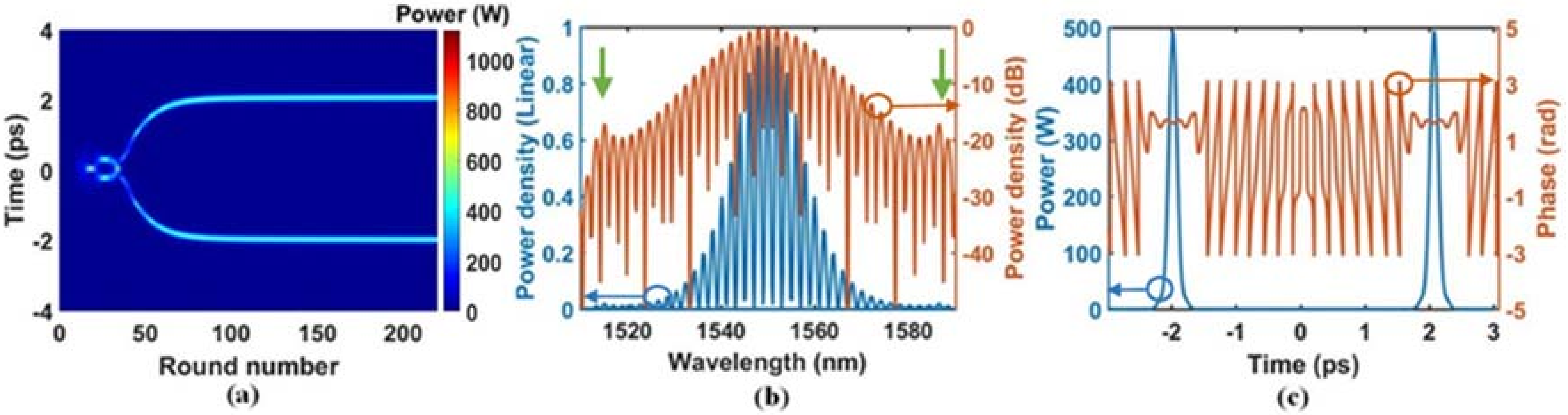
4.2. In-Phase Two-Soliton Bound States
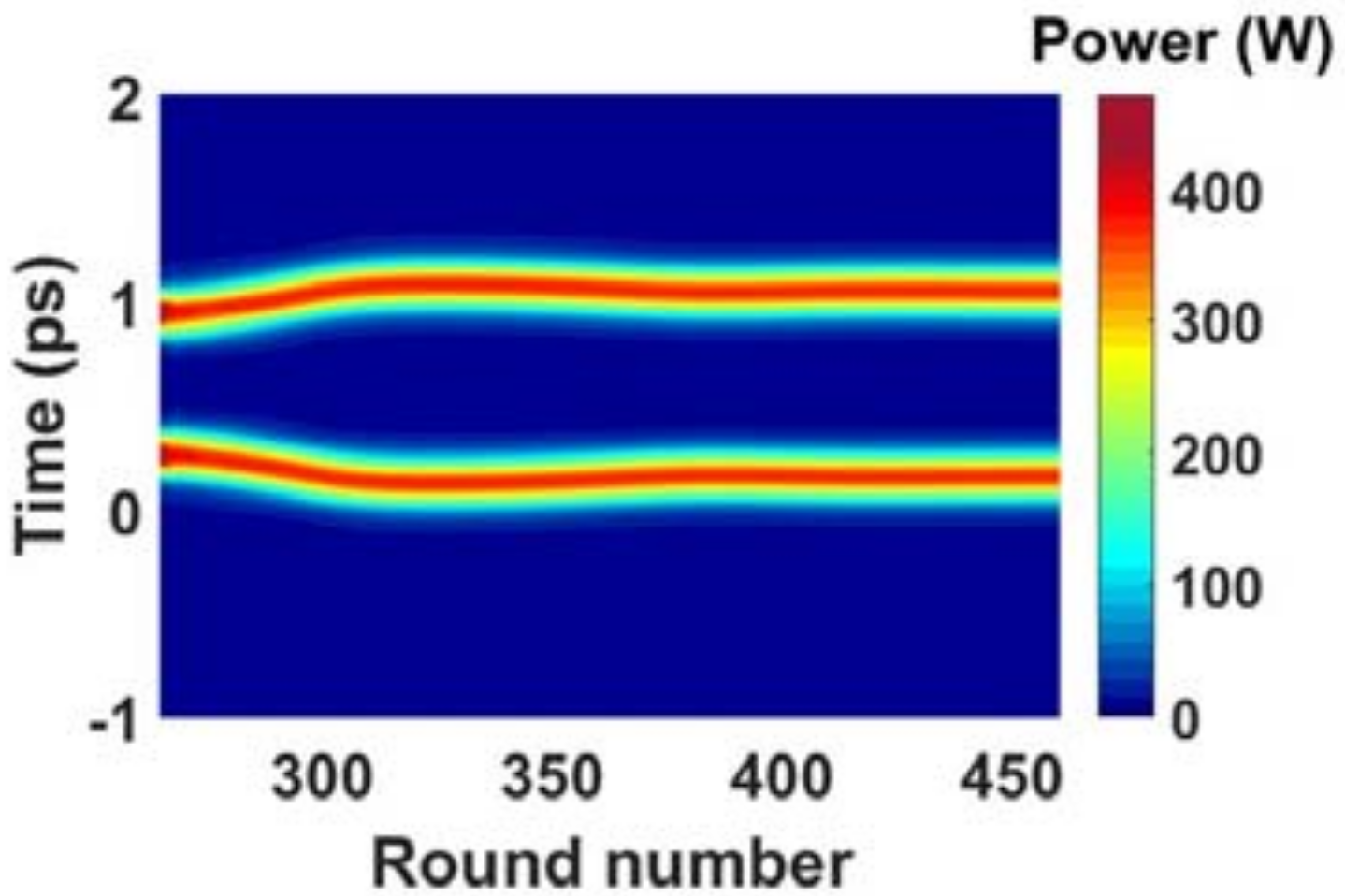
4.3. Influence of Gain
4.4. Influence of Third-Order Dispersion
5. Discussion on Generation and Stability of Various Soliton Molecules
5.1. Key Parameters for Generation of Soliton Molecules
5.2. Stability of Soliton Molecules
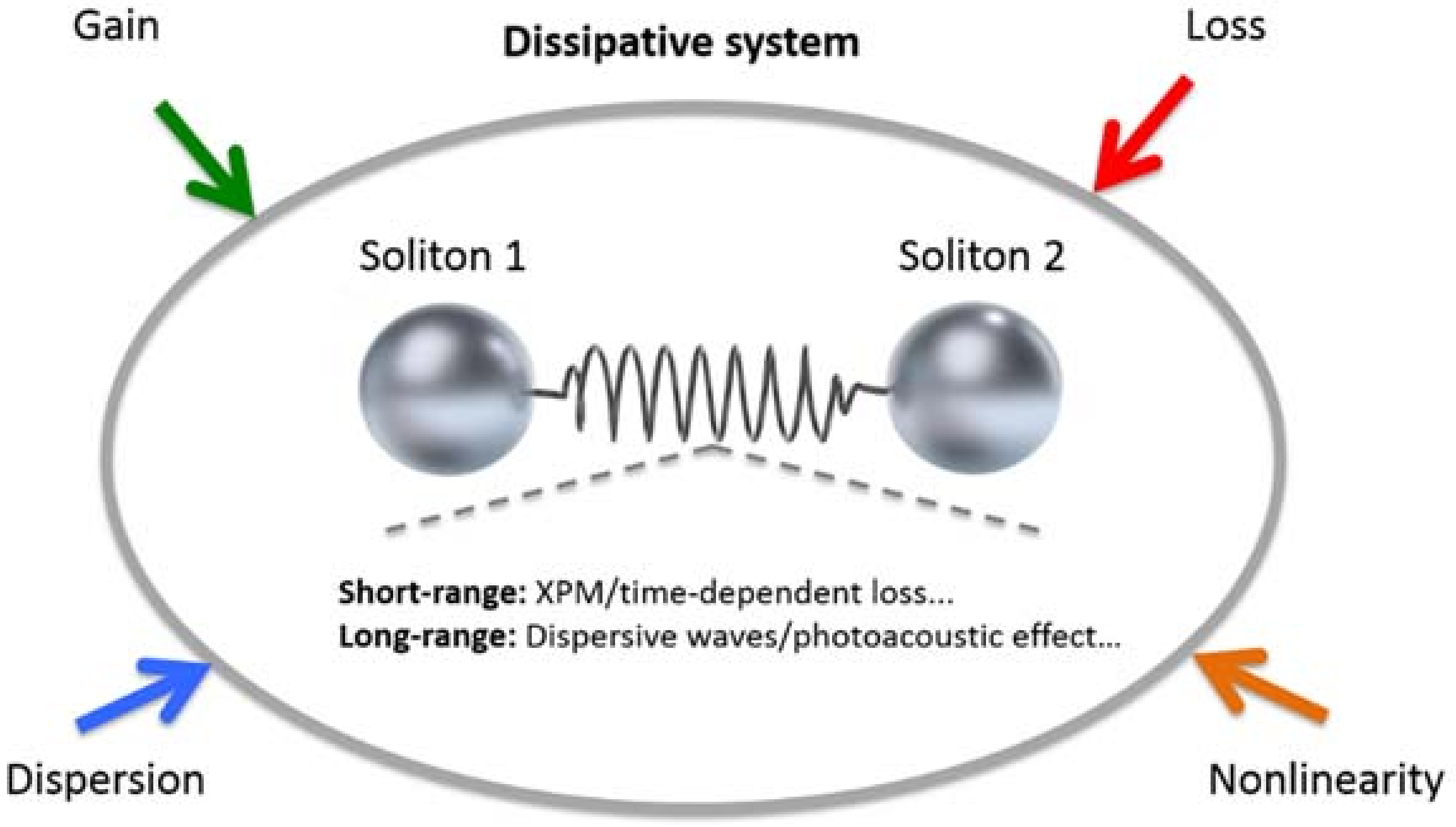
5.3. Interaction Mechanisms
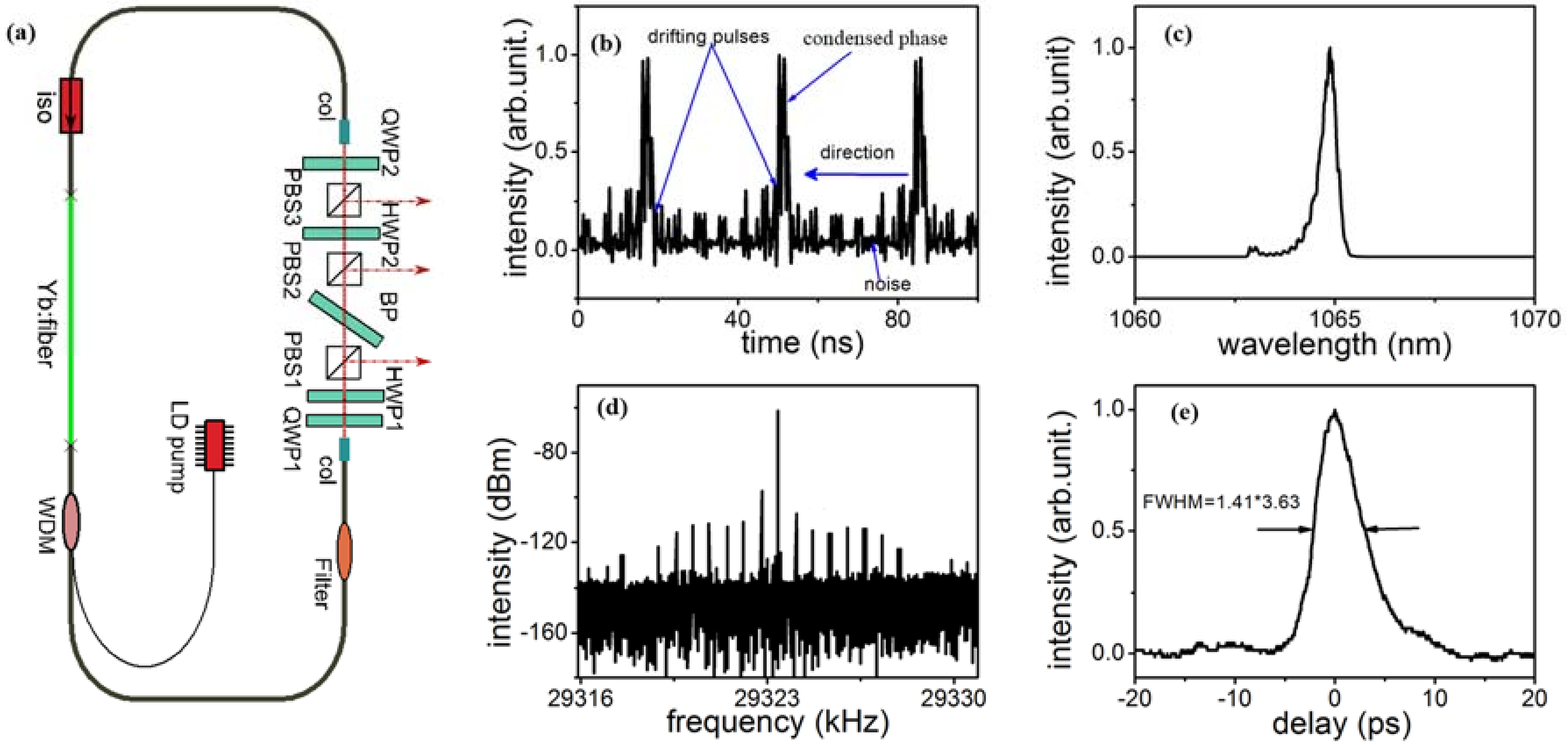
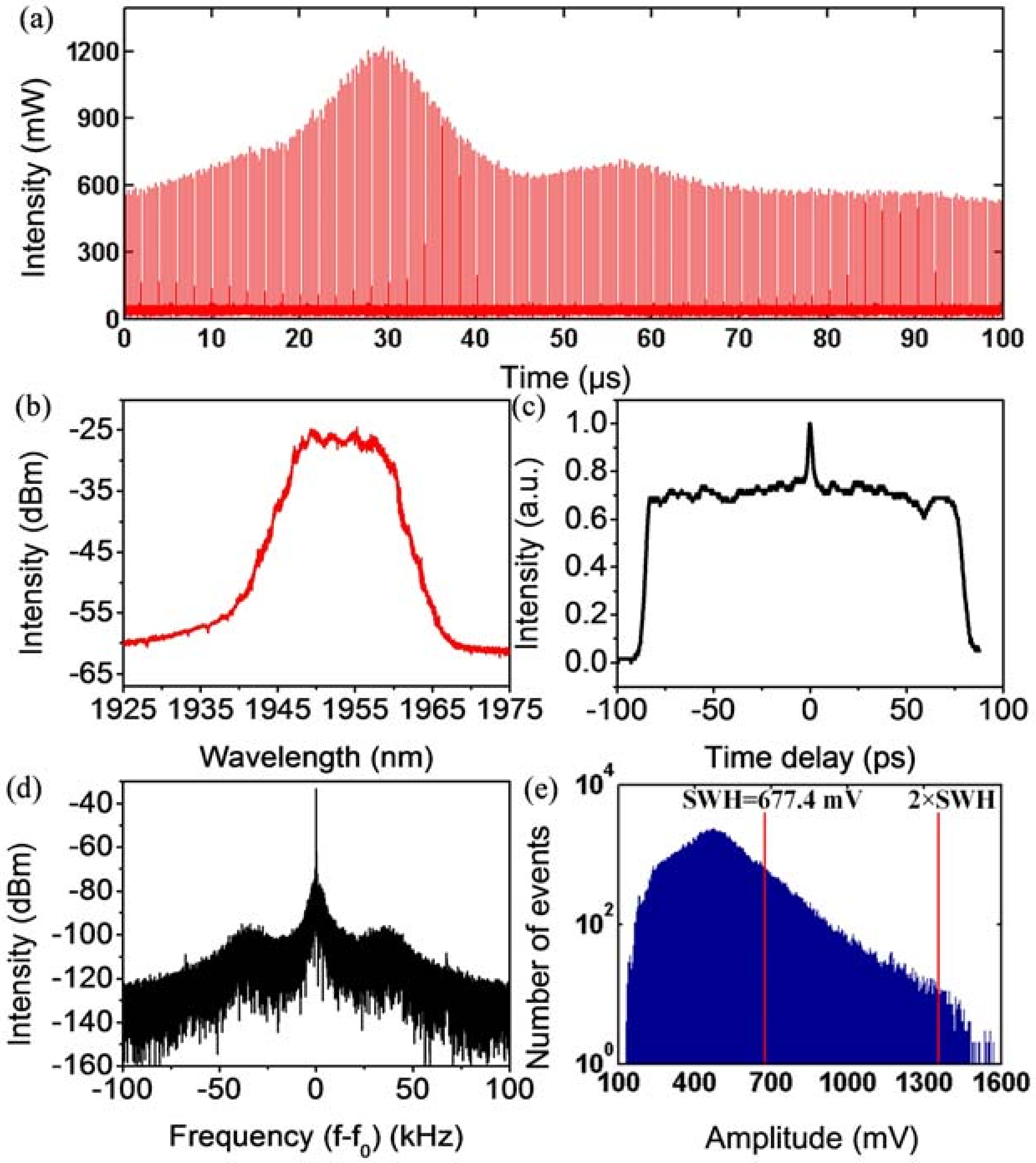
6. Other Multisoliton States and Dissipative Soliton Dynamics
7. Conclusion and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, C.; Wise, F. Recent advances in fibre lasers for nonlinear microscopy. Nat. Photonics 2013, 7, 875–882. [Google Scholar] [CrossRef] [PubMed]
- Fermann, M.E.; Hartl, I. Ultrafast fibre lasers. Nat. Photonics 2013, 7, 868–874. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Olivier, M.; PichÚ, M. Origin of the bound states of pulses in the stretched-pulse fibre laser. Opt. Express 2009, 17, 405–418. [Google Scholar] [CrossRef] [PubMed]
- Ortaç, B.; Zaviyalov, A.; Nielsen, C.K.; Egorov, O.; Iliew, R.; Limpert, J.; Lederer, F.; Tünnermann, A. Observation of soliton molecules with independently evolving phase in a mode-locked fibre laser. Opt. Lett. 2010, 35, 1578–1580. [Google Scholar] [CrossRef] [PubMed]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental observation of temporal soliton molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef] [PubMed]
- Komarov, A.; Komarov, K.; Sanchez, F. Quantization of binding energy of structural solitons in passive mode-locked fibre lasers. Phys. Rev. A 2009, 79, 033807. [Google Scholar] [CrossRef]
- Yun, L.; Liu, X. Generation and propagation of bound-state pulses in a passively mode-locked figure-eight laser. IEEE Photonics J. 2012, 4, 512–519. [Google Scholar]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.R.; Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 2017, 356, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Krupa, K.; Nithyanandan, K.; Andral, U.; Tchofo-Dinda, P.; Grelu, P. Real-time observation of internal motion within ultrafast dissipative optical soliton molecules. Phys. Rev. Lett. 2017, 118, 243901. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Bound solitons in the nonlinear Schrödinger-Ginzburg-Landau equation. Phys. Rev. A 1991, 44, 6954–6957. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Bound solitons in coupled nonlinear Schrödinger equations. Phys. Rev. A 1992, 45, R8321–R8323. [Google Scholar] [CrossRef] [PubMed]
- Afanasjev, V.V.; Akhmediev, N. Soliton interaction in nonequilibrium dynamical systems. Phys. Rev. E 1996, 53, 6471–6475. [Google Scholar] [CrossRef]
- Afanasjev, V.V.; Malomed, B.A.; Chu, P. Stability of bound states of pulses in the Ginzburg-Landau equations. Phys. Rev. E 1997, 56, 6020. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J. Multisoliton solutions of the complex Ginzburg-Landau equation. Phys. Rev. Lett. 1997, 79, 4047–4051. [Google Scholar] [CrossRef]
- Tang, D.Y.; Man, W.S.; Tam, H.Y.; Drummond, P.D. Observation of bound states of solitons in a passively mode-locked fibre laser. Phys. Rev. A 2001, 64, 033814. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, B.; Shen, D.Y.; Lu, C.; Man, W.; Tam, H. Compound pulse solitons in a fibre ring laser. Phys. Rev. A 2003, 68, 013816. [Google Scholar] [CrossRef]
- Grelu, P.; Belhache, F.; Gutty, F.; Soto-Crespo, J. Phase-locked soliton pairs in a stretched-pulse fibre laser. Opt. Lett. 2002, 27, 966–968. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Tang, D.; Wu, X.; Lei, D.; Wen, S. Bound states of gain-guided solitons in a passively mode-locked fibre laser. Opt. Lett. 2007, 32, 3191–3193. [Google Scholar] [CrossRef] [PubMed]
- Ortac, B.; Hideur, A.; Brunel, M.; Chedot, C.; Limpert, J.; Tunnermann, A.; Ilday, F.O. Generation of parabolic bound pulses from a Yb-fibre laser. Opt. Express 2006, 14, 6075–6083. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Zhan, L.; Luo, S.; Shen, Q.S. Generation of soliton molecules in a normal-dispersion fibre laser. IEEE Photonics Technol. Lett. 2013, 25, 948–951. [Google Scholar] [CrossRef]
- Grelu, P.; Béal, J.; Soto-Crespo, J. Soliton pairs in a fibre laser: From anomalous to normal average dispersion regime. Opt. Express 2003, 11, 2238–2243. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Bao, C.Y.; Fu, B.; Xiao, X.S.; Grelu, P.; Yang, C.X. Generation of wavelength-tunable soliton molecules in a 2-mu m ultrafast all-fibre laser based on nonlinear polarization evolution. Opt. Lett. 2016, 41, 2254–2257. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xiao, X.; Yang, C. Quantized pulse separations of phase-locked soliton molecules in a dispersion-managed mode-locked Tm fibre laser at 2 μm. Opt. Lett. 2017, 42, 29–32. [Google Scholar] [CrossRef] [PubMed]
- Seong, N.; Kim, D. Experimental observation of stable bound solitons in a figure-eight fibre laser. Opt. Lett. 2002, 27, 1321–1323. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, C.K.; Ortac, B.; Schreiber, T.; Limpert, J.; Hohmuth, R.; Richter, W.; Tunnermann, A. Fibre Lasers III: Technology, Systems and Applications Vol. 6102 Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE); Brown, A.J.W., Nilsson, J., Harter, D.J., Tunnermann, A., Eds.; SPIE International Society for Optics and Photonics: Bellingham, WA, USA, 2006; p. 10217. [Google Scholar]
- Wu, X.; Tang, D.; Luan, X.; Zhang, Q. Bound states of solitons in a fibre laser mode locked with carbon nanotube saturable absorber. Opt. Commun. 2011, 284, 3615–3618. [Google Scholar] [CrossRef]
- Gui, L.; Xiao, X.; Yang, C. Observation of various bound solitons in a carbon-nanotube-based erbium fibre laser. J. Opt. Soc. Am. B Opt. Phys. 2013, 30, 158–164. [Google Scholar] [CrossRef]
- Tsatourian, V.; Sergeyev, S.V.; Mou, C.B.; Rozhin, A.; Mikhailov, V.; Rabin, B.; Westbrook, P.S.; Turitsyn, S.K. Polarisation dynamics of vector soliton molecules in mode locked fibre laser. Sci. Rep. 2013, 3, srep03154. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, S.; Meng, Y.; Hao, Y.; Li, H.; Du, J.; Yang, Z. Observation of soliton bound states in a graphene mode locked erbium-doped fibre laser. Laser Phys. 2012, 22, 774–777. [Google Scholar] [CrossRef]
- Gui, L.; Li, X.; Xiao, X.; Zhu, H.; Yang, C. Widely spaced bound states in a soliton fibre laser with graphene saturable absorber. IEEE Photonics Technol. Lett. 2013, 25, 1184–1187. [Google Scholar] [CrossRef]
- Luo, A.P.; Liu, H.; Zhao, N.; Zheng, X.W.; Liu, M.; Tang, R.; Luo, Z.C.; Xu, W.C. Observation of Three Bound States From a Topological Insulator Mode-Locked Soliton Fibre Laser. IEEE Photonics J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, D.; Gan, X.; Han, L.; Ma, C.; Xi, T.; Zhang, Y.; Shang, W.; Hua, S.; Zhao, J. Harmonic mode locking of bound-state solitons fibre laser based on MoS2 saturable absorber. Opt. Express 2015, 23, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xu, Y.; Dhanabalan, S.C.; Sophia, J.; Zhao, C.; Xu, C.; Xiang, Y.; Li, J.; Zhang, H. Black phosphorus quantum dots as an efficient saturable absorber for bound soliton operation in an erbium doped fibre laser. IEEE Photonics J. 2016, 8, 1503310. [Google Scholar] [CrossRef]
- Gui, L.; Yang, X.; Zhao, G.; Yang, X.; Xiao, X.; Zhu, J.; Yang, C. Suppression of continuous lasing in a carbon nanotube polyimide film mode-locked erbium-doped fibre laser. Appl. Opt. 2011, 50, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chen, T.; Li, M.; Zhang, B.; Lu, Y.; Chen, K.P. All-fibre ultrafast thulium-doped fibre ring laser with dissipative soliton and noise-like output in normal dispersion by single-wall carbon nanotubes. Appl. Phys. Lett. 2013, 103, 011103. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, P.; Wang, X.; Xiao, H.; Liu, Z. Pulse bundles and passive harmonic mode-locked pulses in Tm-doped fibre laser based on nonlinear polarization rotation. Opt. Express 2014, 22, 6147–6153. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Song, Y.-L.; Du, G.-G.; Yan, P.-G.; Guo, C.-Y.; Zheng, G.-L.; Ruan, S.-C. Soliton dynamic patterns of a passively mode-locked fibre laser operating in a 2 μm region. Laser Phys. Lett. 2015, 12, 045108. [Google Scholar] [CrossRef]
- Bao, C.; Yang, C. Harmonic mode-locking in a tm-doped fibre laser: Characterization of its timing jitter and ultralong starting dynamics. Opt. Commun. 2015, 356, 463–467. [Google Scholar] [CrossRef]
- Chernysheva, M.; Bednyakova, A.; Al Araimi, M.; Howe, R.C.T.; Hu, G.H.; Hasan, T.; Gambetta, A.; Galzerano, G.; Rummeli, M.; Rozhin, A. Double-Wall Carbon Nanotube Hybrid Mode-Locker in Tm-doped Fibre Laser: A Novel Mechanism for Robust Bound-State Solitons Generation. Sci. Rep. 2017, 7, srep44314. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Tang, D.; Cheng, T.; Lu, C. Gain-guided solitons in dispersion-managed fibre lasers with large net cavity dispersion. Opt. Lett. 2006, 31, 2957–2959. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Tang, D.; Wu, J. Gain-guided soliton in a positive group-dispersion fibre laser. Opt. Lett. 2006, 31, 1788–1790. [Google Scholar] [CrossRef] [PubMed]
- Ilday, F.; Buckley, J.; Clark, W.; Wise, F. Self-similar evolution of parabolic pulses in a laser. Phys. Rev. Lett. 2004, 92, 213902. [Google Scholar] [CrossRef] [PubMed]
- Grelu, P.; Belhache, F.; Gutty, F.; Soto-Crespo, J.M. Relative phase locking of pulses in a passively mode-locked fibre laser. J. Opt. Soc. Am. B Opt. Phys. 2003, 20, 863–870. [Google Scholar] [CrossRef]
- Zhao, B.; Tang, D.; Shum, P.; Guo, X.; Lu, C.; Tam, H. Bound twin-pulse solitons in a fibre ring laser. Phys. Rev. E 2004, 70, 067602. [Google Scholar] [CrossRef] [PubMed]
- Ortaç, B.; Hideur, A.; Chartier, T.; Brunel, M.; Grelu, P.; Leblond, H.; Sanchez, F. Generation of bound states of three ultrashort pulses with a passively mode-locked high-power Yb-doped double-clad fibre laser. IEEE Photonics Technol. Lett. 2004, 16, 1274–1276. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, D.; Cheng, T.; Tam, H.; Lu, C. Bound states of dispersion-managed solitons in a fibre laser at near zero dispersion. Appl. Opt. 2007, 46, 4768–4773. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.-H.; Chan, C.-W.; Lee, H.-Y.; Chen, Y.-H. Bound states of dispersion-managed solitons from single-mode Yb-doped fibre laser at net-normal dispersion. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar]
- Lu, B.L.; Wang, Y.; Qi, X.Y.; Chen, H.W.; Jiang, M.; Hou, L.; Huang, K.X.; Kang, J.; Bai, J.T. Observation of bound state solitons in tunable all-polarization-maintaining Yb-doped fibre laser. Laser Phys. 2017, 27, 075102. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, D.; Zhang, H.; Wu, X. Bound states of vector dissipative solitons. IEEE Photonics J. 2015, 7, 1–8. [Google Scholar] [CrossRef]
- Li, L.; Ruan, Q.J.; Yang, R.H.; Zhao, L.M.; Luo, Z.Q. Bidirectional operation of 100 fs bound solitons in an ultra-compact mode-locked fibre laser. Opt. Express 2016, 24, 21020–21026. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.-J.; Wang, S.-M.; Lai, Y. Bound soliton fibre laser mode-locking without saturable absorption effect. IEEE Photonics J. 2016, 8, 1–9. [Google Scholar]
- Wang, Z.Q.; Zhan, L.; Majeed, A.; Zou, Z.X. Harmonic mode locking of bound solitons. Opt. Lett. 2015, 40, 1065–1068. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Huo, J.; Wu, G.; Tian, X. Soliton molecules in a fibre laser mode-locked by a graphene-based saturable absorber. Laser Phys. 2015, 25, 075103. [Google Scholar] [CrossRef]
- Liu, H.H.; Chow, K.K. High Fundamental-Repetition-Rate Bound Solitons in Carbon Nanotube-Based Fibre Lasers. IEEE Photonics Technol. Lett. 2015, 27, 867–870. [Google Scholar] [CrossRef]
- Song, Y.F.; Zhang, H.; Zhao, L.M.; Shen, D.Y.; Tang, D.Y. Coexistence and interaction of vector and bound vector solitons in a dispersion-managed fibre laser mode locked by graphene. Opt. Express 2016, 24, 1814–1822. [Google Scholar] [CrossRef] [PubMed]
- Al Khawaja, U. Stability and dynamics of two-soliton molecules. Phys. Rev. E 2010, 81, 056603. [Google Scholar] [CrossRef] [PubMed]
- Afanasjev, V.V.; Akhmediev, N. Soliton interaction and bound states in amplified-damped fibre systems. Opt. Lett. 1995, 20, 1970–1972. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J. Stable soliton pairs in optical transmission lines and fibre lasers. J. Opt. Soc. Am. B Opt. Phys. 1998, 15, 515–523. [Google Scholar] [CrossRef]
- Bahloul, F.; Salhi, M.; Guesmi, K.; Sanchez, F.; Attia, R. Numerical demonstration of generation of bound solitons in figure of eight microstructured fibre laser in normal dispersion regime. Opt. Commun. 2013, 311, 282–287. [Google Scholar] [CrossRef]
- Liu, X. Dynamic evolution of temporal dissipative-soliton molecules in large normal path-averaged dispersion fibre lasers. Phys. Rev. A 2010, 82, 063834. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fibre Optics, 4th ed.; Academic Press: Boston, MA, USA, 2007; pp. 153–154. ISBN 13 978-0-12-369516-1. [Google Scholar]
- Komarov, A.; Amrani, F.; Dmitriev, A.; Komarov, K.; Meshcheriakov, D.; Sanchez, F. Dispersive-wave mechanism of interaction between ultrashort pulses in passive mode-locked fibre lasers. Phys. Rev. A 2012, 85, 013802. [Google Scholar] [CrossRef]
- Soto-Crespo, J.; Akhmediev, N. Multisoliton regime of pulse generation by lasers passively mode locked with a slow saturable absorber. J. Opt. Soc. Am. B Opt. Phys. 1999, 16, 674–677. [Google Scholar] [CrossRef]
- Cundiff, S.; Collings, B.; Knox, W. Polarization locking in an isotropic, modelocked soliton Er/Yb fibre laser. Opt. Express 1997, 1, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Grudinin, A.; Gray, S. Passive harmonic mode locking in soliton fibre lasers. J. Opt. Soc. Am. B Opt. Phys. 1997, 14, 144–154. [Google Scholar] [CrossRef]
- Soto-Crespo, J.; Akhmediev, N.; Grelu, P.; Belhache, F. Quantized separations of phase-locked soliton pairs in fibre lasers. Opt. Lett. 2003, 28, 1757–1759. [Google Scholar] [CrossRef] [PubMed]
- Weill, R.; Bekker, A.; Smulakovsky, V.; Fischer, B.; Gat, O. Spectral sidebands and multipulse formation in passively mode-locked lasers. Phys. Rev. A 2011, 83, 043831. [Google Scholar] [CrossRef]
- Pilipetskii, A.; Golovchenko, E.; Menyuk, C. Acoustic effect in passively mode-locked fibre ring lasers. Opt. Lett. 1995, 20, 907–909. [Google Scholar] [CrossRef] [PubMed]
- Kutz, J.; Collings, B.; Bergman, K.; Knox, W. Stabilized pulse spacing in soliton lasers due to gain depletion and recovery. IEEE J. Quantum Electron. 1998, 34, 1749–1757. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Grelu, P.; Lederer, F. Impact of slow gain dynamics on soliton molecules in mode-locked fibre lasers. Opt. Lett. 2012, 37, 175–177. [Google Scholar] [CrossRef] [PubMed]
- Kagi, N.; Oyobe, A.; Nakamura, K. Temperature dependence of the gain in erbium-doped fibres. J. Lightw. Technol. 1991, 9, 261–265. [Google Scholar] [CrossRef]
- Bolshtyansky, M.; Wysocki, P.; Conti, N. Model of temperature dependence for gain shape of erbium-doped fibre amplifier. J. Lightw. Technol. 2000, 18, 1533–1540. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: New York, NY, USA, 1977; ISBN 13 978-0471024019. [Google Scholar]
- Gumenyuk, R.; Okhotnikov, O.G. Impact of gain medium dispersion on stability of soliton bound states in fibre laser. IEEE Photonics Technol. Lett. 2013, 25, 133–135. [Google Scholar] [CrossRef]
- Luo, Y.; Cheng, J.; Liu, B.; Sun, Q.; Li, L.; Fu, S.; Tang, D.; Zhao, L.; Liu, D. Group-velocity-locked vector soliton molecules in fibre lasers. Sci. Rep. 2017, 7, 2369. [Google Scholar] [CrossRef] [PubMed]
- Komarov, A.; Sanchez, F. Structural dissipative solitons in passive mode-locked fibre lasers. Phys. Rev. E 2008, 77, 066201. [Google Scholar] [CrossRef] [PubMed]
- Komarov, A.; Haboucha, A.; Sanchez, F. Ultrahigh-repetition-rate bound-soliton harmonic passive mode-locked fibre lasers. Opt. Lett. 2008, 33, 2254–2256. [Google Scholar] [CrossRef] [PubMed]
- Olivier, M.; Roy, V.; Piché, M. Influence of the Raman effect on bound states of dissipative solitons. Opt. Express 2006, 14, 9728–9742. [Google Scholar] [CrossRef] [PubMed]
- Dianov, E.; Luchnikov, A.; Pilipetskii, A.; Prokhorov, A. Long-range interaction of picosecond solitons through excitation of acoustic waves in optical fibres. Appl. Phys. B Lasers Opt. 1992, 54, 175–180. [Google Scholar] [CrossRef]
- Kelly, S.M.J. Characteristic sideband instability of periodically amplified average soliton. Electron. Lett. 1992, 28, 806. [Google Scholar] [CrossRef]
- Gordon, J.P. Dispersive perturbations of solitons of the nonlinear Schrödinger equation. J. Opt. Soc. Am. B Opt. Phys. 1992, 9, 91–97. [Google Scholar] [CrossRef]
- Grapinet, M.; Grelu, P. Vibrating soliton pairs in a mode-locked laser cavity. Opt. Lett. 2006, 31, 2115–2117. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.M.; Grelu, P.; Akhmediev, N.; Devine, N. Soliton complexes in dissipative systems: Vibrating, shaking and mixed soliton pairs. Phys. Rev. E 2007, 75, 016613. [Google Scholar] [CrossRef] [PubMed]
- Zaviyalov, A.; Iliew, R.; Egorov, O.; Lederer, F. Multi-soliton complexes in mode-locked fibre lasers. Appl. Phys. B Lasers Opt. 2011, 104, 513–521. [Google Scholar] [CrossRef]
- Zavyalov, A.; Iliew, R.; Egorov, O.; Lederer, F. Dissipative soliton molecules with independently evolving or flipping phases in mode-locked fibre lasers. Phys. Rev. A 2009, 80, 043829. [Google Scholar] [CrossRef]
- Gui, L.; Xiao, X.; Yang, C.; Yang, X.; Zhu, J.; Li, X.; Zhu, H. Observation of various bound solitons of a fibre laser with carbon nanotubes and graphene as saturable absorbers. In Proceedings of Quantum Electronics Conference & Lasers and Electro-Optics (CLEO/IQEC/PACIFIC RIM), Sydney, NSW, Australia, 28 August–1 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1397–1399.
- Chouli, S.; Grelu, P. Rains of solitons in a fibre laser. Opt. Express 2009, 17, 11776–11781. [Google Scholar] [CrossRef] [PubMed]
- Chouli, S.; Grelu, P. Soliton rains in a fibre laser: An experimental study. Phys. Rev. A 2010, 81, 063829. [Google Scholar] [CrossRef]
- Niang, A.; Amrani, F.; Salhi, M.; Grelu, P.; Sanchez, F. Rains of solitons in a figure-of-eight passively mode-locked fibre laser. Appl. Phys. B 2014, 116, 771–775. [Google Scholar] [CrossRef]
- Chong, A.; Renninger, W.H.; Wise, F.W. Properties of normal-dispersion femtosecond fibre lasers. J. Opt. Soc. Am. B Opt. Phys. 2008, 25, 140–148. [Google Scholar] [CrossRef]
- Bao, C.; Xiao, X.; Yang, C. Soliton rains in a normal dispersion fibre laser with dual-filter. Opt. Lett. 2013, 38, 1875–1877. [Google Scholar] [CrossRef] [PubMed]
- Renninger, W.H.; Chong, A.; Wise, F.W. Area theorem and energy quantization for dissipative optical solitons. J. Opt. Soc. Am. B Opt. Phys. 2010, 27, 1978–1982. [Google Scholar] [CrossRef] [PubMed]
- Kovalsky, M.G.; Hnilo, A.A.; Tredicce, J.R. Extreme events in the Ti: Sapphire laser. Opt. Lett. 2011, 36, 4449–4451. [Google Scholar] [CrossRef] [PubMed]
- Finot, C.; Hammani, K.; Fatome, J.; Dudley, J.M.; Millot, G. Selection of extreme events generated in Raman fibre amplifiers through spectral offset filtering. IEEE J. Quantum Electron. 2010, 46, 205–213. [Google Scholar] [CrossRef]
- Hammani, K.; Finot, C. Experimental signatures of extreme optical fluctuations in lumped Raman fibre amplifiers. Opt. Fibre Technol. 2012, 18, 93–100. [Google Scholar] [CrossRef]
- Hammani, K.; Finot, C.; Millot, G. Emergence of extreme events in fibre-based parametric processes driven by a partially incoherent pump wave. Opt. Lett. 2009, 34, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.; Grelu, P.; Akhmediev, N. Dissipative rogue waves: Extreme pulses generated by passively mode-locked lasers. Phys. Rev. E 2011, 84, 016604. [Google Scholar] [CrossRef] [PubMed]
- Lecaplain, C.; Grelu, P.; Soto-Crespo, J.; Akhmediev, N. Dissipative rogue waves generated by chaotic pulse bunching in a mode-locked laser. Phys. Rev. Lett. 2012, 108, 233901. [Google Scholar] [CrossRef] [PubMed]
- Lecaplain, C.; Grelu, P.; Soto-Crespo, J.; Akhmediev, N. Dissipative rogue wave generation in multiple-pulsing mode-locked fibre laser. J. Opt. 2013, 15, 064005. [Google Scholar] [CrossRef]
- Lecaplain, C.; Grelu, P. Rogue waves among noiselike-pulse laser emission: An experimental investigation. Phys. Rev. A 2014, 90, 013805. [Google Scholar] [CrossRef]
- Runge, A.F.; Aguergaray, C.; Broderick, N.G.; Erkintalo, M. Raman rogue waves in a partially mode-locked fibre laser. Opt. Lett. 2014, 39, 319–322. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, S.; Wise, F.W. Rogue waves in a normal-dispersion fibre laser. Opt. Lett. 2015, 40, 1366–1369. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Cai, Z.-R.; Hu, S.; Luo, A.-P.; Zhao, C.-J.; Zhang, H.; Xu, W.-C.; Luo, Z.-C. Dissipative rogue waves induced by long-range chaotic multi-pulse interactions in a fibre laser with a topological insulator-deposited microfibre photonic device. Opt. Lett. 2015, 40, 4767–4770. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Luo, A.-P.; Xu, W.-C.; Luo, Z.-C. Dissipative rogue waves induced by soliton explosions in an ultrafast fibre laser. Opt. Lett. 2016, 41, 3912–3915. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Tarasov, N.; Sugavanam, S.; Churkin, D. Rogue waves generation via nonlinear soliton collision in multiple-soliton state of a mode-locked fibre laser. Opt. Express 2016, 24, 21256–21263. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Hu, D.K.; Zhao, K.J.; Jiao, L.Y.; Xiao, X.S.; Yang, C.X. Dissipative rogue waves among noise-like pulses in a Tm fibre laser mode locked by a monolayer MoS2 saturable absorber. IEEE J. Select. Topics Quantum Electron. 2018, 24. [Google Scholar] [CrossRef]
- Pottiez, O.; Grajales-Coutiño, R.; Ibarra-Escamilla, B.; Kuzin, E.A.; Hernández-García, J.C. Adjustable noiselike pulses from a figure-eight fibre laser. Appl. Opt. 2011, 50, E24–E31. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Akhmediev, N.; Ankiewicz, A. Pulsating, creeping and erupting solitons in dissipative systems. Phys. Rev. Lett. 2000, 85, 2937. [Google Scholar] [CrossRef] [PubMed]
- Cundiff, S.T.; Soto-Crespo, J.M.; Akhmediev, N. Experimental evidence for soliton explosions. Phys. Rev. Lett. 2002, 88, 59. [Google Scholar] [CrossRef] [PubMed]
- Runge, A.F.; Broderick, N.G.; Erkintalo, M. Observation of soliton explosions in a passively mode-locked fibre laser. Optica 2015, 2, 36–39. [Google Scholar] [CrossRef]
- Bao, C.; Chang, W.; Yang, C.; Akhmediev, N.; Cundiff, S.T. Observation of coexisting dissipative solitons in a mode-locked fibre laser. Phys. Rev. Lett. 2015, 115, 253903. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.M.; Akhmediev, N. Composite solitons and two-pulse generation in passively mode-locked lasers modeled by the complex quintic Swift-Hohenberg equation. Phys. Rev. E 2002, 66, 066610. [Google Scholar] [CrossRef] [PubMed]


| Wavelength | Dispersion | Saturable Absorber | Pulse Width | Pulse Separation | Phase Difference | Reference |
|---|---|---|---|---|---|---|
| 1 μm | 0.047 ps2 | NPE | 4.3 ps | 20.33 ps | - | [46] |
| 1 μm | 0.0054 ps2 | NPE | 0.39 ps | 21 ps | - | [48] |
| 1 μm | 0.18 ps2 | SESAM | 13.4 ps | 14.8 ps | π/2 | [49] |
| 1.5 μm | −0.381ps2 | MoS2 | 1.2 ps | 3.4 ps | π | [33] |
| 1.5 μm | −0.28 ps2 | CNT | 0.9 ps | 3–20 ps | π, 0, ±π/2 | [28] |
| 1.5 μm | −0.28 ps2 | Graphene | 0.62 ps | 55 ps | - | [31] |
| 1.5 μm | anomalous | CNT | 370 fs | 1.5 ps | π | [29] |
| 1.5 μm | −0.1 ps2 | NPE | 1.5 ps | 18.5 ps | - | [21] |
| 1.55 μm | 0.038 ps2 | SESAM | 20.3 ps | 91 ps | - | [50] |
| 1.55 μm | 0.0017 ps2 | CNT | 0.18 ps | 1.53 ps | ±π/2 | [51] |
| 1.55 μm | −0.12 ps2 | NALM | 1.3 ps | 2.2 ps | π | [8] |
| 1.55 μm | anomalous | Soliton shaping | 2 ps | 5.2 ps | π | [52] |
| 1.5 μm | −0.047 ps2 | NPE | 0.58 ps | 1.5 ps | π | [53] |
| 1.5 μm | −0.03 ps2 | Graphene | 0.307 ps | 35 ps | - | [54] |
| 1.5 μm | −0.02 ps2 | CNT | 0.71 ps | 2.5 ps/3.5 ps | ±π/2 | [55] |
| 1.5 μm | −0.277 ps2 | Black phosphorus | 0.787 ps | 7.5 ps | - | [34] |
| 1.5 μm | anomalous | Graphene | 0.39 ps | 8.1 ps | - | [56] |
| 2 μm | −0.329 ps2 | NPE | 0.78 ps | 2.5 ps | π | [23] |
| 2 μm | −0.098 ps2 | NPE | 0.93 ps | 7–15 ps | π, 0 | [24] |
| Fibre Segment | Second-Order Dispersion β2 (ps2/km) | Third-Order Dispersion β3 (ps3/km) | Nonlinear Kerr Coefficient (W−1·km−1) | Length L (m) |
|---|---|---|---|---|
| SMF 1 | −7.5 | 0 | 2.3 | 0.2 |
| SMF 2 | −22 | 0 | 1.2 | 0.2 |
| EDF | −18 | 0 | 3.2 | 0.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, L.; Wang, P.; Ding, Y.; Zhao, K.; Bao, C.; Xiao, X.; Yang, C. Soliton Molecules and Multisoliton States in Ultrafast Fibre Lasers: Intrinsic Complexes in Dissipative Systems. Appl. Sci. 2018, 8, 201. https://doi.org/10.3390/app8020201
Gui L, Wang P, Ding Y, Zhao K, Bao C, Xiao X, Yang C. Soliton Molecules and Multisoliton States in Ultrafast Fibre Lasers: Intrinsic Complexes in Dissipative Systems. Applied Sciences. 2018; 8(2):201. https://doi.org/10.3390/app8020201
Chicago/Turabian StyleGui, Lili, Pan Wang, Yihang Ding, Kangjun Zhao, Chengying Bao, Xiaosheng Xiao, and Changxi Yang. 2018. "Soliton Molecules and Multisoliton States in Ultrafast Fibre Lasers: Intrinsic Complexes in Dissipative Systems" Applied Sciences 8, no. 2: 201. https://doi.org/10.3390/app8020201
APA StyleGui, L., Wang, P., Ding, Y., Zhao, K., Bao, C., Xiao, X., & Yang, C. (2018). Soliton Molecules and Multisoliton States in Ultrafast Fibre Lasers: Intrinsic Complexes in Dissipative Systems. Applied Sciences, 8(2), 201. https://doi.org/10.3390/app8020201




