Wind Power Forecasting Using Multi-Objective Evolutionary Algorithms for Wavelet Neural Network-Optimized Prediction Intervals
Abstract
:1. Introduction
2. PI Assessments
2.1. PI Coverage Probability
2.2. PIs’ Normalized Average Width
3. Multi-Objective Optimization Model for WNN-Based PI Construction
3.1. PI Multi-Objective Optimization Criteria
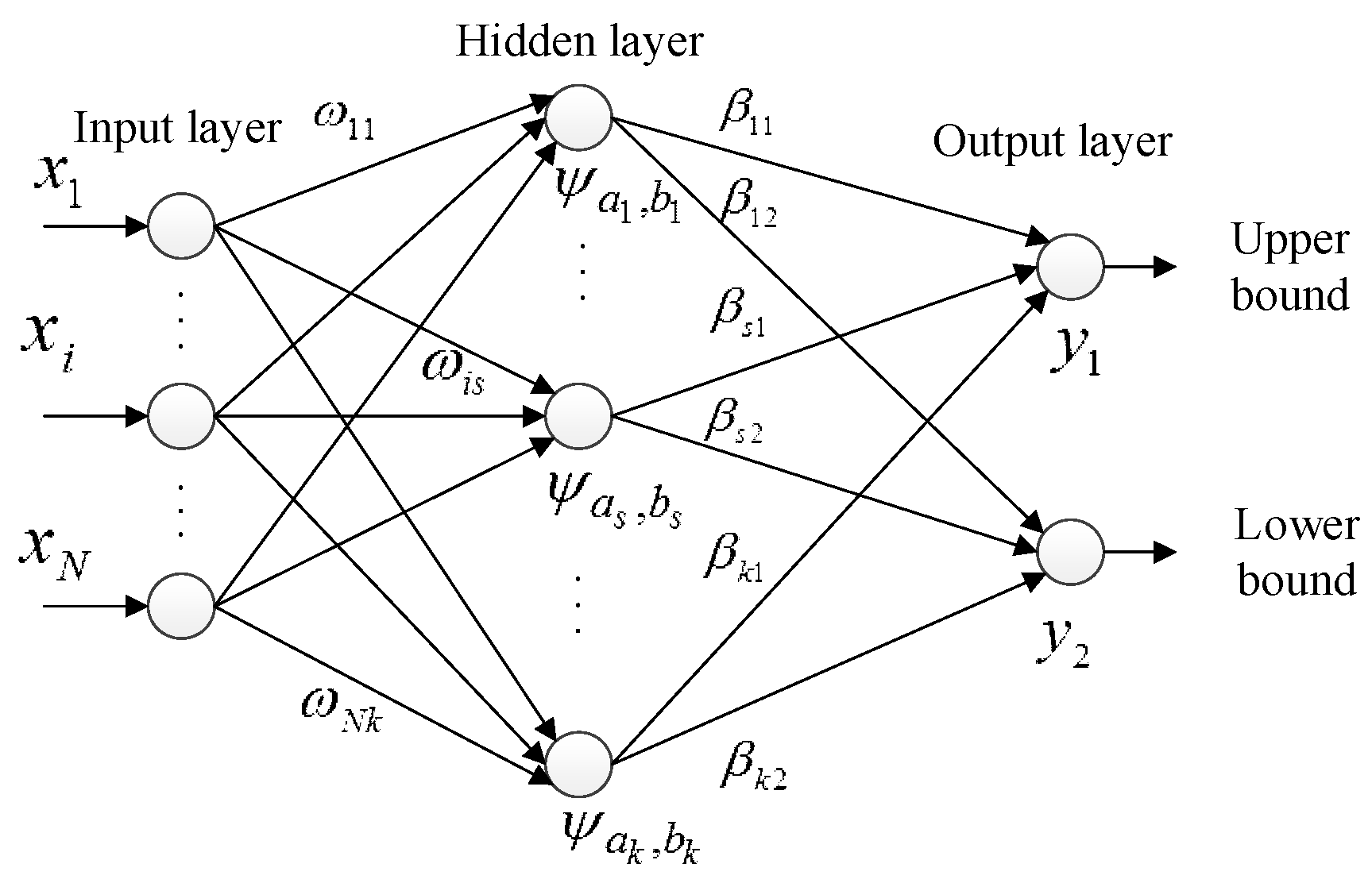
3.2. WNN-Based PI Construction
4. Evolution Knowledge MOABC Algorithm (EKMOABC) for WNN-Optimized Construction of PIs
4.1. Initialization
4.2. Preliminary Iteration
4.3. Pareto Dominance
4.4. Employed Bees Evolution Based on Guidance of Elite Population Knowledge
4.5. Probability Choice Equation Combining the Dominance and Distribution Relationships
4.6. Onlooker Bees Evolution
4.7. Strategy to Update the Archive
4.8. Scout Bees Evolution
4.9. Termination
5. Experiments and Results
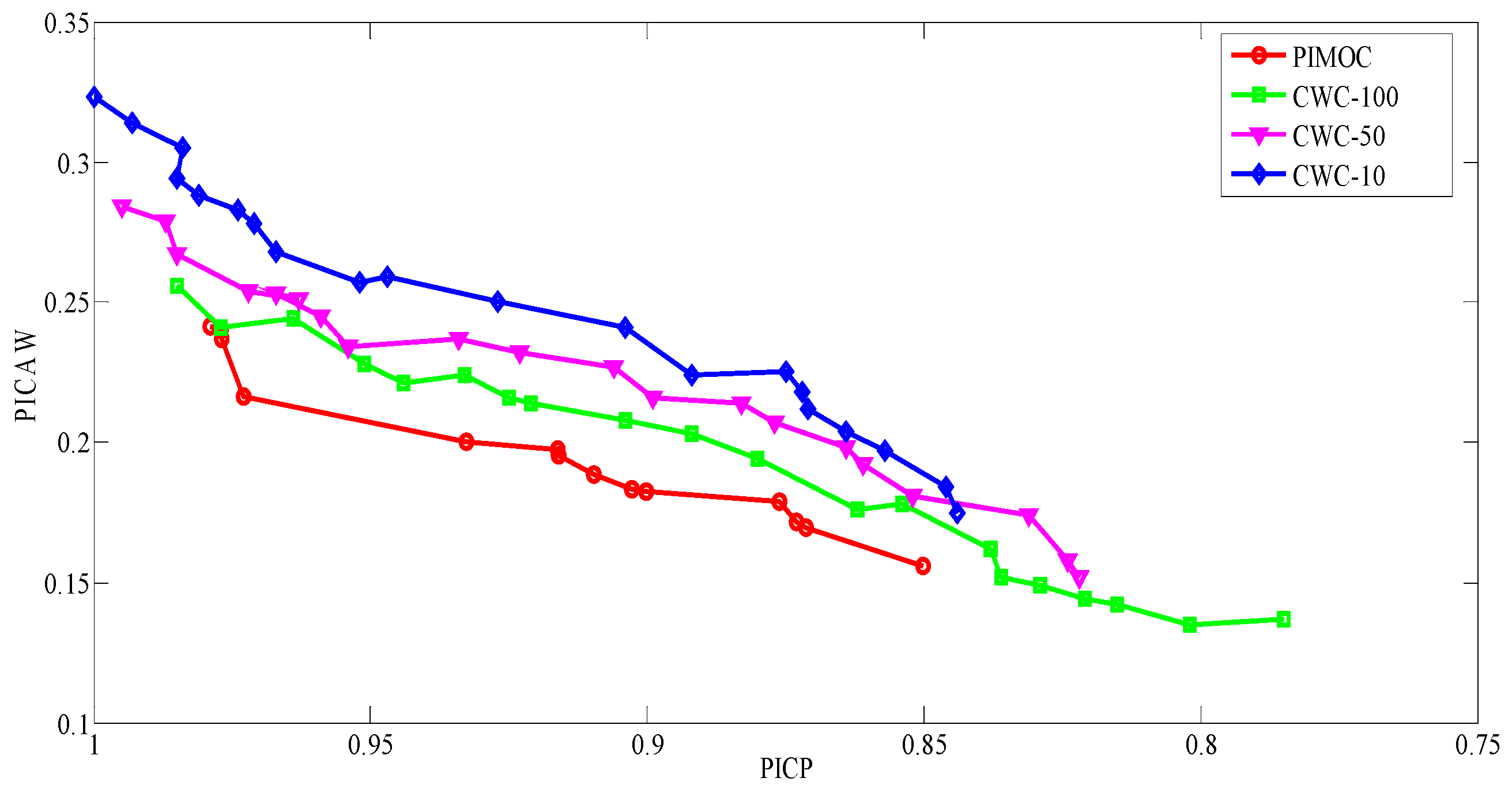
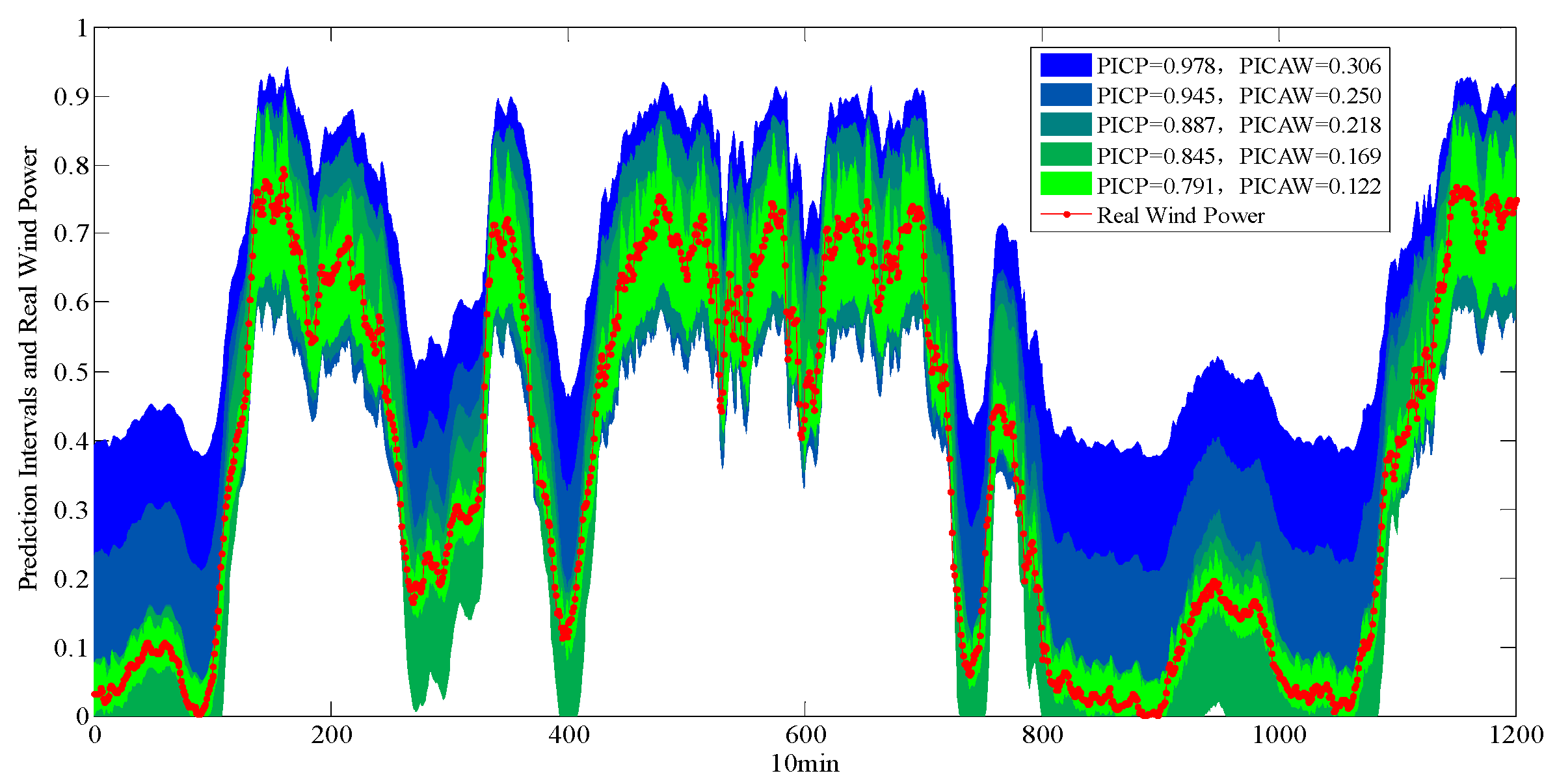
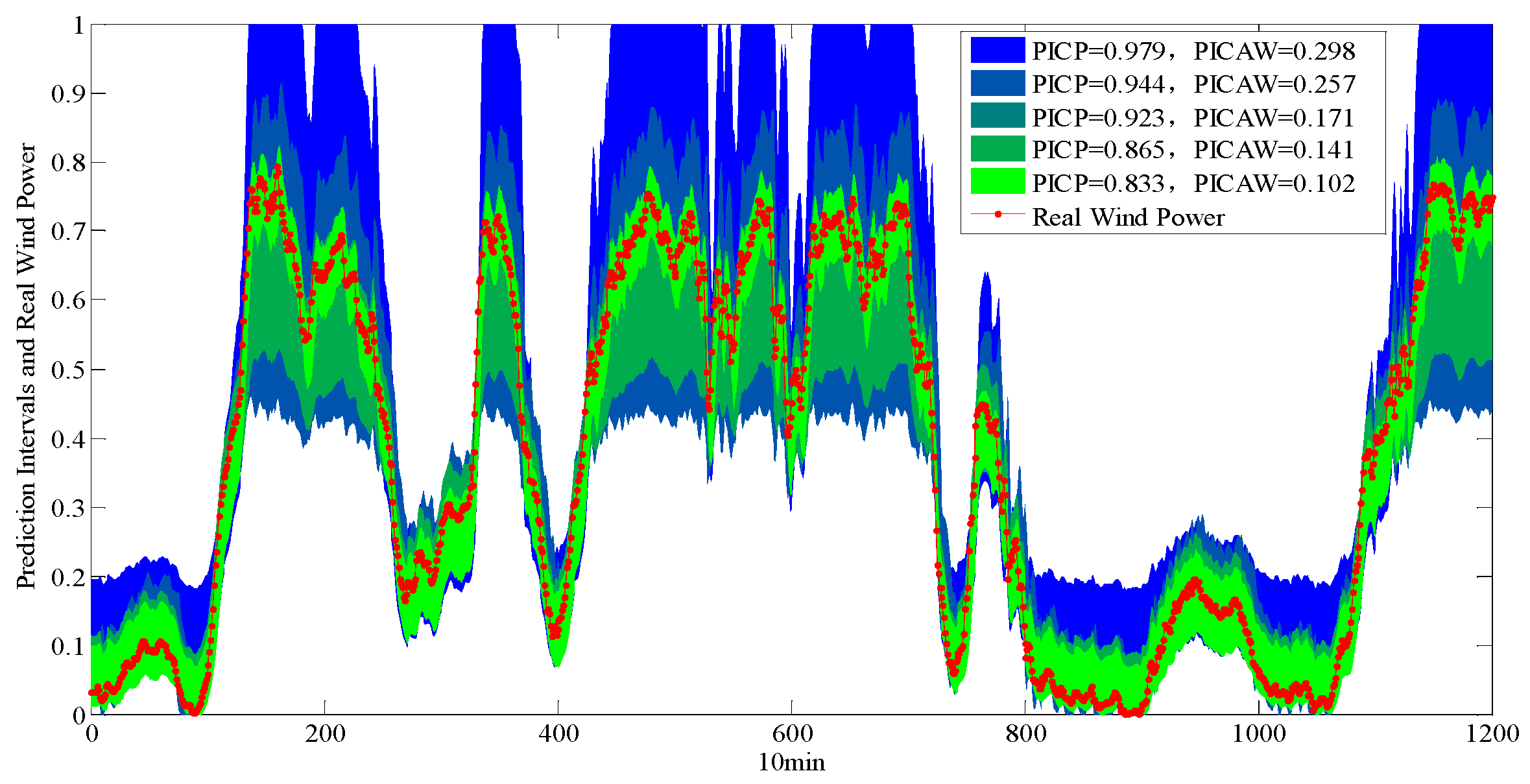
5.1. Performance Comparisons between CWC with Different Parameters and PIMOC
5.2. Performances of the Multi-Objective Evolution Algorithm in PI Construction
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Q.; Martinez-Anido, C.B.; Wu, H.; Florita, A.R.; Hodge, B.M. Quantifying the economic and grid reliability impacts of improved wind power forecasting. IEEE Trans. Sustain. Energy 2016, 7, 1525–1537. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Haque, A.U.; Nehrir, M.H.; Mandal, P. A hybrid intelligent model for deterministic and quantile regression approach for probabilistic wind power forecasting. IEEE Trans. Power Syst. 2014, 29, 1663–1672. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Short-term wind speed prediction using empirical wavelet transform and Gaussian process regression. Energy 2015, 93, 1456–1466. [Google Scholar] [CrossRef]
- Che, Y.; Peng, X.; Monache, L.D.; Kawaguchi, T.; Xiao, F. A wind power forecasting system based on the weather research and forecasting model and Kalman filtering over a wind-farm in Japan. J. Renew. Sustain. Energy 2016, 8, 319–329. [Google Scholar] [CrossRef]
- Zuluaga, C.D.; Álvarez, M.A.; Giraldo, E. Short-term wind speed prediction based on robust Kalman filtering: An experimental comparison. Appl. Energy 2015, 156, 321–330. [Google Scholar] [CrossRef]
- Yan, J.; Li, K.; Bai, E.; Yang, Z.; Foley, A. Time series wind power forecasting based on variant Gaussian Process and TLBO. Neurocomputing 2016, 189, 135–144. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Li, Z.; Song, X.; Lang, Y.; Su, J. A novel bidirectional mechanism based on time series model for wind power forecasting. Appl. Energy 2016, 177, 793–803. [Google Scholar] [CrossRef]
- Osório, G.J.; Matias, J.C.O.; Catalão, J.P.S. Short-term wind power forecasting using adaptive neuro-fuzzy inference system combined with evolutionary particle swarm optimization, wavelet transform and mutual information. Renew. Energy 2015, 75, 301–307. [Google Scholar] [CrossRef]
- Ata, R. Artificial neural networks applications in wind energy systems: A review. Renew. Sustain. Energy Rev. 2015, 49, 534–562. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Wind power forecasting using neural network ensembles with feature selection. IEEE Trans. Sustain. Energy 2017, 6, 1447–1456. [Google Scholar] [CrossRef]
- Tewari, S.; Geyer, C.J.; Mohan, N. A statistical model for wind power forecast error and its application to the estimation of penalties in liberalized markets. IEEE Trans. Power Syst. 2011, 26, 2031–2039. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Short-term load and wind power forecasting using neural network-based prediction intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 303. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.; Srinivasan, D.; Khosravi, A. Incorporating wind power forecast uncertainties into stochastic unit commitment using neural network-based prediction intervals. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2123–2135. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.; Srinivasan, D.; Khosravi, A. Particle swarm optimization for construction of neural network-based prediction intervals. Neurocomputing 2014, 127, 172–180. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Lower upper bound estimation method for construction of neural network-based prediction intervals. IEEE Trans. Neural Netw. 2011, 22, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Construction of optimal prediction intervals for load forecasting problems. IEEE Trans. Power Syst. 2010, 25, 1496–1503. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew. Energy 2011, 36, 1245–1251. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Khooban, M.H. Probabilistic forecasting of hourly electricity price by generalization of elm for usage in improved wavelet neural network. IEEE Trans. Ind. Inform. 2016, 13, 71–79. [Google Scholar] [CrossRef]
- Ibrahim, A.; Rahnamayan, S.; Martin, M.V.; Deb, K. Elite NSGA-III: An improved evolutionary many-objective optimization algorithm. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 973–982. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B. A quick artificial bee colony (qABC) algorithm and its performance on optimization problems. Appl. Soft Comput. J. 2014, 23, 227–238. [Google Scholar] [CrossRef]
- Akbari, R.; Hedayatzadeh, R.; Ziarati, K.; Hassanizadeh, B. A multi-objective artificial bee colony algorithm. Swarm Evol. Comput. 2012, 2, 39–52. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
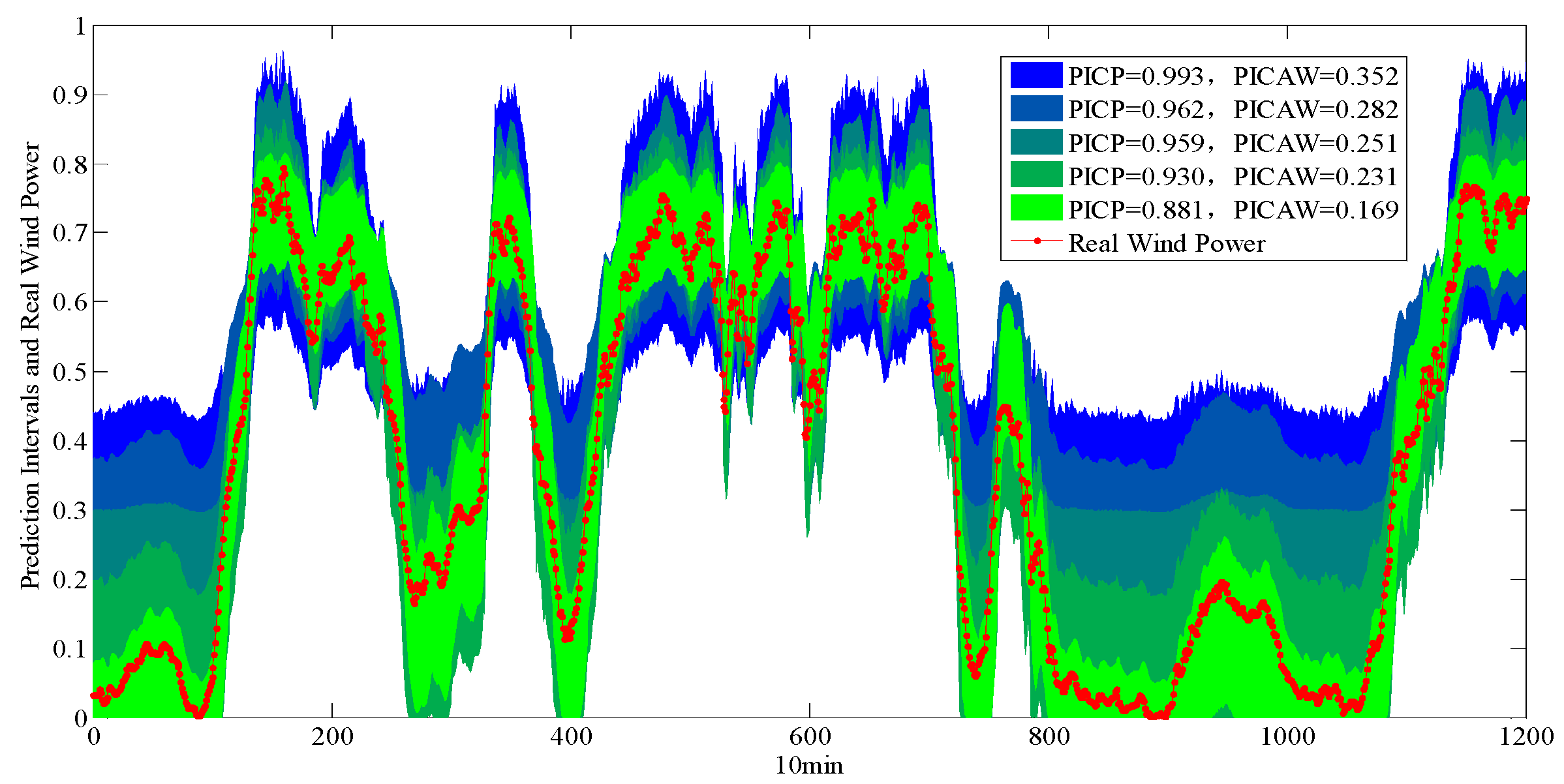
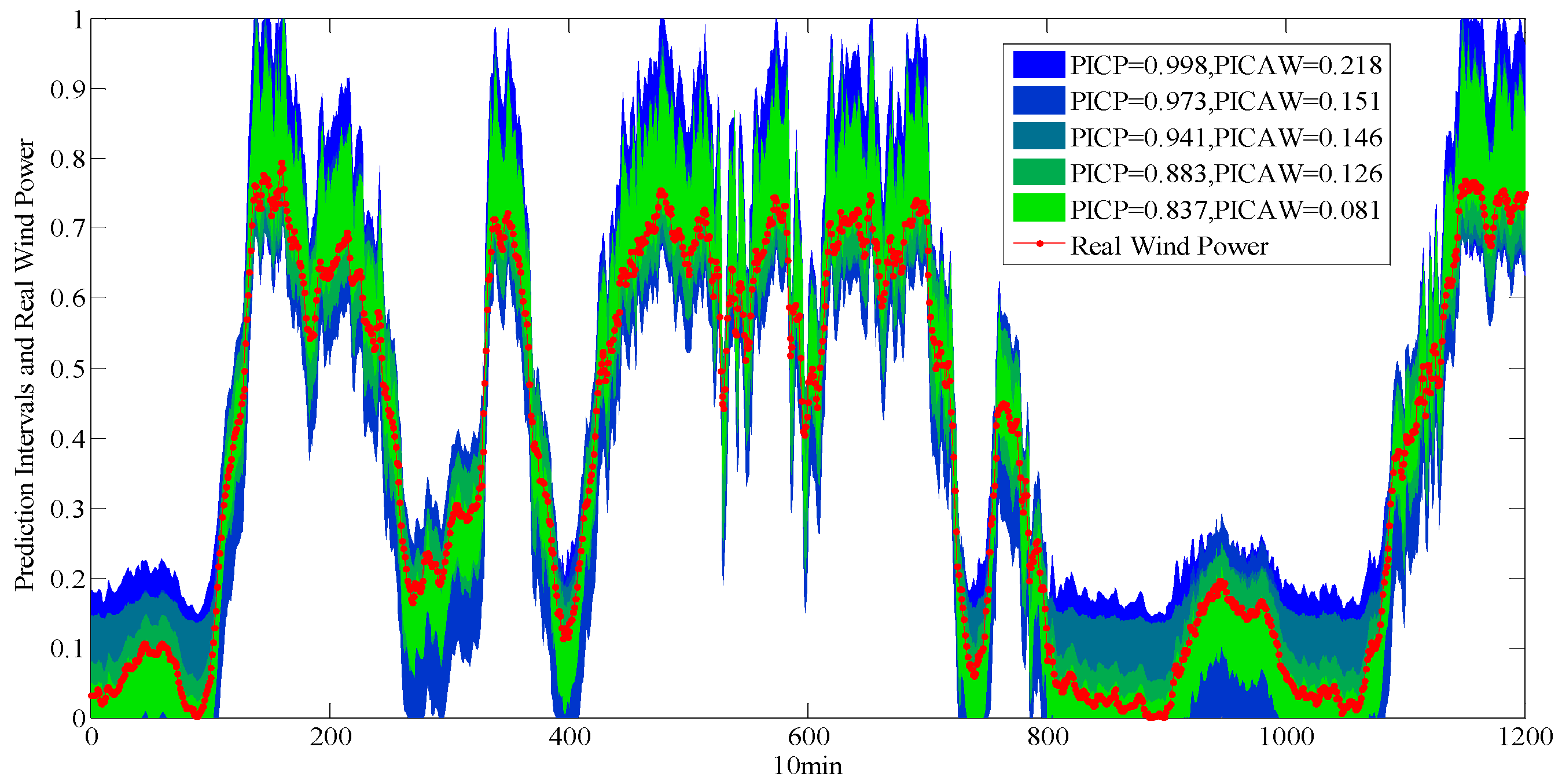

| Name | |||||||
| PICP | 0.785 | 0.836 | 0.892 | 0.944 | 0.985 | ||
| PICAW | 0.137 | 0.152 | 0.203 | 0.235 | 0.256 | ||
| PICP | 0.822 | 0.864 | 0.923 | 0.963 | 0.995 | ||
| PICAW | 0.152 | 0.198 | 0.232 | 0.251 | 0.284 | ||
| PICP | 0.844 | 0.872 | 0.947 | 0.981 | 1.000 | ||
| PICAW | 0.175 | 0.218 | 0.259 | 0.288 | 0.323 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Wang, X.; Chen, J. Wind Power Forecasting Using Multi-Objective Evolutionary Algorithms for Wavelet Neural Network-Optimized Prediction Intervals. Appl. Sci. 2018, 8, 185. https://doi.org/10.3390/app8020185
Shen Y, Wang X, Chen J. Wind Power Forecasting Using Multi-Objective Evolutionary Algorithms for Wavelet Neural Network-Optimized Prediction Intervals. Applied Sciences. 2018; 8(2):185. https://doi.org/10.3390/app8020185
Chicago/Turabian StyleShen, Yanxia, Xu Wang, and Jie Chen. 2018. "Wind Power Forecasting Using Multi-Objective Evolutionary Algorithms for Wavelet Neural Network-Optimized Prediction Intervals" Applied Sciences 8, no. 2: 185. https://doi.org/10.3390/app8020185
APA StyleShen, Y., Wang, X., & Chen, J. (2018). Wind Power Forecasting Using Multi-Objective Evolutionary Algorithms for Wavelet Neural Network-Optimized Prediction Intervals. Applied Sciences, 8(2), 185. https://doi.org/10.3390/app8020185




