The Fundamental Contribution of Phytoplankton Spectral Scattering to Ocean Colour: Implications for Satellite Detection of Phytoplankton Community Structure
Abstract
1. Introduction
Study Objectives and Outline
2. Methods: Modelling Approach
2.1. The Requirement for a Biophysically Consistent PFT Optical Model
2.2. Equivalent Algal Populations Model: Principal Attributes
2.3. Case Study Methods
2.3.1. Southern Ocean Case Study: Separating the Effects of Biomass From the Effects of Change
2.3.2. Benguela-Like Case Study: Addressing Pigment Variability
2.3.3. Spectral Shape and Sensitivity Analyses
3. Results and Discussion
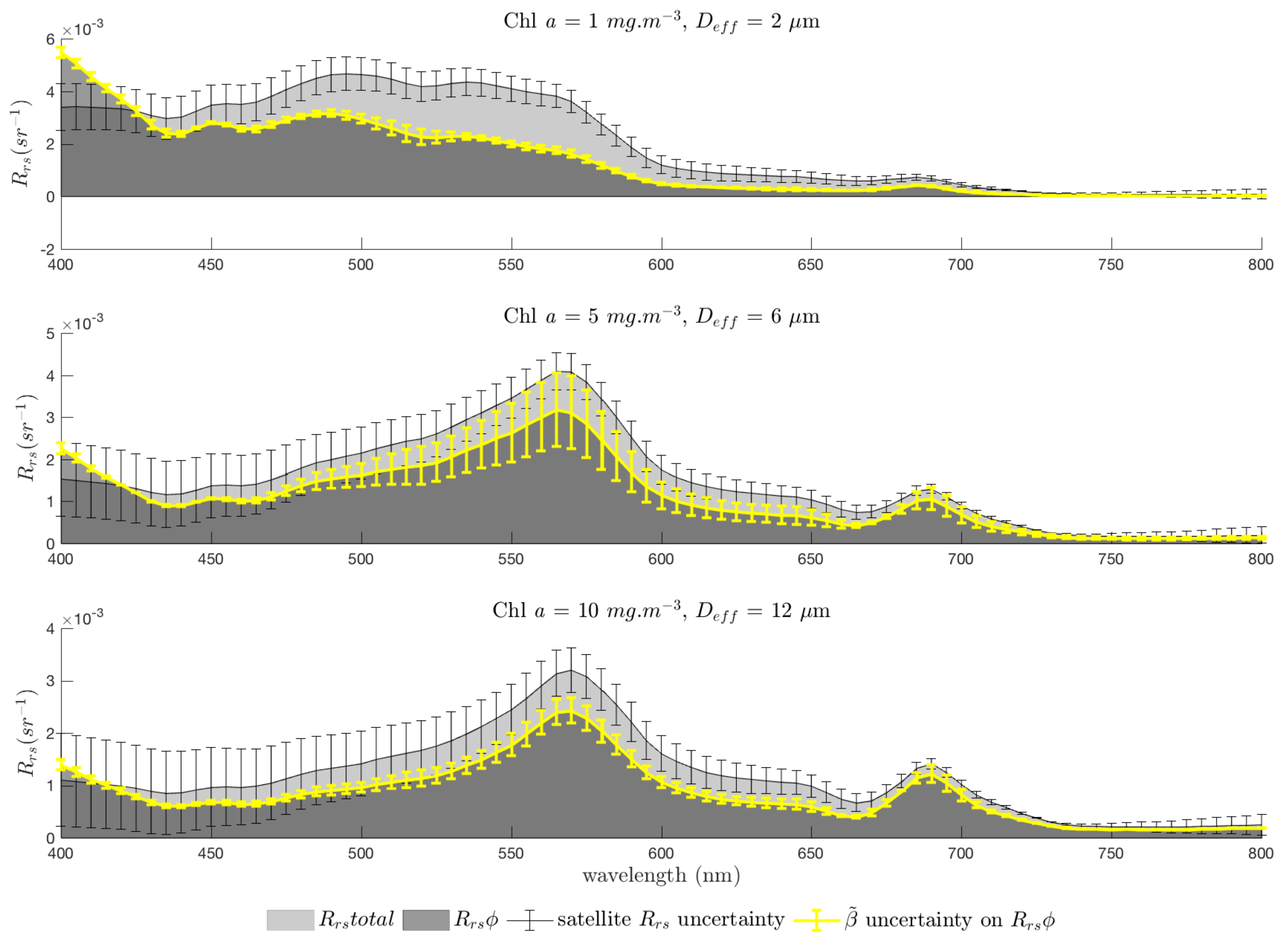
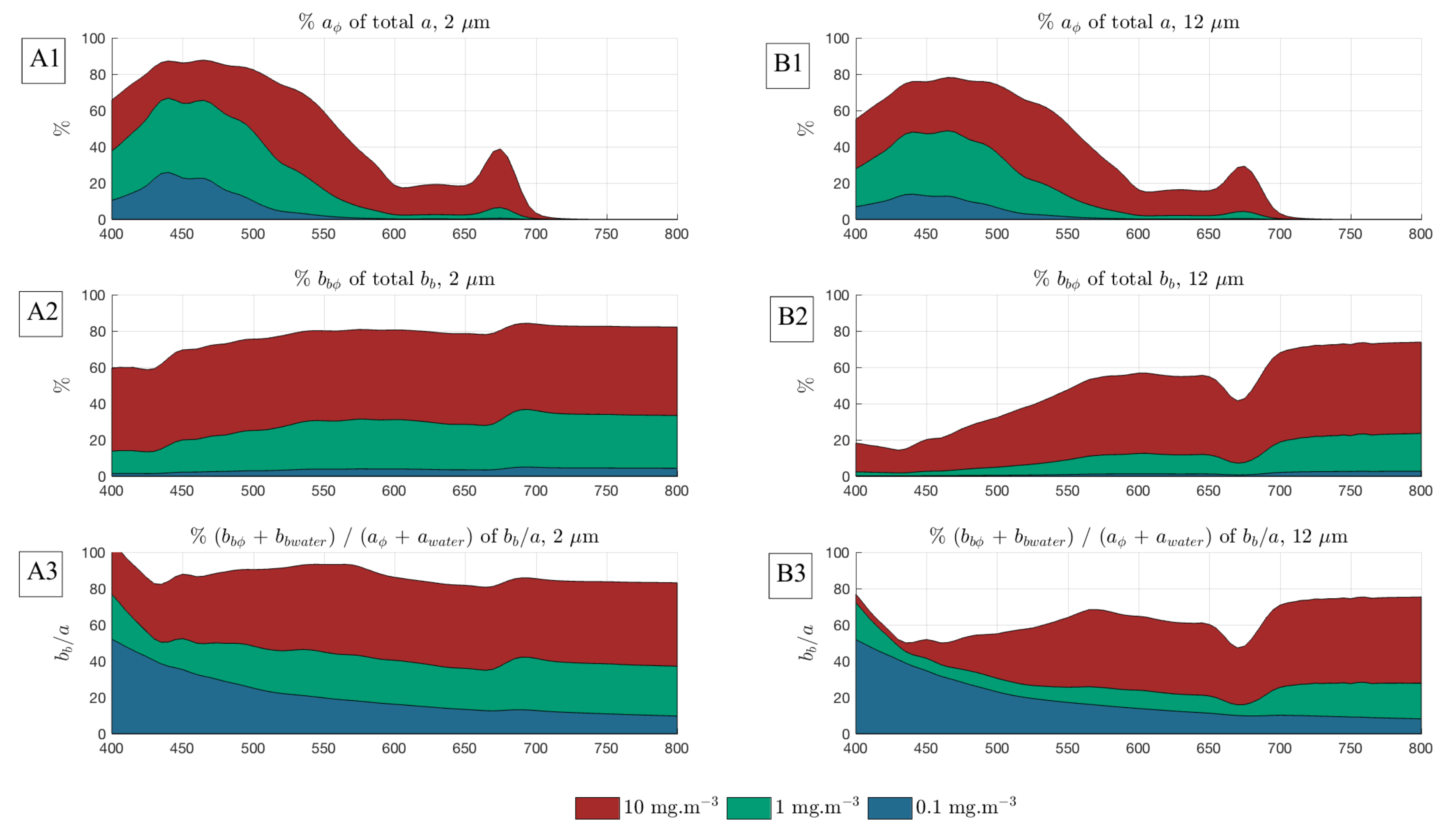
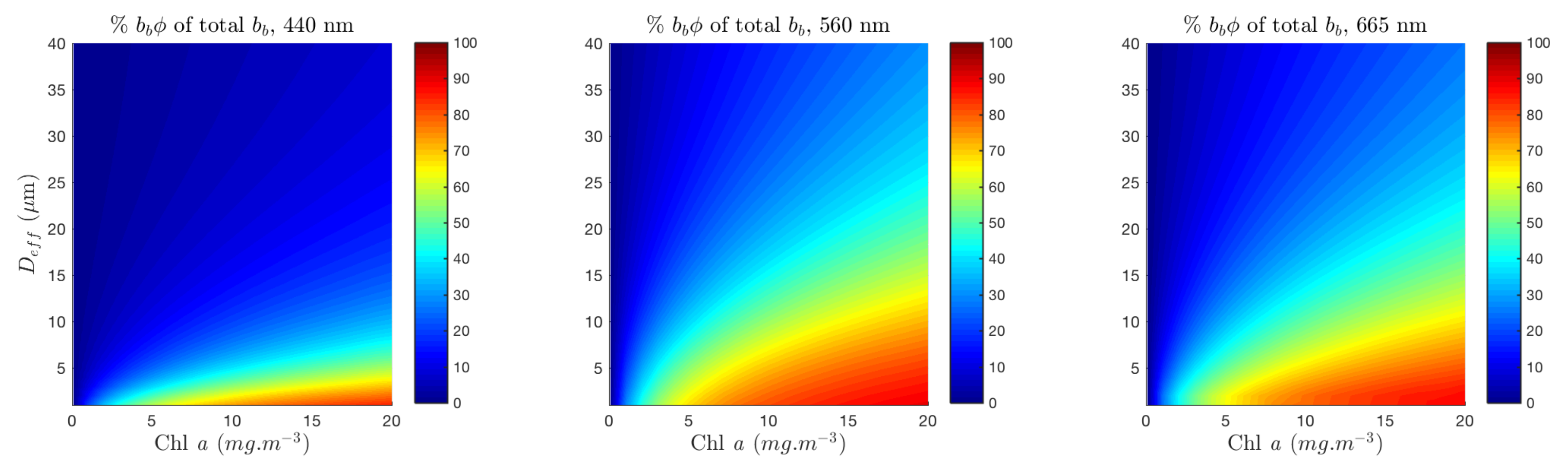
3.1. Quantifying the Contribution of Phytoplankton to the Signal
3.2. Case Study 1: Separating the Effects of Biomass from the Effects of Change
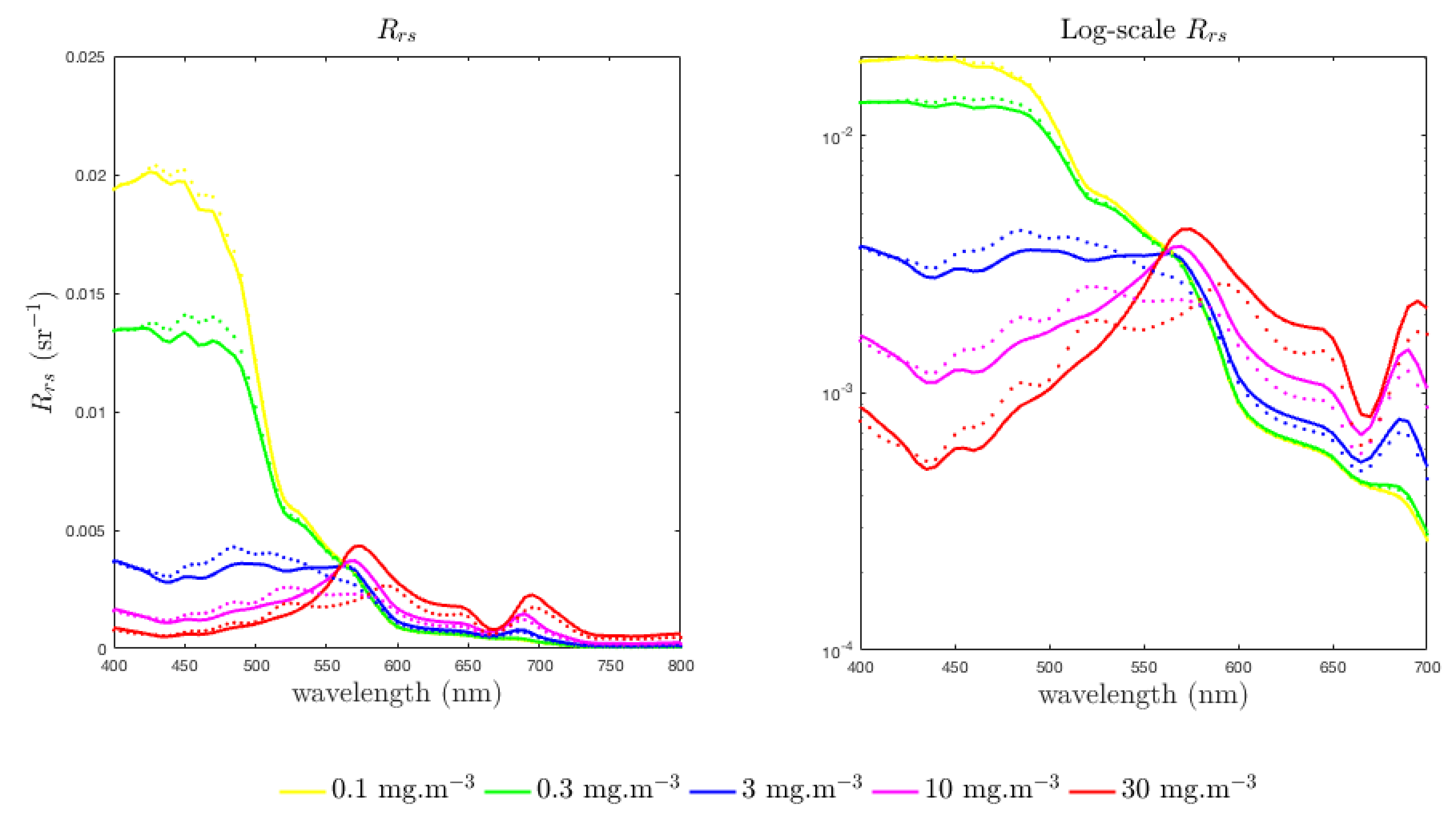
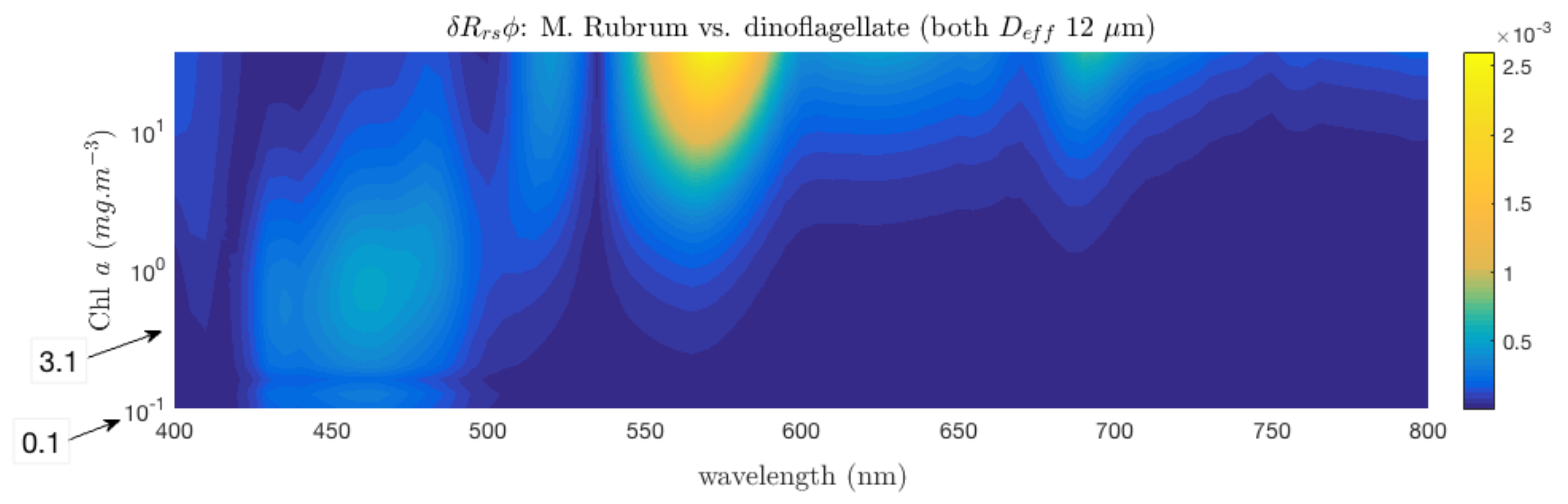
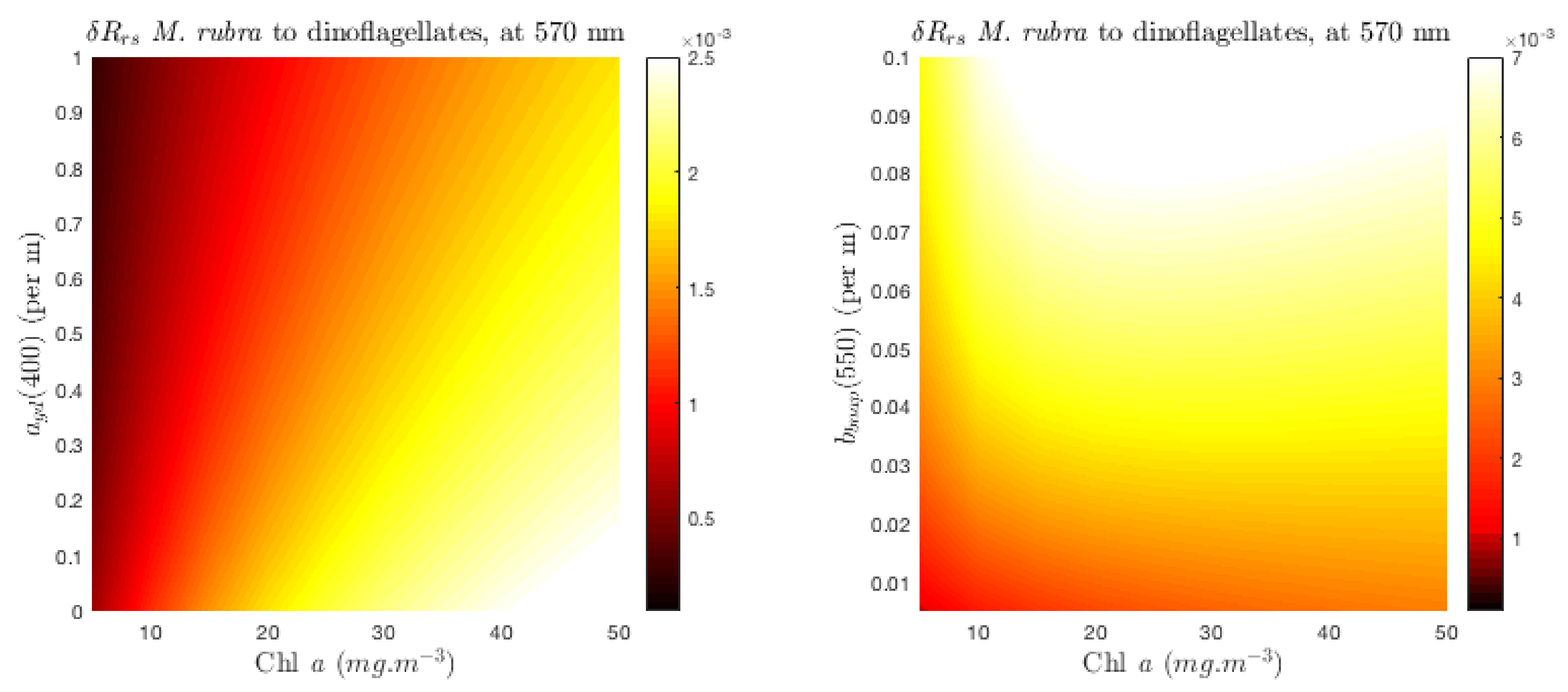
3.3. Case Study 2: Addressing Pigment Variability
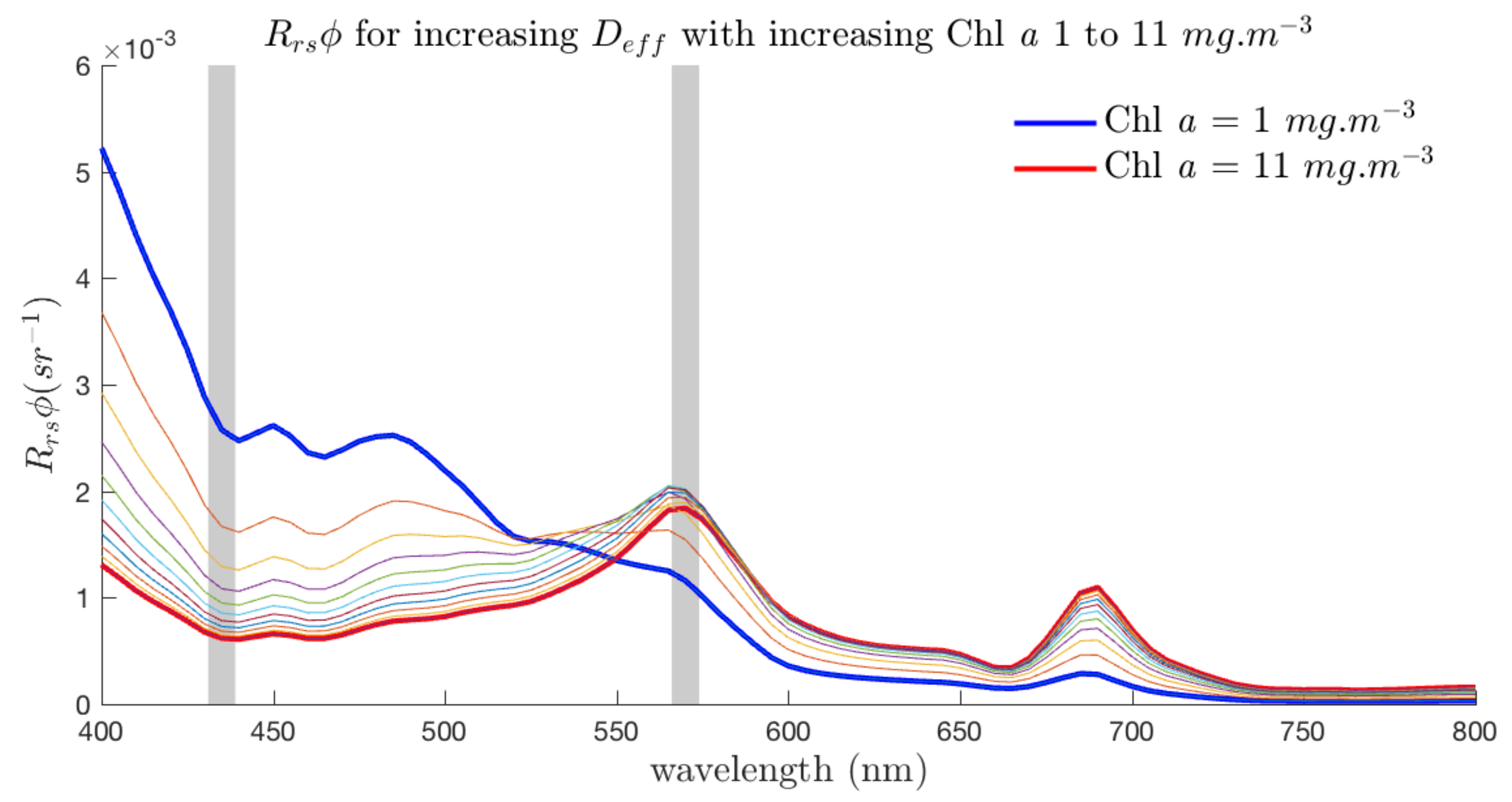
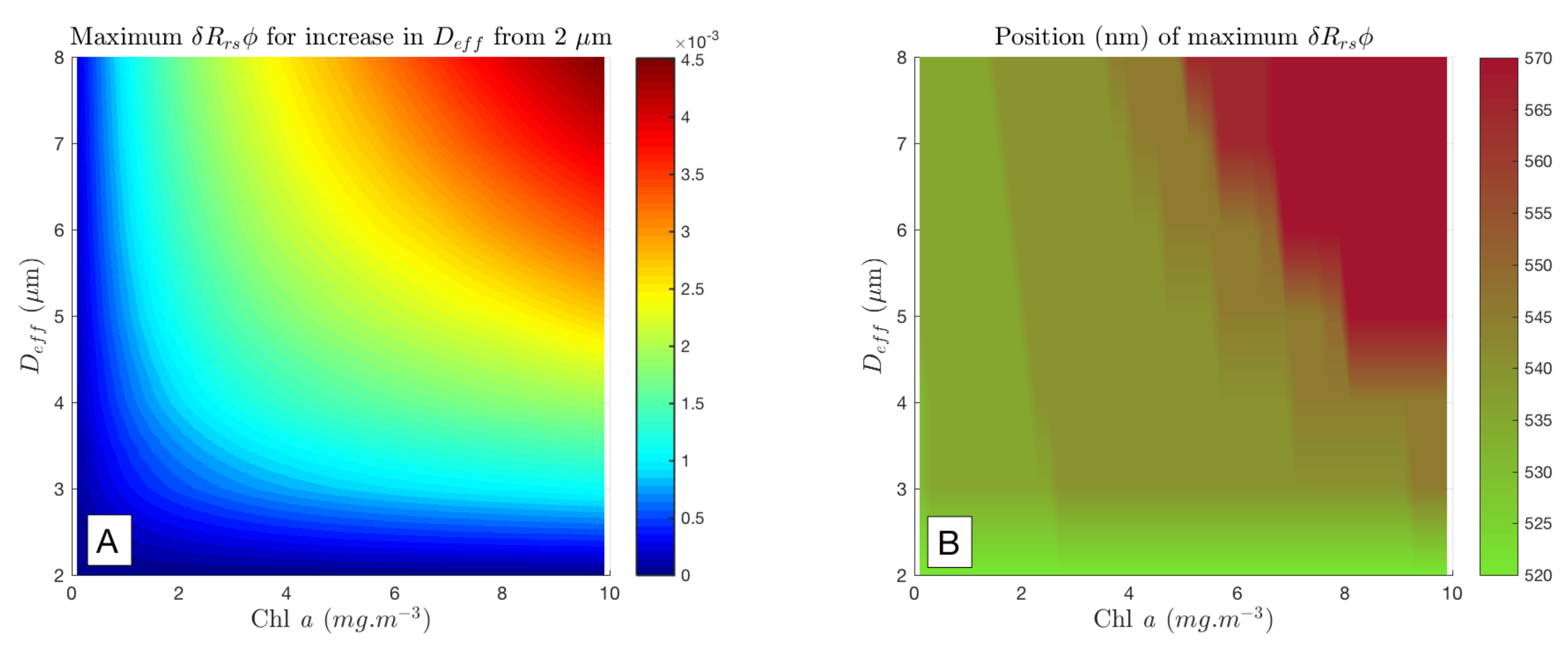
3.4. Radiometric Sensitivity of EAP Size-Based PFT Detection—Magnitude of
3.5. Spectral Shape Sensitivity of EAP Size-Based PFT Detection
3.6. Considering Uncertainties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Phytoplankton Assemblage Variability in the EAP Model
Appendix A.1. Justification for Using Measurement-Derived Refractive Indices across Wide Size Ranges
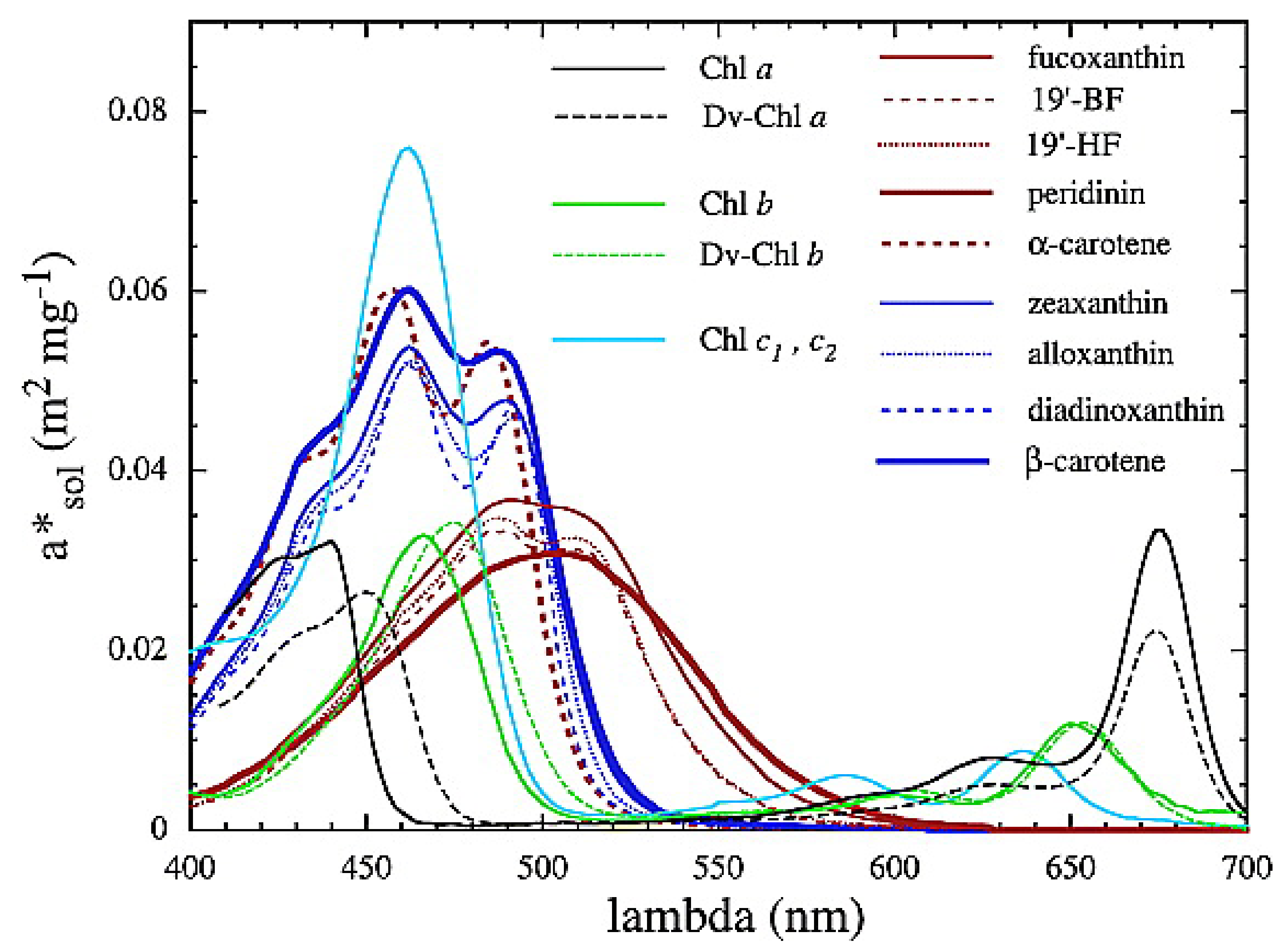
Appendix A.2. EAP Phytoplankton IOPss

Appendix A.3. EAP agd(λ) Parameterisation
Appendix A.4. EAP bbnap(λ) Parameterisation
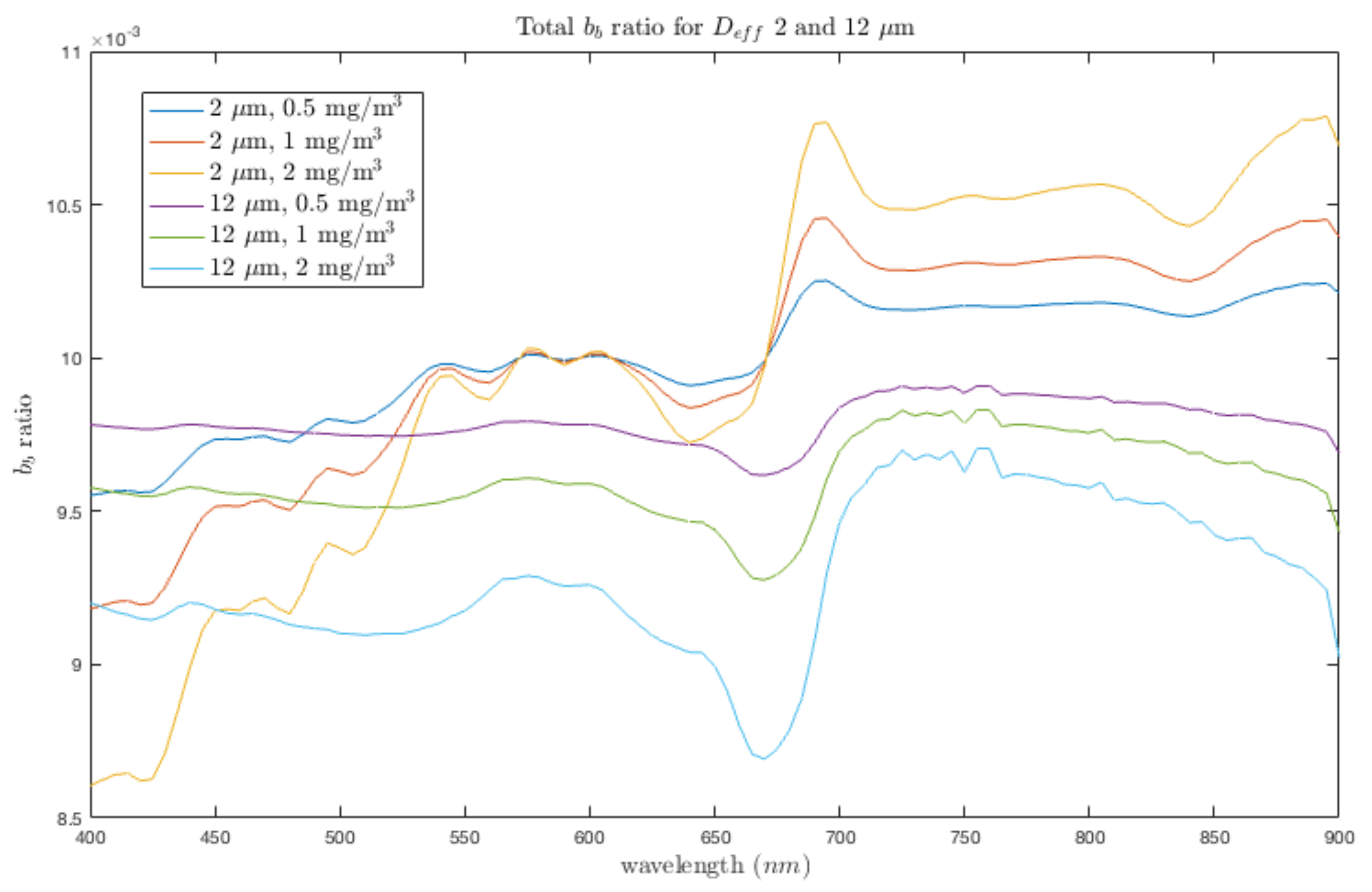
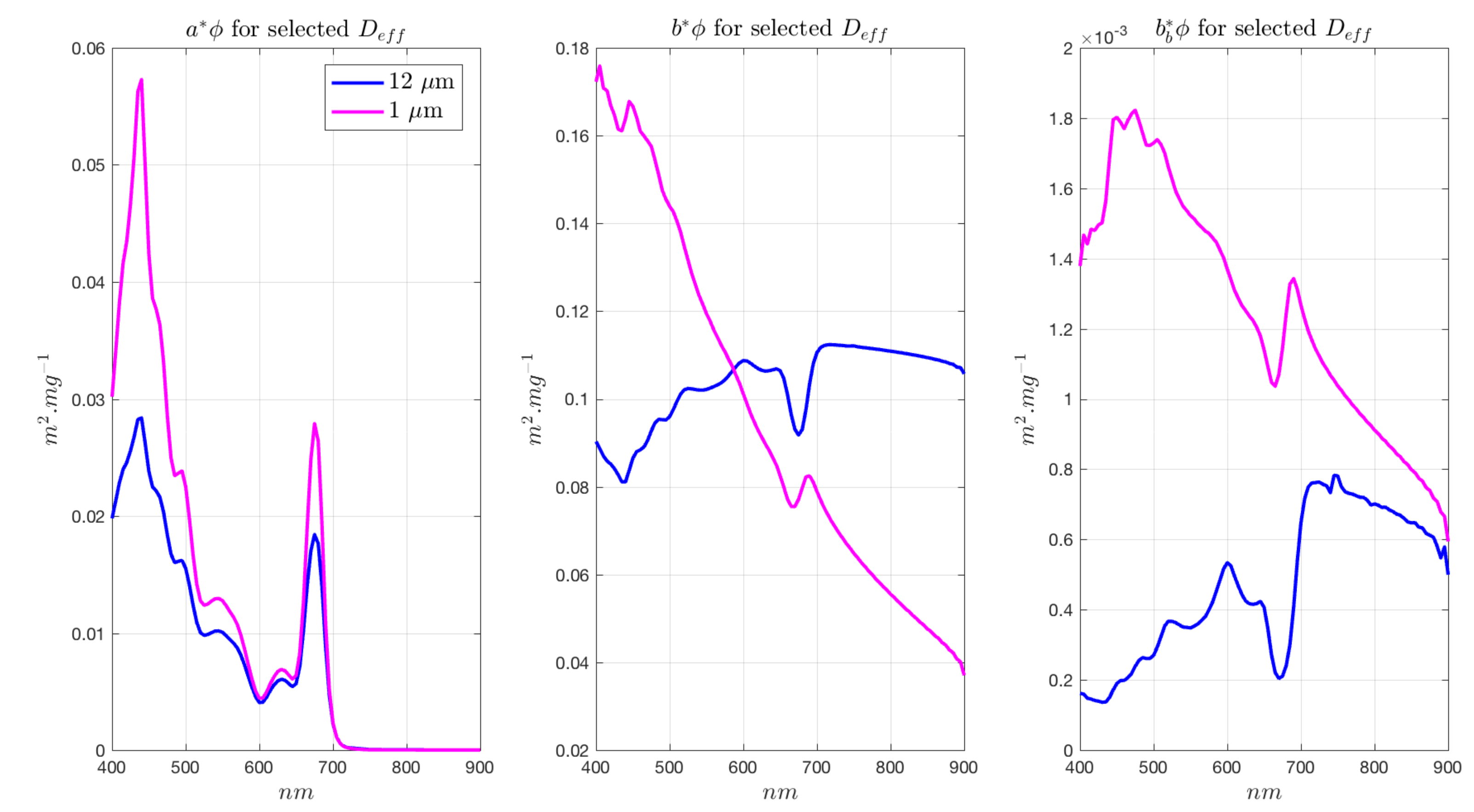
Appendix B. Measurements and Modelling Parameters
Appendix B.1. Chl a
Appendix B.2. Model Parameters Used for Hydrolight-Ecolights
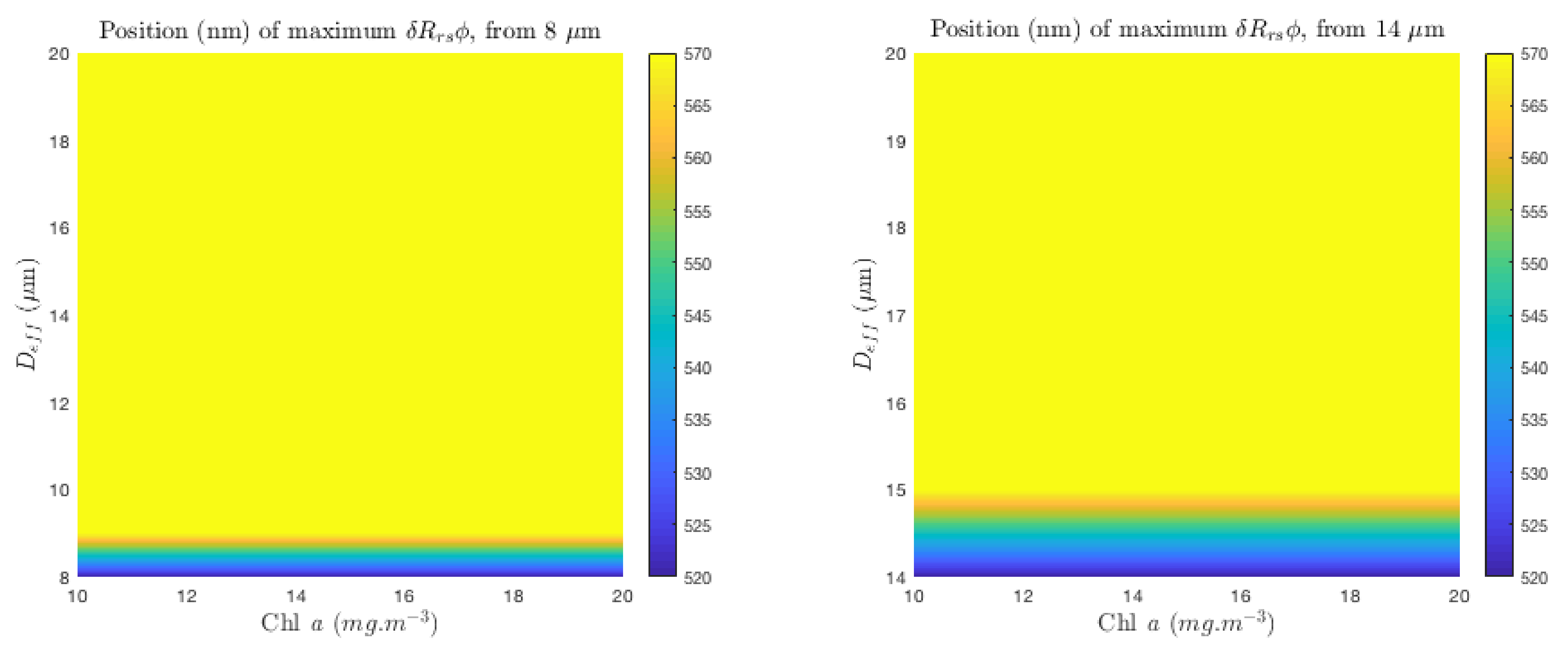
Appendix C. Position of Maximum δRrsϕ
Appendix D. Uncertaintiess
References
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T. Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef] [PubMed]
- McClain, C.R. A decade of satellite ocean color observations. Annu. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed]
- Swart, S.; Chang, N.; Fauchereau, N.; Joubert, W.; Lucas, M.; Mtshali, T.; Roychoudhury, A.; Tagliabue, A.; Thomalla, S.; Waldron, H.; et al. Southern Ocean Seasonal Cycle Experiment 2012: Seasonal scale climate and carbon cycle links. S. Afr. J. Sci. 2012, 108, 11–13. [Google Scholar] [CrossRef]
- Thomalla, S.; Fauchereau, N.; Swart, S.; Monteiro, P. Regional scale characteristics of the seasonal cycle of chlorophyll in the Southern Ocean. Biogeosciences 2011, 8, 2849. [Google Scholar] [CrossRef]
- Ryan-Keogh, T.J.; Thomalla, S.J.; Mtshali, T.N.; Little, H. Modelled estimates of spatial variability of iron stress in the Atlantic sector of the Southern Ocean. Biogeosciences 2017, 14, 3883–3897. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Ciavatta, S.; Sathyendranath, S.; Jackson, T.; Tilstone, G.; Curran, K.; Airs, R.L.; Cummings, D.; Brotas, V.; Organelli, E.; et al. Uncertainty in Ocean-Color Estimates of Chlorophyll for Phytoplankton Groups. Front. Mar. Sci. 2017, 4, 104. [Google Scholar] [CrossRef]
- Antoine, D.; d’Ortenzio, F.; Hooker, S.B.; Bécu, G.; Gentili, B.; Tailliez, D.; Scott, A.J. Assessment of uncertainty in the ocean reflectance determined by three satellite ocean color sensors (MERIS, SeaWiFS and MODIS-A) at an offshore site in the Mediterranean Sea (BOUSSOLE project). J. Geophys. Res. Oceans 2008, 113, 2156–2202. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Watts, L.; Devred, E.; Platt, T.; Caverhill, C.; Maass, H. Discrimination of diatoms from other phytoplankton using ocean-colour data. Mar. Ecol. Prog. Ser. 2004, 272, 59–68. [Google Scholar] [CrossRef]
- Alvain, S.; Loisel, H.; Dessailly, D. Theoretical analysis of ocean color radiances anomalies and implications for phytoplankton groups detection in Case 1 waters. Opt. Express 2012, 20, 1070–1083. [Google Scholar] [CrossRef]
- Kostadinov, T.; Siegel, D.; Maritorena, S. Retrieval of the particle size distribution from satellite ocean color observations. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Kostadinov, T.S. Carbon-based phytoplankton size classes retrieved via ocean color estimates of the particle size distribution. Ocean Sci. 2016, 12, 561. [Google Scholar] [CrossRef]
- Anderson, T.R. Plankton functional type modelling: Running before we can walk? J. Plankton Res. 2005, 27, 1073–1081. [Google Scholar] [CrossRef]
- Brown, C.A.; Huot, Y.; Werdell, P.J.; Gentili, B.; Claustre, H. The origin and global distribution of second order variability in satellite ocean color and its potential applications to algorithm development. Remote Sens. Environ. 2008, 112, 4186–4203. [Google Scholar] [CrossRef]
- MÉlin, F.; Sclep, G.; Jackson, T.; Sathyendranath, S. Uncertainty estimates of remote sensing reflectance derived from comparison of ocean color satellite data sets. Remote Sens. Environ. 2016, 177, 107–124. [Google Scholar] [CrossRef]
- Lee, Z.P. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms and Applications. Rep. Int. Ocean Colour Coord. Group 2006, 5, 1–122. [Google Scholar]
- Mélin, F.; Zibordi, G.; Berthon, J.F. Assessment of satellite ocean color products at a coastal site. Remote Sens. Environ. 2007, 110, 192–215. [Google Scholar] [CrossRef]
- Mouw, C.B.; Hardman-Mountford, N.J.; Alvain, S.; Bracher, A.; Brewin, R.J.W.; Bricaud, A.; Ciotti, A.M.; Devred, E.; Fujiwara, A.; Hirata, T.; et al. A Consumer’s Guide to Satellite Remote Sensing of Multiple Phytoplankton Groups in the Global Ocean. Front. Mar. Sci. 2017, 4, 41. [Google Scholar] [CrossRef]
- Hirata, T.; Hardman-Mountford, N.J.; Brewin, R.J.W.; Aiken, J.; Barlow, R.; Suzuki, K.; Isada, T.; Howell, E.; Hashioka, T.; Noguchi-Aita, M.; et al. Synoptic relationships between surface Chlorophyll-a and diagnostic pigments specific to phytoplankton functional types. Biogeosciences 2011, 8, 311–327. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Hardman-Mountford, N.J.; Lavender, S.J.; Raitsos, D.E.; Hirata, T.; Uitz, J.; Devred, E.; Bricaud, A.; Ciotti, A.; Gentili, B. An intercomparison of bio-optical techniques for detecting dominant phytoplankton size class from satellite remote sensing. Remote Sens. Environ. 2011, 115, 325–339. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Hirata, T.; Lavender, S.J.; Barciela, R.M.; Hardman-Mountford, N.J. A three-component model of phytoplankton size class for the Atlantic Ocean. Ecol. Modell. 2010, 221, 1472–1483. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Bréon, F.M. Remote sensing of phytoplankton groups in Case 1 waters from global SeaWiFS imagery. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 1989–2004. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Loisel, H. Seasonal distribution and succession of dominant phytoplankton groups in the global ocean: A satellite view. Glob. Biogeochem. Cycles 2008, 22, 1–15. [Google Scholar] [CrossRef]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Platt, T. A three component classification of phytoplankton absorption spectra: Application to ocean-color data. Remote Sens. Environ. 2011, 115, 2255–2266. [Google Scholar] [CrossRef]
- Ciotti, A.M.; Bricaud, A. Retrievals of a size parameter for phytoplankton and spectral light absorption by colored detrital matter from water-leaving radiances at SeaWiFS channels in a continental shelf region off Brazil. Limnol. Oceanogr. Methods 2006, 4, 237–253. [Google Scholar] [CrossRef]
- Bracher, A.; Vountas, M.; Dinter, T.; Burrows, J.; Röttgers, R.; Peeken, I. Quantitative observation of cyanobacteria and diatoms from space using PhytoDOAS on SCIAMACHY data. Biogeosciences 2009, 6, 751–764. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Siegel, D.A.; Maritorena, S. Global variability of phytoplankton functional types from space: assessment via the particle size distribution. Biogeosciences 2010, 7, 3239–3257. [Google Scholar] [CrossRef]
- Bernard, S.; Probyn, T.A.; Quirantes, A. Simulating the optical properties of phytoplankton cells using a two-layered spherical geometry. Biogeosci. Discuss. 2009, 6, 1497–1563. [Google Scholar] [CrossRef]
- Uitz, J.; Stramski, D.; Reynolds, R.A.; Dubranna, J. Assessing phytoplankton community composition from hyperspectral measurements of phytoplankton absorption coefficient and remote-sensing reflectance in open-ocean environments. Remote Sens. Environ. 2015, 171, 58–74. [Google Scholar] [CrossRef]
- Torrecilla, E.; Stramski, D.; Reynolds, R.A.; Millán-Núñez, E.; Piera, J. Cluster analysis of hyperspectral optical data for discriminating phytoplankton pigment assemblages in the open ocean. Remote Sens. Environ. 2011, 115, 2578–2593. [Google Scholar] [CrossRef]
- Xi, H.; Hieronymi, M.; Röttgers, R.; Krasemann, H.; Qiu, Z. Hyperspectral differentiation of phytoplankton taxonomic groups: A comparison between using remote sensing reflectance and absorption spectra. Remote Sens. 2015, 7, 14781–14805. [Google Scholar] [CrossRef]
- Sadeghi, A.; Dinter, T.; Vountas, M.; Taylor, B.; Altenburg-Soppa, M.; Bracher, A. Remote sensing of coccolithophore blooms in selected oceanic regions using the PhytoDOAS method applied to hyper-spectral satellite data. Biogeosciences 2012, 9, 2127–2143. [Google Scholar] [CrossRef]
- Stramski, D.; Bricaud, A.; Morel, A. Modeling the inherent optical properties of the ocean based on the detailed composition of the planktonic community. Appl. Opt. 2001, 40, 2929–2945. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, A.; Huot, Y.; Shimada, K.; Saitoh, S.I.; Babin, M. Bio-optical characteristics of the western Arctic Ocean: Implications for ocean color algorithms. Can. J. Remote Sens. 2007, 33, 503–518. [Google Scholar] [CrossRef]
- Bernard, S.; Shillington, F.A.; Probyn, T.A. The use of equivalent size distributions of natural phytoplankton assemblages for optical modeling. Opt. Express 2007, 15, 1995–2007. [Google Scholar] [CrossRef] [PubMed]
- Lain, L.R.; Bernard, S.; Matthews, M.W. Understanding the contribution of phytoplankton phase functions to uncertainties in the water colour signal. Opt. Express 2017, 25, A151–A165. [Google Scholar] [CrossRef] [PubMed]
- Morel, A. Consequences of a Synechococcus bloom upon the optical properties of oceanic (case 1) waters. Limnol. Oceanogr. 1997, 42, 1746–1754. [Google Scholar] [CrossRef]
- Evers-King, H.; Bernard, S.; Lain, L.R.; Probyn, T.A. Sensitivity in reflectance attributed to phytoplankton cell size: Forward and inverse modelling approaches. Opt. Express 2014, 22, 11536–11551. [Google Scholar] [CrossRef]
- Organelli, E.; Nuccio, C.; Lazzara, L.; Uitz, J.; Bricaud, A.; Massi, L. On the discrimination of multiple phytoplankton groups from light absorption spectra of assemblages with mixed taxonomic composition and variable light conditions. Appl. Opt. 2017, 56, 3952. [Google Scholar] [CrossRef]
- Defoin-Platel, M.; Chami, M. How ambiguous is the inverse problem of ocean color in coastal waters? J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Kirk, J. A theoretical analysis of the contribution of algal cells to the attenuation of light within natural waters I. General treatment of suspensions of pigmented cells. New Phytol. 1975, 75, 11–20. [Google Scholar] [CrossRef]
- Morel, A.; Bricaud, A. Theoretical results concerning light absorption in a discrete medium, and application to specific absorption of phytoplankton. Deep Sea Res. 1981, 28, 1375–1393. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Lazzara, L.; Prieur, L. Variations in the spectral values of specific absorption of phytoplankton. Limnol. Oceanogr. 1987, 32, 403–415. [Google Scholar] [CrossRef]
- Bricaud, A.; Bédhomme, A.; Morel, A. Optical properties of diverse phytoplanktonic species: Experimental results and theoretical interpretation. J. Plankton Res. 1988, 10, 851–873. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Bricaud, A.; Morel, A. Light backscattering efficiency and related properties of some phytoplankters. Deep Sea Res. Part A Oceanogr. Res. Pap. 1992, 39, 1835–1855. [Google Scholar] [CrossRef]
- Bricaud, A.; Stramski, D. Spectral absorption coefficients of living phytoplankton and nonalgal biogenous matter: A comparison between the Peru upwelling areaand the Sargasso Sea. Limnol. Oceanogr. 1990, 35, 562–582. [Google Scholar] [CrossRef]
- Le Quéré, C.; Harrison, S.P.; Prentice, I.C.; Buitenhuis, E.T.; Aumont, O.; Bopp, L.; Claustre, H.; Cotrim Da Cunha, L.; Geider, R.; Giraud, X.; et al. Ecosystem dynamics based on plankton functional types for global ocean biogeochemistry models. Glob. Chang. Biol. 2005, 11, 2016–2040. [Google Scholar]
- Nair, A.; Sathyendranath, S.; Platt, T.; Morales, J.; Stuart, V.; Forget, M.H.; Devred, E.; Bouman, H. Remote sensing of phytoplankton functional types. Remote Sens. Environ. 2008, 112, 3366–3375. [Google Scholar] [CrossRef]
- IOCCG. Phytoplankton Functional Types from Space. In Reports of the International Ocean Colour Coordinating Group; IOCCG: Dartmouth, NS, Canada, 2014. [Google Scholar]
- Dutkiewicz, S.; Hickman, A.; Jahn, O.; Gregg, W.; Mouw, C.; Follows, M. Capturing optically important constituents and properties in a marine biogeochemical and ecosystem model. Biogeosciences 2015, 12, 4447–4481. [Google Scholar] [CrossRef]
- Moutier, W.; Duforet-Gaurier, L.; Thyssen, M.; Loisel, H.; Meriaux, X.; Courcot, L.; Dessailly, D.; Reve, A.H.; Gregori, G.; Alvain, S.; et al. Evolution of the scattering properties of phytoplankton cells from flow cytometry measurements. PLoS ONE 2017, 12, e0181180. [Google Scholar] [CrossRef]
- Stramski, D.; Morel, A. Optical properties of photosynthetic picoplankton in different physiological states as affected by growth irradiance. Deep Sea Res. 1990, 37, 245–266. [Google Scholar] [CrossRef]
- Reynolds, R.A.; Stramski, D.; Kiefer, D.A. The effect of nitrogren limitation on the absorption and scattering properties of the marine diatom Thalassiosira pseudonana. Limnol. Oceanogr. 1997, 42, 881–892. [Google Scholar] [CrossRef]
- Stramski, D.; Sciandra, A.; Claustre, H. Effects of temperature, nitrogen, and light limitation on the optical properties of the marine diatom Thalassiosira pseudonana. Limnol. Oceanogr. 2002, 47, 392–403. [Google Scholar] [CrossRef]
- Stramski, D.; Reynolds, R.A. Diel variations in the optical properties of a marine diatom. Limnol. Oceanogr. 1993, 38, 1347–1364. [Google Scholar] [CrossRef]
- Stramski, D.; Shalapyonok, A.; Reynolds, R.A. Optical characterization of the oceanic unicellular cyanobacterium Synechococcus grown under a day-night cycle in natural irradiance. J. Geophys. Res. Oceans 1995, 100, 13295–13307. [Google Scholar] [CrossRef]
- Sauer, M.J.; Roesler, C.; Werdell, P.; Barnard, A. Under the hood of satellite empirical chlorophyll a algorithms: Revealing the dependencies of maximum band ratio algorithms on inherent optical properties. Opt. Express 2012, 20, 20920–20933. [Google Scholar] [CrossRef] [PubMed]
- Sathyendranath, S.; Brewin, R.J.; Jackson, T.; Mélin, F.; Platt, T. Ocean-colour products for climate-change studies: What are their ideal characteristics? Remote Sens. Environ. 2017, 203, 125–138. [Google Scholar] [CrossRef]
- Mobley, C.D.; Stramski, D. Effects of microbial particles on oceanic optics: Methodology for radiative transfer modeling and example simulations. Limnol. Oceanogr. 1997, 42, 550–560. [Google Scholar] [CrossRef]
- Stramski, D.; Mobley, C.D. Effects of microbial particles on oceanic optics: A database of single-particle optical properties. Limnol. Oceanogr. 1997, 42, 538–549. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 11–23. [Google Scholar] [CrossRef]
- Olson, R.; Zettler, E.; Anderson, O. Discrimination of eukaryotic phytoplankton cell types from light scatter and autofluorescence properties measured by flow cytometry. Cytom. Part A 1989, 10, 636–643. [Google Scholar] [CrossRef] [PubMed]
- Matthews, M.W.; Bernard, S. Using a two-layered sphere model to investigate the impact of gas vacuoles on the inherent optical properties of M. aeruginosa. Biogeosciences 2013, 10, 8139–8157. [Google Scholar] [CrossRef]
- Smith, M.E.; Lain, L.R.; Bernard, S. An optimized Chlorophyll a switching algorithm for MERIS and OLCI in phytoplankton-dominated waters. Remote Sens. Environ. 2018, 215, 217–227. [Google Scholar] [CrossRef]
- Lain, L.R.; Bernard, S.; Evers-King, H. Biophysical modelling of phytoplankton communities from first principles using two-layered spheres: Equivalent Algal Populations (EAP) model. Opt. Express 2014, 22, 16745–16758. [Google Scholar] [CrossRef] [PubMed]
- Stramski, D.; Boss, E.; Bogucki, D.; Voss, K. The role of seawater constituents in light backscattering in the ocean. Prog. Oceanogr. 2004, 61, 27–56. [Google Scholar] [CrossRef]
- Toll, J.S. Causality and the Dispersion Relation: Logical Foundations. Phys. Rev. 1956, 104, 1760–1770. [Google Scholar] [CrossRef]
- Aas, E. Refractive index of phytoplankton derived from its metabolite composition. J. Plankton Res. 1996, 18, 2223–2249. [Google Scholar] [CrossRef]
- Bernard, S.; Probyn, T.; Barlow, R. Measured and modelled optical properties of particulate matter in the southern Benguela. S. Afr. J. Sci. 2001, 97, 410–420. [Google Scholar]
- Stramski, D. Refractive index of planktonic cells as a measure of cellular carbon and chlorophyll a content. Deep Sea Res. Part I Oceanogr. Res. Pap. 1999, 46, 335–351. [Google Scholar] [CrossRef]
- Johnsen, G.; Samset, O.; Granskog, L.; Sakshaug, E. In vivo absorption characteristics in 10 classes of bloom-forming phytoplankton: Taconomic characteristics and responses to photoadaptation by means of discriminant and HPLC analysis. Mar. Ecol. Prog. Ser. 1994, 149–157. [Google Scholar] [CrossRef]
- Bricaud, A.; Babin, M.; Morel, A.; Claustre, H. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. Oceans 1995, 100, 13321–13332. [Google Scholar] [CrossRef]
- Constable, A.J.; Melbourne-Thomas, J.; Corney, S.P.; Arrigo, K.R.; Barbraud, C.; Barnes, D.; Bindoff, N.L.; Boyd, P.W.; Brandt, A.; Costa, D.P.; et al. Climate change and Southern Ocean ecosystems I: How changes in physical habitats directly affect marine biota. Glob. Chang. Biol. 2014, 20, 3004–3025. [Google Scholar] [CrossRef] [PubMed]
- Mtshali, T.N. SANAE 55 Cruise Report; South African National Antarctic Programme (SANAP): Cape Town, South Africa, 2016. [Google Scholar]
- Del Castillo, C.E.; Miller, R.L. Horizontal and vertical distributions of colored dissolved organic matter during the Southern Ocean Gas Exchange Experiment. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Reynolds, R.; Stramski, D.; Mitchell, B. A chlorophyll-dependent semianalytical reflectance model derived from field measurements of absorption and backscattering coefficients within the Southern Ocean. J. Geophys. Res. Oceans 2001, 106, 7125–7138. [Google Scholar] [CrossRef]
- Gustafson, D.E., Jr.; Stoecker, D.K.; Johnson, M.D.; Van Heukelem, W.F.; Sneider, K. Cryptophyte algae are robbed of their organelles by the marine ciliate Mesodinium rubrum. Nature 2000, 405, 1049. [Google Scholar] [CrossRef] [PubMed]
- Stramska, M.; Stramski, D.; Mitchell, B.G.; Mobley, C.D. Estimation of the absorption and backscattering coefficients from in water radiometric measurements. Limnol. Oceanogr. 2000, 45, 628–641. [Google Scholar] [CrossRef]
- Oubelkheir, K.; Claustre, H.; Bricaud, A.; Babin, M. Partitioning total spectral absorption in phytoplankton and colored detrital material contributions. Limnol. Oceanogr. Methods 2007, 5, 384–395. [Google Scholar] [CrossRef]
- Chami, M.; McKee, D.; Leymarie, E.; Khomenko, G. Influence of the angular shape of the volume-scattering function and multiple scattering on remote sensing reflectance. Appl. Opt. 2006, 45, 9210–9220. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Atmos. 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
- Boyd, P.; Ellwood, M. The biogeochemical cycle of iron in the ocean. Nat. Geosci. 2010, 10, 675–682. [Google Scholar] [CrossRef]
- Bernard, S.; Pitcher, G.; Evers-King, H.; Robertson, L.; Matthews, M.; Rabagliati, A.; Balt, C. Ocean Colour Remote Sensing of Harmful Algal Blooms in the Benguela System. In Remote Sensing of the African Seas; Springer: Berlin, Germany, 2014; pp. 185–203. [Google Scholar]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Maass, H.; Ulloa, O.; Platt, T. A two-component model of phytoplankton absorption in the open ocean: Theory and applications. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Tan, H.; Oishi, T.; Tanaka, A.; Doerffer, R. Accurate estimation of the backscattering coefficient by light scattering at two backward angles. Appl. Opt. 2015, 54, 7718–7733. [Google Scholar] [CrossRef] [PubMed]
- Harmel, T.; Hieronymi, M.; Slade, W.; Röttgers, R.; Roullier, F.; Chami, M. Laboratory experiments for inter-comparison of three volume scattering meters to measure angular scattering properties of hydrosols. Opt. Express 2016, 24, 234–256. [Google Scholar] [CrossRef] [PubMed]
- Bricaud, A.; Claustre, H.; Ras, J.; Oubelkheir, K. Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal populations. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Kudela, R.M.; Ryan, J.P. Red and black tides: Quantitative analysis of water-leaving radiance and perceived color for phytoplankton, colored dissolved organic matter, and suspended sediments. Limnol. Oceanogr. 2006, 51, 2646–2659. [Google Scholar] [CrossRef]
- Quirantes, A.; Bernard, S. Light-scattering methods for modelling algal particles as a collection of coated and/or nonspherical scatterers. J. Quant. Spectrosc. Radiat. Transf. 2006, 100, 315–324. [Google Scholar] [CrossRef]
- Ishikawa, A.; Wright, S.W.; van den Enden, R.; Davidson, A.T.; Marchant, H.J. Abundance, size structure and community composition of phytoplankton in the Southern Ocean in the austral summer 1999/2000. Pol. Biosci. 2002, 15, 11–26. [Google Scholar]
- Wright, S.; Thomas, D.; Marchant, H.; Higgins, H.; Mackey, M.; Mackey, D. Analysis of phytoplankton of the Australian sector of the Southern Ocean: Comparisons of microscopy and size frequency data with interpretations of pigment HPLC data using the∖’CHEMTAX∖’matrix factorisation program. Mar. Ecol. Prog. Ser. 1996, 144, 285–298. [Google Scholar] [CrossRef]
- Wright, S.W.; Jeffrey, S. Fucoxanthin pigment markers of marine phytoplankton analysed by HPLC and HPTLC. Mar. Ecol. Prog. Ser. 1987, 259–266. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Prieur, L. Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnol. Oceanogr. 1981, 26, 43–53. [Google Scholar] [CrossRef]
- Roesler, C.S.; Perry, M.J.; Carder, K.L. Modeling in situ phytoplankton absorption from total absorption spectra in productive inland marine waters. Limnol. Oceanogr. 1989, 34, 1510–1523. [Google Scholar] [CrossRef]
- Bernard, S.; Probyn, T.A.; Shillington, F.A. Towards the validation of SeaWiFS in southern African waters: The effects of gelbstoff. S. Afr. J. Mar. Sci. 1998, 19, 15–25. [Google Scholar] [CrossRef]
- Roesler, C.S.; Perry, M.J. In situ phytoplankton absorption, fluorescence emission, and particulate backscattering spectra determined from reflectance. J. Geophys. Res. 1995, 100, 13279–13294. [Google Scholar] [CrossRef]
- Chami, M.; Shybanov, E.B.; Khomenko, G.A.; Lee, M.E.G.; Martynov, O.V.; Korotaev, G.K. Spectral variation of the volume scattering function measured over the full range of scattering angles in a coastal environment. Appl. Opt. 2006, 45, 3605–3619. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.S.; Boss, E.; Macdonald, J.B.; Pegau, W.S.; Barnard, A.H.; Zaneveld, J.R.V. Model for estimating bulk refractive index from the optical backscattering ratio and the implications for understanding particle composition in case I and case II waters. J. Geophys. Res 2001, 106, 14129–14142. [Google Scholar] [CrossRef]
- Boss, E.; Pegau, W.; Lee, M.; Twardowski, M.; Shybanov, E.; Korotaev, G.; Baratange, F. Particulate backscattering ratio at LEO 15 and its use to study particle composition and distribution. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Holm-Hansen, O.; Lorenzen, C.J.; Holmes, R.W.; Strickland, J.D. Fluorometric determination of chlorophyll. ICES J. Mar. Sci. 1965, 30, 3–15. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Westberry, T.K.; Boss, E. Satellite-detected fluorescence reveals global physiology of ocean phytoplankton. Biogeosciences 2009, 779–794. [Google Scholar] [CrossRef]
- Ostrowska, M.; Woźniak, B.; Dera, J. Modelled quantum yields and energy efficiency of fluorescence photosynthesis and heat production by phytoplankton in the World Ocean. Oceanologia 2012, 54, 565–610. [Google Scholar] [CrossRef]
- Greene, R.M.; Geider, R.J.; Kolber, Z.; Falkowski, P.G. Iron-induced changes in light harvesting and photochemical energy conversion processes in eukaryotic marine algae. Plant Physiol. 1992, 100, 565–575. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lain, L.R.; Bernard, S. The Fundamental Contribution of Phytoplankton Spectral Scattering to Ocean Colour: Implications for Satellite Detection of Phytoplankton Community Structure. Appl. Sci. 2018, 8, 2681. https://doi.org/10.3390/app8122681
Lain LR, Bernard S. The Fundamental Contribution of Phytoplankton Spectral Scattering to Ocean Colour: Implications for Satellite Detection of Phytoplankton Community Structure. Applied Sciences. 2018; 8(12):2681. https://doi.org/10.3390/app8122681
Chicago/Turabian StyleLain, Lisl Robertson, and Stewart Bernard. 2018. "The Fundamental Contribution of Phytoplankton Spectral Scattering to Ocean Colour: Implications for Satellite Detection of Phytoplankton Community Structure" Applied Sciences 8, no. 12: 2681. https://doi.org/10.3390/app8122681
APA StyleLain, L. R., & Bernard, S. (2018). The Fundamental Contribution of Phytoplankton Spectral Scattering to Ocean Colour: Implications for Satellite Detection of Phytoplankton Community Structure. Applied Sciences, 8(12), 2681. https://doi.org/10.3390/app8122681




