Abstract
Flow shop scheduling problems have a wide range of real-world applications in intelligent manufacturing. Since they are known to be NP-hard for more than two machines, we propose a hybrid genetic simulated annealing (HGSA) algorithm for flow shop scheduling problems. In the HGSA algorithm, in order to obtain high-quality initial solutions, an MME algorithm, combined with the MinMax (MM) and Nawaz–Enscore–Ham (NEH) algorithms, was used to generate the initial population. Meanwhile, a hormone regulation mechanism for a simulated annealing (SA) schedule was introduced as a cooling scheme. Using MME initialization, random crossover and mutation, and the cooling scheme, we improved the algorithm’s quality and performance. Extensive experiments have been carried out to verify the effectiveness of the combination approach of MME initialization, random crossover and mutation, and the cooling scheme for SA. The result on the Taillard benchmark showed that our HGSA algorithm achieved better performance relative to the best-known upper bounds on the makespan compared with five state-of-the-art algorithms in the literature. Ultimately, 109 out of 120 problem instances were further improved on makespan criterion.
1. Introduction
The flow shop scheduling problem (FSSP) was first proposed by Johnson in 1954 [1]. Due to its extensive production applications in industries such as food processing, steel manufacturing, plastics production, and chemical manufacturing, the problem has received much attention since it was introduced. Researchers from all over the world have conducted in-depth research on this issue, and in the literature [2,3], they have developed branch-and-bound algorithms to solve the flow shop scheduling problem. However, these exact solution algorithms are only suitable for small-sized scheduling problems, as the calculation time increases exponentially with the problem size. As FSSP has proved to be an NP-hard problem [4], exact algorithms have not been suitable for large-scale scheduling problems. After that, several heuristic algorithms were proposed. Among them, the Nawaz–Enscore–Ham (NEH) heuristic algorithm [5], proposed by Nawaz et al., was used to solve an FFSP with n workpieces and m machines. The comparison between NEH and 15 other algorithms showed that it can quickly obtain better solutions and is suitable for solving large-scale flow shop scheduling problems. However, the quality of the feasible solutions obtained by the NEH algorithm is not high [6]. After the NEH algorithm was proposed, many researchers combined NEH with other optimization algorithms to achieve better results. Marichelvam et al. [7] combined NEH with the cuckoo search algorithm to form an improved cuckoo search algorithm (ICS), which proved to be more effective at achieving optimal solutions than the other algorithms in the literature. Qi et al. [6] proposed an improved variable neighborhood search algorithm and proved that the NEH heuristic algorithm could generate better initial solutions. Burdett and Kozan [8] addressed the representation and construction of accurate train schedules by a hybrid job shop approach and proposed a constructive algorithm to construct a schedule using NEH insertion, backtracking, and dynamic route selection mechanisms. The experiment results showed the constructive algorithm required less CPU time and obtained better solutions.
Rathinam [9] used the decision tree (DT) algorithm to minimize the makespan of the FSSP. In addition, Govindan et al. [10] provided a hybrid algorithm (ADE) that combined a scatter search algorithm with decision tree which exceeded other existing hybrid algorithms. The main disadvantage is that the tree size of the ADE and DT algorithms increases with the number of jobs and machines in large-scale FSSPs. In [11], three kinds of hybrid discrete artificial bee colony (ABC) algorithm (hDABC1, hDABC2, and hDABC3), with the initial solution generated by MME-A and MME-B and new solutions generated by the adaptation strategy and distribution estimation, were proposed. Pan and Huang [12] developed a hybrid genetic algorithm (GA) based on two different local search strategies (insertion search and the insertion search repair and cut) and an orthogonal-array-based crossover. Gao et al. [13] proposed two Bertollisi heuristics [14], which were based on a job pair comparison approach, to generate a sequence of jobs and constructive heuristics combined with standard deviation heuristics. The algorithms integrated with local search strategies to improve the quality of the solution. The results showed the effectiveness of the proposed algorithm, especially for large-scale FSSPs. Nowicki and Smutnicki [15] proposed an approximation algorithm based on a tabu search technique with a specific neighborhood definition to solve a permutation flow shop problem. Sayoti et al. [16] proposed an adaptation of a new approach called the golden ball algorithm (GBA), which was inspired by concepts and strategies for soccer playing. The result showed GBA was able to find the optimal schedule rapidly for the small-scale flow shop schedule problem. In [17], a genetic algorithm integrated with a Hopfield network was proposed and proved to be an effective method to solve NP-hard problems. Although researchers have developed many algorithms to solve FSSPs, there still exist some shortcomings in these algorithms, such as local optimization and high computational cost, especially when solving large-scale problems. Table 1 summarizes some of the algorithms proposed for FSSPs in the literature. Most of these studies demonstrate that combinational heuristic and metaheuristic approaches which include advantages of more than one algorithm are very useful for solving flow shop problems. For instance, Tseng et al. [18] studied a hybrid genetic algorithm for a no-wait flow shop problem. Ding et al. [19] presented an improved iterated greedy algorithm with a tabu-based reconstruction strategy. An iterated greedy algorithm in [20], a high-performing memetic algorithm in [21], and a discrete self-organizing migrating algorithm in [22] have been used for flow shop problems with the minimum makespan criterion and obtained better results. Eddaly et.al [23] proposed a hybrid combinatorial particle swarm optimization (HCPSO) algorithm as a resolution technique for solving this problem. Burdett and Kozans [24] proposed a new multiparent operator which could greatly improve the performance of a GA search.

Table 1.
Survey of algorithms for solving the flow shop scheduling problem (FSSP).
The GA and the simulated annealing (SA) algorithm are well-known metaheuristics that have been successfully used in flow shop problems. The genetic algorithm has the advantages of strong global optimization ability, fast speed, strong versatility, and easy implementation. However, it has the drawback of poor local search ability, which decreases search efficiency, especially in the late period of optimization. On the other hand, the simulated annealing algorithm has strong local search capabilities to make up the shortcomings of the genetic algorithm. GA + SA has been used to solve job shop [25], open shop [26], and flexible flow shop problems [27]. However, to the best of our knowledge, there are no reports on its application in flow shop scheduling, especially with improved crossover and mutation operators and adaptive simulated annealing.
Therefore, we propose a hybrid genetic simulated annealing (HGSA) algorithm to solve flow shop scheduling problems. The main contributions of this paper include the following:
- (1)
- We propose the novel HGSA algorithm to solve FSSPs. It is characterized by an operational coding in GA and a hormone regulation mechanism in the simulated annealing part of the algorithm. The MME [28] algorithm, combined with the NEH [5] and MinMax (MM) [29] heuristic algorithms, is used for initialization of the population. We use location-based intersection and two-point intersection for crossover operations with either one of these two being randomly selected. In the mutation process, twors mutation or inversion mutation [30] is randomly employed to mutate the population. After the crossover and mutation operation is completed, the best individuals are retained, and the simulated annealing operation is performed on these solutions.
- (2)
- Using the widely adopted Taillard benchmark FSSPs, we conducted extensive experiments and showed that our HGSA algorithm achieved better results than the baseline algorithms to which it was compared in our study. We showed that our HGSA algorithm’s high performance for FSSPs is based on its hybrid search strategy, twors/inversion mutation, location-based/two-point crossovers, and their combination with the MME heuristic algorithm for population initialization.
2. Flow Shop Scheduling Problem Description
The flow shop scheduling problem can be described as follows: There are n jobs with the same process route to be processed, which need to be processed continuously on m machines. The layout of the flow shop is shown in Figure 1. The machining process satisfies the following assumptions: (1) All jobs and machines are available at time zero. (2) There is no prior priority among jobs. (3) Each job has m processing steps. (4) Every process must be processed on different machines and the process sequence cannot be changed. (5) Each machine can only process only one job at a time, and each workpiece can only be machined by one machine at a time. (6) The machining process cannot be interrupted during the processing. (7) All jobs must obey the first-in/first-out rule during processing. Note that the symbols used in this paper and their meanings are shown in Table 2.
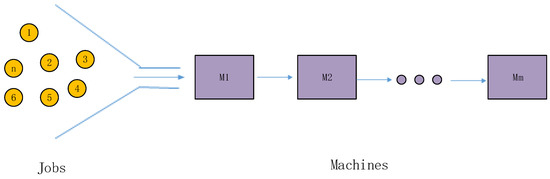
Figure 1.
Layout of the flow shop processing environment.

Table 2.
The meaning of the parameters used in this paper.
The mathematical model of the FSSP makespan can be expressed as [4]
S.t.
Formula (2) is a constraint which indicates that different processes of the same job cannot be proceeded at the same time. Formula (3) is a machine constraint which indicates that one machine can only process one job at a time. Formula (4) is time constraint which indicates that the next process of a job cannot start before the current process is completed. Formula (5) indicates that if the subsequent machine j + 1 is in the machining state, the job will delay at machine j until machine j + 1 is idle. Formula (6) shows that for any job i, the completion time is determined by the starting time and the processing time on machine j. Therefore, Cmax(π) and Cij can be calculated from Formulas (7) to (8):
3. Hybrid Genetic Simulated Annealing Algorithm
3.1. Overview of the HGSA Algorithm
There are many algorithms which have been used to solve flow shop problems, such as the GA, particle swam optimization (PSO), the SA algorithm, the harmony search (HS) algorithm, ant colony optimization (ACO), the ABC, etc. Among these algorithms, the genetic algorithm has the advantages of strong global optimization ability, fast speed, strong versatility, and easy implementation. However, it has the drawback of poor local search ability, which decreases search efficiency, especially in the late period of optimization. Fortunately, the simulated annealing algorithm has strong local search capabilities to make up the shortcomings of the genetic algorithm. Hence, in this paper, the advantages of the two algorithms are combined. GA is employed to get an optimal or near-optimal solution among the solution space, and then SA is utilized to seek a better one based on the solution. In addition, in order to improve the search efficiency of SA, an annealing rate method based on the hormone regulation mechanism is used in this paper. The flowchart of the algorithm is shown in Figure 2. The simple pseudocode of HGSA is as follows:
| HGSA {Hybrid Genetic Simulated Annealing Algorithm} Initialize population by MME while (not stop condition) do Step 1: Select the population Step 2: Crossover operation If(random==0) location-based Crossover else two-point Crossover Step 3: Mutation operation If(random==0) Insertion Mutation else Reverse order Mutation Step 4: Simulated annealing opearation end_while |
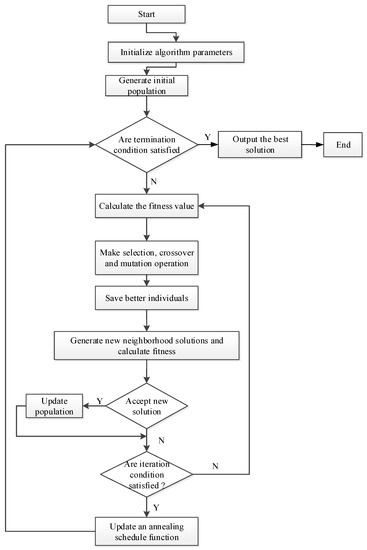
Figure 2.
Algorithm flowchart of the hybrid genetic simulated annealing (HGSA) algorithm.
3.2. Encoding Representation
In this paper, the job ordering is used as the solution chromosome. The number of genes in the chromosome is equal to the quantity of jobs to be processed, which is n. If there are 10 jobs to be processed, p1 = [3, 5, 8, 7, 9, 6, 4, 2, 1, 10] can be taken as one of the chromosomes in the population. The number in the chromosome indicates the ID of the jobs being machined, and the position in the chromosome indicates the processing order of the jobs.
3.3. Initial Population
The initial population quality has a significant impact on the performance of an evolutionary algorithm. Good initial solutions can significantly improve the convergence rate and solution quality of the algorithm [51]. In this paper, the MME algorithm, combined with the NEH [5] and MM [29] heuristic algorithms, is used to generate the initial population. Ronconi [28] proved that the MME algorithm has better performance than the NEH algorithm for solving FSSPs. In [52], it was also proved that the initial solutions obtained by the MME algorithm explored the specific characteristics of the blocking condition, which made it outperform the NEH for minimizing the makespan of the Blocking Flow-Shop Scheduling (BFSS) problem.
The basic flow of the MME algorithm is as follows:
(1) Calculate the total machining time required for all the steps of each jobs. Rank the job with the smallest total processing time in the first position of the job sorting. Rank the job with the second smallest processing time in the last position of the job sorting and set i = 2.
(2) The rest of the n-2 jobs are arranged in ascending order according to the label function value of Formula (9). The job that takes ai will be sorted on i-th position of the job sequence, fixes the order, and records as π0:
In Formula (9), r is a random number between [0, 1], means the modulus of the difference between the two consecutive jobs on the adjacent machines, and indicates the job with a smaller total machining time is prioritized.
(3) i = i + 1. If i < n, go to step 2, otherwise go to step 4.
(4) Exchange the first two jobs in π0 and add them to the machining sequence π1. Calculate the makespan before and after the order exchanging. Then, reserve the sequence with the least makespan and fix the order of the two jobs. Denote the sequence as π1 and set k = 2.
(5) Randomly select a job in the unprocessed sequence to insert to possible positions of π1. Calculate the makespan after the job is added, then select the position that can minimize the completion time.
(6) Delete a job from the unprocessed sequence after its position is determined. Perform step 5 until all job positions are determined to form a new chromosome. Repeat the above steps 1–6 for p times to generate an initial population of p size individuals.
3.4. Crossover Operation
In this paper, we randomly select location-based crossover and two-point crossover, both of which are often used in genetic algorithms. The process is to generate an integer out of 0 and 1 randomly. If it is 0, select the location-based crossover operation; otherwise, select the two-point crossover operation. In the following description, P1 and P2 represent two parent individuals, and C1 and C2 represent two child individuals. The specific steps are shown as follows.
3.4.1. Location-Based Crossover
(1) Exchange the genes at several randomly selected positions of P1 and P2. Keep the genes in other locations unchanged.
(2) Perform conflict detection to delete the same gene as the exchange position in the original parent gene.
(3) Fill the gene vacancy with unused genes sequentially.
As shown in Figure 3a, there are 10 genes in this chromosome. Select positions 1, 3, 5, and 8 for exchange. The genes at the exchange position of P1 and P2 are directly exchanged to the same position of C2 and C1. Then, delete the same genes as the swap position in C1 and C2 and fill them with unused genes.
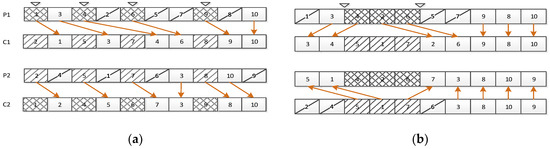
Figure 3.
Procedure of location-based crossover operation (a) and two-point crossover operation (b).
3.4.2. Two-Point Crossover
(1) Two intersections are randomly generated, the gene fragments between the two points are copied from P1 and P2 to the corresponding positions of C1 and C2, and their positions and order are kept unchanged.
(2) The genes contained in the intersections between P1 and P2 are removed, the jobs not included in the intersections are copied to C2 and C1, and their order is maintained.
As shown in Figure 3b, the chromosome contains 10 genes (jobs). Select positions 3 and 6 for crossover. Then, the genes in P1 and P2 located between position 3 and 6 are directly copied to C1 and C2. The repetitive gene is removed, the remaining genes in P2 (white gene fragments in the figure) are sequentially filled into C1 to produce new individuals, and C2 is produced in the same manner.
3.5. Mutation Operation
In the genetic algorithm, the role of the mutation operator is to perturb the original chromosome to improve the local search ability and capability to jump out of local optima. In this paper, two commonly used mutation operations twors mutation and inversion mutation are randomly selected [53].
3.5.1. Twors Mutation
(1) Two positions in the chromosome are randomly selected.
(2) Insert the top-ranked gene into the back of another gene.
As shown in Figure 4a, the chromosome contains 10 genes (jobs). Positions 3 and 8 are selected. The gene 3 is inserted after the gene 8. Then, the other genes are sequentially moved back to obtain a new chromosome.

Figure 4.
Procedure of insert mutation operation (a) and reverse mutation operation (b).
3.5.2. Inversion Mutation
(1) Two positions in the gene are randomly selected.
(2) The genes between the two positions were reversed, and the other gene positions are unchanged. The specific operation mode is shown in Figure 4b.
3.6. Simulated Annealing Operation
In the process of the HGSA algorithm, better individuals obtained from GA are sent to SA for improvement. The SA operation can help solutions to avoid falling into local optima. SA starts from a higher temperature (i.e., the initial temperature) and randomly finds the global optimal solution of the objective function in the neighborhood along with the continuous decrease at a certain annealing rate of temperature. At last, the algorithm ends and outputs the optimal solution when the termination condition of the algorithm is reached. The search efficiency of the SA is affected by some parameters such as the initial temperature, the neighborhood structure, the annealing rate, and the termination condition. These factors play a significant role in the performance of the HGSA and should be carefully implemented as follows.
3.6.1. Neighborhood Structure
The neighborhood structure will directly affect the local search efficiency. This paper adopts the more common neighborhood structure in the production scheduling problem, namely, exchange and insertion [54].
(1) Two points exchange. Exchange the genes at two positions which are randomly generated. For example, the coding of a chromosome is “154837629. The randomly generated gene positions are 3 and 6. Then, the new chromosome produced by exchanging genes at these two positions is “15783429”.
(2) Insertion. Select two gene positions randomly. Then, the gene with the larger position number is inserted into the previous position of the gene with the smaller position number, and the smaller number position gene and the subsequent gene sequence is postponed. For example, the code of one chromosome is “15783429”, the two randomly selected position numbers are 2 and 4, and the new chromosome obtained after the insertion operation is “18573429”.
3.6.2. Initial Temperature
The initial temperature T0 of the SA should be properly set because a too high initial temperature causes waste of calculation time, and a too small initial temperature causes the efficiency of the global search to decrease. This article uses the following formula to set the initial temperature:
In the formula, Umax is the maximum value of all feasible solutions generated by the MME algorithm, and Umin is the minimum value of all feasible solutions generated by the MME algorithm.
3.6.3. Annealing Rate
The annealing rate has a significant effect on the efficiency of the simulated annealing algorithm [55]. In order to improve the search efficiency of the algorithm, a new annealing rate method based on the hormone regulation mechanism [27] is used in this paper. The annealing rate can be obtained by Formulas (10)–(12):
where α is a small constant, k represents the number of iterations, n represents the Hill coefficient (n ≥ 1), ΔT is the difference between the current temperature (k + 1) and the previous temperature (k), and ΔT < 0. The effect of the annealing rate function in the case of k = 20, n = 1; 1.2; 1.5; 2.5 is shown in Figure 5. In this paper, the value of n is chosen to be 1.5.
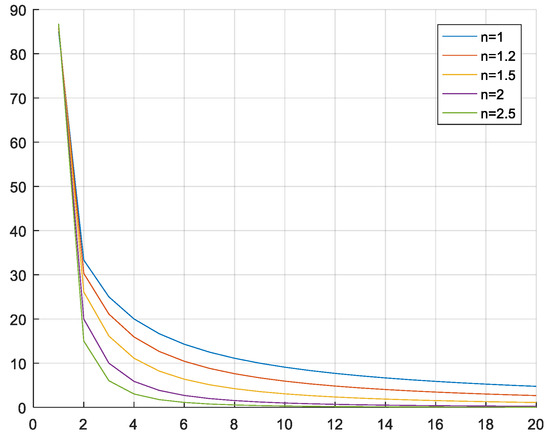
Figure 5.
Annealing rate function.
3.6.4. The Terminating Condition
In SA, the termination criterion of the annealing procedure consists of the Metropolis sampling stability criterion of the inner loop and the external loop termination criterion. That is, when the new state or the current state’s neighborhood solution space has been searched, the inner loop is jumped out, and the temperature is returned to the outside cycle. The outer loop termination criterion is also the algorithm termination criterion. In the algorithm design, the termination temperature is adopted. When the current temperature reaches the termination temperature requirement, the outer loop is terminated and the algorithm ends.
3.7. Benchmark Selected
In this work, 120 problems that were contributed to the OR-Library by E. TAILLARD [56] were used. The 120 problems called Ta001, Ta002… Ta120, respectively, were by E. TAILLARD (1993) and are often used to test the algorithm performance in flow shop problems. All these benchmarks can be downloaded from: http://mistic.heig-vd.ch/taillard/problemes.dir/ordonnancement.dir/ordonnancement.html.
3.8. Computational Complexity
In this section, we derive the algorithmic complexity of the proposed scheme. The meanings of the symbols used are as follows: n is the number of jobs, m is the number of machines, T0 is the initial temperature, Tf is the termination temperature, P is the population size, and G is the number of iterations. At first, the complexity of MME is O (n2m). In GA, the complexity of selection and mutation are O(n × logn) and O(nm), respectively. The computational complexity of SA is O(Pn2m2logTf/T0). The total computational complexity of HGSA is O (n2m) + G × O(n × logn) + G × O(n2m) + G × O(nm) + G × O(Pn2m2logTf/T0). It can be seen that the complexity of the proposed algorithm is related to population size, iterations, problem size, and parameters.
4. Experimental Results and Analysis
The algorithm of this paper was coded in Matlab language. The program running environment was Intel Corei5, 2.19 GHz CPU, and 8 GB RAM. We selected 120 classic examples proposed by Taillard as test data, and the data size of the Taillard benchmark was from 20jobs-5machines to 500jobs-20machines. The experimental parameters of the algorithm were set as follows [57,58]: the population size was 100, the crossover probability was 0.9, and the mutation probability was 0.1. In order to compare the performance of the HGSA with different Hill coefficients (n = 1; 1.2; 1.5; 2.5), the average relative percentage deviation (ARPD) values of different Hill coefficients with other parameters fixed are shown in Table 3. In these experiments, we chose the 200 × 20 and 500 × 20 instance in Talliard as the benchmarks. The results show that algorithm obtained the minimum ARPD when the Hill coefficient was equal to 1.5. So, the value of the Hill coefficient was chosen to be 1.5.

Table 3.
The average relative percentage deviation (ARPD) value of different Hill coefficients on the performance of HGSA.
In order to analyze the performance of the proposed algorithm, it was compared with the hybrid genetic algorithm (HGA) in [18], the improved iterated greedy algorithm (IIGA) in [19], the iterated greedy algorithm with a referenced insertion scheme (IG-RIS) in [20], the memetic algorithm (MA) in [21], and the discrete self-organizing migrating algorithm (DSOMA) in [22]. Table 4 shows the makespan results of the proposed algorithm and the other four algorithms tested in different sizes of Taillard benchmark. Each data scale has 10 sets of data, and the boldface figure in Table 4 represents the optimal solution obtained by the algorithms. It can be seen from the table that the algorithm proposed in this paper improved the results of 109 out of 120 examples, which indicates that the best results obtained by HGSA are better than the other four metaheuristics, reflecting the better search quality of HGSA. Compared with the MA, IG-RIS, and HIGA algorithms, the results of HGSA were greatly improved. Only in 11 cases with a small problem size were the results of HGSA slightly inferior to DSOMA. As the scale of the study increased, HGSA reflected a more obvious advantage. At the same time, the comparison with the HIGA and HGA algorithms showed that the MME initial population generation method and SA local search method based on hormone regulation mechanism could improve the optimization effect of the algorithm more effectively, especially for large-scale examples. Figure 6 is the Gantt chart of the ta001. The chart shows that the makespan obtained by proposed algorithm was 1324. The optimal schedule we got was [3, 17, 15, 16, 8, 6, 9, 18, 4, 2, 14, 5, 7, 11, 12, 10, 1, 19, 13, 20]. In order to further compare the advantages and disadvantages of the proposed algorithm and the other algorithms, three parameters of average error (AE), improvement percentage (IP), and ARPD were introduced to compare the effects of each algorithm.

Table 4.
Makespan comparison of different algorithms on Taillard benchmarks.
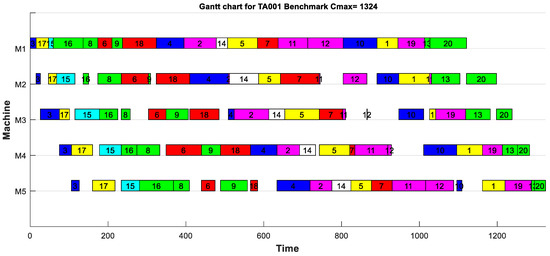
Figure 6.
Gantt chart of the Ta001.
(1) AE represents the average error between the makespan of the algorithms and the lowest known upper bound values. The formula is
where zopt is the known upper bound value for each instance, zi is the optimal makespan of each algorithm, and K is the number of instances. The average error comparison results of several algorithms are shown in Figure 7. As can be seen from the figure, the lowest AE value of HGSA in this paper was 5.58, which was lower than the lowest value of 20.516 for the DSOMA algorithm.
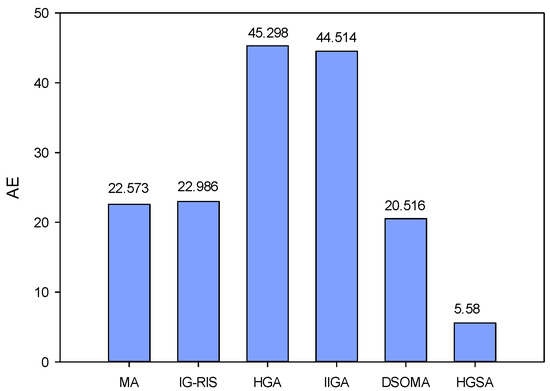
Figure 7.
Comparison of average errors (AEs) on Taillard benchmarks.
(2) IP represents the improvement percentage on makespan of the HGSA algorithm compared with the other algorithms. The formula is
where CHGSA is the minimum makespan obtained by the HGSA algorithm, and CX is the minimum makespan obtained by the other algorithms. Figure 8 shows the percentage improvement on makespan of the HGSA algorithm compared to the MA, IG-RIS, IIGA, and DSOMA algorithms. It can be seen from the figure that the superiority of the HGSA algorithm is not obvious compared with other algorithms when the scale of the benchmark is small. In the 20 × 20 instances, the HGSA algorithm performed slightly weaker than the DSOMA algorithm. However, with the increase of instances scale, that is, the increasing of workpieces and machine tools number, the advantages of HGSA became increasingly obvious. In the 500 × 20 instances, HGSA had an improvement of 31.7%, 30.5%, 80.6%, 36.1%, and 71.9% compared to MA, G-RIS, HGA, DSOMA, and IIGA, respectively. As the scale of instances increased, the improvement effect was more obvious, indicating that the algorithm performed better when the schedule was larger.
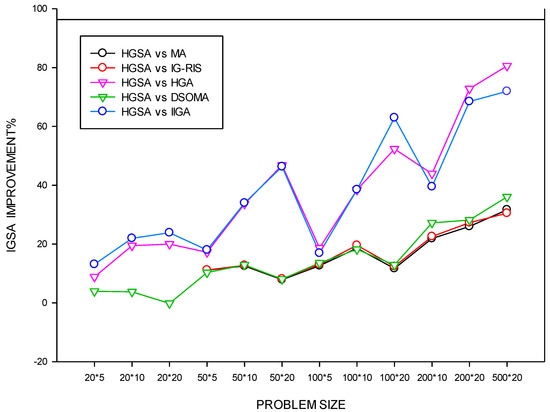
Figure 8.
Improvement percentage (IP) of HGSA with other algorithms for makespan criterion.
(3) ARPD represents the average relative percentage deviation between the result obtained by the algorithm and the optimal value. The formula is
where K is the number of the same scale instances, Cxi is the makespan of the algorithm x on the ith instance of the same size, and Copti is the optimal value on the ith instance of the same size. Figure 9 shows that the ARPD of HGSA was similar to that of the DSOMA algorithm in the 20 × 20 instances, which was approximately 6%. In the other instances, the ARPD of HGSA, which were all less than 9%, was significantly lower than that of the existing algorithms. This demonstrates that the results obtained by our HGSA algorithm can be closer to the theoretical optimal values (upper bound) of these benchmark instances. Furthermore, the results show that HGSA performs well when the population size of jobs and the number of machines increases. Furthermore, the results show that HGSA performs well when the population size of jobs and the number of machines increases.
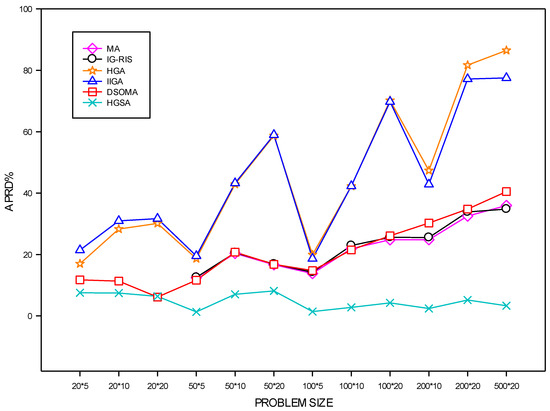
Figure 9.
Comparison of ARPD on Taillard benchmarks.
5. Conclusions and Future Work
In this paper, a hybrid genetic simulated annealing algorithm based on the hormone regulation mechanism was designed for the flow shop scheduling problem. In order to ensure the quality of the initial population, the MME algorithm, combined with the NEH and MM algorithms, was used to generate the initial population with a certain quality and diversity. Then, SA based on the hormone regulation mechanism was combined with GA to balance the efficiency and global search ability of the algorithm. Furthermore, randomly selected cross-mutation methods were introduced in GA to obtain promising results. Through the test on Talliard benchmarks, the results of HGSA were compared with MA, IG-RIS, HGA, IIGA, and DSOMA in terms of makespan, AE, IP, and ARPD. The results of our HGSA algorithm were closer to the upper bound of the Talliard benchmarks, which verified the effectiveness of the HGSA. In future research, we plan to add an energy consumption objective into the flow shop problem. We will also adapt our algorithm and apply it to the flow shop scheduling problem with job random arrivals together with an energy saving model. In addition, the proposed algorithm can also be extended to solve hybrid flow shop scheduling and job shop scheduling problems.
Author Contributions
H.W., S.L., and J.H. conceived of and designed the study. H.W., H.J., and J.H. worked on the algorithm design. H.W. and J.H. wrote the manuscript, made the figures, and reformatted the manuscript. All authors have read and approved the final manuscript.
Funding
This work is supported by the National Natural Science Foundation of China under Grant No. 51475097, 91746116, and 51741101; and Science and Technology Foundation of Guizhou Province under Grant No. [2015]4011, [2016]5013, [2015]02, and [2017]239.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson, S.M. Optimal two- and three-stage production schedules with setup times included. Naval Res. Logist. Q. 2010, 1, 61–68. [Google Scholar] [CrossRef]
- Hong, Z.Y.; Pang, H.L. Study on a constructive heuristic algorithm based on compromise policy for Blocking flow-shop scheduling. Syst. Eng. Theory Pract. 2008, 28, 114–118. [Google Scholar]
- Ignall, E.; Schrage, L. Application of the Branch and Bound Technique to Some Flow-Shop Scheduling Problems. Oper. Res. 1965, 13, 400–412. [Google Scholar] [CrossRef]
- Bansal, S.P. Minimizing the Sum of Completion Times of n Jobs over m Machines in a Flowshop A Branch and Bound Approach. AIIE Trans. 1977, 9, 306–311. [Google Scholar] [CrossRef]
- Nawaz, M.E.E.E., Jr.; Ham, I. A heuristic algorithm for the m -machine, n -job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Cui, Q.; Xiuli, W.U.; Jianjun, Y.U. Improved genetic algorithm variable neighborhood search for solving hybrid flow shop scheduling problem. Comput. Integr. Manuf. Syst. 2017, 23, 1917–1927. [Google Scholar]
- Marichelvam, M.K.; Prabaharan, T.; Yang, X.S. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan. Appl. Soft Comput. 2014, 19, 93–101. [Google Scholar] [CrossRef]
- Burdett, R.L.; Kozan, E. A sequencing approach for creating new train timetables. OR Spectr. 2010, 32, 163–193. [Google Scholar] [CrossRef]
- Rathinam, B. Rule based heuristic approach for minimizing total flow time in permutation flow shop scheduling. Teh. Vjesn. 2015, 22, 25–32. [Google Scholar] [CrossRef]
- Govindan, K.; Balasundaram, R.; Baskar, N.; Asokan, P. A Hybrid Approach for Minimizing Makespan In Permutation Flowshop Scheduling. J. Syst. Sci. Syst. Eng. 2017, 26, 50–76. [Google Scholar] [CrossRef]
- Han, Y.Y.; Gong, D.; Sun, X. A discrete artificial bee colony algorithm incorporating differential evolution for the flow-shop scheduling problem with blocking. Eng. Optim. 2015, 47, 927–946. [Google Scholar] [CrossRef]
- Pan, C.H.; Huang, H.C. A hybrid genetic algorithm for no-wait job shop scheduling problems. Expert Syst. Appl. 2009, 36, 5800–5806. [Google Scholar] [CrossRef]
- Gao, K.; Pan, Q.; Suganthan, P.N.; Li, J. Effective heuristics for the no-wait flow shop scheduling problem with;total flow time minimization. Int. J. Adv. Manuf. Technol. 2013, 66, 1563–1572. [Google Scholar] [CrossRef]
- Bertolissi, E. Heuristic algorithm for scheduling in the no-wait flow-shop. J. Mater. Process. Technol. 2000, 107, 459–465. [Google Scholar] [CrossRef]
- Nowicki, E.; Smutnicki, C. A fast tabu search algorithm for the permutation flow-shop problem. Eur. J. Oper. Res. 1996, 91, 160–175. [Google Scholar] [CrossRef]
- Sayoti, F.; Ri, M.E. Golden Ball Algorithm for solving Flow Shop Scheduling Problem. Ijimai 2016, 4, 15–18. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.B.M.; Mansor, M.A.B.; Sathasivam, S. Genetic Algorithm for Restricted Maximum k-Satisfiability in the Hopfield Network. Int. J. Interact. Multimedia Artif. Intell. 2016, 4, 52. [Google Scholar]
- Tseng, L.; Lin, Y. A hybrid genetic algorithm for no-wait flowshop scheduling problem. Int. J. Prod. Econ. 2010, 128, 144–152. [Google Scholar] [CrossRef]
- Ding, J.Y.; Song, S.; Gupta, J.N.; Zhang, R.; Chiong, R.; Wu, C. An improved iterated greedy algorithm with a Tabu-based reconstruction strategy for the no-wait flowshop scheduling problem. Appl. Soft Comput. 2015, 30, 604–613. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Kizilay, D.; Pan, Q.K.; Suganthan, P.N. Iterated greedy algorithms for the blocking flowshop scheduling problem with makespan criterion. Comput. Oper. Res. 2017, 77, 111–126. [Google Scholar] [CrossRef]
- Pan, Q.K.; Wang, L.; Sang, H.Y.; Li, J.Q.; Liu, M. A High Performing Memetic Algorithm for the Flowshop Scheduling Problem with Blocking. IEEE Trans. Autom. Sci. Eng. 2013, 10, 741–756. [Google Scholar]
- Davendra, D.; Bialicdavendra, M. Scheduling flow shops with blocking using a discrete self-organising migrating algorithm. Int. J. Prod. Res. 2013, 51, 2200–2218. [Google Scholar] [CrossRef]
- Eddaly, M.; Jarboui, B.; Siarry, P. Combinatorial particle swarm optimization for solving blocking flowshop scheduling problem. J. Comput. Des. Eng. 2016, 3, 295–311. [Google Scholar] [CrossRef]
- Burdett, R.L.; Kozan, E. Evolutionary algorithms for flowshop sequencing with non-unique jobs. Int. Trans. Oper. Res. 2000, 7, 401–418. [Google Scholar] [CrossRef]
- Yin, H.L. Genetic Algorithm Nested with Simulated Annealing for Big Job Shop Scheduling Problems. In Proceedings of the 2013 9th International Conference on Computational Intelligence and Security (CIS), Emei Moutain, China, 14–15 December 2013. [Google Scholar]
- Andresen, M.; BräSel, H.; MöRig, M.; Tusch, J.; Werner, F.; Willenius, P. Simulated annealing and genetic algorithms for minimizing mean flow time in an open shop. Math. Comput. Model. 2008, 48, 1279–1293. [Google Scholar] [CrossRef]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A.; Li, W.D. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm. Robot. Comput.-Integr. Manuf. 2013, 29, 418–429. [Google Scholar] [CrossRef]
- Ronconi, D.P. A note on constructive heuristics for the flowshop problem with blocking. Int. J. Prod. Econ. 2004, 87, 39–48. [Google Scholar] [CrossRef]
- Merz, P.; Freisleben, B. Memetic Algorithms for the Traveling Salesman Problem. Complex Syst. 1997, 13, 297–345. [Google Scholar]
- Abdoun, O.; Abouchabaka, J.; Tajani, C. Analyzing the Performance of Mutation Operators to Solve the Travelling Salesman Problem. Int. J. Emerg. Sci. 2012, 2, 61–77. [Google Scholar]
- Koulamas, C.; Kyparisis, G.J. The three-stage assembly flowshop scheduling problem. Comput. Oper. Res. 2001, 28, 689–704. [Google Scholar] [CrossRef]
- Chang, P.; Hsieh, J.; Lin, S. The development of gradual-priority weighting approach for the multi-objective flowshop scheduling problem. Int. J. Prod. Econ. 2002, 79, 171–183. [Google Scholar] [CrossRef]
- Fink, A.; Vos, S. Solving the continuous flow-shop scheduling problem by metaheuristics. Eur. J. Oper. Res. 2003, 151, 400–414. [Google Scholar] [CrossRef]
- Wang, J.; Xia, Z.Q. Flow-shop scheduling with a learning effect. J. Oper. Res. Soc. 2005, 56, 1325–1330. [Google Scholar] [CrossRef]
- Agarwal, A.; Colak, S.; Eryarsoy, E. Improvement heuristic for the flow-shop scheduling problem: An adaptive-learning approach. Eur. J. Oper. Res. 2006, 169, 801–815. [Google Scholar] [CrossRef]
- Rajendran, C.; Ziegler, H. Ant-colony algorithms for permutation flowshop scheduling to minimize makespan/total flowtime of jobs. Eur. J. Oper. Res. 2007, 155, 426–438. [Google Scholar] [CrossRef]
- Yagmahan, B.; Yenisey, M.M. Ant colony optimization for multi-objective flow shop scheduling problem. Comput. Ind. Eng. 2008, 54, 411–420. [Google Scholar] [CrossRef]
- Zhang, G.; Shao, X.; Li, P.; Gao, L. An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem. Comput. Ind. Eng. 2009, 56, 1309–1318. [Google Scholar] [CrossRef]
- Sayadi, M.K.; Ramezanian, R.; Ghaffarinasab, N. A discrete firefly meta-heuristic with local search for makespan minimization in permutation flow shop scheduling problems. Int. J. Ind. Eng. Comput. 2010, 1, 1–10. [Google Scholar] [CrossRef]
- Pan, Q.K.; Tasgetiren, M.F.; Suganthan, P.N.; Chua, T.J. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem. China Mech. Eng. 2011, 181, 2455–2468. [Google Scholar] [CrossRef]
- Deng, G.; Gu, X. A hybrid discrete differential evolution algorithm for the no-idle permutation flow shop scheduling problem with makespan criterion. Comput. Oper. Res. 2012, 39, 2152–2160. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. A hybrid cuckoo search via Lévy flights for the permutation flow shop scheduling problem. Int. J. Prod. Res. 2013, 51, 4732–4754. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, C.; Shao, X.; Lin, W.; Zhu, H. An effective hybrid teaching–learning-based optimization algorithm for permutation flow shop scheduling problem. Adv. Eng. Softw. 2014, 77, 35–47. [Google Scholar] [CrossRef]
- Lin, Q.; Gao, L.; Li, X.; Zhang, C. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem minimizing makespan and energy consumption. Comput. Ind. Eng. 2015, 85, 437–446. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, S. An effective hybrid biogeography-based optimization algorithm for the distributed assembly permutation flow-shop scheduling problem. Comput. Ind. Eng. 2016, 97, 128–136. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L.; Wang, S.Y.; Zheng, X.L. A competitive memetic algorithm for the distributed two-stage assembly flow-shop scheduling problem. Int. J. Prod. Res. 2017, 54, 3561–3577. [Google Scholar] [CrossRef]
- Chen, P.; Wen, W.; Li, R.; Li, X. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem minimizing makespan and energy consumption. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017. [Google Scholar]
- Bewoor, L.; Prakash, V.C.; Sapkal, S. Evolutionary Hybrid Particle Swarm Optimization Algorithm for Solving NP-Hard No-Wait Flow Shop Scheduling Problems. Algorithms 2017, 10, 121. [Google Scholar] [CrossRef]
- Sun, Z.; Gu, X. Hybrid Algorithm Based on an Estimation of Distribution Algorithm and Cuckoo Search for the No Idle Permutation Flow Shop Scheduling Problem with the Total Tardiness Criterion Minimization. Sustainability 2017, 9, 953. [Google Scholar]
- Meng, T.; Pan, Q.K.; Li, J.Q.; Sang, H.Y. An improved migrating birds optimization for an integrated lot-streaming flow shop scheduling problem. Swarm Evol. Comput. 2018, 38, 64–78. [Google Scholar] [CrossRef]
- Yahyaoui, A.; Fnaiech, N.; Fnaiech, F. A Suitable Initialization Procedure for Speeding a Neural Network Job-Shop Scheduling. IEEE Trans. Ind. Electron. 2011, 58, 1052–1060. [Google Scholar] [CrossRef]
- Liu, S.Q.; Kozan, E. Scheduling a flow shop with combined buffer conditions. Int. J. Prod. Econ. 2009, 117, 371–380. [Google Scholar] [CrossRef]
- Tao, S.; Wang, S. An algorithm for weighted sub-graph matching based on gradient flows. Inf. Sci. 2016, 340–341, 104–121. [Google Scholar] [CrossRef]
- Ku, L. An Adaptive Variable Neighbourhood Search Algorithm for the Hybrid Flowshop Scheduling Problem. Syst. Eng. 2015, 11, 121–129. [Google Scholar]
- Dai, M.; Tang, D.; Zheng, K.; Cai, Q. An Improved Genetic-Simulated Annealing Algorithm Based on a Hormone Modulation Mechanism for a Flexible Flow-Shop Scheduling Problem. Adv. Mech. Eng. 2013, 5, 124903. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Giret, A.; Barber, F. A genetic algorithm for energy-efficiency in job-shop scheduling. Int. J. Adv. Manuf. Technol. 2016, 85, 1303–1314. [Google Scholar] [CrossRef]
- Rajkumar, R.; Shahabudeen, P. An improved genetic algorithm for the flowshop scheduling problem. Int. J. Prod. Res. 2009, 47, 233–249. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).