RETRACTED: Laplacian Eigenmaps Feature Conversion and Particle Swarm Optimization-Based Deep Neural Network for Machine Condition Monitoring
Abstract
1. Introduction
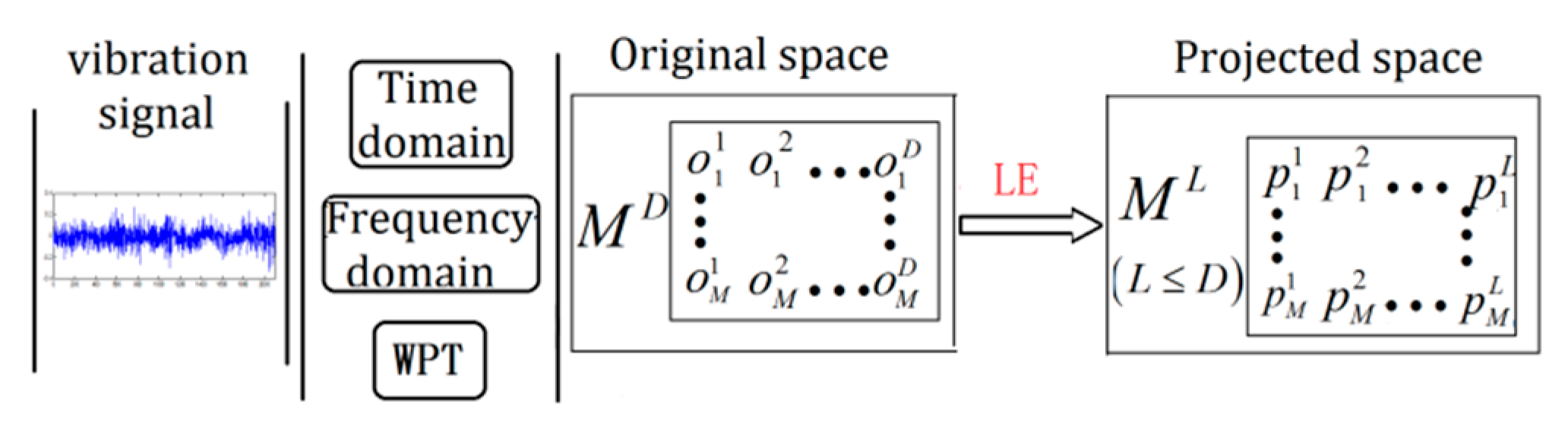
2. The Proposed Method
2.1. Original Features Extraction
2.1.1. Time and Frequency Analysis
2.1.2 WPT
2.2. LE Feature Space Conversion
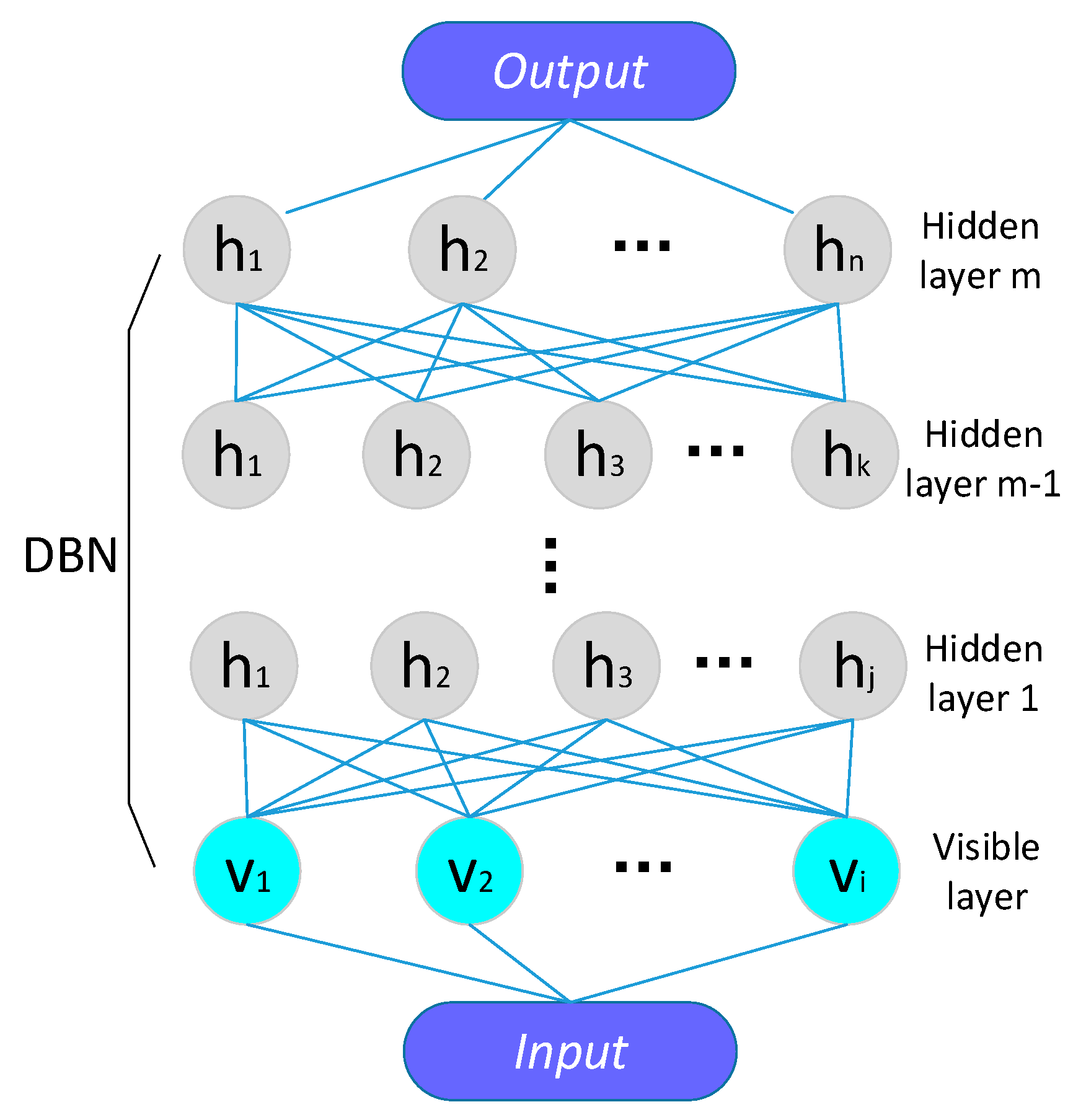
2.3. DNN Training and Optimization
2.3.1. Construction of Deep Neural Network
2.3.2. DNN Optimization Based on PSO
2.4. Condition Assessment
3. Experiments and Analysis
3.1. Test Rig and Data
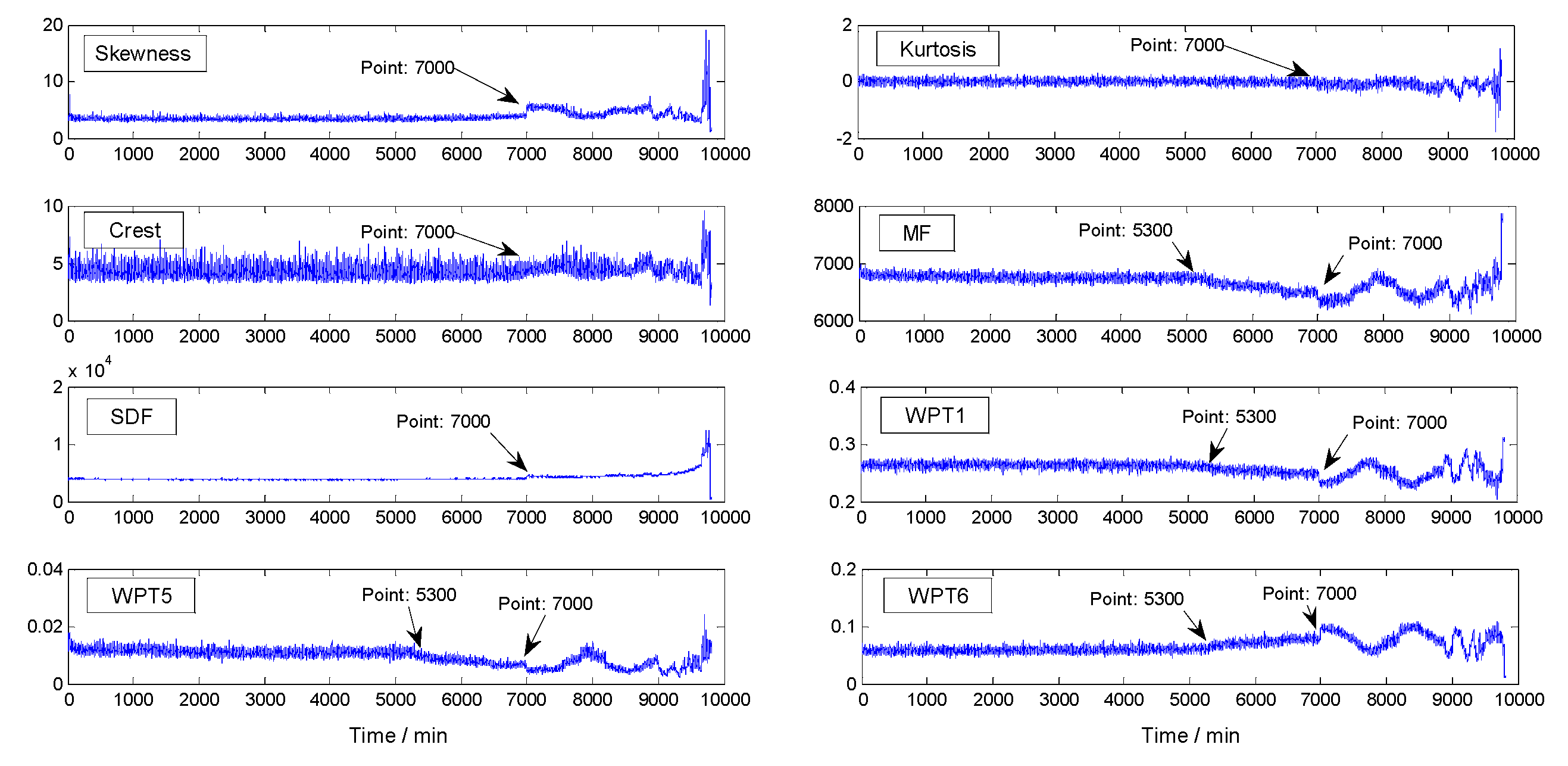
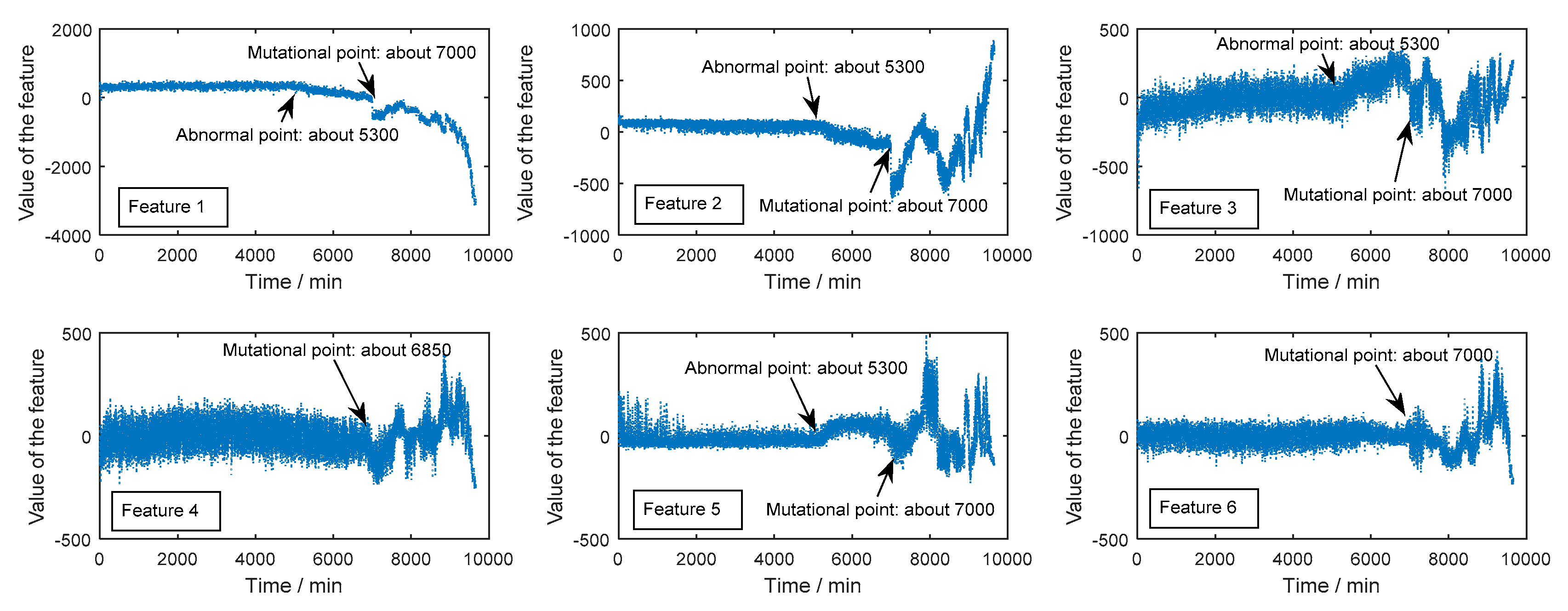
3.2. Feature Space Conversion
3.3. DNN Condition Assessment
3.3.1. DNN Construction and Training
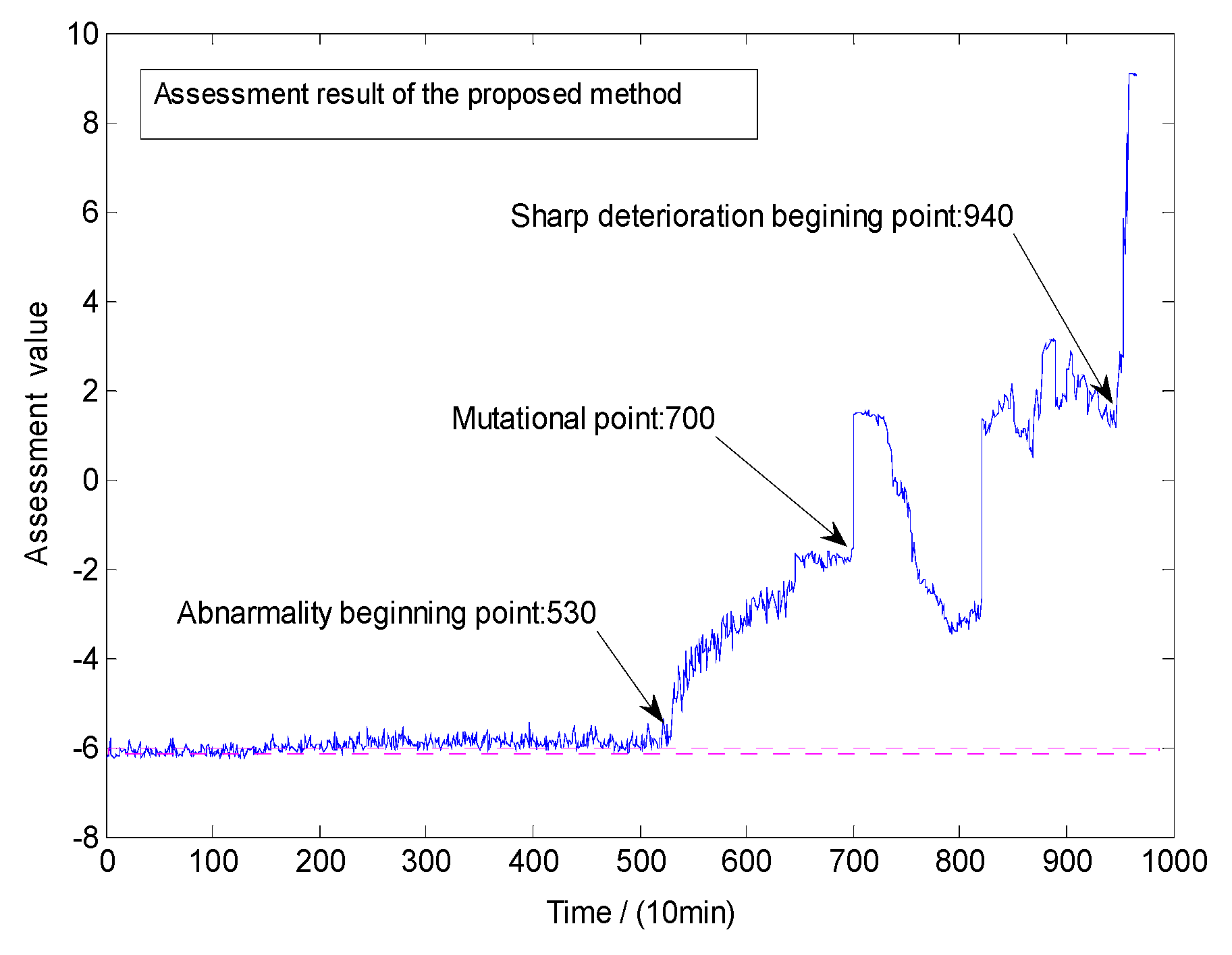
3.3.2. Assessment and Results
3.4. Comparison Experiments and Analysis
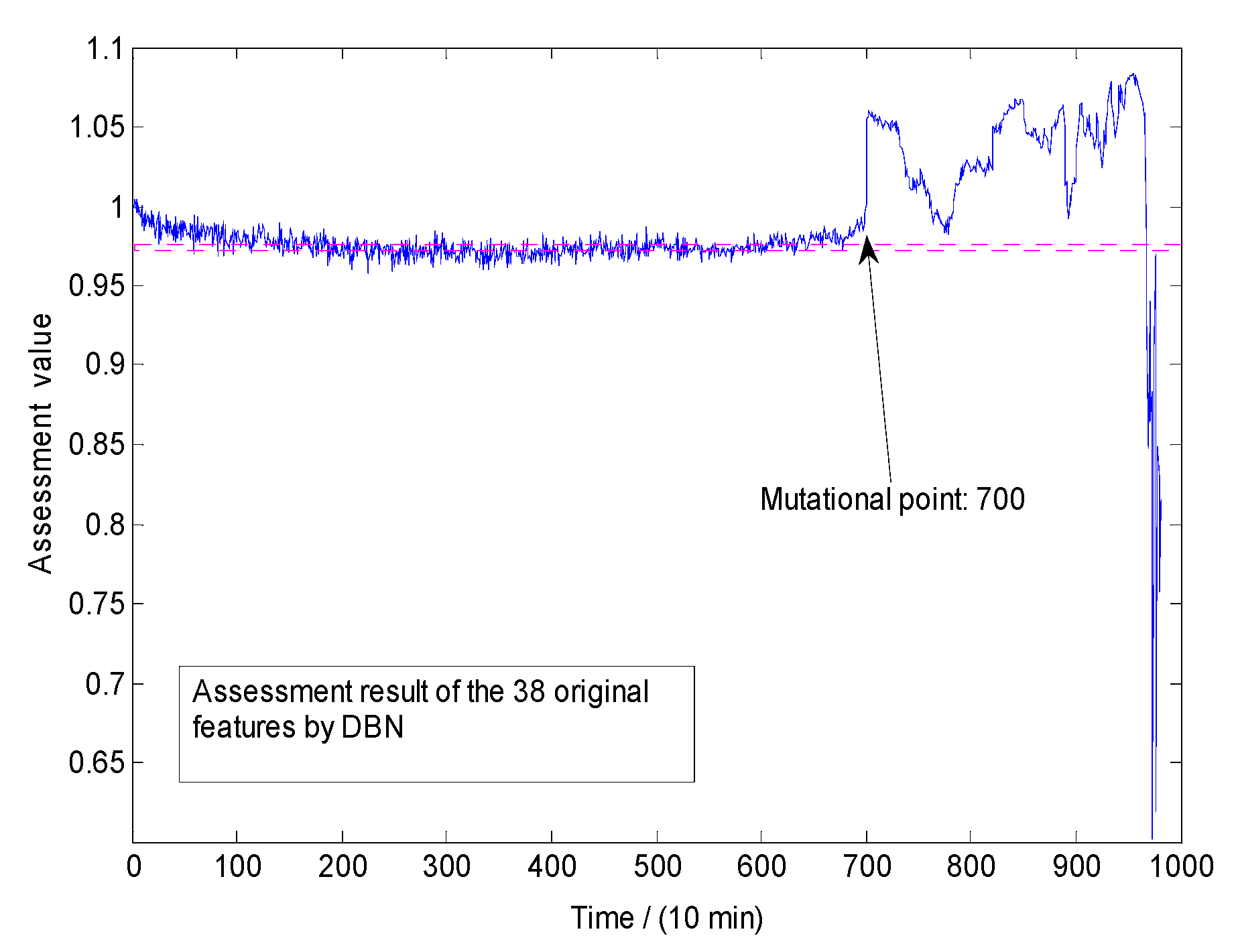
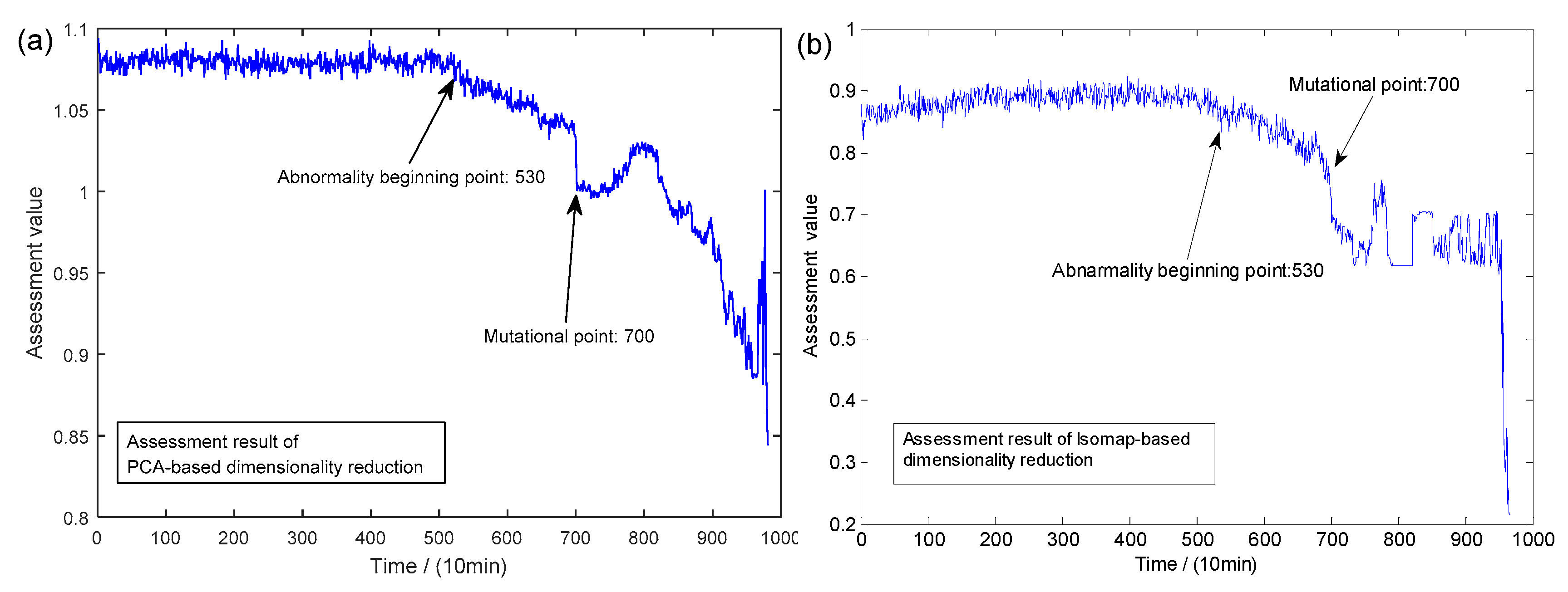
3.4.1. Comparisons of Space Conversion Methods
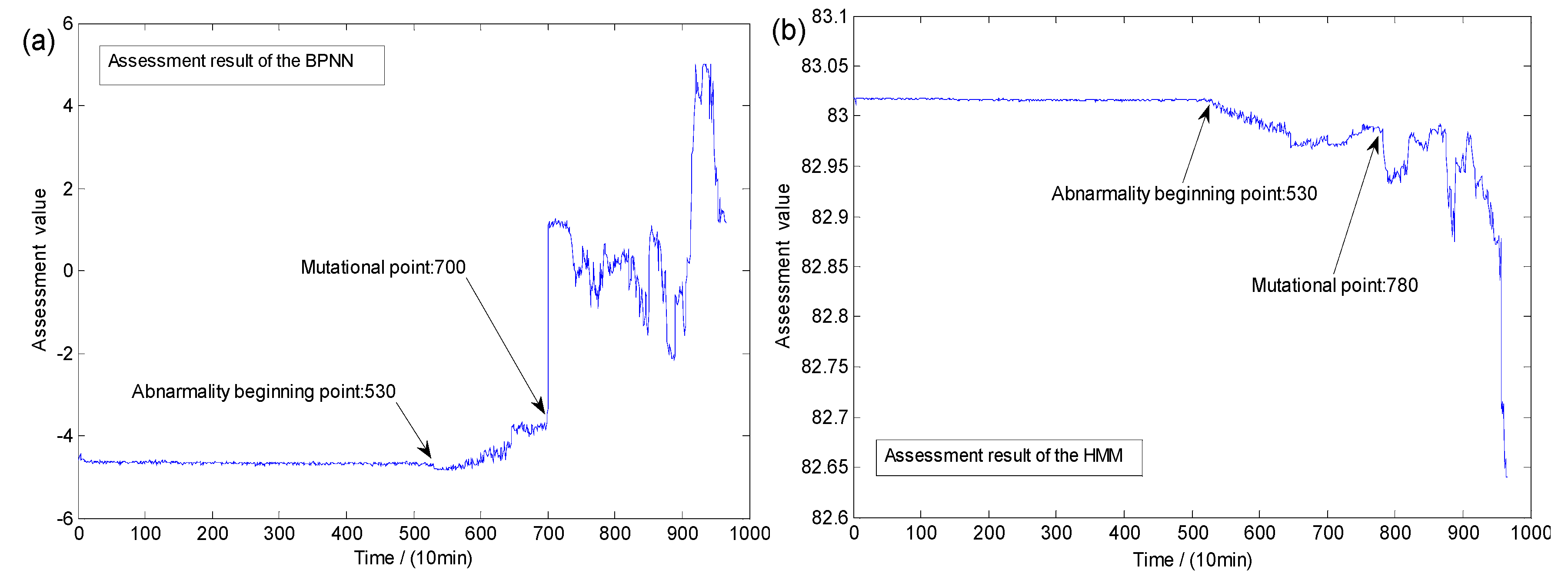
3.4.2. Comparisons of Assessment Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuan, N.; Yang, W.; Kang, B.; Xu, S.; Li, C. Signal fusion-based deep fast random forest method for machine health assessment. J. Manuf. Syst. 2018, 48, 1–8. [Google Scholar] [CrossRef]
- Loutridis, S. Instantaneous energy density as a feature for gear fault detection. Mech. Syst. Signal Process. 2006, 20, 1239–1253. [Google Scholar] [CrossRef]
- Öztürk, H.; Sabuncu, M.; Yesilyurt, I. Early detection of pitting damage in gears using mean frequency of scalogram. J. Vib. Control 2008, 14, 469–484. [Google Scholar] [CrossRef]
- Loutridis, S. Self-similarity in vibration time series: Application to gear fault diagnostics. J. Vib. Acoust. 2008, 130, 031004. [Google Scholar] [CrossRef]
- Yu, D.; Yang, Y.; Cheng, J. Application of time–frequency entropy method based on Hilbert–Huang transform to gear fault diagnosis. Measurement 2007, 40, 823–830. [Google Scholar] [CrossRef]
- Cui, J.; Wang, Y. A novel approach of analog circuit fault diagnosis using support vector machines classifier. Measurement 2011, 44, 281–289. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, Z.; Song, Z. HMM-driven robust probabilistic principal component analyzer for dynamic process fault classification. IEEE Trans. Ind. Electron. 2015, 62, 3814–3821. [Google Scholar] [CrossRef]
- Yan, J.; Guo, C.; Wang, X. A dynamic multi-scale Markov model based methodology for remaining life prediction. Mech. Syst. Signal Process. 2011, 25, 1364–1376. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Yang, B.-S.; Oh, M.-S.; Tan, A.C.C. Fault diagnosis of induction motor based on decision trees and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2009, 36, 1840–1849. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Wang, C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings. Mech. Syst. Signal Process. 2016, 72, 92–104. [Google Scholar] [CrossRef]
- Lin, Q.; Liu, S.; Zhu, Q.; Tang, C.; Song, R.; Chen, J.; Coello, C.A.C.; Wong, K.-C.; Zhang, J. Particle swarm optimization with a balanceable fitness estimation for many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 22, 32–46. [Google Scholar] [CrossRef]
- Klein, R.; Ingman, D.; Braun, S. Non-stationary signals: Phase-energy approach—Theory and simulations. Mech. Syst. Signal Process. 2001, 15, 1061–1089. [Google Scholar] [CrossRef]
- Baydar, N.; Ball, A. A comparative study of acoustic and vibration signals in detection of gear failures using Wigner–Ville distribution. Mech. Syst. Signal Process. 2001, 15, 1091–1107. [Google Scholar] [CrossRef]
- He, Q. Vibration signal classification by wavelet packet energy flow manifold learning. J. Sound Vib. 2013, 332, 1881–1894. [Google Scholar] [CrossRef]
- Gharavian, M.; Ganj, F.A.; Ohadi, A.; Bafroui, H.H. Comparison of FDA-based and PCA-based features in fault diagnosis of automobile gearboxes. Neurocomputing 2013, 121, 150–159. [Google Scholar] [CrossRef]
- Zhu, Z.-B.; Song, Z.-H. A novel fault diagnosis system using pattern classification on kernel FDA subspace. Expert Syst. Appl. 2011, 38, 6895–6905. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Hemmati, F.; Orfali, W.; Gadala, M.S. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar] [CrossRef]
- Hauberg, S. Principal curves on Riemannian manifolds. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1915–1921. [Google Scholar] [CrossRef] [PubMed]
- Jafari, A.; Almasganj, F. Using Laplacian eigenmaps latent variable model and manifold learning to improve speech recognition accuracy. Speech Commun. 2010, 52, 725–735. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Yuan, N.; Yang, W.; Kang, B.; Xu, S.; Wang, X.; Li, C. Manifold learning-based fuzzy k-principal curve similarity evaluation for wind turbine condition monitoring. In Energy Science & Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018. [Google Scholar]


| Features | Names | Equations | Features | Names | Equations |
|---|---|---|---|---|---|
| Mean | Kurtosis index | ||||
| variance | Peak factor | ||||
| Square root amplitude | Margin indicator | ||||
| Valid value | Waveform indicator | ||||
| Peak | Pulse indicator | ||||
| Skewness index |
| Features | Names | Equations | Features | Names | Equations |
|---|---|---|---|---|---|
| Mean frequency | None | ||||
| Standard deviation frequency | None | ||||
| Spectral skewness | None | ||||
| Spectral kurtosis | None | ||||
| First-order center of gravity | None | ||||
| Second-order center of gravity | None | ||||
| Second order moment of spectrum |
| Type | Number | Ball Diameter (mm) | Contact Angle (deg) | Rotation Speed (RPM) | Load (kN·m) | Sampling Rate (kHz) |
|---|---|---|---|---|---|---|
| ZA-2115 | 4 | 10 | 0 | 1500 | 26.50 | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, N.; Yang, W.; Kang, B.; Xu, S.; Wang, X. RETRACTED: Laplacian Eigenmaps Feature Conversion and Particle Swarm Optimization-Based Deep Neural Network for Machine Condition Monitoring. Appl. Sci. 2018, 8, 2611. https://doi.org/10.3390/app8122611
Yuan N, Yang W, Kang B, Xu S, Wang X. RETRACTED: Laplacian Eigenmaps Feature Conversion and Particle Swarm Optimization-Based Deep Neural Network for Machine Condition Monitoring. Applied Sciences. 2018; 8(12):2611. https://doi.org/10.3390/app8122611
Chicago/Turabian StyleYuan, Nanqi, Wenli Yang, Byeong Kang, Shuxiang Xu, and Xiaolin Wang. 2018. "RETRACTED: Laplacian Eigenmaps Feature Conversion and Particle Swarm Optimization-Based Deep Neural Network for Machine Condition Monitoring" Applied Sciences 8, no. 12: 2611. https://doi.org/10.3390/app8122611
APA StyleYuan, N., Yang, W., Kang, B., Xu, S., & Wang, X. (2018). RETRACTED: Laplacian Eigenmaps Feature Conversion and Particle Swarm Optimization-Based Deep Neural Network for Machine Condition Monitoring. Applied Sciences, 8(12), 2611. https://doi.org/10.3390/app8122611






