Analysis of SNR for High-Orbit Target Detected by Ground-Based Photoelectric System
Abstract
:Featured Application
Abstract
1. Introduction
2. Signal-to-Noise Model of Satellite
3. Parameters for Simulation
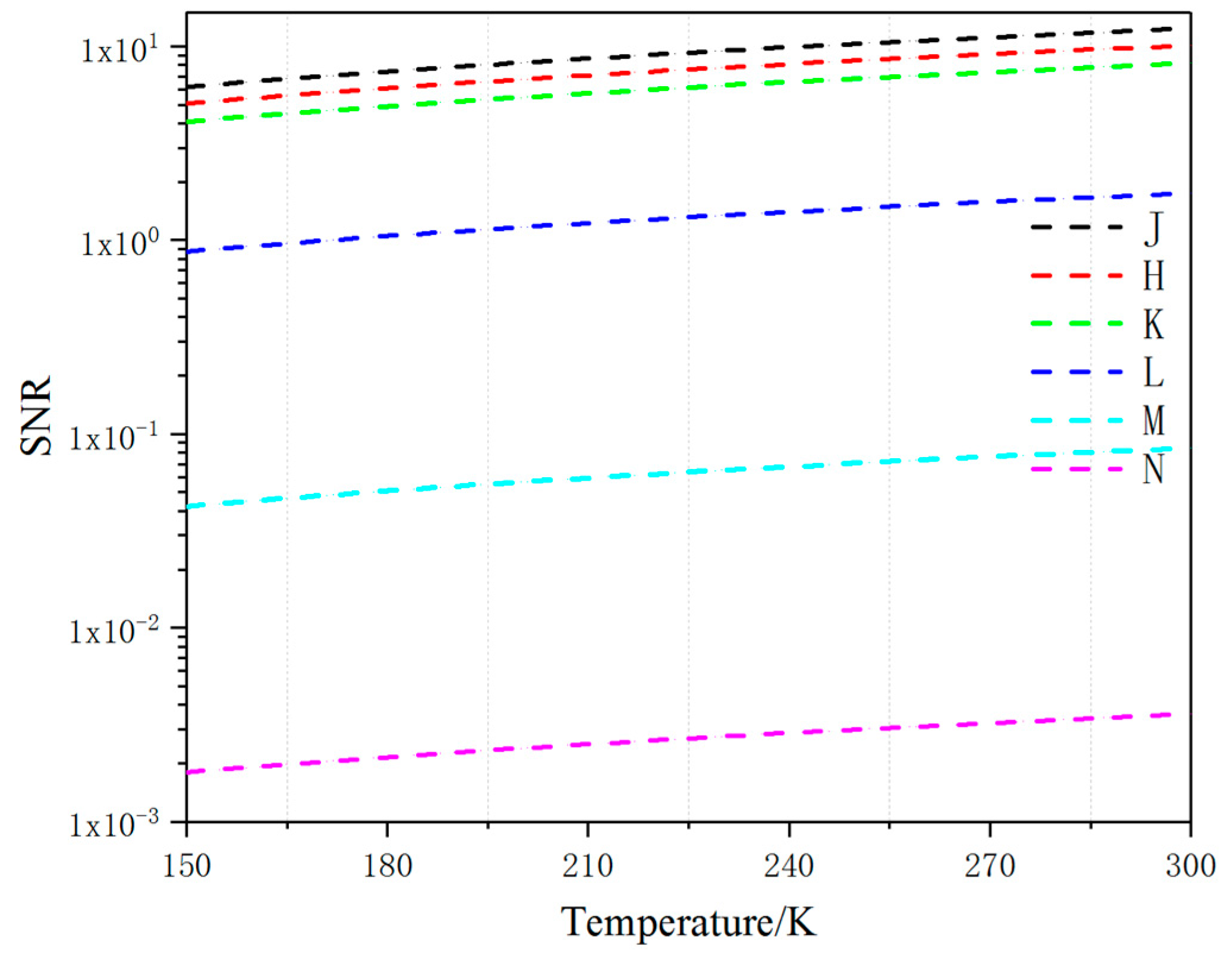
4. Simulation Results
5. Experiment
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Ciuonzo, D.; Maio, A.D.; Orlando, D. A unifying framework for adaptive radar detection in homogeneous plus structured interference—Part II: Detectors design. IEEE Trans. Signal Process. 2016, 64, 2907–2919. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Maio, A.D.; Orlando, D. A Unifying Framework for Adaptive Radar Detection in Homogeneous Plus Structured Interference—Part I: On the Maximal Invariant Statistic. IEEE Trans. Signal Process. 2016, 64, 2907–2919. [Google Scholar] [CrossRef]
- Shi, X.; Xu, X. Detector material and sensitivity analysis for space-based infrared sensors. Optoelectron. Lett. 2010, 6, 27–30. [Google Scholar] [CrossRef]
- Lambert, J.V.; Africano, J.L.; Kervin, P. Radiometric Sizing of Small Orbital Objects. In Proceedings of the 2002 Space Control Conference, Lexington, KY, USA, 23–25 April 2002. [Google Scholar]
- Jin, H.; Song, Y.; Lee, Y.; Kim, K.S.; Lee, C.U.; Choi, Y.; Moon, H.K.; Lee, D.J.; Yoon, J.N. The light curves of a Geostationary Satellite and its model. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 14–17 September 2010. [Google Scholar]
- Chaudhary, A.; Payne, T.; Wilhelm, S.; Gregory, S.; Skinner, M.A.; Rudy, R.; Russell, R.; Brown, J.; Dao, P. Analysis of Unresolved Spectral Infrared Signature for the Extraction of Invariant Features. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 14–17 September 2010. [Google Scholar]
- Liu, Y.; Yang, Q.; Liu, J.; Wang, B.; Zhang, Z.; Wang, H. MWIR imaging experiments with large F-number optics on LEO spacecraft. Infrared Phys. Technol. 2014, 67, 315–317. [Google Scholar] [CrossRef]
- Jim, K.T.C.; Scott, B.; Knox, R. Simulations of Non-resolved, Infrared Imaging of Satellites. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 1–4 September 2009; pp. 636–645. [Google Scholar]
- Liu, Y. Inversion of space target infrared multi-band temperature distribution. Infrared Laser Eng. 2013, 42, 556–561. [Google Scholar]
- Hardie, R.C.; Baxley, F.; Brys, B.; Hytla, P. Scene-Based Nonuniformity Correction with Reduced Ghosting Using a Gated LMS Algorithm. Opt. Express 2009, 17, 14918–14933. [Google Scholar] [CrossRef] [PubMed]
- Cognion, R. Observations and Modeling of GEO Satellites at Large Phase Angles. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 10–13 September 2013. [Google Scholar]
- Butkus, A.; Roe, K.; Mitchell, B.; Payne, T. Space Surveillance Network and Analysis Model (SSNAM) Performance Improvements. In Proceedings of the 2007 DoD High Performance Computing Modernization Program Users Group Conference, Pittsburgh, PA, USA, 18–21 June 2007; pp. 469–473. [Google Scholar]
- Yan, M.; Luo, P.L.; Iwakuni, K.; Millot, G.; Hänsch, T.W.; Picqué, N. Mid-infrared dual-comb spectroscopy with electro-optic modulators. Light Sci. Appl. 2017, 6, e17076. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Ma, T.; Danesh, M.; Shivananju, B.N.; Gan, S.; Song, J.; Qiu, C.W.; Cheng, H.M.; Ren, W.; Bao, Q. Effects of edge on graphene plasmons as revealed by infrared nanoimaging. Light Sci. Appl. 2017, 6, e16204. [Google Scholar] [CrossRef] [PubMed]
- Chadwick, S.R.; Pavioursmith, M. The Great Canoes in the Sky; Springer International Publishing: Berlin, Germany, 2017. [Google Scholar]
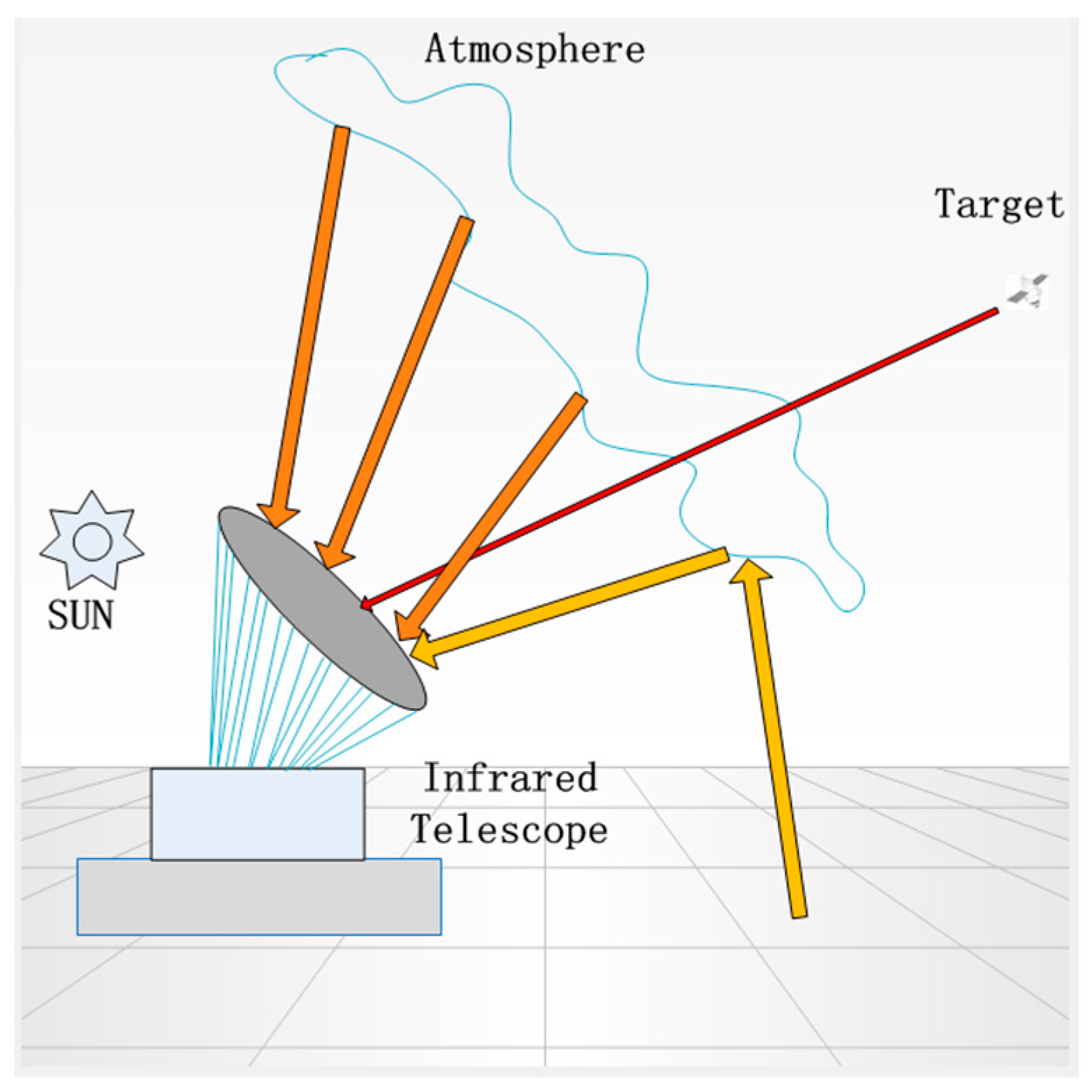
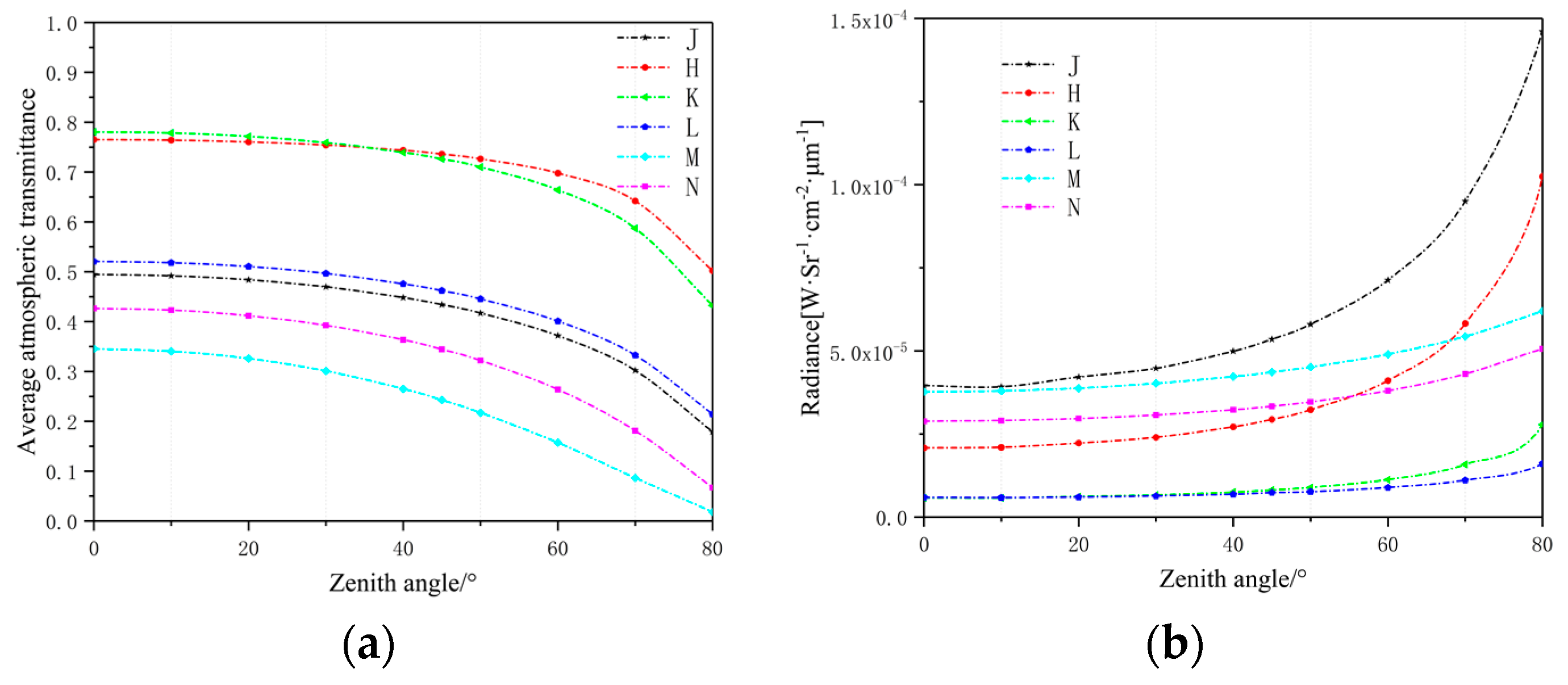
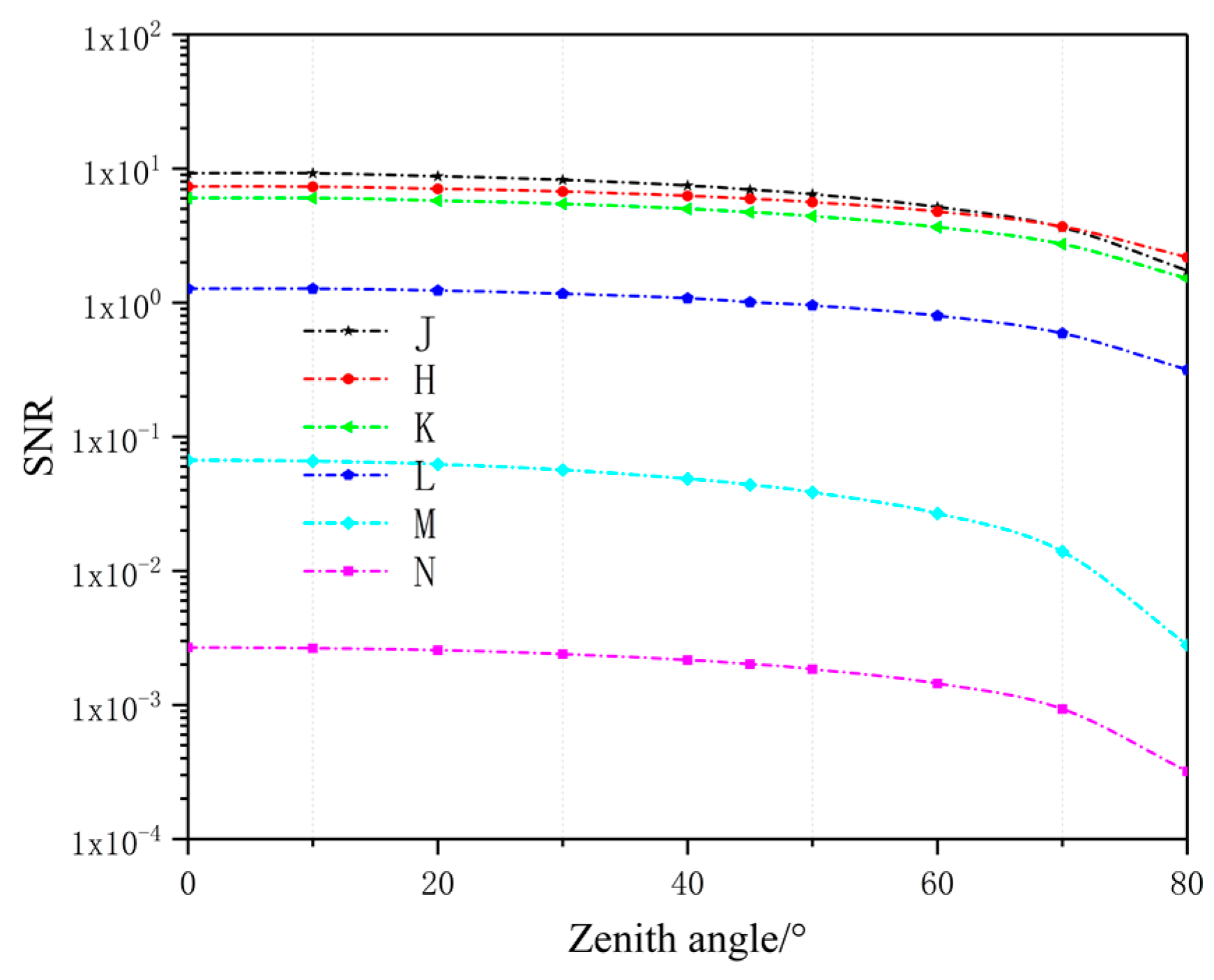
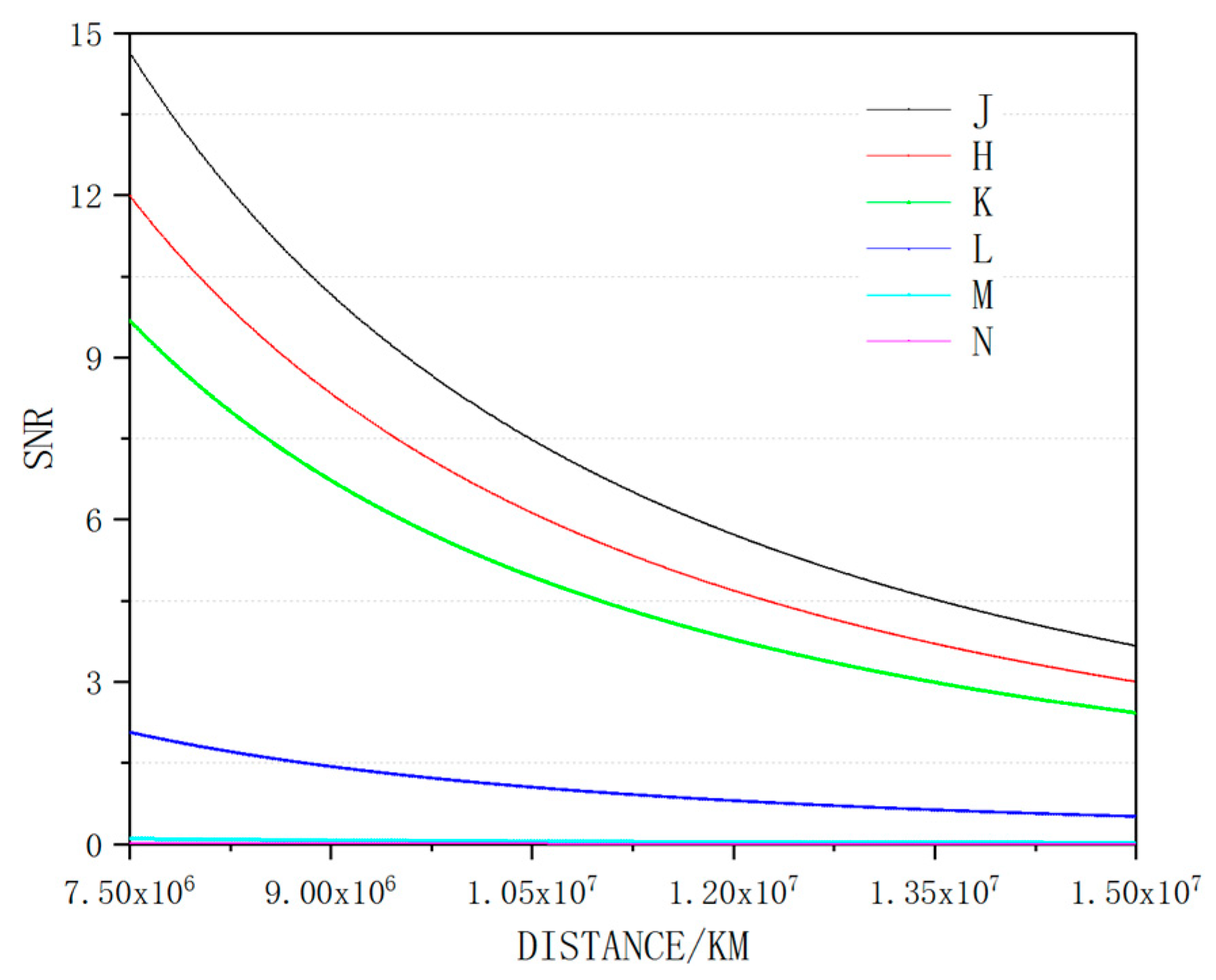

| Spectrum | Wavelength (Micrometers) | Astronomical Band |
|---|---|---|
| Near Infrared | 1.1–1.4 | J |
| Short Infrared | 1.5–1.8 | H |
| Short Infrared | 2.0–2.4 | K |
| Mid Infrared | 3.0–4.0 | L |
| Mid Infrared | 4.6–5.0 | M |
| Long Infrared | 7.5–14.5 | N |
| Name | Default Value |
|---|---|
| Optics transmission | 0.75 |
| Quantum efficiency | 0.85 |
| Pixel size | 30 |
| F-number | 4 |
| Focal length | 4.8 m |
| Dark current | 450 e-rms |
| Readout noise | 6400 e-/pix/s |
| Name | Time (UTC) | Average SNR |
|---|---|---|
| 1962-060-A | 00:22:42 | 10.71 |
| 13114 | 10:08:54 | 15.63 |
| 13777 | 10:33:30 | 13.48 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Huang, R.; Xue, X. Analysis of SNR for High-Orbit Target Detected by Ground-Based Photoelectric System. Appl. Sci. 2018, 8, 2604. https://doi.org/10.3390/app8122604
Huang Z, Huang R, Xue X. Analysis of SNR for High-Orbit Target Detected by Ground-Based Photoelectric System. Applied Sciences. 2018; 8(12):2604. https://doi.org/10.3390/app8122604
Chicago/Turabian StyleHuang, Zhiguo, Rui Huang, and Xiaojun Xue. 2018. "Analysis of SNR for High-Orbit Target Detected by Ground-Based Photoelectric System" Applied Sciences 8, no. 12: 2604. https://doi.org/10.3390/app8122604
APA StyleHuang, Z., Huang, R., & Xue, X. (2018). Analysis of SNR for High-Orbit Target Detected by Ground-Based Photoelectric System. Applied Sciences, 8(12), 2604. https://doi.org/10.3390/app8122604




