Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink
Abstract
:1. Introduction
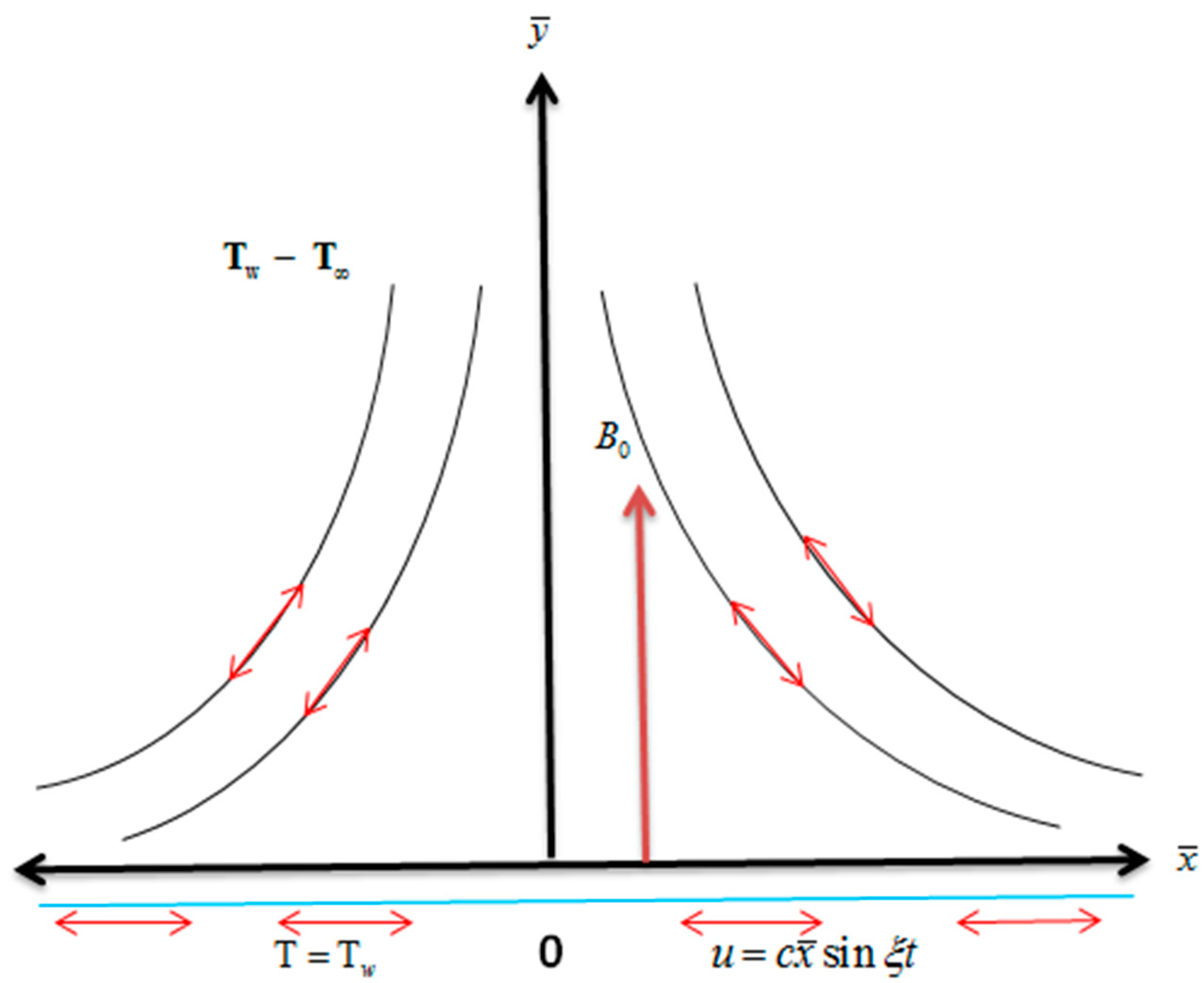
2. Mathematical Modeling
2.1. Physical Quantities of Interest
2.2. Entropy Generation and Bejan Number
2.3. Solution by HAM
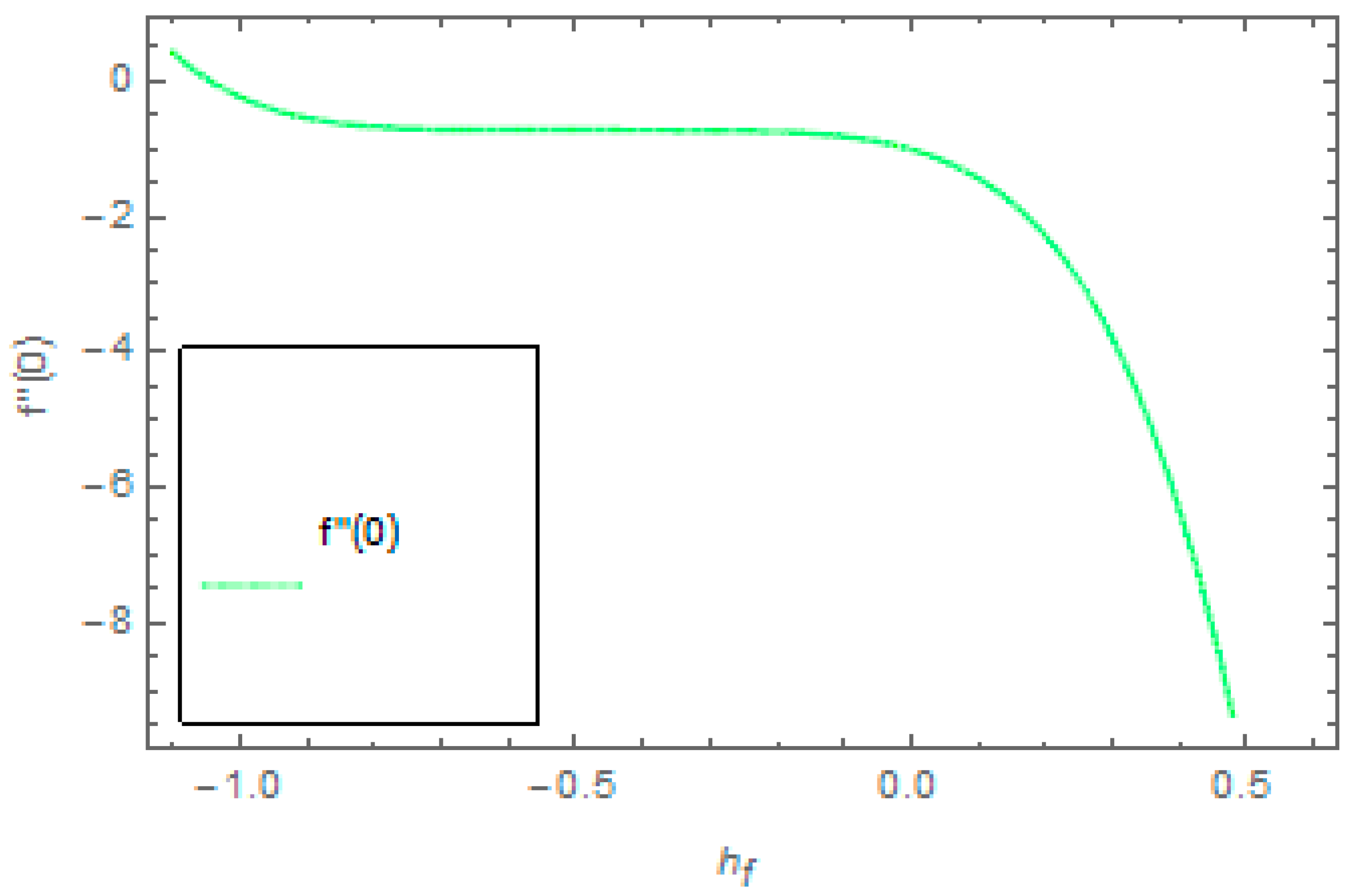
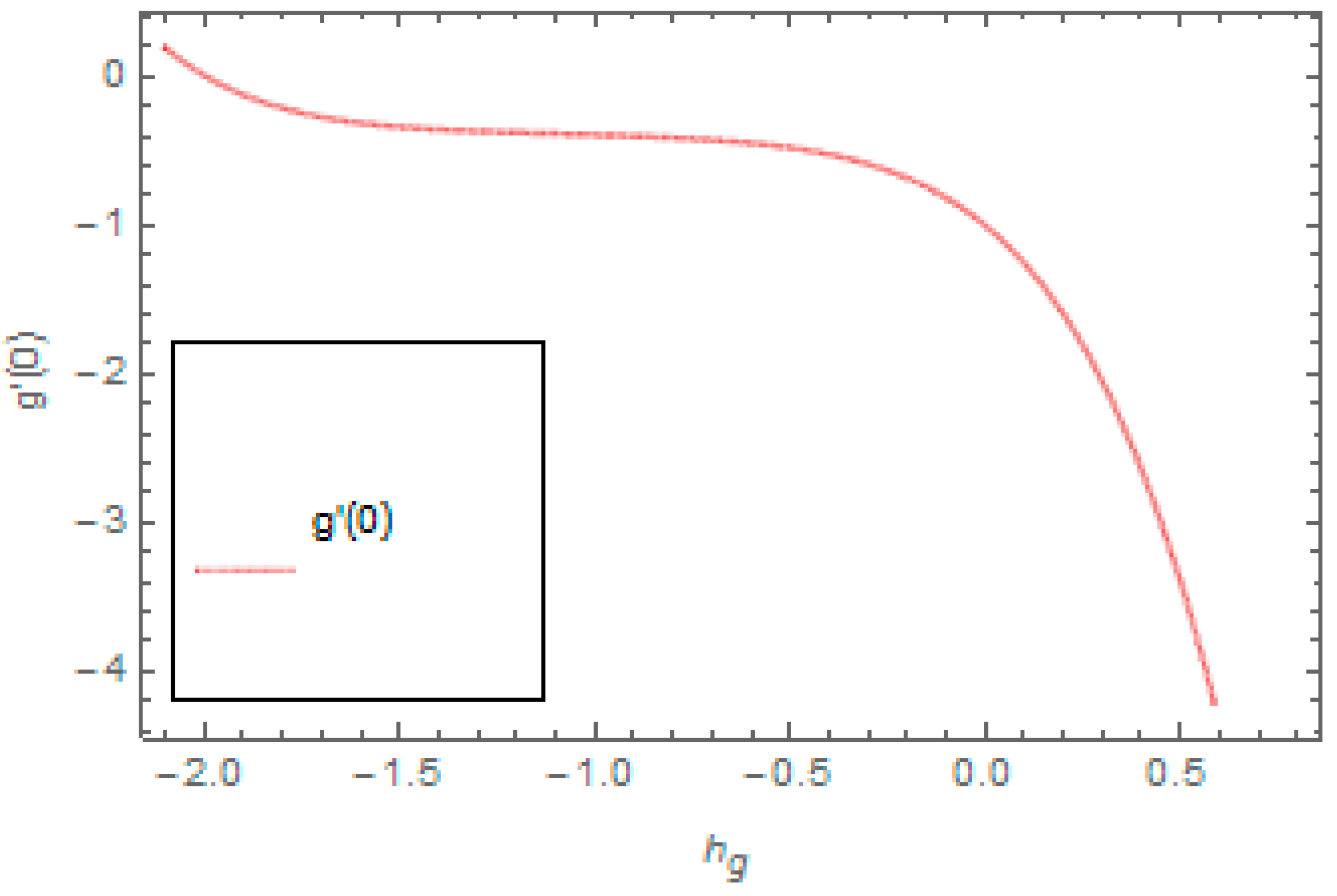
2.4. HAM Convergence
3. Results and Discussion
3.1. Tables Discussion
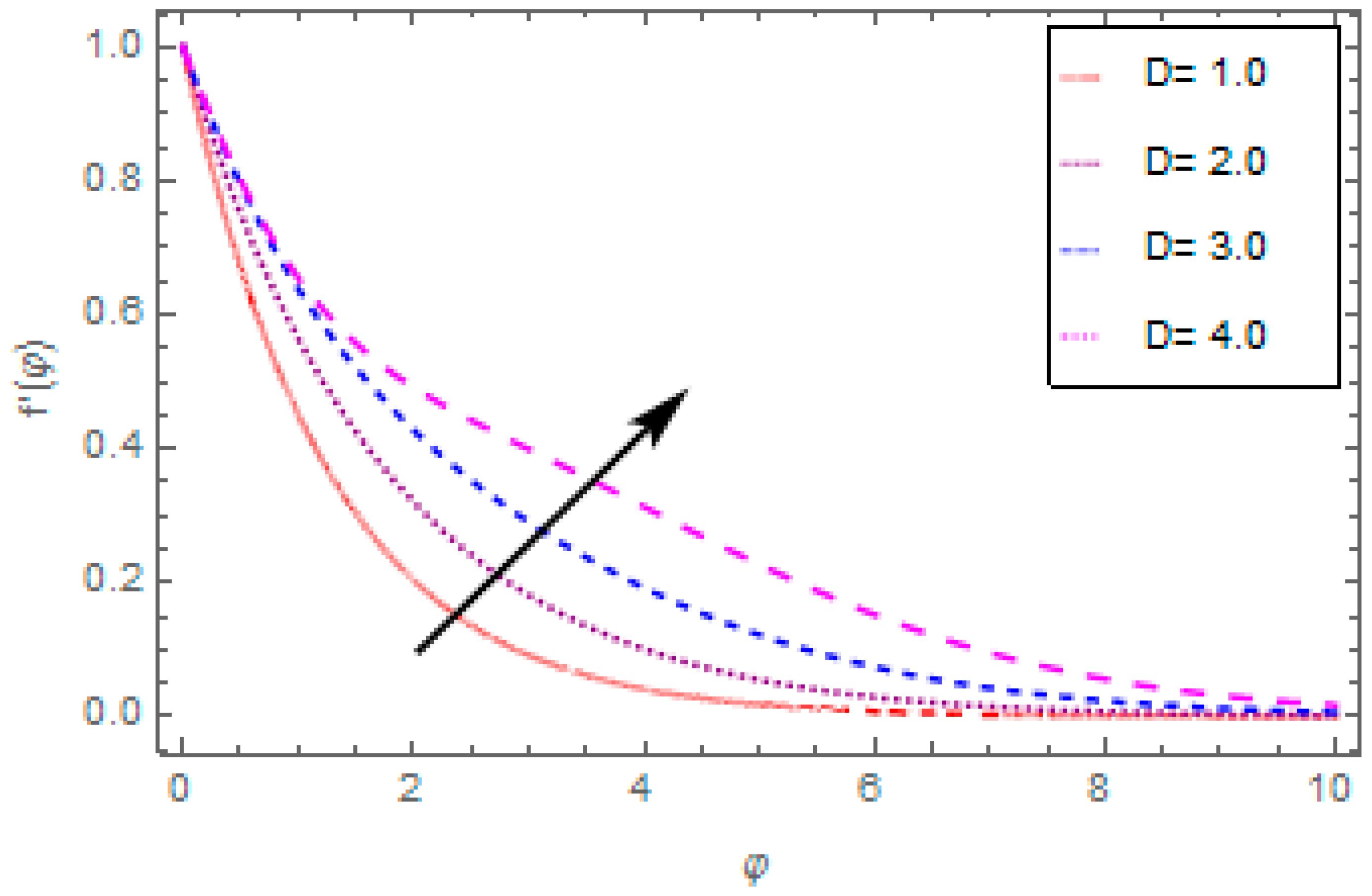
3.2. Graphical Discussion
4. Conclusions
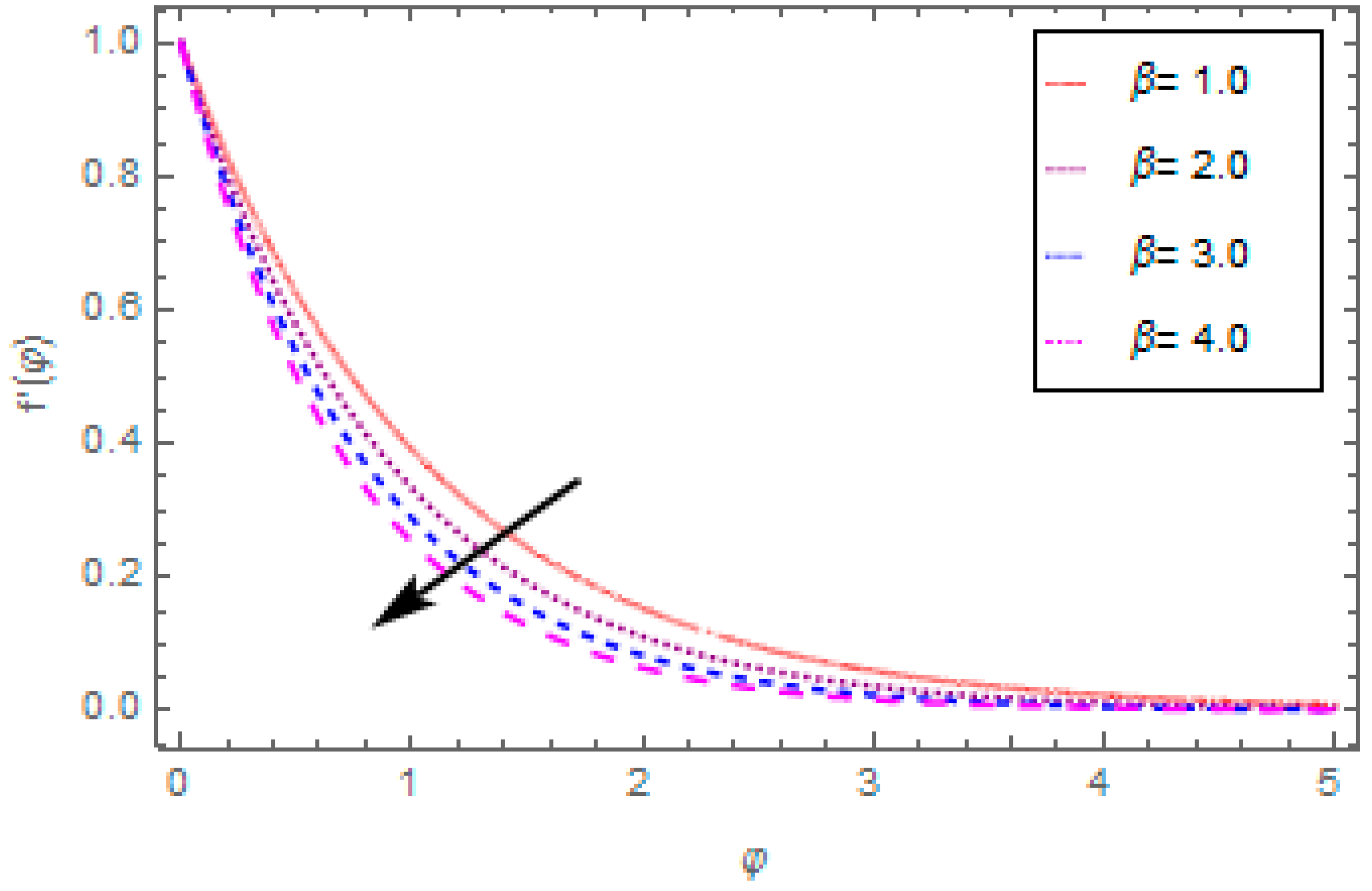
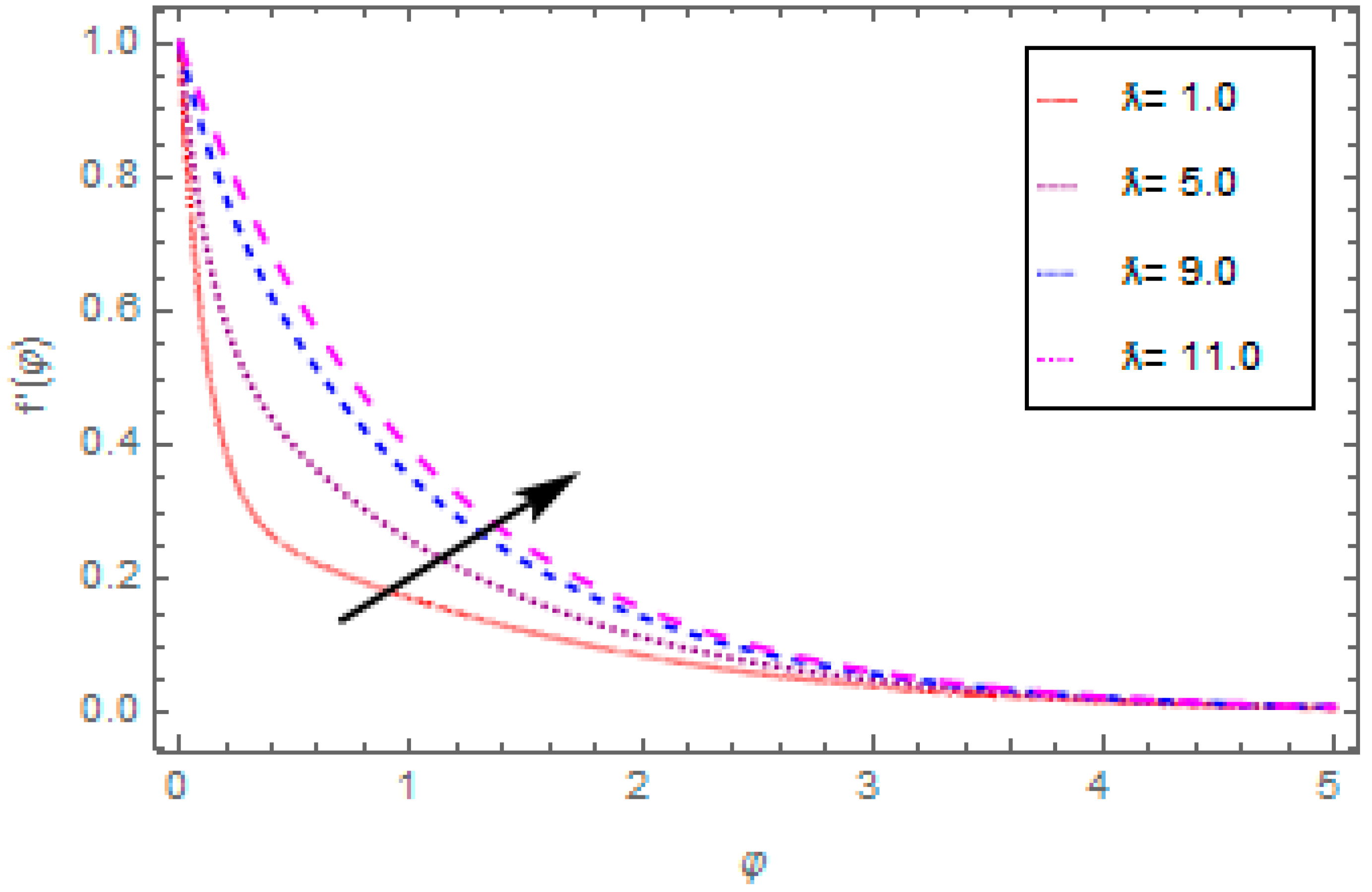
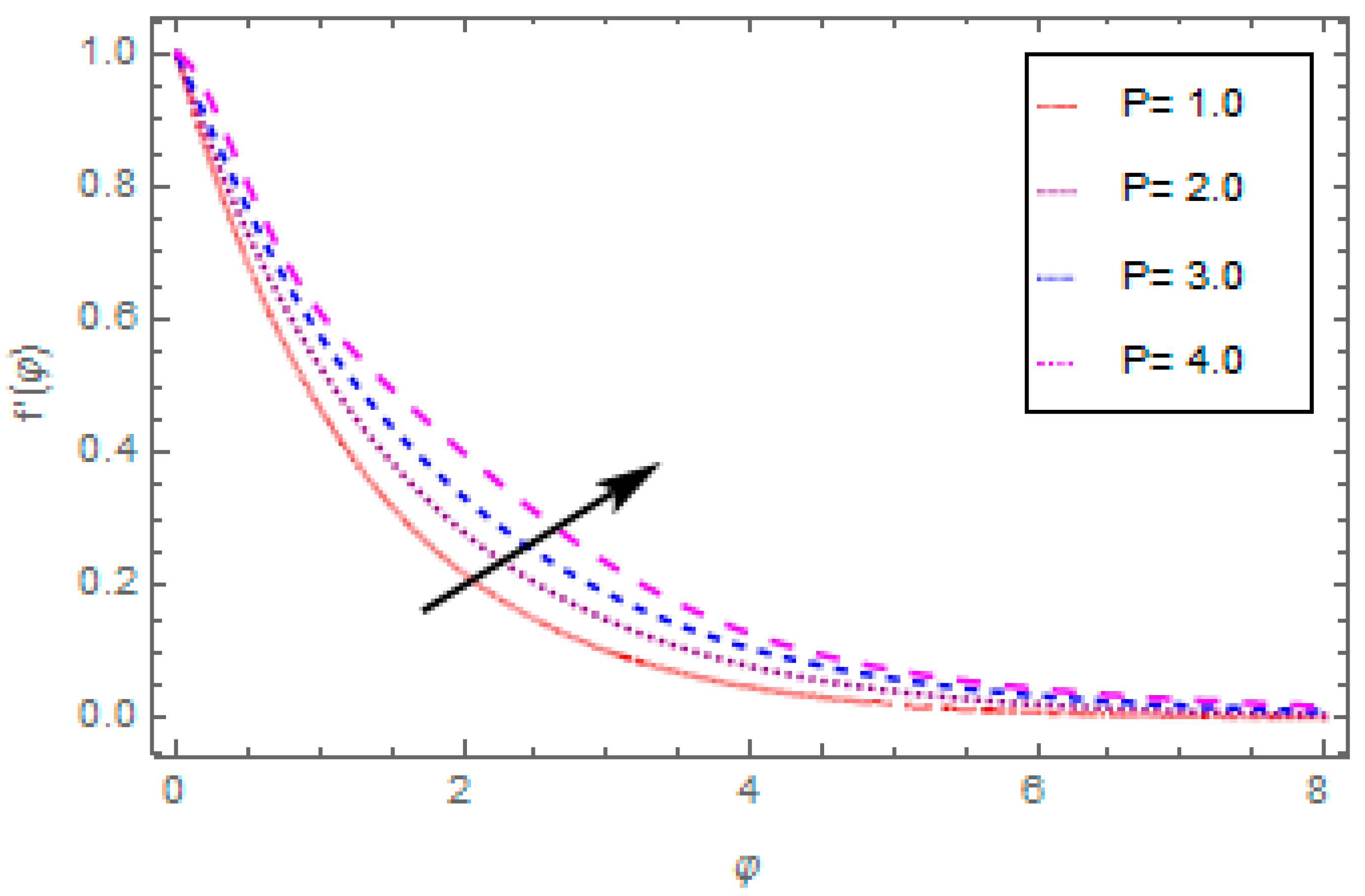
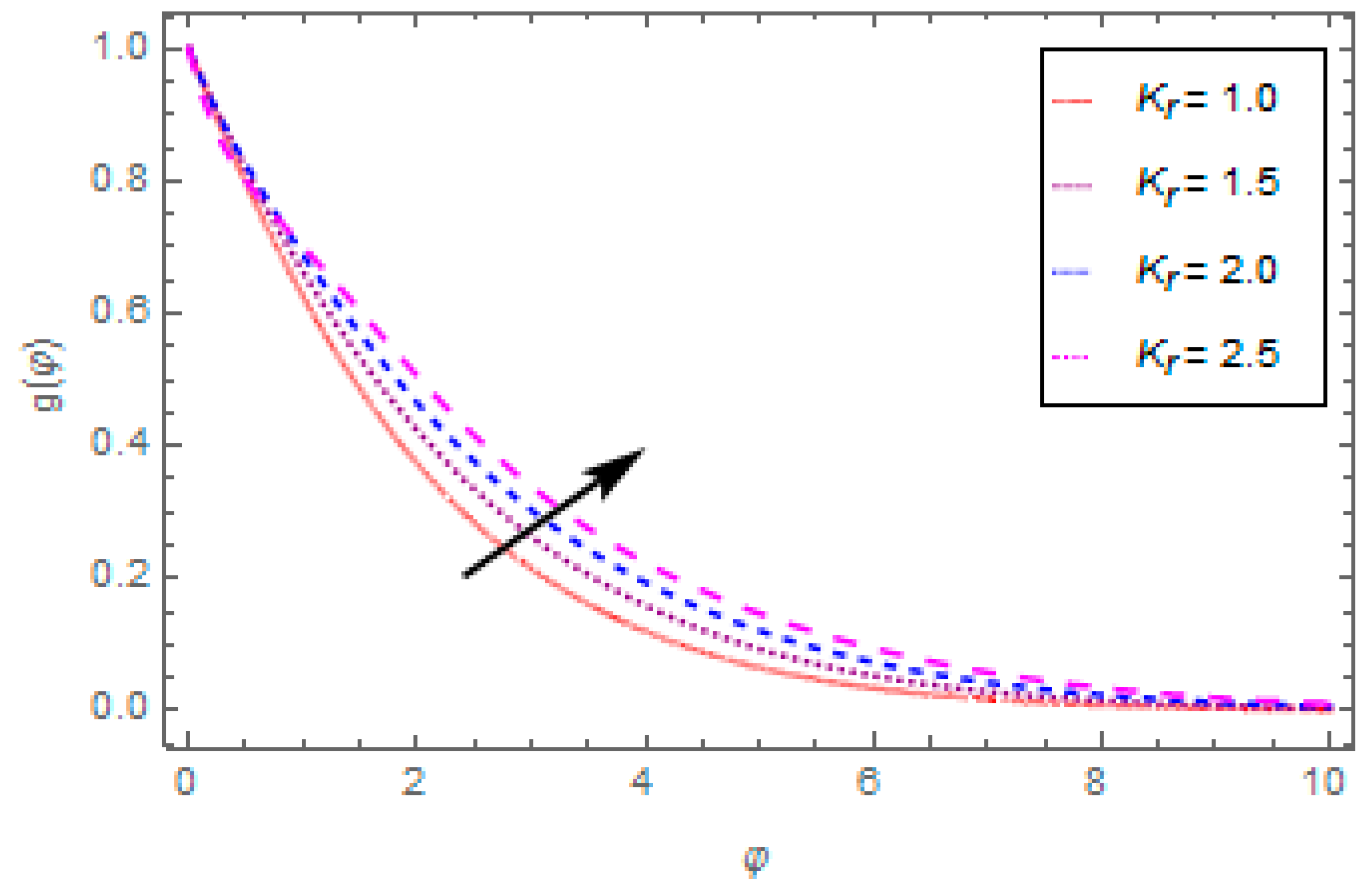
- The velocity function reduces with the enhancement in magnetic field and porosity parameter, and escalates with the enhancement in oscillating frequency and fluid parameters.
- The temperature function reduces with the enhancement in oscillating frequency and Prandtl number, and escalates with the enhancement in heat source/sink and radiation parameter.
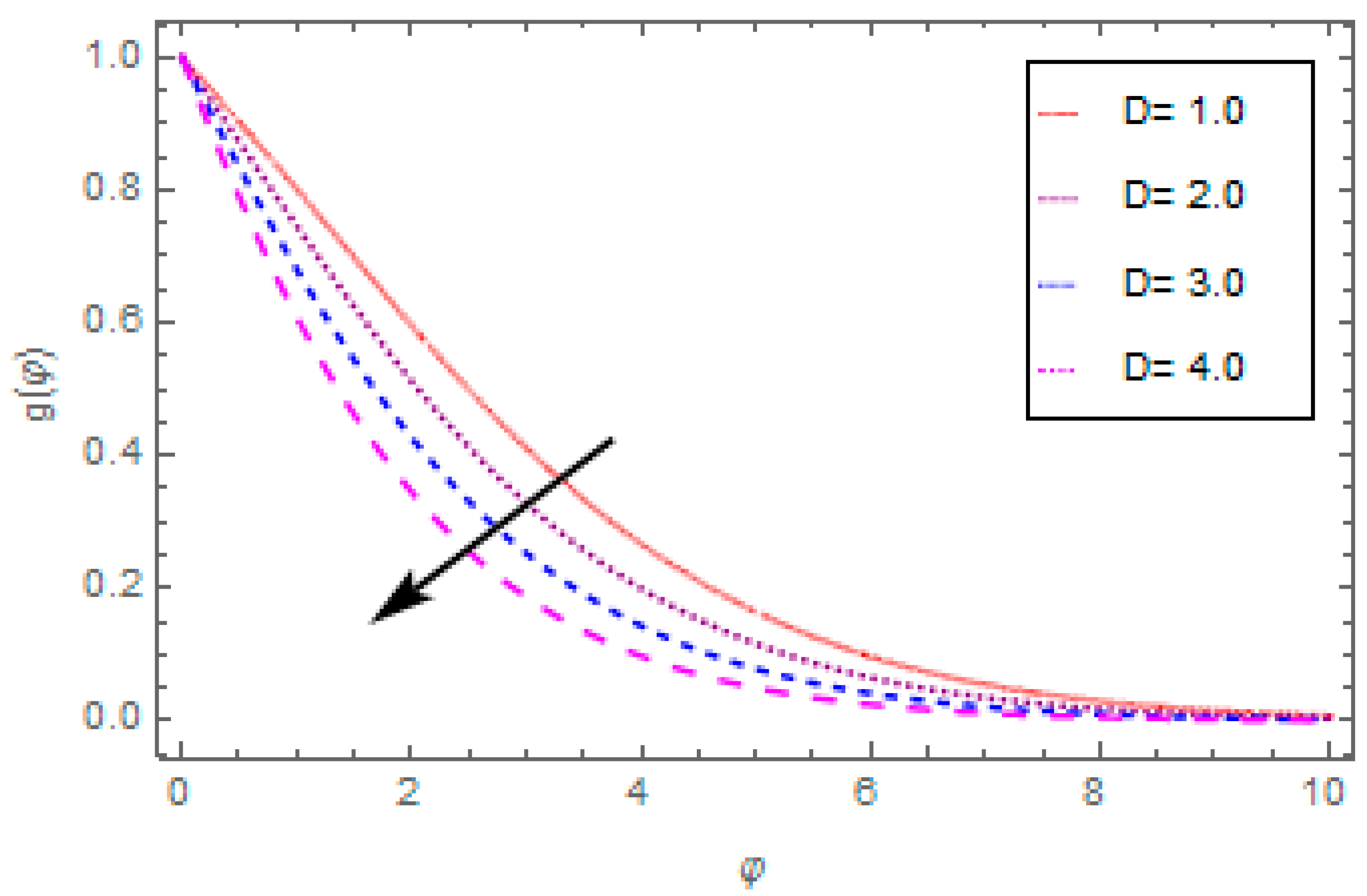
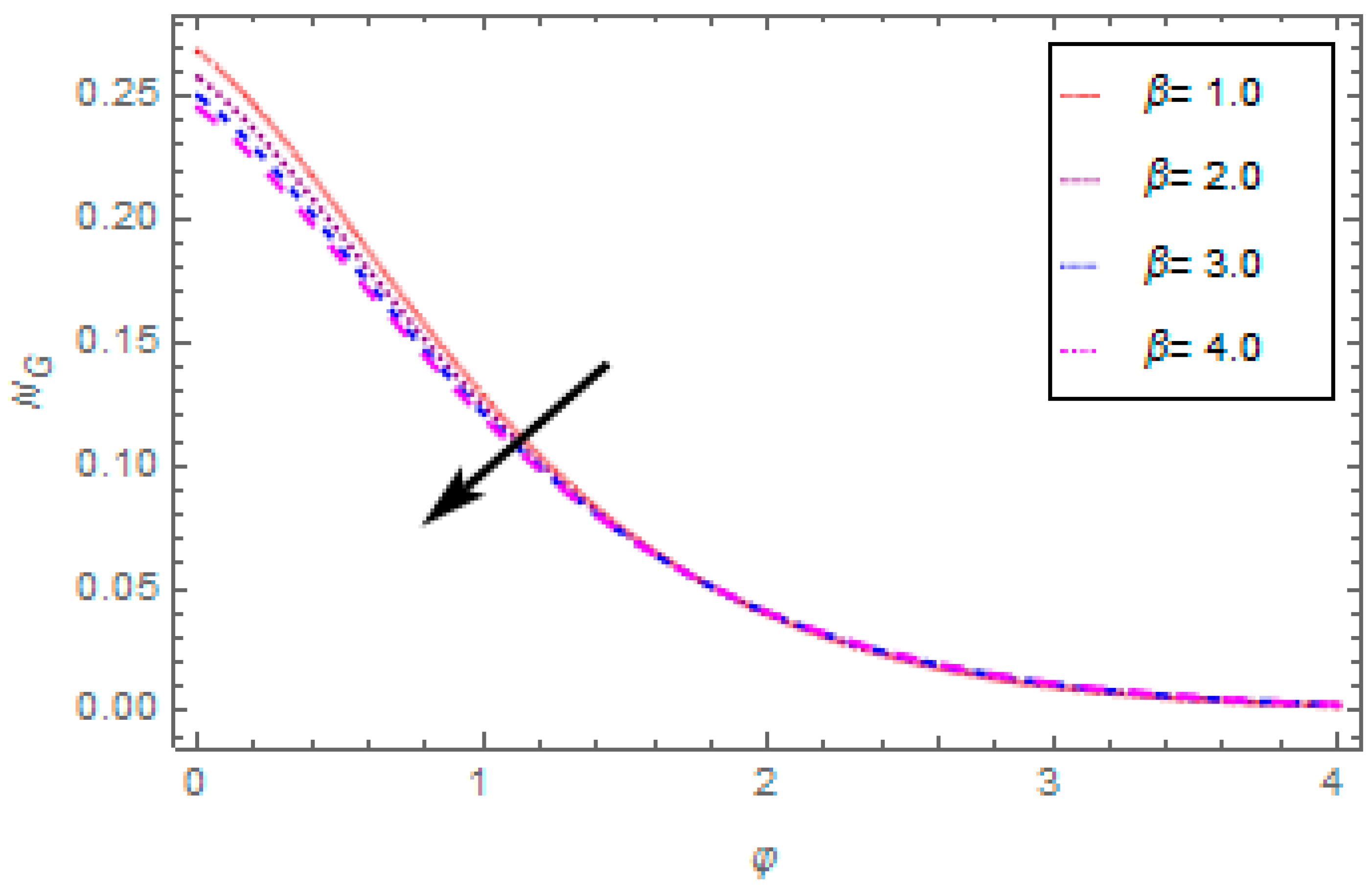
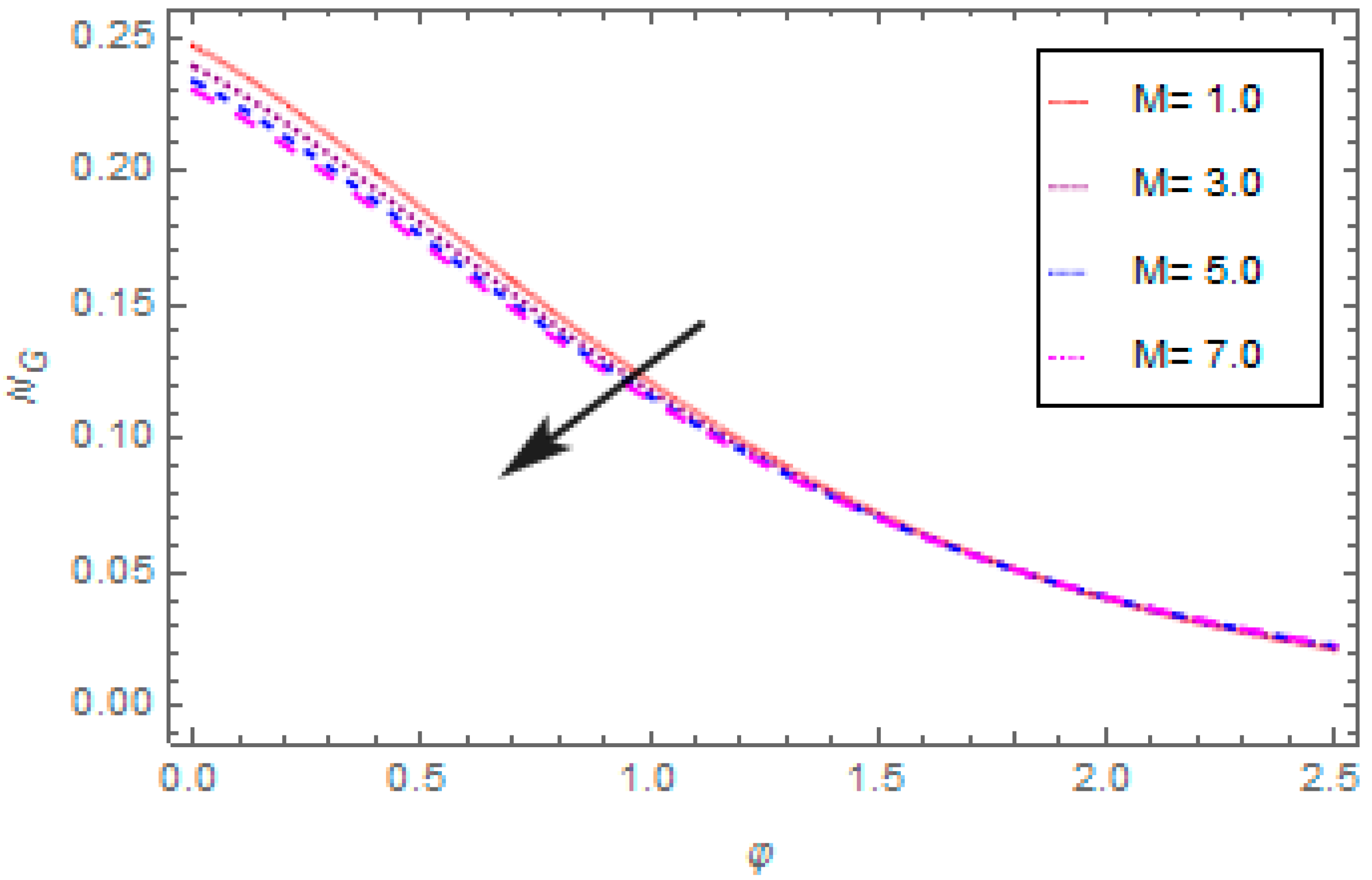
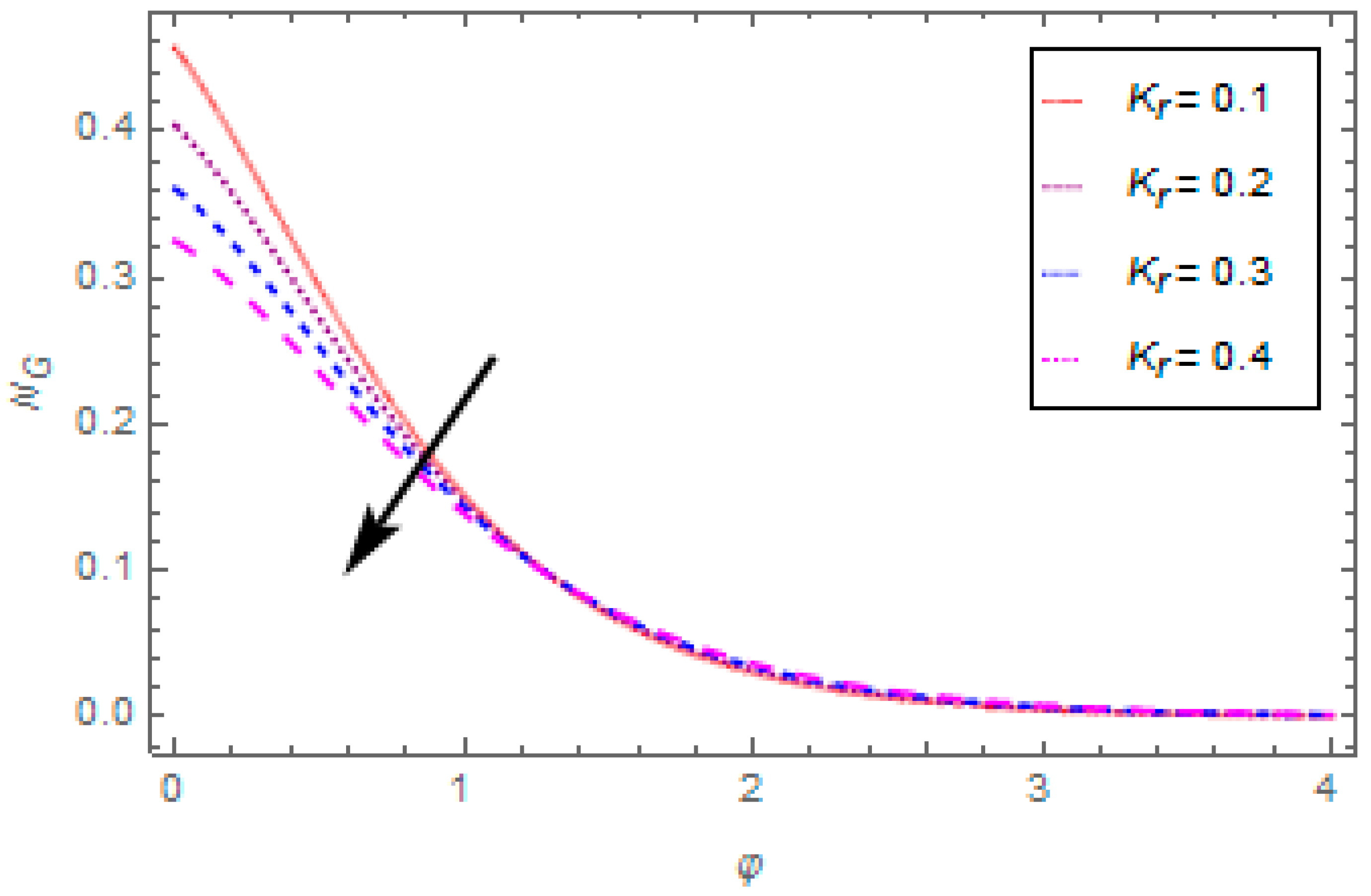
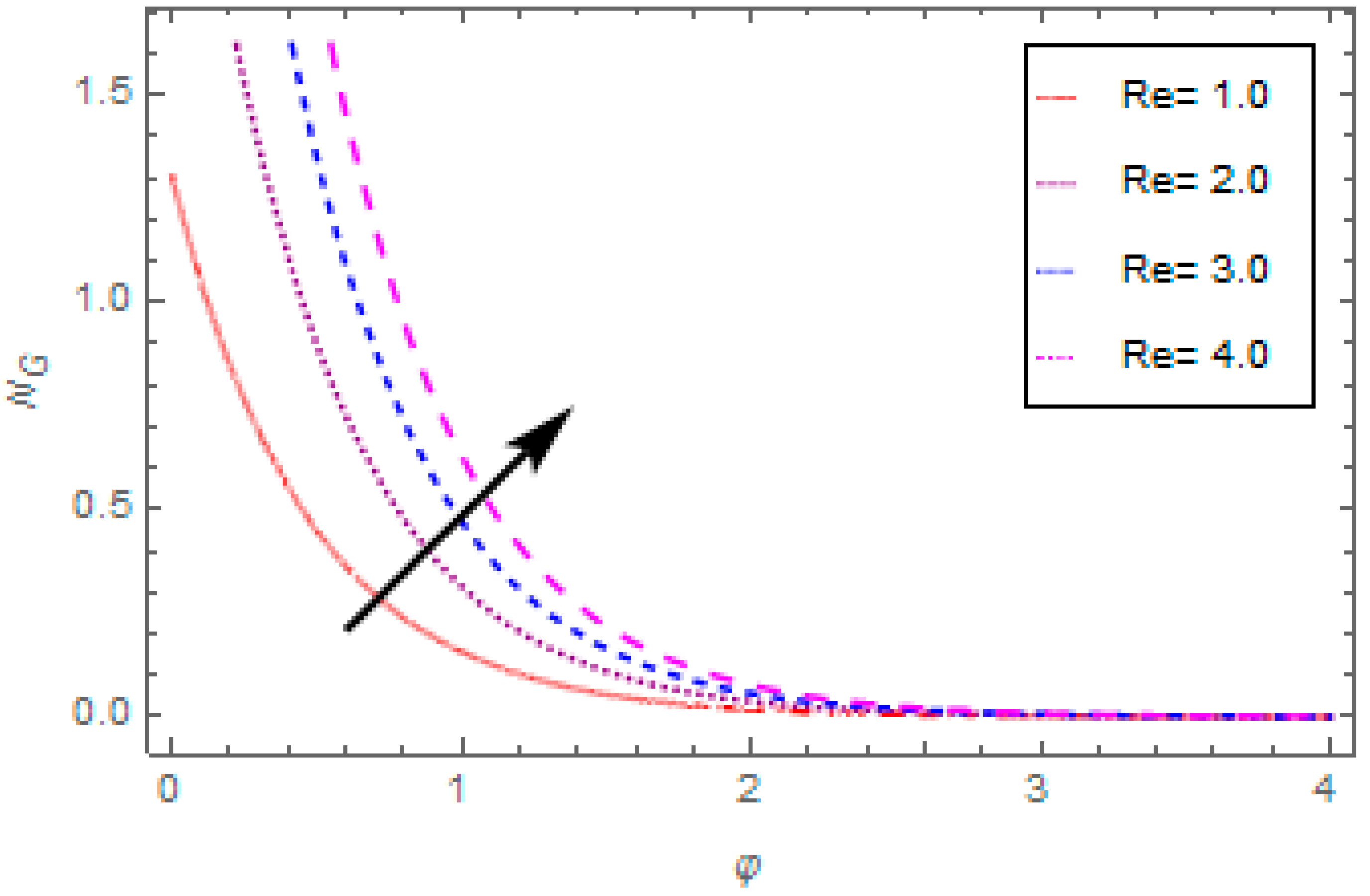
- The entropy generation rate reduces with the escalation in porosity parameter, thermal radiation, magnetic field, and escalates with the enhancement in Reynolds number.
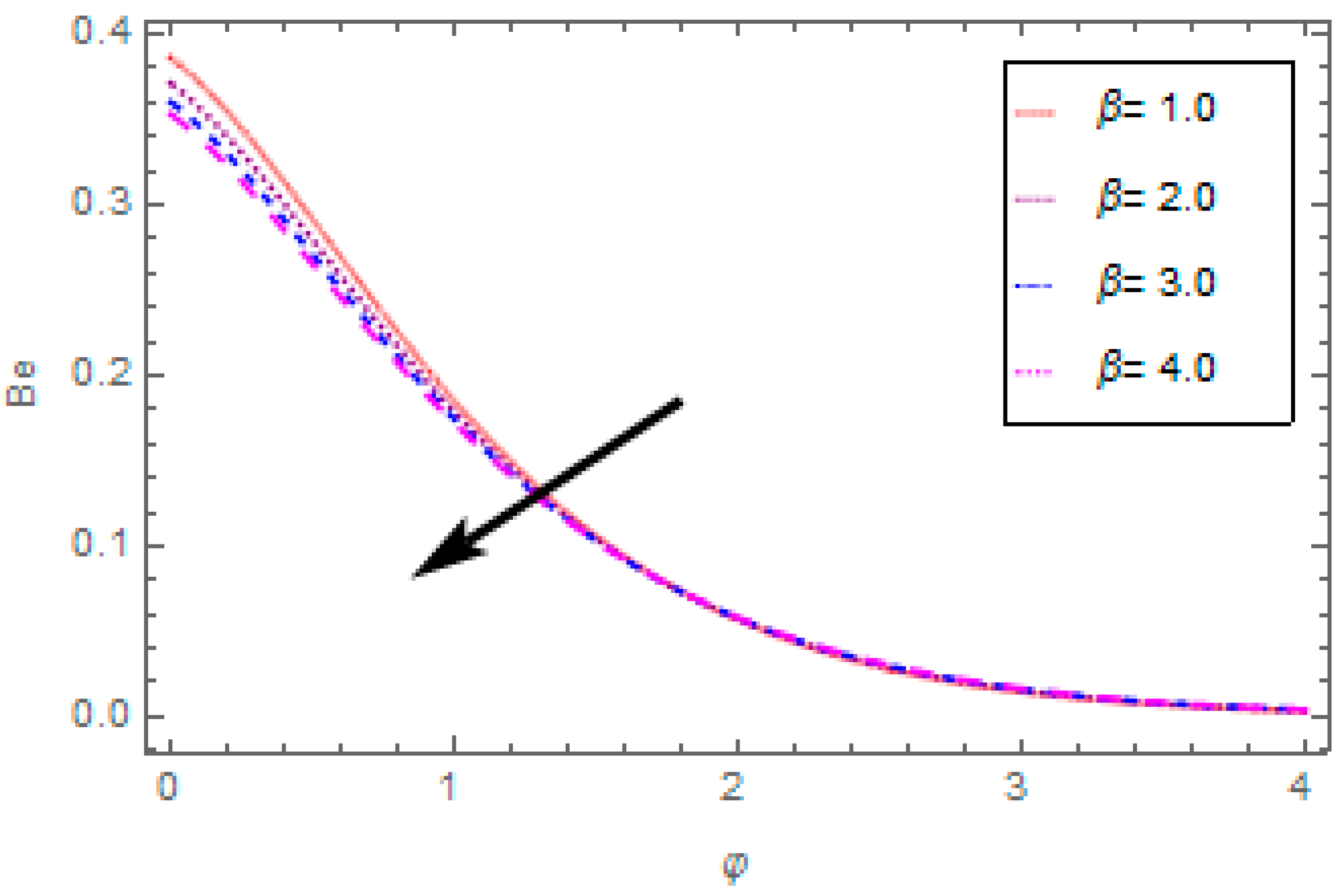
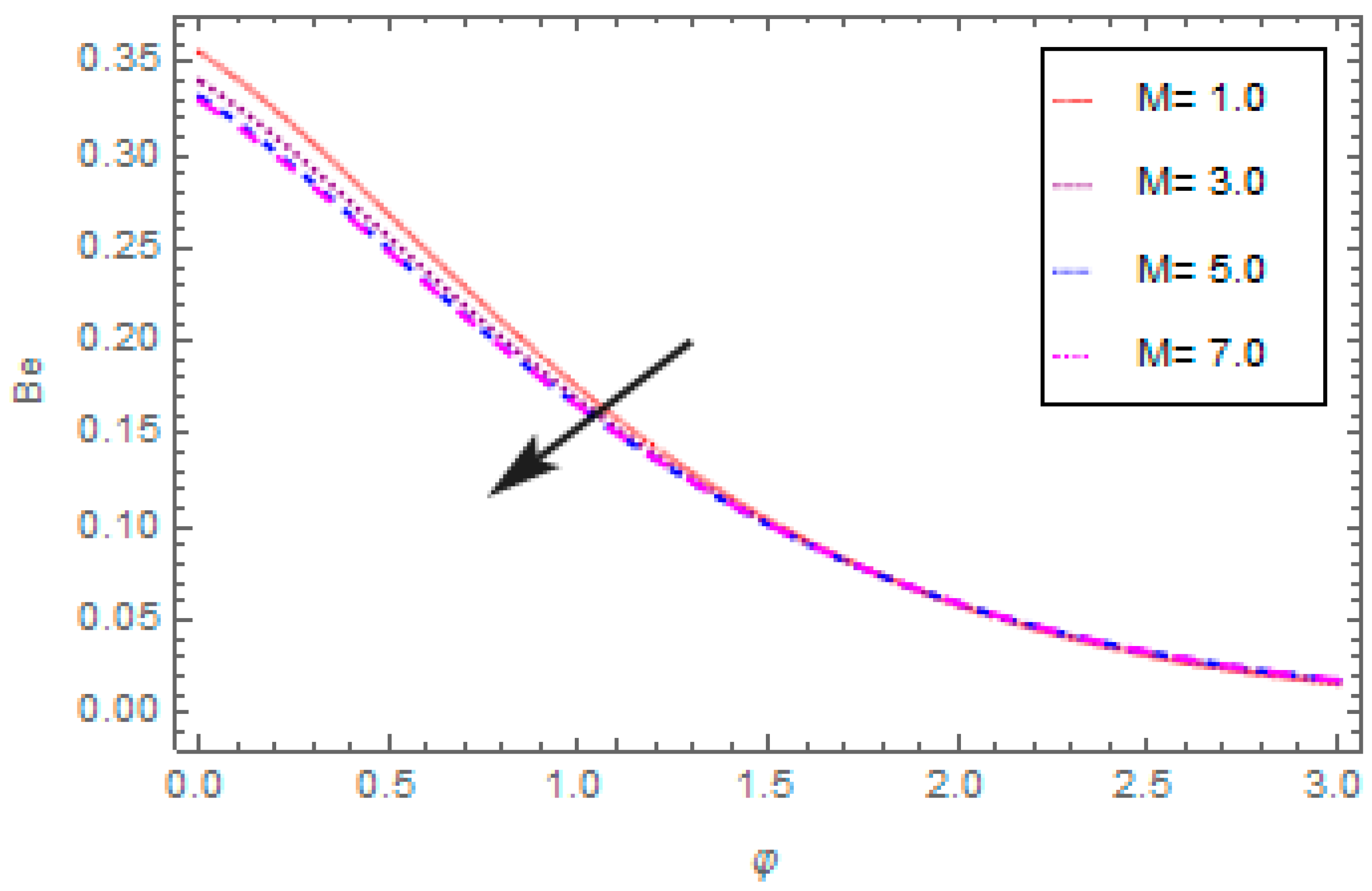
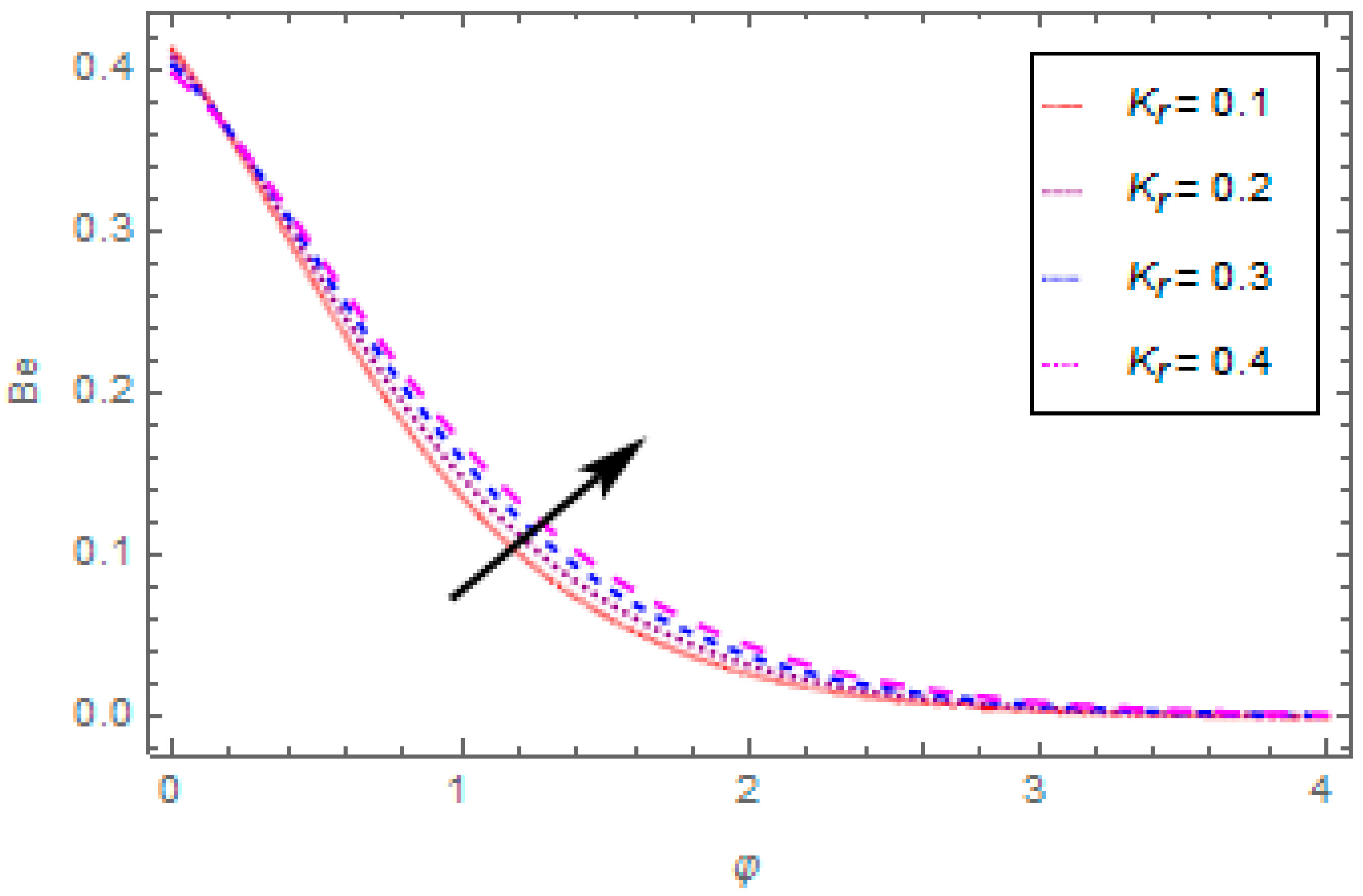
- The Bejan number reduces with the enhancement in porosity parameter and magnetic field, and increases with the enhancement in thermal radiation parameter.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| magnetic field | |
| Brinkman number | |
| specific heat | |
| skin friction coefficient | |
| oscillating frequency | |
| thermal conductivity () | |
| absorption coefficient | |
| radiation parameter | |
| magnetic parameter | |
| Nusselt number | |
| P | fluid parameter |
| Prandtl number | |
| heat source | |
| heat flux | |
| fluid temperature | |
| infinity temperature | |
| surface temperature | |
| , | velocity components |
| coordinates | |
| topological spaces | |
| homotopic functions | |
| Greek Letters | |
| fluid material | |
| kinematic viscosity, | |
| fluid density | |
| electrical conductivity of fluid | |
| Stefan–Boltzmann constant | |
| assisting parameter | |
| fluid parameter | |
| porosity parameter | |
| heat source/sink | |
| dimensionless temperature |
References
- Hayat, T.; Iqbal, Z.; Qasim, M.; Obaidat, S. Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 1817–1822. [Google Scholar] [CrossRef]
- Patel, M.; Timol, M.G. Numerical treatment of Powell–Eyring fluid flow using method of satisfaction of asymptotic boundary conditions. Appl. Numer. Math. 2009, 59, 2584–2592. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Idrees, M.; Khan, W.; Islam, S.; Gul, T. Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface. Math. Comput. Appl. 2018, 23, 20. [Google Scholar] [CrossRef]
- Jalil, M.; Asghar, S.; Imran, S.M. Self similar solutions for the flow and heat transfer of Powell-Eyring fluid over a moving surface in a parallel free stream. Int. J. Heat Mass Transf. 2013, 65, 73–79. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Radiation effects on the flow of Powell-Eyring fluid past an unsteady inclined stretching sheet with non-uniform heat source/sink. PLoS ONE 2014, 9, e103214. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Wang, W. A Frcatal model for water flow through unsaturated porous rocks. Fractals 2018, 26, 1840015. [Google Scholar] [CrossRef]
- Long, G.; Xu, G. Effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Chen, H.; Cia, H.; Deng, L. A Novel Fractal Model for Relative Permeability of Gas Diffusion Layer in Proton Exchange Membrane Fuel Cell with Capillary Pressure Effect. Fractals 2018. [Google Scholar] [CrossRef]
- Xiao, B.; Chen, H.; Xiao, S.; Cai, J. Research on Relative Permeability of Nanofibers with Capillary Pressure Effect by Means of Fractal-Monte Carlo Technique. J. Nanosci. Nanotechnol. 2017, 17, 6811–6817. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Fan, J.; Chen, H.; Hu, X.; Zhao, D.; Zhang, X.; Ren, W. Optimization of the fractal-like architecture of porous fibtous materials related to permeability, diffusivity and thermal conductivity. Fractals 2017, 25, 1750030. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Sarojamma, G.; Vajravelu, K.; Sreelakshmi, K. A study on entropy generation on thin film flow over an unsteady stretching sheet under the influence of magnetic field, thermocapillarity, thermal radiation and internal heat generation/absorption. Commun. Numer. Anal. 2017, 2, 141–156. [Google Scholar] [CrossRef]
- Soomro, F.A.; Haq, R.U.; Khan, Z.H.; Zhang, Q. Numerical study of entropy generation in MHD water-based carbon nanotubes along an inclined permeable surface. Eur. Phys. J. Plus 2017, 132, 412. [Google Scholar] [CrossRef]
- Mansour, R.B.; Sahin, Z. Entropy generation in developing laminar fluid flow through a circular pipe with variable properties. Heat Mass Transf. 2005, 42, 1–11. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohammadi, F.; Abbasbandy, S.; Alhuthali, M.S. Entropy Generation Analysis for Stagnation Point Flow in a Porous Medium over a Permeable Stretching Surface. J. Appl. Fluid Mech. 2015, 8, 753–765. [Google Scholar] [CrossRef]
- Bég, O.A.; Rashidi, M.M.; Kavyani, N.; Islam, M.N. Entropy generation in hydromagnetic convective on Karman swirling flow. Int. J. Appl. Math. Mech. 2013, 9, 37–65. [Google Scholar]
- Hayat, T.; Rafiq, M.; Ahmad, B.; Asghar, S. Entropy generation analysis for peristaltic flow of nanoparticles in a rotating frame. Int. J. Heat Mass Transf. 2017, 108, 1775–1786. [Google Scholar] [CrossRef]
- Nouri, D.; Pasandideh-Fard, M.; Oboodi, M.J.; Mahian, O.; Sahin, A.Z. Entropy generation analysis of nanofluid flow over a spherical heat source inside a channel with sudden expansion and contraction. Int. J. Heat Mass Transf. 2018, 116, 1036–1043. [Google Scholar] [CrossRef]
- Dalir, N.; Dehsara, M.; Nourazar, S.S. Entropy analysis for magnetohydrodynamic flow and heat transfer of a Jeffrey nanofluid over a stretching sheet. Energy 2015, 79, 351–362. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. Entropy generation optimization and unsteady squeezing flow of viscous fluid with five different shapes of nanoparticles. Physicochem. Eng. Asp. 2018, 554, 197–210. [Google Scholar] [CrossRef]
- Mohammad, I.; Gohar, A.; Shah, Z.; Islam, S.; Muhammad, S. Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet. Entropy 2018, 20, 412. [Google Scholar] [CrossRef]
- Makinde, O.D.; Eegunjobi, A.S. Effects of convective heating on entropy generation rate in a channel with permeable walls. Entropy 2013, 15, 220–233. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and das’ model. Entropy 2015, 18, 9. [Google Scholar] [CrossRef]
- Sheremet, M.; Pop, I.; Öztop, H.F.; Abu-Hamdeh, N. Natural convection of nanofluid inside a wavy cavity with a non-uniform heating: Entropy generation analysis. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 958–980. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer Flow of Radiative Carbon Nanotubes with Microstructure and Inertial Characteristics in the Rotating Frame. Case Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative Heat and Mass Transfer Analysis of Micropolar Nanofluid Flow of Casson Fluid between Two Rotating Parallel Plates with Effects of Hall Current. ASME J. Heat Transf. 2018. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The Elcerical MHD and Hall Current Impact on Micropolar Nanofluid Flow between Rotating Parallel Plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Khan, S.; Khan, W.; Khan, Z.A. Darcy–Forchheimer flow of micropolar nanofluid between two plates in the rotating frame with non-uniform heat generation/absorption. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, D.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liquids 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Lattice Boltzmann Method simulation of MHD non-Darcy nanofluid free convection. Physics B 2017, 516, 55–71. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann Method. J. Mol. Liquids 2017, 234, 364–374. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using Lattice Boltzmann Method. J. Mol. Liquids 2017, 231, 555–565. [Google Scholar] [CrossRef]
- Liao, S.J. An Explicit, Totally Analytic Approximate Solution for Blasius Viscous Flow Problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall, CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef] [PubMed]
- Jawad, M.; Shah, Z.; Islam, S.; Islam, S.; Bonyah, E.; Khan, Z.A. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018. [Google Scholar] [CrossRef]
- Khan, N.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 2018, 8, 115302. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Ali, A.; Sulaiman, M.; Islam, S.; Shah, Z.; Bonyah, E. Three-dimensional magnetohydrodynamic (MHD) flow of Maxwell nanofl uid containing gyrotactic micro-organisms with heat source/sink. AIP Adv. 2018, 8, 085303. [Google Scholar] [CrossRef]
- Hammed, H.; Haneef, M.; Shah, Z.; Islam, S.; Khan, W. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]



| Previous Result Ref. [3]. | Present Study | |||
|---|---|---|---|---|
| 0.5 | −1.29447 | −1.29876 | ||
| 0.7 | −1.39927 | −1.40331 | ||
| 0.9 | −1.50053 | −1.50452 | ||
| 1.1 | 1.0 | −1.59913 | −1.60303 | |
| 1.3 | −1.68426 | −1.68834 | ||
| 1.5 | −1.73747 | −1.74168 | ||
| 1.7 | 0.5 | −1.78810 | −1.79324 | |
| 0.6 | −1.81316 | −1.81795 | ||
| 0.7 | −1.84069 | −1.84533 |
| Previous Results, Ref [3]. | Present Study | |||
|---|---|---|---|---|
| 1.0 | 1.82770 | 1.82748 | ||
| 1.2 | 1.80574 | 1.80200 | ||
| 1.4 | 1.78404 | 1.77763 | ||
| 1.6 | 2.5 | 1.76259 | 1.75229 | |
| 2.6 | 1.79740 | 1.79024 | ||
| 2.7 | 1.83133 | 1.82557 | ||
| 2.8 | 0.3 | 1.85965 | 1.85951 | |
| 0.4 | 1.97571 | 1.97496 | ||
| 0.5 | 2.08693 | 2.08544 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, S.O.; Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S.; Khan, I. Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink. Appl. Sci. 2018, 8, 2588. https://doi.org/10.3390/app8122588
Alharbi SO, Dawar A, Shah Z, Khan W, Idrees M, Islam S, Khan I. Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink. Applied Sciences. 2018; 8(12):2588. https://doi.org/10.3390/app8122588
Chicago/Turabian StyleAlharbi, Sayer Obaid, Abdullah Dawar, Zahir Shah, Waris Khan, Muhammad Idrees, Saeed Islam, and I. Khan. 2018. "Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink" Applied Sciences 8, no. 12: 2588. https://doi.org/10.3390/app8122588
APA StyleAlharbi, S. O., Dawar, A., Shah, Z., Khan, W., Idrees, M., Islam, S., & Khan, I. (2018). Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink. Applied Sciences, 8(12), 2588. https://doi.org/10.3390/app8122588






