Magnetooptics in Cylindrical Structures
Abstract
1. Introduction
2. Maxwell Equations
3. Helmholtz Equations
4. A Simple Cylindrically Layered Structure
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Relations among Amplitudes
Appendix B. Recursion Relations
References
- Collin, R.E. Foundation for Microwave Engineering, 2nd ed.; Wiley Interscience: New York, NY, USA, 2001; pp. 450–476. ISBN 0-7803-6031-1. [Google Scholar]
- Yeh, P. Optics of anisotropic layered media: A new 4 × 4 matrix algebra. Surf. Sci. 1980, 96, 41–53. [Google Scholar] [CrossRef]
- Gismyatov, I.F.; Sementsov, D.I. Magneto-Optical Effects upon Reflection of Light from a Ferrodielectric with an Arbitrary Orientation of Magnetization. Opt. Spectrosc. 2002, 92, 588–592. [Google Scholar] [CrossRef]
- Bukhanko, A.F. Effects of Nonreciprocity in Structure with Noncollinear Orientation of Magnetization of Layers. Opt. Spectrosc. 2011, 110, 281–286. [Google Scholar] [CrossRef]
- Tabor, W.J.; Chen, F.S. Electromagnetic Propagation through Materials Possessing Both Faraday Rotation and Birefringence: Experiments with Ytterbium Orthoferrite. J. Appl. Phys. 1969, 40, 2760–2765. [Google Scholar] [CrossRef]
- Tien, P.K. Integrated optics and new wave phenomena in optical waveguides. Rev. Mod. Phys. 1977, 49, 361–419. [Google Scholar] [CrossRef]
- Stadler, B.J.H.; Mizumoto, T. Integrated Magneto-Optical Materials and Isolators: A Review. IEEE Photonics J. 2014, 6, 0600215. [Google Scholar] [CrossRef]
- Gloge, D. Weakly guiding fibers. Appl. Opt. 1971, 10, 2252–2258. [Google Scholar] [CrossRef] [PubMed]
- Marcuse, D. Theory of Dielectric Optical Waveguides; Academic Press: New York, NY, USA; London, UK, 1974; Chapter 2; pp. 60–78. ISBN 0-12-470950-8. [Google Scholar]
- Snyder, A.W. Understanding Monomode Optical Fibers. Proc. IEEE 1981, 69, 6–13. [Google Scholar] [CrossRef]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Chapman & Hall: London, UK; New York, NY, USA; Tokyo, Japan; Mebourne, Australia; Madras, India, 1991; Chapter 11; pp. 220–226, Chapter 13, pp. 280–290; ISBN 0-412-24250-8. [Google Scholar]
- Yoshino, T. Theory for the Faraday effect in optical fiber. J. Opt. Soc. Am. B 2005, 22, 1856–1860. [Google Scholar] [CrossRef]
- Bozinovic, N.; Golowich, S.; Kristensen, P.; Ramachandran, S. Control of orbital angular momentum of light with optical fibers. Opt. Lett. 2012, 37, 2451–2453. [Google Scholar] [CrossRef]
- Kales, M.L. Modes in Wave Guides Containing Ferrites. J. Appl. Phys. 1954, 24, 604–608. [Google Scholar] [CrossRef]
- Fallahkhair, A.B.; Li, K.S.; Murphy, T.E. Vector Finite Difference Modesolver for Anisotropic Dielectric Waveguides. J. Ligthtw. Technol. 2008, 26, 1423–1431. [Google Scholar] [CrossRef]
- Pintus, P. Accurate vectorial finite element mode solver for magneto-optic and anisotropic waveguides. Opt. Express 2014, 22, 15737–15756. [Google Scholar] [CrossRef]
- Epstein, P.S. Theory of Wave Propagation in a Gyromagnetic Medium. Rev. Mod. Phys. 1956, 28, 3–17. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Electrodynamique de Milieux Continus; Editions Mir: Moscou, Russia, 1969; Chapitre XI; pp. 429–438. [Google Scholar]
- Pershan, P.S. Magneto-optical effects. J. Appl. Phys. 1967, 38, 1482–1490. [Google Scholar] [CrossRef]
- Freiser, M.J. A Survey of Magnetooptical Effects. IEEE Trans. Magn. 1968, 4, 152–161. [Google Scholar] [CrossRef]
- Dillon, J.F., Jr. Origin and Uses of the Faraday Rotation in Magnetic Crystals. J. Appl. Phys. 1968, 39, 922–929. [Google Scholar] [CrossRef]
- Suits, J.C. Faraday and Kerr Effects in Magnetic Compounds. IEEE Trans. Magn. 1972, 8, 95–105. [Google Scholar] [CrossRef]
- Wettling, W. Magneto-optics in ferrites. J. Magn. Magn. Mater. 1976, 3, 147–160. [Google Scholar] [CrossRef]
- Wangsness, R.K. Susceptibility Tensor and the Faraday Effect in Ferrimagnets. Phys. Rev. 1954, 95, 339–345. [Google Scholar] [CrossRef]
- Krinchik, G.S.; Chetkin, M.V. The problem of determining the dielectric perfmittivity and magnetic permeability tensors of a medium. Sov. Phys. JETP 1959, 36, 1368–1369. [Google Scholar]
- Krinchik, G.S.; Chetkin, M.V. Exchange interaction and magneto-optical effects in ferrite garnets. Sov. Phys. JETP 1962, 14, 485–703. [Google Scholar]
- Chetkin, M.V.; Shalygin, A.N. The Faraday Effect in Garnets in the Infrared Region. J. Appl. Phys. 1968, 39, 561–562. [Google Scholar] [CrossRef]
- Krinchik, G.S.; Gushchin, V.S.; Tsidaeva, N.I. Temperature-independent Faraday effect in rare-earth iron garnets. Sov. Phys. JETP 1984, 59, 410–414. [Google Scholar]
- Druzhinin, A.V.; Lobov, I.D.; Mayevskiy, V.M. A new gyromagnetic effect in the optical frequency range. Pis. Zh. Tekh. Fiz. 1985, 11, 879–882. [Google Scholar]
- Višňovský, Š. Helmholtz Equation in Transverse Circular Representation. Prog. Electromagn. Res. M 2017, 59, 161–170. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogeneous Media; Series on Electromagnetic Waves; IEEE Press: New York, NY, USA, 1995; Chapter 1; p. 22. ISBN 0-7803-4749-8. [Google Scholar]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists; Elsevier Academic Press: Burlington, NJ, USA; San Diego, CA, USA; London, UK, 2005; Chapters 2, 9 and 11; ISBN 0-12-088584-0. [Google Scholar]
- Marcuse, D. Light Transmission Optics; Van Nostrand Reinhold Company: London, UK; Toronto, ON, Canada; Melbourne, Australia, 1972; Chapter 8; pp. 288–305. [Google Scholar]
- Kong, J.A. Electromagnetic Wave Theory; EMW Publishing: Cambridge, MA, USA, 2000; Chapter 3; pp. 450–460. ISBN 0-9668143-9-8. [Google Scholar]
- Anderson, N.R.; Camley, R.E. Multilayer magnetic waveguides: Optimizing nonreciprocal propagation. J. Appl. Phys. 2014, 116, 023903. [Google Scholar] [CrossRef]
- Cooper, R.W.; Crossley, W.A.; Page, J.L.; Pearson, R.F. Faraday Rotation in YIG and TbIG. J. Appl. Phys. 1968, 39, 565–567. [Google Scholar] [CrossRef]
- Doormann, V.; Krumme, J.-P.; Lenz, H. Optical and magneto-optical tensor spectra of bismuth substituted yttrium iron garnet films. J. Appl. Phys. 1990, 68, 3544–3553. [Google Scholar] [CrossRef]
- Sekijima, T.; Funakoshi, T.; Katabe, K.; Tahara, K.; Fujii, T.; Wakino, K.; Okada, M. Growth and Optical Properties of Ce-substituted Fibrous YIG Single Crystals. Jpn. J. Appl. Phys. 1998, 37, 4854–4857. [Google Scholar] [CrossRef]
- Dulal, P.; Block, A.D.; Gage, T.E.; Haldren, H.A.; Sung, S.-Y.; Hutchings, D.C.; Stadler, B.J.H. Optimized Magneto-optical Isolator Designs Inspired by Seedlayer-Free Terbium Iron Garnets with Opposite Chirality. ACS Photonics 2016, 3, 1818–1825. [Google Scholar] [CrossRef]
- Bi, L.; Hu, J.; Jiang, P.; Kim, H.S.; Kim, D.H.; Onbasli, M.C.; Dionne, G.F.; Ross, C.A. Magneto-Optical Thin Films for On-Chip Monolithic Integration of Non-Reciprocal Photonic Devices. Materials 2013, 6, 5094–5117. [Google Scholar] [CrossRef]
- Bohnert, K.; Gabus, P.; Nehring, J.; Braendle, H.; Brunzel, M.G. Fiber-Optic Current Sensor for Electrowinning of Metals. J. Lightw. Technol. 1990, 25, 3544–3553. [Google Scholar] [CrossRef]
- Huang, D.; Srinivasan, S.; Bowers, J.E. Compact Tb doped fiber optic current sensor with high sensitivity. Opt. Express 2015, 23, 247221. [Google Scholar] [CrossRef]
- Andronova, I.A.; Malykin, G.B. Physical problems of fiber gyroscopy based on Sagnac effect. Phys.-Usp. 2002, 45, 793–817. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogeneous Media; Series on Electromagnetic Waves; IEEE Press: New York, NY, USA, 1995; Chapter 3; pp. 161–181. ISBN 0-7803-4749-8. [Google Scholar]
- Snyder, A.W.; Sammut, R.A. Fundamental (HE11) modes of graded optical fibers. J. Opt. Soc. Am. 1979, 69, 1663–1671. [Google Scholar] [CrossRef]
- Fan, F.; Chen, S.; Chang, S.-J. A Review of Magneto-Optical Microstructure Devices at Terahertz Frequencies. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 8500111. [Google Scholar] [CrossRef]
- Firby, C.J.; Elezzabi, A.Y. High-speed nonreciprocal magnetoplasmonic waveguide phase shifter. Optica 2015, 2, 598–606. [Google Scholar] [CrossRef]
- Goell, J.E. A circular-harmonic computer analysis of rectangular dielectric waveguide. Bell Syst. Tech. J. 1969, 48, 2133–2160. [Google Scholar] [CrossRef]
- Pollock, J.G.; Iyer, A.K.; Pratap, D.; Ramakrishna, S.A. A class of circular waveguiding structures containing cylindrically anisotropic metamaterials: Applications from radio frequency/microwave to optical frequencies. J. Appl. Phys. 2016, 119, 083103. [Google Scholar] [CrossRef]
- Poladian, L.; Straton, M.; Docherty, A.; Argyros, A. Pure chiral optical fibres. Opt. Express 2011, 19, 968–980. [Google Scholar] [CrossRef] [PubMed]
- Baltenkov, A.S.; Msezane, A.Z. Electronic quantum confinement in cylindrical potential well. Eur. Phys. J. D 2016, 70, 81. [Google Scholar] [CrossRef]

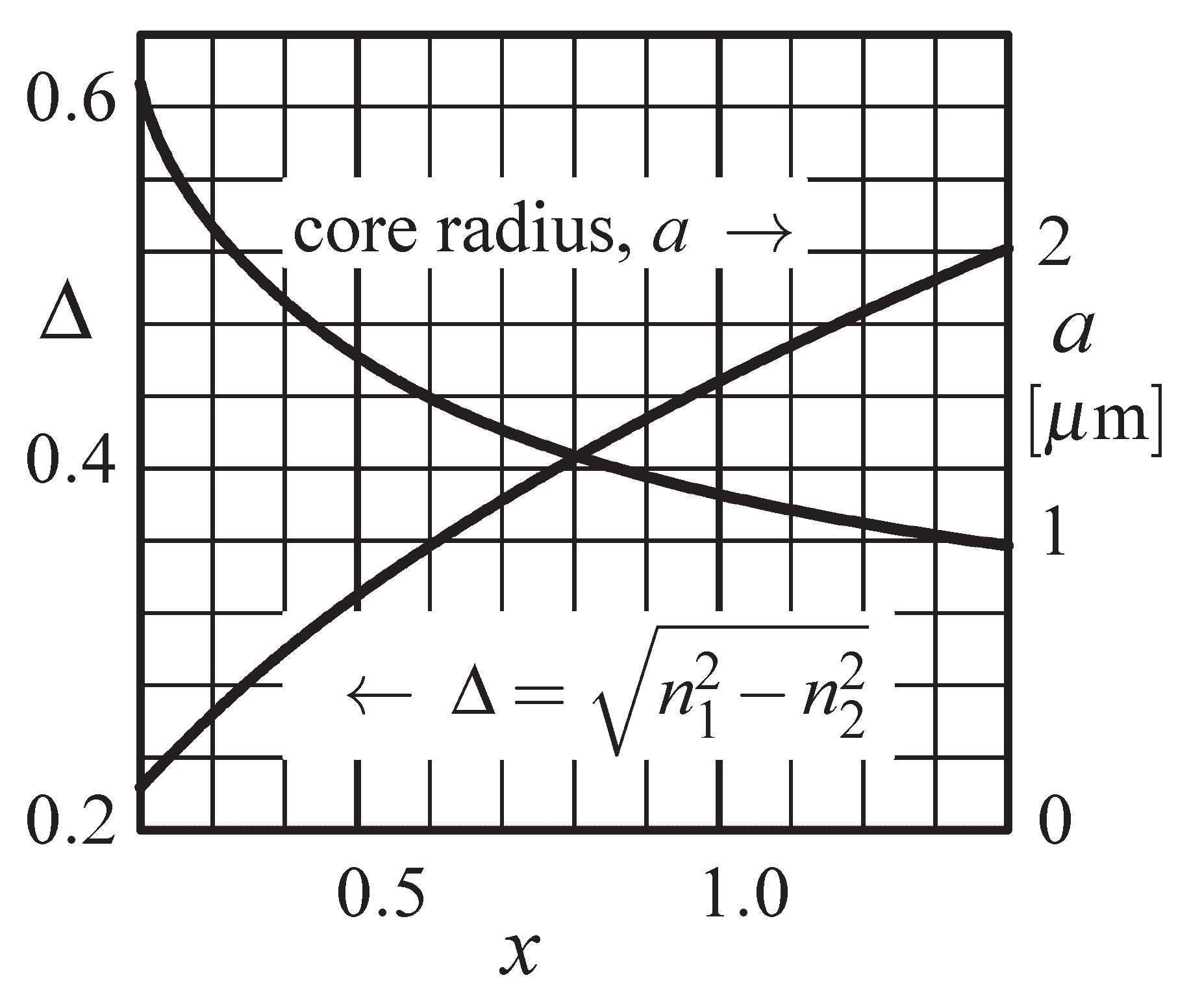
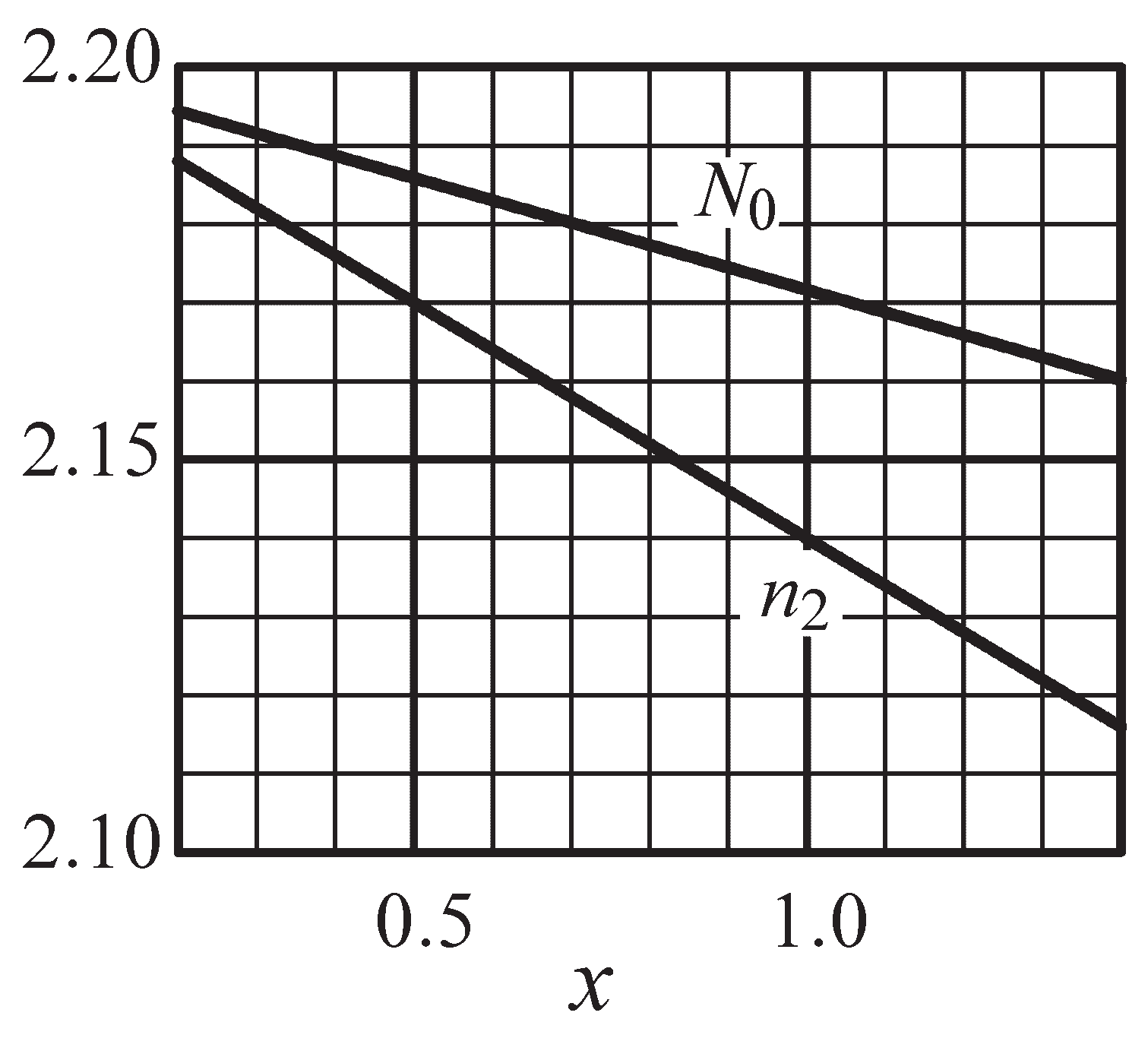
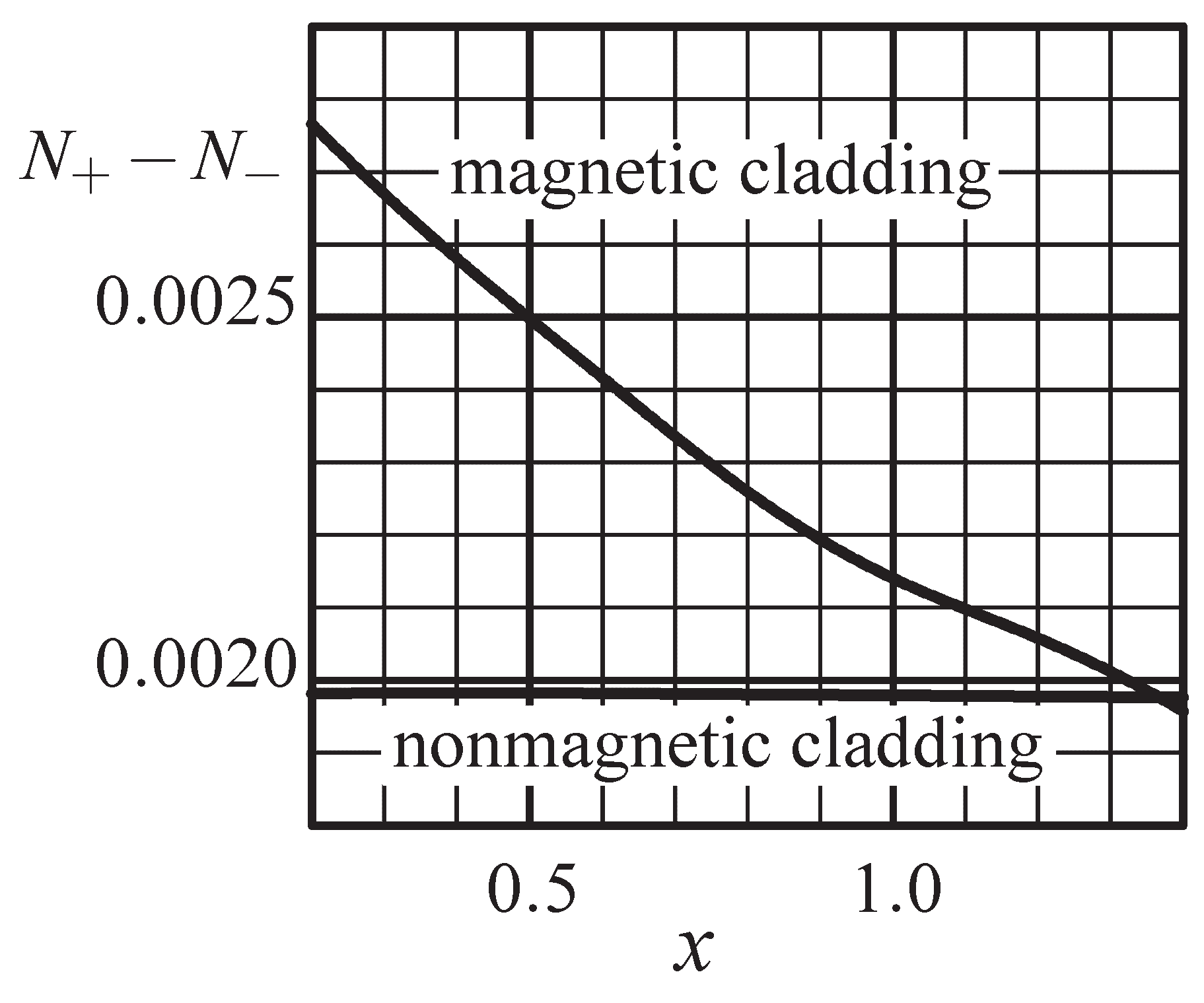
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|---|---|
| n | 2.200 | 2.188 | 2.176 | 2.164 | 2.152 | 2.140 | 2.128 | 2.116 |
| 1 | 0.806 | 0.617 | 0.450 | 0.289 | 0.167 | 0.083 | −0.022 | |
| 2 | 1.611 | 1.233 | 0.90 | 0.578 | 0.333 | 0.167 | −0.044 | |
| 1 | 0.806 | 0.617 | 0.450 | 0.289 | 0.167 | 0.083 | −0.022 |
| x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|---|
| 2.188 | 2.176 | 2.164 | 2.152 | 2.140 | 2.128 | 2.116 | |
| 0.229469 | 0.324074 | 0.396363 | 0.457051 | 0.510294 | 0.558226 | 0.602116 | |
| V | 2.40082 | 2.40011 | 2.40045 | 2.39929 | 2.39953 | 2.39863 | 2.39929 |
| a [m] | 2.581 | 1.827 | 1.494 | 1.295 | 1.160 | 1.060 | 0.983 |
| 2.19435 | 2.18869 | 2.18302 | 2.17732 | 2.17162 | 2.16589 | 2.16017 | |
| [m] | 1.479 | 1.048 | 0.858 | 0.745 | 0.668 | 0.6116 | 0.568 |
| x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|---|
| 1.98134 | 1.98262 | 1.98182 | 1.98028 | 1.97902 | 1.97756 | 1.97642 | |
| 2.76591 | 2.58059 | 2.41696 | 2.25978 | 2.14032 | 2.05772 | 1.95713 | |
| d [m] | 140.099 | 150.159 | 160.325 | 171.477 | 181.048 | 188.315 | 197.994 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Višňovský, Š. Magnetooptics in Cylindrical Structures. Appl. Sci. 2018, 8, 2547. https://doi.org/10.3390/app8122547
Višňovský Š. Magnetooptics in Cylindrical Structures. Applied Sciences. 2018; 8(12):2547. https://doi.org/10.3390/app8122547
Chicago/Turabian StyleVišňovský, Štefan. 2018. "Magnetooptics in Cylindrical Structures" Applied Sciences 8, no. 12: 2547. https://doi.org/10.3390/app8122547
APA StyleVišňovský, Š. (2018). Magnetooptics in Cylindrical Structures. Applied Sciences, 8(12), 2547. https://doi.org/10.3390/app8122547





