Correct Stability Condition and Fundamental Performance Analysis of the α-β-γ-δ Filter
Abstract
:Featured Application
Abstract
1. Introduction
2. The --- Filter
2.1. Problem Definition
2.2. Fundamental Properties Obtained in Conventional Studies
2.2.1. Transfer Function and Stability Conditions
2.2.2. Relationship to Kalman Filter
2.2.3. Relationship to the - and -- Filters
2.2.4. Performance Analysis Method
3. Derivation of Correct Stability Condition
4. Steady-State Performance Index and Optimal Gains
4.1. Derivation of Tracking Performance Index
4.2. Derivation of Smoothing Performance Index
4.3. Comparison of Performance Indices with Those of Conventional Filters
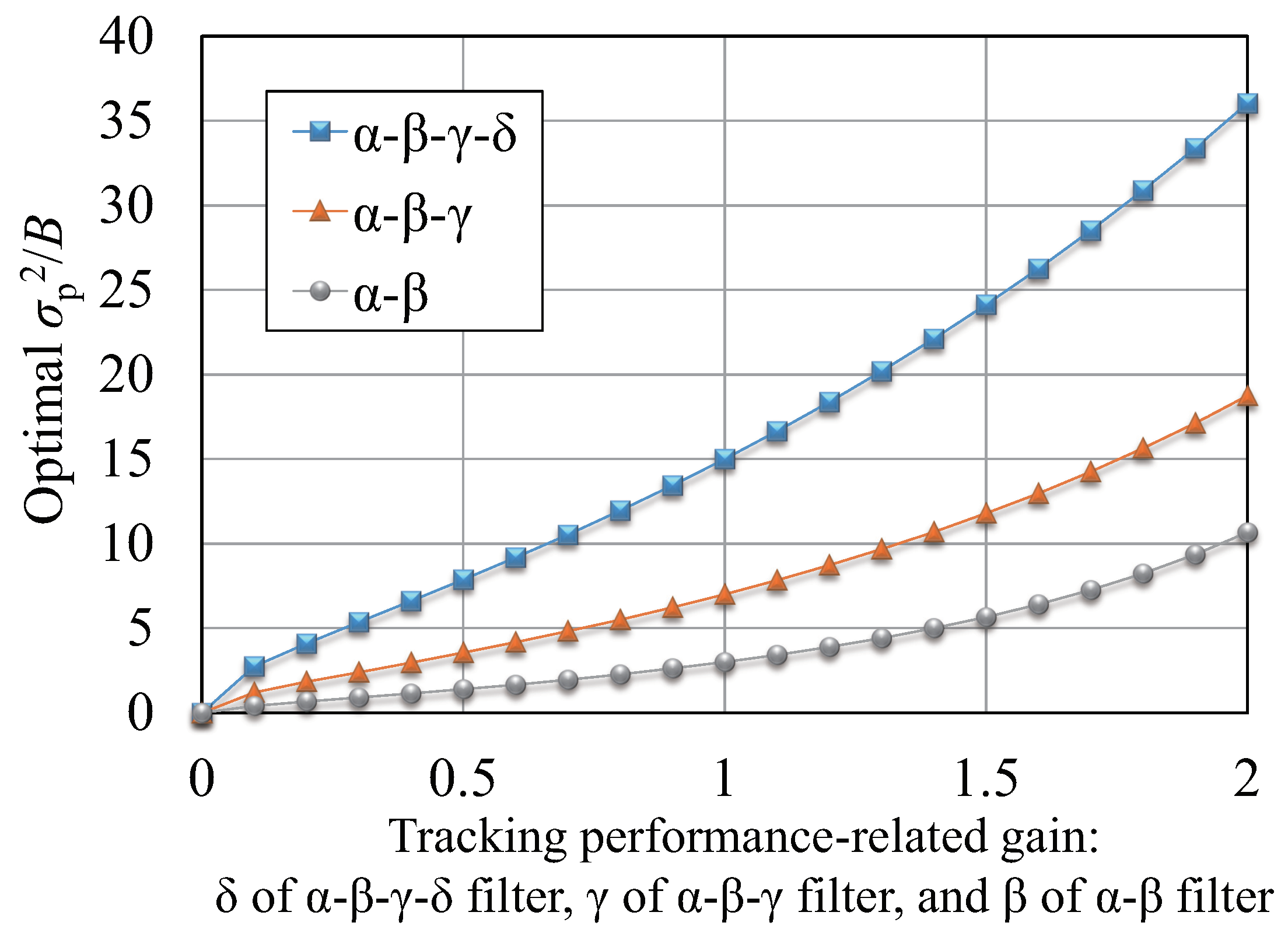
4.4. Calculation of Optimal Smoothing Performance
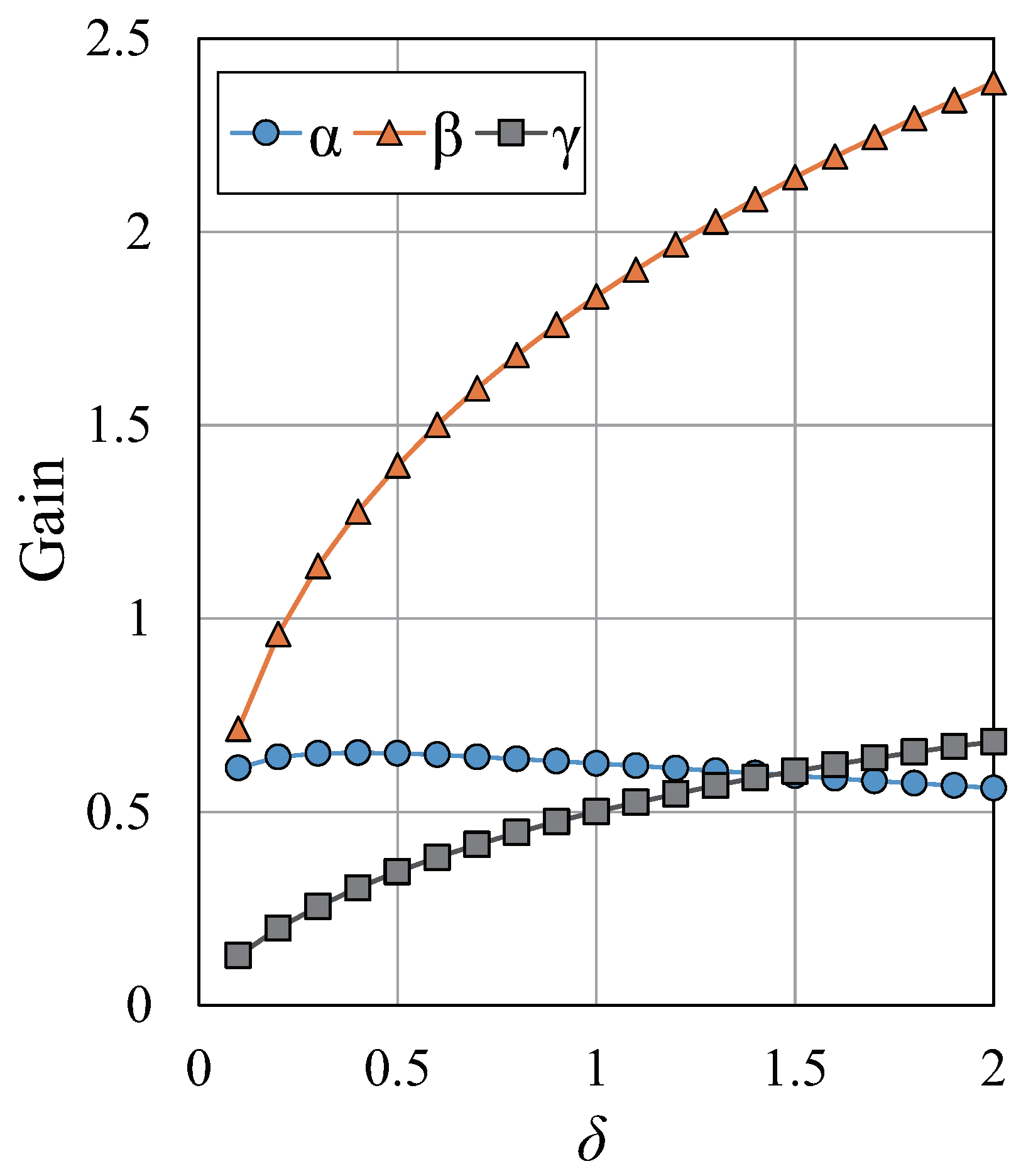
5. Theoretical Analysis Using Performance Indices
6. Numerical Simulation
- Simple-maneuvering target assuming constant acceleration or jerk motion.
- High-maneuvering target assuming complicated motion.
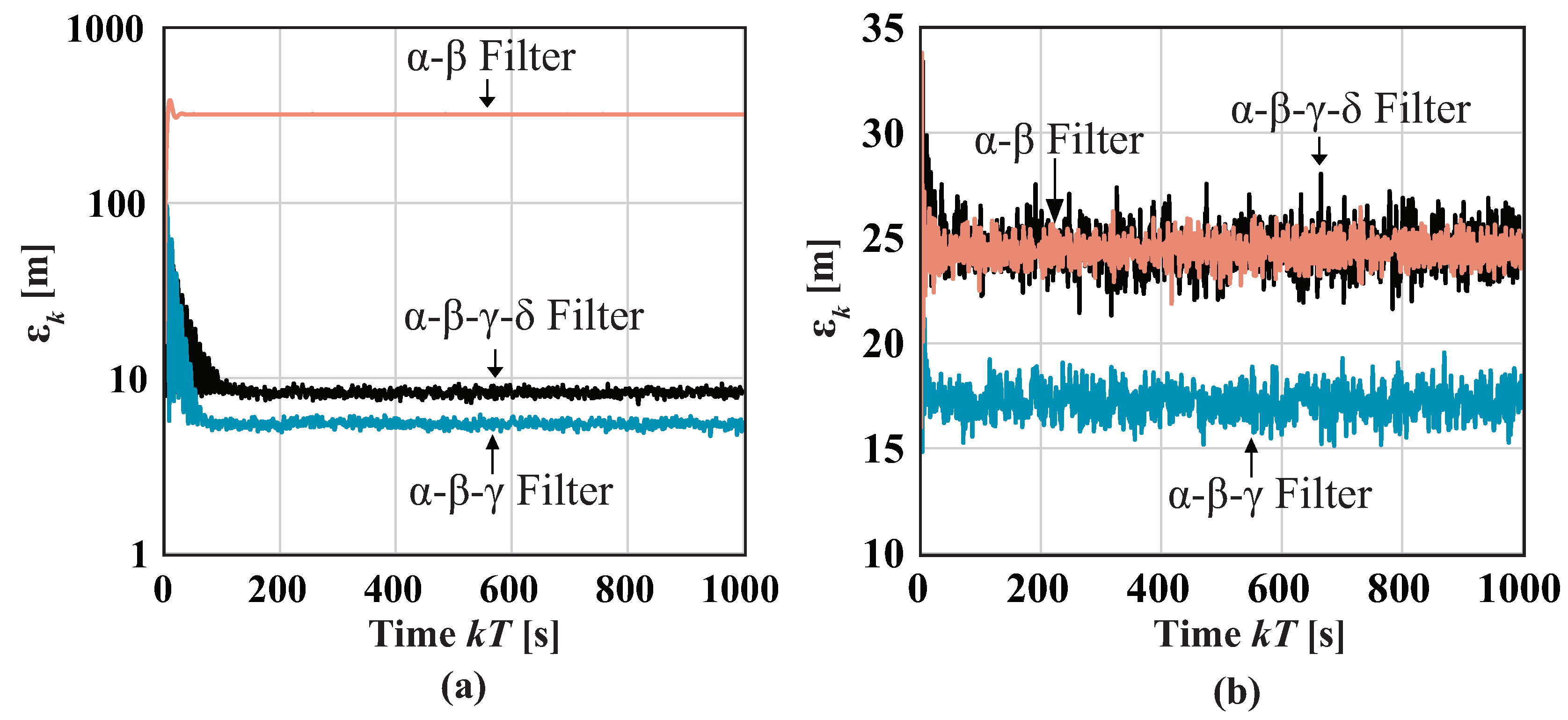
6.1. Tracking of Simple-Maneuvering Target
- Low gain case: ( = 0.266, = 0.1) for the - filter, ( = 0.738, = 0.165, = 0.1) for the -- filter, and ( = 0.613, = 0.715, = 0.128, = 0.1) for the --- filter.
- High gain case: ( = 0.475, = 1.5) for the - filter, ( = 1.354, = 0.560, = 1.5) for the -- filter, and ( = 0.593, = 2.14, = 0.605, = 1.5) for the --- filter.
6.1.1. Scenario 1: Constant Acceleration Target
6.1.2. Scenario 2: Constant-Jerk Target
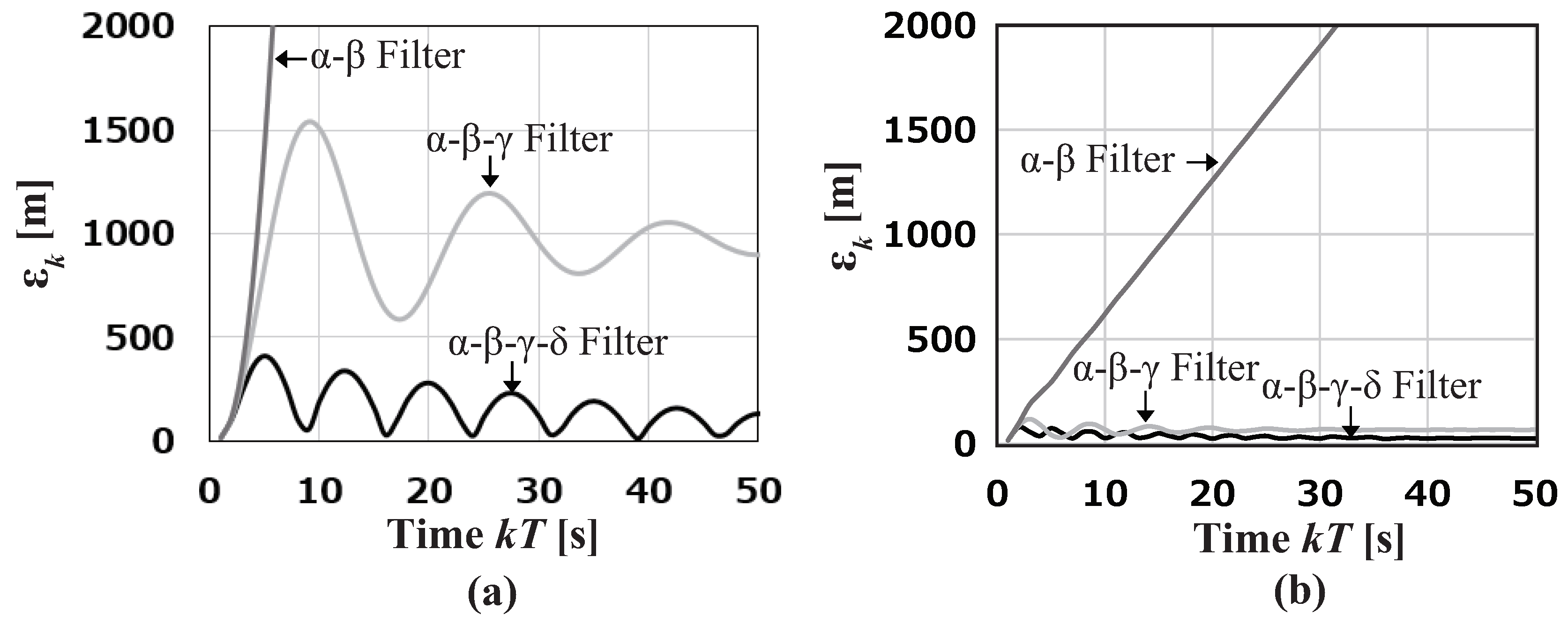
6.2. Tracking of High-Maneuvering Target
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. An Example of Unstable Case that Satisfy the Conventional Stability Conditions
Appendix B. Jury’s Stability Test for α-β-γ-δ Filter
| Row | |||||
|---|---|---|---|---|---|
| a | |||||
| b | |||||
| c | |||||
Appendix C. Derivation of the Tracking Performance Index
Appendix D. Derivation of the Smoothing Performance Index
References
- Liu, Z.; Fu, X.; Gao, X. Co-Optimization of Communication and Sensing for Multiple Unmanned Aerial Vehicles in Cooperative Target Tracking. Appl. Sci. 2018, 8, 899. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Dogancay, K. Instrumental Variable Based Kalman Filter Algorithm for Three-Dimensional AOA Target Tracking. IEEE Sign. Process. Lett. 2018, 25, 1605–1609. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, F.; Zhu, W.; Bai, G.; Yan, L. A Hybrid Model Algorithm for Hypersonic Glide Vehicle Maneuver Tracking Based on the Aerodynamic Model. Appl. Sci. 2017, 7, 159. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Ge, J.; Lu, W.; Zong, B. Adaptive Strong Tracking Square-Root Cubature Kalman Filter for Maneuvering Aircraft Tracking. IEEE Access 2018, 6, 10052–10061. [Google Scholar] [CrossRef]
- Li, T.; Corchado, J.M.; Bajo, J.; Sun, S.; Paz, J.F.D. Effectiveness of Bayesian filters: An information fusion perspective. Inf. Sci. 2016, 329, 670–689. [Google Scholar] [CrossRef]
- Saho, K.; Takahashi, Y.; Masugi, M. Moving object tracker using sensor fusion of ultrasonic range finder and accelerometer. J. Int. Counc. Electric. Eng. 2017, 7, 34–40. [Google Scholar] [CrossRef]
- Yazdani, M.; Gamble, G.; Henderson, G.; Nielsen, R.H. A simple control policy for achieving minimum jerk trajectories. Neural Netw. 2012, 27, 74–80. [Google Scholar] [CrossRef] [PubMed]
- Ekstrand, B. Some aspects on filter design for target tracking. J. Control Sci. Eng. 2012, 2012, 10. [Google Scholar] [CrossRef]
- Kosuge, Y.; Ito, M. Evaluating an α-β filter in terms of increasing a track update-sampling rate and improving measurement accuracy. Electron. Commun. Jpn. Part I Commun. 2003, 86, 10–20. [Google Scholar] [CrossRef]
- Matsunami, I.; Nakamura, R.; Kajiwara, A. Target State Estimation Using RCS Characteristics for 26GHz Short-Range Vehicular Radar. In Proceedings of the 2013 International Conference on Radar, Adelaide, Australia, 9–12 September 2013; pp. 304–308. [Google Scholar]
- Tenne, D.; Singh, T. Characterizing performance of α-β-γ filters. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1072–1087. [Google Scholar] [CrossRef]
- Kosuge, Y.; Ito, M. A necessary and sufficient condition for the stability of an α-β-γ filter. In Proceedings of the 40th SICE Annual Conference, Nagoya, Japan, 25–27 July 2001; pp. 7–12. [Google Scholar]
- Saho, K.; Masugi, M. Performance analysis of α-β-γ filters using position and velocity measurements. EURASIP J. Adv. Sign. Process. 2015, 2015, 35. [Google Scholar] [CrossRef]
- Wu, C.M.; Lin, P.P.; Han, Z.Y.; Li, S.R. Simulation-based Optimal Design of α-β-γ-δ Filter. Int. J. Autom. Comput. 2010, 7, 247–253. [Google Scholar] [CrossRef]
- Wu, C.M. Adaptive parameters for tracking filters innovation system. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Yu, T.Y.; Wu, C.M. Application of Adaptive α-β-γ and α-β-γ-δ Filter to Tracking Systems. Sens. Mater. 2017, 29, 419–427. [Google Scholar]
- Jeong, T.G.; Pan, B.F.; Njonjo, A.W. A Study of Optimization of α-β-γ-η Filter for Tracking a High Dynamic Target. J. Korean Navig. Port Res. 2017, 11, 297–302. [Google Scholar] [CrossRef]
- Jury, E.I. Theory and Application of the z-Transform Method; John Wiley and Sons: New York, NY, USA, 1964. [Google Scholar]
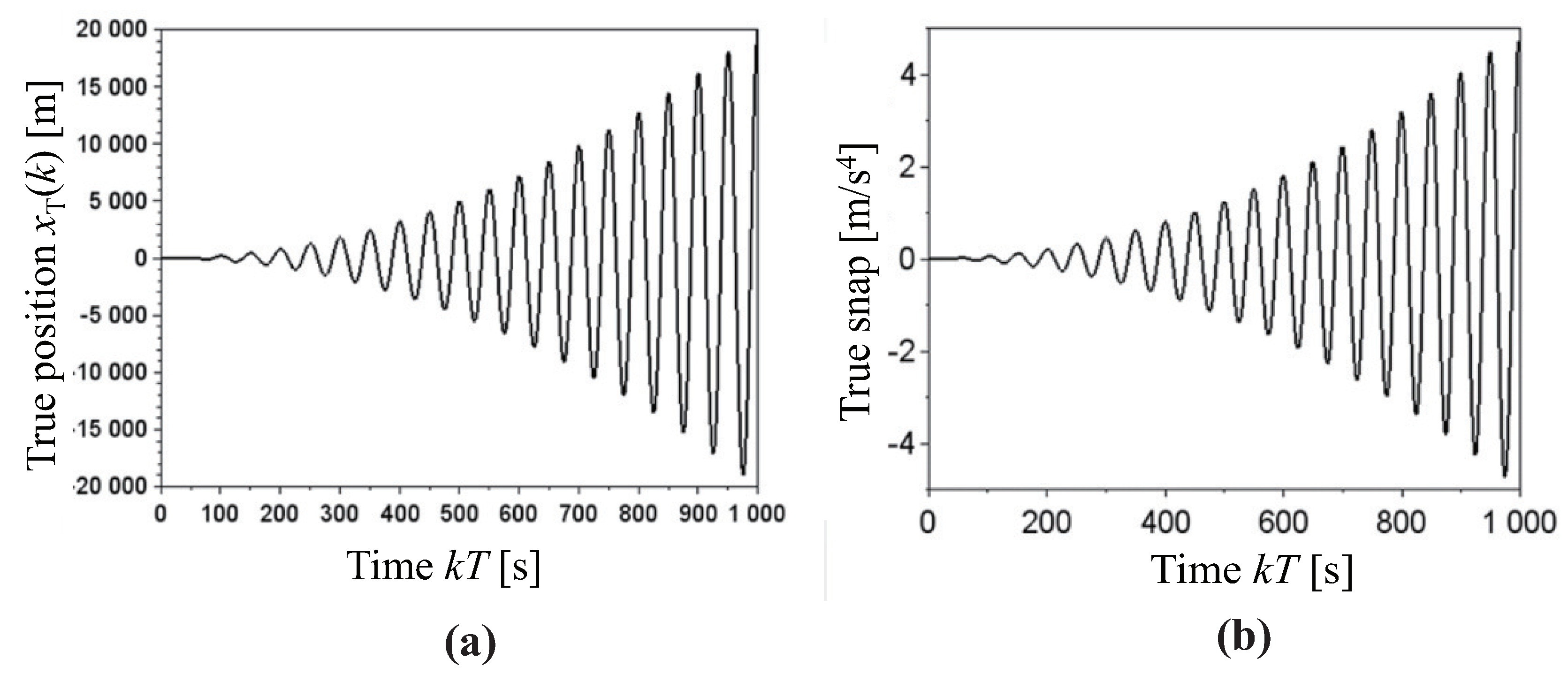
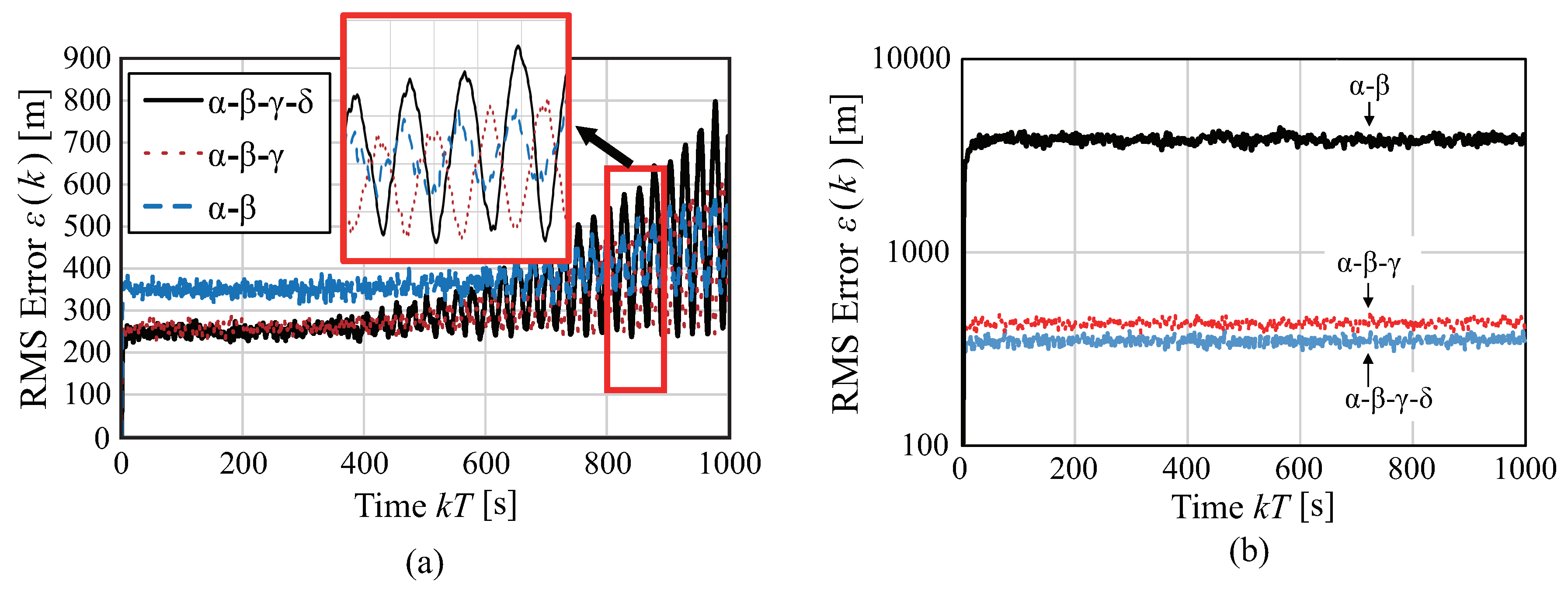
| Variables | Description | Unit |
|---|---|---|
| T | Sampling interval | [s] |
| k | Discrete sampling index | Dimensionless |
| Parameter at index k | ||
| Predicted position | [m] | |
| Predicted velocity | [m/s] | |
| Predicted acceleration | [m/s] | |
| Predicted jerk | [m/s] | |
| Smoothed (estimated) position | [m] | |
| Smoothed (estimated) velocity | [m/s] | |
| Smoothed (estimated) acceleration | [m/s] | |
| Smoothed (estimated) jerk | [m/s] | |
| Observed (measured) position | [m] | |
| Filter gain for | Dimensionless | |
| Filter gain for | Dimensionless | |
| Filter gain for | Dimensionless | |
| Filter gain for | Dimensionless | |
| Error variance of | [m] | |
| E | Mean with respect to k | |
| Smoothing performance index | [m] | |
| Tracking performance index | [m] | |
| Snap assumed in the derivation of | [m/s] | |
| RMS prediction error of Monte Carlo simulations | [m] |
| Tracking Performance (Normalized) | Smoothing Performance (Normalized) | |
|---|---|---|
| - filter | [8] | [8] |
| -- filter | [13] | [13] |
| --- filter | (Equation (43)) | Equations (45)–(47) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shibata, T.; Saho, K. Correct Stability Condition and Fundamental Performance Analysis of the α-β-γ-δ Filter. Appl. Sci. 2018, 8, 2523. https://doi.org/10.3390/app8122523
Shibata T, Saho K. Correct Stability Condition and Fundamental Performance Analysis of the α-β-γ-δ Filter. Applied Sciences. 2018; 8(12):2523. https://doi.org/10.3390/app8122523
Chicago/Turabian StyleShibata, Takanori, and Kenshi Saho. 2018. "Correct Stability Condition and Fundamental Performance Analysis of the α-β-γ-δ Filter" Applied Sciences 8, no. 12: 2523. https://doi.org/10.3390/app8122523
APA StyleShibata, T., & Saho, K. (2018). Correct Stability Condition and Fundamental Performance Analysis of the α-β-γ-δ Filter. Applied Sciences, 8(12), 2523. https://doi.org/10.3390/app8122523





