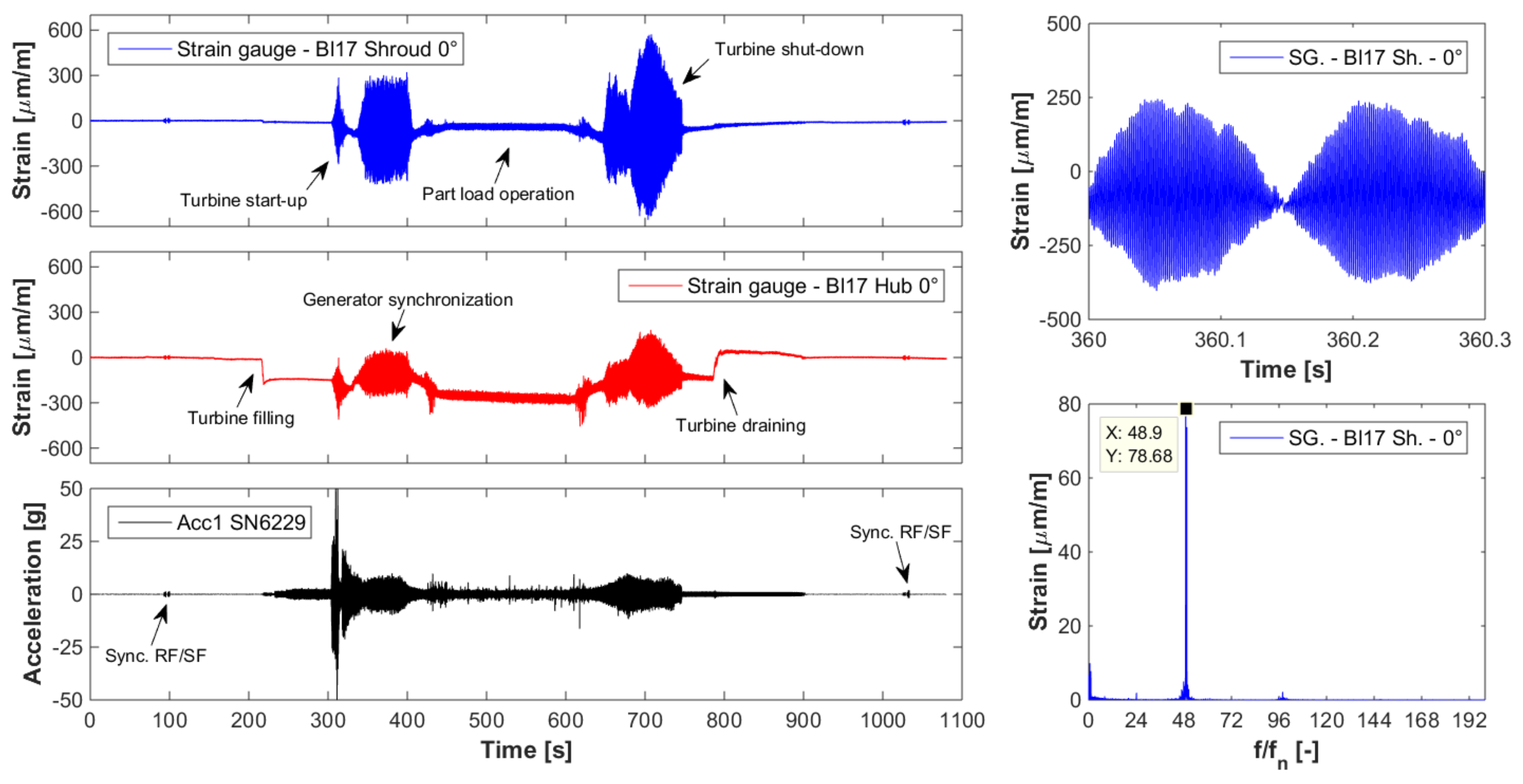
Figure 1.
Evidence of harmful structural loading of the turbine runner blades during the normal start-up and shut-down procedures. Signals recorded with the onboard instrumentation [
37].
Figure 1.
Evidence of harmful structural loading of the turbine runner blades during the normal start-up and shut-down procedures. Signals recorded with the onboard instrumentation [
37].
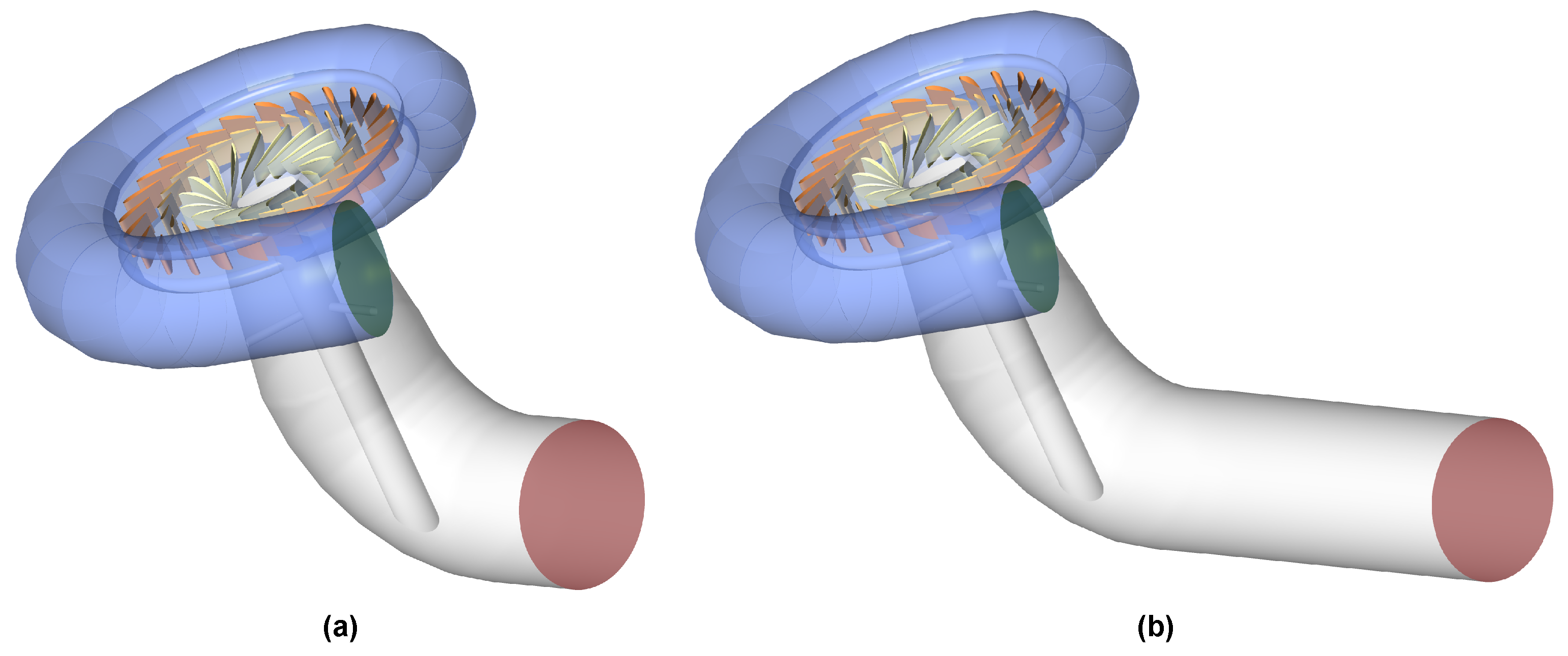
Figure 2.
(a) View of the CFD domain with the standard draft tube. (b) View of the CFD domain with the extended draft tube.
Figure 2.
(a) View of the CFD domain with the standard draft tube. (b) View of the CFD domain with the extended draft tube.
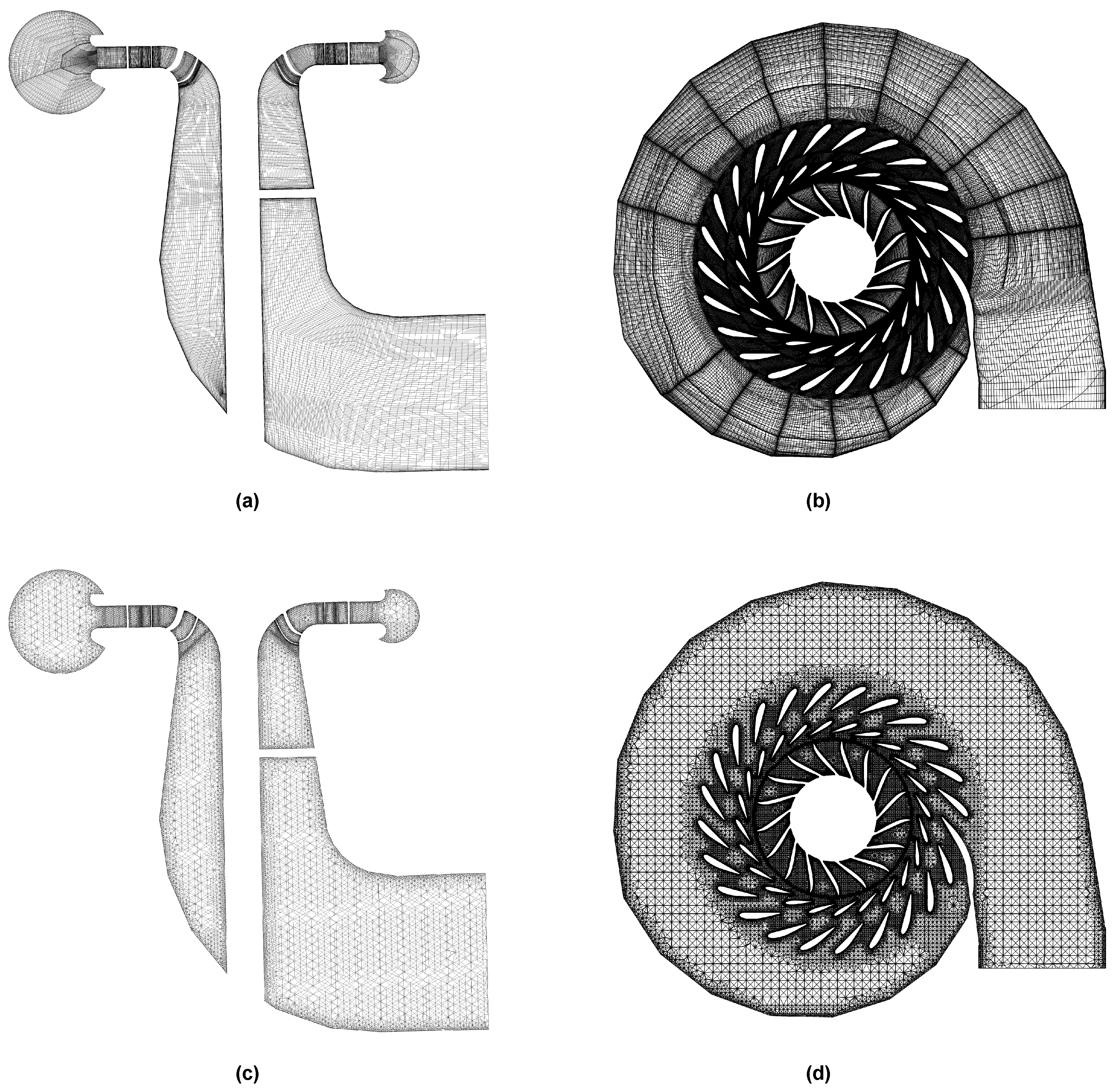
Figure 3.
(a) Structured hexahedral mesh, meridional plane view. (b) Structured hexahedral mesh, zero machine plane view. (c) Unstructured mesh, meridional plane view. (d) Unstructured mesh, zero machine plane view.
Figure 3.
(a) Structured hexahedral mesh, meridional plane view. (b) Structured hexahedral mesh, zero machine plane view. (c) Unstructured mesh, meridional plane view. (d) Unstructured mesh, zero machine plane view.
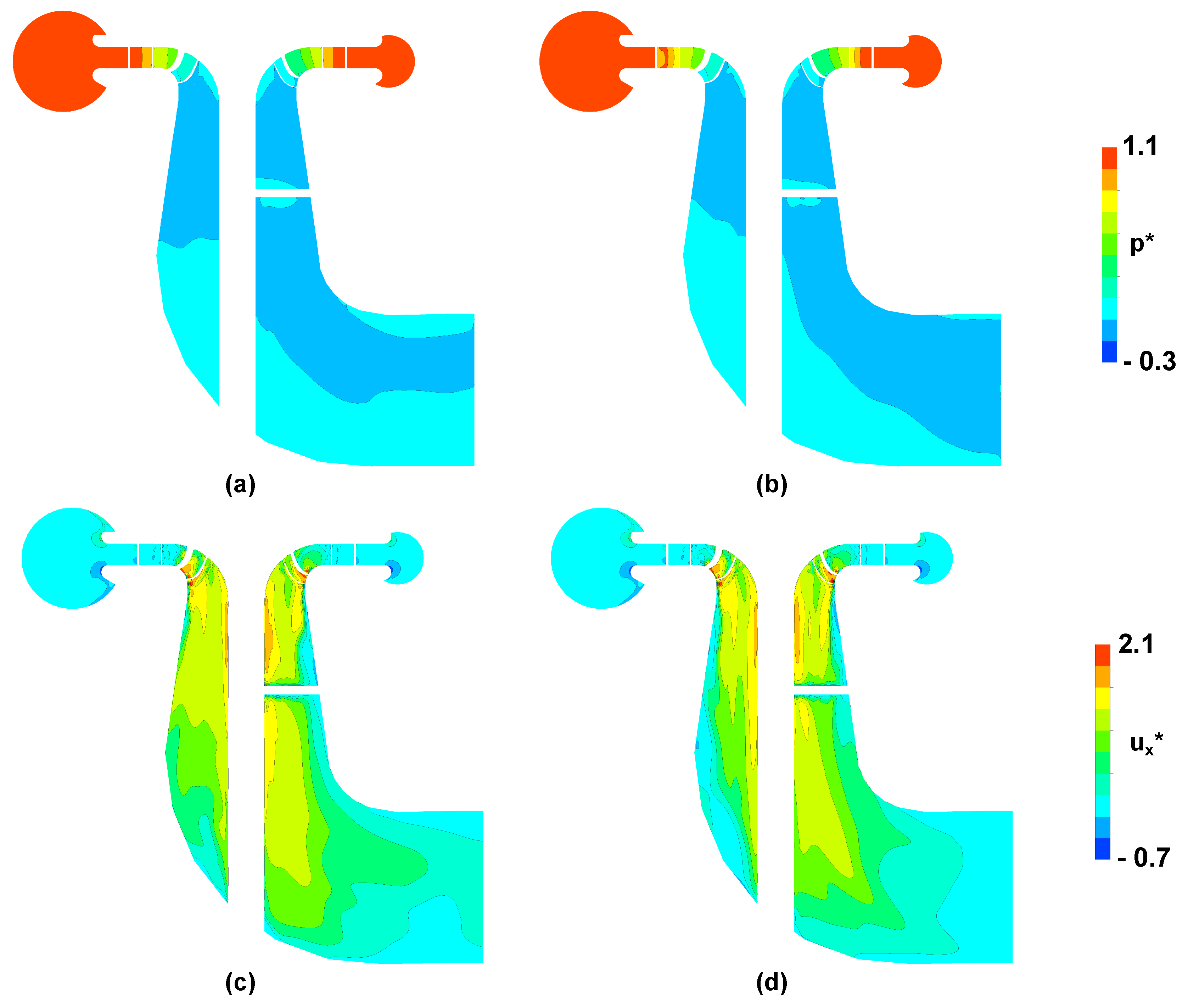
Figure 4.
(a) Dimensionless pressure contours on the meridional plane, CFD1 structured mesh, BEP. (b) Dimensionless pressure contours on the meridional plane, CFD2 refined structured mesh, BEP. (c) Dimensionless axial velocity contours on the meridional plane, CFD1 structured mesh, BEP. (d) Dimensionless axial velocity contours on the meridional plane, CFD2 refined structured mesh, BEP.
Figure 4.
(a) Dimensionless pressure contours on the meridional plane, CFD1 structured mesh, BEP. (b) Dimensionless pressure contours on the meridional plane, CFD2 refined structured mesh, BEP. (c) Dimensionless axial velocity contours on the meridional plane, CFD1 structured mesh, BEP. (d) Dimensionless axial velocity contours on the meridional plane, CFD2 refined structured mesh, BEP.
Figure 5.
Contours of the quantity, BEP. (a) Pressure side of a blade, CFD1 structured mesh. (b) Pressure side of a blade, CFD2 refined structured mesh. (c) Suction side of a blade, CFD1 structured mesh. (d) Suction side of a blade, CFD2 refined structured mesh.
Figure 5.
Contours of the quantity, BEP. (a) Pressure side of a blade, CFD1 structured mesh. (b) Pressure side of a blade, CFD2 refined structured mesh. (c) Suction side of a blade, CFD1 structured mesh. (d) Suction side of a blade, CFD2 refined structured mesh.
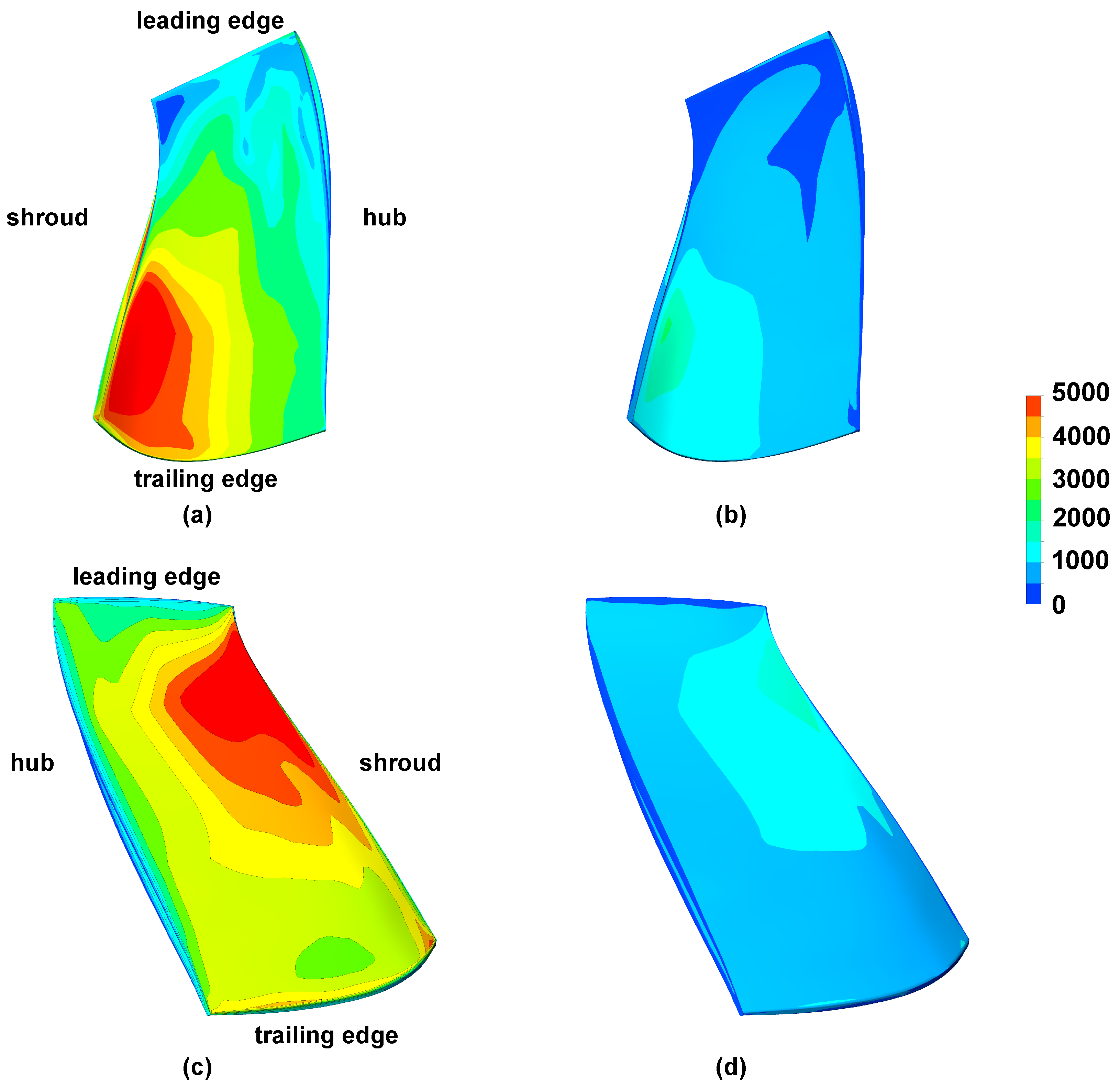
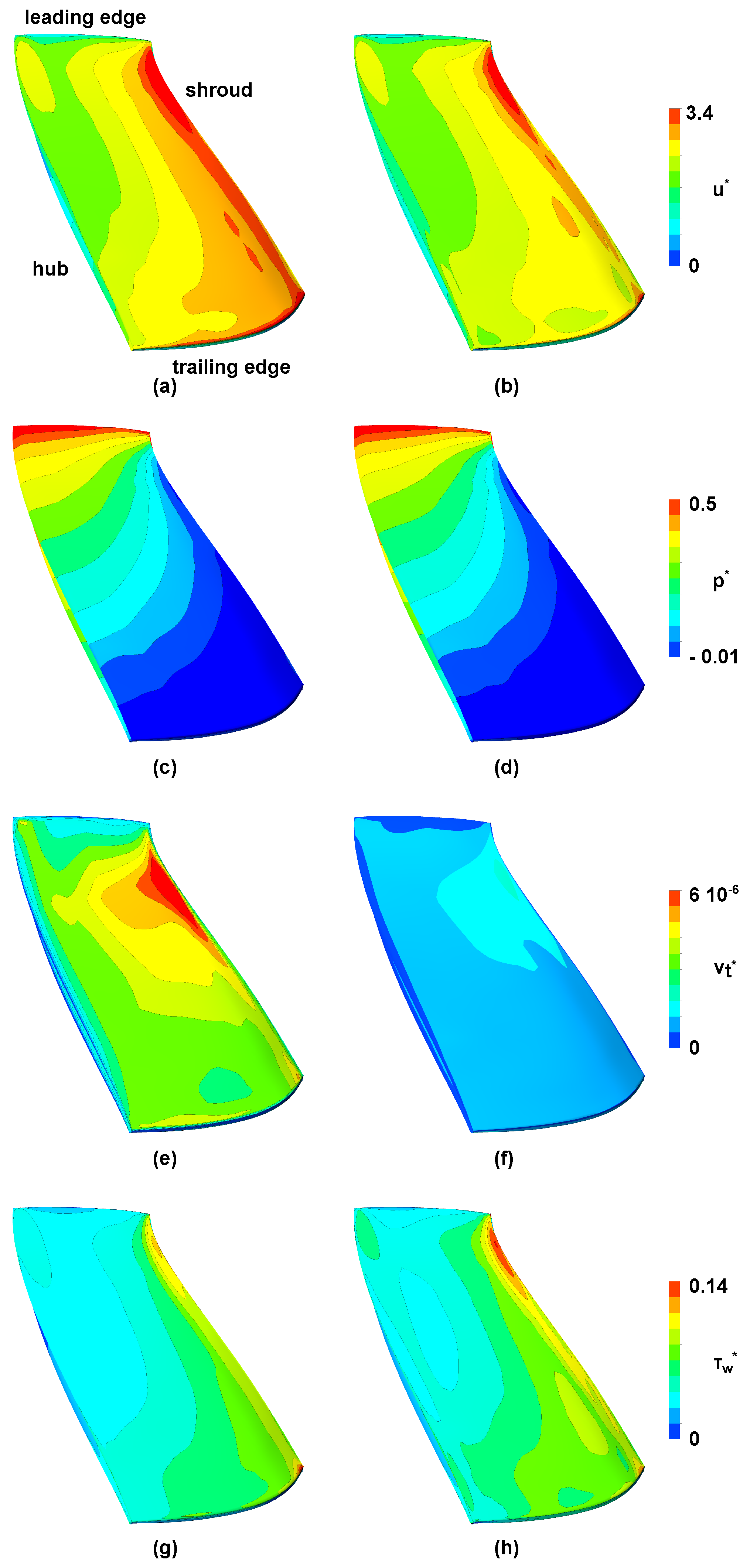
Figure 6.
(a) Contours of the dimensionless magnitude of the relative velocity on the suction side of a blade, CFD1 structured mesh, BEP. (b) Contours of the dimensionless magnitude of the relative velocity on the suction side of a blade, CFD2 refined structured mesh, BEP. (c) Contours of the dimensionless pressure on the suction side of a blade, CFD1 structured mesh, BEP. (d) Contours of the dimensionless pressure on the suction side of a blade, CFD2 refined structured mesh, BEP. (e) Contours of the dimensionless eddy viscosity on the suction side of a blade, CFD1 structured mesh, BEP. (f) Contours of the dimensionless eddy viscosity on the suction side of a blade, CFD2 refined structured mesh, BEP. (g) Contours of the dimensionless wall shear on the suction side of a blade, CFD1 structured mesh, BEP. (h) Contours of the dimensionless wall shear on the suction side of a blade, CFD2 refined structured mesh, BEP.
Figure 6.
(a) Contours of the dimensionless magnitude of the relative velocity on the suction side of a blade, CFD1 structured mesh, BEP. (b) Contours of the dimensionless magnitude of the relative velocity on the suction side of a blade, CFD2 refined structured mesh, BEP. (c) Contours of the dimensionless pressure on the suction side of a blade, CFD1 structured mesh, BEP. (d) Contours of the dimensionless pressure on the suction side of a blade, CFD2 refined structured mesh, BEP. (e) Contours of the dimensionless eddy viscosity on the suction side of a blade, CFD1 structured mesh, BEP. (f) Contours of the dimensionless eddy viscosity on the suction side of a blade, CFD2 refined structured mesh, BEP. (g) Contours of the dimensionless wall shear on the suction side of a blade, CFD1 structured mesh, BEP. (h) Contours of the dimensionless wall shear on the suction side of a blade, CFD2 refined structured mesh, BEP.
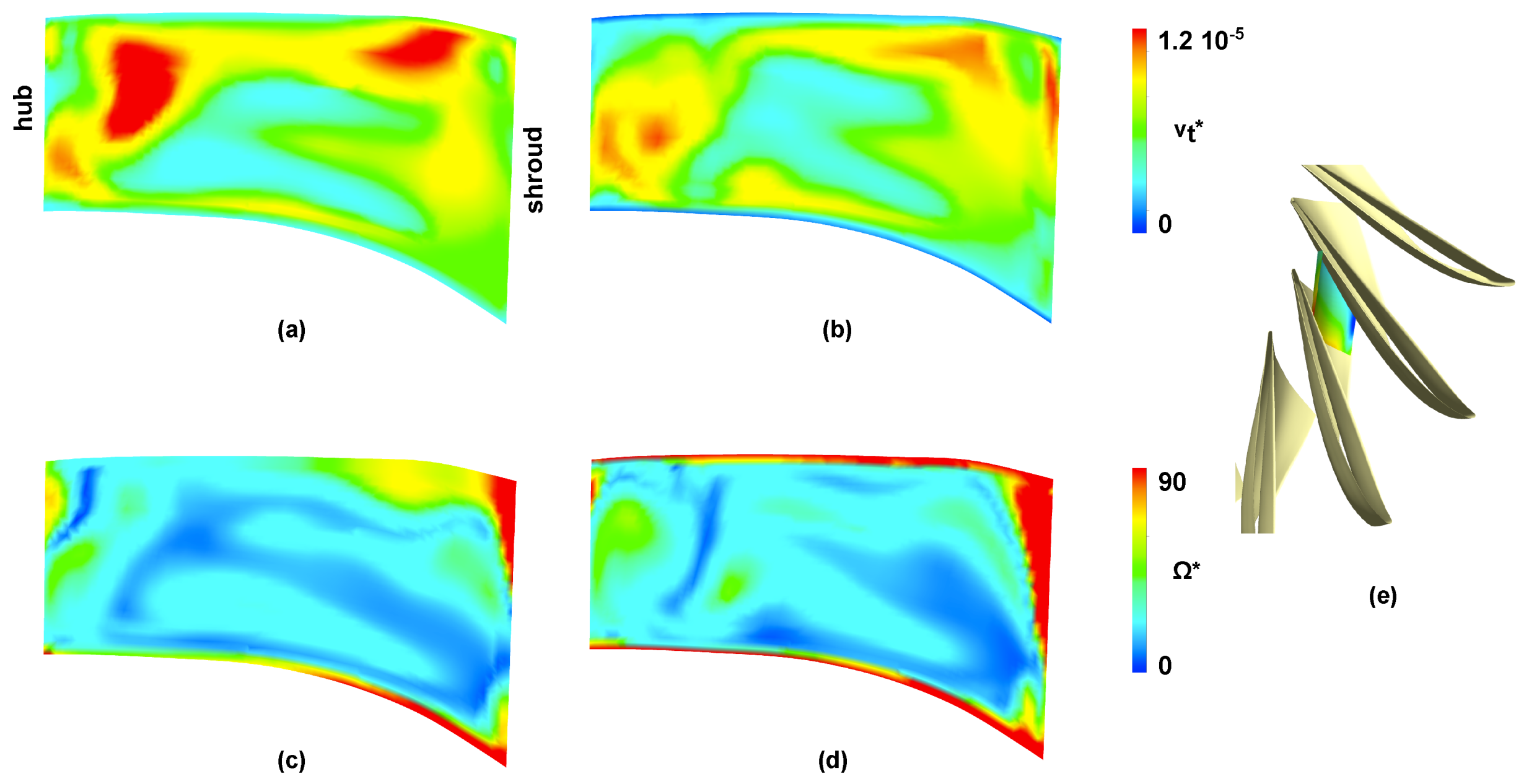
Figure 7.
(a) Contours of the dimensionless eddy viscosity in a cross-section of a blade channel, CFD1 structured mesh, BEP. (b) Contours of the dimensionless eddy viscosity in a cross-section of a blade channel, CFD2 refined structured mesh, BEP. (c) Contours of the dimensionless vorticity in a cross-section of a blade channel, CFD1 structured mesh, BEP. (d) Contours of the dimensionless vorticity in a cross-section of a blade channel, CFD2 refined structured mesh, BEP. (e) Position of the cross-section in a blade channel.
Figure 7.
(a) Contours of the dimensionless eddy viscosity in a cross-section of a blade channel, CFD1 structured mesh, BEP. (b) Contours of the dimensionless eddy viscosity in a cross-section of a blade channel, CFD2 refined structured mesh, BEP. (c) Contours of the dimensionless vorticity in a cross-section of a blade channel, CFD1 structured mesh, BEP. (d) Contours of the dimensionless vorticity in a cross-section of a blade channel, CFD2 refined structured mesh, BEP. (e) Position of the cross-section in a blade channel.
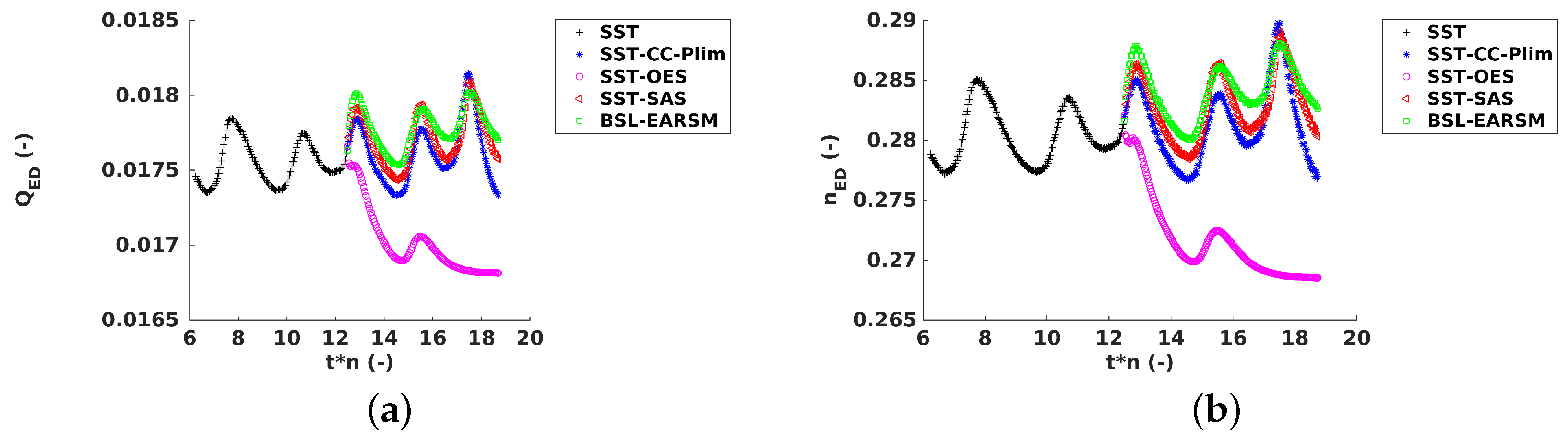
Figure 8.
(a) Time history of the discharge factor , Speed-No-Load (SNL). (b) Time history of the speed factor , SNL. CC, Curvature Correction; Plim, Production limiter; OES, Organised Eddy Simulation; SAS, Scale-Adaptive Simulation; BSL-EARSM, Baseline Explicit Algebraic Reynodlds Stress Model.
Figure 8.
(a) Time history of the discharge factor , Speed-No-Load (SNL). (b) Time history of the speed factor , SNL. CC, Curvature Correction; Plim, Production limiter; OES, Organised Eddy Simulation; SAS, Scale-Adaptive Simulation; BSL-EARSM, Baseline Explicit Algebraic Reynodlds Stress Model.
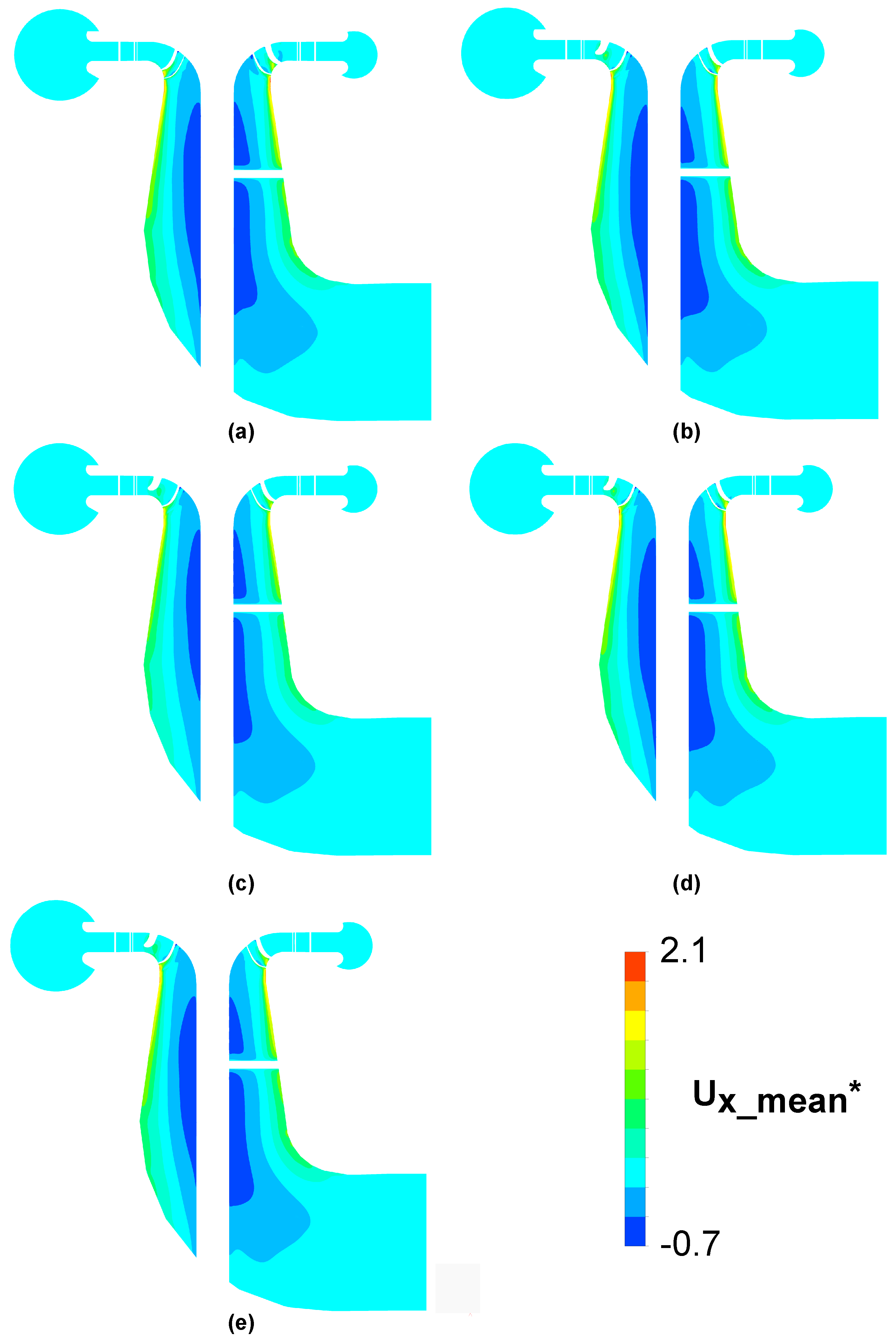
Figure 9.
Contours of the dimensionless mean axial velocity on the meridional plane, SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
Figure 9.
Contours of the dimensionless mean axial velocity on the meridional plane, SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
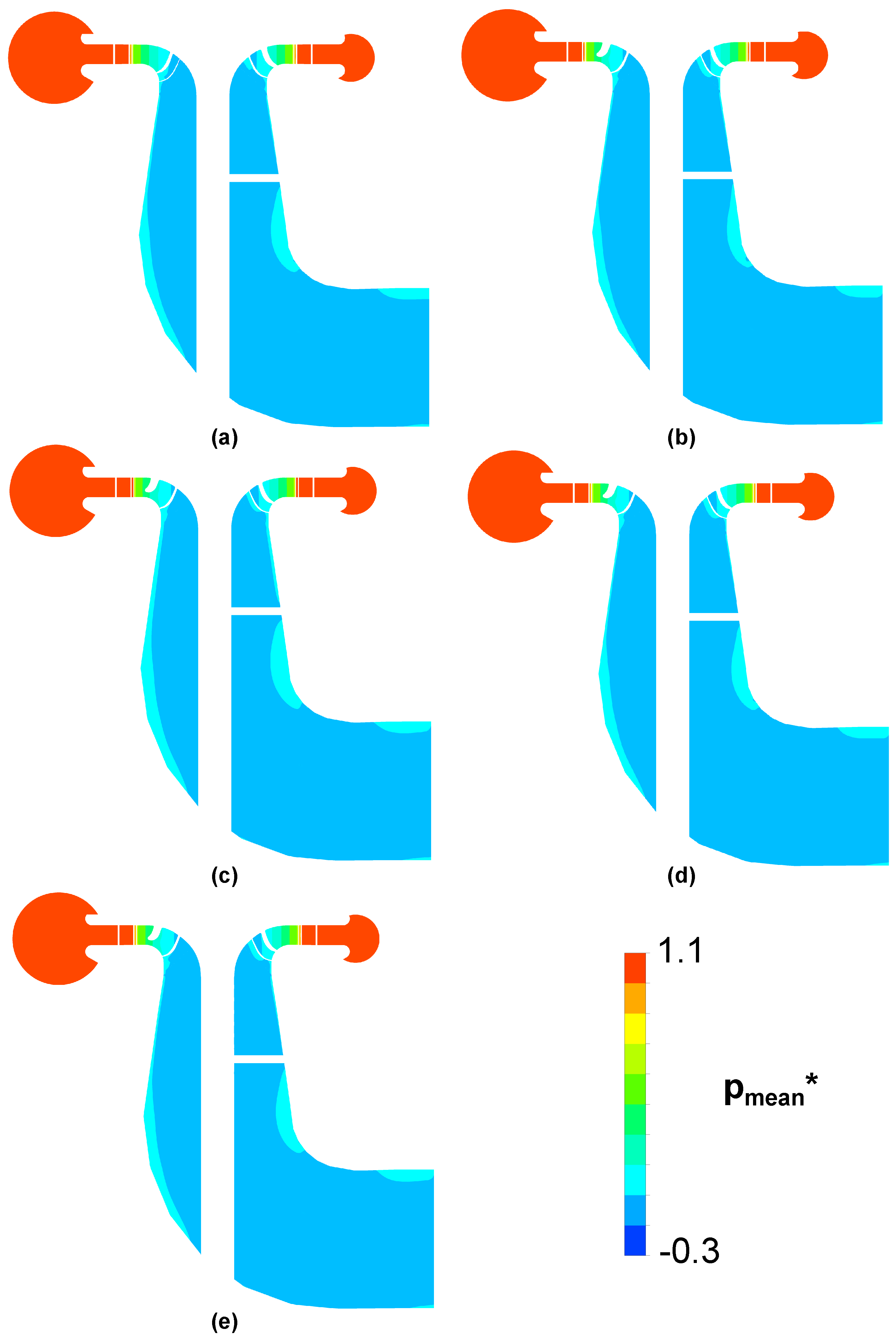
Figure 10.
Contours of the dimensionless mean pressure on the meridional plane, SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
Figure 10.
Contours of the dimensionless mean pressure on the meridional plane, SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
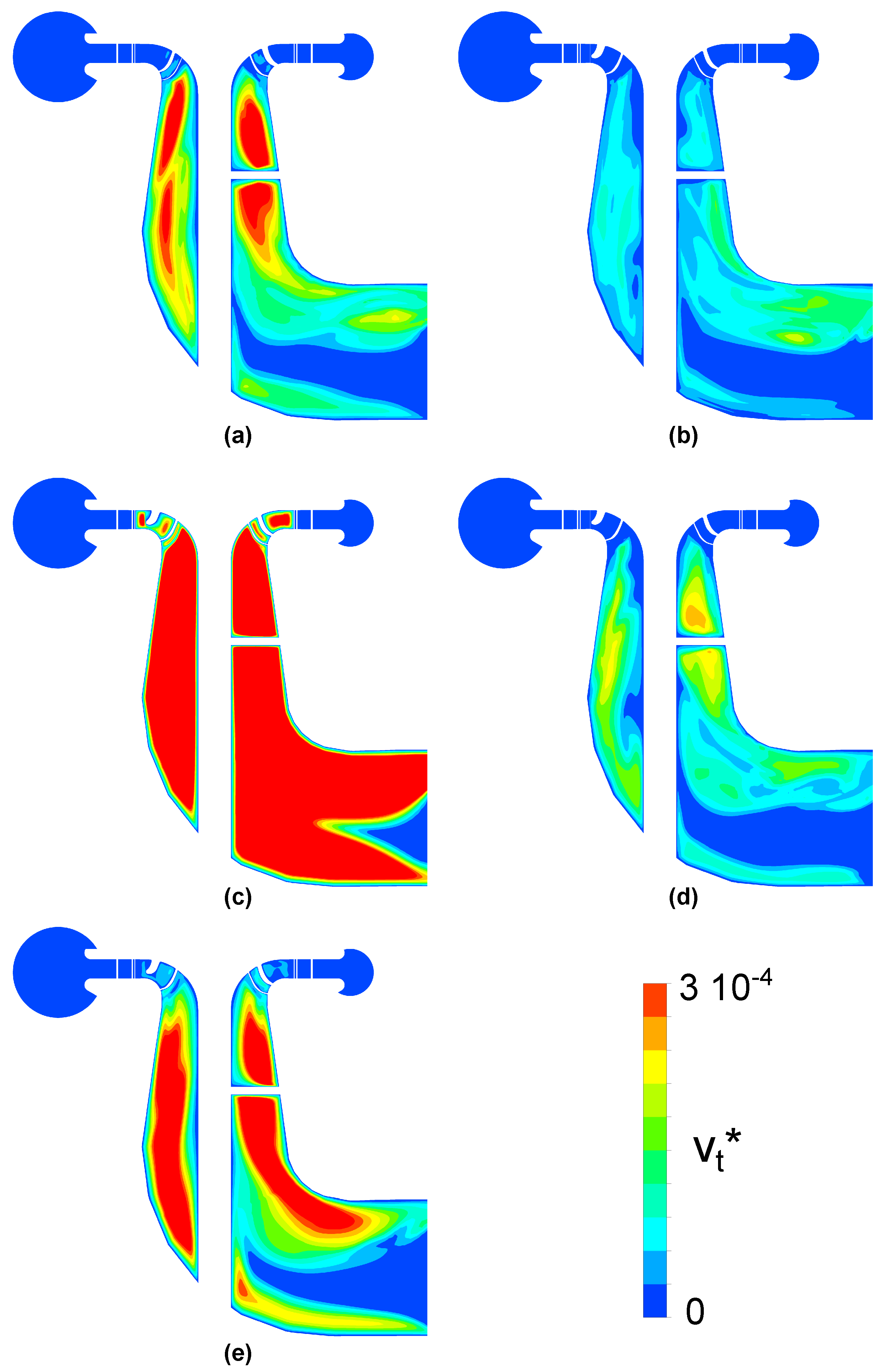
Figure 11.
Instantaneous contours of the dimensionless eddy viscosity on the meridional plane, SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
Figure 11.
Instantaneous contours of the dimensionless eddy viscosity on the meridional plane, SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
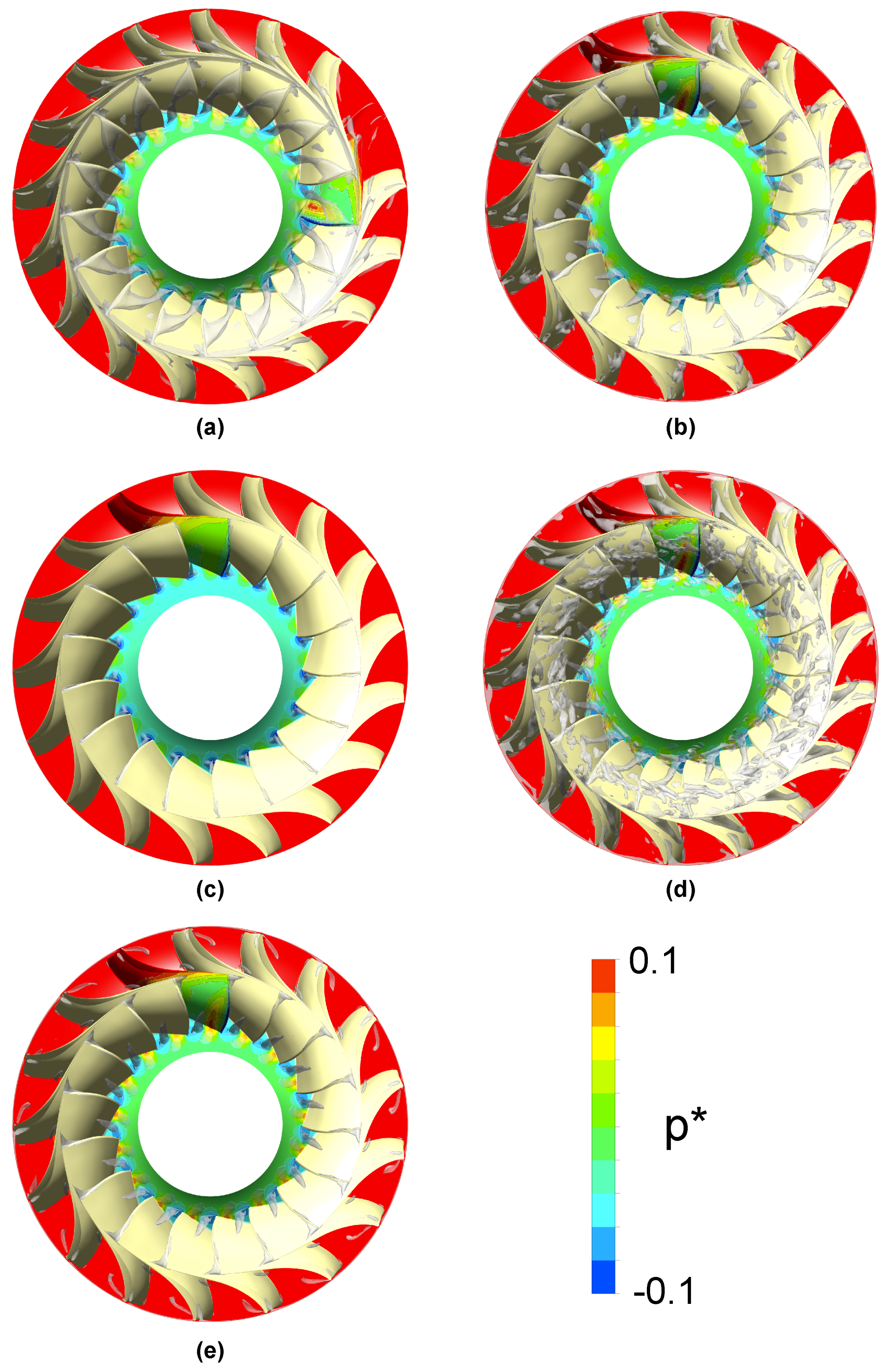
Figure 12.
Instantaneous iso-surface of the Q-criterion and contours of the dimensionless pressure on the hub and one runner blade (downstream view), SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
Figure 12.
Instantaneous iso-surface of the Q-criterion and contours of the dimensionless pressure on the hub and one runner blade (downstream view), SNL. (a) SST . (b) SST-CC-Plim . (c) SST-OES . (d) SST-SAS . (e) BSL-EARSM .
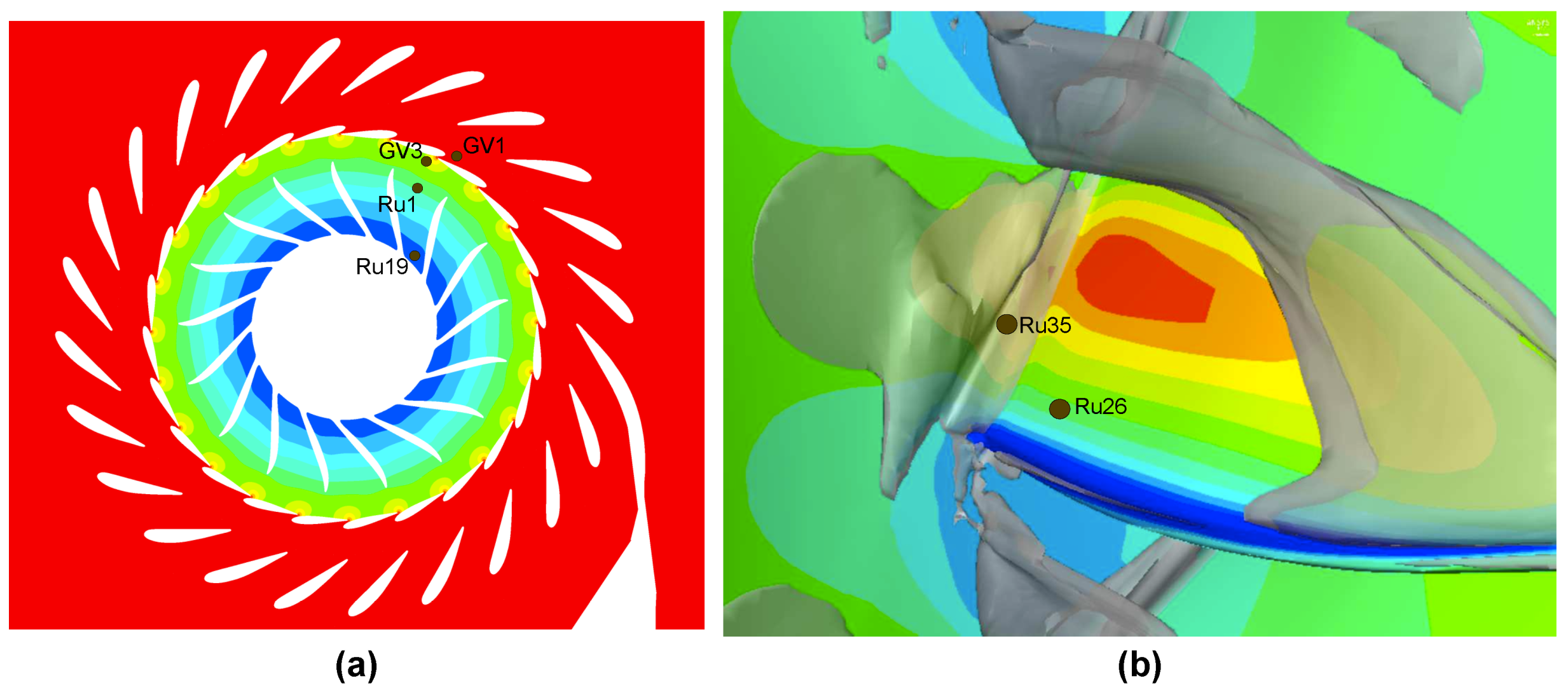
Figure 13.
(a) Positions of the probes in one guide vane and blade channel. (b) Positions of the probes on the suction side of a runner blade close to the trailing edge.
Figure 13.
(a) Positions of the probes in one guide vane and blade channel. (b) Positions of the probes on the suction side of a runner blade close to the trailing edge.
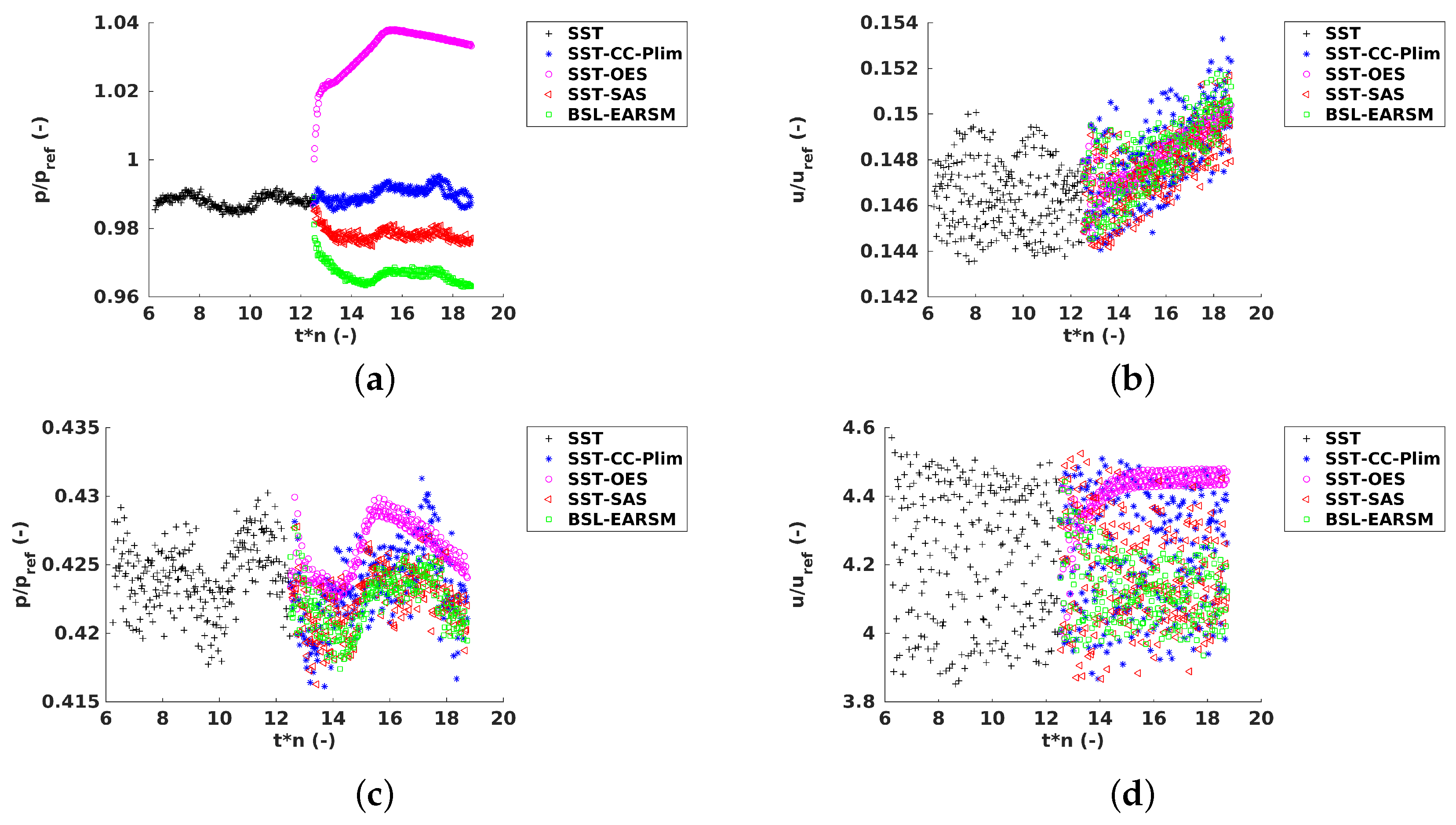
Figure 14.
(a) Time history of the dimensionless pressure, probe GV1. (b) Time history of the dimensionless velocity magnitude, probe GV1. (c) Time history of the dimensionless pressure, probe GV3. (d) Time history of the dimensionless velocity magnitude, probe GV3.
Figure 14.
(a) Time history of the dimensionless pressure, probe GV1. (b) Time history of the dimensionless velocity magnitude, probe GV1. (c) Time history of the dimensionless pressure, probe GV3. (d) Time history of the dimensionless velocity magnitude, probe GV3.
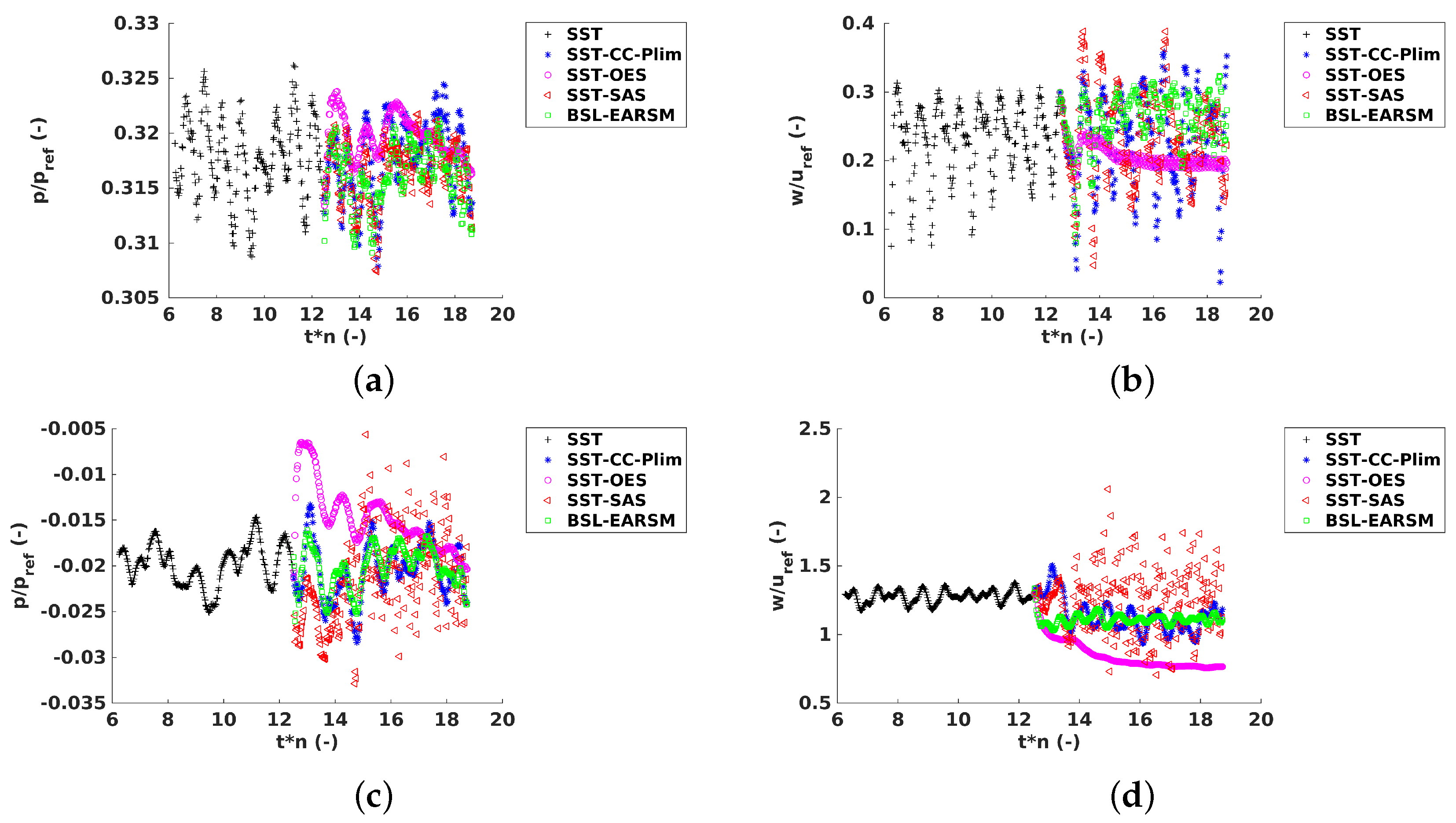
Figure 15.
(a) Time history of the dimensionless pressure, probe Ru1. (b) Time history of the dimensionless velocity magnitude, probe Ru1. (c) Time history of the dimensionless pressure, probe Ru19. (d) Time history of the dimensionless velocity magnitude, probe Ru19.
Figure 15.
(a) Time history of the dimensionless pressure, probe Ru1. (b) Time history of the dimensionless velocity magnitude, probe Ru1. (c) Time history of the dimensionless pressure, probe Ru19. (d) Time history of the dimensionless velocity magnitude, probe Ru19.
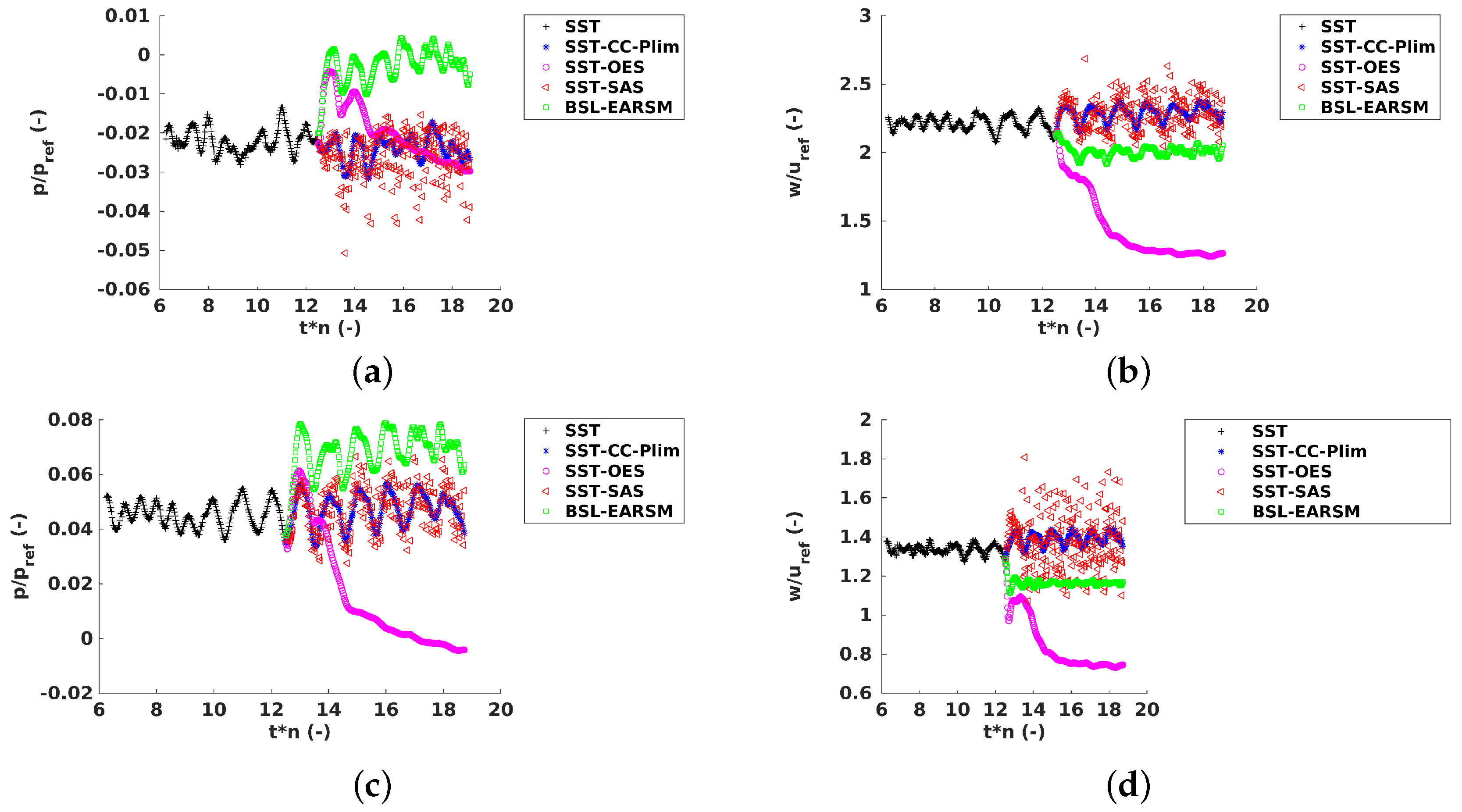
Figure 16.
(a) Time history of the dimensionless pressure, probe Ru26. (b) Time history of the dimensionless velocity magnitude, probe Ru26. (c) Time history of the dimensionless pressure, probe Ru35. (d) Time history of the dimensionless velocity magnitude, probe Ru35.
Figure 16.
(a) Time history of the dimensionless pressure, probe Ru26. (b) Time history of the dimensionless velocity magnitude, probe Ru26. (c) Time history of the dimensionless pressure, probe Ru35. (d) Time history of the dimensionless velocity magnitude, probe Ru35.
Figure 17.
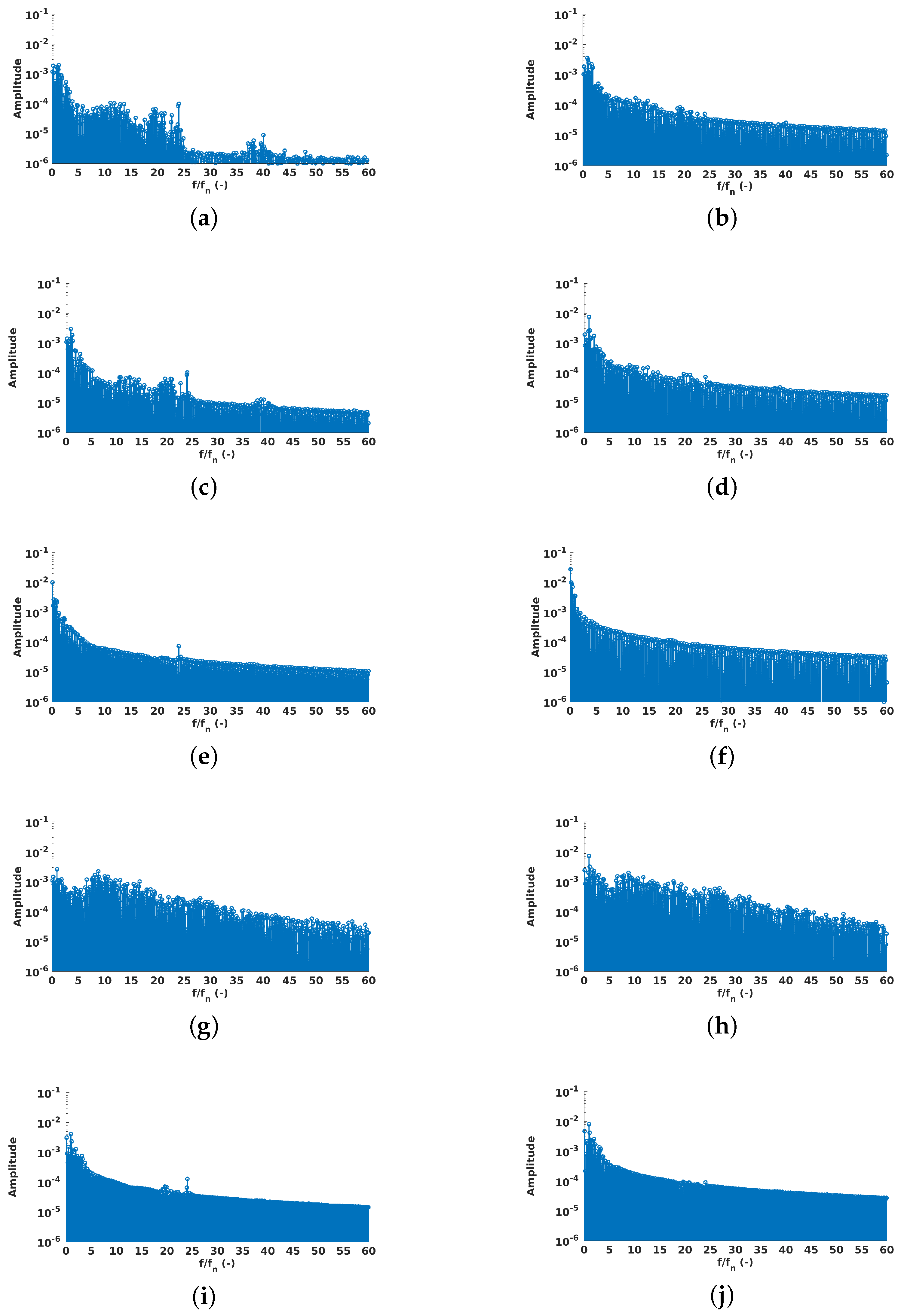
Pressure spectrum at probe Ru26: (a) SST . (c) SST-CC-Plim . (e) SST-OES . (g) SST-SAS . (i) BSL-EARSM . Pressure spectrum at probe Ru35: (b) SST . (d) SST-CC-Plim . (f) SST-OES . (h) SST-SAS . (j) BSL-EARSM .
Figure 17.
Pressure spectrum at probe Ru26: (a) SST . (c) SST-CC-Plim . (e) SST-OES . (g) SST-SAS . (i) BSL-EARSM . Pressure spectrum at probe Ru35: (b) SST . (d) SST-CC-Plim . (f) SST-OES . (h) SST-SAS . (j) BSL-EARSM .
Table 1.
Number of nodes and elements for each mesh.
Table 1.
Number of nodes and elements for each mesh.
| Sub-Domain | Structured Mesh | Unstructured Mesh |
|---|
| Nodes () | Elements () | Nodes () | Elements () |
|---|
| Spiral Case | 3.7 | 3.6 | | |
| Stay Vanes | 2.9 | 2.8 | 2.8 | 8.9 |
| Guide Vanes | 3.7 | 3.5 | | |
| Runner | 2.8 | 2.6 | 2.2 | 6.6 |
| Draft Tube | 1.6 | 1.5 | 0.8 | 2.7 |
| Total | 14.7 | 14.0 | 5.8 | 18.2 |
Table 2.
Minimum angle and aspect ratio for each mesh.
Table 2.
Minimum angle and aspect ratio for each mesh.
| Sub-Domain | Structured Mesh | Refined Structured Mesh | Unstructured Mesh |
|---|
| | Min Angle | Max Aspect | Min Angle | Max Aspect | Min Angle | Max Aspect |
| | (deg) | Ratio | (deg) | Ratio | (deg) | Ratio |
| Spiral Case | 20 | 2248 | 20 | 2248 | | |
| Stay Vanes | 29 | 77 | 29 | 77 | 12 | 592 |
| Guide Vanes | 23 | 62 | 23 | 118 | | |
| Runner | 7 | 75 | 3 | 212 | 30 | 147 |
| Draft Tube | 20 | 171 | 20 | 774 | 20 | 329 |
Table 3.
Average value on solid walls. Best Efficiency Point (BEP).
Table 3.
Average value on solid walls. Best Efficiency Point (BEP).
| Sub-Domain | Structured Mesh | Refined Structured Mesh | Unstructured Mesh |
|---|
| Spiral Case | 720 | 720 | 90 |
| Stay Vanes | 550 | 550 | 160 |
| Guide Vanes | 850 | 285 | 300 |
| Runner | 2700 | 690 | 250 |
| Draft Tube | 330 | 310 | 90 |
Table 4.
List of the computations performed at the BEP.
Table 4.
List of the computations performed at the BEP.
| Reference | Algorithm | Rotor/Stator Interface | Computational Domain | Mesh | Inlet Boundary Condition |
|---|
| CFD1 | Steady | Frozen | standard | structured | mass flow rate |
| CFD2 | Steady | Frozen | standard | refined structured | mass flow rate |
| CFD3 | Steady | Frozen | standard | unstructured | mass flow rate |
| CFD4 | Steady | Frozen | extended | structured | mass flow rate |
| CFD5 | Steady | Frozen | standard | structured | total pressure |
| CFD6 | Unsteady | Transient | standard | structured | mass flow rate |
Table 5.
CFD results at the BEP compared with the measurements.
Table 5.
CFD results at the BEP compared with the measurements.
| Reference | | | | |
|---|
| CFD1 | 0.187 | 0.268 | 0.175 | 1.00 |
| CFD2 | 0.190 | 0.271 | 0.177 | 1.00 |
| CFD3 | 0.188 | 0.269 | 0.177 | 1.01 |
| CFD4 | 0.187 | 0.267 | 0.174 | 0.99 |
| CFD5 | 0.186 | 0.275 | 0.174 | 1.00 |
| CFD6 | 0.187 | 0.268 | 0.178 | 1.01 |
| EXP | 0.183 | 0.271 | 0.171 | 1.00 |
Table 6.
CFD results at the SNL operating point compared with the measurements. Averaged values over 6.25 runner revolutions.
Table 6.
CFD results at the SNL operating point compared with the measurements. Averaged values over 6.25 runner revolutions.
| Turbulence Model | | |
|---|
| SST | 0.0176 | 0.280 |
| SST-CC-Plim | 0.0176 | 0.281 |
| SST-OES | 0.0170 | 0.272 |
| SST-SAS | 0.0177 | 0.283 |
| BSL-EARSM | 0.0178 | 0.284 |
| EXP | 0.0170 | 0.270 |