Three Dimensional CS-FEM Phase-Field Modeling Technique for Brittle Fracture in Elastic Solids
Abstract
1. Introduction
2. Methods
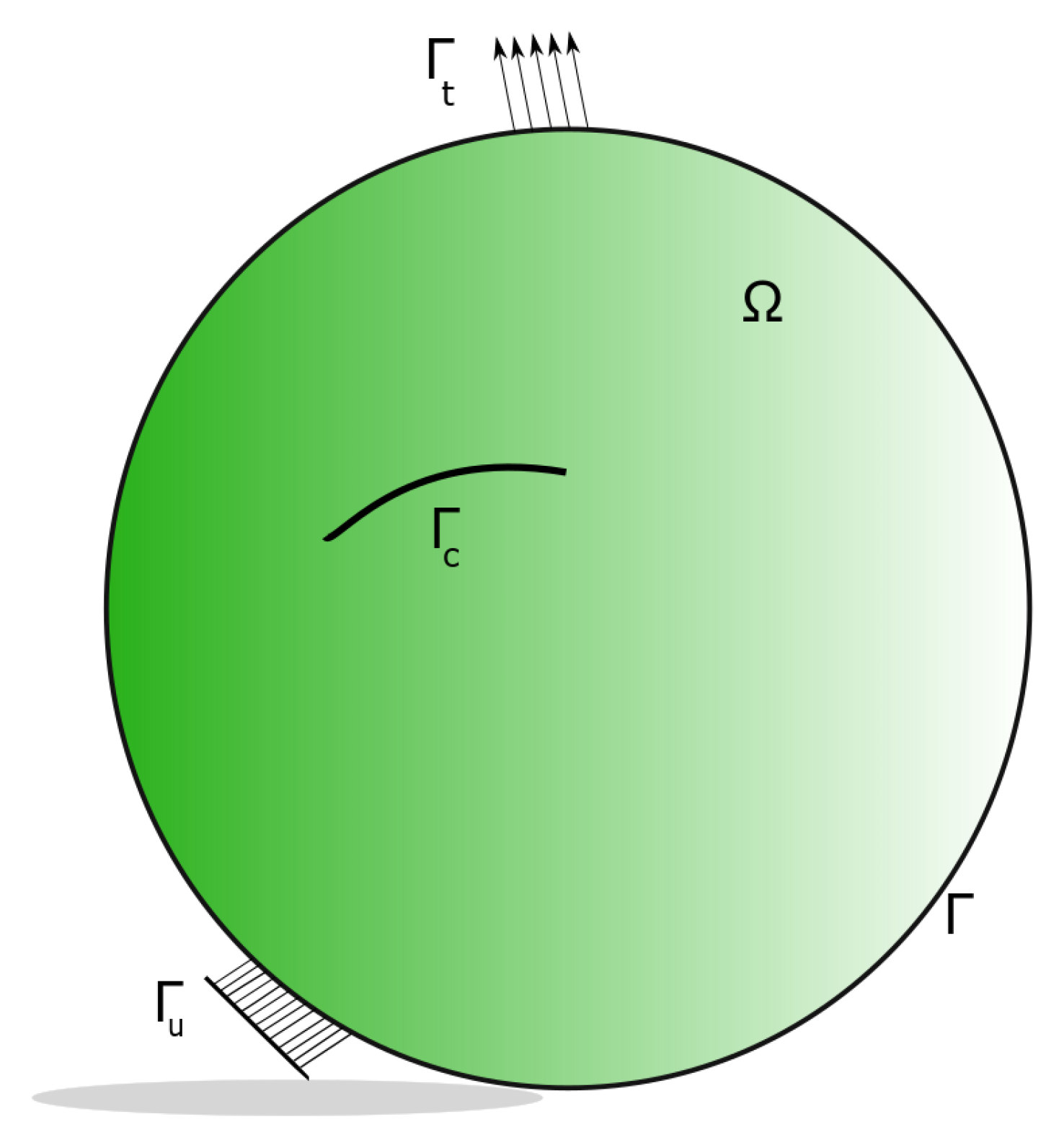
2.1. Governing Equations of a 3D Elastic Solid with Discontinuity
2.2. Review of Phase-Field Model for Brittle Fracture
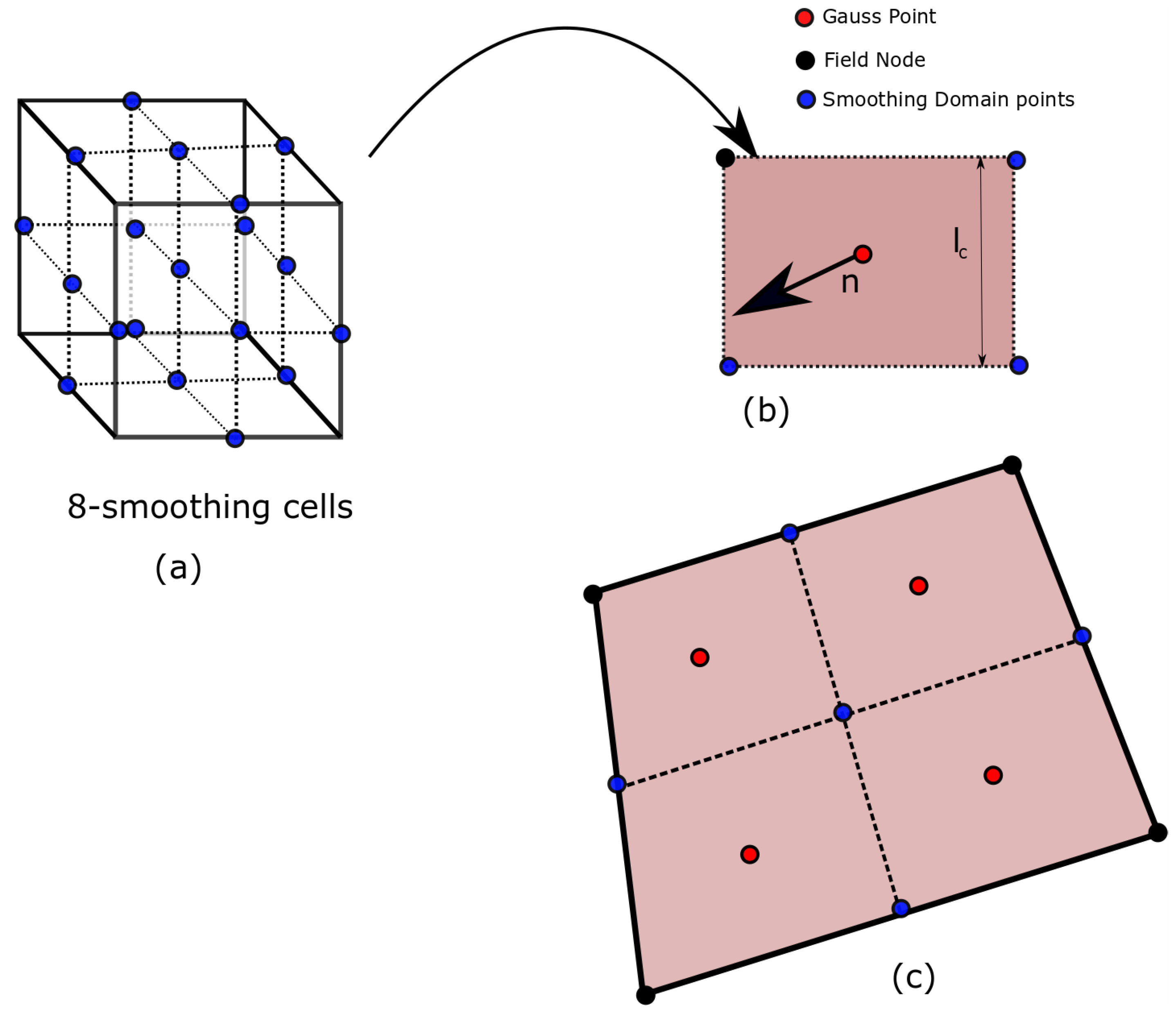
2.3. Three-Dimensional Cell Based Smoothed-Finite Elements
2.4. Implementation in ABAQUS UEL
3. Numerical Modeling
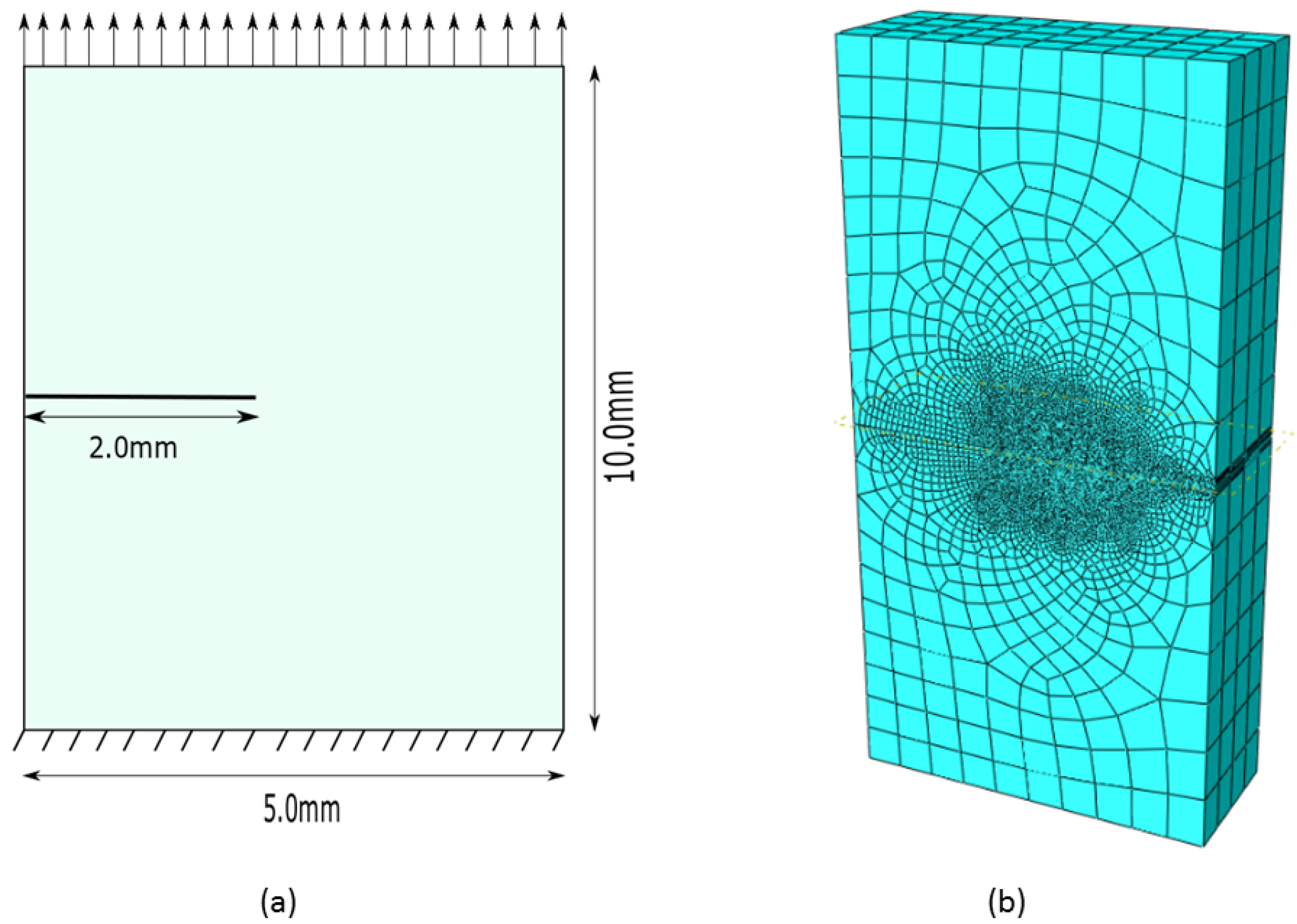
3.1. Single Edge Notched Tensile Sample
3.2. Single Edge Notched Shear Sample
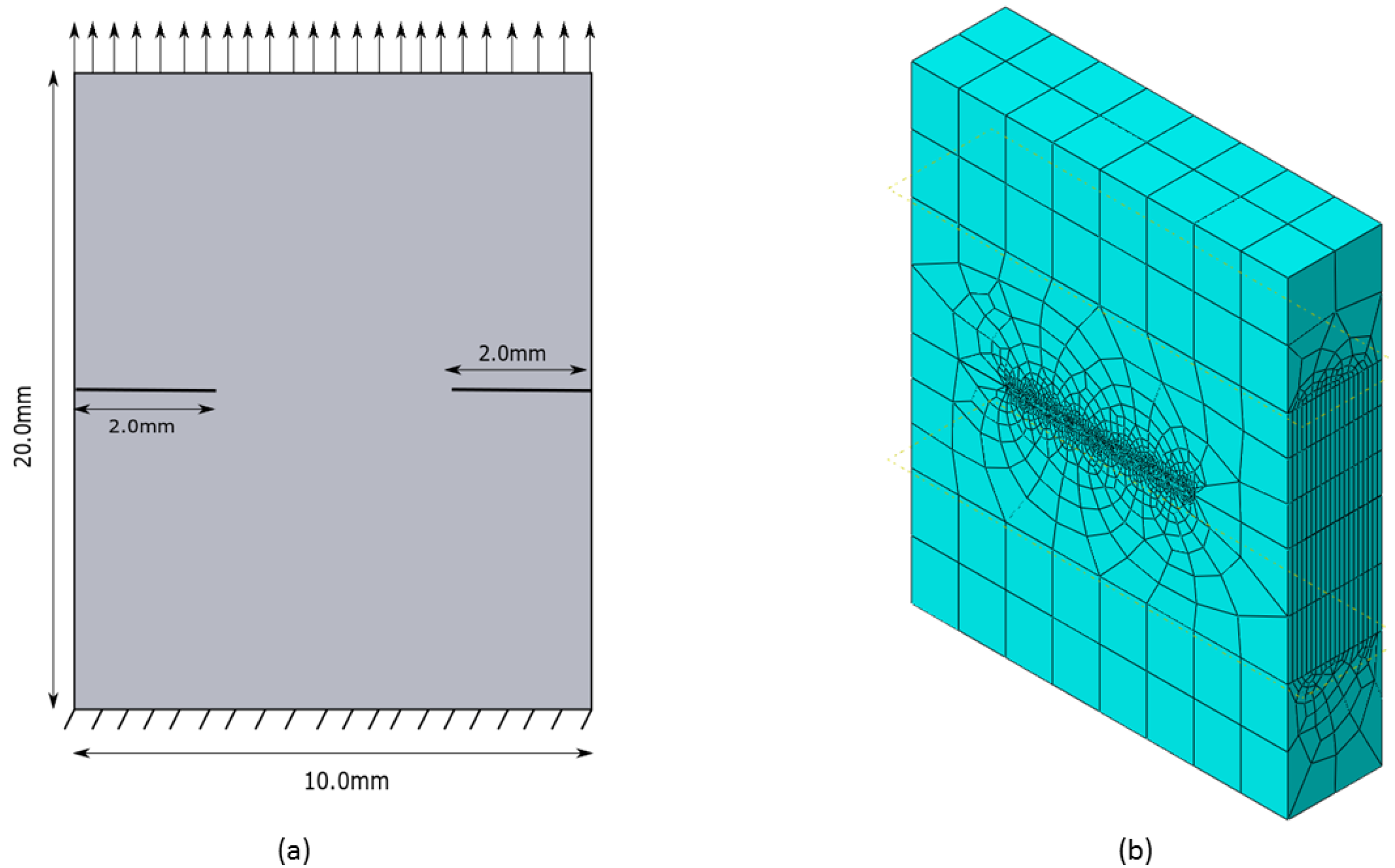
3.3. Double Edge Notched Tensile Sample
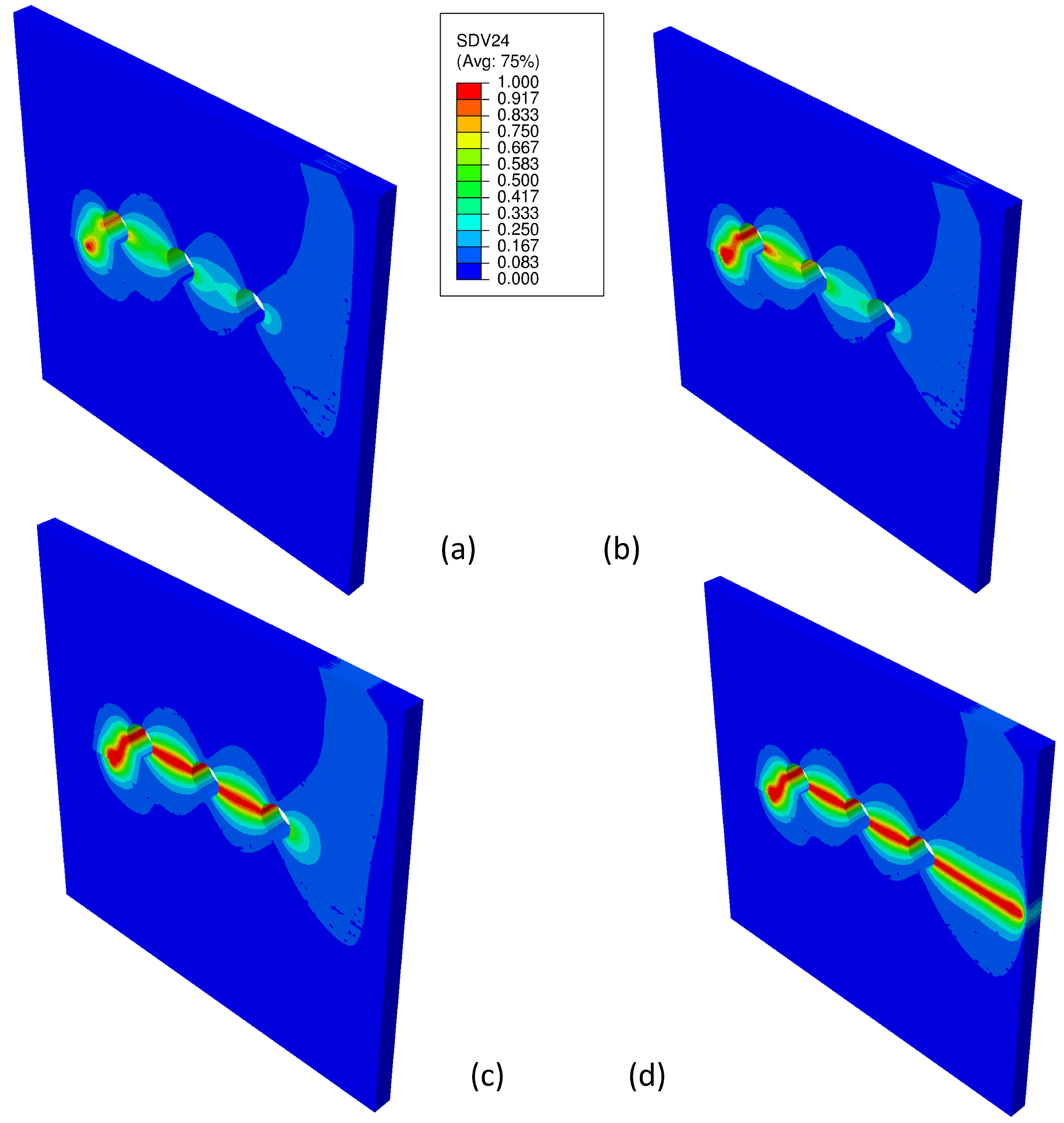
3.4. 3D Specimen with Notch and Three Openings
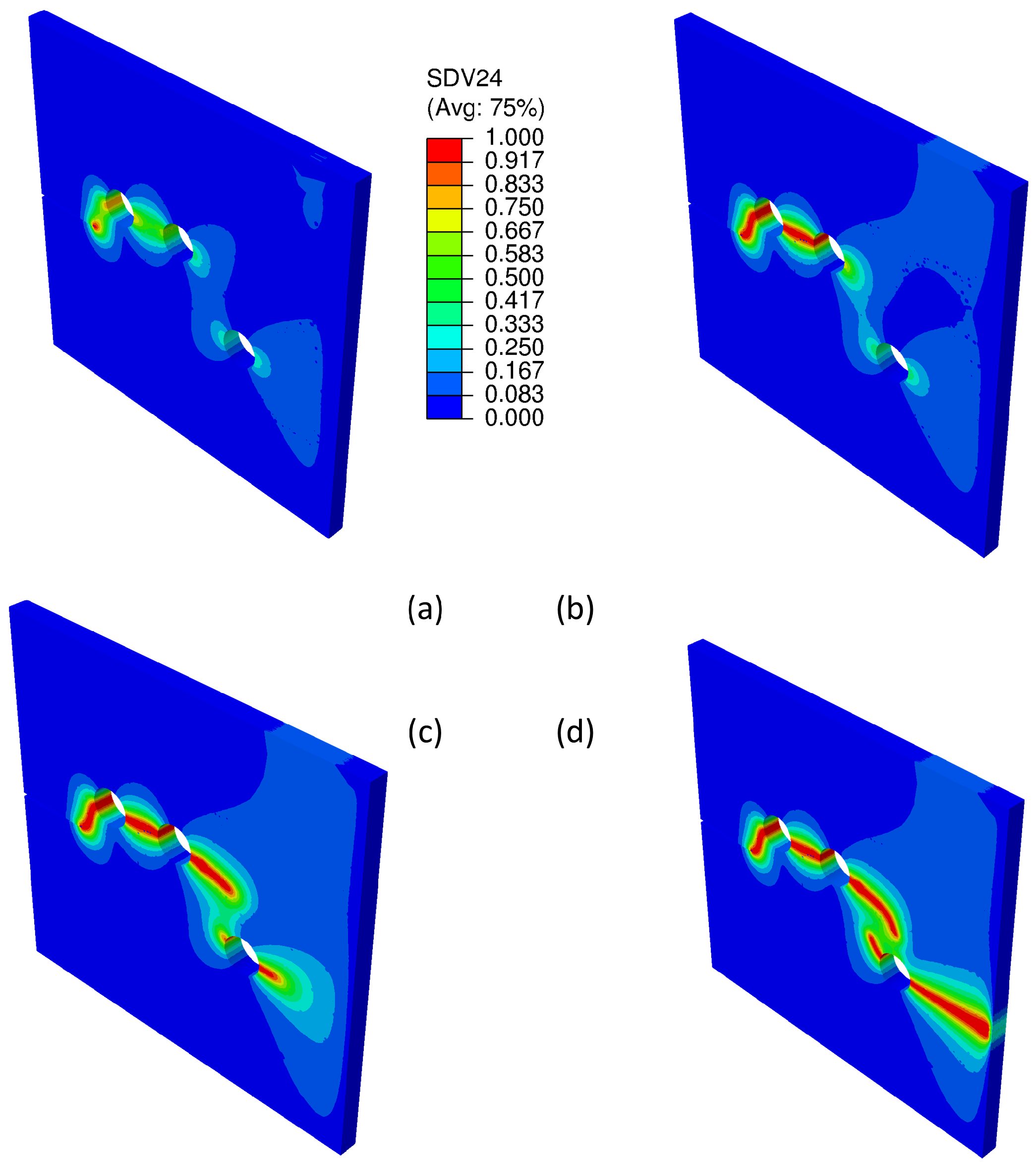
3.5. 3D Bi-Material Notched Specimen
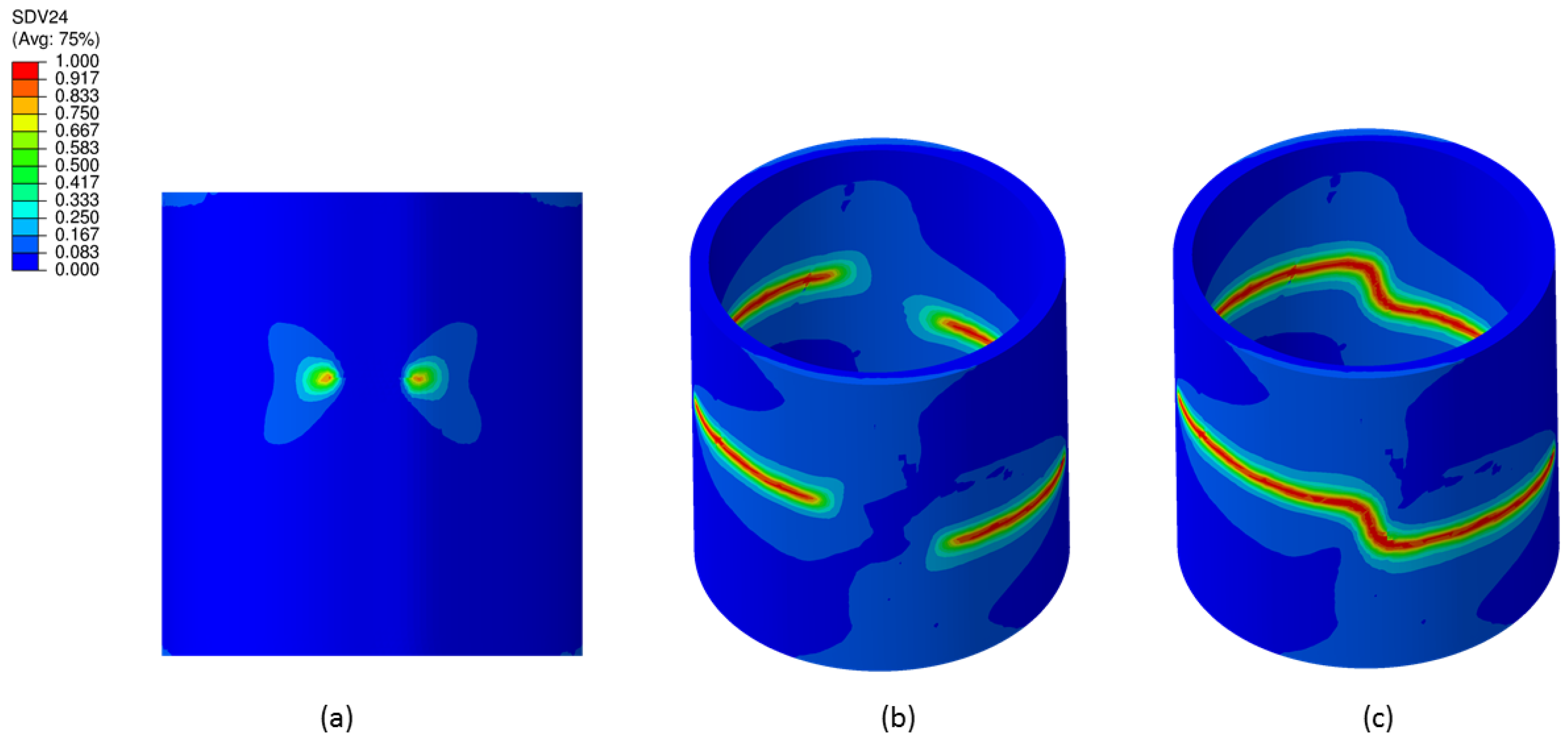
3.6. Crack Propagation in Thick Walled Cylinder
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Liu, G.; Trung, N.T. Smoothed Finite Element Methods; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Liu, G.R.; Dai, K.Y.; Nguyen, T.T. A smoothed finite element method for mechanics problems. Comput. Mech. 2007, 39, 859–877. [Google Scholar] [CrossRef]
- Liu, G.R. Meshfree Methods—Moving Beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Liu, G.R.; Quek, S.S. The Finite Element Method—A Practical Course; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liu, G.R.; Nguyen, T.T.; Dai, K.Y.; Lam, K.Y. Theoretical aspects of the smoothed finite element method (SFEM). Int. J. Numer. Methods Eng. 2007, 71, 902–930. [Google Scholar] [CrossRef]
- Liu, G.; Nguyen-Thoi, T.; Lam, K. A novel alpha finite element method (αFEM) for exact solution to mechanics problems using triangular and tetrahedral elements. Comput. Methods Appl. Mech. Eng. 2008, 197, 3883–3897. [Google Scholar] [CrossRef]
- Liu, G.; Nguyen-Thoi, T.; Nguyen-Xuan, H.; Lam, K. A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems. Comput. Struct. 2009, 87, 14–26. [Google Scholar] [CrossRef]
- Liu, G.; Nguyen-Thoi, T.; Lam, K. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. J. Sound Vib. 2009, 320, 1100–1130. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, G.; Jiang, C.; Nguyen-Thoi, T.; Jiang, Y. A generalized beta finite element method with coupled smoothing techniques for solid mechanics. Eng. Anal. Bound. Elem. 2016, 73, 103–119. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Rabczuk, T.; Bordas, S.; Debongnie, J. A smoothed finite element method for plate analysis. Comput. Methods Appl. Mech. Eng. 2008, 197, 1184–1203. [Google Scholar] [CrossRef]
- Nguyen-Thoi, T.; Liu, G.; Vu-Do, H.; Nguyen-Xuan, H. A face-based smoothed finite element method (FS-FEM) for visco-elastoplastic analyses of 3D solids using tetrahedral mesh. Comput. Methods Appl. Mech. Eng. 2009, 198, 3479–3498. [Google Scholar] [CrossRef]
- Nguyen-Thoi, T.; Vu-Do, H.; Rabczuk, T.; Nguyen-Xuan, H. A node-based smoothed finite element method (NS-FEM) for upper bound solution to visco-elastoplastic analyses of solids using triangular and tetrahedral meshes. Comput. Methods Appl. Mech. Eng. 2010, 199, 3005–3027. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Liu, G.; Thai-Hoang, C.; Nguyen-Thoi, T. An edge-based smoothed finite element method (ES-FEM) with stabilized discrete shear gap technique for analysis of Reissner–Mindlin plates. Comput. Methods Appl. Mech. Eng. 2010, 199, 471–489. [Google Scholar] [CrossRef]
- Nguyen-Thoi, T.; Liu, G.R.; Vu-Do, H.C.; Nguyen-Xuan, H. An edge-based smoothed finite element method for visco-elastoplastic analyses of 2D solids using triangular mesh. Comput. Mech. 2009, 45, 23–44. [Google Scholar] [CrossRef]
- Nourbakhshnia, N.; Liu, G.R. A quasi-static crack growth simulation based on the singular ES-FEM. Int. J. Numer. Methods Eng. 2001, 88, 473–492. [Google Scholar] [CrossRef]
- Jiun-Shyan, C.; Cheng-Tang, W.; Sangpil, Y.; Yang, Y. A stabilized conforming nodal integration for Galerkin mesh-free methods. Int. J. Numer. Methods Eng. 2000, 50, 435–466. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Liu, G.; Bordas, S.; Natarajan, S.; Rabczuk, T. An adaptive singular ES-FEM for mechanics problems with singular field of arbitrary order. Comput. Methods Appl. Mech. Eng. 2013, 253, 252–273. [Google Scholar] [CrossRef]
- Bhowmick, S.; Liu, G. On singular ES-FEM for fracture analysis of solids with singular stress fields of arbitrary order. Eng. Anal. Bound. Elem. 2018, 86, 64–81. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, Y.; Ma, H.; Huang, S. A fast multipole boundary element method for modeling 2-D multiple crack problems with constant elements. Eng. Anal. Bound. Elem. 2014, 47, 1–9. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.; Gu, L. Crack propagation by element-free Galerkin methods. Eng. Fract. Mech. 1995, 51, 295–315. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, G.; Kitamura, Y.; Nguyen-Xuan, H. A three-dimensional ES-FEM for fracture mechanics problems in elastic solids. Eng. Fract. Mech. 2013, 114, 127–150. [Google Scholar] [CrossRef]
- Liu, G.; Nourbakhshnia, N.; Zhang, Y. A novel singular ES-FEM method for simulating singular stress fields near the crack tips for linear fracture problems. Eng. Fract. Mech. 2011, 78, 863–876. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Molnár, G.; Gravouil, A. 2D and 3D ABAQUS implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. ABAQUS implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Miehe, C.; Schänzel, L.M. Phase field modeling of fracture in rubbery polymers. Part I: Finite elasticity coupled with brittle failure. J. Mech. Phys. Solids 2014, 65, 93–113. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Miehe, C.; Schänzel, L.M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Hofacker, M.; Miehe, C. A phase field model of dynamic fracture: Robust field updates for the analysis of complex crack patterns. Int. J. Numer. Methods Eng. 2012, 93, 276–301. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: a simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Areias, P.; Msekh, M.; Rabczuk, T. Damage and fracture algorithm using the screened Poisson equation and local remeshing. Eng. Fract. Mech. 2016, 158, 116–143. [Google Scholar] [CrossRef]
- Areias, P.; Rabczuk, T.; de Sá, J.C. A novel two-stage discrete crack method based on the screened Poisson equation and local mesh refinement. Comput. Mech. 2016, 58, 1003–1018. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Nguyen, H.V.; Bordas, S.; Rabczuk, T.; Duflot, M. A cell-based smoothed finite element method for three-dimensional solid structures. KSCE J. Civ. Eng. 2012, 16, 1230–1242. [Google Scholar] [CrossRef]
- Bhowmick, S.; Liu, G.R. A phase-field modeling for brittle fracture and crack propagation based on the cell-based smoothed finite element method. Eng. Fract. Mech. 2018, 204, 369–387. [Google Scholar] [CrossRef]
- Msekh, M.A. Phase Field Modeling for Fracture with Applications to Homogeneous and Heterogeneous Materials. Ph.D. Thesis, Bauhaus-Universität Weimar, Weimar, Germany, 2017. [Google Scholar] [CrossRef]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhowmick, S.; Liu, G.-R. Three Dimensional CS-FEM Phase-Field Modeling Technique for Brittle Fracture in Elastic Solids. Appl. Sci. 2018, 8, 2488. https://doi.org/10.3390/app8122488
Bhowmick S, Liu G-R. Three Dimensional CS-FEM Phase-Field Modeling Technique for Brittle Fracture in Elastic Solids. Applied Sciences. 2018; 8(12):2488. https://doi.org/10.3390/app8122488
Chicago/Turabian StyleBhowmick, Sauradeep, and Gui-Rong Liu. 2018. "Three Dimensional CS-FEM Phase-Field Modeling Technique for Brittle Fracture in Elastic Solids" Applied Sciences 8, no. 12: 2488. https://doi.org/10.3390/app8122488
APA StyleBhowmick, S., & Liu, G.-R. (2018). Three Dimensional CS-FEM Phase-Field Modeling Technique for Brittle Fracture in Elastic Solids. Applied Sciences, 8(12), 2488. https://doi.org/10.3390/app8122488



