Featured Application
Considered technique allows the segmentation of histological images by means of semisupervised learning using Histogram-based Autoencoder Neural Networks. Data analysis applying fractal estimators is proposed for the evaluation of the method-induced errors of autopsy lung images.
Abstract
The designing of Computer-Aided Diagnosis (CADx) is necessary to improve patient condition analysis and reduce human error. HistAENN (Histogram-based Autoencoder Neural Network, the first hierarchy level) and the fractal-based estimator (the second hierarchy level) are assumed for segmentation and image analysis, respectively. The aim of the study is to investigate how to select or preselect algorithms at the second hierarchy level algorithm using small data sets and the semisupervised training principle. Method-induced errors are evaluated using the Monte Carlo test and an overlapping table is proposed for the rejection or tentative acceptance of particular segmentation and fractal analysis algorithms. This study uses lung histological slides and the results show that 2D box-counting substantially outweighs lacunarity for considered configurations. These findings also suggest that the proposed method is applicable for further designing of classification algorithms, which is essential for researchers, software developers, and forensic pathologist communities.
1. Introduction
The digital analysis of medical microscopic images is very important from an application point of view. The designing of such systems is necessary for improving patient condition analysis and to reducing human errors. Advances in image acquisition of microscopic slides have improved the performance of CADx (Computer-Aided Diagnosis) [1,2]. CADx systems are large data systems, because microscopic slides are very large images and many of them are processed in a typical workflow. A typical microscope slide is approximately mm and submicrometer resolution can be achieved using optical scanners. In most cases, the biological content does not occupy the entire slide, but image size is still large enough.
The problem of image size is important, but automated analysis is much more significant. Large data sets require fully automated or computer-assisted processing (Human in The Loop). The extraction of important parameters for medical analysis of a patient is a very complicated task. The essential problem is complexity of visible structures and their variability in different patients. The designing of CADx systems is seemingly one of the most challenging tasks for researchers nowadays.
Reliable CADx systems are available for the morphologically simplest biological structures. A good example is the use of liquid cytology with removed artefacts instead of traditional pap smear in cervical cancer screening, which leads to clearer background of obtained cytological images and therefore enables preliminary computer interpretation of cytology for example with Focal Point BS, Burlington, NC, [3]. Automated microscopy system Cellavision DM96 is also used for the examination of peripheral blood smears essential in hematological diagnosis [4,5].
A typical CADx system is based on a data classification system with numerous application- oriented complex algorithms. One of them is the estimation of a type of microscopic structure and the determination of malignancy. This could be achieved by analyzing microscopic structures, which are tissue dependent. The analysis of lung microscopic slides shows the importance of fractal structures for classification purposes. Quantitative analysis of the fractal dimension seems to be a promising method, but the segmentation of an acquired image is needed. Additional image analysis algorithms as well as a large data set are required for the design of CADx systems.
Two main approaches could be applied for the design of a CADx system. The first one is the black-box approach using machine learning methods, where overall process is based on training using a large data set. The primary drawback of this approach is the need for a very large data set with man-made segmentation. The secondary drawback is the lack of knowledge about obtained data processing details, therefore such a system is a black box and determination of reliability of such a CADx system is questionable. The second approach is the hierarchical system which is much more promising, because particular parts of the system could be tested independently, thus the determination of reliability of such a CADx system is possible. The hierarchical system allows the reduction of the data set, because increased control of particular algorithms is possible.
This work uses hierarchical design. The first hierarchy level is based on segmentation using dedicated HistAENN (Histogram-based Autoencoder Neural Network) and semisupervised learning principle. The second hierarchy level is the fractal-based estimator for complex structure analysis.
The field of research has a broad spectrum of application, and therefore the contribution is listed in a few main points:
- This work assumes hierarchical design using autoencoder neural network (the first hierarchy level) and the fractal-based estimator for complex structure analysis (the second hierarchy level) of segmented images and shows how to select or preselect algorithms in the second hierarchy level algorithm using small data sets and the semisupervised training principle. The choice of the best algorithm can be automated. Manual segmentation of entire images, required for supervised learning for creating training pairs, is not required in this case. It is the main contribution of this paper.
- This paper demonstrates a different approach to the design of image segmentation algorithms, because in majority of papers’ single results of neural networks are provided. There are numerous reasons why single results are provided, such as learning time, but it leads to false final conclusions about the architecture of the neural network. Neural network should be learned multiple times, because such empirical verification leads to different non-optimal networks, and the distribution for most quality parameters is achieved. Single learning gives a single value of neural network quality parameters, so the comparison of two different neural network architectures leads to significant errors.
- This paper addresses the problem of lung autopsy microscopic image analysis that is completely different from examination of regular histological slides of lung tissue. The issue of result variability due to the selection of image segmentation, and image analysis algorithms are discussed. The outcome has good potential for further designing of classification algorithms, which is essential not only for researchers and software developers but also for the forensic pathologist community. Moreover, methods described and discussed in this paper are appropriate for different types of digital images.
- The segmentation algorithm with the use of machine learning approach and comparison of results for two fractal-based algorithms—2D box-counting and fractals related lacunarity—are discussed in this paper. Binary images from the classification algorithm should be achieved, but the inherited properties of histological slides do not allow the discovery of an exact solution. The segmentation algorithm introduces errors and could be considered as noise. Segmented images are processed by fractal algorithms and input data including noise influence on the final variability of estimated fractal descriptors. Low variability of the system is especially important for semisupervised learning, because this type of learning is preferred for the processing of large images with some control of this process by specialists (patomorphologists or cytomorphologists.
- Method-induced errors could be estimated using the Monte Carlo approach. This work uses 100 HistAENNs trained for every image for the determination of algorithm influence on results. Overlapping tables could be achieved and analyzed for the determination of variability. The selection of a possibly more acceptable algorithm (e.g., fractal) and the selection of parameters for particular algorithm could be attained. The analysis of variability which may be applied for data sets with very raw manual segmentation is most important. Moreover, providing the expected classification results for the selection of segmentation and fractal analysis algorithms is not necessary.
- This paper shows the viability of the designing of segmentation algorithms with the use of neural networks if the appropriate rotational invariance algorithm is applied. It is possible by the application of the Sliding Window Local Histogram (SWLH) to achieve desired invariance. The training of such rotational invariance inside much deeper and larger CNN (Convolutional Neural Network [6,7,8]) is feasible, but SWLH that is a part of HistAENN simplifies training. SWLH reduces the size of the neural network as well as training time, so Monte Carlo tests are possible with a few days of processing.
Additional estimators are necessary for proper classification if the fractal estimators are not sufficient [9]. Such additional estimators and classification parts of system are not dealt with in this paper.
The related works are introduced in Section 2. A brief introduction to lung tissue as well as image acquisition parameters is presented in Section 3. Image complexity and variability of structures are presented using example images. Semisupervised learning and analysis of method-induced errors are considered in Section 4. Quantitative analysis of variability of estimators is considered in Section 4.1. Manual Segmentation Techniques in Semisupervised Learning are considered in Section 4.2. The first hierarchy level uses proposed HistAENN architecture (Section 4.3) that is trained using developed HistAENNseg software (Section 4.4). The second hierarchy level is based on the fractal estimator that is promising as one of the descriptors for lung structures observed in microscopic images. Box-counting and lacunarity are considered in Section 4.5 as fractal estimators with the multi-parameter output. Results based on Monte Carlo tests [10,11], related to variability, can be found in Section 5. Discussions of selected solutions are provided in Section 6.1 (All-in-One and Hierarchical Segmentation), Section 6.2 (Selection of Learning Principles), and Section 6.3 (Invariant Image Representation). Discussion of obtained numerical results that leads to the selection of a better fractal-based image analysis algorithm is presented in Section 6.4. Final conclusions and further work are provided in Section 7.
2. Related Works
Semisupervised learning of neural networks (including CNNs) and other pattern recognition algorithms are recognized as the most promising techniques for large data sets due to the limited number of labels [12,13,14,15]. Fractal analysis is used very often for analysis of microscopic structures in medical images [16]. The application of fractal geometry for automated segmentation of lung parenchyma image sequences is discussed in [17]. The problem of variability of fractal estimators is well known and is described in numerous works [9,18]. The bias problem is not relevant if the same algorithm is used.
The analysis of variability is possible using numerical tests. Two variants are possible using the Monte Carlo approach. The best variant is based on the synthetically generated large data sets of known properties (e.g., fractal dimension). This variant allows testing of the variability for a particular system. It is robust, but limited, because it is impossible to generate microscopic images of a lung. A typical augmentation process used during neural network training cannot be used, because augmentation could change the structure of images and influence values of fractal estimators. Another variant of the Monte Carlo approach is used in this paper. The source of noise is the learning process itself, because the starting parameters and order of training samples influence the achieved neural network and segmentation results. This is a source of noise for variation testing of system (neural network with fractal estimator). Uncertainty in deep convolutional encoder–decoder architectures using the Monte Carlo approach is considered in [19,20].
Method-induced errors are considered in numerous works, and two techniques are possible: analysis of direct distributions or mean and standard deviation pairs, the latter being more convenient. In both cases, multi-parameter estimation is used for an arbitrary set of scales. Standard deviation and mean are considered, for example in [18,21,22]. Average fit error is considered in [23]. Coefficient of variation, as well as standard deviation and mean, are used in [9]. Standard deviation and mean for 2D and 3D box-counting are considered in [24]. Method-induced error analysis using the Monte Carlo test could be regarded as a kind of software testing, especially to achieve high reliability [25,26]. The Monte Carlo test is time-consuming, so adaptive techniques [27], including Markov Chain Monte Carlo are used [28].
Overlapping tables are used for quantitative comparison of fractal algorithms. This = allows the overlapping of empirical distribution analysis. It is the adjacency matrix for undirected graphs in graph theory. Numerous measurement criteria are available for the analysis of adjacency matrix, especially in the context of ecological niche analysis [29]. Niche overlaps are usually considered to be a 2D overlapping problem [30] and in this work 3D overlapping is considered.
Rotational invariance is considered, and it is important for image classification purposes. Numerous techniques for rotational invariance of overall image are proposed [31,32,33,34,35]. Multiple images with specific rotation of faces are used in [31]. Similar input technique is used in [32] for multiple parallel CNNs and their outputs are processed by dense layers which are the data fusion parts of system. An additional rotational invariant layer is applied in [33,34]. Two techniques to encode rotational invariance are considered in [35] by applying rotation to the input images and rotations to the convolutional filter. Rotational invariance for small-scale areas are considered in this paper as a simpler solution.
Advances in image segmentation algorithms offer some alternatives to machine learning-based segmentation. The most important are turbopixel/superpixel segmentation methods [36,37], watershed segmentation methods [38,39], and active contour methods [40,41].
3. Data
Histopathological examination of tissues is useful in undiagnosed and suspected cases to confirm the diagnosis. The involvement of lung is observed in infectious and malignant conditions and cases of cardiovascular events and lung autopsy is indispensable in forensic medicine, because this examination may often provide the information about the cause of death [42].
The morphology of lung tissue is shown in Figure 1 and it is remarkable that alveolar septa are fractal in structure and therefore are essential for the segmentation task. Various morphological changes are observed in autopsy lungs. Lung pathological findings contain cases of pneumonia, emphysema, tuberculosis, and malignant lesions [43].
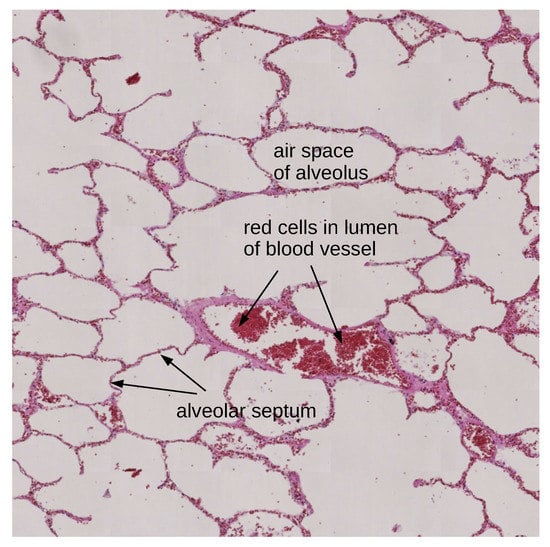
Figure 1.
Example of lung tissue.
The fundamental basis of fractals and analysis of fractal dimension and associated measurements, such as lacunarity (texture) for lung are considered in [44]. In [45] most commonly observed examples of terminal changes in lung at autopsy are pulmonary edema and changes due to cardiac causes and pneumonia whereas acute respiratory distress syndrome and mycotic abscess and metastatic lung cancer were observed as rare findings. Normal morphology of lung tissue is also observed in autopsy lung [42]. It is reported that in cases of autopsy lung autolytic changes are often observed which are also found in other types of tissues. Moreover, for some cases, histology is unremarkable [46,47], making the segmentation of lung autopsy histological slides is a challenging task due to the presence of autolytic changes of different grading causing indistinct tissue structure. Various morphological findings connected with age, coexistence of additional diseases, and hormonal stage of the patient are also significant and influence lung tissue. The examples of histological findings in autopsy lungs are shown in Figure 2. Very often, more than two changes are found in one histological slide, so this is another reason digital classification is a challenging task.
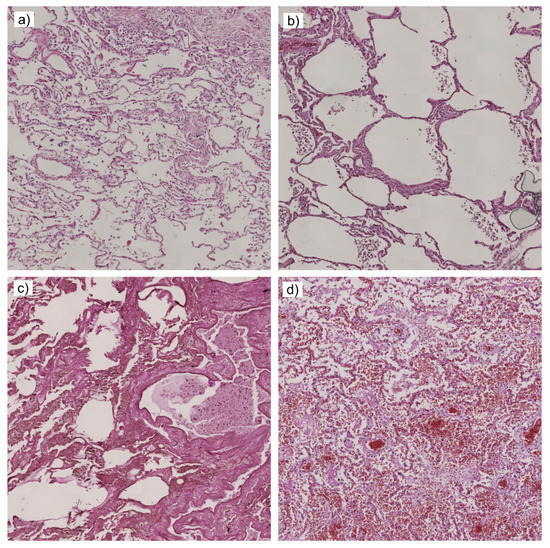
Figure 2.
Examples of lung autopsy images ((a) emphysema, (b) edema, (c) autolysis, (d) blood cells in alveoli and congestion).
Eight colors were used for the segmentation due to the presence of various morphological structures, dependent on the state of the patient, additional diseases, age etc. It has been observed that medical images have very complex morphological structure due to many diagnostic issues. Four colors were used for the estimation of fractal dimension. Therefore, the fractal dimension is estimated in some individuals from pneumocytes of alveolar septa. The structure of the fractal is created not only by pneumocytes, but also in cases of congestion is created additionally by erythrocytes present or neutrophils and macrophages if present in alveolar septa in an inflammation state for example. This is the reason more than one color is included in fractal dimension analysis; furthermore, in some images only one color is presented in septa, and in other cases even four colors connected with morphological structures are present. Four additional colors were used in segmentation for further purposes. This issue is strongly-based in the area of medical analysis which is not included in our present analysis, and outside of the paper scope.
Experimental evaluation of box-counting and lacunarity is based on parts of 52 autopsy images stained with Hematoxyline–Eosine. They are acquired using 3DHistech Panoramic MIDI scanner with Hitachi HV-F22CL camera. The pixel size is about 0.234 m and virtual slide (MRXS format) uses JPEG compression with compression factor 60. The input images from slide scanner are RGB, but we tested grayscale variant, because many features are visible without color. Color could improve results but using a grayscale image is interesting from the research point of view. The inputs in this work are TIFF images with resolution. They are extracted from MRXS virtual slides using OpenSlide Viewer v.3.4.1 [48] and VIPS v.8.4.5 [49].
4. Methods
The analysis of method-induced errors allows the comparison of the algorithm. Multiple tests are required for the determination of variability of results and the most important fact is that the overall process could be automated if quantitative algorithm quality criterion is defined. Method-induced errors could be estimated for complex systems or particular parts of such a system.
4.1. Variability of Estimators
The problem of variability is very complex from different points of view. Single segmentation and corresponding fractal-based estimation results are insufficient for the variability analysis.
Low variability (small method-induced errors) is required for the user. Semisupervised learning is applied for every image by the user, so the user expects good classification, therefore the proper value of fractal dimension (FD) for classification algorithm should be delivered. Segmented image could be visualized for the user’s acceptance or rejection of classifier results. Low variability of system means also that the number of tests and trials is very low for the user.
Variability testing is possible by multiple repetitions of training and estimation of fractal parameters (a kind of Monte Carlo test). This process allows estimation of some empirical distribution which is valuable for the analysis of variability. This process could be repeated for the same input image. Neural network learning process is sophisticated, so achieving a global minimum is not usually possible. Multiple runs of the training algorithm will deliver similar but not identical segmentation algorithms. The small data set used in the second phase of a learning of classifier does not guarantee correct convergence but testing of this convergence is needed.
The distributions of FD or lacunarity, obtained by multiple tests of the same input image and particular segmentation provided by the user, are the results of Monte Carlo tests. Different images can have similar distributions. Images with the same image content are expected to deliver similar distributions. The question is, how can a pathomorphologist use distributions from a Monte Carlo test without a large database or precise classification?
The solution for the abovementioned problems is as follows. The hypothesis about the possible correct structure of neural network and fractal estimator could be checked with a Monte Carlo test, with a decision rule defined as an acceptance by the lack of reasons for the rejection. The rejection of this hypothesis and rejection of a particular system configuration is possible in cases of significant overlapping of all distributions. Two different images with different content should be with two different distributions without overlapping or with very low probability of overlapping. The testing of all distribution pairs provides the quality coefficient.
Analysis of bounding boxes defined by means and standard deviations could be proposed as criteria for possible rejection or acceptance of the hypothesis. Three selected mean values define the center of box and standard deviations define nearest distances between center and particular box faces.
The lack of significant overlapping for two images, in the standard deviation sense, means that there are box pairs related to two different images without common content even if the learning process is repeated multiple times. Overlapping occurs if there is a common content. Comparison of all pairs/boxes gives an overlapping table . This table is diagonally symmetrical, but diagonal results are not used. All possible pairs are tested, and the following formula shows how this table is filled with logical ‘0’ or ‘1’ values:
where x and y are indexes of boxes and . The minimal number of comparisons in is defined by the formula:
where P is the number of images ( in this work). The density of overlapping D is the assumed criteria of analysis, so sum of logic ‘0’ values could be calculated using values below or above diagonal:
Relative overlapping is defined by formula:
and it is a scalar indicator of the system quality that is related to method-induced errors. Minimal value (zero) is the best case (acceptance) and maximal value is 100% (full rejection).
It should be noted that classification assignment is not considered in this technique. Significant overlapping of distributions is the source of strong rejection of the system. This is not a proof that such system will function. Lack of significant overlapping suggests the ability of classification for achieved parameters from a particular system. Partial overlapping of distribution shows that the system requires additional image descriptors for the correct classification. Such additional tests are not considered in this work.
The value of could be used for the comparison of different algorithms or system configurations. The variability analysis could be based on testing of standard deviation and mean. An alternative approach is possible with the use of distributions directly.
4.2. Manual Segmentation Techniques in Semisupervised Learning
Semisupervised learning assumes labeling of a small part of an image. There are three possible methods of labeling (Figure 3) for small areas depicted as a white line. The first one assumes labeling of the inner part of an object (Figure 3a) far from region edges. The second one assumes labeling of region boundaries (edges). This method requires finding edges between each possible pair of objects of different classes (Figure 3b). The third one requires near-to-edge labeling of objects without edges crossing (Figure 3c). The first and the third methods were used jointly in this paper.
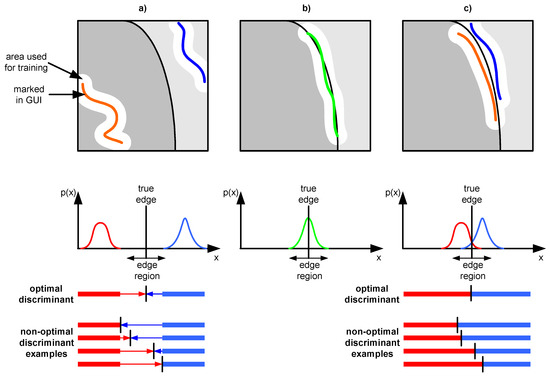
Figure 3.
Examples of manual labeling, achieved distribution and possible regions discriminations ((a) inner regions labeling, (b) regions edge labeling, (c) near-to-edge labeling).
Manual selection, depicted as a color curve, allows the local selection of surrounding pixels around such a curve which are depicted as fat white curves corresponding to particular selection. White and color curves allow the extraction of image parts, so small image pieces with fixed window size could be processed directly during training or are an input image for other parametric or non-parametric estimators. Single- or multi-dimensional distribution for particular selections are achieved in all the abovementioned cases (they are also shown in Figure 3):
- The inner part of region labeling is straightforward for the user but leads to numerous problems. Separation between two regions could be significant and both distributions do not overlap (Figure 3a). There are numerous possible discriminants which could be achieved during the training of a classifier using typical neural network training algorithms. Optimal discriminant is between both distributions and it is usually not achieved.
- The near-to-edge selection uses previously mentioned properties of distributions to achieve better discrimination. Both selections in this method overlap and both distributions overlap too. This means that the distance between them is much smaller compared to the first method (Figure 3a), but full overlapping is not achieved as in the distribution shown in Figure 3b. The application of typical neural network training algorithms leads to positioning of the discriminant between both overlapped distributions. There is no gap between them, thus an optimal or very close to optimal solution is achieved.
The first and the third method should be used together, because they are related to different distributions. The first method is not feasible for near-to-edge regions and the third could fail in inner-region areas. Combining them allows efficient training in the semisupervised approach. Manual segmentation rules are rather simple for users if the GUI is correctly designed. User actions are related to the segmentation using color curves as in Figure 3 and white regions are not depicted in any way. Single pixels of the selection curve depicted in GUI define the center of the window, used for the extraction of the pixels. It is not necessary to select from both sides of edges in the same image part area. Two different image part areas could be successfully used for the selection of classes.
Proposed inner-region and near-to-edge labeling could be applied for sharp and fuzzy edges, which is very important for the processing of histological images. It should be noted that segmentation using strict assignment of objects to particular classes leads to segmentation errors. The difference between classes is sharp, but edges between objects in the image are fuzzy. This is a result of acquisition errors during the scanning, slide preparation errors or numerous stereology effects [50]. Thick section could contain entire microscopic objects or pieces of microscopic objects. Slides are three-dimensional with some volumetric transparency, but a two-dimensional image is obtained by slide scanner [50].
4.3. Architecture of HistAENN and Two-Step Learning
A local histogram with low number of bins (SWLH) is applied for image preprocessing and the window size is pixels. This preprocessing is responsible for local rotational invariance. The architecture of applied neural network is variable with two phases and corresponding configurations (Figure 4).
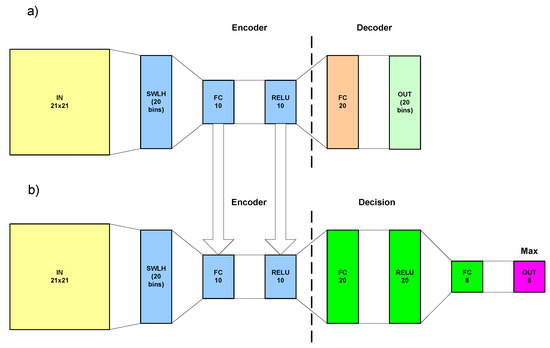
Figure 4.
Scheme of HistAENN architecture for both training phases (RELU—REctified Linear Unit Layer, FC—Full Connection Layer) ((a) autoencoder phase, (b) classifier phase).
During the first phase, HistAENN works as an autoencoder [8,51,52] with input vectors (histograms) and exactly the same output vectors. A bottleneck in the inner part of an autoencoder (FC10 together with RELU10) forces data clustering. Two parts of an autoencoder are achieved after training: encoder and decoder, which correspond to the input-to-bottleneck and bottleneck-to-output parts of neural network. This phase uses 100,000 random fragments of the image for training, so this autoencoder is obtained by unsupervised learning.
The encoder is reused in the second phase with fixed weights. The outputs of the encoder are connected to the new neural network which is a classifier. Inputs are vectors (histograms), as in the previous phase. The classifier uses N independent outputs which are assigned to particular classes. The position of maximal value from the output vector is a recognized class number. Every position of the sliding window corresponds to a single output class number.
Desired outputs are manually assigned labels by the user before training HistAENN, so the number of training pairs is much smaller (e.g., 500 for each class) compared to the number of training cases in the first phase. This phase uses the supervised learning principle.
A typical testing using an additional data set is not used during both phases. It is intentional, because the segmented image is evaluated by a human. Test cases could deliver quality information to the user, but this is not discussed in this paper. This paper is related to the automatic evaluation of variability of HistAENNs and fractal estimators. The application of test cases leads to the rejection of badly fitted HistAENNs. The acceptance of such HistAENNs is required for the increasing of variability range.
The processing of entire image begins after the end of the second phase of training. The obtained segmentation could be accepted by the user or not, because it is semisupervised learning with a Human in The Loop. We observed that additional iterations are not so frequent, and they are related in most cases to human labeling errors.
4.4. HistAENNseg—Image Segmentation Software
Manual segmentation techniques and semisupervised learning were implemented in developed software (HistAENNseg). Qt library v.5.5.1 is used for GUI implementation. User activities and GUI are reduced to the desired minimum and manual labeling process requires mouse or graphical tablet (Figure 5) actions. Labels are related to the desired classes. The selection of hundreds up to a few thousand pixels for every class is typically sufficient. The selection should be based on boundary regions between two classes (Figure 3). The selection of regions is possible in the left window. The right window shows achieved segmentation results, with colors assigned to the particular classes which are mixed with original input grayscale image.
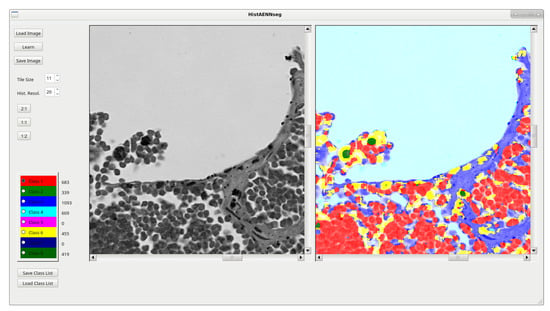
Figure 5.
Exemplary view of HistAENNseg.
Further fractal analysis is based on a binary image, so for the particular image some classes are merged following segmentation. Image resolution for the fractal analysis is reduced four times, because fractal estimation is costly without optimal code for GPU. Additional processing [53] using dilation (disk diameter 1), erosion (disk diameter 4) and removal of an island with the area size of less than 8 pixels area is applied for local artefact filtering.
There are a lot of machine learning frameworks with the support of CNNs. This software uses dlib v.19.10 [54] and NVidia cuDNN library v.7.0.5 [55] for CUDA v.9.1. The selection of dlib was prompted by C++11 [56] direct support of CPU parallel processing and stable memory management of GPU. Overall software was developed and runs on Debian 9. MATLAB is used [53] for the further fractal analysis of labeled output images.
4.5. Fractal-Based Analysis of Microscopic Lung Images
Fractal estimators are frequently used indicators of the complexity in binary and grayscale images [57,58,59]. Different fractal and similar estimators are proposed i.e., box-counting [57], lacunarity [60], variogram [61,62], TPM (Triangular Prism Method) [63,64], SIM (Slit Island Method) [65], APR (Area Perimeter Relation) [66] and others.
The difference between conventional fractal and multi-parameter fractal techniques is in the number of obtained parameters [67,68]. Classical fractal estimators assume single output scalar value-estimated FD. This value is related to the slope of linear function of Richardson’s plot [65,69]. This plot uses a logarithmic axis and typically the linear function in this plot is observed for synthetic fractals. The FD could be a function of scale. Vectors with scale-dependent FD is the output of multi-parameter estimators. The scale range and number of scales should be selected to obtain a smooth Richardson’s curve.
FD value could be calculated for non-fractal objects without relation to object structure. This phenomenon is known as a “fractal rabbit” [69]. Image analysis applications accept “fractal rabbits” if the achieved FD values are useful for a particular application.
Two well-known algorithms are considered in this paper—2D box-counting and 2D lacunarity. Both algorithms use the sliding window approach for binary images and holes are analyzed by box-counting and lacunarity in this work.
Box-counting allows the estimation of using the following formula:
and the can be estimated from the least squares linear fit of against , where is the number of boxes of side length r required to cover the set.
Two extensions of box-counting output are also used, because could be a function of r. Vectors with the local s for multi-parameter box-counting algorithm could be obtained using the following formula:
for neighborhood measurements and .
Another possibility is based on the estimation of s for selected regions from nonlinear Richardson’s plot. Local s are obtained as the results and correspond to region boundaries [69].
There is some redundancy in full vector, but the vector length is fixed which is important for the simplification of classifier design. Regions-based approach uses variable-length vector with s and boundaries pairs.
Lacunarity is not exactly the fractal algorithm in the strict sense, because FD is not estimated and the results of lacunarity depend on texture [60]. Fractal textures give a unique response to the lacunarity algorithm. Lacunarity estimation uses the following formulas [60]:
where r is the sliding window height and width, and are moments of distribution Q. The table n is the counting table that is addressed by r and number of counted pixels s with the specific value (‘0’s or ‘1’s for binary image). The distribution Q is achieved from n by normalization.
5. Results
There are 100 HistAENNs trained using the same single labeling for every image with random starting weights. Both training phases use the SGD (Stochastic Gradient Descent) algorithm [70,71] and 10,000 training steps. The labeling process is controlled by a human using additional training steps before the Monte Carlo test and iteratively corrected if the segmentation results are insufficient. It is expected from the user’s perspective that similar results should be achieved if single segmentation is visually checked.
Example results for box-counting and lacunarity are shown in Figure 6 and Figure 7 respectively. All Monte Carlo results (Richardson’s and lacunarity plots) are shown, for illustrative purposes for a single image as a set of 100 overlapping curves. Raw discrete distributions derived from these distributions are shown as vertical lines with grayscale coding. Direct analysis of such raw distributions is possible, but it leads to a very large set of parameters. The reductive approach is possible by simplification, so only mean and standard deviation are used. Mean values and standard deviations are depicted for particular r values as a continuous line (red) and vertical lines (black), respectively. More precise visualization with median and range is possible, with the use of box and whisker plot. Furthermore, local FDs are shown for box-counting.
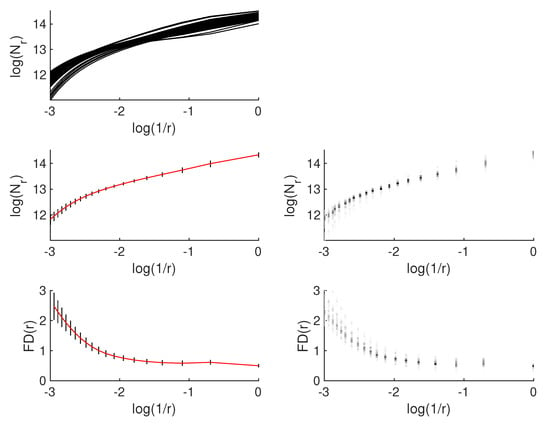
Figure 6.
Exemplary results for box-counting analysis for single image (standard deviations are shown as a vertical line in left figures; raw distributions are shown in right figures).
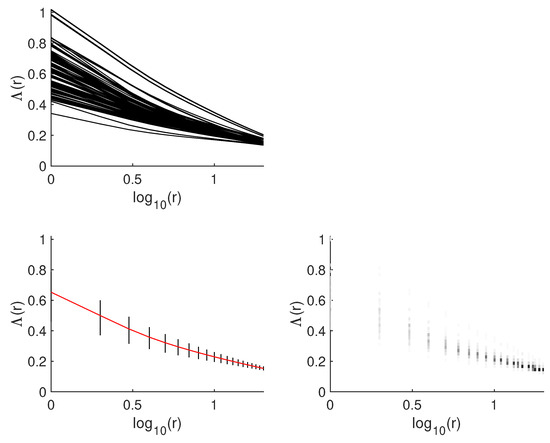
Figure 7.
Exemplary results for lacunarity analysis for single image (standard deviations are shown as a vertical line in left figures; raw distributions are shown in right figures).
NVIDIA Titan X (Maxwell) GPU card was used for training of HistAENNs. Calculations of local histograms (SWLH) were on the CPU. It is possible to process SWLH on GPU, but it will be considered in further versions of HistAENNseg software, because the integration with dlib is necessary.
Multi-parameter box-counting and lacunarity are selected for the analysis of method-induced errors. There are about 19 and 20 results for both algorithms, respectively, so the analysis in this high-dimensional space is difficult and unnecessary. Smooth curves are obtained for every image to avoid sampling problems. A few parameters are sufficient for the analysis. The problem depends on their selection and their equidistant selection is the direct solution, so three values out of four are tested.
Four cases of multi-parameter box-counting and lacunarity are calculated for the configurations and are shown in Table 1.

Table 1.
Configuration of multi-parameter methods and obtained results.
Overlapping table is shown graphically in Figure 8.

Figure 8.
Examples of overlapping: (a) box-counting (Case 1), (b) box-counting (Case 2), (c) lacunarity case (Case 3), (d) lacunarity (Case 4). Black is for overlapping.
6. Discussion
6.1. All-in-One and Hierarchical Segmentations
There are numerous image segmentation [72] and classification [73] algorithms. Machine learning techniques are especially important because the segmentation by training is possible. An alternative approach based on the analysis of images and design of entire segmentation algorithm manually, by long trial and error sequences, is very difficult for complex image content. Parallel processing is possible for machine learning, so different configurations of machine learning algorithms may be automatically trained and tested for the optimization of segmentation performance.
Two main approaches are applied for the design of image segmentation systems using machine learning algorithms:
- All-in-One approach, where a single machine learning algorithm is used for overall image processing. Such an approach could also be used for the final classification purposes, so the input is the image and the output is the recognized class.
- Hierarchical approach, with well-defined processing stages where some of them could be machine learning-based and others could be typical image processing algorithms, such as filters.
The solution proposed in this paper for the segmentation of autopsy lung images uses the hierarchical approach with the HistAENN and additional preprocessing.
6.2. Selection of Learning Principles
The learning of the classifier for the segmentation purposes is a very challenging task. The first problem is related to the selected: supervised, semisupervised, or unsupervised variant [74,75]. This selection is non-trivial, influencing the possibilities of the final system and user experience during regular work:
- Supervised learning requires input and output image pairs. The input image from each pair is available directly, but the desired output image should be manually segmented. Large slide images and their large data set lead to extremely high costs of design. The advantage is the possibility of designing a fully automatic CADx system.
- Unsupervised learning requires input images only, so the problem of manual segmentation of desired output images is avoided. This approach is based on automatic clustering. The number of classes could be arbitrarily selected or could be estimated automatically [76,77]. Unsupervised learning could be applied for well separated classes directly, but in most cases requires manual fitting of algorithms for a particular data set. This additional effort depends on the image content.
- Semisupervised learning is a promising solution for cost reduction of manual segmentation. This process assumes labeling of very small parts of images that belong to the specific classes. Semisupervised learning could be used for CADx system development or as a CADx working principle. In the latter case, semisupervised learning is used by patomorphologists during the analysis of a particular image. Obtained results are checked and corrected iteratively (Human in The Loop) for segmentation improving to the desired level. A very significant advantage of this learning principle is the possibility of an image segmentation system design without access to all possible image variants.
Semisupervised principle is selected in the present paper.
6.3. Invariant Image Representation and Neural Networks
One of the most important problems of neural network-based system is the selection of architecture of the neural network. The invariance of input image on the scale, rotation, skew, and other image transformations is crucial for the correct processing of real images. Sometimes a physical relation of objects and acquisition system (camera) guarantees fixed relation for some of the transformations. The system should be non-sensitive to the object transformations. There are two possible approaches for achieving this extremely important property:
- Invariant transformations guaranteed by machine learning,
- Invariant transformations guaranteed by preprocessing algorithms.
The first approach may be achieved by neural network, using augmentation of data with different combinations of scale, rotation, skews, and other transformations. Data augmentation requires a great deal of additional computation power for the preparation of augmented images and learning time is also significantly increased. Moreover, the achieving of input image invariance requires additional layers.
An alternative approach is used in hierarchical systems, which are designed with the knowledge about possible image transformations, when object-to-acquisition system relations could be estimated. Preprocessing algorithms could be applied for achieving image transformation invariance. Such algorithms use image features as control points for the desired transformation. Achieved compensation reduces learning cost, which is the main advantage of this approach. It is important for users of the system, because the selected segmentation is based on semisupervised learning (one particular image, one learning process). The drawback is the lack of feature points in microscopic lung images, due to isotropy, so rotational invariance should be achieved without control points.
The problem of rotational invariance is addressed in this work by the conversion of input image part from particular sliding window position to another space. This technique is very often applied for images or non-image input data. Statistical parameters, such as mean, standard deviation, etc. are independent of the data order, so desired rotational invariance may be achieved. Some researchers use tens of these parameters for input data preprocessing, instead of directly processing a part of the image.
The selection of parameters is not trivial. Another difficulty is the correlation of multiple statistical parameters used at the same time. Mean and standard deviations are not correlated, but for example mean and median values could share some properties. Output results may depend on one parameter or multiple parameters with some weights. Another problem lies in the possibility of interpolation, not the approximation (data generalization) due to redundant preprocessing parameters.
Non-parametric statistical approach is selected in this paper (SWLH). Histograms preserve information about the distribution using a set of values using a less reductive approach. Details about distribution, including modal properties, are preserved that could be important for segmentation purposes. Different image classes could be very often described by different distributions, due to differences in local brightness and contrast. Edge regions are their mixture. The hypothesis concerning a possibility of preprocessing of input image by the SWLH is also empirically tested in this work.
6.4. Selection of Fractal Descriptors for Image Analysis
The proposed technique demonstrates the possibility of the evaluation of the system with the neural network and fractal descriptors. The achieved method-induced errors may be evaluated graphically (Figure 8) or using relative overlapping for different configurations (Table 1, column).
This work is related to fixed configuration of HistAENN (Figure 4) and a few variants of the parameter selection from fractal descriptors (Table 1). It should be noted that it is possible to test different configurations. Such optimization is valuable in the search for an optimal system configuration.
The selection of scales for box-counting and lacunarity is important for computational cost reduction (Table 1). This work uses arbitrary selected scales, and a further option is the application of the non-gradient optimization algorithm.
Multi-parameter box-counting changes the quality of parameter selection twofold (Table 1, Case 1 and Case 2). The best is Case 1 and the maximal box width is 52 pixels of the input image that corresponds to the value. The minimal box width is 4 pixels. Case 2 uses different ranges for boxes (maximal box width is 76 and the minimal is 28 pixels).
Achieved results show advantages of box-counting over lacunarity. Relative overlapping is much lower for box-counting and this algorithm could be selected as estimator for the designed system. Lacunarity gives significant overlapping in more than in 2/3 cases (Table 1, Case 3 and Case 4), and should be rejected.
Increased overlapping (Figure 8) in some cases may be seen. This is depicted as a series of black pixels in vertical or horizontal directions. It means that there are some input images with very high values of standard deviation in the Monte Carlo test and the bounding box overlaps many others. The application of multi-parameter box-counting classification system is not possible for these images, and some other image descriptors are needed for classification improvement. The image of overlapping for multi-parameter lacunarity is filled with many black pixel series and significant overlapping could be detected visually.
7. Final Conclusions and Further Work
The design and performance of CADx systems is a time-consuming task with a high cost of development. An early rejection or acceptance of the considered configuration of neural networks and other algorithms is essential, because there are many factors that influence the optimal configuration. A hierarchical approach is especially important, because the system could be developed step by step.
A Monte Carlo test is a useful tool for unbiased testing of algorithms if synthetically generated data are available. Images as an empirical source of test data for the determination of system quality are used in this work. The analysis of results could be based on graphical analysis of overlapping tables or in quantitative form using the relative overlapping formula. The main difficulty with the Monte Carlo approach is the computation cost, but computer clusters could be applied for processing.
Full classification systems are not discussed in this paper. Considered box-counting is not sufficient as only one technique for the classification purposes, because there are some cases of overlapping in particular images and additional parameters are necessary. The design of classification systems will be considered in further work.
The present paper shows the possibility of the analysis of complex systems. A final system without this analysis is a black box and the proposed method allows us to regard this system as a grey box.
Author Contributions
D.O.-M., M.P. and P.M. conceived and designed the experiments; A.S. performed the acquisition; P.M. and D.O.-M. analyzed the data; P.M. developed HistAENNseg; D.O.-M. and P.M. wrote the paper.
Acknowledgments
This study was supported by grant from budget resources for science—National Science Center, Poland NR DEC-2017/01/X/ST6/00914. We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan X GPU used for this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doi, K. Computer-Aided Diagnosis in Medical Imaging: Historical Review, Current Status and Future Potential. Comput. Med. Imaging Graph. Off. J. Comput. Med. Imaging Soc. 2007, 31, 198–211. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Nishikawa, R.M. (Eds.) Computer-Aided Detection and Diagnosis in Medical Imaging; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Yu, K.; Hyun, N.; Fetterman, B.; Lorey, T.; Raine-Bennett, T.R.; Zhang, H.; Stamps, R.E.; Poitras, N.E.; Wheeler, W.; Befano, B.; et al. Automated Cervical Screening and Triage, Based on HPV Testing and Computer-Interpreted Cytology. J. Natl. Cancer Inst. 2018, 110, 1222–1228. [Google Scholar] [CrossRef] [PubMed]
- Ceelie, H.; Dinkelaar, R.B.; van Gelder, W. Examination of peripheral blood films using automated microscopy; evaluation of Diffmaster Octavia and Cellavision DM96. J. Clin. Pathol. 2007, 60, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Stouten, K.; Riedl, J.A.; Levin, M.D.; Gelder, W. Examination of peripheral blood smears: Performance evaluation of a digital microscope system using a large-scale leukocyte database. Int. J. Lab. Hematol. 2015, 37, e137–e140. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 253–256. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning (Adaptive Computation and Machine Learning); MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sun, W.; Xu, G.; Gong, P.; Liang, S. Fractal analysis of remotely sensed images: A review of methods and applications. Int. J. Remote Sens. 2006, 27, 4963–4990. [Google Scholar] [CrossRef]
- Metropolis, N. Monte Carlo Method. In From Cardinals to Chaos: Reflection on the Life and Legacy of Stanislaw Ulam; CUP Archive: Cambridge, UK, 1989; p. 125. [Google Scholar]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Lee, D.H. Pseudo-Label: The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks. In Proceedings of the ICML 2013 Workshop: Challenges in Representation Learning (WREPL), Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Gan, H.; Sang, N.; Huang, R.; Tong, X.; Dan, Z. Using clustering analysis to improve semi-supervised classification. Neurocomputing 2013, 101, 290–298. [Google Scholar] [CrossRef]
- Schwenker, F.; Trentin, E. Pattern classification and clustering: A review of partially supervised learning approaches. Pattern Recognit. Lett. 2014, 37, 4–14. [Google Scholar] [CrossRef]
- Feng, Z.; Nie, D.; Wang, L.; Shen, D. Semi-supervised learning for pelvic MR image segmentation based on multi-task residual fully convolutional networks. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 885–888. [Google Scholar]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Zhao, J.; Qiang, Y.; Wang, H.; Xiao, Y.; Zhang, X.; Zhang, Y. An Automated Segmentation Method for Lung Parenchyma Image Sequences Based on Fractal Geometry and Convex Hull Algorithm. Appl. Sci. 2018, 8, 832. [Google Scholar] [CrossRef]
- Wen, R.; Sinding-Larsen, R. Uncertainty in Fractal Dimension Estimated from Power Spectra and Variogram. Math. Geol. 1997, 29, 727–753. [Google Scholar] [CrossRef]
- Kendall, A.; Badrinarayanan, V.; Cipolla, R. Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding. arXiv, 2015; arXiv:1511.02680. [Google Scholar]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2016. [Google Scholar]
- Polychronaki, G.E.; Ktonas, P.Y.; Gatzonis, S.; Siatouni, A.; Asvestas, P.A.; Tsekou, H.; Sakas, D.; Nikita, K.S. Comparison of fractal dimension estimation algorithms for epileptic seizure onset detection. J. Neural Eng. 2010, 7, 046007. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.T. Signal Pattern Recognition Based on Fractal Features and Machine Learning. Appl. Sci. 2018, 8, 1327. [Google Scholar] [CrossRef]
- Li, J.; Sun, C.; Du, Q. A New Box-Counting Method for Estimation of Image Fractal Dimension. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 3029–3032. [Google Scholar]
- Sanghera, B.; Banerjee, D.; Khan, A.; Simcock, I.; Stirling, J.J.; Glynne-Jones, R.; Goh, V. Reproducibility of 2D and 3D Fractal Analysis Techniques for the Assessment of Spatial Heterogeneity of Regional Blood Flow in Rectal Cancer. Radiology 2012, 263, 865–873. [Google Scholar] [CrossRef] [PubMed]
- Zio, E. Practical Applications of Monte Carlo Simulation for System Reliability Analysis. In The Monte Carlo Simulation Method for System Reliability and Risk Analysis; Chapter: The Monte Carlo Simulation Method for System Reliability and Risk Analysis; Springer: London, UK, 2013; pp. 83–107. [Google Scholar]
- Singh, H.; Pal, P. Article: Software Reliability Testing using Monte Carlo Methods. Int. J. Comput. Appl. 2013, 69, 41–44. [Google Scholar]
- Thompson, N.A.; Weiss, D.J. A Framework for the Development of Computerized Adaptive Tests. Pract. Assess. Res. Eval. 2011, 16, 1–9. [Google Scholar]
- Zhou, B.; Okamura, H.; Dohi, T. Markov Chain Monte Carlo Random Testing. In Advances in Computer Science and Information Technology; Kim, T.H., Adeli, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 447–456. [Google Scholar]
- Schatzmann, E.; Gerrard, R.; Barbour, A.D. Measures of Niche Overlap, I. Math. Med. Biol. J. IMA 1986, 3, 99–113. [Google Scholar] [CrossRef]
- Cornell, H. Encyclopedia of Theoretical Ecology; Chapter: Niche Overlap; University of California Press: Berkeley, CA, USA, 2011; pp. 489–497. [Google Scholar]
- Fasel, B.; Gatica-Perez, D. Rotation-Invariant Neoperceptron. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; Volume 3, pp. 336–339. [Google Scholar]
- Dieleman, S.; Willett, K.W.; Dambre, J. Rotation-invariant convolutional neural networks for galaxy morphology prediction. MNRAS 2015, 450, 1441–1459. [Google Scholar] [CrossRef]
- Cheng, G.; Zhou, P.; Han, J. RIFD-CNN: Rotation-Invariant and Fisher Discriminative Convolutional Neural Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Cheng, G.; Zhou, P.; Han, J. Learning Rotation-Invariant Convolutional Neural Networks for Object Detection in VHR Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Marcos, D.; Volpi, M.; Tuia, D. Learning rotation invariant convolutional filters for texture classification. In Proceedings of the 23rd International Conference on Pattern Recognition, Cancun, Mexico, 4–8 December 2016; pp. 2012–2017. [Google Scholar]
- Levinshtein, A.; Stere, A.; Kutulakos, K.N.; Fleet, D.J.; Dickinson, S.J.; Siddiqi, K. TurboPixels: Fast Superpixels Using Geometric Flows. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2290–2297. [Google Scholar] [CrossRef] [PubMed]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vis. Image Underst. 2018, 166, 1–27. [Google Scholar] [CrossRef]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed Cuts: Thinnings, Shortest Path Forests, and Topological Watersheds. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 925–939. [Google Scholar] [CrossRef] [PubMed]
- Ciecholewski, M. River channel segmentation in polarimetric SAR images: Watershed transform combined with average contrast maximisation. Expert Syst. Appl. 2017, 82, 196–215. [Google Scholar] [CrossRef]
- Ciecholewski, M. Malignant and Benign Mass Segmentation in Mammograms Using Active Contour Methods. Symmetry 2017, 9, 277. [Google Scholar] [CrossRef]
- Ding, K.; Xiao, L.; Weng, G. Active contours driven by region-scalable fitting and optimized Laplacian of Gaussian energy for image segmentation. Signal Process. 2017, 134, 224–233. [Google Scholar] [CrossRef]
- Panchonia, A. Histopathological Evaluation of Lung Autopsy: 100 Cases Study. J. Res. Med. Dent. Sci. 2018, 6, 109–112. [Google Scholar] [CrossRef]
- Chauhan, G.; Agrawal, M.; Thakkar, N.; Parghi, B. Spectrum of histopathological lesions in lung autopsy. J. Res. Med. Dent. Sci. 2015, 3, 109. [Google Scholar] [CrossRef]
- Lennon, F.E.; Cianci, G.C.; Cipriani, N.A.; Hensing, T.A.; Zhang, H.J.; Chen, C.T.; Murgu, S.D.; Vokes, E.E.; Vannier, M.; Salgia, R. Lung cancer—A fractal viewpoint. Nat. Rev. Clin. Oncol. 2015, 12, 664–675. [Google Scholar] [CrossRef] [PubMed]
- Kurawar, R.R.; Vasaikar, M.S. Spectrum of Histomorphological Changes in Lungs at Autopsy: A 5 Year Study. Ann. Pathol. Lab. Med. 2017, 4, A106–A112. [Google Scholar] [CrossRef]
- Khare, P.; Gupta, R.; Ahuja, M.; Khare, N.; Agarwal, S.; Bansal, D. Prevalence of Lung Lesions at Autopsy: A Histopathological Study. J. Clin. Diagn. Res. 2017, 11, EC13–EC16. [Google Scholar] [CrossRef] [PubMed]
- Andra Cocariu, E.; Mageriu, V.; Staniceanu, F.; Bastian, A.; Socoliuc, C.; Zurac, S. Correlations Between the Autolytic Changes and Postmortem Interval in Refrigerated Cadavers. Rom. J. Internal Med. 2016, 54, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Goode, A.; Gilbert, B.; Harkes, J.; Jukic, D.; Satyanarayanan, M. OpenSlide: A Vendor-Neutral Software Foundation for Digital Pathology. J. Pathol. Informat. 2013, 4, 8. [Google Scholar]
- Martinez, K.; Cupitt, J. VIPS—A highly tuned image processing software architecture. In Proceedings of the IEEE International Conference on Image Processing, Genova, Italy, 14 September 2005; pp. 574–577. [Google Scholar]
- Baddeley, A.; Jensen, E.B.V. Stereology for Statisticians; Chapman & Hall/CRC: London, UK, 2005. [Google Scholar]
- Mei, S.; Wang, Y.; Wen, G. Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model. Sensors 2018, 18, 1064. [Google Scholar] [CrossRef] [PubMed]
- Liang, P.; Shi, W.; Zhang, X. Remote Sensing Image Classification Based on Stacked Denoising Autoencoder. Remote Sens. 2018, 10, 16. [Google Scholar] [CrossRef]
- MathWorks. Image Processing Toolbox. User’s Guide; MathWorks: Natick, MA, USA, 2018. [Google Scholar]
- King, D.E. Dlib-ml: A Machine Learning Toolkit. J. Mach. Learn. Res. 2009, 10, 1755–1758. [Google Scholar]
- NVIDIA. cuDNN Developer Guide; NVDIA: Santa Clara, CA, USA, 2018. [Google Scholar]
- Stroustrup, B. Programming: Principles and Practical Using C++, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2014. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of the Nature; W. H. Freeman and Company: Stuttgart, Germany, 1983. [Google Scholar]
- Peitgen, H.; Jürgens, H.; Saupe, D. Fractals for the Classrooms: Part One: Introduction to Fractals and Chaos; Springer-Verlag: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Peitgen, H.; Jürgens, H.; Saupe, D. Fractals for the Classrooms: Part Two: Complex Systems and Mandelbrot; Springer-Verlag: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Plotnick, R.; Gardner, R.; Hargrove, W.; Prestegaard, K.; Perlmutter, M. Lacunarity analysis: A general technique for the analysis of spatial patterns. Phys. Rev. E 1996, 53, 5461–5468. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics. A Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Clarke, K. Computation of the Fractal Dimension of Topographic Surfaces using the Triangular Prism Surface Area Method. Comput. Geosci. 1986, 12, 713–722. [Google Scholar] [CrossRef]
- Sun, W. Three New Implementations of the Triangular Prism Method for Computing the Fractal Dimension of Remote Sensing Images. Photogramm. Eng. Remote Sens. 2006, 72, 372–382. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Passoja, D.; Paullay, A. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Mazurek, P.; Oszutowska-Mazurek, D. From Slit–Island Method to Ising Model—Analysis of Grayscale Images. Int. J. Appl. Math. Comput. Sci. 2014, 24, 49–63. [Google Scholar] [CrossRef]
- Harte, D. Multifractals. Theory and Applications; Chapman & Hall/CRC: London, UK, 2001. [Google Scholar]
- Seuront, L. Fractals and Multifractals in Ecology and Aquatic Science; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Kaye, B. A Random Walk Through Fractal Dimensions; Wiley-VCH: Weinheim, Germany, 1994. [Google Scholar]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Mei, S.; Montanari, A.; Nguyen, P.M. A mean field view of the landscape of two-layer neural networks. Proc. Natl. Acad. Sci. USA 2018, 1–7. [Google Scholar] [CrossRef] [PubMed]
- El-Baz, A.; Jilang, X.; Suri, J.S. (Eds.) Biomedical Image Segmentation: Advances and Trends; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we Need Hundreds of Classifiers to Solve Real World Classification Problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Chapella, O.; Schölkopf, B.; Zien, A. (Eds.) Semi–Supervised Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Albalate, A.; Minker, W. Semi–Supervised and Unsupervised Machine Learning; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gan, G.; Ma, C.; Wu, J. Data Clustering. Theory, Algorithms, and Applications; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Aggarwal, C.C.; Reddy, C.K. (Eds.) Data Clustering. Algorithms and Applications; Chapman & Hall/CRC: London, UK, 2014. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).