An Improved Empirical Wavelet Transform and Its Applications in Rolling Bearing Fault Diagnosis
Abstract
1. Introduction
2. Exposition of Traditional EWT Method
2.1. EWT Method
2.2. Drawbacks of the EWT Method
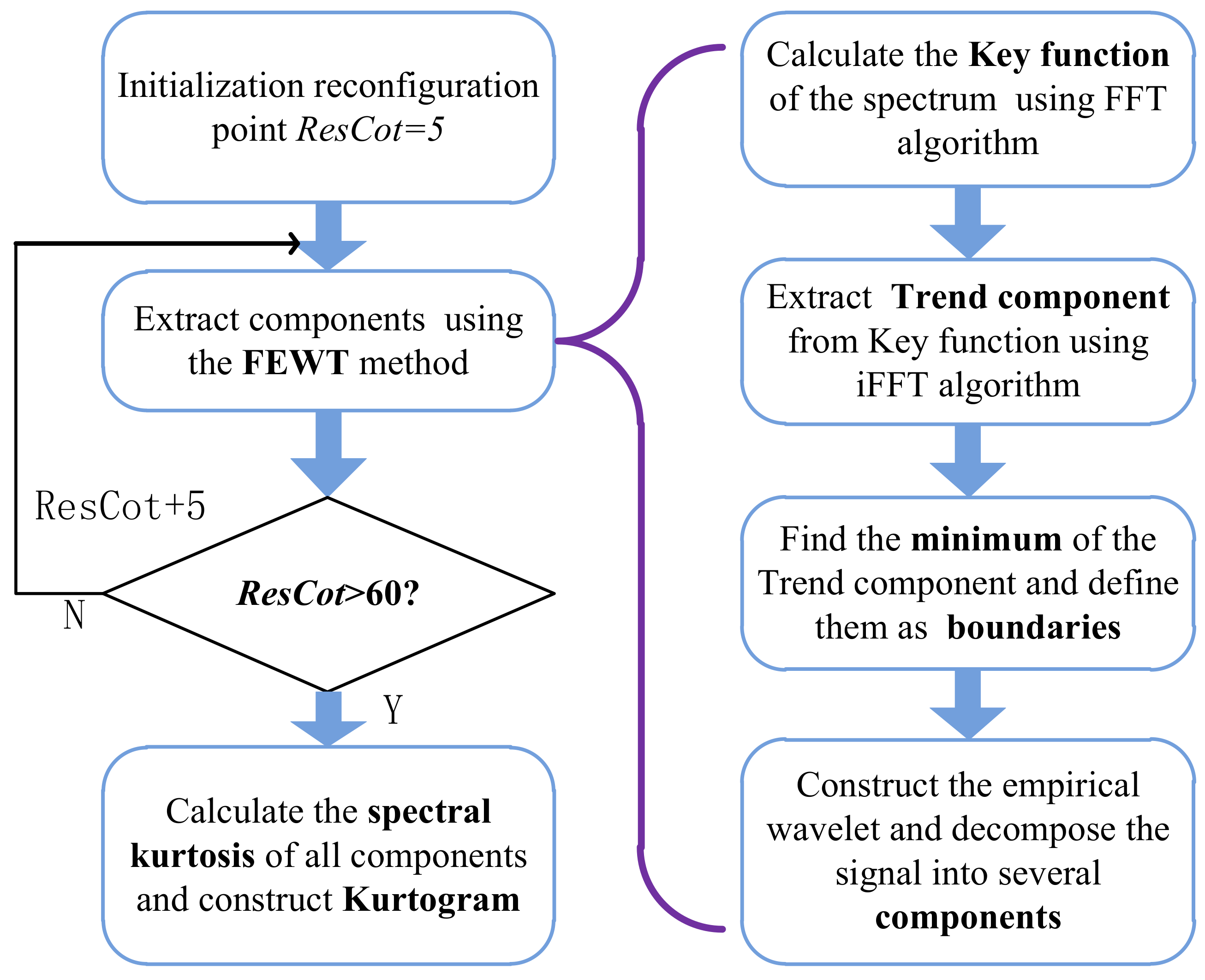
3. Proposed Method of Fast Empirical Wavelet Transform
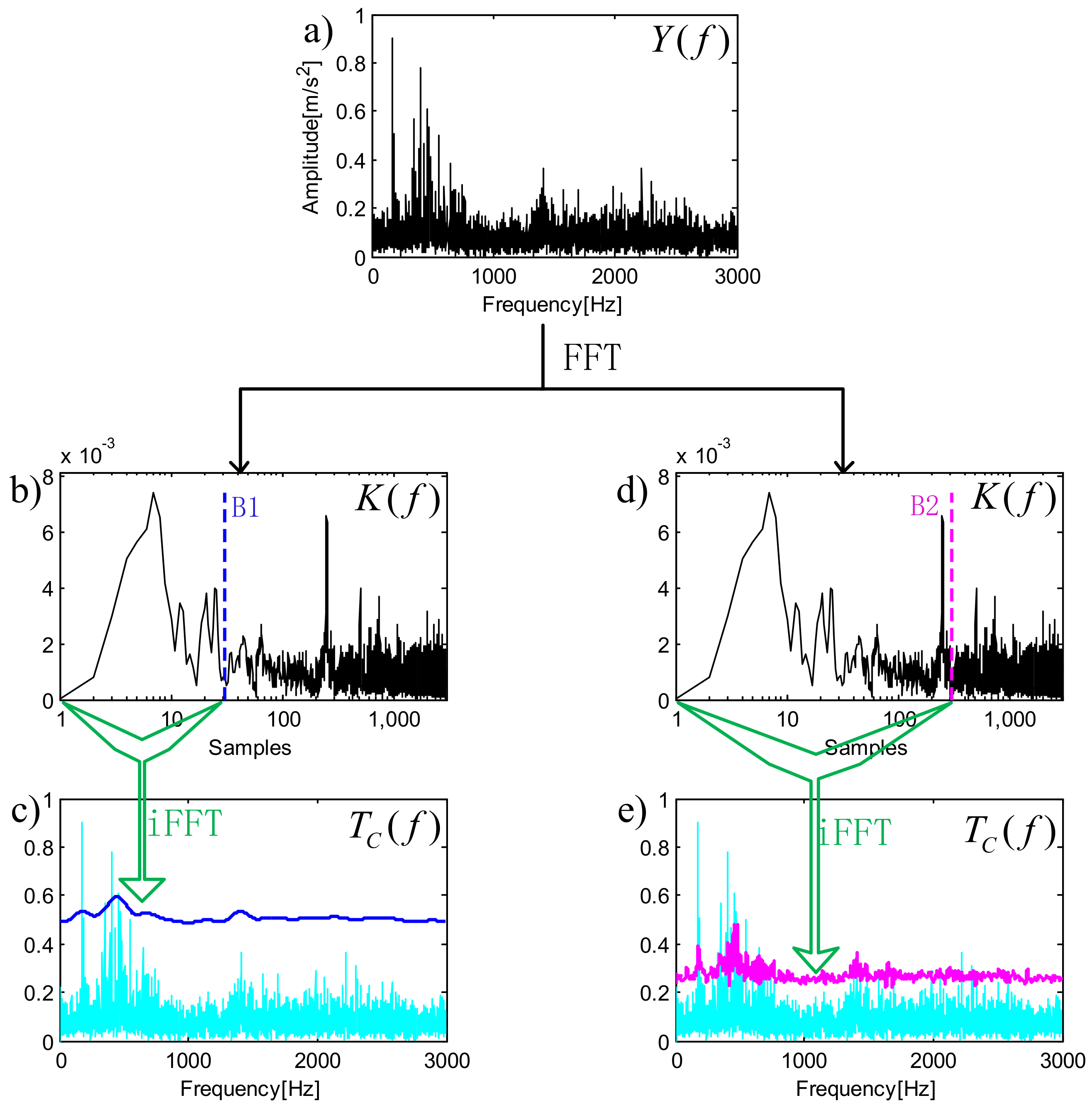
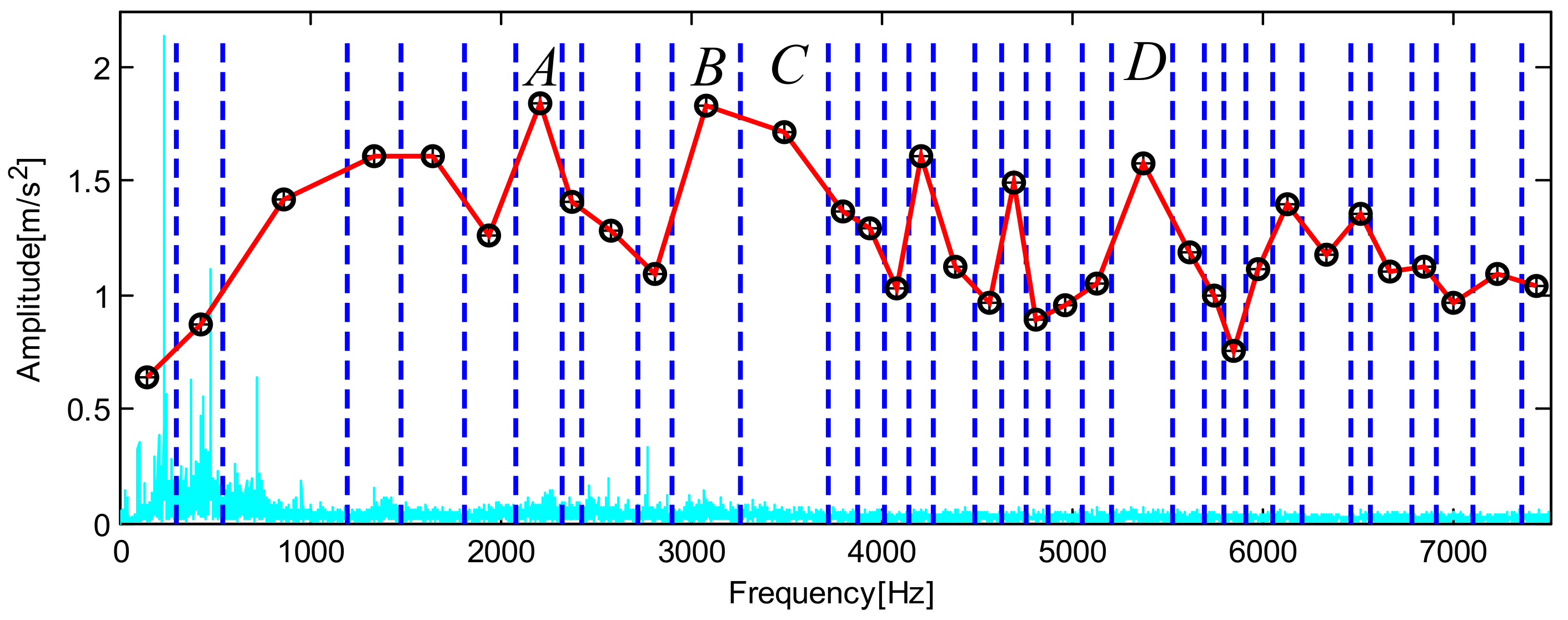
3.1. Trend Estimation Method Based on the Key Function
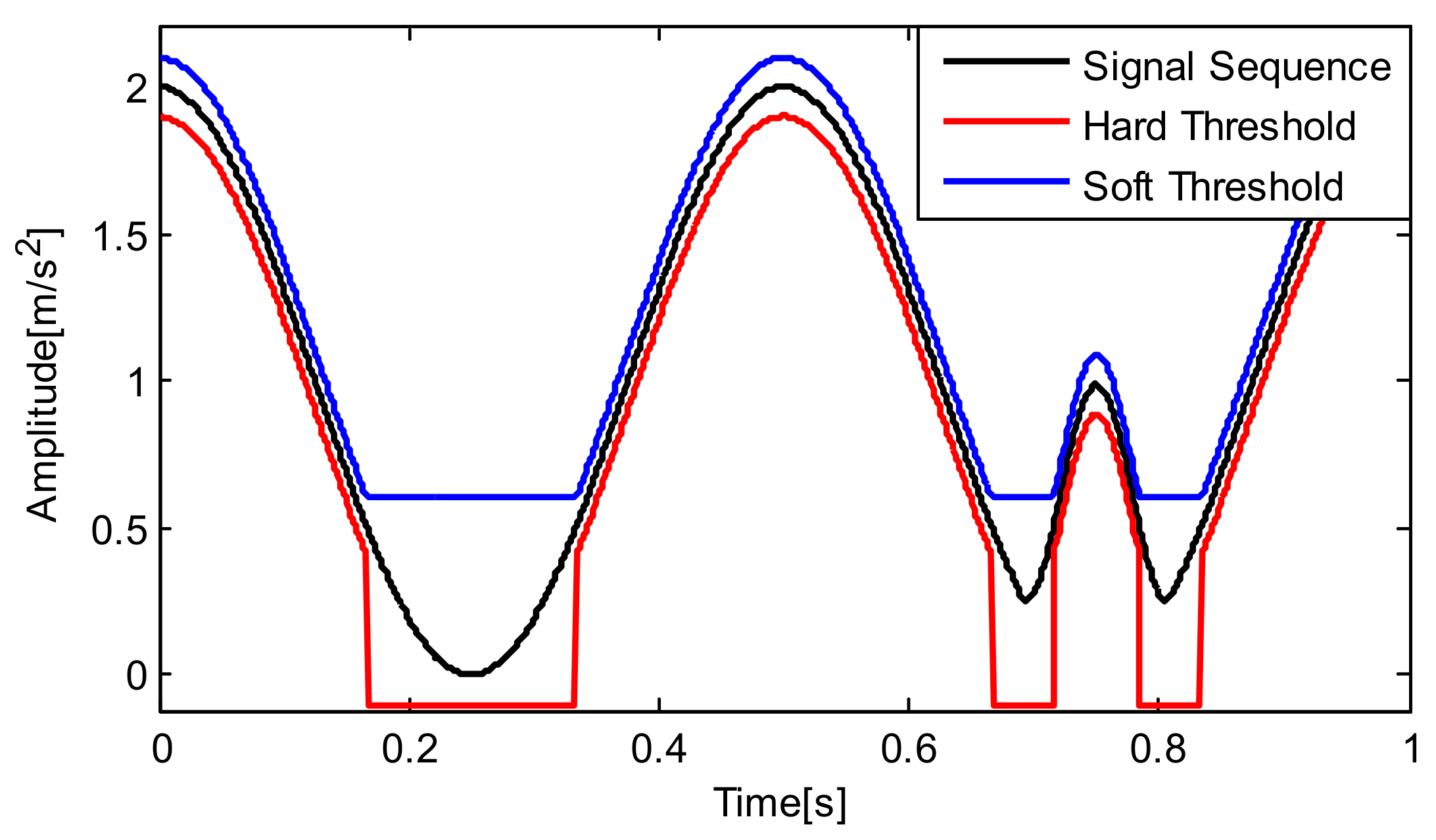
3.2. Threshold Denoising Method
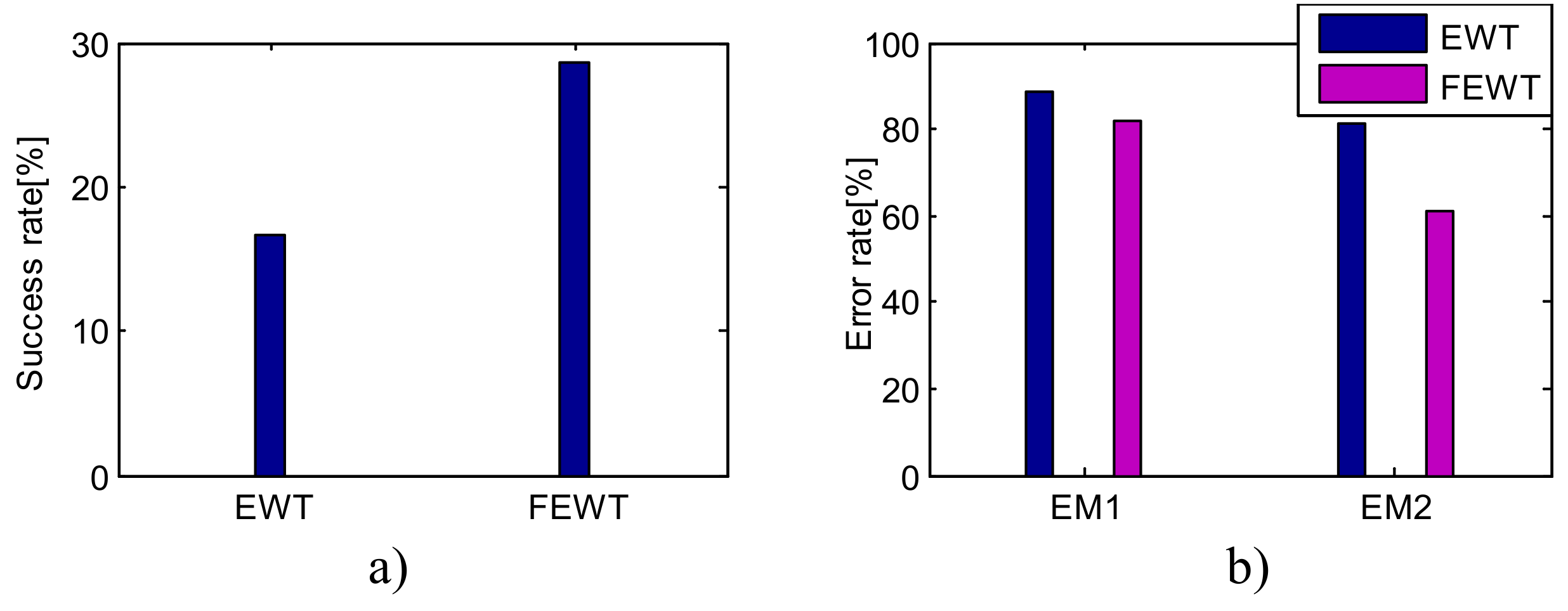
4. Simulated Signal Verification
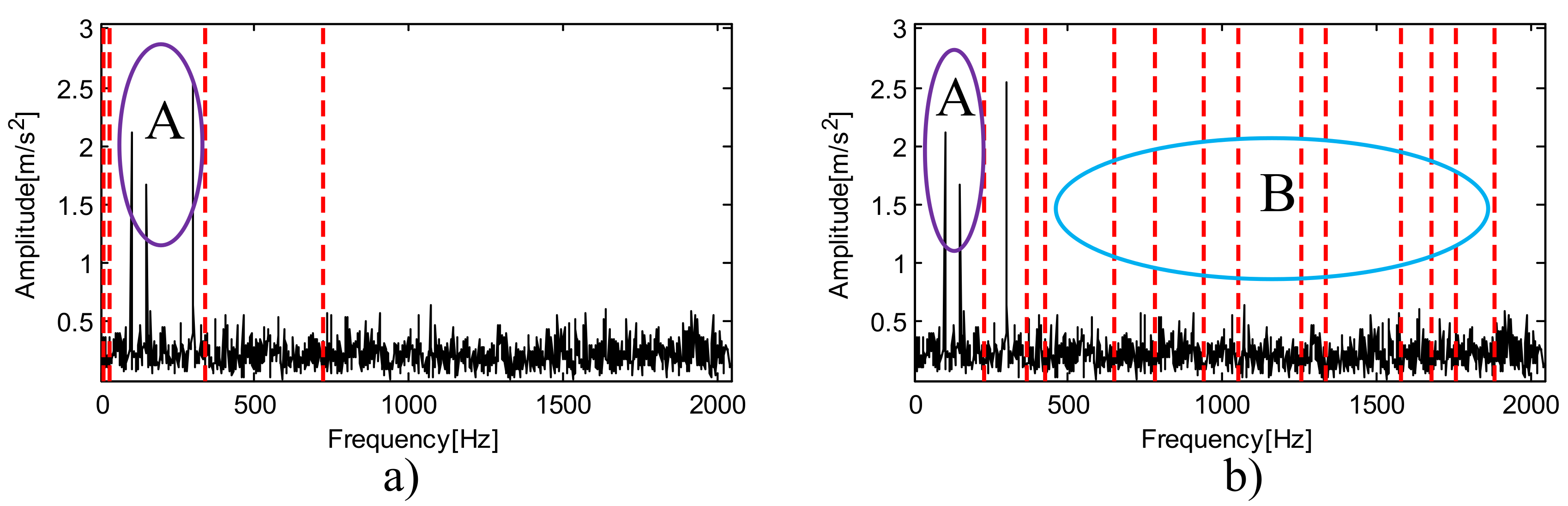
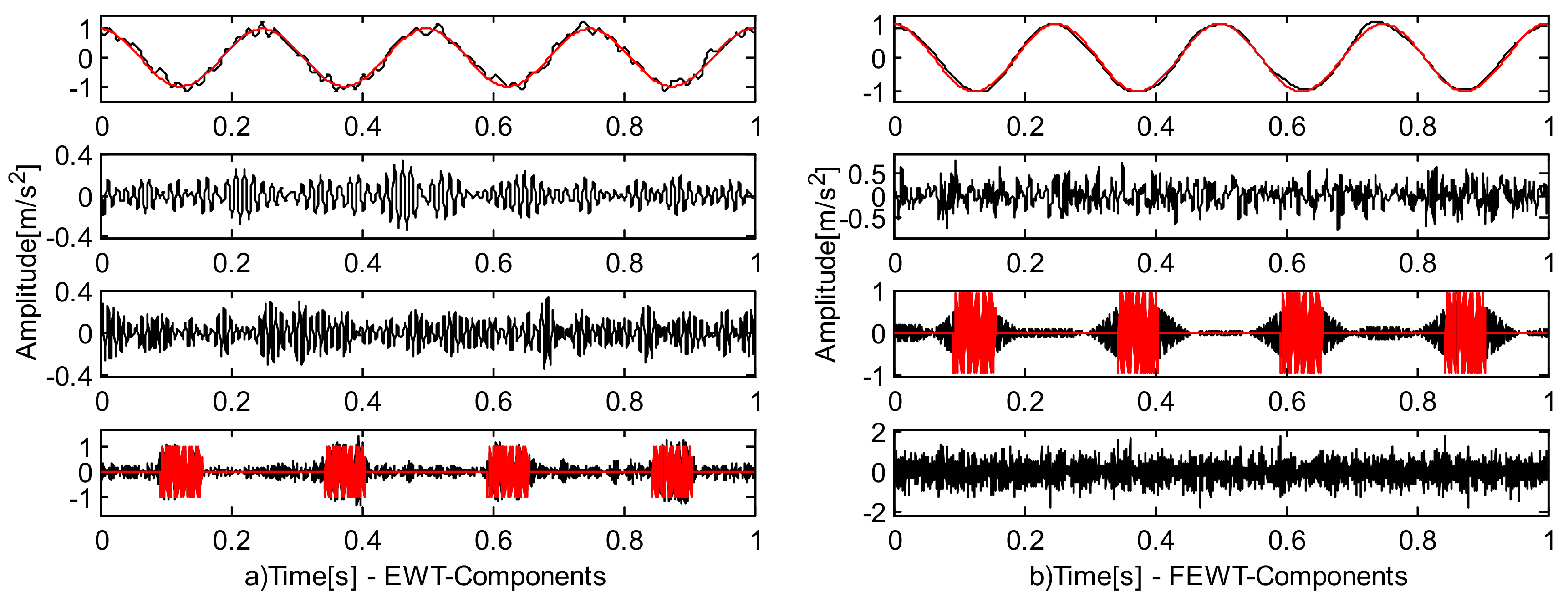
4.1. Case Study 1
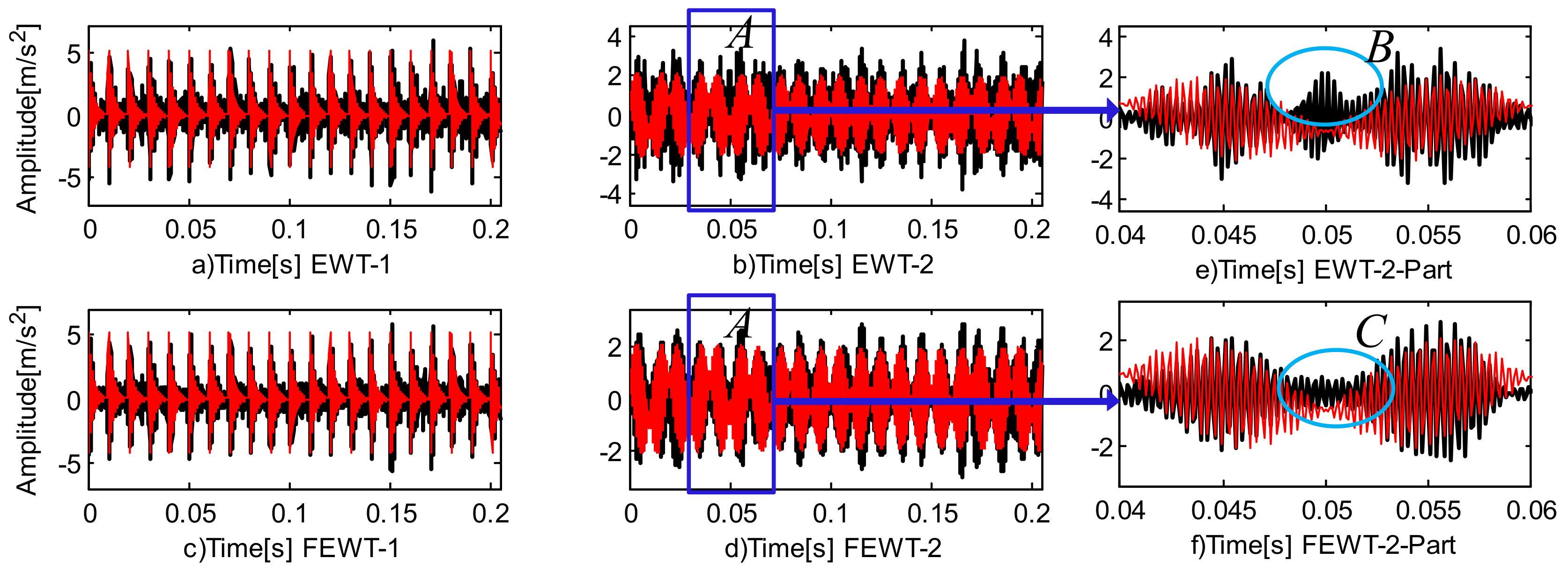
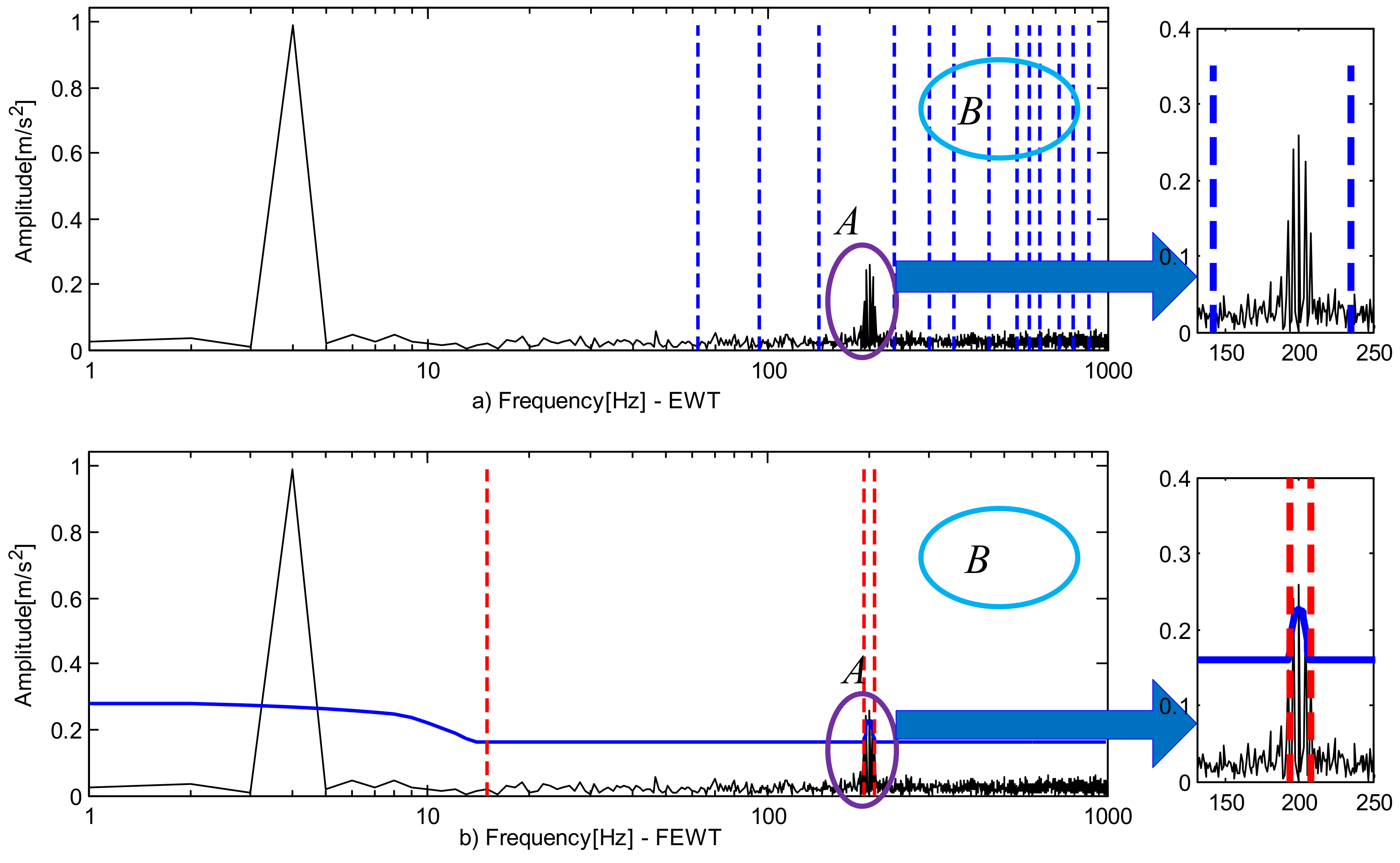
4.2. Case Study 2
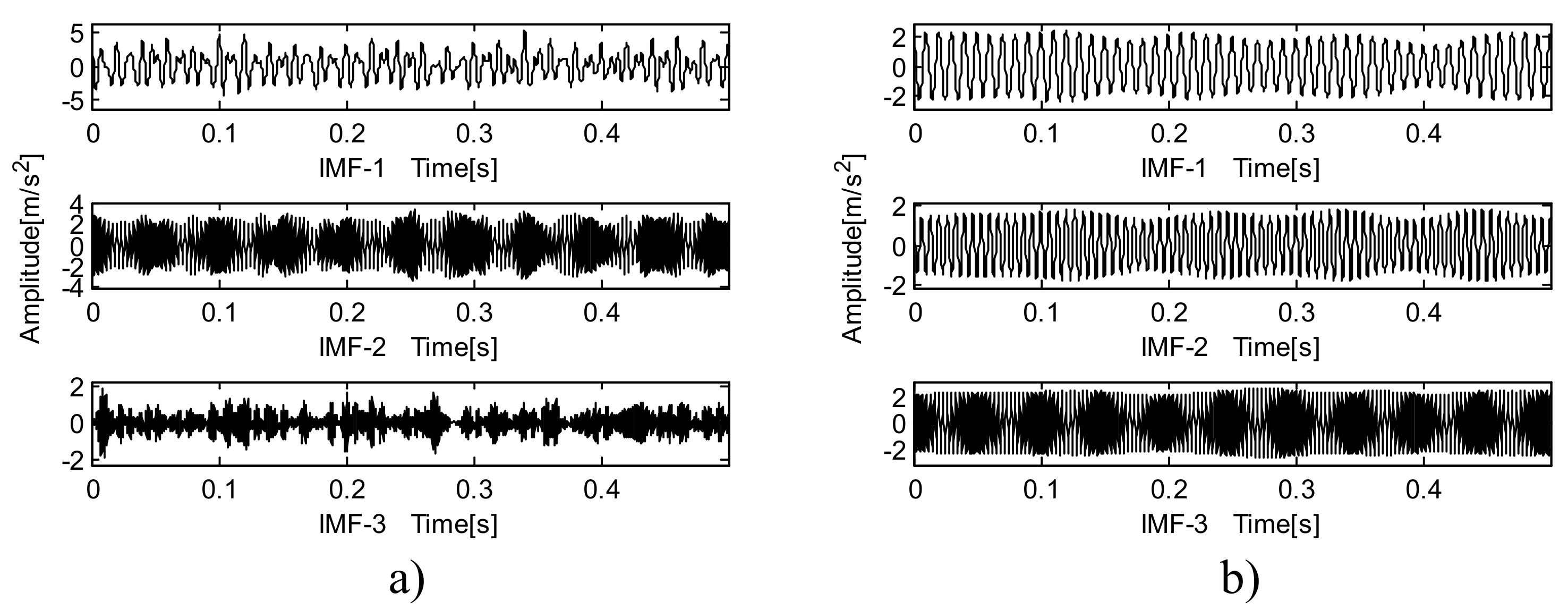
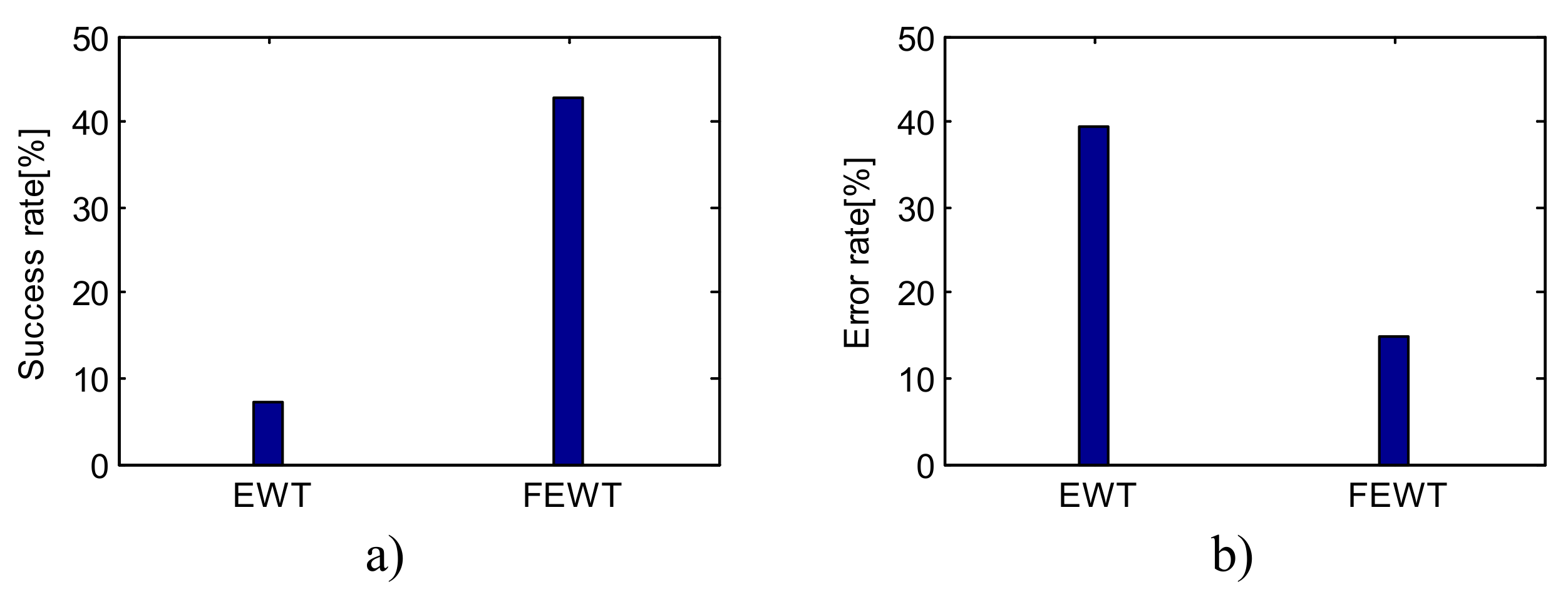
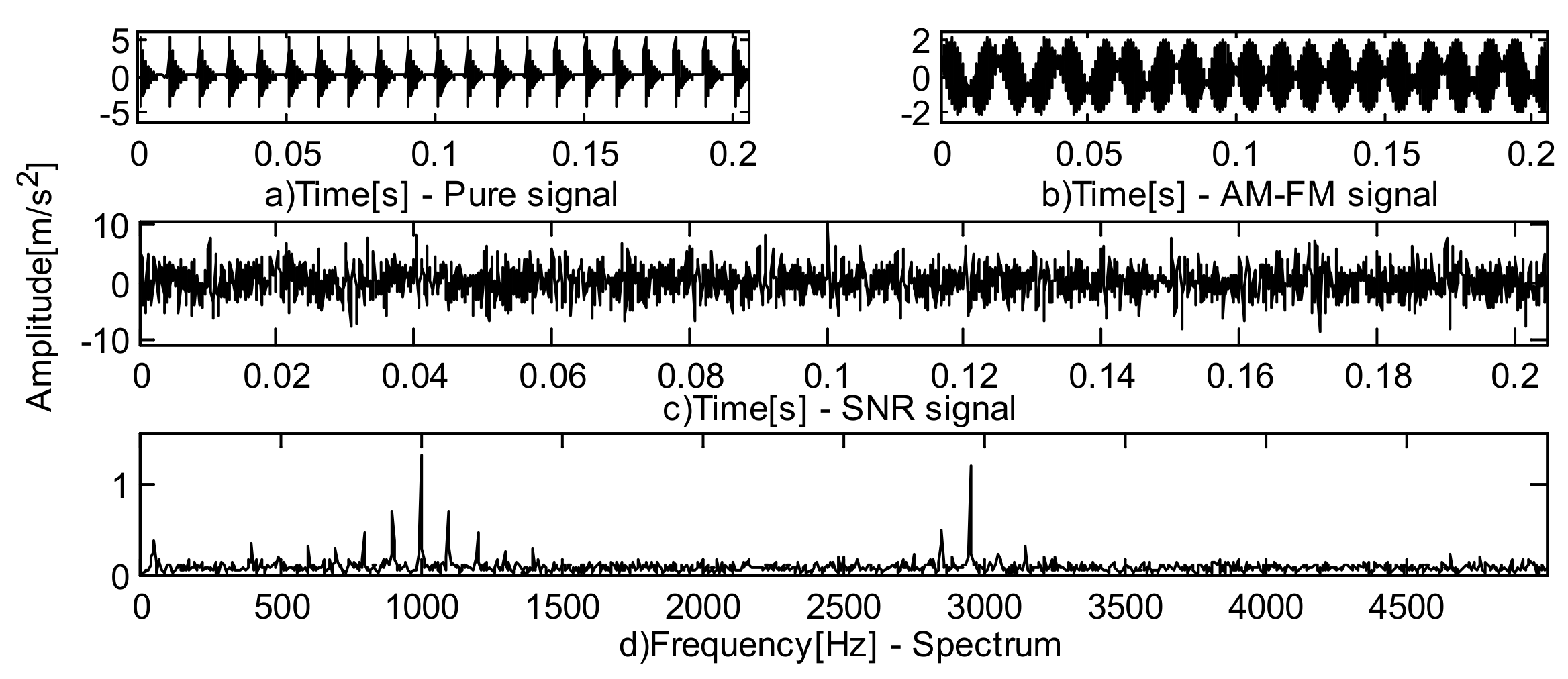
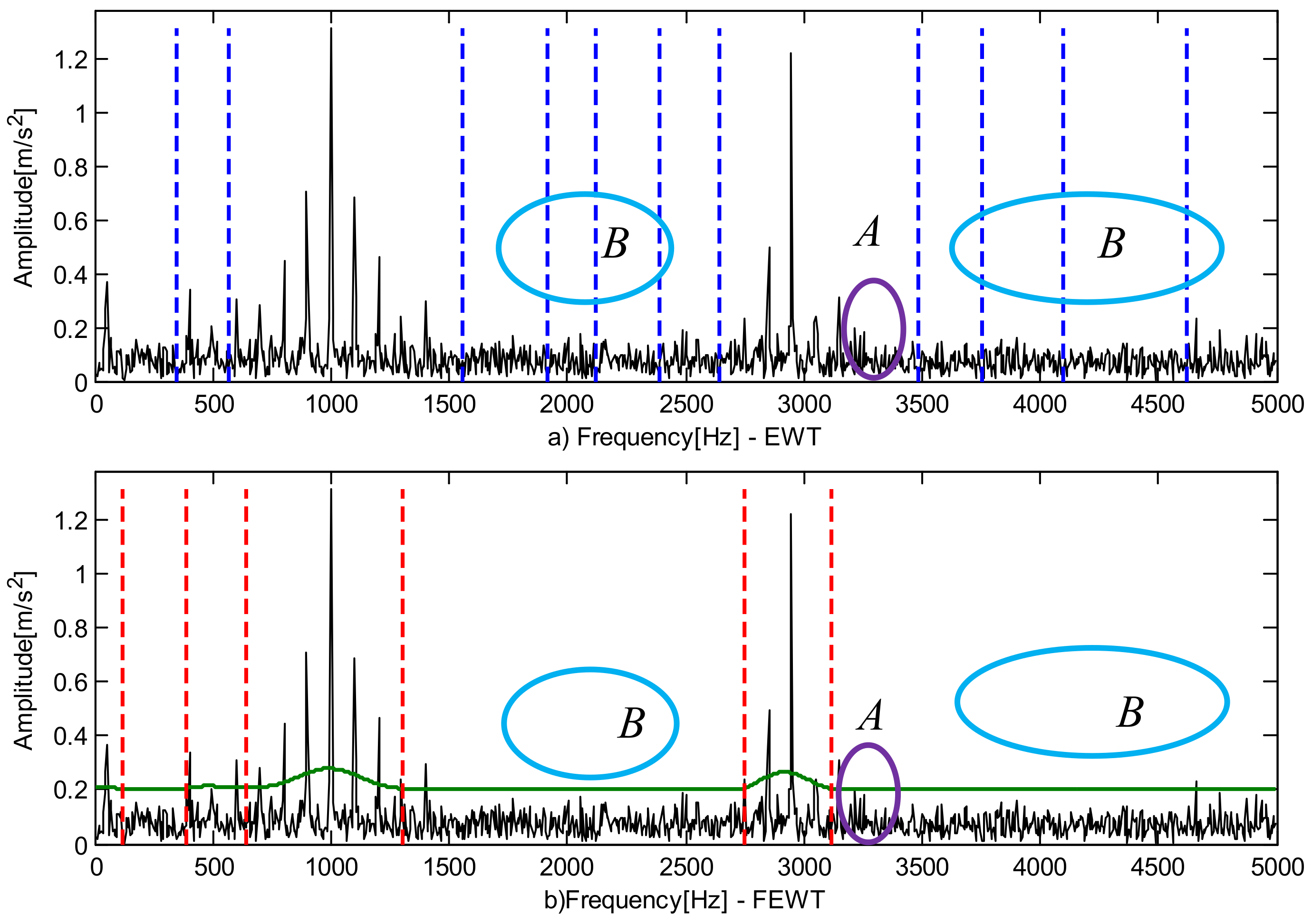
4.3. Case Study 3
5. Applications
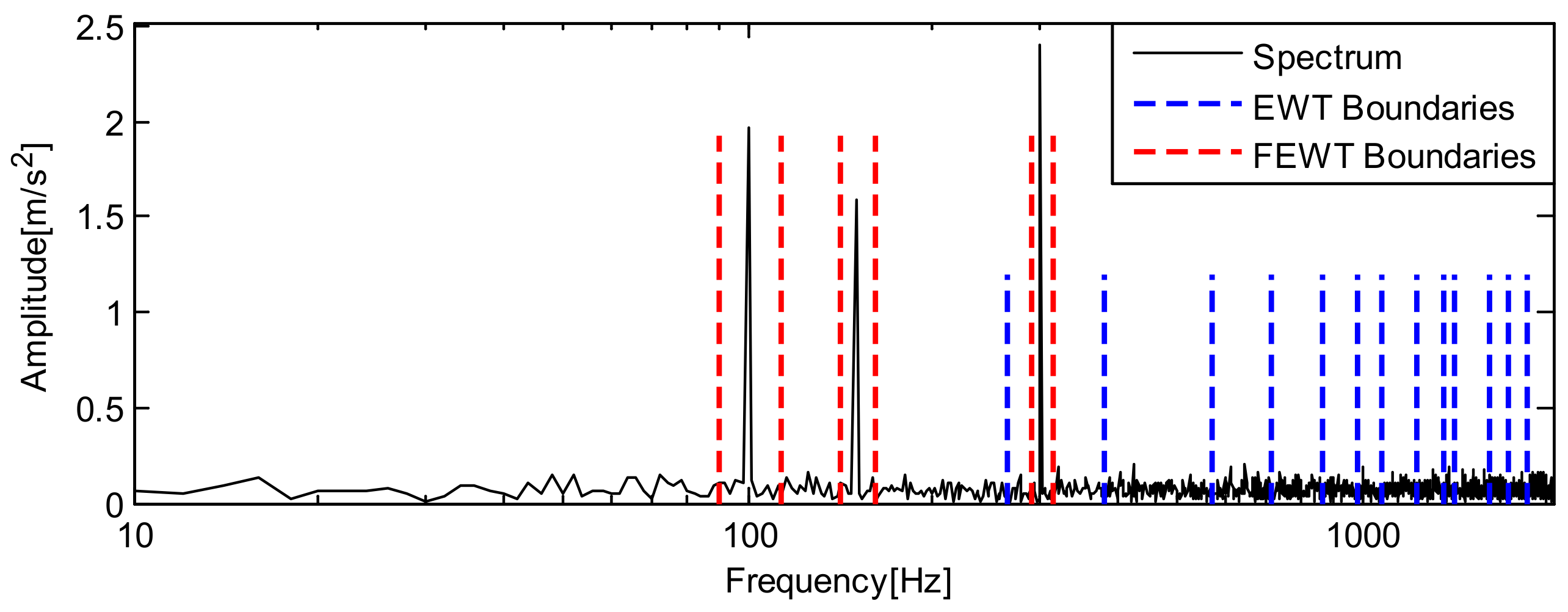
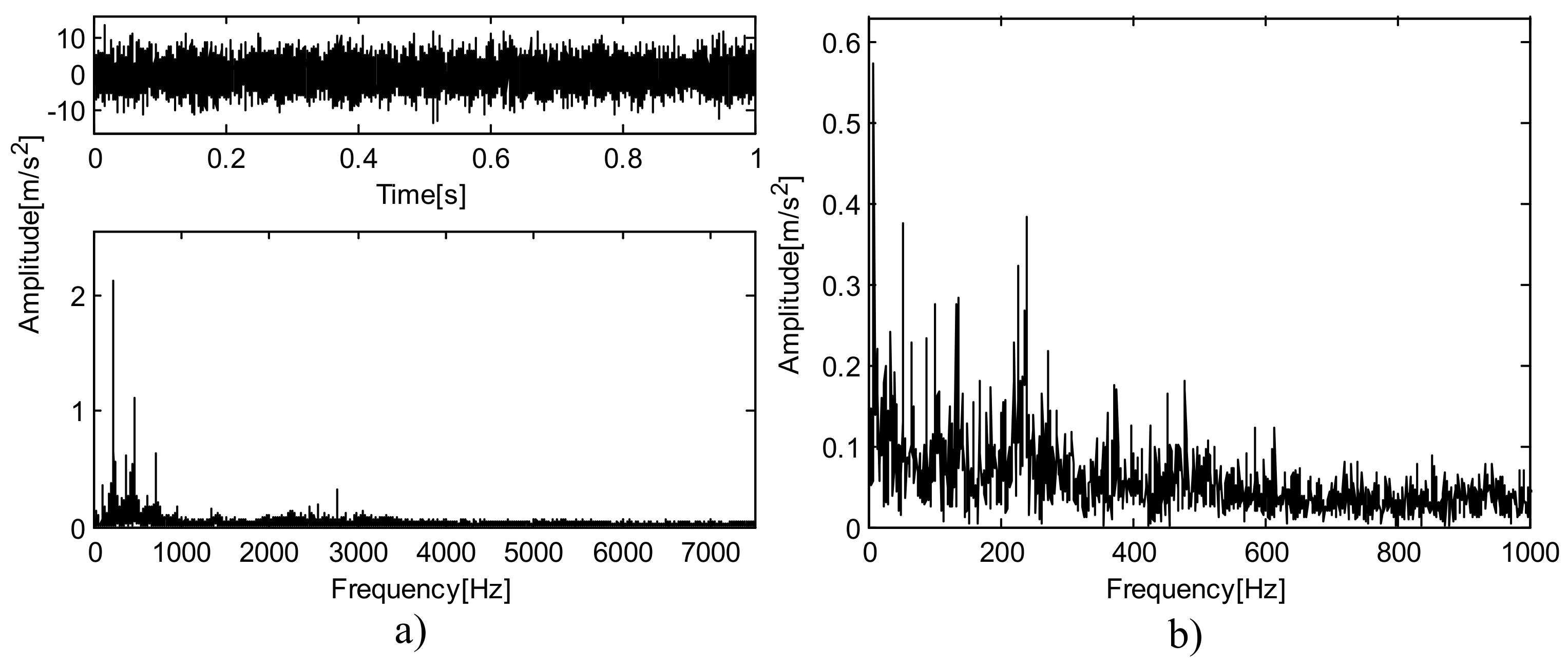
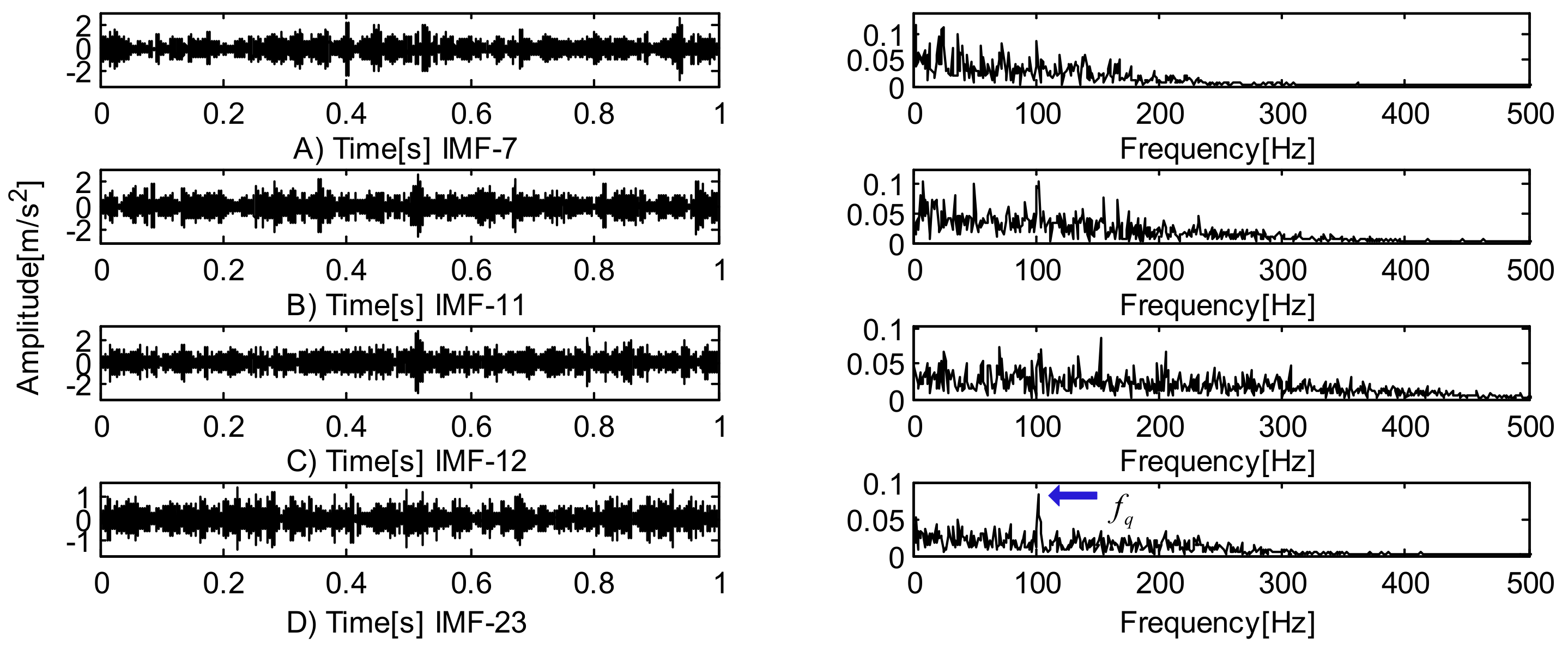
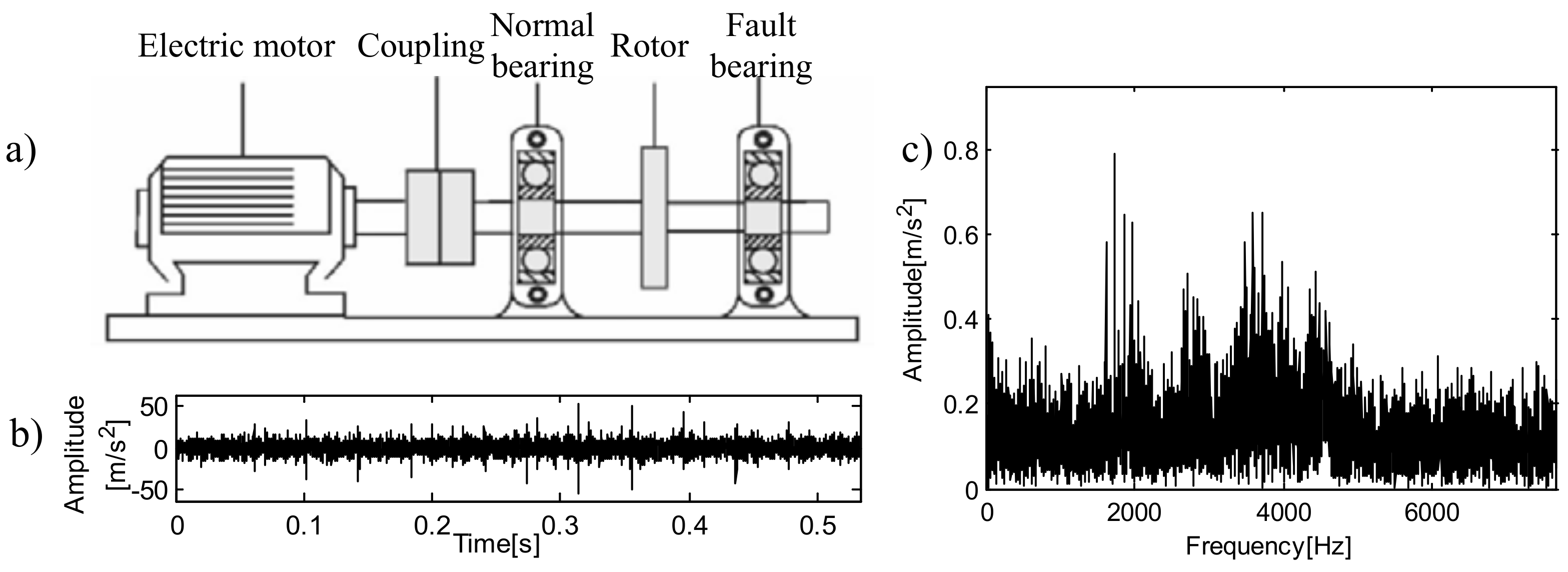
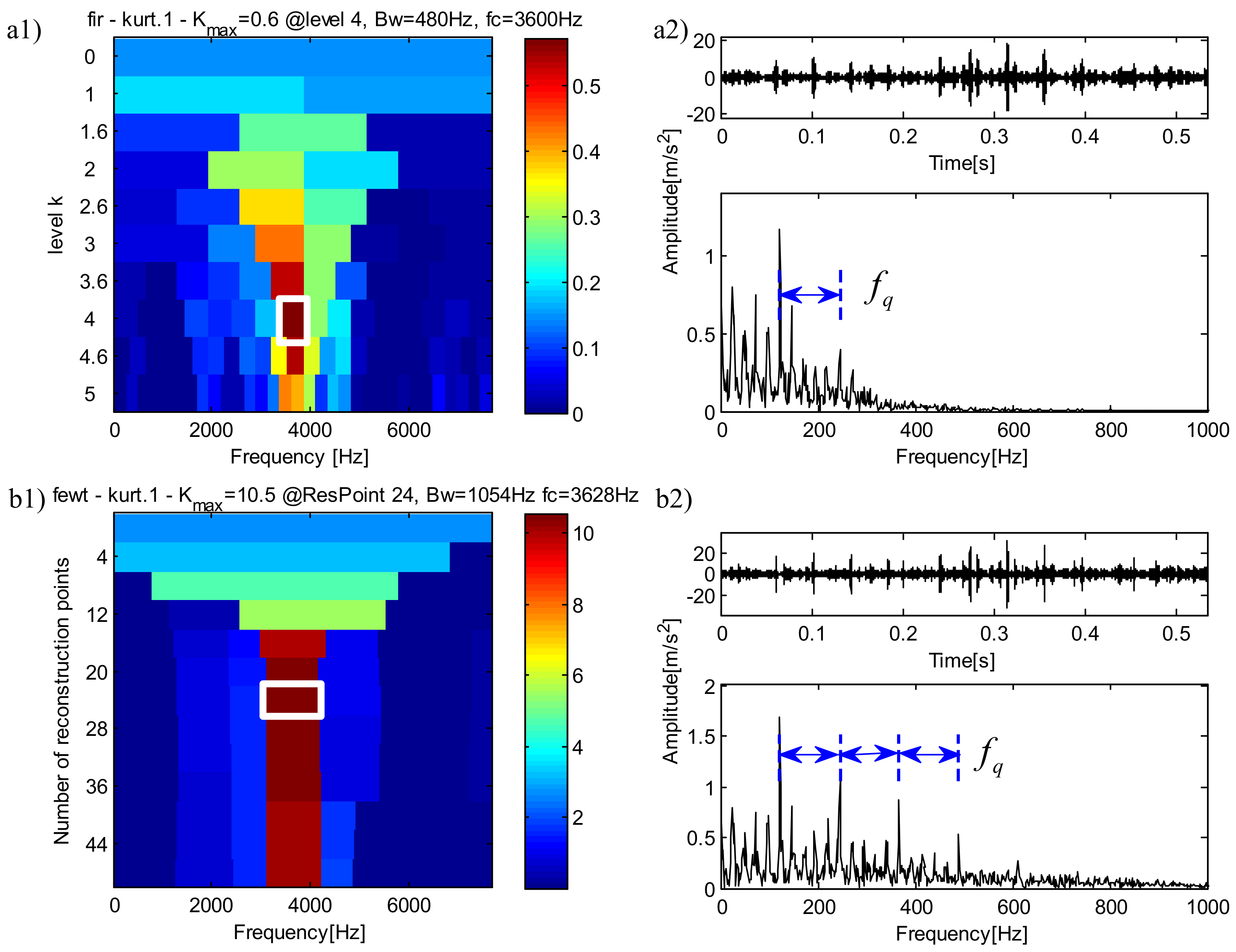
5.1. Analysis of Bearing Outer Ring Fault Data
5.2. Analysis of Bearing Inner Ring Fault Data
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cui, L.L.; Li, B.B.; Ma, J.F.; Jin, Z. Quantitative trend fault diagnosis of a rolling bearing based on Sparsogram and Lempel-Ziv. Measurement 2018, 128, 410–418. [Google Scholar] [CrossRef]
- Song, L.Y.; Wang, H.Q.; Chen, P. Step-by-step Fuzzy Diagnosis Method for Equipment Based on Symptom Extraction and Trivalent Logic Fuzzy Diagnosis Theory. IEEE Trans. Fuzzy Syst. 2018, 26, 3467–3478. [Google Scholar] [CrossRef]
- Cui, L.L.; Huang, J.F. Quantitative and localization diagnosis of a defective ball bearing based on vertical-horizontal synchronization signal analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8705. [Google Scholar] [CrossRef]
- Chen, J.L.; Li, Z.P.; Pan, J. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70, 1–35. [Google Scholar] [CrossRef]
- Song, L.Y.; Wang, H.Q.; Chen, P. Vibration-Based Intelligent Fault Diagnosis for Roller Bearings in Low-Speed Rotating Machinery. IEEE Trans. Instrum. Meas. 2018, 67, 1887–1899. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math Phys. Eng. Sci. 1998, 454, 903–9955. [Google Scholar] [CrossRef]
- Li, H.G.; Hu, Y.; Li, F.C. Succinct and fast empirical mode decomposition. Mech. Syst. Signal Process. 2017, 85, 879–895. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, J.; Chen, J. Fast Empirical Mode Decomposition Based on Gaussian Noises. In Proceedings of the Third International Conference on Mathematics and Computers in Sciences and in Industry, IEEE, Chania, Greece, 27–29 August 2016; pp. 282–288. [Google Scholar]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Cao, H.R.; Fan, F.; Zhou, K. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, H.; Li, Z. A new compound faults detection method for rolling bearings based on empirical wavelet transform and chaotic oscillator. Chaos Solitons Fractals 2016, 89, 8–19. [Google Scholar] [CrossRef]
- Chen, J.L.; Pan, J.; Li, Z.P. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Thirumala, K.; Umarikar, A.C.; Jain, T. Estimation of Single-Phase and Three-Phase Power-Quality Indices Using Empirical Wavelet Transform. IEEE Trans. Power Deliv. 2015, 30, 445–454. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A comparative study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to bearing defect diagnosis. Mech. Syst. Signal Process. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Zheng, J.D.; Pan, H.Y.; Yang, S.B. Adaptive parameterless empirical wavelet transform based time-frequency analysis method and its application to rotor rubbing fault diagnosis. Signal Process. 2017, 130, 305–314. [Google Scholar] [CrossRef]
- Jiang, X.M.; Wu, L.; Ge, M.T. A Novel Faults Diagnosis Method for Rolling Element Bearings Based on EWT and Ambiguity Correlation Classifiers. Entropy 2017, 19, 231. [Google Scholar] [CrossRef]
- Hu, Y.; Li, F.C.; Li, H.G. An enhanced empirical wavelet transform for noisy and non-stationary signal processing. Digit. Signal Process. 2017, 60, 220–229. [Google Scholar] [CrossRef]
- Pan, J.; Chen, J.L.; Zi, Y.Y. Mono-component feature extraction for mechanical fault diagnosis using modified empirical wavelet transform via data-driven adaptive Fourier spectrum segment. Mech. Syst. Signal Process. 2016, 72, 160–183. [Google Scholar] [CrossRef]
- Song, Y.H.; Zeng, S.K.; Ma, J.M. A fault diagnosis method for roller bearing based on empirical wavelet transform decomposition with adaptive empirical mode segmentation. Measurement 2018, 117, 266–276. [Google Scholar] [CrossRef]
- Ge, M.T.; Wang, J.; Zhang, F.F.; Bai, K. A Novel Fault Diagnosis Method of Rolling Bearings Based on AFEWT-KDEMI. Entropy 2018, 20, 455. [Google Scholar] [CrossRef]
- Ge, M.T.; Wang, J.; Ren, X.Y. Fault Diagnosis of Rolling Bearings Based on EWT and KDEC. Entropy 2017, 19, 633. [Google Scholar] [CrossRef]
- Liu, T.; Li, J.; Cai, X.F. A time-frequency analysis algorithm for ultrasonic waves generating from a debonding defect by using empirical wavelet transform. Appl. Acoust. 2018, 131, 16–27. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Singh, L. Automatic detection of a wheelset bearing fault using a multi-level empirical wavelet transform. Digit. Signal Process. 2018, 78, 185–192. [Google Scholar] [CrossRef]
- Luo, Z.J.; Liu, T.; Yan, S.Z. Revised empirical wavelet transform based on auto-regressive power spectrum and its application to the mode decomposition of deployable structure. J. Sound Vib. 2018, 431, 70–87. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, Y.; Yi, C. Sparsity guided empirical wavelet transform for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2018, 101, 292–308. [Google Scholar] [CrossRef]
- Hu, Y.; Tu, X.T.; Li, F.C. An adaptive and tacholess order analysis method based on enhanced empirical wavelet transform for fault detection of bearings with varying speeds. J. Sound Vib. 2017, 409, 241–255. [Google Scholar] [CrossRef]
- Juan, P.A.; Adeli, H. A new music-empirical wavelet transform methodology for time–frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Process. 2015, 45, 55–68. [Google Scholar]
- Kedadouche, M.; Liu, Z.H.; Vu, V.H. A new approach based on OMA-empirical wavelet transforms for bearing fault diagnosis. Measurement 2016, 90, 292–308. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, T.Y.; Chu, F.L. Meshing frequency modulation assisted empirical wavelet transform for fault diagnosis of wind turbine planetary ring gear. Renew. Energy 2018, 132, 1373–1388. [Google Scholar] [CrossRef]
- Ding, J.M.; Ding, C.C. Automatic detection of a wheelset bearing fault using a multi-level empirical wavelet transform. Measurement 2018, 134, 179–192. [Google Scholar] [CrossRef]
- Cui, L.L.; Yao, T.C.; Zhang, Y.; Gong, X.; Kang, C. Application of pattern recognition in gear faults based on the matching pursuit of a characteristic waveform. Measurement 2017, 104, 212–222. [Google Scholar] [CrossRef]
- Cui, L.L.; Huang, J.F.; Zhang, F.B.; Chu, F.L. HVSRMS localization formula and localization law: Localization diagnosis of a ball bearing outer ring fault. Mech. Syst. Signal Process 2019, 120, 608–629. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]









© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhang, K.; Ma, C.; Li, X.; Zhang, J. An Improved Empirical Wavelet Transform and Its Applications in Rolling Bearing Fault Diagnosis. Appl. Sci. 2018, 8, 2352. https://doi.org/10.3390/app8122352
Xu Y, Zhang K, Ma C, Li X, Zhang J. An Improved Empirical Wavelet Transform and Its Applications in Rolling Bearing Fault Diagnosis. Applied Sciences. 2018; 8(12):2352. https://doi.org/10.3390/app8122352
Chicago/Turabian StyleXu, Yonggang, Kun Zhang, Chaoyong Ma, Xiaoqing Li, and Jianyu Zhang. 2018. "An Improved Empirical Wavelet Transform and Its Applications in Rolling Bearing Fault Diagnosis" Applied Sciences 8, no. 12: 2352. https://doi.org/10.3390/app8122352
APA StyleXu, Y., Zhang, K., Ma, C., Li, X., & Zhang, J. (2018). An Improved Empirical Wavelet Transform and Its Applications in Rolling Bearing Fault Diagnosis. Applied Sciences, 8(12), 2352. https://doi.org/10.3390/app8122352







