Effective Prediction of Bearing Fault Degradation under Different Crack Sizes Using a Deep Neural Network
Abstract
:1. Introduction
2. Fault Data Acquisition System
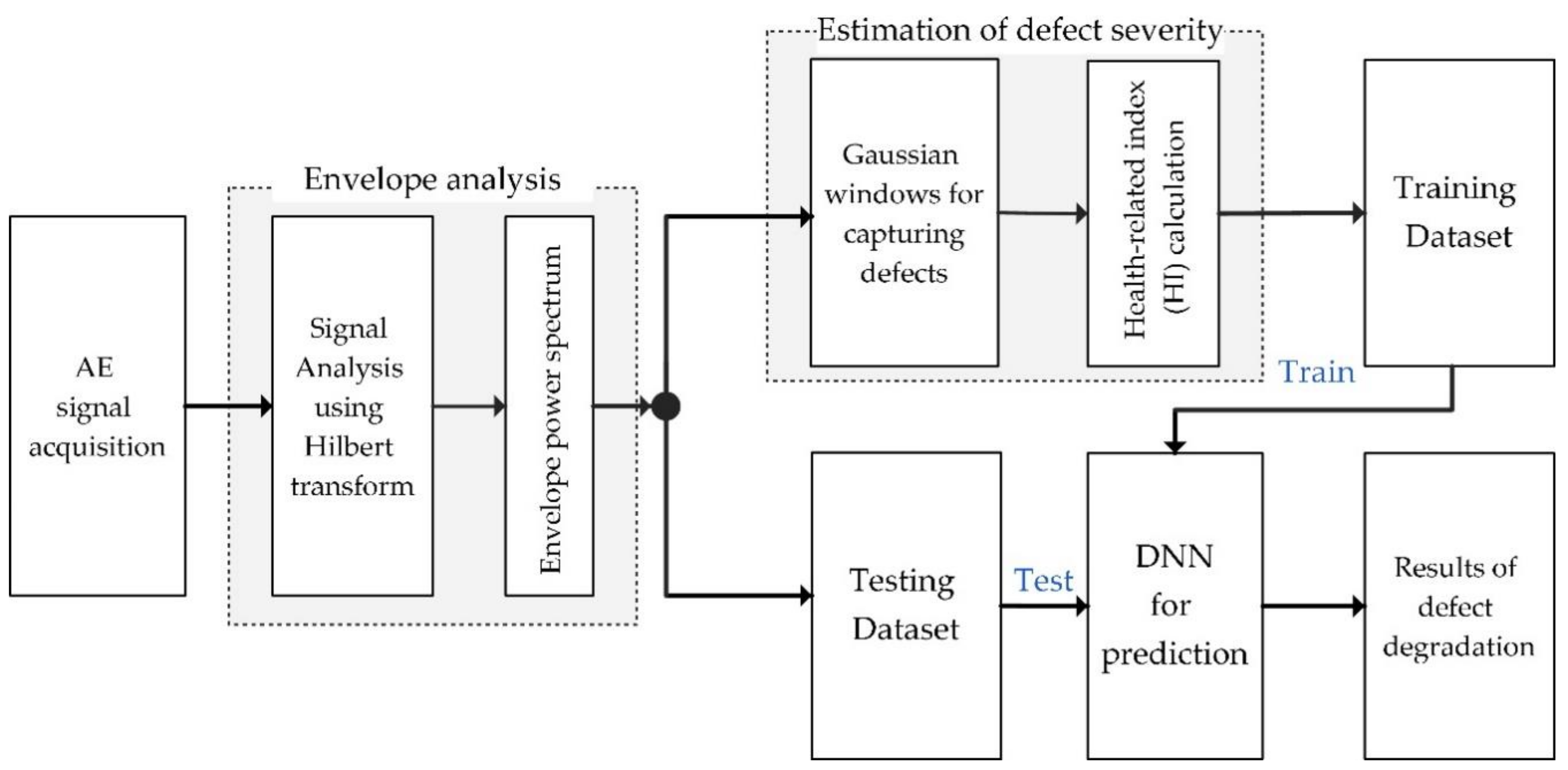
3. The Proposed Methodology for Prediction of Bearing Defect Degradation Using Deep Neural Network
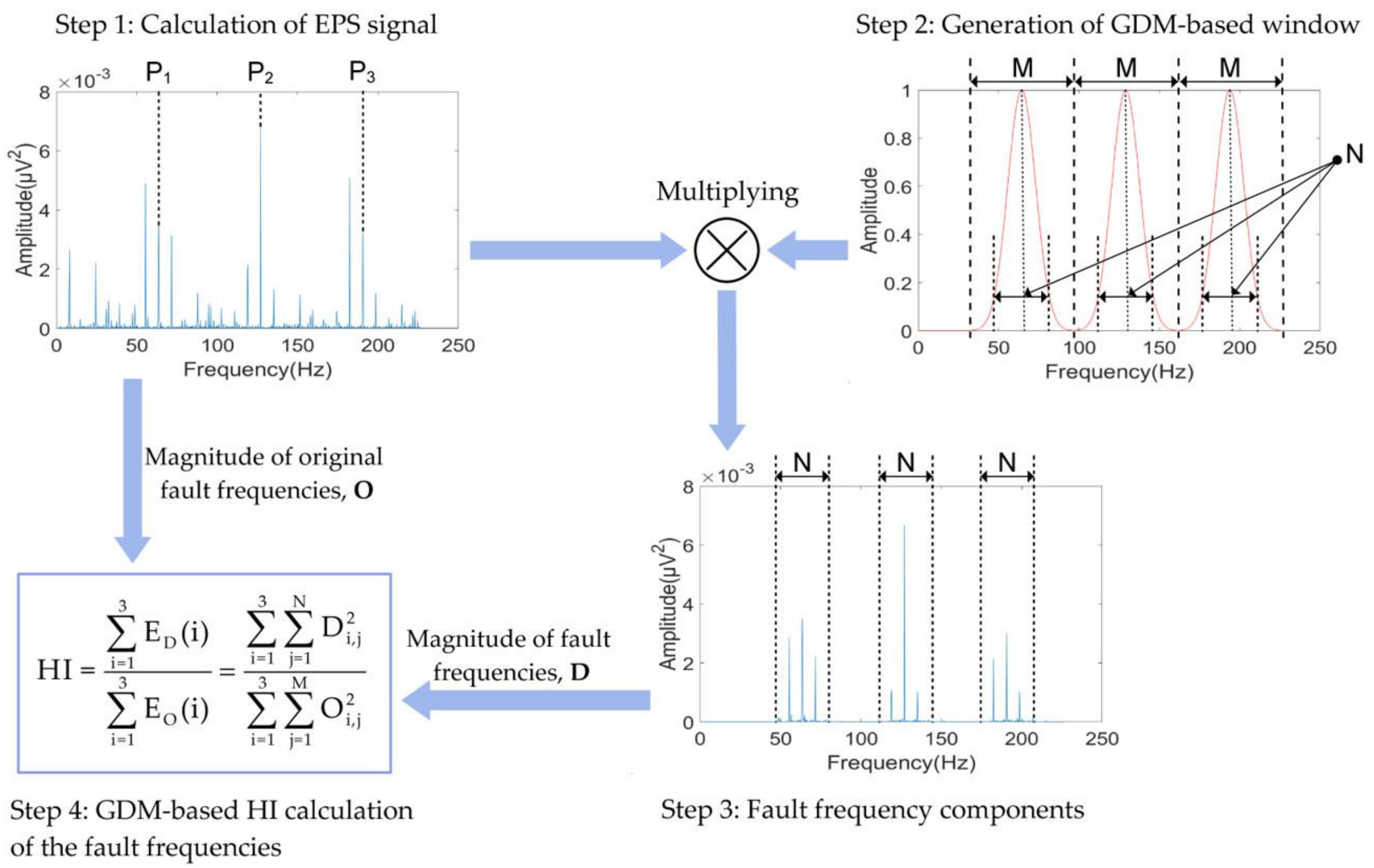
3.1. Estimation of Bearing Defect Severity Using the Gaussian Window Method
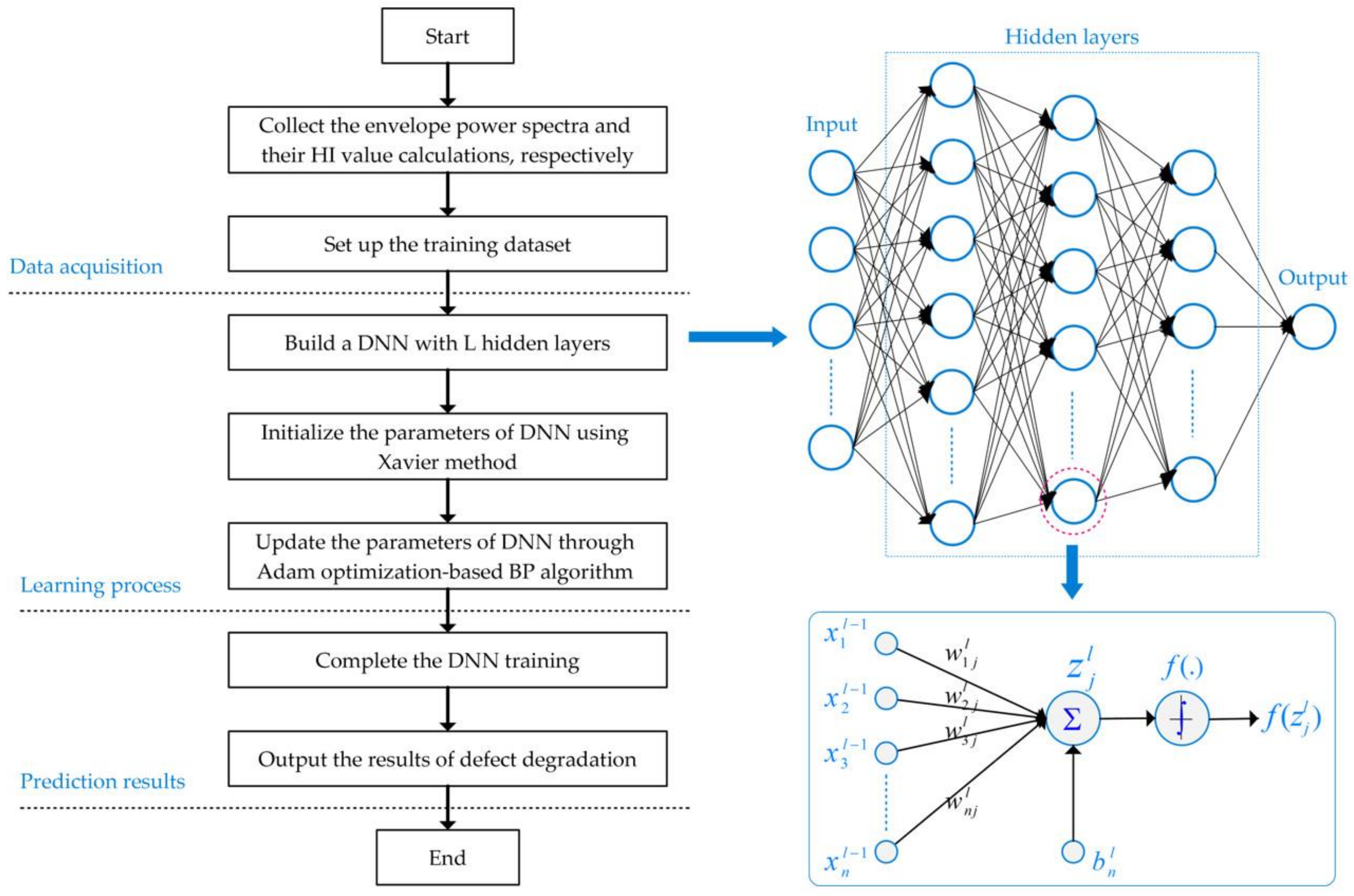
3.2. DNN for Defect Degradation Prediction
3.3. Adam Optimization-Based Backpropagation Algorithm and Xavier Weight Initialization
- ▪
- Set the learning rate: exponential decay rates for the moment: the loss function with the model’s parameters .
- ▪
- Start at time step : initialization of , 1st moment , and 2nd moment .While do not converge, do: calculating gradient of the loss function at: updating the first moment estimation: updating the second moment estimation: calculating the bias-corrected first moment: calculating the bias-corrected second moment.Update the parameters:end while, return .
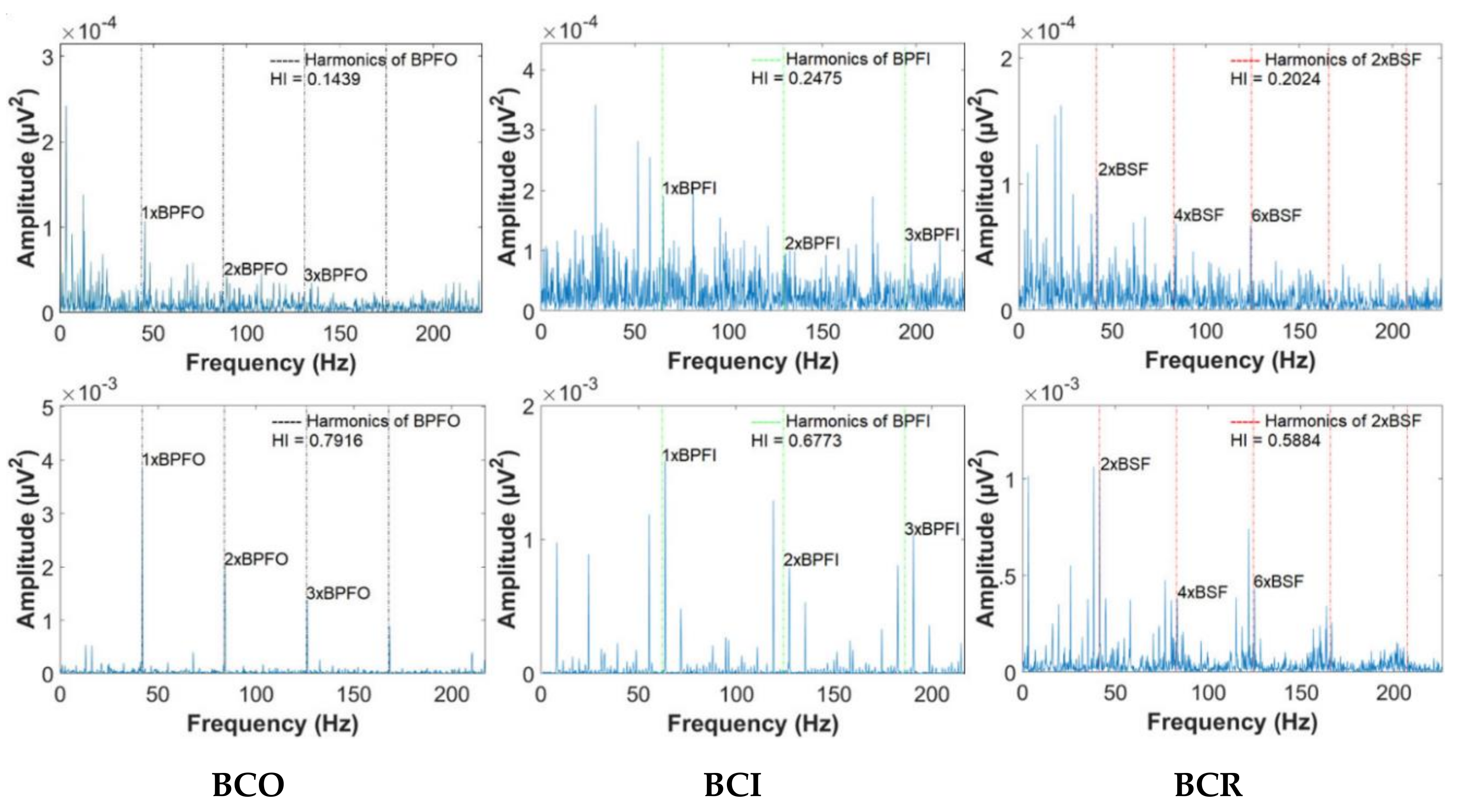
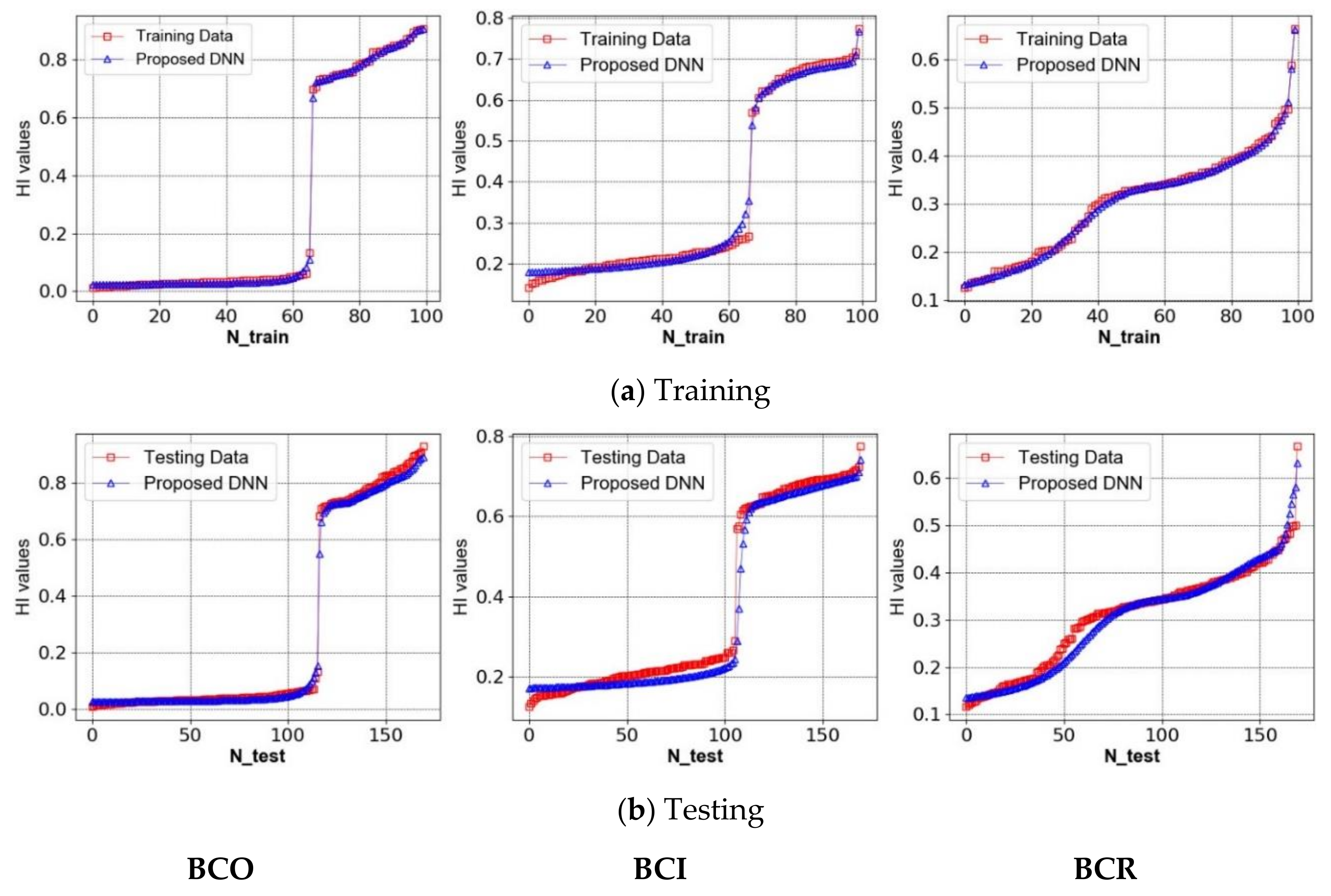
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Nguyen, P.; Kang, M.; Kim, J.-M.; Ahn, B.-H.; Ha, J.-M.; Choi, B.-K. Robust condition monitoring of rolling element bearings using de-noising and envelope analysis with signal decomposition techniques. Expert Syst. Appl. 2015, 42, 9024–9032. [Google Scholar] [CrossRef]
- Climente-Alarcon, V.; Antonino-Daviu, J.A.; Riera-Guasp, M.; Vlcek, M. Induction Motor Diagnosis by Advanced Notch FIR Filters and the Wigner-Ville Distribution. IEEE Trans. Ind. Electron. 2014, 61, 4217–4227. [Google Scholar] [CrossRef]
- Leite, V.C.M.N.; Silva, J.G.B.D.; Torres, G.L.; Veloso, G.F.C.; Silva, L.E.B.D.; Bonaldi, E.L.; Oliveira, L.E.d.L.D. Bearing Fault Detection in Induction Machine Using Squared Envelope Analysis of Stator Current. In Bearing Technology; Darji, P.H., Ed.; InTech: Rijeka, Croatia, 2017; 67145p. [Google Scholar] [Green Version]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; Wills, L.M.; Kim, J.M. Time-Varying and Multiresolution Envelope Analysis and Discriminative Feature Analysis for Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 7749–7761. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Y.; Meng, G.; Ding, J.; Xiao, Y. Fault Severity Monitoring of Rolling Bearings Based on Texture Feature Extraction of Sparse Time–Frequency Images. Appl. Sci. 2018, 8, 1538. [Google Scholar] [CrossRef]
- Nguyen, H.; Kim, J.; Kim, J.-M. Optimal Sub-Band Analysis Based on the Envelope Power Spectrum for Effective Fault Detection in Bearing under Variable, Low Speeds. Sensors 2018, 18, 1389. [Google Scholar] [CrossRef] [PubMed]
- Zorzi, M. A New Family of High-Resolution Multivariate Spectral Estimators. IEEE Trans. Autom. Control 2014, 59, 892–904. [Google Scholar] [CrossRef]
- Zorzi, M. An interpretation of the dual problem of the THREE-like approaches. Automatica 2015, 62, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Wang, D.; Kong, F.; Tse, P.W. Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier. Measurement 2013, 46, 1551–1564. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; Kim, J.; Tan, A.C.C.; Kim, E.Y.; Choi, B. Reliable Fault Diagnosis for Low-Speed Bearings Using Individually Trained Support Vector Machines with Kernel Discriminative Feature Analysis. IEEE Trans. Power Electron. 2015, 30, 2786–2797. [Google Scholar] [CrossRef]
- Li, K.; Su, L.; Wu, J.; Wang, H.; Chen, P. A Rolling Bearing Fault Diagnosis Method Based on Variational Mode Decomposition and an Improved Kernel Extreme Learning Machine. Appl. Sci. 2017, 7, 1004. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, S.; Chen, X.; Li, C.; Sanchez, R.-V.; Qin, H. Deep neural networks-based rolling bearing fault diagnosis. Microelectron. Reliab. 2017, 75, 327–333. [Google Scholar] [CrossRef]
- Zhang, R.; Peng, Z.; Wu, L.; Yao, B.; Guan, Y. Fault Diagnosis from Raw Sensor Data Using Deep Neural Networks Considering Temporal Coherence. Sensors 2017, 17, 549. [Google Scholar] [CrossRef] [PubMed]
- L’Heureux, A.; Grolinger, K.; Elyamany, H.F.; Capretz, M.A.M. Machine Learning with Big Data: Challenges and Approaches. IEEE Access 2017, 5, 7776–7797. [Google Scholar] [CrossRef]
- Chi, M.; Plaza, A.; Benediktsson, J.A.; Sun, Z.; Shen, J.; Zhu, Y. Big Data for Remote Sensing: Challenges and Opportunities. Proc. IEEE 2016, 104, 2207–2219. [Google Scholar] [CrossRef]
- Yin, J.; Chen, B.; Lai, K.R.; Li, Y. Automatic Dangerous Driving Intensity Analysis for Advanced Driver Assistance Systems From Multimodal Driving Signals. IEEE Sens. J. 2018, 18, 4785–4794. [Google Scholar] [CrossRef]
- Yin, J.; Chen, B. An Advanced Driver Risk Measurement System for Usage-Based Insurance on Big Driving Data. IEEE Trans. Intell. Veh. 2018. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, Y.; Wan, J.; Liu, X.; Song, Z. Industrial Big Data for Fault Diagnosis: Taxonomy, Review, and Applications. IEEE Access 2017, 5, 17368–17380. [Google Scholar] [CrossRef]
- Bediaga, I.; Mendizabal, X.; Arnaiz, A.; Munoa, J. Ball bearing damage detection using traditional signal processing algorithms. IEEE Instrum. Meas. Mag. 2013, 16, 20–25. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Fan, X.; Huang, H.-Z. Rolling element bearing fault detection using an improved combination of Hilbert and wavelet transforms. J. Mech. Sci. Technol. 2009, 23, 3292–3301. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Gu, S.; Zhang, L. Learning a Deep Single Image Contrast Enhancer from Multi-Exposure Images. IEEE Trans. Image Process. 2018, 27, 2049–2062. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Krishna Kumar, S. On weight Initialization in Deep Neural Networks. arXiv, 2017; arXiv:1704.08863. [Google Scholar]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing Health Monitoring Based on Hilbert-Huang Transform, Support Vector Machine, and Regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]

| Crack sizes | Length (mm) | Width (mm) | Depth (mm) |
| 3 | 0.35 | 0.30 | |
| 6 | 0.49 | 0.50 | |
| 12 | 0.60 | 0.50 | |
| Shaft speed | 500 revolutions per minute (r/min) | ||
| Defect frequencies | BPFO = 43.68 Hz, BPFI = 64.65 Hz, and 2 × BSF = 41.44 Hz | ||
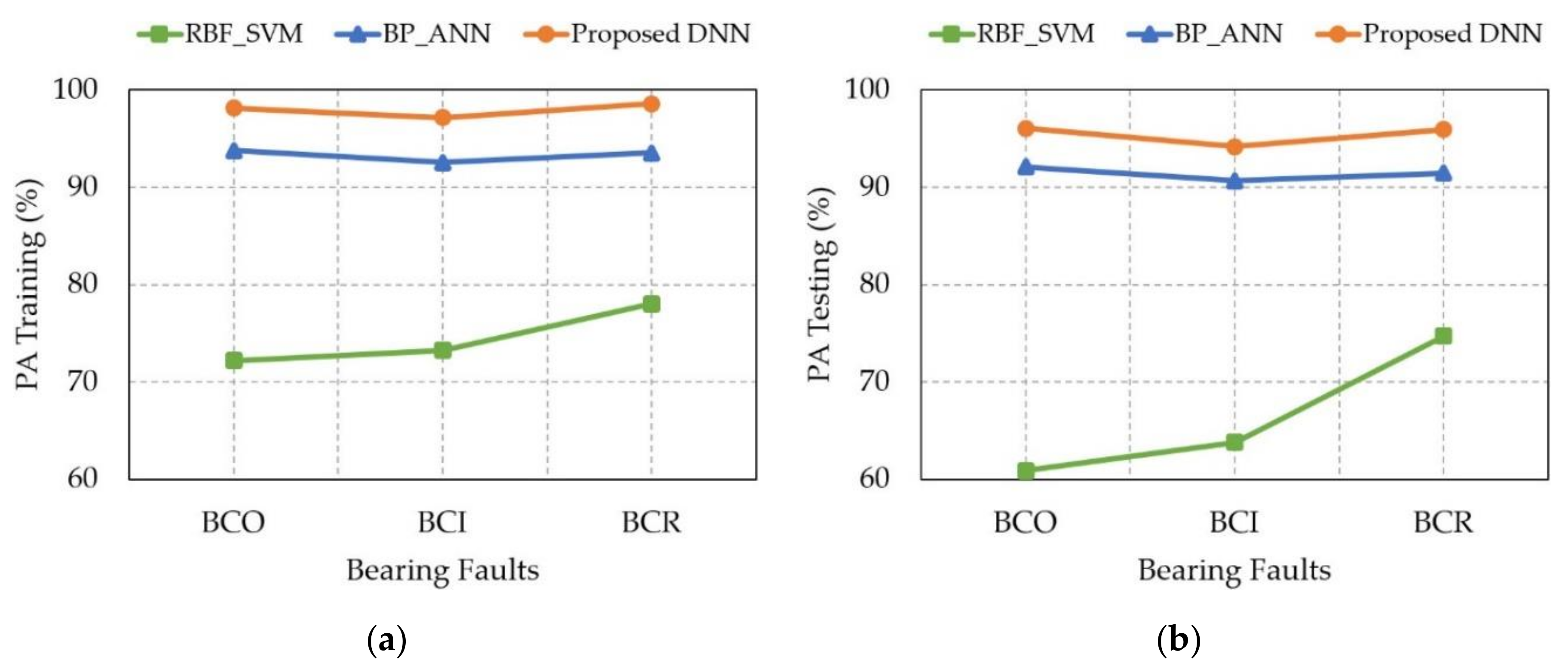
| Methodologies | The Prediction Accuracy (PA) of Bearing Fault Degradation Levels | |||||
|---|---|---|---|---|---|---|
| Training (%) | Testing (%) | |||||
| BCO | BCI | BCR | BCO | BCI | BCR | |
| RBF_SVM [29] | 72.19 | 73.26 | 78.01 | 60.88 | 63.79 | 74.70 |
| BP_ANN [14] | 93.76 | 92.53 | 93.50 | 92.08 | 90.67 | 91.45 |
| Proposed DNN | 98.14 | 97.12 | 98.54 | 96.05 | 94.17 | 95.91 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.N.; Kim, C.-H.; Kim, J.-M. Effective Prediction of Bearing Fault Degradation under Different Crack Sizes Using a Deep Neural Network. Appl. Sci. 2018, 8, 2332. https://doi.org/10.3390/app8112332
Nguyen HN, Kim C-H, Kim J-M. Effective Prediction of Bearing Fault Degradation under Different Crack Sizes Using a Deep Neural Network. Applied Sciences. 2018; 8(11):2332. https://doi.org/10.3390/app8112332
Chicago/Turabian StyleNguyen, Hung Ngoc, Cheol-Hong Kim, and Jong-Myon Kim. 2018. "Effective Prediction of Bearing Fault Degradation under Different Crack Sizes Using a Deep Neural Network" Applied Sciences 8, no. 11: 2332. https://doi.org/10.3390/app8112332
APA StyleNguyen, H. N., Kim, C.-H., & Kim, J.-M. (2018). Effective Prediction of Bearing Fault Degradation under Different Crack Sizes Using a Deep Neural Network. Applied Sciences, 8(11), 2332. https://doi.org/10.3390/app8112332







